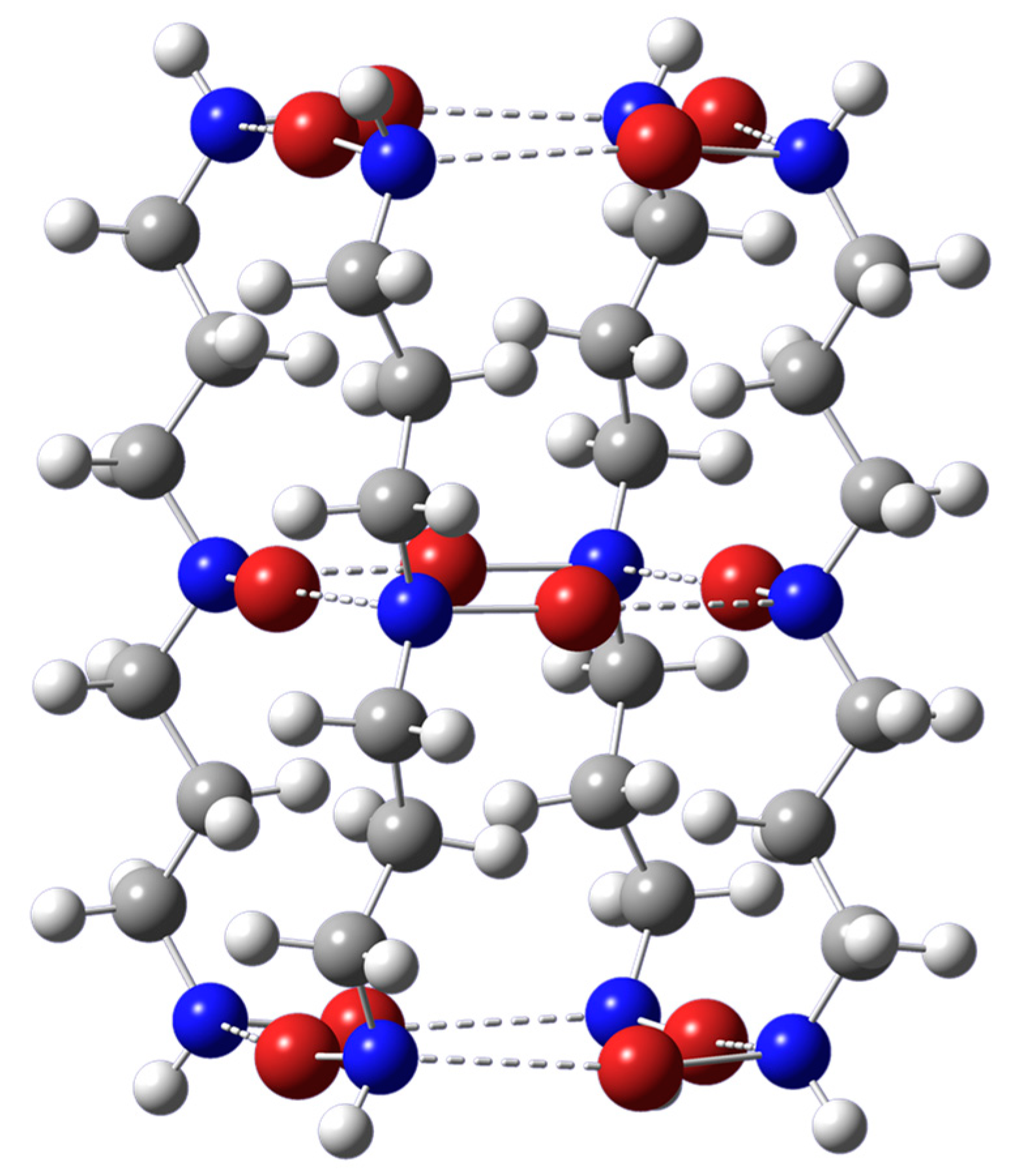
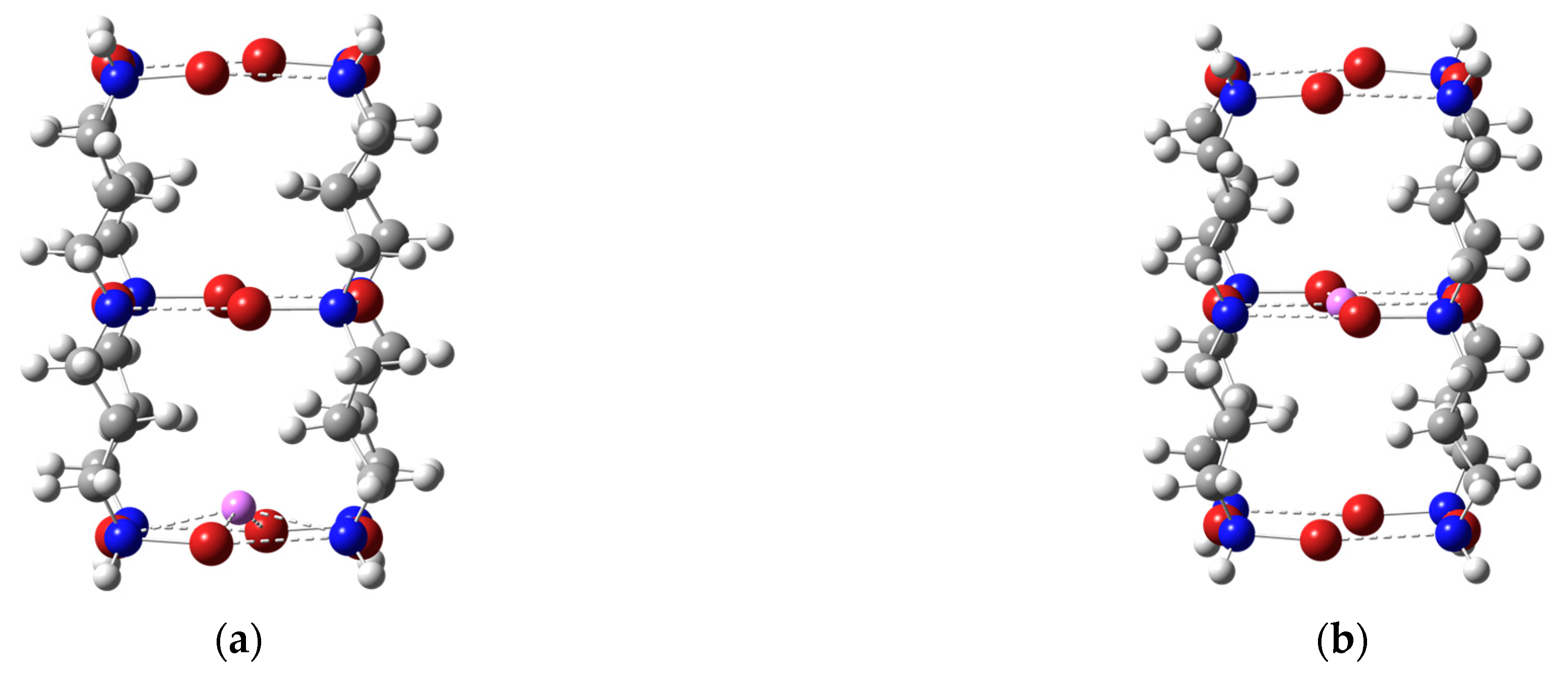Next Article in Journal
Preparation of Environmentally Friendly BiVO4@SiO2 Encapsulated Yellow Pigment with Remarkable Thermal and Chemical Stability
Next Article in Special Issue
Probing the Electronic Structure of Dinuclear Carbon-Rich Complexes Containing an Octa-3,5-diene-1,7-diyndiyl Bridging Ligand
Previous Article in Journal
Paramagnetic Nuclear Magnetic Resonance: The Toolkit
Previous Article in Special Issue
Modulation of Ferrocene–Ferrocene Interactions by Varying Their Reciprocal Positions in L-Dap/Aib Helical Peptides
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 12
Issue 1
10.3390/inorganics12010016
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Model Halogen-Bonded Network as a Potential Tube-like Host for Li+: A DFT Study

by
Rubén D. Parra
†
Department of Chemistry and Biochemistry, DePaul University, Chicago, IL 60614, USA
†
To the memory of Professor Alberto Bolaños, a dear friend and my undergraduate inorganic chemistry thesis advisor.
Inorganics 2024, 12(1), 16; https://doi.org/10.3390/inorganics12010016
Submission received: 4 December 2023 / Revised: 26 December 2023 / Accepted: 28 December 2023 / Published: 30 December 2023
(This article belongs to the Special Issue 10th Anniversary of Inorganics: Organometallic Chemistry)
Browse Figures
Versions Notes

Abstract

:
The formation of a halogen-bonded network using four NHX-(CH2)3-NX-(CH2)3-NHX molecules (X = Cl, Br, or I) is investigated using DFT. The self-assembly of the four basic motifs results in a tube-like structure with C4h symmetry, with one halogen-bonded network located at each end of the structure and one at its center. Each halogen-bonded network has four quasi-planar N-X···N interactions with binding energies that increase with the size of X. The structure is found to bind Li+ at each of the halogen-bonded networks, albeit more strongly at its center. The binding of Li+ is driven by halogen atom lone pairs that produce a rich electron density orthogonal to the halogen bond. The presence and strength of the interactions are further examined using AIM and NBO calculations. Lastly, IRC calculations are performed to examine the transitions between the Li+ complex minima and, thus, the potential for transporting the metal ion from one end of the tube to the other. Based on the tetrameric structure, a model intramolecular structure is built and considered as a potential host for Li+. In this case, the central intermolecular N-X···N network is replaced by an intramolecular Si-C≡C-Si network. Interestingly, both intermolecular and intramolecular structures exhibit similar Li+ binding abilities.

Graphical Abstract

1. Introduction

Halogen-bonding interactions have captivated the attention of many researchers, especially over the last two decades [1,2,3,4,5,6,7,8]. Spanning from fundamental studies to practical applications, publications pertaining to the halogen bond have become ever more familiar in the scientific literature. Fundamental studies, for example, have led researchers to rationalize a halogen bond, D-X…A, as a Lewis acid–base interaction [9,10,11,12,13,14,15,16,17,18,19]. Accordingly, a halogen-bond acceptor, A, acts as a base affording an electron-rich region that attractively interacts with an electron-poor region on the halogen-bond donor, D-X. The electron-rich region in the Lewis base is generally associated with an electron lone pair, although it can also be associated with π electrons like those found in unsaturated compounds or aromatic rings [20,21,22,23]. In turn, the electron-deficient region in the halogen-bond donor is found opposite to the covalent bond between the halogen atom, X, and the atom covalently attached to it in the D-X moiety. Indeed, analysis of the electrostatic potential of D-X reveals the existence of a positive electrostatic potential along the line opposite to the D-X bond. This positive electrostatic potential is known as the sigma hole or σ hole [24,25]. Many computational studies have shown a correlation between the strength of a halogen bond with the size and magnitude of the σ hole, for a given halogen-bond acceptor [26]. In particular, the size and magnitude of the sigma hole increase with the size of the halogen atom, X.
Because of its highly directional and tunable character [26,27,28,29,30,31,32], the halogen bond has found applications in a wide variety of fields including organic synthesis [33,34], catalysis [35,36,37,38], medicinal chemistry [39,40,41,42,43], and supramolecular chemistry [44,45,46,47,48,49,50,51,52,53,54,55]. The sigma hole of the halogen atom in D-X has also found applications in the recognition, binding, and even transport of electron-rich species such as anions and certain metals that effectively act as halogen-bond acceptors [56,57,58,59,60,61,62,63,64,65,66,67,68,69]. In contrast, the ability of the halogen atom, in halogen-bonded systems, for binding cations has been largely overlooked [70,71,72,73,74,75,76]. The binding of a cation may be expected as a Lewis acid–base interaction, wherein the halogen atom participating in a halogen bond concurrently acts as a Lewis base, and the cation acts as a Lewis acid. The Lewis base character of the halogen atom in D-X arises from the halogen atom lone pairs that give rise to an electron-rich region orthogonal to the sigma hole, endowing the halogen atom with an interesting amphoteric Lewis acid–base character [77,78,79,80].
The work presented here contributes to the field of halogen bonds regarding their potential for binding metal cations. Accordingly, this work addresses, in part, the scarcity of studies that examine and capitalize on the dual role of the halogen atom as a Lewis acid for halogen bonding via the sigma hole and as a Lewis base for metal cation binding via the halogen atom lone pairs. Indeed, building on previous work by the author, this paper presents a DFT computational investigation on the ability of a tube-like halogen-bonded network to host a metal ion [75]. The model tubular network is designed with binding sites at both ends of the tube and within the interior of the tube. Consequently, the binding of a metal ion may be conceived to occur first at one end of the tubular network, and then the metal ion can, in principle, jump from the initial binding site to the next binding site in the interior of the tube. The process for moving the metal ion from one binding site to the next in the interior of the tube, until the metal ion reaches the other end of the tube, is examined in terms of geometries, binding energies, and energy barriers. In this study, Li+ is conveniently chosen as a proof of principle or case study given its relatively small size, which makes it suitable for computational studies involving molecular assemblies containing a large number of atoms. The computational results of this work should stimulate others to pursue the intentional design, synthesis, and application of halogen-bonded network systems for metal ion binding, recognition, and transport.

2. Results and Discussion

2.1. Model Halogen-Bonded Networks

Both an intermolecular and an intramolecular halogen-bonded network are considered as potential hosts for binding Li+ via halogen atoms acting as both Lewis acids for halogen bonding and as Lewis bases for metal ion binding. The formation and stability of the tube-like intermolecular halogen-bonded network is first examined using the model system shown in Figure 1. The model system is based on that of a previous study by the author, in which Li+ was complexed by a cyclic bromoamine tetramer, (Br-NH2)4 [75]. Here, however, the simple bromoamine unit is replaced with a longer chain motif containing two terminal HN-X units and a central N-X amine unit, NHX-(CH2)3-NX-(CH2)3-NHX with X = Cl, Br, or I. The tetrameric self-assembly of the longer chain motifs results in a symmetric C4h tube-like structure with three halogen-bonded networks separated by corresponding methylene groups (Figure 1). Each halogen-bonded network consists of four quasi-planar N-X···N halogen-bond interactions. Frequency calculations of the fully optimized geometries confirm their nature as energy minima with no imaginary frequencies.
BSSE-corrected interaction energies, ∆E, upon formation of the halogen-bonded tetrameric structures, are listed in Table 1. The interaction energies are calculated as the difference between the total energy of the tetramer and the sum of the energies of the individual monomers with the same geometry as they have in the optimized tetramer. Dividing the interaction energy by the number of halogen bonds (total of 12) in the tube-like structure yields the corresponding average binding energy, <∆E>. An inspection of Table 1 reveals that the magnitude of the interaction energies for the formation of the tubular networks linearly increases with the size of the halogen atom, Cl < Br < I. In particular, the changes in the average interaction energies reflect the strengthening of the halogen bond from weak (X = Cl) to medium (X = Br) to moderately strong (X = I). It is worth noting that the presence of a relatively large number of N-X···N interactions helps produce a robust tetrameric structure with an energetically favorable self-assembly process.
Important geometrical parameters for the intermolecular halogen bonds in the tube-like tetrameric structure are listed in Table 2. In all cases, the halogen-bond distances, X···N, are smaller than the sum of the van der Waals radii (3.30, 3.40, and 3.53 Å for Cl···N, Br···N, and I···N, respectively) [81]. Likewise, the distances between opposing halogen atoms in either the terminal or central halogen-bonded networks are substantially larger than the sum of the van der Waals radii (3.50, 3.70, and 3.96 Å for Cl···Cl, Br···Br, and I···I, respectively). These X···X distances provide a sense of the cavity size through which a metal ion guest can pass through. The corresponding distances between adjacent halogen atoms, though significantly smaller than the opposing counterparts, are nonetheless larger than the sum of the van der Waals radii, which help minimize X···X repulsive interactions. Of pertinent importance is the solvent-accessible volume of each tube-like structure. The calculated results, obtained at the same level of theory used for the geometry optimizations, show molecular spherical cavities with radii close to one another, especially for the lighter X, with corresponding values of 7.56, 7.53, and 8.10 Ǻ for X = Cl, Br, and I, respectively. The directional character of the halogen bond is manifested in related angles that are close to linear, ranging from 168° to 172°. A close examination of Table 2 suggests that the halogen bonds in the center of the tubular system are somewhat stronger given their relatively short distances and wider angles. On geometrical grounds, the increasing strength of the halogen bond with the increasing size of the halogen atom, X, can be gleaned by comparing normalized halogen-bond distances. The normalized distances are, in turn, obtained as the ratio of X···N distances to the sum of the respective van der Waals radii. For the halogen bonds at the ends of the tubular system, for example, the largest normalized distance is that for X = Cl (0.93), while the smallest is that for X = I (0.87). In turn, the corresponding normalized Br···N distance (0.89) is midway between the other two values.
The relative strength of the halogen bonds is further examined using topological analyses, within the framework of the AIM theory, and using delocalization energy analyses, within the framework of the NBO method. The AIM and NBO results are reported in Table 3. Specifically for all systems, Table 3 lists the second-order NBO delocalization energies, <E2>, associated with the charge transfer from the halogen-bond acceptor lone pair into the antibonding orbital of the halogen-bond donor, nN→σ*N–X. Also shown in Table 3 are the electron densities at each halogen bond critical point. Both the AIM and NBO results indicate stronger halogen-bond interactions in the central part of the tubular tetramer. The results also show a steady strengthening of the halogen bond with the increasing size of the halogen atom, in agreement with the interaction energies and geometrical results previously discussed. In fact, a linear correlation is found between the average interaction energies and the second-order stabilization energies averaged over the terminal and the central N-X···N halogen bonds. Similarly, a linear correlation is found between the average interaction energies and the ρc values averaged over the terminal and the central N-X···N halogen bonds. Despite the small number of points considered, these linear correlations are in accord with the more general findings reported by other researchers [8,9,10,11,12].
The aforementioned linear correlation between the average halogen-bond interaction energies, <∆E>, and the average second-order delocalization energies, <E2>, is made apparent in Equation (1) below (R2 = 0.998), in energy units of kcal/mol.
<∆E> = −0.7964<E2> + 0.1684
Likewise, the linear correlation between the average halogen-bond interaction energies, <∆E>, and the halogen-bond critical points, ρc, is made apparent in Equation (2) below (R2 = 0.998), in units of kcal/mol for <∆E> and in atomic units for ρc.
<∆E> = −861.82 ρc + 9.6475
In addition to the strength and the directionality of the pertinent intermolecular interactions, the entropic cost of bringing several molecules together to form a supramolecular system should be considered, especially when it plays a major role in hampering the formation of the supramolecular assembly [82]. One way to address the entropic cost is to design a system where the relevant functional groups are already in the desired geometrical location and orientation. For example, it may be possible to design an intramolecular system wherein the desired interactions and binding sites are pre-organized in a way that the entropic cost is taken care of in advance [83]. In this study, a tube-like intramolecular halogen-bonded network for Li+ binding is proposed (Figure 2). In this case, the central halogen-bonded network of Figure 1 is replaced by a sequence of covalent-bonding interactions involving silicon atoms instead of nitrogen atoms, with acetylene groups replacing the halogen atoms. The choice of silicon and acetylene groups is made because the geometry of the resulting intramolecular system largely retains the key geometrical features of its intermolecular counterpart, thus facilitating comparison.
The halogen-bond geometrical distances listed in Table 4 appear somewhat shorter than those shown in Table 2 for the terminal intermolecular halogen bonds, by about 0.02, 0.07, and 0.11 Å for X = Cl, Br, and I, respectively. The intramolecular halogen-bond angles are also close to their intermolecular counterparts. Lastly the X···X distances appear smaller in the intramolecular structures, with the distances between adjacent halogen atoms more closely resembling those of the central halogen bonds of the intermolecular tetrameric structure. Regarding the solvent-accessible volume, calculations resulted in radii for the molecular spherical cavities that are close to one another and to those of their intermolecular counterparts mentioned in the previous section. Specifically, the calculated spherical cavity radii values are 7.56, 7.86, and 7.80 Ǻ for X = Cl, Br, and I, respectively.
The AIM and NBO parameters listed in Table 5 allow for further comparison of the halogen-bond strength in the networks. Comparing the second-order NBO delocalization energies, <E2>, in Table 5 with those of the terminal halogen-bonded network listed in Table 3 shows that the intramolecular X···N interactions tend to be stronger than the intermolecular counterparts, especially for the heavier halogens. A similar observation can be made when comparing the electron density at each halogen bond critical point listed in Table 5 with those of the terminal halogen bonds listed in Table 3. It is possible to obtain a rough estimate of the average interaction energies for the intramolecular N-X···N halogen interactions, <∆E>, by using the fitting line equations shown in Equations 1 and 2. From Equation (1), the estimated average halogen-bond interaction energies are −1.99, −4.47, and −7.98 kcal/mol for X = Cl, Br, and I, respectively. Likewise, the estimated values using Equation (2) are −0.95, −4.49, and −8.36 kcal/mol for X = Cl, Br, and I, respectively. The results from the two different fitting line equations are comparable for X = Br and I, though not so much for X = Cl, for which a difference of more than 1 kcal/mol is seen between the two estimates. Nevertheless, the estimated intramolecular interaction energies exhibit the same pattern of increasing in magnitude with the increasing size of the halogen atom, as seen in Table 1. Lastly, the estimated halogen-bond interaction energies in the intramolecular system are consistently more negative for the heavier halogen atoms and less negative for X = Cl than the related average values listed in Table 1.
Given the existence and relative robustness of the halogen bonds in the networks shown in Figure 1 and Figure 2, respectively, it is of interest to examine the ability of these networks to bind a metal cation. To this end, the molecular electrostatic potential is calculated for the networks. The results displayed in Figure 3 show the presence of distinctive negative electrostatic potential regions along the vertical axis of both tubular networks. A view from the top shows also the negative potential above the upper halogen-bonded network. Thus, in principle, a metal cation can be attracted to the negative potential at the outer top of the tubular system and then make its way into the tube as it feels the electrostatic attractive interaction arising from the interior negative potentials. The metal ion can then continue moving through the tubular network all the way to its other end. The specific geometries and energetics of the Li+ binding interactions are examined in the sections below.

2.2. Model Intermolecular Halogen-Bonded Network and Li+ Binding

Full geometry optimization demonstrated the ability for the tetrameric tube-like structure to bind Li+ through the halogen-bonded network either at the end of the tube or at its center, as shown in Figure 4. Frequency calculations confirm that the optimized complexes are indeed minimum-energy structures with no imaginary frequencies.
The BSSE-corrected Li+ complexation energies are listed in Table 6. The complexation energies are calculated as the difference between the total energy of the complex and the sum of the energies of both the metal ion and the whole tetrameric network. Table 6 shows that, for any given X, the magnitude of the complexation energies is larger for the central complexes and that it also steadily decreases with the size of X.
Binding of the metal ion brings about changes in the geometrical parameters of the host (the free tetrameric tube-like structure). For example, the halogen-bond distances and angles of the terminal complex are listed in Table 7. A comparison with the values listed in Table 2 for the free host indicates that the most affected X···N distances are those directly involved in the binding of Li+. Specifically, a reduction in these halogen-bond distances occurs upon metal ion complexation. The magnitude of the percentage change in the X···N distances decreases with the size of X as 4.2% > 2.6% > 2.1% for X = Cl, Br, and I, respectively. The changes in the other halogen-bond distances and for all halogen-bond angles are negligible for any given X, however. Table 7 also lists the X···Li+ distances and X···Li+···X angles. Close inspection reveals a linear relationship between the Li+ complexation energy and either the X···Li+ distances or the X···Li+···X angles. Indeed, shorter X···Li+ distances favor a more effective electrostatic interaction between the metal ion and the halogen atoms’ electron density. Particularly interesting is the relationship of the complexation energies with the X···Li+···X angles. Here, a larger angle indicates that Li+ sits closer to the plane formed by the halogen atoms, permitting the metal ion to more effectively experience the combined electron density of the four halogen atoms directly involved in its binding.
Key geometrical parameters for the Li+ central complexes are displayed in Table 8. Comparison with the corresponding parameters in Table 2 shows that the changes in the X···N distances are all small (about ±1%), regardless of X. For those of the central halogen-bonded network binding Li+, for example, the Cl···N distances are shortened by 1.4%, while the Br···N and I···N distances are lengthened by 0.6% and 1.1%, respectively. These changes are smaller than those previously noted for the terminal complex. The changes in the halogen-bond angles are negligible, with the largest change being a 2.3% decrease in the central N-I···N angles. Like the terminal Li+ complexes, the X···Li+ distances listed in Table 8 have a linear relationship with the central Li+ complexation energies shown in Table 6. No such linear relationship is found, though, with the X···Li+···X angles, as is the case with the terminal Li+ complexes. For the central Li+ complex, the X···Li+···X angles for X = Cl and X = Br reach 180° for the maximum effective interaction, while the I···Li+···I angles (~159°) are still far from this maximum.
The existence of a critical point between the Li+ and each of the halogen atoms participating in its complexation gives further evidence of the binding of the metal ion. For the terminal complex, Table 9 shows that the electron density, ρc, at the N-X···Li+ bond critical point decreases with the size of X. Moreover, the reductions in ρc appear to linearly correlate with the changes in X in the Li+ complexation energies of the terminal complexes (Table 6). Table 9 also shows that for any given X, ρc is larger in the central complexes, in agreement with the larger magnitude of the respective Li+ complexation energies. The second-order NBO delocalization energies, <E2>, in Table 9 pertaining to the N-X···Li+ interactions refer to the charge transfer from the halogen atom lone pairs into the anti-lone pair orbital of Li+, nX→lp*Li+. Interestingly, the changes in these delocalization energies, with respect to X, run opposite to the changes in the corresponding interaction energies for both the terminal and central complexes. That is, the smaller the charge transfer, nX→ lp*Li+, is, the larger the magnitude of the Li+ complexation energy is; this is a result that highlights the pivotal role played by the electrostatic interactions in the binding of Li+ in these complexes [84].
In addition to the values specific to the N-X···Li+ interactions, Table 9 lists the <E2> and ρc values pertaining to the halogen-bond interactions, N-X···N, that are present in the terminal and central Li+ complexes. A comparison with the related values listed in Table 3 for the free host structures shows that the largest changes occur for the N-X···N interactions that participate in the binding of Li+. In general, the change in the <E2> and ρc values upon Li+ binding aligns with the change in the geometrical parameters previously discussed. For instance, the reduction in the halogen-bond distances, N-X···N, correlates with a sizeable percentage increase in the ρc values of 31%, 18%, and 14% for X = Cl, Br, and I, respectively. Similarly, the comparable <E2> values also show a percentage increase of 55%, 28%, and 21%.

2.3. Model Intramolecular Halogen-Bonded Network and Li+ Binding

The optimized geometries of the complexes of Li+ with the intramolecular tube-like structure are shown in Figure 5. The absence of imaginary frequencies confirms their nature as minimum-energy structures.
The BSSE-corrected Li+ complexation energies listed in Table 10 show similarities with those listed in Table 6 for the analogous Li+ complexes with the tetrameric hosts. For example, the binding of the metal ion both weakens with the size of X and becomes stronger in the central complex. It is worth noting that the ability of the halogen atoms to bind Li+ in both kinds of complexes is practically the same, as indicated by the Li+ complexation energies that are within 1% of each other for a given X. An important structural difference between the intermolecular and intramolecular host complexes is that the central part of the latter contains a sequence of four silicon-linked alkyne groups providing the electron density for binding the metal ion. A comparison with Table 6 reveals that the magnitude of the central Li+ complexation energies is larger for the intramolecular hosts, with the difference increasing by 2% < 5% < 8% for X = Cl, Br, and I, respectively. Nonetheless, the ability to bind Li+ at the central part is comparable for both the halogen-bonded network and the silicon-linked alkyne groups.
Key geometrical parameters for the Li+ terminal complexes are displayed in Table 11. These geometrical parameters are remarkably close to those listed in Table 7 for their intermolecular counterparts for any given X. The closeness of the geometrical parameters mirrors the similar complexation energies between the applicable inter- and intramolecular Li+ complex systems discussed earlier.
The relevant geometrical parameters for the intramolecular Li+ central complexes are displayed in Table 12. With respect to the intermolecular counterparts (Table 8), the X···N distances are slightly shortened, while the N-X···N angles remain mostly unchanged. Table 12 also lists the distance between Li+ and the midpoint of the triple-bonded carbon atoms, (C≡C)···Li+. This distance is effectively independent of X. When compared with the X···Li+ values listed in Table 8, it is apparent that the metal ion is closer to the midpoint of each C≡C moiety than it is to the halogen atoms. This is especially true for the heavier bromine and iodine atoms, for which the X···Li+ values are 4.5% and 11.4% longer, respectively, than the (C≡C)···Li+ values. The (C≡C)···Li+···(C≡C) angles are all linear, indicating that Li+ lies in the plane of symmetry of the system for any given X. Linearity is also noted for the intermolecular counterparts, except for X = I. The more favorable geometrical features regarding the binding of Li+ by the intramolecular guest system are consistent with the larger magnitude of the Li+ complexations’ energies discussed before.
The binding of Li+ by the terminal N-X···N or the central (C≡C)···Li+ networks of the intramolecular host structure is evidenced by the existence of a critical point found in a pathway between the metal ion and each of the halogen atoms or the midpoint of each C≡C unit participating in its complexation. Table 13 shows that the electron density at the (C≡C)···Li+ critical point, ρc, is independent of X and smaller than that of the N-X···Li+ bond critical points. The second-order stabilization energies, <E2>, associated with the charge transfer from the alkyne triple bond moiety to the metal ion, C≡C→lp*Li+, also listed in Table 13, are negligible and independent of X. They are also much smaller than the corresponding N-X···Li+ values referring to the charge transfer from the halogen atom lone pairs into the lithium ion, nX→lp*Li+.
Regarding the halogen-bond interactions, N-X···N, Table 13 shows that, in the terminal complex, both ρc and <E2> increase with X and that they are larger for those halogen bonds responsible for binding Li+. Indeed, the ρc and <E2> values for the N-X···N interactions that are not participating in the binding of Li+ are much closer to those of the free intramolecular hosts (Table 5). Interestingly, Table 13 reveals that binding Li+ in the central complex brings about a small-yet-sizable increase for both ρc and <E2> values for the N-X···N interactions, when compared with those of the free hosts. That is, binding the metal ion by the central silicon-linked alkyne groups seems to strengthen the terminal halogen-bonded networks. These results for the central complex are congruent with the decrease in the halogen-bond distances in the intramolecular complexes (Table 12), when compared with those of the free intramolecular hosts (Table 4).

2.4. Transition State Geometries and Barrier Heights

Given the ability of the inter- or intramolecular host structures to bind Li+ in two different modes (terminal or central Li+ complexes), it is important to investigate the energy barrier that needs to be overcome for the Li+ complex to transition from one binding mode to the other. To this end, a geometry optimization is conducted to find the transition-state structure linking the two Li+ binding modes for both the intermolecular and the intramolecular Li+ complexes of any given X. The optimized geometries of the optimized transition-state structures are shown in Figure 6. The presence of a single imaginary frequency confirms their nature as saddle points of the first order.
Further confirmation that the optimized transition-state structures indeed connect the two intended minima is provided by intrinsic reaction coordinate (IRC) calculations. Figure 7 illustrates the IRC calculations for the intermolecular Li+ complex using X = Br as an example. For this system, the IRC calculations successfully advanced in the forward and reverse coordinates to points quite close to the pertinent actual minima structures. The leftmost side of Figure 7 corresponds to the terminal complex, which has an electronic energy of about 3 kcal/mol relative to the more stable central complex. The transition-state structure is located about 6 kcal/mol above the terminal complex structure. Once the energy barrier is overcome, the left terminal complex can transition into the central complex. From the central complex, an electronic energy barrier of about 9 kcal/mol needs to be surpassed to transition back into the left terminal complex or forward into the right terminal complex. Transitioning to the latter would effectively result in the transport of the metal ion from one end of the tube-like host to the other, passing through the central complex.
Figure 8 illustrates the IRC calculations for the intramolecular Li+ complex using X = Cl as an example. For this system, the IRC calculations successfully advanced in the forward and reverse coordinates to points quite close to the pertinent actual minima structures. The leftmost side of Figure 8 corresponds to the terminal complex, which has an electronic energy of about 2 kcal/mol relative to the more stable central complex. The transition-state structure is located about 12 kcal/mol above the terminal complex structure. Once the energy barrier is overcome, the left terminal complex can transition into the central complex. From the central complex, an electronic energy barrier of about 14 kcal/mol needs to be surpassed to transition back into the left terminal complex or forward into the right terminal complex. Transitioning to the latter would effectively result in the transport of the metal ion from one end of the tube-like host to the other, passing through the central complex. Interestingly, Figure 8 shows a flat region in the direction from the transition-state structure to the terminal complex structure. Moreover, the appearance of a small shoulder is seen just before the system dives into the terminal complex structure.
The calculated relative electronic energies, Erel, and Gibbs free energies, Grel, of the Li+ terminal complexes with the intermolecular or intramolecular host networks are listed in Table 14. In all cases, the terminal complexes are found to be higher in energy than the corresponding central complexes. For X = Cl and I, Grel is larger than Erel, while the opposite is true for X = Br. The relative electronic energy and Gibbs free energy barriers, Eǂ and Gǂ, respectively, are larger in the intramolecular complexes than in their intermolecular counterparts. The largest energy barriers are consistently found for X = Cl, while the lowest are found for X = I.
It is worth noting that, for the lowest energy Li+ complex structure with the intermolecular host, when X = I, the metal ion does not sit in the middle of the central halogen-bonded network but rather off this plane with an N-I···N angle of 158.7° (See Table 8). In fact, the structure with Li+ sitting in the center of symmetry with N-I···N angles of 180° is found to be a first-order saddle point connecting the two symmetrical energy minima (at either side of the central plane). Although the calculated electronic energy barrier, Eǂ, is only 0.34 kcal/mol, the corresponding Gǂ is much higher, 1.57 kcal/mol. Another aspect worth mentioning, with respect to the Li+ complex with the intermolecular host when X = I, is that the Gǂ listed in Table 14 is smaller than Grel, suggesting a larger stability of the transition-state structure compared with the terminal complex itself. This larger stability is not reflected in the corresponding electronic energies, which show Eǂ to be more than twice Erel. Under these circumstances, the transition from the terminal complex to the lowest energy structure seems to be a favorable energetic process as far as the Gibbs free energy is concerned. Because the lowest energy structure is off the center, it can transition to the other side of the center upon overcoming the Gibbs energy barrier of 1.57 kcal/mol and passing through a transition-state structure located at the center of the central N-I···N network.
To some extent, the origins of the energy barriers for the transition between the terminal and central complexes can be traced to both a loss of attractive Li+ binding interactions and an increase in the repulsive interactions of the metal ion with nearby hydrogen atoms carrying a partial positive charge. For example, Table 15 lists the calculated NBO charges for the metal ion, qLi+, and its closest hydrogen atoms, qH, in the central, terminal, and TS complexes with both intermolecular and intramolecular host complexes. Also listed in Table 15 are the related distances, Li+···H. An inspection of Table 15 reveals, for example, that the Li+···H distances are substantially smaller in the TS structures than they are in their central or terminal counterparts, even more conspicuously so in the intramolecular complexes. The reduction in the Li+···H distances noted for the transition state complexes is expected to greatly contribute to the energy barriers due to the resulting repulsive Li+···H interactions. The charges on the hydrogen atoms closest to Li+ are generally found around 0.20 a.u., whereas the charge on the metal ion is much higher and tends to decrease with the size of X. Evidence of the loss of attractive interactions with Li+ is found in the AIM calculations on the TS structures. For instance, the intermolecular TS complexes, when X = Cl, show only two critical points connecting the metal ion with two opposing Cl atoms, in contrast to the related four critical points found in either minimum-energy complex (central or terminal). One critical point in the TS complex connects Li+ with a Cl atom from the central Cl-bonded network, and the other connects Li+ with a Cl atom from the closer terminal one. The average Li+···Cl distance is also much larger (3.01 Ǻ) than that found in the central or terminal complexes, 2.60 or 2.63 Ǻ, respectively, also suggesting weaker interactions. Similar results are found when X = Br. In this case, the average Li+···Br distance is also larger (3.09 Ǻ) than that found in the in the central or terminal complexes, 2.72 or 2.77 Ǻ, respectively. Interestingly, when X = I, three critical points are found connecting Li+ to three I atoms, one from the central network and two from the terminal network. Again, the average Li+···I distance (3.37 Ǻ) is larger than that either in the central complex (2.93 Ǻ) or in the terminal complex (3.01 Ǻ). The presence of an additional Li+···I critical point in the TS complex reveals the further stabilization of the TS complex, leading to a smaller energy barrier relative to that when X = Cl or Br. For a more refined and robust understanding of the energy barriers, the author is currently conducting in-depth analyses of the energy and reaction force profiles along the entire calculated IRC for all Li+-bound complexes, and the results will be published elsewhere.

3. Computational Methods

All calculations were performed with the ωB97XD/DGDZVP model using the Gaussian 16 program [85]. The DFT model employed here has been shown to be adequate and cost-effective for studying intermolecular interactions, especially halogen bonding in relatively large systems [86,87,88,89]. The geometries for all molecular systems were fully optimized, and their nature as minima or transition-state structures was determined by the absence or presence of imaginary frequencies resulting from the corresponding frequency calculations. It is worth noting that no symmetry was imposed for any of the geometry optimization calculations. Intrinsic reaction coordinate (IRC) calculations were carried out to confirm the predicted connection between different minima through the relevant transition-state structures. Calculated binding energies for all complexes were corrected for the basis set superposition error (BSSE) [90]. Additional insight into the strength and nature of the various interactions was gained by carrying out analyses based on the theory of atoms in molecules (AIM) [91,92,93,94], and natural bond orbital (NBO) analysis [95].

4. Future Perspectives

In this study, the ability of N-X···N halogen bonds to drive the formation of robust tube-like structures was demonstrated using DFT ωB97XD/DGDZVP calculations. Specifically, four NHX-(CH2)3-NX-(CH2)3-NHX molecules (X = Cl, Br, or I) were shown to self-assemble into a tube-like structure of C4h symmetry, without imposing any symmetry constraints, with one halogen-bonded network consisting of four quasi-planar N-X···N halogen-bond interactions located at each end of the structure and one at its center. In the tubular system, the four monomers were bound together by three homodromic halogen-bonded systems with alternating directions. The case in which the three halogen-bonded systems do not alternate was not considered in this study because they are generally higher in energy. For example, relative to the system with alternating halogen-bond directions, the Gibbs free energies of the non-alternating systems were 2.67, 1.98, and 3.49 kcal/mol for X = Cl, Br, and I, respectively. The robustness of the tube-like structures was seen in the calculated BSSE-corrected interaction energies; the second-order stabilization energies, <E2>; and the electron density accumulated at halogen-bond critical points, ρc. The potential of the tetrameric tube-like structure for binding Li+ at each of its terminal and central halogen-bonded networks was demonstrated, as was the potential to have the metal ion transition from one end of the tubular host to the other via IRC calculations. These results suggested the possible use of the tube-like host as a Li+ channel. The generality of the results presented here should be investigated by further computational and experimental work. For example, the effect of increasing the size and charge of the metal ion, i.e., Na+, K+, Mg2+, Ca2+, etc., on the binding abilities of the tubular host should be examined. Another aspect that remains the subject of future work is the self-assembly of five or more building molecules that could accommodate larger metal ions or, more generally, other cations. Moreover, the length of the building molecule can also be increased, for example, by adding more NX motifs to the interior of the molecule, such as in NHX-(CH2)3-NX-(CH2)3-NX-(CH2)3-NHX molecules (X = Cl, Br, or I). A longer length of the molecular building block results in a longer tubular structure, with the intriguing possibility for binding and transporting a metal ion over longer distances. Lastly, the use of isoelectronic alternatives in the molecular motifs merits examination. For example, in a previous study on (BrX)n cyclic complexes, with X = F, OH, or NH2 and n = 3–5, the author examined a set of relevant isolectronic species. It was found that the average dissociation electronic energies for the tetramers are comparable, with values of 3.19, 3.54, and 3.91 for X = F, NH2, and OH, respectively [96]. For the purpose of the work presented here, X = NH2 was chosen as a compromise. However, the examination of molecules with other isoelectronic motifs like OH should be considered in future work.
It is often desirable to design a single molecule with the pertinent functional groups properly placed to perform the intended function, namely, binding a metal ion. In particular, having the N-X···N halogen bonds already formed in a single molecular structure, rather than by the self-assembly of several molecular building motifs, may actually be desired. To this end, the tetrameric structure was modified into an intramolecular structure wherein the central intermolecular N-X···N network was replaced by an intramolecular Si-C≡C-Si network. The silicon-linked alkyne motif was chosen because it maintained the main geometrical halogen-bonded features of the intermolecular tetrameric parent system. It is worth noting that very similar Li+ binding abilities were seen for both inter- and intramolecular structures. Additional computational and experimental studies will help gauge the generality of the results pertaining to the intramolecular tube-like host structure for binding and transporting metal ions.
It is noteworthy that a recent study demonstrated the use of halogen bonds for the binding of Li+ and for the solid–liquid extraction of lithium halide salts. Specifically, phenanthroline-based heteroditopic macrocycles containing halogen-bond donors were designed for the ion-pair recognition of lithium halides [97]. In these systems, the binding of Li+ by the phenanthroline motif was accompanied by the binding of the halide through halogen-bond formation with the strategically located halogen-bond donors in the hosts. It was found that these systems selectively bind LiCl over LiBr or LiI. Follow-up studies were reported to extend the applicability of the approach to other alkali metal halides [98,99]. It is hoped that the DFT computational results presented in this work provide a foundation and motivation to help expand research in the field of halogen bonds. The use of halogen atoms for a dual role in forming halogen bonds and in binding metal ions, as presented here, is a novel approach that remains highly unexplored, especially for the possible channeling or transporting of metal ions.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available in article.

Acknowledgments

The author would like to acknowledge that this research was greatly facilitated by a DePaul University Internal Grant as part of the Paid Leave program in the spring of 2023. The author is also grateful to the Department of Chemistry and Biochemistry at DePaul University for its continuing support.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Che. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
  2. Erdélyi, M.; Esterhuysen, C.; Zhu, W. Halogen Bonding: From Fundamentals to Applications. ChemPlusChem 2021, 86, 1229–1230. [Google Scholar] [CrossRef] [PubMed]
  3. Politzer, P.; Lane, P.; Concha, M.C.; Ma, Y.; Murray, J.S. An overview of halogen bonding. J. Mol. Mod. 2007, 13, 305–311. [Google Scholar] [CrossRef] [PubMed]
  4. Politzer, P.; Murray, J.S. Halogen bonding: An interim discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef]
  5. Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen bonding: A halogen-centered noncovalent interaction yet to be understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef]
  6. Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The many faces of halogen bonding: A review of theoretical models and methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
  7. Neaton, J.B. A direct look at halogen bonds. Science 2017, 358, 167–168. [Google Scholar] [CrossRef] [PubMed]
  8. Costa, P.J. The halogen bond: Nature and applications. Phys. Sci. Rev. 2017, 2, 20170136. [Google Scholar] [CrossRef]
  9. Grabowski, S.J. Halogen bond and its counterparts: Bent’s rule explains the formation of nonbonding interactions. J. Phys. Chem. A 2011, 115, 12340–12347. [Google Scholar] [CrossRef]
  10. Grabowski, S.J. QTAIM characteristics of halogen bond and related interactions. J. Phys. Chem. A 2012, 116, 1838–1845. [Google Scholar] [CrossRef]
  11. Wang, C.; Danovich, D.; Mo, Y.; Shaik, S. On the nature of the halogen bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. [Google Scholar] [CrossRef] [PubMed]
  12. Syzgantseva, O.A.; Tognetti, V.; Joubert, L. On the physical nature of halogen bonds: A QTAIM study. J. Phys. Chem. A 2013, 117, 8969–8980. [Google Scholar] [CrossRef] [PubMed]
  13. Oliveira, V.; Kraka, E.; Cremer, D. The intrinsic strength of the halogen bond: Electrostatic and covalent contributions described by coupled cluster theory. Phys. Chem. Chem. Phys. 2016, 18, 33031–33046. [Google Scholar] [CrossRef] [PubMed]
  14. Clark, T.; Murray, J.S.; Politzer, P. Role of polarization in halogen bonds. Aust. J. Chem. 2013, 67, 451–456. [Google Scholar] [CrossRef]
  15. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
  16. Scheiner, S. Does a halogen bond require positive potential on the acid and negative potential on the base? Phys. Chem. Chem. Phys. 2023, 25, 7184–7194. [Google Scholar] [CrossRef] [PubMed]
  17. Eskandari, K.; Zariny, H. Halogen bonding: A lump–hole interaction. Chem. Phys. Lett. 2010, 492, 9–13. [Google Scholar] [CrossRef]
  18. Stone, A.J. Are halogen bonded structures electrostatically driven? J. Am. Chem. Soc. 2013, 135, 7005–7009. [Google Scholar] [CrossRef]
  19. Inscoe, B.; Rathnayake, H.; Mo, Y. Role of charge transfer in halogen bonding. J. Phys. Chem. A 2021, 125, 2944–2953. [Google Scholar] [CrossRef]
  20. Wang, H.; Wang, W.; Jin, W.J. σ-Hole bond vs π-hole bond: A comparison based on halogen bond. Chem. Rev. 2016, 116, 5072–5104. [Google Scholar] [CrossRef]
  21. Kellett, C.W.; Kennepohl, P.; Berlinguette, C.P. π covalency in the halogen bond. Nat. Commun. 2020, 11, 3310. [Google Scholar] [CrossRef] [PubMed]
  22. Sharber, S.A.; Mullin, W.J.; Thomas III, S.W. Bridging the void: Halogen bonding and aromatic interactions to program luminescence and electronic properties of π-conjugated materials in the solid state. Chem. Mater. 2021, 33, 6640–6661. [Google Scholar] [CrossRef]
  23. van Terwingen, S.; Wang, R.; Englert, U. Three for the Price of One: Concomitant I⋯N, I⋯O, and I⋯π Halogen Bonds in the Same Crystal Structure. Molecules 2022, 27, 7550. [Google Scholar] [CrossRef]
  24. Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Mod. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
  25. Clark, T. Halogen bonds and σ-holes. Faraday Discuss. 2017, 203, 9–27. [Google Scholar] [CrossRef] [PubMed]
  26. Kolář, M.; Hostaš, J.; Hobza, P. The strength and directionality of a halogen bond are co-determined by the magnitude and size of the σ-hole. Phys. Chem. Chem. Phys. 2014, 16, 9987–9996. [Google Scholar] [CrossRef] [PubMed]
  27. Huber, S.M.; Scanlon, J.D.; Jimenez-Izal, E.; Ugalde, J.M.; Infante, I. On the directionality of halogen bonding. Phys. Chem. Chem. Phys. 2013, 15, 10350–10357. [Google Scholar] [CrossRef]
  28. Scheiner, S. Enhancement of Halogen Bond Strength by Intramolecular H-Bonds. J. Phys. Chem. A. 2023, 127, 4695–4703. [Google Scholar] [CrossRef]
  29. Riley, K.E.; Murray, J.S.; Fanfrlík, J.; Řezáč, J.; Solá, R.J.; Concha, M.C.; Ramos, F.M.; Politzer, P. Halogen bond tunability I: The effects of aromatic fluorine substitution on the strengths of halogen-bonding interactions involving chlorine, bromine, and iodine. J. Mol. Mod. 2011, 17, 3309–3318. [Google Scholar] [CrossRef]
  30. Riley, K.E.; Murray, J.S.; Fanfrlík, J.; Řezáč, J.; Solá, R.J.; Concha, M.C.; Ramos, F.M.; Politzer, P. Halogen bond tunability II: The varying roles of electrostatic and dispersion contributions to attraction in halogen bonds. J. Mol. Mod. 2013, 19, 4651–4659. [Google Scholar] [CrossRef]
  31. Parra, R.D.; Grabowski, S.J. Enhancing Effects of the Cyano Group on the CX∙∙∙ N Hydrogen or Halogen Bond in Complexes of X-Cyanomethanes with Trimethyl Amine: CH3−n (CN)nX∙∙∙ NMe3,(n = 0–3; X = H, Cl, Br, I). Int. J. Mol. Sci. 2022, 23, 11289. [Google Scholar] [CrossRef]
  32. Lu, Y.; Liu, Y.; Li, H.; Zhu, X.; Liu, H.; Zhu, W. Mutual influence between halogen bonds and cation–π interactions: A theoretical study. ChemPhysChem 2012, 13, 2154–2161. [Google Scholar] [CrossRef]
  33. Meyer, F.; Dubois, P. Halogen bonding at work: Recent applications in synthetic chemistry and materials science. CrystEngComm 2013, 15, 3058–3071. [Google Scholar] [CrossRef]
  34. Yamada, S.; Konno, T. Recent advances in halogen bond-assisted organic synthesis. Curr. Org. Chem. 2020, 24, 2118–2152. [Google Scholar] [CrossRef]
  35. Bulfield, D.; Huber, S.M. Halogen bonding in organic synthesis and organocatalysis. Chem. Eur. J. 2016, 22, 14434–14450. [Google Scholar] [CrossRef]
  36. Sutar, R.L.; Huber, S.M. Catalysis of organic reactions through halogen bonding. ACS Catal. 2019, 9, 9622–9639. [Google Scholar] [CrossRef]
  37. Kaasik, M.; Kanger, T. Supramolecular halogen bonds in asymmetric catalysis. Front. Chem. 2020, 8, 599064. [Google Scholar] [CrossRef]
  38. Yang, H.; Wong, M.W. Application of halogen bonding to organocatalysis: A theoretical perspective. Molecules 2020, 25, 1045. [Google Scholar] [CrossRef]
  39. Wilcken, R.; Zimmermann, M.O.; Lange, A.; Joerger, A.C.; Boeckler, F.M. Principles and applications of halogen bonding in medicinal chemistry and chemical biology. J. Med. Chem. 2013, 56, 1363–1388. [Google Scholar] [CrossRef]
  40. Ho, P.S. Halogen bonding in medicinal chemistry: From observation to prediction. Future Med. Chem. 2017, 9, 637–640. [Google Scholar] [CrossRef]
  41. Mendez, L.; Henriquez, G.; Sirimulla, S.; Narayan, M. Looking back, looking forward at halogen bonding in drug discovery. Molecules 2017, 22, 1397. [Google Scholar] [CrossRef]
  42. Ford, M.C.; Ho, P.S. Computational tools to model halogen bonds in medicinal chemistry. J. Med. Chem. 2016, 59, 1655–1670. [Google Scholar] [CrossRef]
  43. Parra, R.D.; Djordjevic, V. Exploring the potential of halogen bonding in the development of protein tyrosine kinase inhibitors. J. Undergrad. Chem. Res. 2015, 14, 93–95. [Google Scholar]
  44. Metrangolo, P.; Giuseppe, R. Halogen bonding: A paradigm in supramolecular chemistry. Chem. Eur. 2001, 7, 2511–2519. [Google Scholar] [CrossRef]
  45. Priimagi, A.; Cavallo, G.; Metrangolo, P.; Resnati, G. The halogen bond in the design of functional supramolecular materials: Recent advances. Acc. Chem. Res. 2013, 46, 2686–2695. [Google Scholar] [CrossRef]
  46. Li, B.; Zang, S.Q.; Wang, L.Y.; Mak, T.C. Halogen bonding: A powerful, emerging tool for constructing high-dimensional metal-containing supramolecular networks. Coord. Chem. Rev. 2016, 308, 1–21. [Google Scholar] [CrossRef]
  47. Rissanen, K. Halogen bonded supramolecular complexes and networks. CrystEngComm 2008, 10, 1107–1113. [Google Scholar] [CrossRef]
  48. Zheng, J.; Suwardi, A.; Wong, C.J.E.; Loh, X.J.; Li, Z. Halogen bonding regulated functional nanomaterials. Nanoscale Adv. 2021, 3, 6342–6357. [Google Scholar] [CrossRef]
  49. Wang, H.; Bisoyi, H.K.; Urbas, A.M.; Bunning, T.J.; Li, Q. The halogen bond: An emerging supramolecular tool in the design of functional mesomorphic materials. Chem. Eur. 2019, 25, 1369–1378. [Google Scholar] [CrossRef]
  50. Resnati, G.; Pennington, W.T. The halogen bond: A new avenue in recognition and self-assembly. New J. Chem. 2018, 42, 10461–10462. [Google Scholar] [CrossRef]
  51. Saccone, M.; Catalano, L. Halogen bonding beyond crystals in materials science. J. Phys. Chem. B 2019, 123, 9281–9290. [Google Scholar] [CrossRef]
  52. Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen bonding in supramolecular chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef]
  53. Pennington, W.T.; Resnati, G.; Taylor, M.S. Halogen bonding: From self-assembly to materials and biomolecules. CrystEngComm 2013, 15, 3057. [Google Scholar] [CrossRef]
  54. Wu, W.X.; Liu, M.; Wang, H.; Jin, W.J. A Simple Rotor Guest Molecule Mediates the Formation of Cage or Channel Structures of Halogen-Bonding Host Cocrystals. Cryst. Growth Des. 2019, 19, 4378–4384. [Google Scholar] [CrossRef]
  55. Parra, R.D.; Castillo, A. Cyclic networks of halogen-bonding interactions in molecular self-assemblies: A theoretical N—X⋯ N versus C—X⋯ N investigation. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2017, 73, 179–187. [Google Scholar] [CrossRef]
  56. Turunen, L.; Erdélyi, M. Halogen bonds of halonium ions. Chem. Soc. Rev. 2020, 49, 2688–2700. [Google Scholar] [CrossRef]
  57. Cavallo, G.; Metrangolo, P.; Pilati, T.; Resnati, G.; Sansotera, M.; Terraneo, G. Halogen bonding: A general route in anion recognition and coordination. Chem. Soc. Rev. 2010, 39, 3772–3783. [Google Scholar] [CrossRef]
  58. Pancholi, J.; Beer, P.D. Halogen bonding motifs for anion recognition. Coord. Chem. Rev. 2020, 416, 213281. [Google Scholar] [CrossRef]
  59. Brown, A.; Beer, P.D. Halogen bonding anion recognition. Chem. Commun. 2016, 52, 8645–8658. [Google Scholar] [CrossRef] [PubMed]
  60. Taylor, M.S. Anion recognition based on halogen, chalcogen, pnictogen and tetrel bonding. Coord. Chem. Rev. 2020, 413, 213270. [Google Scholar] [CrossRef]
  61. Vargas Jentzsch, A.; Hennig, A.; Mareda, J.; Matile, S. Synthetic ion transporters that work with anion−π interactions, halogen bonds, and anion–macrodipole interactions. Acc. Chem. Res. 2013, 46, 2791–2800. [Google Scholar] [CrossRef] [PubMed]
  62. Vargas Jentzsch, A.; Emery, D.; Mareda, J.; Metrangolo, P.; Resnati, G.; Matile, S. Ditopic ion transport systems: Anion–π interactions and halogen bonds at work. Angew. Chem. 2011, 123, 11879–11882. [Google Scholar] [CrossRef]
  63. Tepper, R.; Schubert, U.S. Halogen bonding in solution: Anion recognition, templated self-assembly, and organocatalysis. Angew. Chem. Int. Ed. 2018, 57, 6004–6016. [Google Scholar] [CrossRef] [PubMed]
  64. Ivanov, D.M.; Bokach, N.A.; Kukushkin, V.Y.; Frontera, A. Metal Centers as Nucleophiles: Oxymoron of Halogen Bond-Involving Crystal Engineering. Chem. Eur. 2022, 28, e202103173. [Google Scholar] [CrossRef] [PubMed]
  65. Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Kirina, Y.V.; Kukushkin, V.Y. Halogen Bonding between Metal Centers and Halocarbons. Chem. Commun. 2016, 52, 5565–5568. [Google Scholar] [CrossRef] [PubMed]
  66. Dabranskaya, U.; Ivanov, D.M.; Novikov, A.S.; Matveychuk, Y.V.; Bokach, N.A.; Kukushkin, V.Y. Metal-Involving Bifurcated Halogen Bonding C–Br···η2 (Cl–Pt). Cryst. Growth Des. 2018, 19, 1364–1376. [Google Scholar] [CrossRef]
  67. Aliyarova, I.S.; Tupikina, E.Y.; Soldatova, N.S.; Ivanov, D.M.; Postnikov, P.S.; Yusubov, M.; Kukushkin, V.Y. Halogen Bonding Involving Gold Nucleophiles in Different Oxidation States. Inorg. Chem. 2022, 61, 15398–15407. [Google Scholar] [CrossRef] [PubMed]
  68. Brammer, L.; Espallargas, G.M.; Libri, S. Combining metals with halogen bonds. CrystEngComm 2008, 10, 1712–1727. [Google Scholar] [CrossRef]
  69. Eliseeva, A.A.; Khazanova, M.A.; Cheranyova, A.M.; Aliyarova, I.S.; Kravchuk, R.I.; Oganesyan, E.S.; Ryabykh, A.V.; Maslova, O.A.; Ivanov, D.M.; Beznosyuk, S.A. Metal-Involving Halogen Bonding Confirmed Using DFT Calculations with Periodic Boundary Conditions. Crystals 2023, 13, 712. [Google Scholar] [CrossRef]
  70. Berger, G.; Frangville, P.; Meyer, F. Halogen bonding for molecular recognition: New developments in materials and biological sciences. Chem. Commun. 2020, 56, 4970–4981. [Google Scholar] [CrossRef]
  71. Shan, H.; Zhou, L.; Ji, W.; Zhao, A. Flexible Alkali–Halogen Bonding in Two Dimensional Alkali-Metal Organic Frameworks. J. Phys. Chem. Lett. 2021, 12, 10808–10814. [Google Scholar] [CrossRef] [PubMed]
  72. Carreras, L.; Benet-Buchholz, J.; Franconetti, A.; Frontera, A.; van Leeuwen, P.W.; Vidal-Ferran, A. Halogen bonding effects on the outcome of reactions at metal centres. Chem. Commun. 2019, 55, 2380–2383. [Google Scholar] [CrossRef] [PubMed]
  73. Parra, R.D. Concerted halogen bonding and orthogonal metal-halogen interactions in dimers of lithium formamidinate and halogenated formamidines: An ab Initio study. Molecules 2014, 19, 1069–1084. [Google Scholar] [CrossRef] [PubMed]
  74. Parra, R.D. Metal–ion binding by cyclic halogen-bonded structures: A theoretical study using M–(BrZ)4 clusters (Z = F or NH2; M = Li+, Na+, or Mg2+). Chem. Phys. Lett. 2015, 637, 177–181. [Google Scholar] [CrossRef]
  75. Parra, R.D. Metal-ion binding via a cyclic network of intramolecular halogen-bonded interactions: A theoretical study. Mol. Phys. 2016, 114, 1485–1493. [Google Scholar] [CrossRef]
  76. Parra, R.D. Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions. Sci 2022, 4, 9. [Google Scholar] [CrossRef]
  77. Voth, A.R.; Khuu, P.; Oishi, K.; Ho, P.S. Halogen bonds as orthogonal molecular interactions to hydrogen bonds. Nat. Chem. 2009, 1, 74–79. [Google Scholar] [CrossRef]
  78. Nelyubina, Y.V.; Antipin, M.Y.; Dunin, D.S.; Kotov, V.Y.; Lyssenko, K.A. Unexpected “amphoteric” character of the halogen bond: The charge density study of the co-crystal of N- methylpyrazine iodide with I2. Chem. Commun. 2010, 46, 5325–5327. [Google Scholar] [CrossRef]
  79. Zhou, P.-P.; Qiu, W.-Y.; Liu, S.; Jinc, N.-Z. Halogen as halogen-bonding donor and hydrogen-bonding acceptor simultaneously in ring-shaped H3N.X(Y).HF (X = Cl, Br and Y = F, Cl, Br) Complexes. Phys. Chem. Chem. Phys. 2011, 13, 7408–7418. [Google Scholar] [CrossRef]
  80. Dikundwar, A.G.; Row, T.N.G. Evidence for the “Amphoteric” nature of fluorine in halogen bonds: An instance of Cl···F contact. Cryst. Growth Des. 2012, 12, 1713–1716. [Google Scholar] [CrossRef]
  81. Bondi, J. van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
  82. Voelkel, M.H.; Wonner, P.; Huber, S.M. Preorganization: A powerful tool in intermolecular halogen bonding in solution. ChemistryOpen 2020, 9, 214–224. [Google Scholar] [CrossRef] [PubMed]
  83. Riel, A.M.S.; Decato, D.A.; Sun, J.; Massena, C.J.; Jessop, M.J.; Berryman, O.B. The intramolecular hydrogen bonded–halogen bond: A new strategy for preorganization and enhanced binding. Chem. Sci. 2018, 9, 5828–5836. [Google Scholar] [CrossRef] [PubMed]
  84. Liu, C.; Zeng, Y.; Li, X.; Zheng, S.; Zhang, X. Cation···π interactions: QTAIM and NBO studies on the interaction of alkali metal cations with heteroaromatic rings. J. Struct. Chem. 2014, 25, 1553–1561. [Google Scholar] [CrossRef]
  85. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  86. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
  87. Siiskonen, A.; Priimagi, A. Benchmarking DFT methods with small basis sets for the calculation of halogen-bond strengths. J. Mol. Model. 2017, 23, 50. [Google Scholar] [CrossRef] [PubMed]
  88. Yurieva, A.G.; Poleshchuk, O.K.; Filimonov, V.D. Filimonov, Comparative analysis of a full-electron basis set and pseudopotential for the iodine atom in DFT quantum-chemical calculations of iodine-containing compounds. J. Struct. Chem. 2008, 49, 548–552. [Google Scholar] [CrossRef]
  89. Kozuch, S.; Martin, J.M. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef]
  90. Boys, S.F.; Bernardi, F. Calculation of small molecular interactions by differences of separate total energies—Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  91. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  92. Zou, J.-W.; Lu, Y.-X.; Yu, Q.-S.; Zhang, H.-X.; Jiang, Y.-J. Halogen bonding: An AIM analysis of the weak interactions. Chin. J. Chem. 2006, 24, 1709–1715. [Google Scholar] [CrossRef]
  93. Biegler-König, F.; Schönbohm, J.; Bayles, D. AIM2000—A program to analyze and visualize atoms in molecules. J. Comput. Chem. 2001, 22, 545–554. [Google Scholar]
  94. Keith, T.A. AIMAll, version 13.11.04; TK Gristmill Software: Overland Park, KS, USA, 2013.
  95. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor–acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  96. Parra, R.D. Cooperative effects and energy barriers to bromonium ion transfer in cyclic (BrX)n halogen-bonded clusters (X = F, OH, or NH2; n = 3–5): An ab initio study. Comput. Theor. Chem. 2015, 1006, 47–54. [Google Scholar] [CrossRef]
  97. Tse, Y.C.; Docker, A.; Zhang, Z.; Beer, P.D. Lithium halide ion-pair recognition with halogen bonding and chalcogen bonding heteroditopic macrocycles. Chem. Commun. 2021, 57, 4950–4953. [Google Scholar] [CrossRef]
  98. Tay, H.M.; Tse, Y.C.; Docker, A.; Gateley, C.; Thompson, A.L.; Kuhn, H.; Zhang, Z.; Beer, P.D. Halogen-Bonding Heteroditopic [2]Catenanes for Recognition of Alkali Metal/Halide Ion Pairs. Angew. Chem. Int. Ed. 2023, 62, e202214785. [Google Scholar] [CrossRef]
  99. Tay, H.M.; Docker, A.; Tse, Y.C.; Beer, P.D. Alkali Metal Halide Ion-Pair Binding in Conformationally Dynamic Halogen Bonding Heteroditopic [2]Rotaxanes. Chem. Eur. J. 2023, 29, e202301316. [Google Scholar]
Inorganics 12 00016 g001
Figure 1. Optimized geometry of the [NHX-(CH2)3-NX-(CH2)3-NHX]4 self-assembled tube-like structure with C4h symmetry. Dashed lines represent N-X···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), and red (Br). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Figure 1. Optimized geometry of the [NHX-(CH2)3-NX-(CH2)3-NHX]4 self-assembled tube-like structure with C4h symmetry. Dashed lines represent N-X···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), and red (Br). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Inorganics 12 00016 g001
Inorganics 12 00016 g002
Figure 2. Optimized geometry of the intramolecular tube-like structure based on the intermolecular [NHX-(CH2)3-NX-(CH2)3-NHX]4 self-assembled structure. Dashed lines represent N-X···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), red (Br), and green (Si). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Figure 2. Optimized geometry of the intramolecular tube-like structure based on the intermolecular [NHX-(CH2)3-NX-(CH2)3-NHX]4 self-assembled structure. Dashed lines represent N-X···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), red (Br), and green (Si). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Inorganics 12 00016 g002
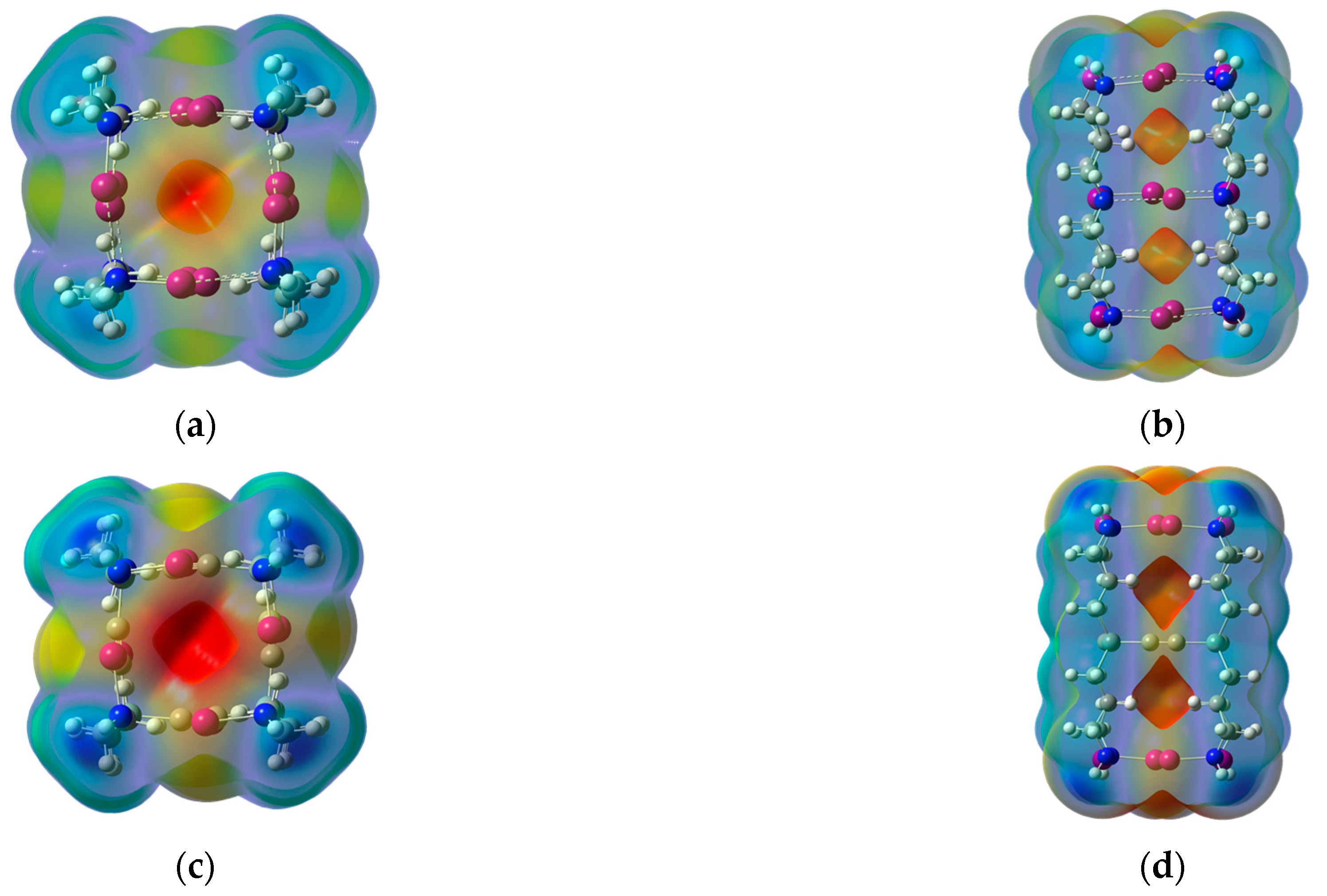
Inorganics 12 00016 g003
Figure 3. Top views and side views of the ωB97XD/DGDZVP molecular electrostatic potential at the 0.001 au molecular surface of the intermolecular tube-like structures shown in the upper panel, (a,b). The corresponding intramolecular structures are shown in the lower panel, (c,d). Red areas represent the most negative potential and blue areas the most positive ones. The results shown are for X = I. Similar results are obtained for X = Cl or Br.
Figure 3. Top views and side views of the ωB97XD/DGDZVP molecular electrostatic potential at the 0.001 au molecular surface of the intermolecular tube-like structures shown in the upper panel, (a,b). The corresponding intramolecular structures are shown in the lower panel, (c,d). Red areas represent the most negative potential and blue areas the most positive ones. The results shown are for X = I. Similar results are obtained for X = Cl or Br.
Inorganics 12 00016 g003
Inorganics 12 00016 g004
Figure 4. Optimized geometries of the terminal (a) and central (b) Li+ complexes with the tetrameric tube-like host structure. Dashed lines represent N-X···N halogen bonds and Li+···X binding interactions. The color representation is as follows: white (H), gray (C), blue (N), red (Br), and green (Si). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Figure 4. Optimized geometries of the terminal (a) and central (b) Li+ complexes with the tetrameric tube-like host structure. Dashed lines represent N-X···N halogen bonds and Li+···X binding interactions. The color representation is as follows: white (H), gray (C), blue (N), red (Br), and green (Si). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Inorganics 12 00016 g004
Inorganics 12 00016 g005
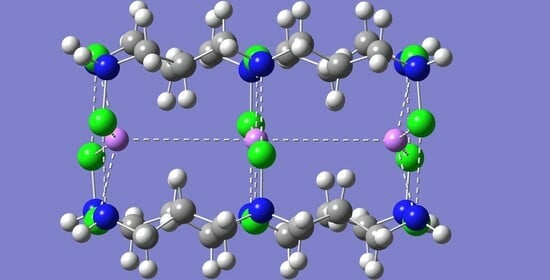
Figure 5. Optimized geometries of the terminal (a) and central (b) Li+ complexes with the intramolecular tube-like host structure. Dashed lines represent N-X···N halogen bonds and Li+···X binding interactions. The color representation is as follows: white (H), gray (C), blue (N), red (Br), pink (Li+), and green (Si). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Figure 5. Optimized geometries of the terminal (a) and central (b) Li+ complexes with the intramolecular tube-like host structure. Dashed lines represent N-X···N halogen bonds and Li+···X binding interactions. The color representation is as follows: white (H), gray (C), blue (N), red (Br), pink (Li+), and green (Si). Shown are the results for X = Br. The optimized geometries for X = Cl or I essentially look the same.
Inorganics 12 00016 g005
Inorganics 12 00016 g006
Figure 6. Optimized geometries of the transition-state structures connecting the two Li+ complexes (terminal and central) with the tetrameric host (a) and intramolecular host (b). Dashed lines represent N-X···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), red (Br), pink (Li+), and green (Si). Shown are the results for X = Br. The related optimized geometries for X = Cl or I essentially look the same.
Figure 6. Optimized geometries of the transition-state structures connecting the two Li+ complexes (terminal and central) with the tetrameric host (a) and intramolecular host (b). Dashed lines represent N-X···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), red (Br), pink (Li+), and green (Si). Shown are the results for X = Br. The related optimized geometries for X = Cl or I essentially look the same.
Inorganics 12 00016 g006
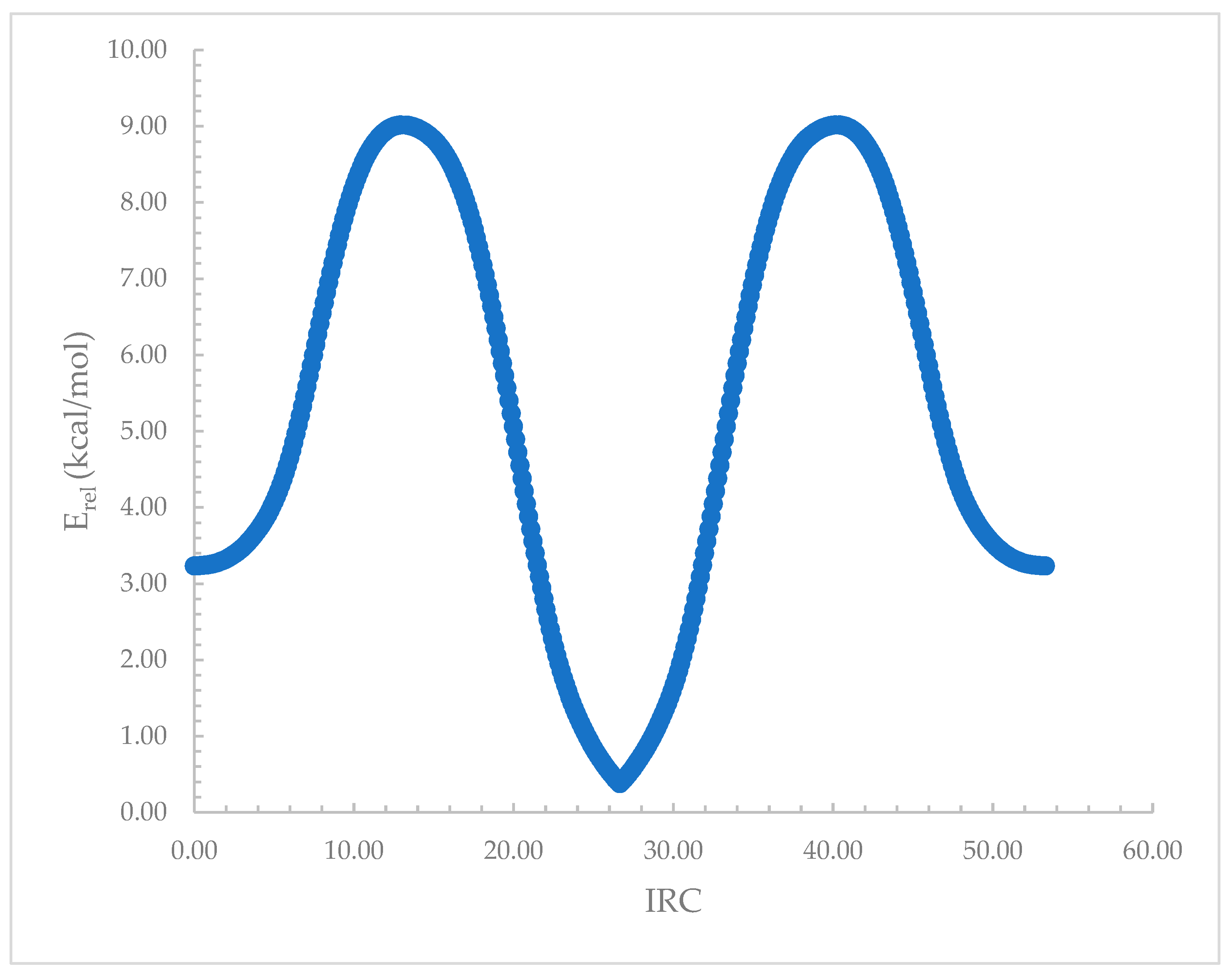
Inorganics 12 00016 g007
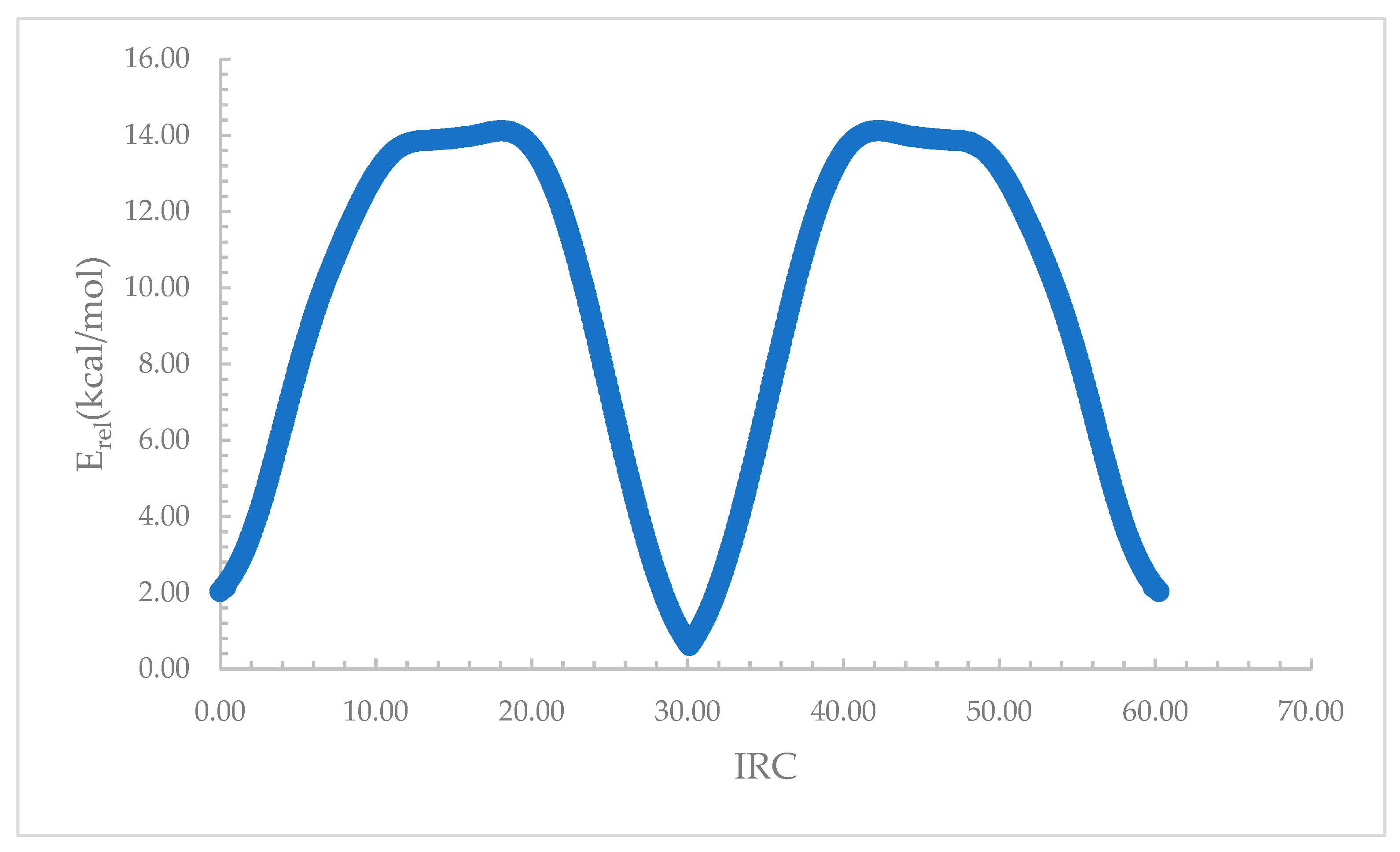
Figure 7. Relative electronic energy, Erel, along the intrinsic reaction coordinate (IRC), connecting the terminal and central complexes for the Li+ complexes with the [NHX-(CH2)3-NX-(CH2)3-NHX]4 hosts. Shown are the results for when X = Br.
Figure 7. Relative electronic energy, Erel, along the intrinsic reaction coordinate (IRC), connecting the terminal and central complexes for the Li+ complexes with the [NHX-(CH2)3-NX-(CH2)3-NHX]4 hosts. Shown are the results for when X = Br.
Inorganics 12 00016 g007
Inorganics 12 00016 g008
Figure 8. Relative electronic energy, Erel, along the intrinsic reaction coordinate (IRC), connecting the terminal and central complexes for the Li+ complexes with the intramolecular host for when X = Cl.
Figure 8. Relative electronic energy, Erel, along the intrinsic reaction coordinate (IRC), connecting the terminal and central complexes for the Li+ complexes with the intramolecular host for when X = Cl.
Inorganics 12 00016 g008
Table 1. BSSE-corrected interaction energies, ∆E, and corresponding average values, averaged over 12 such interactions present, <∆E>, for the formation of the tetrameric halogen-bonded structures. Energy values in kcal/mol.
Table 1. BSSE-corrected interaction energies, ∆E, and corresponding average values, averaged over 12 such interactions present, <∆E>, for the formation of the tetrameric halogen-bonded structures. Energy values in kcal/mol.
X∆E<∆E>
Cl−24.87−2.07
Br−50.13−4.18
I−74.10−6.18
Table 2. Halogen-bond distances (Å) and angles (degrees) for the optimized intermolecular halogen-bonded tetramers. Also listed are the distance between opposing or adjacent halogen atoms, X = Cl, Br, or I, in the corresponding terminal or central halogen-bonded network. Values for the terminal halogen bonds in the tubular structure are listed first, followed by those of the central halogen bonds.
Table 2. Halogen-bond distances (Å) and angles (degrees) for the optimized intermolecular halogen-bonded tetramers. Also listed are the distance between opposing or adjacent halogen atoms, X = Cl, Br, or I, in the corresponding terminal or central halogen-bonded network. Values for the terminal halogen bonds in the tubular structure are listed first, followed by those of the central halogen bonds.
Distances
ClBrI
X···N3.0583.0363.085
X···X a5.3295.4405.710
X···X b3.7683.8474.038
X···N2.9432.9343.023
X···X a5.2685.3595.663
X···X b3.7253.7904.005
Angles
ClBrI
N-X···N168.0167.9168.5
N-X···N168.2169.4171.7
a Opposite and b adjacent interhalogen distances in the terminal or central halogen-bonded networks.
Table 3. Second-order delocalization energies, <E2> (kcal/mol), and electron density at halogen bond critical point, ρc (a.u.), in the intermolecular halogen-bonded tetramers. Values for the terminal halogen bonds in the tubular structure are listed first, followed by those of the central halogen bonds.
Table 3. Second-order delocalization energies, <E2> (kcal/mol), and electron density at halogen bond critical point, ρc (a.u.), in the intermolecular halogen-bonded tetramers. Values for the terminal halogen bonds in the tubular structure are listed first, followed by those of the central halogen bonds.
ρc
ClBrI
X···N0.01190.01440.0171
X···N0.01520.01790.0195
<E2>
ClBrI
N-X···N2.514.697.48
N-X···N3.255.978.57
Table 4. Halogen-bond distances (Å) and angles (degrees) for the optimized halogen bonds in the intramolecular halogen-bonded network model system. Also listed are the distance between opposing and adjacent halogen atoms, X = Cl, Br, or I, in the corresponding halogen-bonded network.
Table 4. Halogen-bond distances (Å) and angles (degrees) for the optimized halogen bonds in the intramolecular halogen-bonded network model system. Also listed are the distance between opposing and adjacent halogen atoms, X = Cl, Br, or I, in the corresponding halogen-bonded network.
Distances
ClBrI
X···N3.0382.9672.974
X···X a5.3005.3625.604
X···X b3.7483.7923.963
Angles
ClBrI
N-X···N169.4168.9166.9
a Opposite and b adjacent interhalogen distances in the halogen-bonded networks.
Table 5. Second-order delocalization energies, <E2> (kcal/mol), and electron density at halogen bond critical point, ρc (a.u.), in the intramolecular tubular halogen-bonded networks.
Table 5. Second-order delocalization energies, <E2> (kcal/mol), and electron density at halogen bond critical point, ρc (a.u.), in the intramolecular tubular halogen-bonded networks.
ClBrI
ρc0.01230.01640.0209
<E2>2.715.8210.23
Table 6. BSSE-corrected complexation energies, ∆E, for both the terminal and central Li+ complexes with the X-bonded intermolecular networks. Energy values in kcal/mol.
Table 6. BSSE-corrected complexation energies, ∆E, for both the terminal and central Li+ complexes with the X-bonded intermolecular networks. Energy values in kcal/mol.
XTerminal ComplexCentral Complex
Cl−80.61−84.41
Br−78.61−81.62
I−75.84−77.86
Table 7. Relevant distances (Å) and angles (degrees) for the optimized Li+ terminal complex with the intermolecular halogen-bonded tetramers. Values for the terminal end of the tubular structure that binds Li+ are listed first, followed by those of the central halogen bonds and then by those at the other end of the tube.
Table 7. Relevant distances (Å) and angles (degrees) for the optimized Li+ terminal complex with the intermolecular halogen-bonded tetramers. Values for the terminal end of the tubular structure that binds Li+ are listed first, followed by those of the central halogen bonds and then by those at the other end of the tube.
Distances
ClBrI
X···N2.9282.9593.020
X···N2.9592.9543.048
X···N3.0463.0193.076
X···Li+2.6302.7723.005
Angles
ClBrI
N-X···N168.2167.4167.1
N-X···N168.6169.8169.8
N-X···N168.2168.1167.6
X···Li+···X161.0153.2141.6
Table 8. Relevant distances (Å) and angles (degrees) for the optimized Li+ central complex with the intermolecular halogen-bonded tetramers. Values for the terminal end of the tubular structure are listed first, followed by those of the central part that binds Li+ and then by those at the other end of the tube.
Table 8. Relevant distances (Å) and angles (degrees) for the optimized Li+ central complex with the intermolecular halogen-bonded tetramers. Values for the terminal end of the tubular structure are listed first, followed by those of the central part that binds Li+ and then by those at the other end of the tube.
Distances
ClBrI
X···N3.0273.0103.064
X···N2.9022.9523.057
X···N3.0273.0103.072
X···Li+2.6042.7222.935
Angles
ClBrI
N-X···N168.1168.3167.9
N-X···N169.0167.9167.8
N-X···N168.1168.3167.7
X···Li+···X180.0180.0158.7
Table 9. Second-order delocalization energies, <E2> (kcal/mol), and electron density at halogen bond critical point, ρc (a.u.), in the Li+ central and terminal complexes. Also listed are the corresponding values for the N-X···Li+ interactions. Values for the terminal halogen bonds are listed first, followed by those of the central halogen bonds and then by those at the other end of the tube.
Table 9. Second-order delocalization energies, <E2> (kcal/mol), and electron density at halogen bond critical point, ρc (a.u.), in the Li+ central and terminal complexes. Also listed are the corresponding values for the N-X···Li+ interactions. Values for the terminal halogen bonds are listed first, followed by those of the central halogen bonds and then by those at the other end of the tube.
Terminal ComplexCentral Complex
ρcρc
ClBrIClBrI
N-X···N0.01560.01700.01940.01260.01510.0177
N-X···N0.01480.01720.01870.01680.01770.0186
N-X···N0.01210.01490.01730.01260.01510.0174
N-X···Li+0.00860.00840.00780.00910.00920.0088
Terminal ComplexCentral Complex
<E2><E2>
ClBrIClBrI
N-X···N3.895.989.052.775.108.03
N-X···N3.145.708.093.915.697.65
N-X···N2.614.957.712.775.107.82
N-X···Li+11.1717.0929.5010.2514.9228.25
Table 10. BSSE-corrected complexation energies, ∆E, for both the terminal and the central Li+ complexes with the X-bonded intramolecular networks. Energy values in kcal/mol.
Table 10. BSSE-corrected complexation energies, ∆E, for both the terminal and the central Li+ complexes with the X-bonded intramolecular networks. Energy values in kcal/mol.
XTerminal ComplexCentral Complex
Cl−81.20−86.14
Br−78.74−85.33
I−75.02−83.90
Table 11. Relevant distances (Å) and angles (degrees) for the optimized Li+ terminal complex with the intramolecular halogen-bonded host systems. Values for the terminal halogen-bonded network of the tubular structure that binds Li+ are listed first, followed by those of the halogen-bonded network at the other end of the tube and then the values pertaining to the Li+ binding interaction.
Table 11. Relevant distances (Å) and angles (degrees) for the optimized Li+ terminal complex with the intramolecular halogen-bonded host systems. Values for the terminal halogen-bonded network of the tubular structure that binds Li+ are listed first, followed by those of the halogen-bonded network at the other end of the tube and then the values pertaining to the Li+ binding interaction.
Distances
ClBrI
X···N2.9112.9242.958
X···N3.0212.9522.964
X···Li+2.6172.7332.930
Angles
ClBrI
N-X···N169.0167.3165.4
N-X···N169.6168.9166.8
X···Li+···X163.4159.3149.4
Table 12. Relevant distances (Å) and angles (degrees) for the optimized Li+ central complex with the intramolecular halogen-bonded host systems. Values for the terminal halogen-bonded networks are listed first, followed by those with respect to the midpoint of each C≡C bond in the silicon-linked alkyne network that binds the metal ion.
Table 12. Relevant distances (Å) and angles (degrees) for the optimized Li+ central complex with the intramolecular halogen-bonded host systems. Values for the terminal halogen-bonded networks are listed first, followed by those with respect to the midpoint of each C≡C bond in the silicon-linked alkyne network that binds the metal ion.
Distances
ClBrI
X···N2.9952.9342.956
(C≡C)···Li+2.5992.5992.601
Angles
ClBrI
N-X···N169.7169.1167.0
(C≡C)···Li+···(C≡C)180.0180.0180.0
Table 13. Second-order delocalization energies, <E2> (kcal/mol), and electron density at key bond critical points, ρc (a.u.), in the Li+ central and terminal complexes with the intramolecular host system. Values for the terminal halogen bonds binding Li+ are listed first.
Table 13. Second-order delocalization energies, <E2> (kcal/mol), and electron density at key bond critical points, ρc (a.u.), in the Li+ central and terminal complexes with the intramolecular host system. Values for the terminal halogen bonds binding Li+ are listed first.
Terminal Complex
ρc<E2>
ClBrIClBrI
N-X···N0.01610.01820.02184.146.6510.62
N-X···N0.01270.01690.02132.866.0910.54
N-X···Li+0.00880.00910.009111.9618.8231.61
Central Complex
ρc<E2>
ClBrIClBrI
N-X···N0.01340.01750.02153.116.4410.81
(C≡C)···Li+0.00700.00700.00700.670.670.67
Table 14. Electronic (Erel) and Gibbs (Grel) free energies of the terminal complex relative to the central complex of the Li+ complexes with the inter- and intramolecular hosts. Energy barriers to the transition from the terminal to central complex are indicated with a dagger symbol as superscript, Eǂ and Gǂ, respectively. All relative energies are in kcal/mol.
Table 14. Electronic (Erel) and Gibbs (Grel) free energies of the terminal complex relative to the central complex of the Li+ complexes with the inter- and intramolecular hosts. Energy barriers to the transition from the terminal to central complex are indicated with a dagger symbol as superscript, Eǂ and Gǂ, respectively. All relative energies are in kcal/mol.
Intermolecular
ErelGrelEǂGǂ
Cl3.814.0212.8411.70
Br3.252.289.028.16
I2.403.195.292.80
Intramolecular
ErelGrelEǂGǂ
Cl1.403.4814.1413.94
Br3.402.6613.7212.62
I5.645.7213.5112.51
Table 15. NBO charges (in a.u.) for lithium ion, qLi+, and the closest hydrogen atoms, qH, in the central, terminal, and transition state (TS) complexes of Li+ with the inter- and intra-molecular tube-like X-bonded hosts, X = Cl, Br, or I. Also listed are the distances (in Ǻ) between Li+ and the corresponding hydrogen atoms, Li+···H.
Table 15. NBO charges (in a.u.) for lithium ion, qLi+, and the closest hydrogen atoms, qH, in the central, terminal, and transition state (TS) complexes of Li+ with the inter- and intra-molecular tube-like X-bonded hosts, X = Cl, Br, or I. Also listed are the distances (in Ǻ) between Li+ and the corresponding hydrogen atoms, Li+···H.
IntermolecularIntramolecular
ClCl
CentralTSTerminalCentralTSTerminal
qLi+0.890.870.910.930.910.91
qH0.210.200.210.210.190.21
Li+···H3.552.383.473.912.423.63
BrBr
CentralTSTerminalCentralTSTerminal
qLi+0.880.850.880.930.900.88
qH0.210.210.210.210.200.21
Li+···H3.652.473.463.942.483.62
II
CentralTSTerminalCentralTSTerminal
qLi+0.820.770.810.930.860.82
qH0.210.200.210.210.190.21
Li+···H3.502.863.514.042.503.57
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Parra, R.D. A Model Halogen-Bonded Network as a Potential Tube-like Host for Li+: A DFT Study. Inorganics 2024, 12, 16. https://doi.org/10.3390/inorganics12010016

AMA Style

Parra RD. A Model Halogen-Bonded Network as a Potential Tube-like Host for Li+: A DFT Study. Inorganics. 2024; 12(1):16. https://doi.org/10.3390/inorganics12010016

Chicago/Turabian Style

Parra, Rubén D. 2024. "A Model Halogen-Bonded Network as a Potential Tube-like Host for Li+: A DFT Study" Inorganics 12, no. 1: 16. https://doi.org/10.3390/inorganics12010016

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop