Next Article in Journal
New Advances into Nanostructured Oxides
Previous Article in Journal
Destabilization of the LiBH4–NaBH4 Eutectic Mixture through Pore Confinement for Hydrogen Storage
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 11
Issue 3
10.3390/inorganics11030129
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

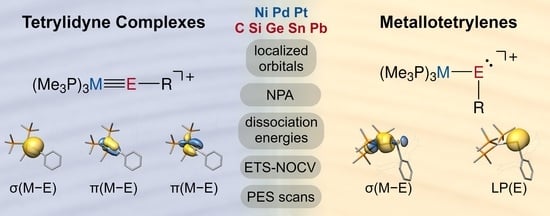
The Electronic Nature of Cationic Group 10 Ylidyne Complexes

by
Leonard R. Maurer
†,
Jens Rump
† and
Alexander C. Filippou
*
Institute of Inorganic Chemistry, University of Bonn, D-53121 Bonn, Germany
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Inorganics 2023, 11(3), 129; https://doi.org/10.3390/inorganics11030129
Submission received: 16 February 2023 / Revised: 13 March 2023 / Accepted: 15 March 2023 / Published: 18 March 2023
(This article belongs to the Special Issue Density Functional Theory (DFT) and Semi-empirical Quantum Mechanical (SQM) Methods in Organometallic Chemistry)
Browse Figures
Versions Notes

Abstract

:
We report a broad theoretical study on [(PMe3)3MER]+ complexes, with M = Ni, Pd, Pt, E = C, Si, Ge, Sn, Pb, and R = ArMes, Tbb, (ArMes = 2,6-dimesitylphenyl; Tbb = C6H2-2,6-[CH(SiMe3)2]2-4-tBu). A few years ago, our group succeeded in obtaining heavier homologues of cationic group 10 carbyne complexes via halide abstraction of the tetrylidene complexes [(PMe3)3M=E(X)R] (X = Cl, Br) using a halide scavenger. The electronic structure and the M-E bonds of the [(PMe3)3MER]+ complexes were analyzed utilizing quantum-chemical tools, such as the Pipek–Mezey orbital localization method, the energy decomposition analysis (EDA), and the extended-transition state method with natural orbitals of chemical valence (ETS-NOCV). The carbyne, silylidyne complexes, and the germylidyne complex [(PMe3)3NiGeArMes]+ are suggested to be tetrylidyne complexes featuring donor–acceptor metal tetrel triple bonds, which are composed of two strong π(M→E) and one weaker σ(E→M) interaction. In comparison, the complexes with M = Pd, Pt; E = Sn, Pb; and R = ArMes are best described as metallotetrylenes and exhibit considerable M−E−C bending, a strong σ(M→E) bond, weakened M−E π-components, and lone pair density at the tetrel atoms. Furthermore, bond cleavage energy (BCE) and bond dissociation energy (BDE) reveal preferred splitting into [M(PMe3)3]+ and [ER] fragments for most complex cations in the range of 293.3–618.3 kJ·mol−1 and 230.4–461.6 kJ·mol−1, respectively. Finally, an extensive study of the potential energy hypersurface varying the M−E−C angle indicates the presence of isomers with M−E−C bond angles of around 95°. Interestingly, these isomers are energetically favored for M = Pd, Pt; E = Sn, Pb; and R = ArMes over the less-bent structures by 13–29 kJ·mol−1.

Graphical Abstract

1. Introduction

Complexes of the general formula LnM≡E−R (M = d-block element, E = Si–Pb, R = singly bonded substituent, and Ln = ligand sphere), featuring a triple bond between a transition metal and the tetrels Si–Pb, are an intriguing class of compounds [1,2]. As heavier homologues of the Fischer-type carbyne complexes [3,4,5,6,7], these compounds, which are called tetrylidyne complexes, have a synthetic potential in organoelement and organometallic chemistry. Following the first reports of germylidyne complexes by P. P. Power et al. [8,9], numerous group 6 germylidyne complexes [10,11,12,13,14] as well as first representatives featuring metal–tin triple bonds [15,16] and metal–lead triple bonds [17,18,19] were obtained by our group using an efficient N2 or PMe3 elimination reaction of d6 metal complexes with organotetrel(II)halides. Later on, the first group 6 silylidyne complexes were prepared from tailor-made 18 VE carbonyl metalates with NHC-stabilized silicon(II)halides [20,21], 1,2-dihalodisilenes [22,23], and base-supported silyliumylidene ions [24], or from the reactions of chloro/hydrosilylidene complexes with Lewis acids [25,26,27,28]. The isolation of these compounds is demanding and requires a fine stereoelectronic tuning of the metal fragment (MLn) as well as a steric protection of the electrophilic tetrel center by a bulky substituent R, circumventing head-to-tail dimerization [29] or intra- and intermolecular σ-bond activation by the M≡E−R functionality.
Previous quantum chemical analyses suggest that tetrylidyne complexes of the heavier group 14 elements have a similar electronic structure to that of Fischer-type carbyne complexes [6,10,16,17,18,30,31,32,33,34]. The M≡E bonds are quite polar and composed of a σ bond, which is slightly less polarized toward the tetrel atom E than in Fischer-type carbyne complexes, and two π bonds, which are considerably more polarized to the metal center M than in their carbon analogues. This leads to partially positively charged ER ligands in the heavier tetrylidyne complexes, whereas the CR ligands in the related Fischer-type carbyne complexes bear a negative partial charge. The M≡E−R bonding can be well described using the Dewar–Chatt–Duncanson model [35,36], comprising an ER+→MLn− σ donation and two MLn−→ER+ π back donations (Figure 1a). Alternatively, the M≡E−R bonding in tetrylidyne complexes can be described by the interaction of the neutral, open-shell fragments (MLn) and ER in their doublet electronic state (Figure 1b). In comparison, the related Schrock-type alkylidyne complexes [37,38] feature M≡C bonds with two rather nonpolar π components. The M≡C bonding in these compounds can be best described by electron pairing between the neutral open-shell fragments MLn and ER in their quartet electronic state (Figure 1c) [30].
While earlier experimental work focused on group 6 metal tetrylidyne complexes [8,9,10,11,12,13,14,15,16,17,18,19,20,39,40,41,42], more recent studies have shown that group 4 (Ti) [43], group 5 (Nb, Ta) [22,44], group 7 (Mn, Re) [45,46,47], group 8 (Fe, Os) [26,48], and group 9 metals (Co, Rh) [49,50] can also be incorporated into triple bonding with the heavier tetrels Si–Pb, significantly expanding this promising field of chemistry (Scheme 1).
In this context, access to compounds where even the carbon analogues are very rare is particularly appealing. Illustrative examples are the tetrylidyne complexes of the group 10 metals. In fact, after the first report of a cationic nickel aminocarbyne complex, [(CO)2(PPh3)Ni≡CNiPr2][BCl4], by E. O. Fischer et al. ca. 40 years ago [51], no other group 10 carbyne complexes have been isolated to date. Some years ago, a two-step approach to the first group 10 tetrylidyne complexes was developed by our group (Scheme 2) [52]. The first step involves a thermal ligand substitution reaction of [M(PMe3)3L] (M = Ni, Pt; L = PMe3, GaCp*, Cp* = C5(CH3)5) with organotetrel(II)halides leading to the ylidene complexes [(PMe3)3M=E(X)R], which, in the second step, are transformed into the targeted tetrylidyne complexes after halide abstraction with Na[B(ArF)4] (Scheme 2). Thereby, the nickel silylidyne, germylidyne, and stannylidyne complex cations [(PMe3)3Ni≡ER]+ (E = Si, R = Tbb (NiSiTbbexp); E = Ge, R = ArMes (NiGeArMesexp); E = Sn, R = ArMes (NiSnArMesexp)) and the platinum silylidyne and germylidyne complex cations [(PMe3)3Pt≡ER]+ (E = Si, R = Tbb (PtSiTbbexp); E = Ge, R = ArMes (PtGeArMesexp)) were isolated as red-brown (NiSiTbbexp), violet-brown (NiGeArMesexp and NiSnArMesexp), and orange (PtSiTbbexp) borate salts and fully characterized (Scheme 2). More recently, the analogous triphenylphosphane nickel complex salts [(PPh3)3Ni≡EN(SiiPr3)(Dipp)][B(ArF)4] were also prepared by T. J. Hadlington et al. using the same approach [53].
We present here an extensive theoretical study of the whole series of the tetrylidyne complex cations [(PMe3)3MER]+ (MER: M = Ni, Pd, Pt; E = C, Si, Ge, Sn, Pb; R = ArMes, Tbb (Si)), employing a comprehensive quantum chemical toolset that includes the Pipek–Mezey orbital localization and the extended-transition state method with natural orbitals of chemical valence (ETS-NOCV), among others. This study shows that most complexes have considerable M-E triple bond characteristics and a similar electronic structure to that of Fischer-type carbyne complexes (Figure 1a,b). Remarkably, with increasing atomic number of M and E an increasing bending of the M−E−R unit, an elongation of the M−E bond and a continuous change in the electronic structure from a metal tetrylidyne complex to a metallotetrylene are predicted in theory. This leads in the case of combinations of Pd/Pt−Sn/Pb to complexes featuring increased electron lone pair density at the tetrel atom and a σ(M→E) bond, which therefore can be also viewed as base-stabilized tetryliumylidene cations, in which the 16 VE ML3 fragments act as a Lewis base. Moreover, the potential energy hypersurface of all complexes E = Si, Ge, Sn, Pb except NiSiR suggests the presence of isomers, which feature narrow M−E−C bond angles of around 95° and distorted square-planar coordinated metal centers.

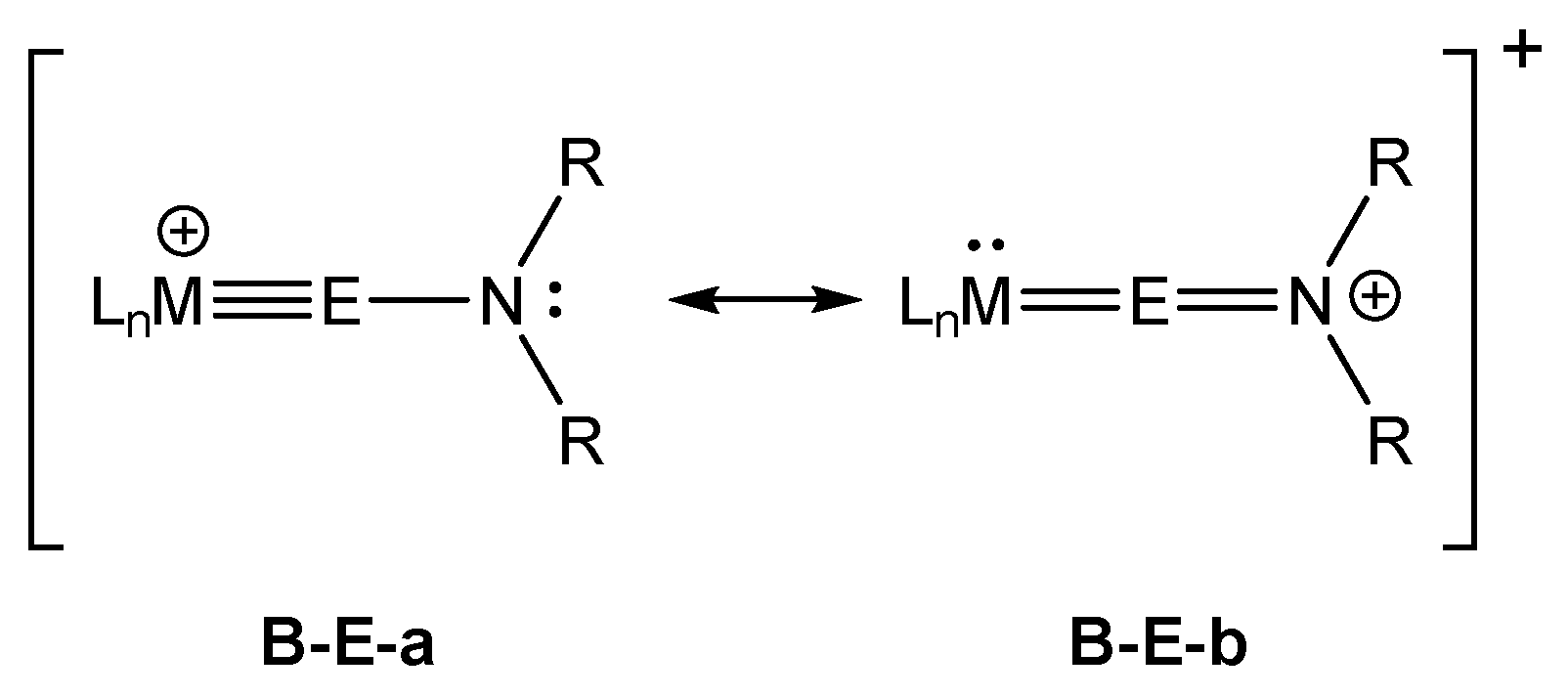
2. Results and Discussion

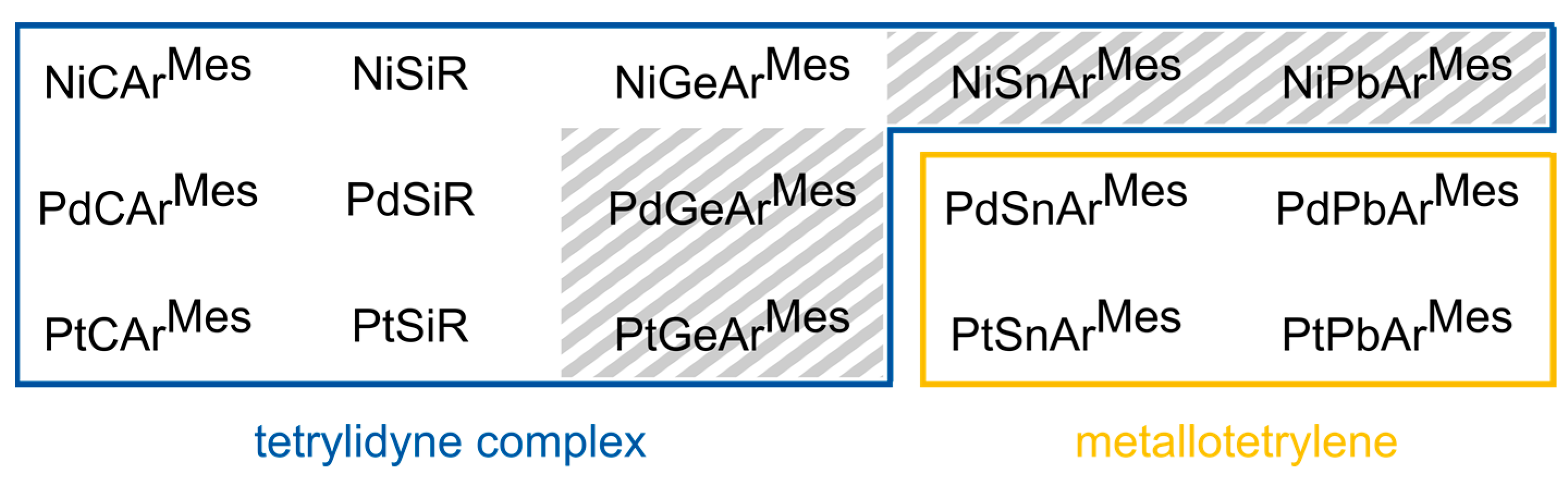
2.1. Structural Results

We decided to use the five experimentally available tetrylidyne complex cations NiSiTbbexp, NiGeArMesexp, NiSnArMesexp, PtSiTbbexp, and PtGeArMesexp from our group as anchor points of this study and completed the homologous series [(PMe3)3MER]+ (M = Ni, Pd, Pt; E = C, Si, Ge, Sn, Pb) by including the 10 hitherto experimentally missing complex cations, resulting in overall 15 metal–tetrel combinations. The substituent was chosen to be ArMes. In case of E = Si, the complex cations MSiTbb were also studied in order to compare them with the experimentally known systems [(PMe3)3Ni≡SiTbb]+ (NiSiTbbexp) and [(PMe3)3Pt≡SiTbb]+ (PtSiTbbexp). For comparison reasons, we also studied the amino derivatives [(PPh3)3Ni≡EN(SiiPr3)(Dipp)]+ (E = Ge (B-Ge), E = Sn (B-Sn)). The structures of all complexes were optimized at the B97-D3 (BJ)-ATM/def2-TZVP level of theory, abbreviated in the following as level I (see also the Materials and Methods section for the full computational details) and confirmed as minima by successive numerical or analytical frequency calculations. A collection of selected bonding parameters is given in Table 1, which indicates several trends, which are discussed in the following.
(a) The calculated M−E bond lengths are in all cases slightly longer than those obtained with single-crystal X-ray diffraction (sc-XRD) analyses. The difference Δ between the calculated and experimental values ranges from 1.4 to 7.0 pm and continuously increases with increasing atomic number of the tetrel (e.g., M = Ni: Δ = 1.4 pm (E = Si); Δ = 3.0 pm (E = Ge, using the mean value of the Ni−Ge bond lengths of the two complex cations found in the asymmetric unit of the crystal lattice); Δ = 7.0 pm (E = Sn)) and with increasing atomic number of the metal (e.g., E = Ge: Δ = 3.0 pm (M = Ni); Δ = 5.8 pm (M = Pt)).
The experimental M≡E bond lengths are the shortest reported to date. For example, the Ni≡Si bond of NiSiTbbexp (203.11(7) pm) is shorter than the Ni=Si bond of [(PMe3)3Ni=Si(Br)Tbb] (210.2(2) pm) and of [(η6-toluene)Ni=Si(C(SiMe3)2CH2)2] (209.4(1) pm), the latter one being the shortest Ni=Si bond reported to date [54,55]. Similarly, the Pt≡Si bond of PtSiTbbexp (213.43(7) pm) is shorter than the Pt=Si bond of [(PMe3)3Pt=Si(Br)Tbb] (219.96(9) pm) and other reported Pt=Si bonds [56]. Furthermore, the Ni≡Ge bond of NiGeArMesexp (210.30(6) pm) is shorter than that of B-Geexp (215.9(1) pm) and shorter than the Ni=Ge bond of [(PMe3)3Ni=Ge(Cl)ArMes] (216.10(4) pm), the latter bond being the shortest Ni=Ge bond reported to date [52]. Finally, the Ni≡Sn bond of NiSnArMesexp (228.08(9) pm) is shorter than that of B-Snexp (235.5(1) pm) and shorter than the Ni=Sn bond of [(PMe3)3Ni=Sn(Cl)ArMes] (234.48(9) pm), the latter bond being the shortest Ni=Sn bond reported to date [57]. All these bonding parameters provide structural evidence for the presence of M≡E triple bonds in these complexes.
At this point, we want to emphasize that the comparison between experimental solid-state structures obtained by single-crystal X-ray diffraction at 100–123 K versus theoretical single-molecule gas-phase calculations at 0 K is likely to exhibit certain deviations. However, we checked the reliability of our calculated structures at the level of theory I with those obtained at the TPSS [58] -D3(BJ)-ATM/def2-TZVP and PW6B95 [59] -D3(BJ)-ATM/def2-TZVP levels of theory and found no considerable differences (see Supplementary Materials). This is somewhat expected as the influence of the density functional approximation (DFA) on the structure is generally considered to be low in contrast to that of the employed basis set [60,61,62,63]. Furthermore, with the large differences found between the experimental and calculated M−E−C1 bond angles of NiSnArMes and PtGeArMes, we assessed the curvature of the potential energy hypersurface (PES) with PES scans, varying the M−E−C1 angle. Surprisingly, altering the angle by ±20° costs only 5.7 kJ·mol−1 (NiSnArMes) and 6.3 kJ·mol−1 (PtGeArMes), indicating a very flat PES (see Section 2.5) with high flexibility regarding the M−E−C1 bond angle.
We also examined the relativistic influence on our compounds by all-electron calculations, explicitly treating relativistic effects with the zero-order regular approximation (ZORA) method [64]. The structure optimization of PtPbArMes at the ZORA-I level of theory using the SARC-ZORA-TZVP basis set for platinum and lead resulted in a structure very similar to the one obtained at the level of theory I, which uses effective core potentials (ECPs) for the heavier atoms (see the SI). This is in line with previous reports that testify to an at least comparable performance of ECPs to explicit relativistic treatment with ZORA or Douglas–Kroll–Hess (DKH) techniques [65,66,67].
(b) The calculated E−C1 bond lengths of the silylidyne complexes MSiTbb compare very well to the experimental ones, but for E = Ge, Sn, the E−C1 bond lengths of the calculated structures are larger. Here, too, the deviation ranging from 2.3 to 5.4 pm continuously increases with increasing atomic number of the tetrel (e.g., M = Ni: Δ = 2.3 pm (E = Ge); Δ = 5.4 pm (E = Sn)) and the metal center (e.g., E = Ge: Δ = 2.3 pm (M = Ni); Δ = 3.9 pm (M = Pt)).
(c) Notably, the calculated M−E bond lengths for E = Si, Ge fit well to those obtained using Pyykkö’s covalent triple bond radii [68], for example, for NiSiArMes (204.2 pm found vs. 203 pm expected), PtSiArMes (215.7 pm found vs. 212 pm expected), or NiGeArMes (213.3 pm found vs. 215 pm expected). However, for E = Sn, Pb, the calculated M−E bond lengths are considerably larger than those suggested by Pyykkö, especially for the compounds PdSnArMes (251.6 pm found vs. 244 pm expected), PdPbArMes (263.1 pm found vs. 249 pm expected), PtSnArMes (255.1 pm found vs. 242 pm expected), and PtPbArMes (267.7 pm found vs. 247 pm expected), which rather appear in the region between metal–tetrel single- and double-bond lengths according to Pyykkö. Of course, conclusions from the latter comparison have to be cautiously made, as Pyykkö’s triple bond radii were obtained by adding up atomic radii that were derived from a limited benchmark set. It should be also considered that the calculated M−E bond lengths significantly depend on the M−E−C1 bond angle (vide infra). For example, a constrained structure optimization with the M−E−C1 bond angle of PdSnArMes, PdPbArMes, PtSnArMes, and PtPbArMes set to 180° yields structures with M−E bond lengths of 245.5 pm, 254.9 pm, 245.5 pm, and 257.1 pm, respectively. These bond lengths are much closer to those predicted using the triple bond radii of Pyykkö.
(d) The E−C1 bond lengths increase within group 14 as expected and stay roughly the same for E = Si when the metal atom is exchanged between Ni, Pd, and Pt. This is not the case for the compounds with E = Ge, Sn, Pb and M = Pd, Pt, for which slightly longer tetrel–carbon bonds are obtained (ca. 3–4 pm longer). This lengthening can be explained in terms of Bent’s rule [69] with the decreased s character of the hybrid orbital of E used for the E−C1 bond reflecting the reluctance for hybridization of the heavier main group elements [70,71,72].
(e) The M−E−C1 bond angles show a high degree of variability with values ranging from 168.4° (NiCArMes, PdCArMes) down to 127.3° (PtPbArMes). The calculated M−E−C1 values of the silylidyne complexes (R = Tbb) only slightly vary with the metal (NiSiTbb: 167.2°, PdSiTbb: 163.1°, and PtSiTbb: 168.1°), being ca. 6° smaller than the experimental values (NiSiTbbexp: 172.40(8)°, PtSiTbbexp: 173.83(9)°) and fall in the range of typical experimental M−E−C angles of heavier tetrylidyne complexes (156–179° [1,73]). This is also the case for NiGeArMes (165.3°), but for M = Pd, Pt and E = Ge, Sn, Pb, the calculated M−E−C1 bond angles (e.g., NiSnArMes: 150.9°, NiPbArMes: 142.7°, PtGeArMes: 149.7°, PtSnArMes: 132.1°, and PtPbArMes: 127.3°) are considerably smaller as graphically shown in Figure 2. The M−E−C1 angles generally decrease in the order C > Si > Ge > Sn > Pb, the decrease being more pronounced for palladium and platinum than for nickel. The only exception to this trend is NiSiArMes with a Ni−Si−C1 angle of 163.8°, which is smaller than the Ni−Ge−C1 angle of NiGeArMes (165.3°).
Based on these trends derived from the structures in combination with the analysis of the molecular orbitals (vide infra), the calculations suggest two different complex classes, namely tetrylidyne complexes with an approximately linear M−E−C1 linkage and a M≡E triple bond and compounds with a considerably bent M−E−C1 moiety and an increased lone pair density at the tetrel center, which are reminiscent of metallotetrylenes. This classification is given in Scheme 3, with all carbon and silicon systems as well as NiGeArMes belonging to the first class, whereas the systems PdSnArMes, PdPbArMes, PtSnArMes, and PtPbArMes belong to the second class of compounds. While NiSnArMes, NiPbArMes, PdGeArMes, and PtGeArMes also feature considerably bent M−E−C1 units, these complexes exhibit electronic structures close to those of the tetrylidyne complexes and therefore lie in between the two complex classes.
As mentioned in the Introduction, we also investigated the geometric and electronic structure of the cationic complexes [L3Ni≡EN(SiiPr3)(Dipp)]+ of T. J. Hadlingtonet al. We performed gas-phase structure optimizations starting from the solid-state structures of B-Geexp and B-Snexp available from ref. [53] at the level of theory I to be consistent with our other results. The structural parameters for both B-Eexp and B-E are listed in Table 1, and a comparison with the calculated structures of ref. [53] can be found in the Supplementary Materials.
The calculated Ni−E and E−N bond lengths of the gas-phase structures are again 1.1–4.1 pm longer than those of the solid-state structures, and the calculated Ni−E−N angles 2.5° (B-Ge) and 5.9° (B-Sn) are smaller than the experimental ones. Compared with our systems, B-Ge and B-Sn feature longer Ni−E bond lengths (218.3 pm in B-Ge vs. 213.3 pm in NiGeArMes; 239.6 pm in B-Sn vs. 235.1 pm in NiSnArMes). The same holds for the solid-state structures. Another salient difference is the larger Ni−E−N angles of the complexes of T. J. Hadlington et al., with values of 173.4° and 167.8° for B-Ge and B-Sn, respectively, compared with the Ni−E−C1 bond angles of NiGeArMes (165.3°) and NiSnArMes (150.9°). A possible explanation is the increased repulsion between the sterically more demanding Ni(PPh3)3 fragment and the tetrylidyne ligand in B-Ge and B-Sn, which is reduced by an elongation of the Ni−E bond and a widening of the Ni−E−N bond angle.
Alternatively, an electronic effect might be present originating from a (N→E) π donation, which in terms of the Lewis formalism is represented by the allenic form B-E-b (Scheme 4). To clarify which is the dominant effect causing the Ni≡E bond elongation and the widening of the Ni−E−N bond angle in B-Ge and B-Sn, the corresponding PMe3-containing complex cation [(PMe3)3Ni≡GeN(SiiPr3)(Dipp)]+ (B-Ge-PMe3) was structurally optimized at the theoretical level I. The obtained Ni−Ge bond length of 214.2 pm is close to that found for NiGeArMes (213.3 pm), and the Ni−Ge−N angle of B-Ge-PMe3 (163.7°) compares well with the Ni−Ge−C1 bond angle of NiGeArMes (165.3°), suggesting that the longer bond length and larger Ni−Ge−N bond angle in B-Ge result from the increased steric repulsion between the sterically demanding PPh3 ligands and the tetrel-bonded amino substituent. A closer look at the MOs of B-Ge and B-Sn suggests a certain extent of (N→E) π donation, but this is apparently much smaller than in Fischer-type aminocarbyne [6,7,74,75,76,77,78] complexes and does not influence the M≡E bond lengths.

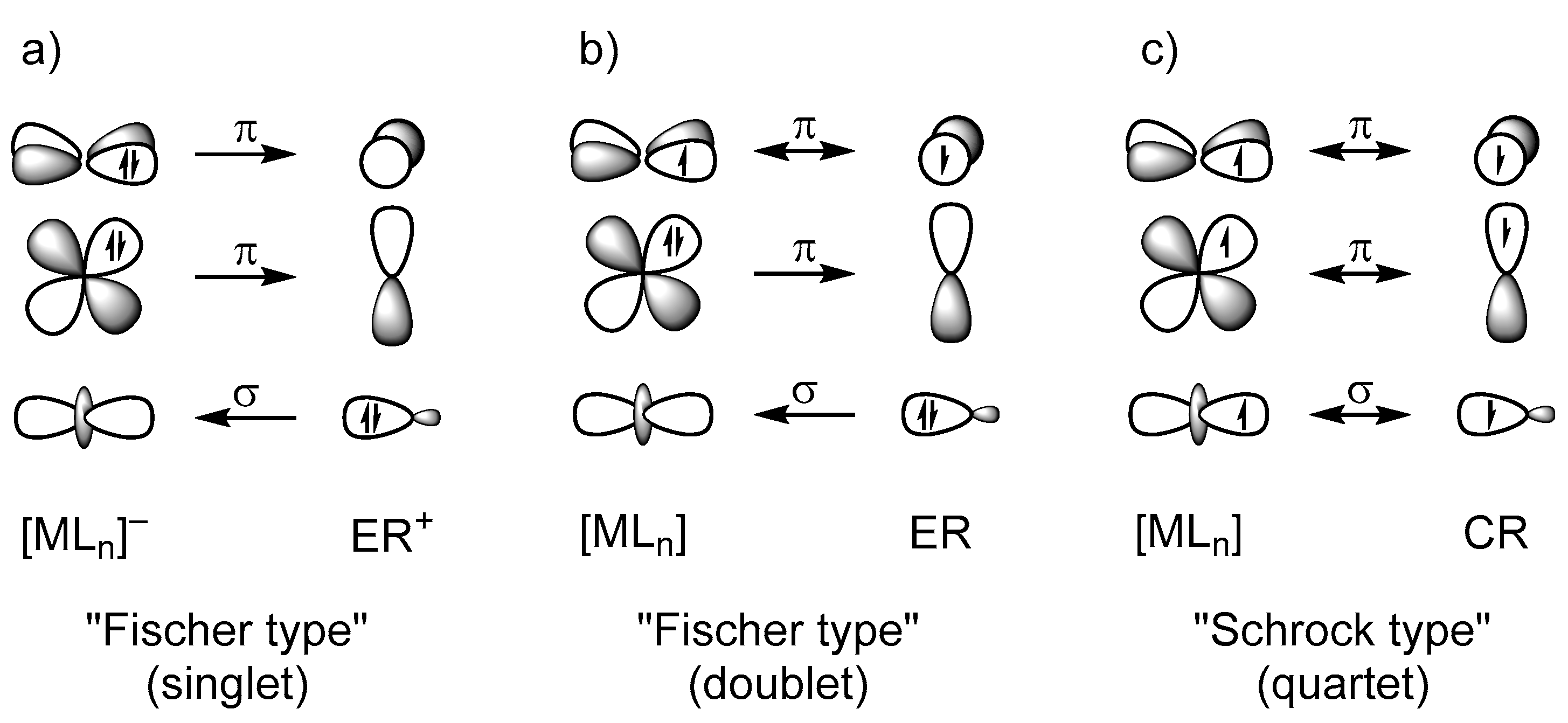
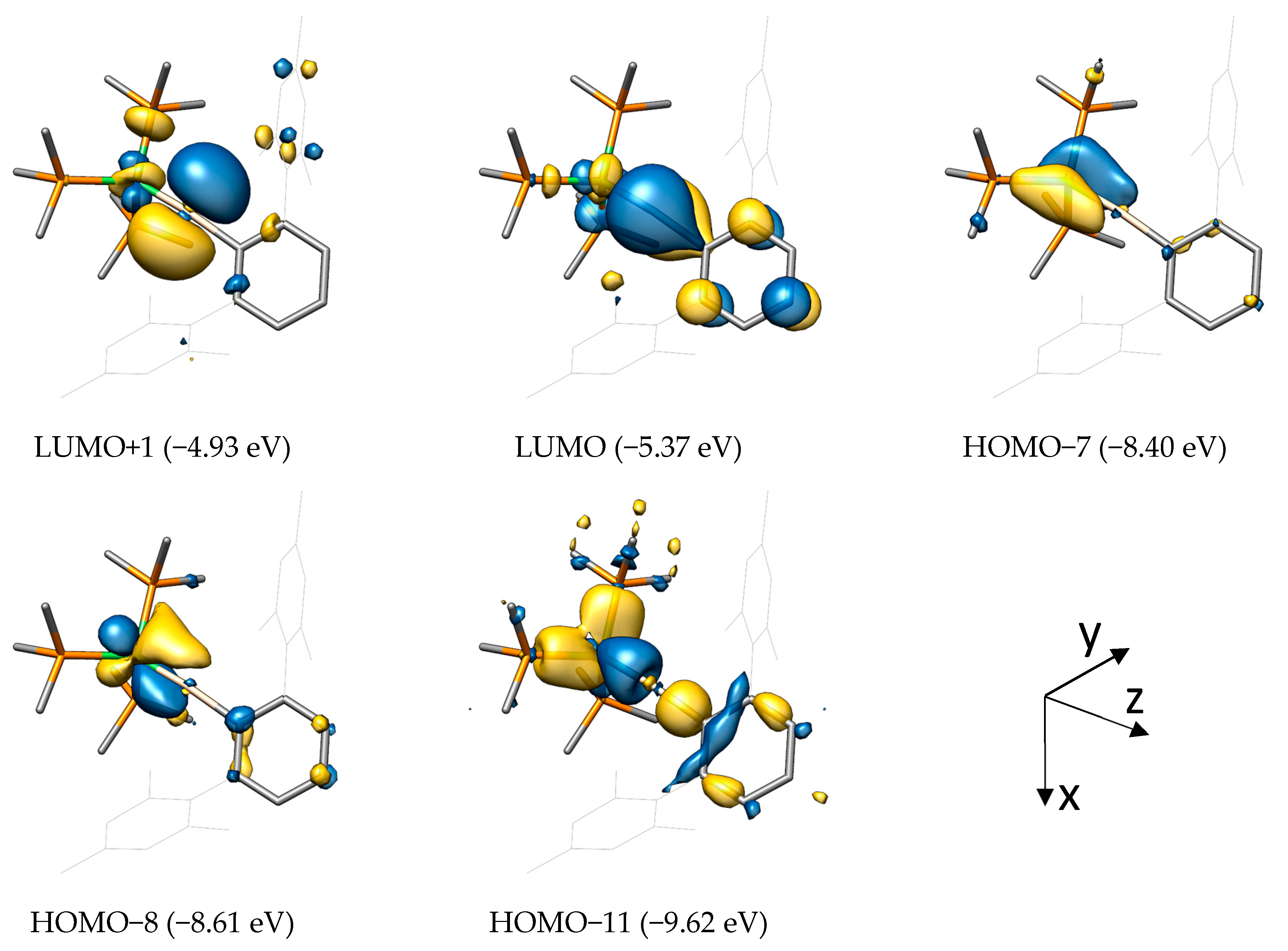
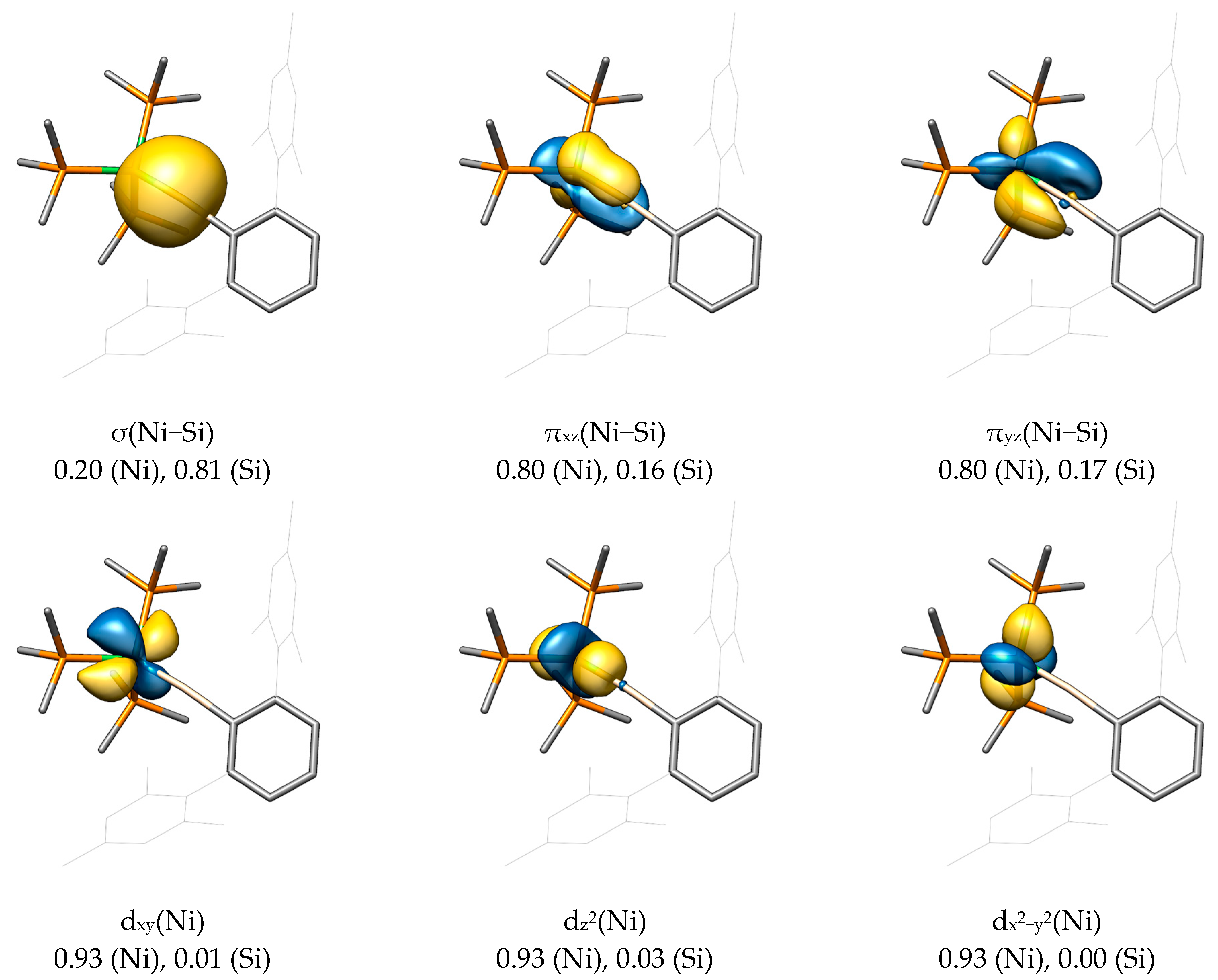
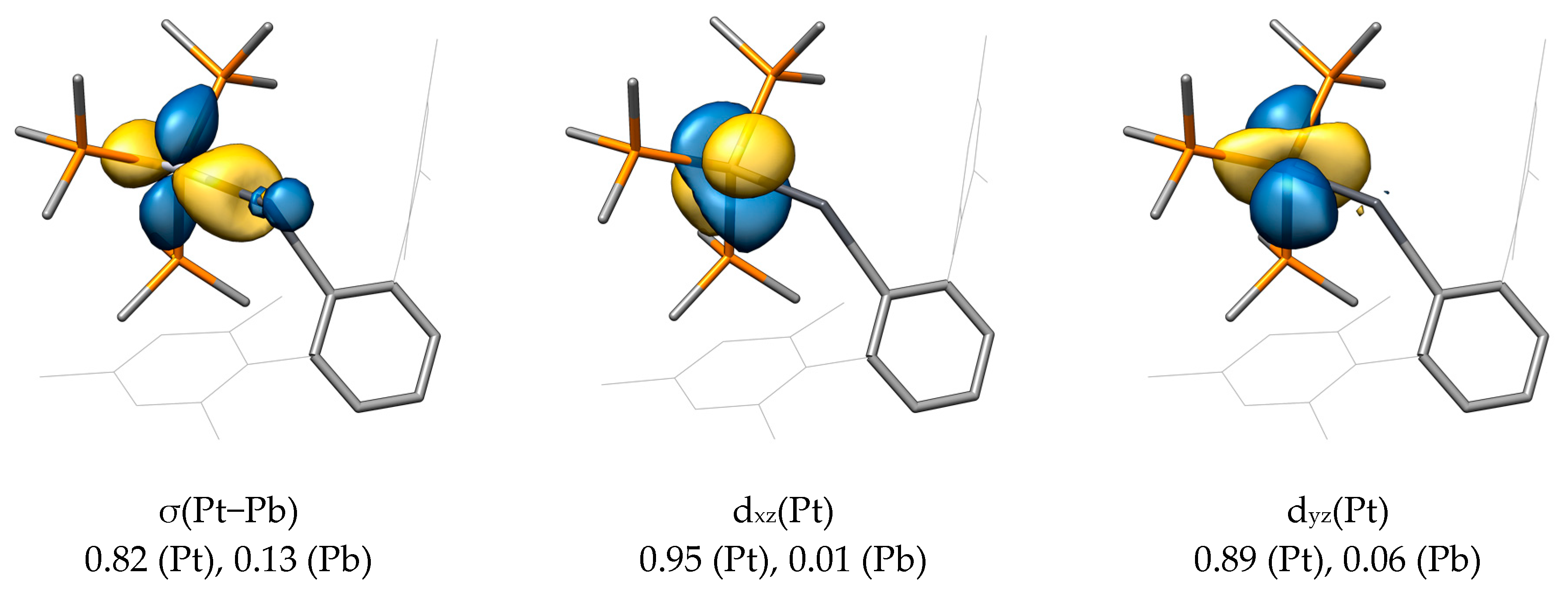
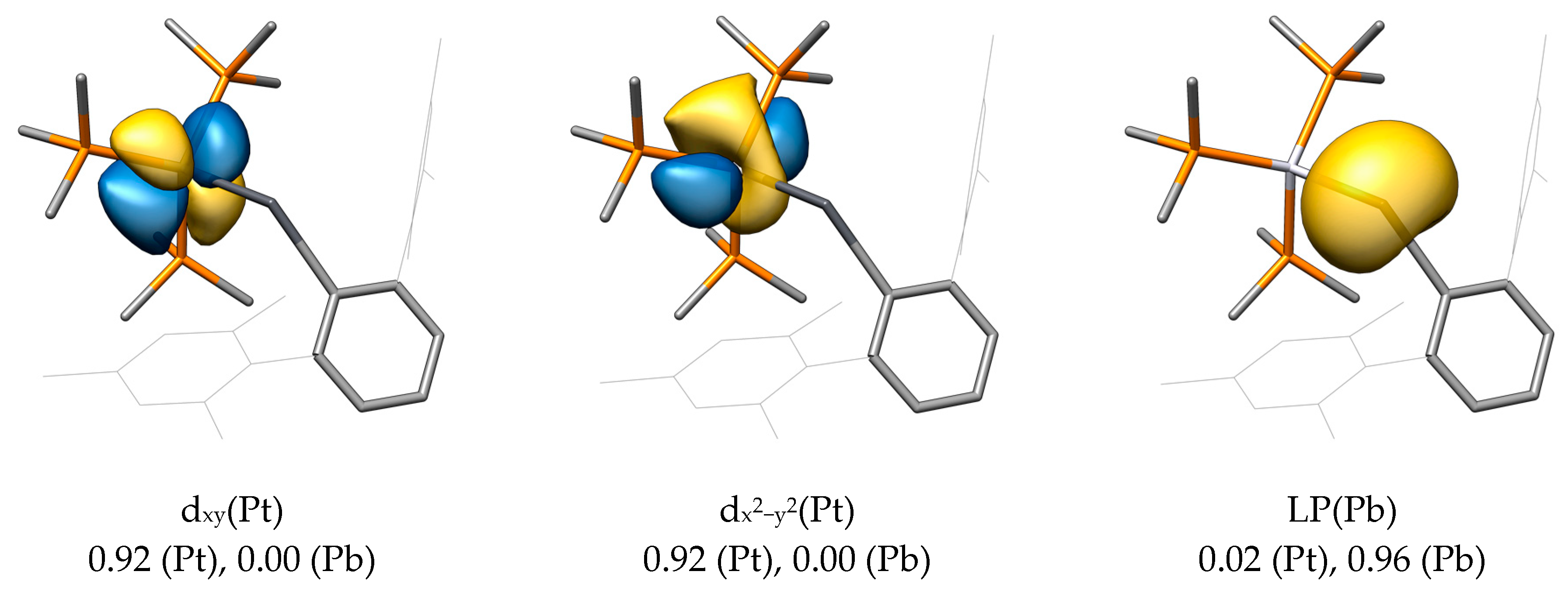
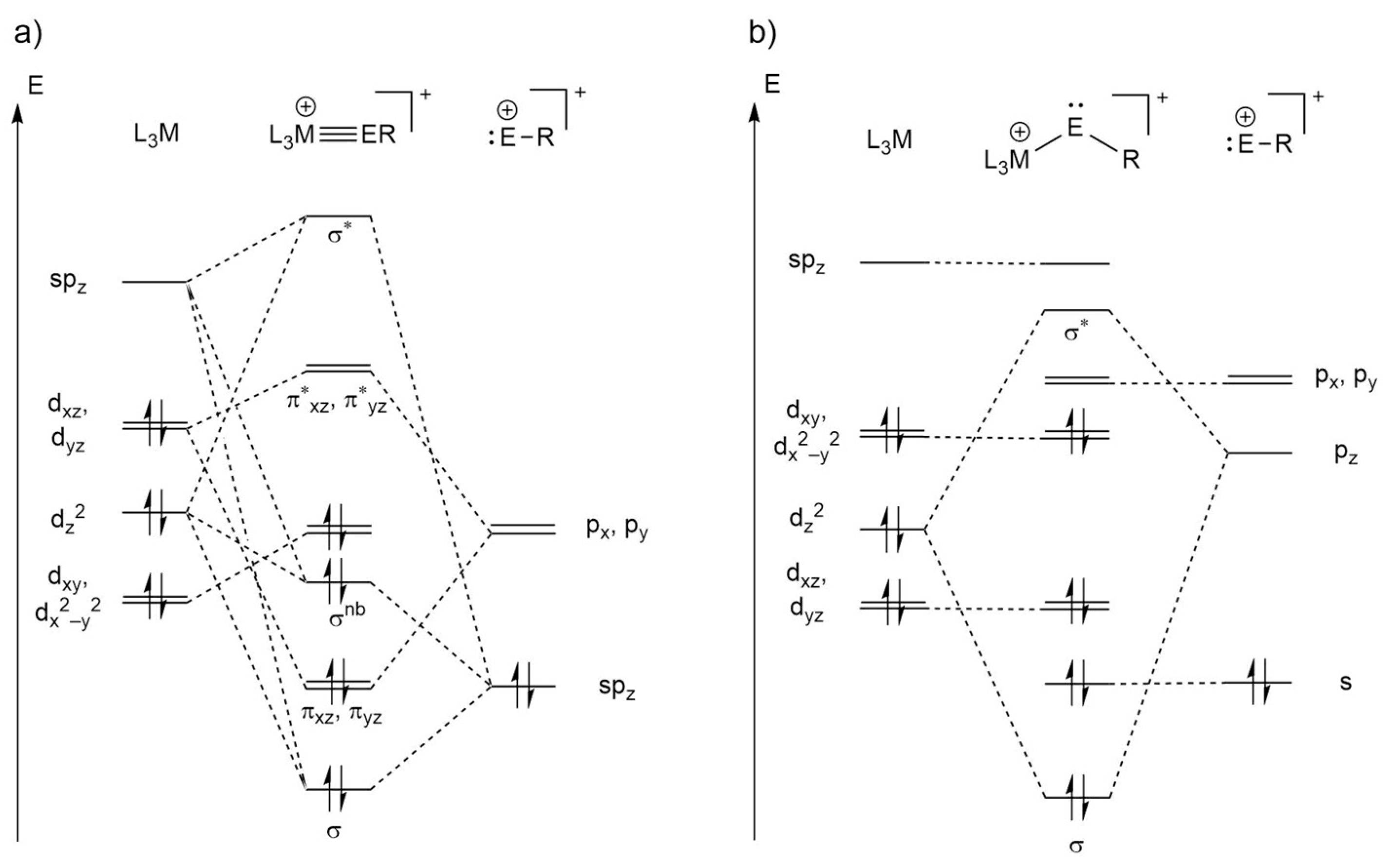
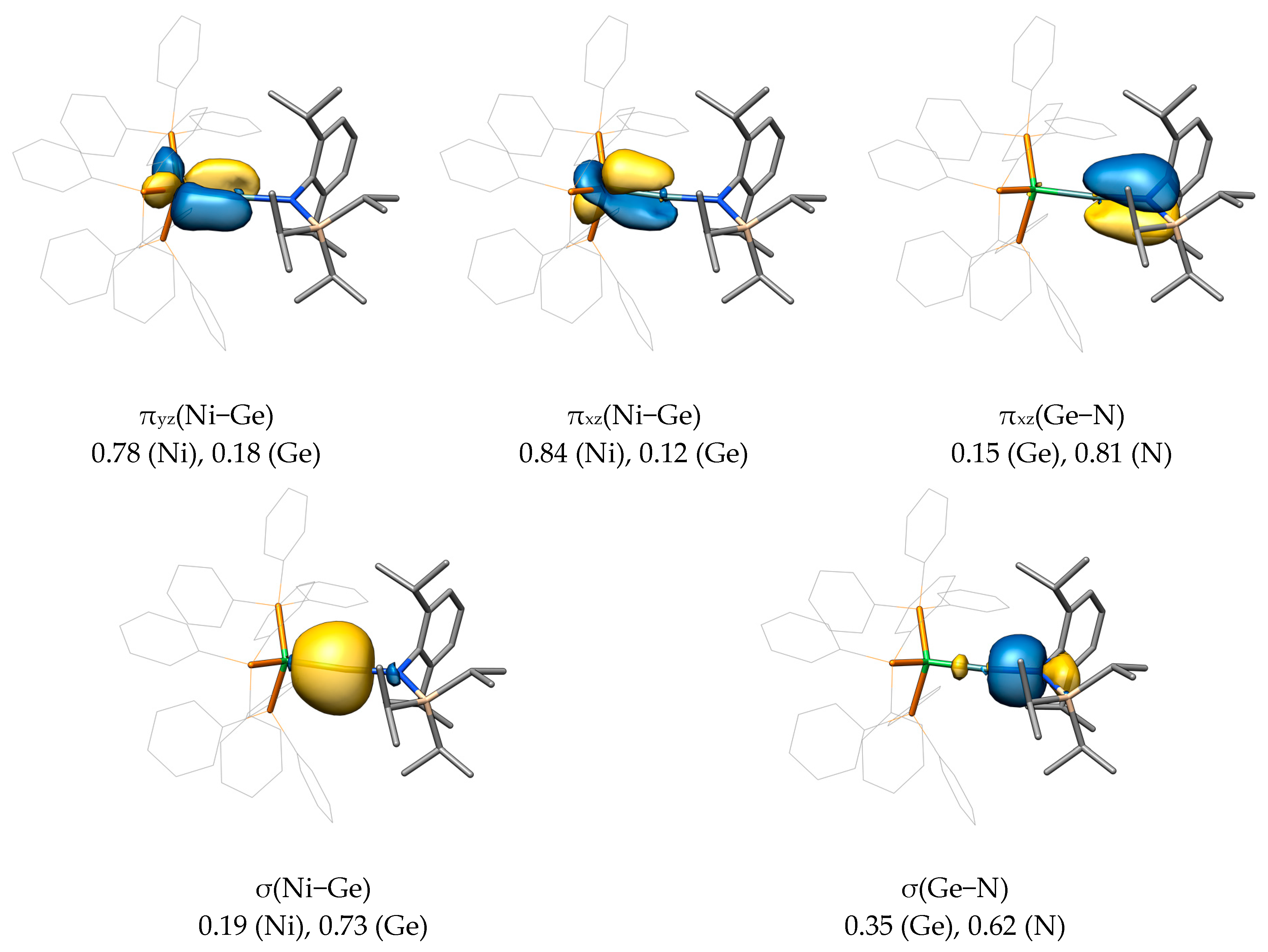
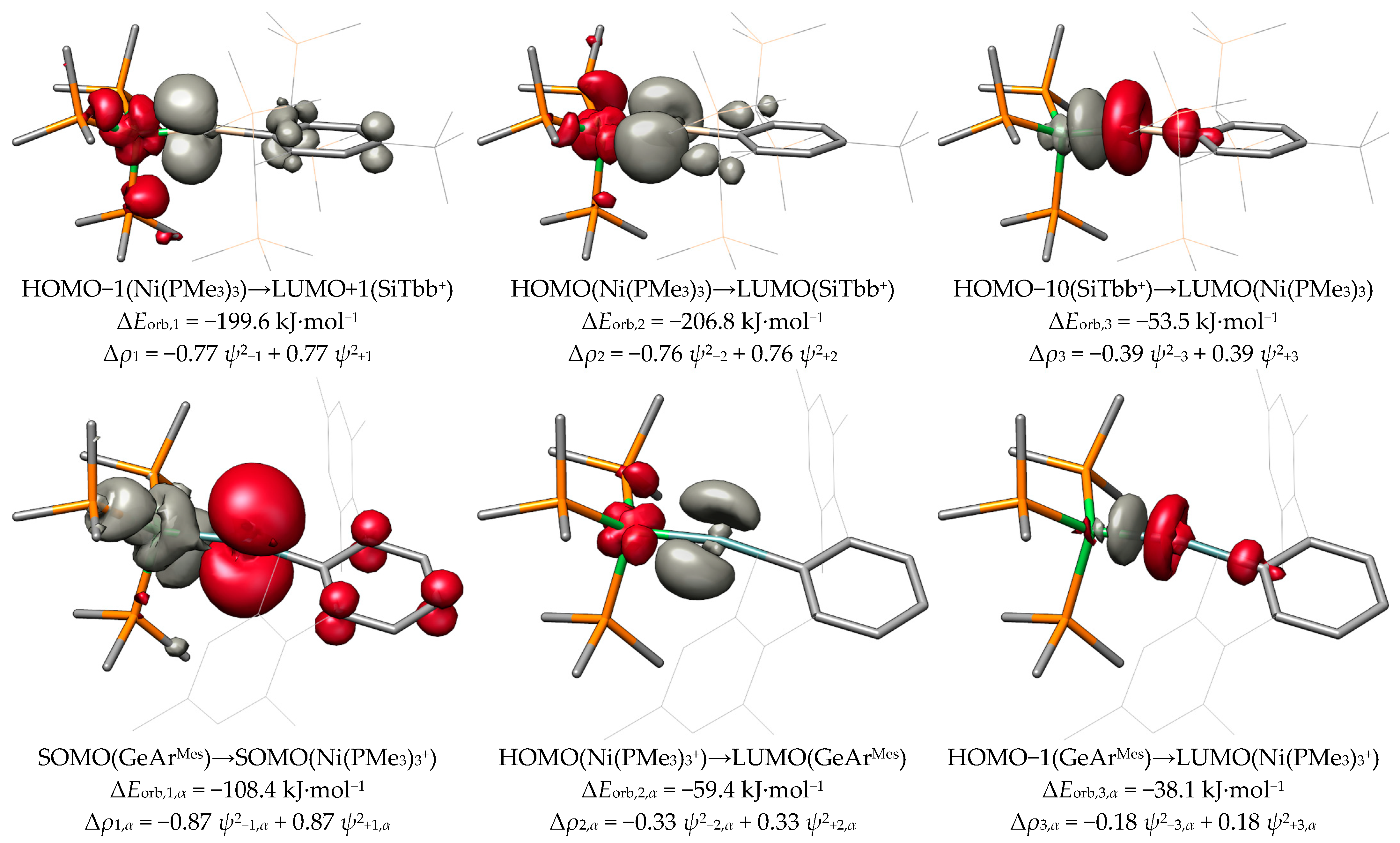
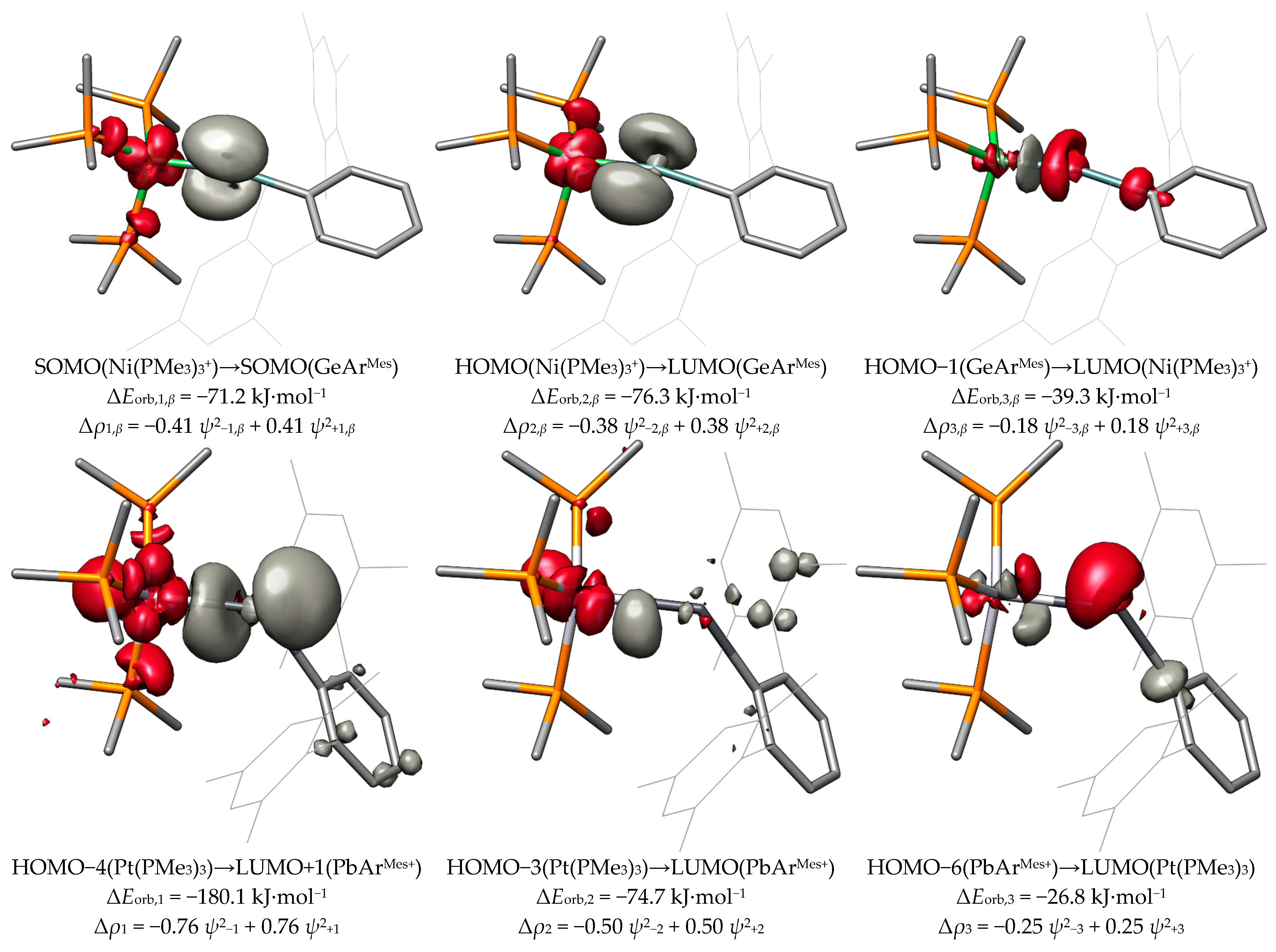
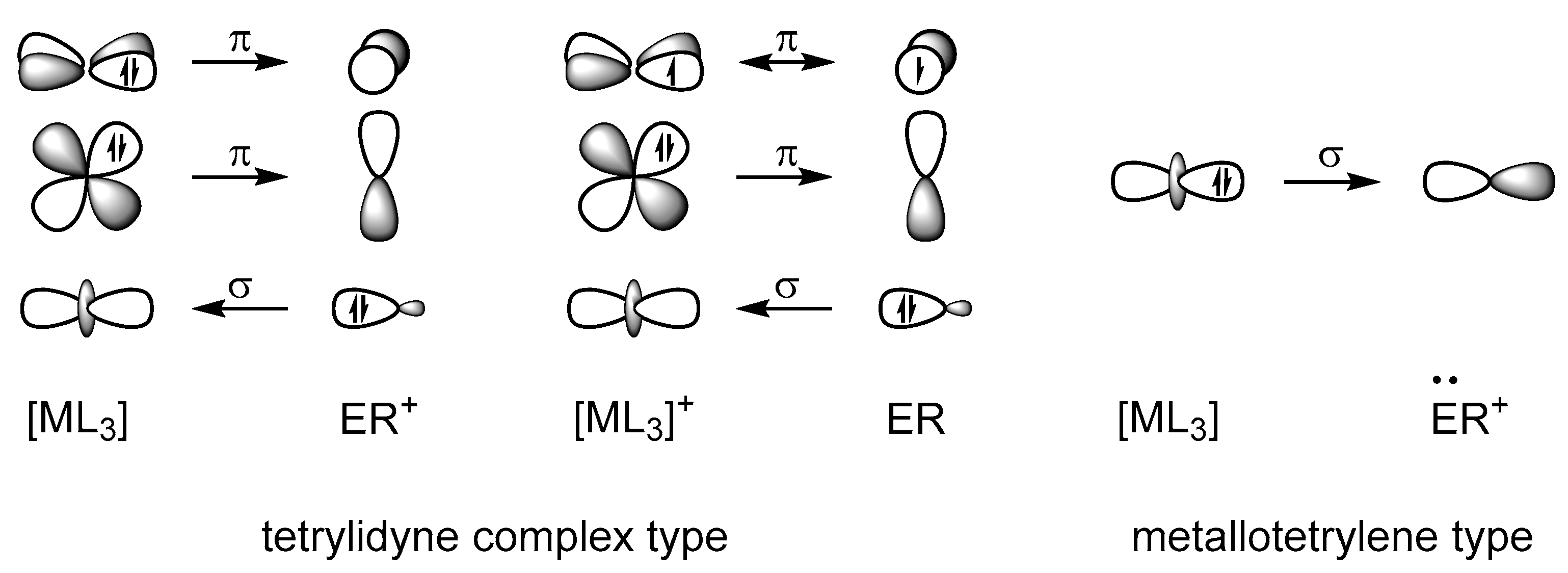
2.2. Molecular Orbital Analysis

As one of the most direct results of an electronic structure calculation, we analyzed the canonical (Kohn−Sham) molecular orbitals (MOs) in the beginning. The MOs of the compounds NiSiArMes (Figure 3) and PtPbArMes (Figure 4) were selected as representatives for the discussion; the selected MOs of the other systems can be found in the SI.
Although heavily delocalized, the low-lying HOMO−11 (highest occupied molecular orbital (HOMO)) in NiSiArMes corresponds to the σ(M−E) bond with σ(E−C) bond character. The metal-centered HOMO−8 and HOMO−7 represent the πxz(M−E) and πyz(M−E) bonds, respectively, with their antibonding, tetrel-centered counterparts being the lowest unoccupied molecular orbital (LUMO) and LUMO+1.
For PtPbArMes, the σ(M−E) bond is represented by HOMO−11, where the participation of the metal dz2 is evident. In contrast to NiSiArMes, no clear π bonds are found between the metal and tetrel, but rather metal-centered dxz (HOMO−10) and dyz (HOMO−9) orbitals without significant orbital contribution from the lead atom. Correspondingly, the antibonding π*(M−E) orbitals have a high contribution from the empty tetrel-px (LUMO, distorted due to M−E−C bending) and tetrel-py (LUMO+1) orbital, and only a small metal d-orbital participation.
As the canonical MOs are challenging to interpret due to their delocalized nature, we applied the Pipek−Mezey localization scheme to generate localized Pipek−Mezey MOs (LMOs) by a unitary transformation, not altering the physical meaningfulness of the orbitals [79]. Again, the LMOs are shown for NiSiArMes (Figure 5) and PtPbArMes (Figure 6), being the anticipated extremes in terms of the bonding situation.
As already expected from the canonical MOs, localized σ(M−E), πxz(M−E), and πyz(M−E) bonds are found for NiSiArMes, resulting in a triply bonded M−E moiety. The corresponding Mulliken populations further show that the σ bond is strongly polarized toward the silicon atom (0.20 for Ni, 0.81 for Si), whereas both π bonds are polarized toward the metal atom (πxz: 0.80 for Ni and 0.16 for Si; πyz: 0.80 for Ni and 0.17 for Si). This bonding situation is reminiscent of that in Fischer-type carbyne complexes discussed in the Introduction. Furthermore, the Ni(0) 3d10 system demands the presence of three more metal-centered orbitals, which can be identified within the LMO framework as dxy, dz2, and dx2−y2, all with negligibly low contributions of the silicon atom (<0.04).
For the sake of completeness, the LMOs for the σ(Si−C1) and σ(Ni−P) bonds were also found and feature the expected orbital polarization toward carbon and phosphorus, respectively, based on electronegativity. It should be mentioned that the central phenyl ring of the Tbb and ArMes substituents is also capable of delocalizing its aromatic π electrons over the formally empty px orbital of the tetrel. Such a π stabilization would, to some extent, compete with the dxz back-donation of the metal atom, thus lowering the bond order between metal and tetrel. This effect, however, is assumed to be small due to the inferior π-donor ability of the phenyl substituent compared with that of the amino (NR2) or alkoxy (OR) substituents (vide supra) and due to a decreasing p-orbital overlap between the tetrel and the phenyl group in the series C > Si > Ge > Sn > Pb. The Mulliken population for this π(E−C) LMO decreases—regardless of the metal—from 0.11 (Si) to rather insignificant values of 0.06 (Ge), 0.03 (Sn), and 0.02 (Pb). This conclusion was also drawn in a study by K. K. Pandey et al. in 2011 on cationic tetrylidyne complexes of molybdenum and tungsten bearing a mesityl substituent [73].
For the main LMOs of PtPbArMes, a σ(Pt-Pb) LMO was found, which—in contrast to NiSiArMes—is not polarized toward the tetrel but toward the metal center (0.82 for Pt and 0.13 for Pb). The involved metal orbital is also different and can be rationalized as a dx2−z2 orbital (in terms of symmetry the same as the dz2 orbital). This orbital is filled, as stated above, due to the presence of a d10 metal system, so it seems clear that this M−E interaction comes from the overlap of a filled metal orbital with an empty p orbital at the tetrel atom.
No π(M−E) LMOs were found for PtPbArMes, although the dxz and dyz orbitals on Pt show the correct orientation. The hereby resulting metallotetrylene picture is confirmed by the presence of an electron lone pair (LP) at Pb without significant contribution of the platinum atom, as shown by the Mulliken population (0.02 for Pt and 0.96 for Pb).
Ultimately, this leads to the formulation of two types of bonding situations, which are qualitatively presented in Scheme 5. Case a involves tetrylidyne complexes for which the M≡E bonding can be described by a σ(E→M) donation and two π(M→E) back donations between a neutral ML3 and an ER+ fragment in the singlet state. As both the empty metal spz (according to a Loewdin population analysis of the LUMO of Ni(PMe3)3) and the filled dz2 orbital have the appropriate symmetry to interact with the filled sp hybrid orbital of the tetrel, three MOs result: a σ-bonding and a σ*-antibonding orbital as well as a nonbonding σnb MO that can be approximately considered as a metal-centered dz2 orbital, as confirmed by the LMOs above (Figure 5). The degenerate πxz and πyz bonds result from the interaction of the filled, almost degenerate metal-dxz and -dyz orbitals (the dxz and dyz orbitals are degenerate only in the case of a C3v-symmetric ML3 fragment) with the empty, approximately degenerate tetrel-px and -py orbitals. The degeneracy of the px and py orbitals is lifted in case of a π-donor substituent at the tetrel atom, such as an amino or alkoxy group, leading to a πoop(E−N) or πoop(E−O) MO as well as a π*oop(M−E) MO with π*(E−N) or π*(E−O) contribution. The remaining orbitals on the metal atom are used for bonding to the phosphane ligands, whereas the second sp hybrid orbital on the tetrel is responsible for the bond to the substituent R.
The other case (b), found especially for PtPbArMes, is the metallotetrylene type, with one σ(M→E) donation constituting the M−E single bond, and an electron lone pair at the tetrel center, causing a considerably bent M−E−C moiety. Here, the sp hybridization on the tetrel is not favored anymore, and the electron lone pair resides in an s orbital, further stabilized by relativistic effects that is not participating in bonding to the metal atom. The empty tetrel-pz acceptor orbital interacts with the filled metal dz2 orbital but is also partially involved in bonding to the substituent R (see HOMO−11 in Figure 4).
After investigating the Mos and LMOs of all compounds in this study, the classification of Scheme 3 was obtained: All carbon and silicon compounds and the NiGeArMes complex can be described as tetrylidyne complexes (case a), whereas PdSnArMes, PdPbArMes, PtSnArMes, and PtPbArMes are best described as metallotetrylenes (case b). The germanium systems PdGeArMes and PtGeArMes as well as NiSnArMes and NiPbArMes lie between cases a and b and show a similar σ bonding to the tetrylidyne complexes, which is why we consider them more like tetrylidyne complexes, albeit with weakened π(M−E) bonds, compared with the silicon compounds.
We also studied the canonical Mos of compound B-Ge and found three Mos resulting from the interaction of the dxz(Ni), px(Ge), and px(N) orbitals (Figure 7), which are the πxz, πnbxz, and π*xz orbitals. The bonding πxz orbital is the low-lying HOMO−27, which shows mostly π(Ge−N) bonding with a very small dxz(M) orbital contribution. The nonbonding combination πnbxz with one nodal plane is HOMO−3. It shows no contribution from the germanium atom but only from the metal and nitrogen atoms. Finally, LUMO+1 comprises the antibonding combination π*xz with a large contribution of the px orbital at the tetrel atom. As can be seen in HOMO−27, some πxz(M−E) bonding interaction is present but is diminished by the presence of the nitrogen atom, leading to a π(E−N) interaction.
The MOs mentioned above were not discussed in the publication of T. J. Hadlington et al. The MO description was limited to HOMO, HOMO−1, and HOMO−2, which were presented by the authors as two π- and one M−E σ-bonding orbital. However, by employing a more modest isosurface value of 0.04 e1/2·Bohr−3/2 and comparing it with similar orbitals in our compounds, we suggest that these orbitals correspond to the metal-centered dx2−y2, dxy, and σnb orbitals, respectively (more details on this can be found in the SI).
The aromatic groups of the triphenylphosphane ligands in B-Ge further amplify the delocalized character of the canonical frontier MOs, making them harder to interpret. This is why we also carried out a Pipek−Mezey orbital localization for B-Ge, and selected LMOs (localized molecular orbitals) are presented in Figure 8. It can be seen that apart from the σ(Ni−Ge) and σ(Ge−N) bonds, three π-type orbitals emerge from the orbital localization (πyz(Ni−Ge), πxz(Ni−Ge), and πxz(Ge−N)). Whereas πyz LMO corresponds to a (Ni−Ge) π bond, the presence of two xz-oriented π-type LMOs (one π(Ni−Ge) and one π(Ge−N) LMO) suggests the presence of both the ylidyne and allenic Lewis resonance forms in compound B-Ge, as discussed in Scheme 4. Furthermore, the Mulliken populations of these LMOs clearly suggest the typical Fischer-type characteristic of these complexes, with high tetrel contributions for the σ bond (0.73, E→M donation) and low ones for the two π bond orbitals (0.18, 0.12, M→E back-donation).
Together with the very similar results obtained for the tin analogue B-Sn (see the SI), the canonical and localized molecular orbital analysis suggests a similar bonding situation as in Fischer-type aminocarbyne complexes. However, the π(E−N) interaction in B-Ge and B-Sn is expected to be weaker than in the Fischer aminocarbyne complexes as evidenced by the small contribution of the tetrel atom in the πxz LMOs.

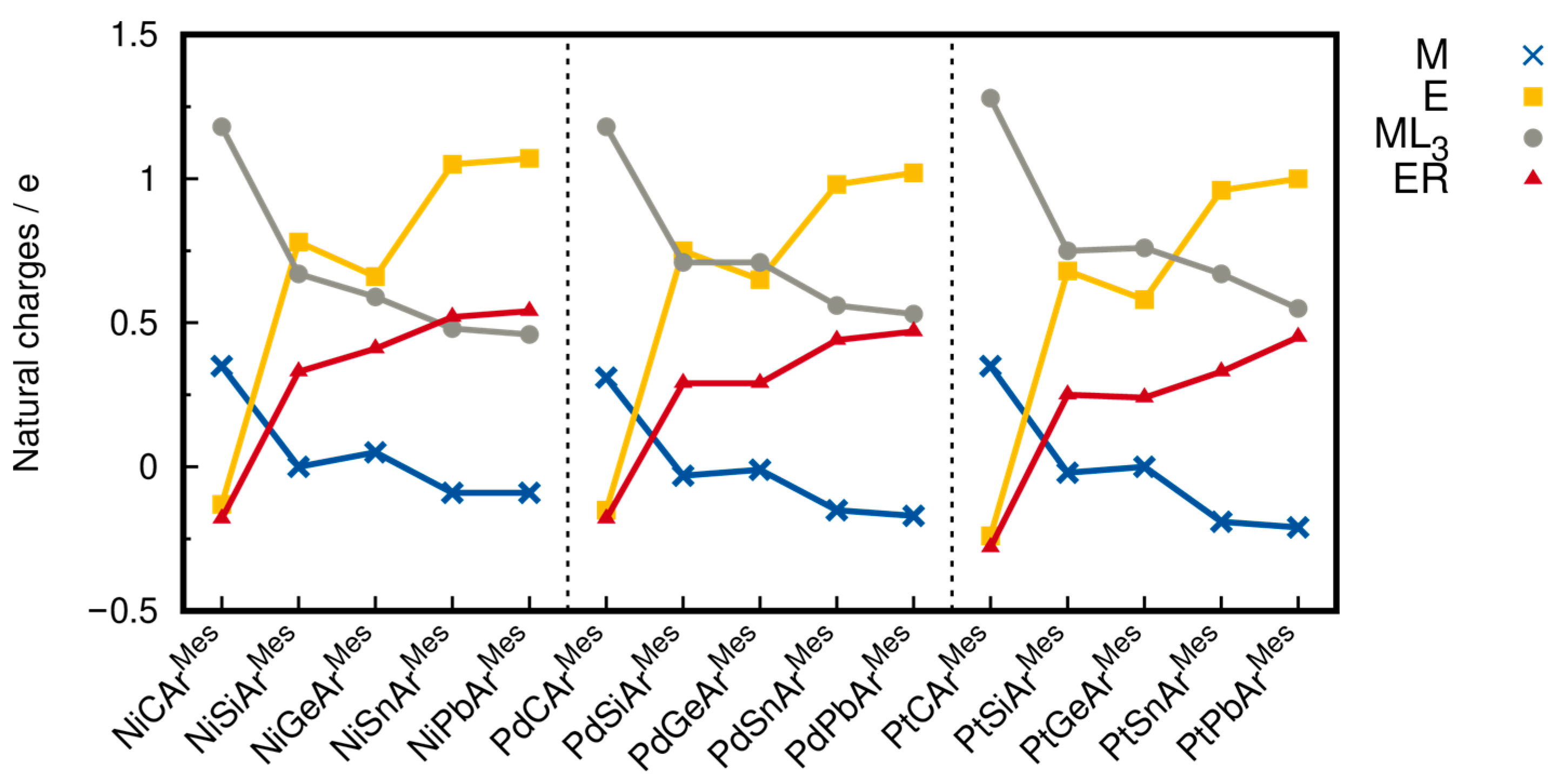
2.3. Bond Dissociation Energies and Natural Population Analysis

Bond dissociation energies provide insights into the strength of bonds and create a basis for the discussion of the correlation between bond strengths and bond orders. Herein, we differentiate between the bond cleavage energy (BCE), which describes the cleavage of a molecule without structural relaxation of the fragments in which the total spin of the fragments must be equal to the spin of the unfragmented molecule, and the bond dissociation energy (BDE), in which the structural relaxation of the fragments is taken into consideration. Both energies are purely electronic. BDEs that were corrected by the zero-point vibrational energies (ZPVEs) as well as the respective inner energies ΔU, enthalpies ΔH°, entropies ΔS°, and Gibbs free energies ΔG° at standard ambient conditions 298.15 K and 1 atm are given in the SI together with their definitions.
The first step in obtaining the lowest possible BCEs and BDEs is determining the charges and spin states of the fragments. For gas-phase calculations, a cleavage into oppositely charged fragments is heavily unfavored due to strong coulombic attraction between the fragments. As a result of the cationic nature of the compounds presented herein, there are two reasonable schemes for the fragmentation of the M−E bond:
  • [(PMe3)3ME−R]+ → [M(PMe3)3] + [E−R]+: An investigation of the electronic states of the fragments [ML3] and [E−R]+ revealed that all fragments have a singlet ground state, with the only exception being the structurally relaxed [C−ArMes]+ fragment, which is stabilized in the triplet state after activation of the Mes substituent (see the calculated structure file). The singlet−triplet excitation energies range from 191.4 kJ·mol−1 ([Ni(PMe3)3]) to 214.3 kJ·mol−1 ([Pd(PMe3)3]) for the metal fragments and from 140.8 kJ·mol−1 ([Si−Tbb]+) to 174.7 kJ·mol−1 ([Sn−ArMes]+) for the tetryliumylidene ions.
  • [(PMe3)3ME−R]+→[M(PMe3)3]+ + [E−R]: This fragmentation scheme involves an interaction of two open-shell fragments either in their doublet or quartet states. The doublet state is preferred by all fragments with doublet−quartet excitation energies ranging from 232.5 kJ·mol−1 ([Ni(PMe3)3]+) to 284.0 kJ·mol−1 ([Pd(PMe3)3]+) for the metal fragments and from 120.3 kJ·mol−1 ([C−ArMes]) to 218.7 kJ·mol−1 ([Pb−ArMes]) for the tetrylidyne fragments (see the SI for details).
The following trends in the BCEs and BDEs given in Table 2 and Figure 9 were found:
(a)
Concerning the BCEs, the fragmentation into the [ML3]+ and [ER] fragments is favored for all compounds by 2.4 kJ·mol−1 (PdSnArMes) to 181.0 kJ·mol−1 (PtCArMes), except for PdPbArMes, for which the cleavage into the [ML3] and [ER]+ fragments is favored by 15.7 kJ·mol−1.
(b)
The BDEs are lower for the dissociation into the [ML3]+ and [ER] fragments in all cases, and the energetic differences between the two fragmentation schemes are lower than for the BCEs in most cases, ranging from 6.1 kJ·mol−1 (NiPbArMes) to 74.7 kJ·mol−1 (PtCArMes).
(c)
When comparing the energetic differences ΔBCE and ΔBDE between the two fragmentation schemes in dependence on the transition metal, the observed trend is Ni ≈ Pt > Pd for the ΔBCEs and Pt > Pd > Ni for the ΔBDEs (ΔBCE = BCE(i) − BCE(ii) and ΔBDE = BDE(i) − BDE(ii), where i and ii denote the fragmentation schemes).
(d)
The energetic difference between the two fragmentation schemes (ΔBCE and ΔBDE) follows the order C >> Si > Ge > Sn > Pb regarding the tetrel for both the ΔBCE and ΔBDE. The substituent effect (ArMes vs. Tbb) in the silylidyne complexes on the BCEs and BDEs is minute. However, because the BCEs of MSiTbb are slightly lower for the fragmentation into the ML3 + ER+ fragments than those of MSiArMes but slightly higher for the fragmentation into the ML3+ + ER fragments, the ∆BCEs of the MSiTbb complexes are lower than the ∆BCEs of the MSiArMes and MGeArMes complexes. For ΔBDE, the difference between Si and Ge is negligible.
For the remaining trends, only the values in Table 2 given in bold are discussed in the following:
(e)
The BCEs, if ordered by transition metal, follow the order Pt > Ni > Pd for E = C and Si and the order Ni > Pt > Pd for E = Ge, Sn and Pb. In comparison, the BDEs, if ordered by the transition metal, follow the order Ni > Pt >Pd for all tetrels. The reason for this difference is a significantly higher structural relaxation energy of the Pt(PMe3)3 fragment (avg. 104.4 kJ·mol−1) followed by the Pd(PMe3)3 (avg. 63.9 kJ·mol−1) and Ni(PMe3)3 fragments (avg. 54.8 kJ·mol−1), which lowers the BDEs of the PtER complexes more than the BDEs of the PdER and NiER complexes in comparison with the respective BCEs.
(f)
If ordered by tetrel, the BCEs and BDEs follow the trend C >> Si > Ge > Sn ≈ Pb. This means that the M−E bonds of the carbyne complexes are, as expected, the strongest. However, the heavier ylidyne complexes exhibit considerable BCEs and BDEs. These are lower than those of the carbyne complexes, with the difference, though, being considerably smaller than those of the ditetrylynes. For example, the experimental dissociation enthalpy ∆H° of acetylene of 964.8 ± 2.9 kJ·mol−1 [81] (∆H°calc(HCCH) = 953.0 kJ·mol−1 at the level of theory I and 970.2 kJ·mol−1 at the level of theory II) is ca. 13 times larger than that of the distannyne ArDippSnSnArDipp (∆Hexp = 72.0 ± 7.1 kJ·mol−1) [82]. Similarly, a calculation of the gas-phase dissociation enthalpy ∆H°calc of ArDippSnSnArDipp at the level of theory I leads to a value of 160.7 kJ·mol−1, which is still only a small fraction of that of the analogous acetylene derivative ArDippC≡CArDipp (∆H°calc = 721.7 kJ·mol−1). In comparison, the BDE of NiSnArMes is still 63 % and 66 % of the BDE of NiCArMes on the level theory I and II, respectively, illustrating the considerable bond strength of the M≡E triple bonds. An important implication of this comparison is that C≡C bonds are stronger than M≡C bonds, whereas the opposite is true for the heavier group 14 elements Si–Pb (i.e., the BDEs of the E−E bonds in E2R2 are smaller than those of the M≡E bonds).
(g)
The choice of tetrel generally has a larger influence on the BCEs and BDEs than the choice of the transition metal. For example, the BCEs of NiGeArMes, PdGeArMes, and PtGeArMes are within 40 kJ·mol−1 of each other, whereas the BDEs of NiSiArMes and NiPbArMes differ by 83.3 kJ·mol−1.
As the charge distribution in the group 10 ylidyne complex cations is an important consideration for the comprehension of these compounds, atomic charges were calculated at the level of theory I from a natural population analysis (NPA) in the natural bond orbital (NBO) framework using natural atomic orbitals (NAOs). The results are given in Table 3 and Figure 10. The metal atoms Ni, Pd, and Pt are either almost electroneutral for E = Si and Ge, with charges in the range of −0.03 e (PdSiR) to +0.05 e (NiGeArMes), or slightly negatively charged for E = Sn, Pb, with charges from −0.21 e (PtPbArMes) to −0.09 e (NiSnArMes, NiPbArMes). A significant positive charge of +0.58 e (PtGeArMes) to +1.07 e (NiPbArMes) is carried by the tetrel atoms Si, Ge, Sn, and Pb, where the positive charges of the Si and Ge atoms are smaller than those of the Sn and Pb atoms. The entire ML3 units carry total charges of +0.46 e (NiPbArMes) to +0.76 e (PtGeArMes), and the ER unit charges range for E = Si–Pb from +0.24 e (PtGeArMes) to +0.54 e (NiPbArMes). Overall, the silylidyne and germylidyne complexes behave very similarly but slightly differ from the charge distribution in the stannylidyne and plumbylidyne complexes. The dependence of the NPA charges on the tetrel atom is also much higher than on the metal atom.
These charges are comparable to the NPA charges for the complexes B-Ge and B-Sn, where the Ni atoms carry only small charges (B-Ge: +0.05 e, B-Sn: −0.19 e), and the tetrel atoms carry high positive charges of +1.01 e (B-Ge) and +1.42 e (B-Sn) [53]. The charges on the Ge and Sn atoms of B-Ge and B-Sn are higher than the charges in the ArMes-containing complexes due to the more electronegative amino substituent.
The group 10 ylidyne complexes with the heavier tetrel atoms have a quite different charge distribution from the group 10 carbyne complexes. This can be attributed to the special position of carbon among the group 14 elements in the periodic table reflected in its much higher electronegativity than that of its heavier congeners. This results in negative partial charges on the carbon atoms in the carbyne complexes, whereas the heavier tetrel atoms carry positive partial charges. Additionally, a clear shift in electron density from the ML3 to the ER unit is observed, leading to negatively charged ER ligands in the carbyne complexes, whereas the heavier tetrylidyne ligands ER (E = Si–Pb) are positively charged. For the same reason, the metal center carries a positive partial charge in the carbyne complexes but is electroneutral or slightly negatively charged in the heavier tetrylidyne complexes, and the ML3 unit carries a much larger positive partial charge in the carbyne complexes than in the heavier group 14 analogues.

2.4. ETS-NOCV and EDA

A very useful tool in the analysis of the chemical bond is the combination of the extended-transition state (ETS) [83] method and natural orbitals of chemical valence (NOCV) [84,85]. The ETS-NOCV analysis was carried out on the level I optimized structures using the ADF program package, as described in Section 3. Within the ETS-NOCV scheme, an energy decomposition analysis (EDA) is used to decompose the interaction energy (ΔEint) of the complexes [L3M≡E−R]+ into chemically meaningful components (Equation (1)):
ΔEint = ΔEorb + ΔEPauli + ΔEelstat + ΔEdisp = −BCE
The orbital interaction energy ΔEorb represents the attractive interactions between the occupied molecular orbitals and the virtual orbitals of the two fragments. The Pauli repulsion energy ΔEPauli results from the destabilizing interaction between the occupied orbitals of the fragments. The third term, ΔEelstat, is the electrostatic interaction energy between the fragments as they are combined in the final molecule with the densities kept frozen, and the dispersion interaction energy ΔEdisp describes the long-ranged dispersive interactions of the fragments.
Because the choice of the electronic reference states of the fragments has a significant influence on all of the energy components and their sum, there is a certain degree of arbitrariness involved in the ETS scheme. The best way to determine the most appropriate electronic reference state of the interacting fragments is dependent on ΔEorb [85]. It is assumed that the combination of electronic reference states for which |ΔEorb| becomes minimal most closely represents the electronic states of the fragments that are formed upon fragmentation. Another argument is that |ΔEorb| could otherwise be arbitrarily increased by the choice of arbitrary electronic states.
Interestingly, the electronic reference states for most fragments are the low-spin singlet states (Table 4), which means the compounds are fragmented into L3M and ER+. This contrasts the preference for the cleavage into the L3M+ and ER fragments according to the BCEs. The electronic reference state of the fragments in case of the carbyne complexes and NiGeArMes and PtGeArMes are the L3M+ and ER fragments in their doublet states, in line with the preferred fragmentation scheme according to the BCEs.
The carbyne complexes prefer fragmentation into L3M+ and ER rather than fragmentation into L3M and ER+ due to the higher electronegativity of the carbon atom compared with its heavier homologs. Because ΔEorb directly depends on the charge transfer between and within the fragments, the fragments in which the atomic charges are closest to the respective atomic charges of the unfragmented molecule are favored. In case of the carbyne complexes, the natural charges of the carbon atoms in the CArMes fragments are +0.23 e (NiCArMes), +0.28 e (PdCArMes), and +0.27 e (PtCArMes); in the [CArMes]+ fragment, they are +0.53 e, independent of the metal. The charges of the carbyne carbon atoms in the carbyne complexes are −0.13 e (NiCArMes), −0.15 e (PdCArMes), and −0.24 e (PtCArMes), which are more similar to the respective charges of the CArMes fragments than to those of the [CArMes]+ fragments.
The ETS-NOCVs were also carried out using the triplet electronic reference states of the ML3 and ER+ fragments and the quartet electronic reference states of the ML3+ and ER fragments, but these resulted in much higher orbital interaction energies than the low-spin calculations.
The notable results are that |ΔEorb| is highest for the carbyne complexes ranging from −645.3 kJ·mol−1 (NiCArMes) to −903.3 kJ·mol−1 (PtCArMes), followed by the silylidyne and germylidyne complexes with a ΔEorb of −426.8 kJ·mol−1 (PdGeArMes) to −585.8 kJ·mol−1 (PtSiTbb), and the Sn and Pb compounds with a ΔEorb of −291.1 kJ·mol−1 (PdPbArMes) to −380.4 kJ·mol−1 (PtSnArMes).
The same trends were observed for ΔEPauli and |ΔEelstat| (see the SI). The dispersion interaction energy is almost identical for all complexes. The total interaction energy corresponds to the BCE, with slightly different values due to the different levels of theory (see Section 2.3).
Interestingly, the NiSnArMes and NiPbArMes complexes show no appreciable differences in the orbital interaction energies from their metallotetrylene counterparts (PdSnArMes, PdPbArMes, PtSnArMes, and PtPbArMes).
The orbital interaction energy can be further split into contributions of individual NOCVs, which allows for a detailed delineation of the bonding situation. Because the NOCVs are related to the fragment MOs, the fragment MOs involved in the bonding can be inferred by inspection of the NOCVs.
For the sake of simplicity, we only discuss the deformation densities of NiSiTbb, NiGeArMes and PtPbArMes. All compounds marked as tetrylidyne complexes in Scheme 3 exhibit similar NOCVs to either NiSiTbb or NiGeArMes, and all compounds marked as metallotetrylenes are similar to PtPbArMes. More details can be found the SI.
As shown in the top row of Figure 11, the three largest contributions to the orbital interaction energy of NiSiTbb are two π-symmetric and one σ-symmetric interaction. The first interaction (ΔEorb,1 = −199.6 kJ·mol−1) is identified as the π-back donation from the HOMO−1 of Ni(PMe3)3 to the LUMO+1 of SiTbb+. This interaction is marginally weaker than the second π-back donation (ΔEorb,2 = −206.8 kJ·mol−1) from the HOMO of Ni(PMe3)3 to the LUMO of SiTbb+. This slight difference is due to the competition of the first π donation with the π interaction of the empty px orbital on the Si atom with the phenyl ring of the substituent R (vide supra). The last interaction is the σ donation (ΔEorb,3 = −53.5 kJ·mol−1) from the HOMO−10 of SiTbb+ to the LUMO of Ni(PMe3)3. Remarkably, there is a substantial difference in the contribution to the bond strength between the π- and σ-type interactions, in which the σ-donation is weaker by a factor of roughly four compared with each of the π-back donations.
Because the interaction of the fragments in NiGeArMes takes place between the two open-shell doublet fragments GeArMes and Ni(PMe3)3+, the orbital interaction energies are further split into the α- and β-spin contributions. The first interaction is a π donation (ΔEorb,1,α = −108.4 kJ·mol−1) from the singly occupied MO (SOMO) of GeArMes to the SOMO of Ni(PMe3)3+, which is completed by the π-back donation (ΔEorb,1,β = −71.2 kJ·mol−1) from the SOMO of Ni(PMe3)3+ to the SOMO of GeArMes. Expectedly, the π donation is significantly stronger than the π-back donation and is accompanied by a larger charge transfer of 0.87 e vs. 0.41 e due to the cationic nature of the Ni(PMe3)3+ fragment. The sum ΔEorb,1,α, + ΔEorb,1,β gives the total orbital interaction energy ΔEorb,1 of −179.6 kJ·mol−1, which is slightly weaker than the first π interaction in NiSiTbb. The second interaction in NiGeArMes is also composed of an α- and β-spin component; both components involve, in this case, a charge transfer in the same direction from the metal to the tetrel (M→E π-back donation). The total interaction energy ΔEorb,2 of −135.7 kJ·mol−1 is albeit weaker than that in NiSiTbb. This is also the case for the third interaction, which is the σ donation (ΔEorb,3 = −77.4 kJ·mol−1) from the HOMO−1 of GeArMes to the LUMO of Ni(PMe3)3+. This σ interaction is slightly stronger than that in NiSiTbb, which can be explained by the direction of the charge flow from the neutral fragment GeArMes to the cationic fragment Ni(PMe3)3+ in NiGeArMes, whereas, in NiSiTbb, the charge flow from SiTbb+ to Ni(PMe3)3 via the σ donation occurs against the charge gradient.
Lastly, the three strongest contributions of the metallotetrylene-like compound PtPbArMes feature one strong σ-back donation (ΔEorb,1 = −180.1 kJ·mol−1) from the HOMO−4 of Pt(PMe3)3 to the LUMO+1 of [PbArMes]+. Notably, the acceptor orbital of this interaction is the pz orbital of the tetrel atom. The direction of the σ donation of the tetrylene-like compounds is opposite to that of the ylidyne complexes. The second interaction can be identified as a weak π-back donation (ΔEorb,2 = −74.7 kJ·mol−1) from the HOMO−3 of Pt(PMe3)3 to the LUMO of [PbArMes]+. This interaction is significantly weaker than in the compounds NiSnArMes (ΔEorb,2 = −136.3 kJ·mol−1) and NiPbArMes (ΔEorb,2 = −113.7 kJ·mol−1). The third interaction still indicates a weak π donation (ΔEorb,3 = −26.8 kJ·mol−1) from the HOMO−6 of PbArMes+ to the LUMO of Pt(PMe3)3. However, there is a significant amount of intrafragment charge-redistribution present, which is why this interaction plays a negligible role in the bonding between the Pt and Pb atoms.
In Figure 12, we present the three bonding situations that describe the cationic group 10 tetrylidyne complexes discussed herein. Additionally, the tetrylidyne complexes with one σ-donating and two π-back interactions can be formulated with one π-type electron spin-pairing interaction bond replacing one of the π-back interactions. Although the formal charge of the latter type is located at the transition metal atom, no notable difference between the two types is observed regarding the charge distribution of the compounds including the heavier group 14 elements. The metallotetrylene type entails a cationic ER+ fragment, which receives electron density from the metal fragment ML3 via a σ bond and features notably smaller M−E−R angles (vide infra).

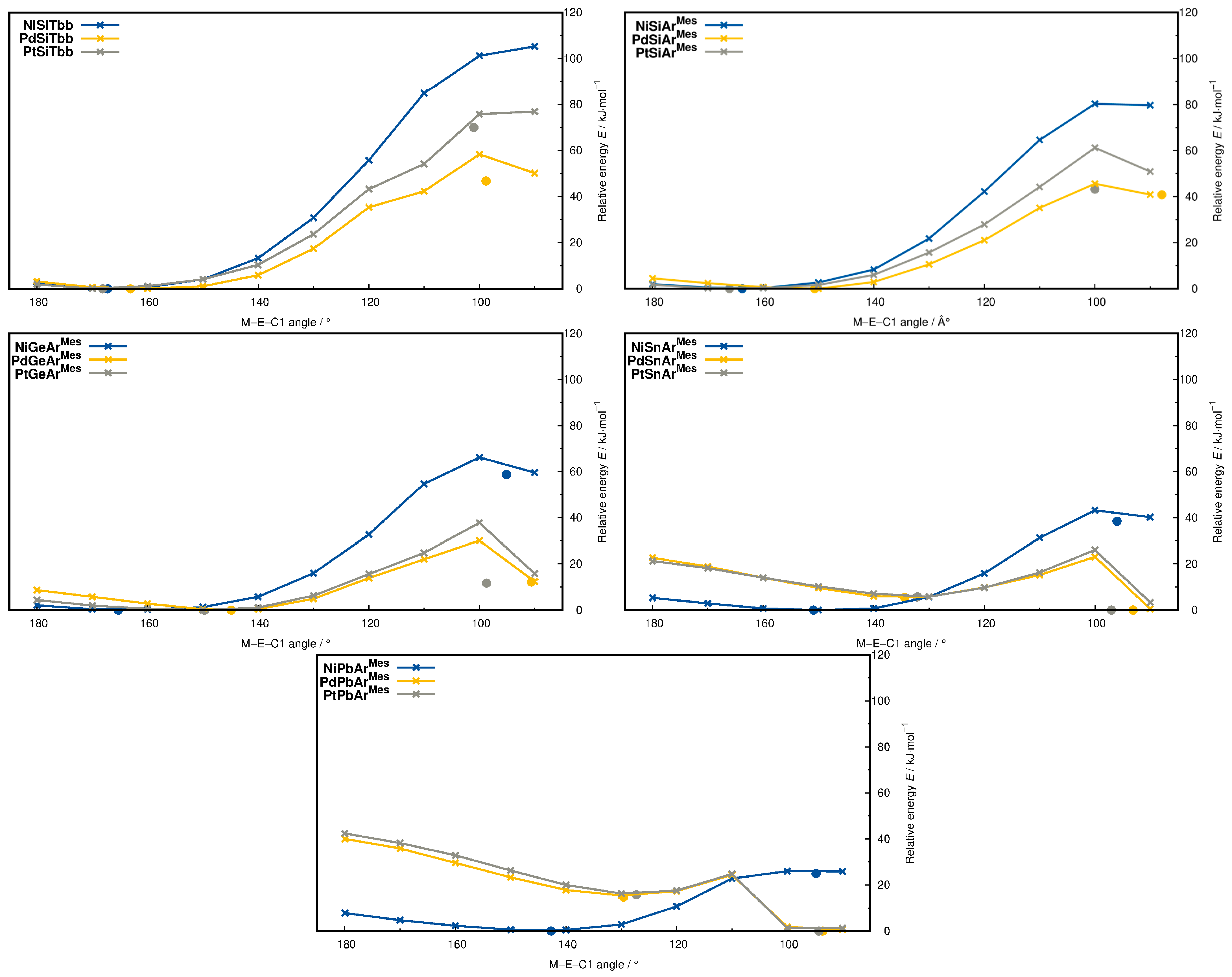
2.5. Metallotetrylene Isomers by PES Scans

When we optimized the structures of our complexes, we were surprised by the variability in the M−E−C1 bond angle, which significantly deviates from 180° for most structures (Table 1). To energetically address this variability, we carried out PES scans of the M−E−C1 angle from 180° to 90° in steps of 10° for all heavier tetrylidyne complexes (Figure 13). As can be seen, the steepness of the PES decreases in the order Si > Ge > Sn > Pb; more importantly, isomers with much smaller M−E−C1 angles of around 95° were found for most systems, abbreviated in the following as MER-2, which were confirmed to be minima on the PES. These isomers are energetically not favored for most compounds as the energy difference between the isomers with the smaller and larger M−E−C angle shows (e.g., PdSiTbb-2: +47.1 kJ·mol−1; NiGeArMes-2: +83.5 kJ·mol−1; NiSnArMes-2: +55.3 kJ·mol−1, at the level of theory II; see the SI). However, the more bent isomers, PdSnArMes-2, PdPbArMes-2, PtSnArMes-2, and PtPbArMes-2, were found to be energetically favored by 13–29 kJ·mol−1. In the following, the isomer PtPbArMes-2 is representatively discussed, and key properties of the other MER-2 isomers are included in the SI.
A comparison of the structural parameters of PtPbArMes-2 (Figure 14) and PtPbArMes (Table 5) shows a further elongation of the M−E bond from 267.7 to 281.9 pm when decreasing the M−E−C1 angle to 94.3°, whereas the E−C1 bond length stays nearly the same (233.7 pm). Notably, the metal adopts a distorted square-planar coordination in PtPbArMes-2 (see the SI) [86].
Expectedly, the analysis of the LMOs of PtPbArMes-2 (Figure 15) shows an electron lone pair at Pb, a σ(Pt−Pb) bond that is highly polarized toward Pt (0.75 at Pt, 0.20 at Pb), and a σ(Pb−C) bond that is highly polarized toward the carbon atom (0.81 at C1, 0.28 at Pb).
The first deformation density of PtPbArMes-2 given in Figure 16 indicates that the σ(Pt−Pb) bond is best described as a donation from the Pt atom to the Pb atom. Notably, the orbital interaction energy ΔEorb,1 of 299.0 kJ·mol−1 is larger in PtPbArMes-2 than the corresponding orbital interaction energy in PtPbArMes, as shown in Table 6. The remaining orbital interactions of PtPbArMes-2 are weaker than those of PtPbArMes. However, the much higher ΔEorb,1 of PtPbArMes-2 compared with that of PtPbArMes ultimately leads to a net preference of the strongly bent isomer of 67.2 kJ·mol−1 based on ΔEorb.

3. Materials and Methods

All calculations except for the ETS-NOCV calculations were carried out using the ORCA 5.0.3 program package [87]. The B97-D3 (BJ)-ATM/def2-TZVP (I) level of theory was employed for the structure optimizations, consisting of the density functional approximation (DFA) B97-D3 (BJ) with Grimme’s D3 correction for the London dispersion interactions including the Becke−Johnson damping [88,89] of the additional three-body contribution of Axilrod, Teller and Muto (ATM) [90,91], and of Ahlrichs’-type triple-ζ basis set def2-TZVP [92].
To obtain high-level electronic energies, single-point energy calculations were performed in addition to the calculated structures using the PWPB95-D3(BJ)-ATM/def2-QZVPP (II) level of theory, consisting of the double-hybrid DFA PWPB95 [93] with the D3(BJ)-ATM dispersion treatment and the quadruple-ζ basis set def2-QZVPP[92]. Thermochemical quantities at the level of theory II were obtained by adding the thermodynamic corrections obtained at the level of theory I to the electronic energies obtained at the level of theory II.
For both levels of theory I and II, Stuttgart/Dresden effective core potentials (ECPs) were employed for Pd [65], Sn [66], Pt [93], and Pb [66] as well as defGrid2 numerical integration settings.
The Coulomb part of the DFAs of the levels of theory I and II was approximated with the RI-J method [94], employing the def2/J auxiliary basis sets. For the DFA PWPB95, the calculation of the exchange and MP2 correlation parts was further accelerated using the RI-JK method [95], with the matching def2/JK basis set [96], and the RI method, with the def2-QZVPP/C auxiliary basis set [97].
NPA charges were calculated with the NBO 7.0 program package [98] using the structures and wave functions obtained at the level of theory I.
The ETS-NOCV calculations were carried out using the ADF 2021.103 program package [99,100] at the B97-D3 (BJ)/TZ2P [101] level of theory, which is comparable to the level of theory I. The ETS-NOCV calculations were carried out using the NumericalQuality good setting along with default settings for all other options.
Cube files of canonical and localized molecular orbitals were generated with the MultiWFN 3.6 program [102] from the wave function obtained on theory level I and visualized with UCSF Chimera version 1.13.1 [103].

4. Conclusions

A systematic theoretical study on the cationic group 10 metal complexes [(PMe3)3MER]+ (MER) with M = Ni, Pd, Pt; E = C, Si, Ge, Sn, Pb; and R = ArMes, Tbb (E = Si), was presented. We employed several quantum chemical tools to assess the electronic structure of these complexes on the basis of compounds that were previously experimentally accessed by our group. This involved (a) a detailed inspection of the bonding parameters of the optimized structures, (b) an investigation of the canonical and Pipek−Mezey-localized MOs, (c) a comparison of the NPA charges and the M−E bond cleavage and bond dissociation energies, and (d) a calculation of the ETS-NOCV interactions. Two classes (a and b) of compounds could be identified: The first class a is tetrylidyne complexes, featuring Fischer-type carbyne complexes with a roughly linear M−E−R linkage and a short M≡E bond, which is composed of a σ(E→M) donor bond and two π(M→E) back bonds. The class b complexes display a considerably bent M−E−R linkage and longer M−E bonds, which are best described as σ(M→E) donor bonds with weak π(M−E) components. Complexes of class b feature an increased lone pair density at the tetrel center, like metallotetrylenes. All carbon and silicon compounds belong to class a, whereas the complexes for E = Sn, Pb and M = Pd, Pt belong to class b. The interjacent germanium compounds as well as NiSnArMes and NiPbArMes show properties of both classes, but the tetrylidyne characteristic is strongly.
We also more closely examined the recently reported cationic group 10 metal complexes [(PPh3)3NiEN(SiiPr3)(Dipp)]+ with E = Ge (B-Ge) and Sn (B-Sn). These compounds feature the same electronic structure as the class a compounds. A certain extent of π(N→E) donation is indicated in these compounds, which is, however, much smaller than in Fischer-type aminocarbyne complexes and does not influence the M≡E bond lengths.
Finally, an extensive study of the potential energy hypersurface varying the M−E−C angles revealed metallotetrylene isomers with M−E−C bond angles of around 95°. Interestingly, these isomers are energetically favored for M = Pd, Pt and E = Sn, Pb over their less bent isomers by 13–29 kJ·mol−1.

Supplementary Materials

The supporting information is available at: https://www.mdpi.com/article/10.3390/inorganics11030129/s1 and contains structural parameters of the MER, MER-2, and B-E complexes; comparisons of computational methods; selected canonical and localized molecular orbitals of the MER and B-E complexes; spin−spin excitation energies of the ML3 and ER fragments, thermodynamically corrected dissociation energies of the MER complexes; and ETS-NOCVs of the MER complexes.

Author Contributions

The data reported herein were produced and presented in equal parts by L.R.M. and J.R. The results presented herein were obtained, analyzed, and discussed through close collaboration of L.R.M., J.R. and A.C.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

We thank the Rheinische Friedrich-Wilhelms Universität Bonn for the financial support of this work. We are very grateful to Ioannis Papazoglou for the synthesis and characterization of the discussed group 10 tetrylidyne complexes. We also highly acknowledge the scientific exchange with Gregor Schnakenburg.

Conflicts of Interest

The authors declare no conflict of interest.

References and Notes

  1. Hashimoto, H.; Tobita, H. Recent Advances in the Chemistry of Transition Metal–Silicon/Germanium Triple-Bonded Complexes. Coord. Chem. Rev. 2018, 355, 362–379. [Google Scholar] [CrossRef]
  2. Saini, S.; Agarwal, A.; Bose, S.K. Transition Metal Chemistry of Heavier Group 14 Congener Triple-Bonded Complexes: Syntheses and Reactivity. Dalton Trans. 2020, 49, 17055–17075. [Google Scholar] [CrossRef]
  3. Fischer, E.O.; Kreis, G.; Kreiter, C.G.; Müller, J.; Huttner, G.; Lorenz, H. trans-Halogeno[alkyl(aryl)carbyne]tetracarbonyl Complexes of Chromium, Molybdenum, and Tungsten—A New Class of Compounds Having a Transition Metal-Carbon Triple Bond. Angew. Chem. Int. Ed. Engl. 1973, 12, 564–565. [Google Scholar] [CrossRef]
  4. Fischer, E.O. Auf dem Weg zu Carben- und Carbin-Komplexen (Nobel-Vortrag). Angew. Chem. 1974, 86, 651–663. [Google Scholar] [CrossRef]
  5. Kim, H.P.; Angelici, R.J. Transition Metal Complexes with Terminal Carbyne Ligands. In Advances in Organometallic Chemistry; Elsevier: Amsterdam, The Netherlands, 1987; Volume 27, pp. 51–111. ISBN 978-0-12-031127-9. [Google Scholar]
  6. Fischer, H.; Hofmann, P.; Kreissl, F.R.; Schrock, R.R.; Schubert, U.; Weiss, K. Carbyne Complexes; Wiley-VCH: Weinheim, Germany, 1988. [Google Scholar]
  7. Mayr, A.; Hoffmeister, H. Recent Advances in the Chemistry of Metal-Carbon Triple Bonds. In Advances in Organometallic Chemistry; Elsevier: Amsterdam, The Netherlands, 1991; Volume 32, pp. 227–324. ISBN 978-0-12-031132-3. [Google Scholar]
  8. Simons, R.S.; Power, P.P. (η5-C5H5)(CO)2MoGeC6H3-2,6-Mes2: A Transition-Metal Germylyne Complex. J. Am. Chem. Soc. 1996, 118, 11966–11967. [Google Scholar] [CrossRef]
  9. Pu, L.; Twamley, B.; Haubrich, S.T.; Olmstead, M.M.; Mork, B.V.; Simons, R.S.; Power, P.P. Triple Bonding to Germanium: Characterization of the Transition Metal Germylynes (η5-C5H5)(CO)2M≡Ge-C6H3-2,6-Mes2 (M = Mo, W; Mes = C6H2-2,4,6-Me3) and (η5-C5H5)(CO)2M≡Ge-C6H3-2,6-Trip2 (M = Cr, Mo, W; Trip = C6H2-2,4,6-i-Pr3) and the Related Single Bonded Metallogermylenes (η5-C5H5)(CO)3M-Ge-C6H3-2,6-Trip2 (M = Cr, W). J. Am. Chem. Soc. 2000, 122, 650–656. [Google Scholar] [CrossRef]
  10. Filippou, A.C.; Philippopoulos, A.I.; Portius, P.; Neumann, D.U. Synthesis and Structure of the Germylyne Complexes trans-[X(dppe)2W≡Ge(η1-Cp*)] (X = Cl, Br, I) and Comparison of the W≡E Bonds (E = C, Ge) by Density Functional Calculations. Angew. Chem. Int. Ed. 2000, 39, 2778–2781. [Google Scholar] [CrossRef]
  11. Filippou, A.C.; Portius, P.; Philippopoulos, A.I. Molybdenum and Tungsten Germylyne Complexes of the General Formula trans-[X(dppe)2M≡Ge-(η1-Cp*)] (X = Cl, Br, I; dppe = Ph2PCH2CH2PPh2; Cp* = C5Me5): Syntheses, Molecular Structures, and Bonding Features of the Germylyne Ligand. Organometallics 2002, 21, 653–661. [Google Scholar] [CrossRef]
  12. Filippou, A.C.; Philippopoulos, A.I.; Portius, P.; Schnakenburg, G. Halide Substitution Reactions of the Germylidyne Complexes trans-[X(dppe)2W≡Ge(η1-Cp*)] (X = Cl, I; dppe = Ph2PCH2CH2PPh2; Cp* = C5Me5). Organometallics 2004, 23, 4503–4512. [Google Scholar] [CrossRef]
  13. Filippou, A.C.; Schnakenburg, G.; Philippopoulos, A.I.; Weidemann, N. Ge2 Trapped by Triple Bonds between Two Metal Centers: The Germylidyne Complexes trans,trans-[Cl(depe)2M≡Ge–Ge≡M(depe)2Cl] (M = Mo, W) and Bonding Analyses of the M≡Ge–Ge≡M Chain. Angew. Chem. Int. Ed. 2005, 44, 5979–5985. [Google Scholar] [CrossRef]
  14. Filippou, A.C.; Weidemann, N.; Philippopoulos, A.I.; Schnakenburg, G. Activation of Aryl Germanium(II) Chlorides by [Mo(PMe3)6] and [W(η2-CH2PMe2)H(PMe3)4]: A New Route to Metal-Germanium Triple Bonds. Angew. Chem. Int. Ed. 2006, 45, 5987–5991. [Google Scholar] [CrossRef]
  15. Filippou, A.C.; Portius, P.; Philippopoulos, A.I.; Rohde, H. Triple Bonding to Tin: Synthesis and Characterization of the Stannylyne Complex trans-[Cl(PMe3)4W≡Sn–C6H3-2,6-Mes2]. Angew. Chem. Int. Ed. 2003, 42, 445–447. [Google Scholar] [CrossRef] [PubMed]
  16. Filippou, A.C.; Philippopoulos, A.I.; Schnakenburg, G. Triple Bonding to Tin: Synthesis and Characterization of the Square-Pyramidal Stannylyne Complex Cation [(dppe)2W≡Sn-C6H3-2,6-Mes2]+ (dppe = Ph2PCH2CH2PPh2, Mes = C6H2-2,4,6-Me3). Organometallics 2003, 22, 3339–3341. [Google Scholar] [CrossRef]
  17. Filippou, A.C.; Weidemann, N.; Schnakenburg, G.; Rohde, H.; Philippopoulos, A.I. Tungsten-Lead Triple Bonds: Syntheses, Structures, and Coordination Chemistry of the Plumbylidyne Complexes trans-[X(PMe3)4W≡Pb(2,6-Trip2C6H3)]. Angew. Chem. Int. Ed. 2004, 43, 6512–6516. [Google Scholar] [CrossRef] [PubMed]
  18. Filippou, A.C.; Rohde, H.; Schnakenburg, G. Triple Bond to Lead: Synthesis and Characterization of the Plumbylidyne Complex trans-[Br(PMe3)4Mo≡Pb–C6H3-2,6-Trip2]. Angew. Chem. Int. Ed. 2004, 43, 2243–2247. [Google Scholar] [CrossRef]
  19. Filippou, A.C.; Weidermann, N.; Schnakenburg, G. Tungsten-Mediated Activation of a PbII-N Bond: A New Route to Tungsten-Lead Triple Bonds. Angew. Chem. Int. Ed. 2008, 47, 5799–5802. [Google Scholar] [CrossRef]
  20. Filippou, A.C.; Chernov, O.; Stumpf, K.W.; Schnakenburg, G. Metal-Silicon Triple Bonds: The Molybdenum Silylidyne Complex [Cp(CO)2Mo≡Si-R]. Angew. Chem. Int. Ed. 2010, 49, 3296–3300. [Google Scholar] [CrossRef]
  21. Filippou, A.C.; Baars, B.; Chernov, O.; Lebedev, Y.N.; Schnakenburg, G. Silicon-Oxygen Double Bonds: A Stable Silanone with a Trigonal-Planar Coordinated Silicon Center. Angew. Chem. Int. Ed. 2014, 53, 565–570. [Google Scholar] [CrossRef] [PubMed]
  22. Filippou, A.C.; Hoffmann, D.; Schnakenburg, G. Triple Bonds of Niobium with Silicon, Germaniun and Tin: The Tetrylidyne Complexes [(κ3-tmps)(CO)2Nb≡E–R] (E = Si, Ge, Sn; tmps = MeSi(CH2PMe2)3; R = aryl). Chem. Sci. 2017, 8, 6290–6299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Ghana, P.; Arz, M.I.; Chakraborty, U.; Schnakenburg, G.; Filippou, A.C. Linearly Two-Coordinated Silicon: Transition Metal Complexes with the Functional Groups M≡Si–M and M═Si═M. J. Am. Chem. Soc. 2018, 140, 7187–7198. [Google Scholar] [CrossRef]
  24. Ghana, P.; Arz, M.I.; Schnakenburg, G.; Straßmann, M.; Filippou, A.C. Metal–Silicon Triple Bonds: Access to [Si(η5-C5Me5)]+ from SiX2(NHC) and Its Conversion to the Silylidyne Complex [TpMe(CO)2MoSi(η3-C5Me5)] (TpMe = κ3-N,N′,N″-hydridotris(3,5-dimethyl-1-pyrazolyl)borate). Organometallics 2018, 37, 772–780. [Google Scholar] [CrossRef]
  25. Mork, B.V.; Tilley, T.D. Multiple Bonding Between Silicon and Molybdenum: A Transition-Metal Complex with Considerable Silylyne Character. Angew. Chem. Int. Ed. 2003, 42, 357–360. [Google Scholar] [CrossRef] [PubMed]
  26. Hayes, P.G.; Xu, Z.; Beddie, C.; Keith, J.M.; Hall, M.B.; Tilley, T.D. The Osmium–Silicon Triple Bond: Synthesis, Characterization, and Reactivity of an Osmium Silylyne Complex. J. Am. Chem. Soc. 2013, 135, 11780–11783. [Google Scholar] [CrossRef]
  27. Fukuda, T.; Yoshimoto, T.; Hashimoto, H.; Tobita, H. Synthesis of a Tungsten–Silylyne Complex via Stepwise Proton and Hydride Abstraction from a Hydrido Hydrosilylene Complex. Organometallics 2016, 35, 921–924. [Google Scholar] [CrossRef]
  28. Yoshimoto, T.; Hashimoto, H.; Hayakawa, N.; Matsuo, T.; Tobita, H. A Silylyne Tungsten Complex Having an Eind Group on Silicon: Its Dimer–Monomer Equilibrium and Cycloaddition Reactions with Carbodiimide and Diaryl Ketones. Organometallics 2016, 35, 3444–3447. [Google Scholar] [CrossRef]
  29. Dübek, G.; Hanusch, F.; Munz, D.; Inoue, S. An Air-Stable Heterobimetallic Si2M2 Tetrahedral Cluster. Angew. Chem. Int. Ed. 2020, 59, 5823–5829. [Google Scholar] [CrossRef] [Green Version]
  30. Vyboishchikov, S.F.; Frenking, G. Structure and Bonding of Low-Valent (Fischer-Type) and High-Valent (Schrock-Type) Transition Metal Carbyne Complexes. Chem.—Eur. J. 1998, 4, 1439–1448. [Google Scholar]
  31. Lein, M.; Szabó, A.; Kovács, A.; Frenking, G. Energy Decomposition Analysis of the Chemical Bond in Main Group and Transition Metal Compounds. Faraday Discuss. 2003, 124, 365–378. [Google Scholar] [CrossRef]
  32. Pandey, K.K.; Lein, M.; Frenking, G. Metal Germylyne Complexes [M≡Ge–R] and Metallogermylenes [M–Ge–R]: DFT Analysis of the Systems [(Cp)(CO)nM≡GeMe] (M = Cr, Mo, W, Fe2+, n = 2; M = Fe, n = 1) and [(Cp)(CO)nM–GeMe] (M = Cr, Mo, W, n = 3; M = Fe, n = 2). J. Am. Chem. Soc. 2003, 125, 1660–1668. [Google Scholar] [CrossRef]
  33. Pandey, K.K.; Lledós, A. Linear M≡E—Me Versus Bent M—E—Me: Bonding Analysis in Heavier Metal-Ylidyne Complexes [(Cp)(CO)2M≡EMe] and Metallo-Ylidenes [(Cp)(CO)3M–EMe] (M = Cr, Mo, W; E = Si, Ge, Sn, Pb). Inorg. Chem. 2009, 48, 2748–2759. [Google Scholar] [CrossRef]
  34. Pandey, K.K.; Patidar, P. Insights into the Nature of M≡E Bonds in [(PMe3)4M≡E(Mes)]+ (M = Mo, W) and [(PMe3)5W≡E(Mes)]+: A Dispersion-Corrected DFT Study. RSC Adv. 2014, 4, 13034. [Google Scholar] [CrossRef]
  35. Dewar, M.J.S. A Review of the π-Complex Theory. Bull. Soc. Chim. Fr. 1951, 18, C71–C79. [Google Scholar]
  36. Chatt, J.; Duncanson, L.A. 586. Olefin Co-Ordination Compounds. Part III. Infra-Red Spectra and Structure: Attempted Preparation of Acetylene Complexes. J. Chem. Soc. (Resumed) 1953, 2939–2947. [Google Scholar] [CrossRef]
  37. Guggenberger, L.J.; Schrock, R.R. A Tantalum Carbyne Complex. J. Am. Chem. Soc. 1975, 97, 2935. [Google Scholar] [CrossRef]
  38. Schrock, R.R. Multiple Metal–Carbon Bonds for Catalytic Metathesis Reactions (Nobel Lecture). Angew. Chem. Int. Ed. 2006, 45, 3748–3759. [Google Scholar] [CrossRef] [PubMed]
  39. Filippou, A.C.; Barandov, A.; Schnakenburg, G.; Lewall, B.; van Gastel, M.; Marchanka, A. Open-Shell Complexes Containing Metal-Germanium Triple Bonds. Angew. Chem. Int. Ed. 2012, 51, 789–793. [Google Scholar] [CrossRef]
  40. Filippou, A.C.; Stumpf, K.W.; Chernov, O.; Schnakenburg, G. Metal Activation of a Germylenoid, a New Approach to Metal-Germanium Triple Bonds: Synthesis and Reactions of the Germylidyne Complexes [Cp(CO)2M≡Ge-C(SiMe3)3] (M = Mo, W). Organometallics 2012, 31, 748–755. [Google Scholar] [CrossRef]
  41. Hicks, J.; Hadlington, T.J.; Schenk, C.; Li, J.; Jones, C. Utilizing Steric Bulk to Stabilize Molybdenum Aminogermylyne and Aminogermylene Complexes. Organometallics 2013, 32, 323–329. [Google Scholar] [CrossRef]
  42. Fukuda, T.; Hashimoto, H.; Tobita, H. Reactions of a Tungsten-Germylyne Complex with Alcohols and Arylaldehydes. Chem. Commun. 2013, 49, 4232–4234. [Google Scholar] [CrossRef]
  43. Wienkenhöver, N. 1,2-Dibromodisilenes: A Rich Source for Titanium Silylidyne Complexes, Acyclic Silylenes and Disilyne Dianions. Dissertation (Dr. rer. nat.), University of Bonn, Bonn, Germany, 2017. [Google Scholar]
  44. Arizpe, L. Synthesis and Characterization of Complexes Featuring Tantalum-Germanium Multiple Bonds. Dissertation (Dr. rer. nat.), University of Bonn, Bonn, Germany, 2019. [Google Scholar]
  45. Filippou, A.C.; Chakraborty, U.; Schnakenburg, G. Rhenium-Germanium Triple Bonds: Syntheses and Reactions of the Germylidyne Complexes mer-[X2(PMe3)3Re≡Ge–R] (X = Cl, I, H; R = m-terphenyl). Chem.—Eur. J. 2013, 19, 5676–5686. [Google Scholar] [CrossRef]
  46. Chakraborty, U. Multiple Bonds between Group 7 Transition Metals and Heavier Tetrel Elements (Ge–Pb). Dissertation (Dr. rer. nat.), University of Bonn, Bonn, Germany, 2013. [Google Scholar]
  47. Filippou, A.C.; Ghana, P.; Chakraborty, U.; Schnakenburg, G. Manganese–Tin Triple Bonds: A New Synthetic Route to the Manganese Stannylidyne Complex Cation trans-[H(dmpe)2Mn≡Sn(C6H3-2,6-Mes2)]+ (dmpe = Me2PCH2CH2PMe2, Mes = 2,4,6-trimethylphenyl). J. Am. Chem. Soc. 2013, 135, 11525–11528. [Google Scholar] [CrossRef] [PubMed]
  48. Blom, B. Reactivity of Ylenes at Late Transition Metal Centers. Dissertation (Dr. rer. nat.), University of Bonn, Bonn, Germany, 2011. [Google Scholar]
  49. Lebedev, Y.N. Multiple Bonding of Low-Valent Silicon and Germanium to Group 6 and 9 Metals. Dissertation (Dr. rer. nat.), University of Bonn, Bonn, Germany, 2014. [Google Scholar]
  50. Widemann, M.; Eichele, K.; Schubert, H.; Sindlinger, C.P.; Klenner, S.; Pöttgen, R.; Wesemann, L. Synthesis and Hydrogenation of Heavy Homologues of Rhodium Carbynes: [(Me3P)2(Ph3P)Rh≡E-Ar*] (E = Sn, Pb). Angew. Chem. Int. Ed. 2021, 60, 5882–5889. [Google Scholar] [CrossRef]
  51. Fischer, E.O.; Schneider, J.R. Übergangsmetallcarbin-komplexe. J. Organomet. Chem. 1985, 295, c29–c34. [Google Scholar] [CrossRef]
  52. Papazoglou, I. Unprecedented Tetrylidyne Complexes of Group 6 and 10 Metals. Dissertation (Dr. rer. nat.), University of Bonn, Bonn, Germany, 2016. [Google Scholar]
  53. Keil, P.M.; Hadlington, T.J. Accessing Cationic Tetrylene-Nickel(0) Systems Featuring Donor–Acceptor E–Ni Triple Bonds (E = Ge, Sn). Chem. Commun. 2022, 58, 3011–3014. [Google Scholar] [CrossRef] [PubMed]
  54. Watanabe, C.; Inagawa, Y.; Iwamoto, T.; Kira, M. Synthesis and Structures of (Dialkylsilylene)Bis(Phosphine)-Nickel, Palladium, and Platinum Complexes and (η6-Arene)(Dialkylsilylene)Nickel Complexes. Dalton Trans. 2010, 39, 9414. [Google Scholar] [CrossRef]
  55. A CSD survey (11.08.2022) gave 6 compounds with Ni=Si double bond lengths ranging from 209.4(1) pm to 222.41(5) pm with a median and mean value of 215.1 pm and 216.4 pm, respectively
  56. A CSD survey (11.08.2022) gave 5 compounds with Pt=Si double bond lengths ranging from 220.8(2) pm to 227.0(2) pm with a median and mean value of 221.2 pm and 223.1 pm, respectively
  57. A CSD survey (11.08.2022) gave 1 compound with a Ni=Sn double bond length of 238.7(2) pm
  58. Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [Green Version]
  59. Zhao, Y.; Truhlar, D.G. Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. 2005, 109, 5656–5667. [Google Scholar] [CrossRef]
  60. Bühl, M.; Kabrede, H. Geometries of Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2006, 2, 1282–1290. [Google Scholar] [CrossRef]
  61. Waller, M.P.; Braun, H.; Hojdis, N.; Bühl, M. Geometries of Second-Row Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2007, 3, 2234–2242. [Google Scholar] [CrossRef] [PubMed]
  62. Bühl, M.; Reimann, C.; Pantazis, D.A.; Bredow, T.; Neese, F. Geometries of Third-Row Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2008, 4, 1449–1459. [Google Scholar] [CrossRef] [Green Version]
  63. Maurer, L.R.; Bursch, M.; Grimme, S.; Hansen, A. Assessing Density Functional Theory for Chemically Relevant Open-Shell Transition Metal Reactions. J. Chem. Theory Comput. 2021, 17, 6134–6151. [Google Scholar] [CrossRef] [PubMed]
  64. van Wüllen, C. Molecular Density Functional Calculations in the Regular Relativistic Approximation: Method, Application to Coinage Metal Diatomics, Hydrides, Fluorides and Chlorides, and Comparison with First-Order Relativistic Calculations. J. Chem. Phys. 1998, 109, 392–399. [Google Scholar] [CrossRef]
  65. Andrae, D.; Häußermann, U.; Dolg, M.; Stoll, H.; Preuß, H. Energy-Adjusted Ab-Initio Pseudopotentials for the Second and Third Row Transition Elements. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
  66. Metz, B.; Stoll, H.; Dolg, M. Small-Core Multiconfiguration-Dirac–Hartree–Fock-Adjusted Pseudopotentials for Post-d Main Group Elements: Application to PbH and PbO. J. Chem. Phys. 2000, 113, 2563–2569. [Google Scholar] [CrossRef]
  67. Hong, G.; Dolg, M.; Li, L. A Comparison of Scalar-Relativistic ZORA and DKH Density Functional Schemes: Monohydrides, Monooxides and Monofluorides of La, Lu, Ac and Lr. Chem. Phys. Lett. 2001, 334, 396–402. [Google Scholar] [CrossRef]
  68. Pyykkö, P. Additive Covalent Radii for Single-, Double-, and Triple-Bonded Molecules and Tetrahedrally Bonded Crystals: A Summary. J. Phys. Chem. A 2015, 119, 2326–2337. [Google Scholar] [CrossRef] [PubMed]
  69. Bent, H.A. An Appraisal of Valence-Bond Structures and Hybridization in Compounds of the First-Row Elements. Chem. Rev. 1961, 61, 275–311. [Google Scholar] [CrossRef]
  70. Power, P.P. An Update on Multiple Bonding between Heavier Main Group Elements: The Importance of Pauli Repulsion, Charge-Shift Character, and London Dispersion Force Effects. Organometallics 2020, 39, 4127–4138. [Google Scholar] [CrossRef]
  71. Kutzelnigg, W. Chemical Bonding in Higher Main Group Elements. Angew. Chem. Int. Ed. Engl. 1984, 23, 272–295. [Google Scholar] [CrossRef]
  72. Desclaux, J.P. Relativistic Dirac-Fock Expectation Values for Atoms with Z = 1 to Z = 120. At. Data Nucl. Data Tables 1973, 12, 311–406. [Google Scholar] [CrossRef]
  73. Pandey, K.K.; Patidar, P.; Power, P.P. Structure and Bonding Energy Analysis of Cationic Metal–Ylyne Complexes of Molybdenum and Tungsten, [(MeCN)(PMe3)4M≡EMes]+ (M = Mo, W; E = Si, Ge, Sn, Pb): A Theoretical Study. Inorg. Chem. 2011, 50, 7080–7089. [Google Scholar] [CrossRef]
  74. Schubert, U.; Fischer, E.O.; Wittmann, D. Structure of [(CO)5CrNEt2]BF4, a Key Organometallic Compound; Reaction to Give the Carbene Complex(CO)5CrC(AsPh2)NEt2. Angew. Chem. Int. Ed. Engl. 1980, 19, 643–644. [Google Scholar] [CrossRef]
  75. Kostic, N.; Fenske, R. Molecular Orbital Calculations on Carbyne Complexes CpMn(CO)2CR+ and (CO)5CrCNEt2+. Frontier-Controlled Nucleophilic Addition to Metal-Carbon Triple Bond. J. Am. Chem. Soc. 1981, 103, 4677–4685. [Google Scholar] [CrossRef]
  76. Filippou, A.C.; Grünleitner, W.; Fischer, E.O.; Imhof, W.; Huttner, G. Übergangsmetall-Carbin-Komplexe: XCIX. Synthese und Röntgenstruktur von (η5-C5Me5)(CO)2Mo≡CNEt2, dem ersten niedervalenten Diethylaminocarbin-Komplex von Molybdän mit einem Pentamethylcyclopentadienyl-Liganden. J. Organomet. Chem. 1991, 413, 165–179. [Google Scholar] [CrossRef]
  77. Filippou, A.C.; Portius, P.; Jankowski, C. Aminomethylene Complexes of Molybdenum(IV) and Tungsten(IV) Bearing 1,2-Dithiolato Ligands. J. Organomet. Chem. 2001, 617–618, 656–670. [Google Scholar] [CrossRef]
  78. Biancalana, L.; Marchetti, F. Aminocarbyne Ligands in Organometallic Chemistry. Coord. Chem. Rev. 2021, 449, 214203. [Google Scholar] [CrossRef]
  79. Pipek, J.; Mezey, P.G. A Fast Intrinsic Localization Procedure Applicable for ab initio and Semiempirical Linear Combination of Atomic Orbital Wave Functions. J. Chem. Phys. 1989, 90, 4916–4926. [Google Scholar] [CrossRef]
  80. Weiss, K. Catalytic Reactions of Carbyne Complexes. In Carbyne Complexes; VCH Verlagsgesellschaft: Weinheim, Germany; VCH Publishers: New York, NY, USA, 1988; p. 205. [Google Scholar]
  81. Ervin, K.M.; Gronert, S.; Barlow, S.E.; Gilles, M.K.; Harrison, A.G.; Bierbaum, V.M.; DePuy, C.H.; Lineberger, W.C.; Ellison, G.B. Bond Strengths of Ethylene and Acetylene. J. Am. Chem. Soc. 1990, 112, 5750–5759. [Google Scholar] [CrossRef]
  82. Lai, T.Y.; Tao, L.; Britt, R.D.; Power, P.P. Reversible Sn–Sn Triple Bond Dissociation in a Distannyne: Support for Charge-Shift Bonding Character. J. Am. Chem. Soc. 2019, 141, 12527–12530. [Google Scholar] [CrossRef]
  83. Ziegler, T.; Rauk, A. On the Calculation of Bonding Energies by the Hartree Fock Slater Method: I. The Transition State Method. Theor. Chim. Acta 1977, 46, 1–10. [Google Scholar] [CrossRef]
  84. Michalak, A.; Mitoraj, M.; Ziegler, T. Bond Orbitals from Chemical Valence Theory. J. Phys. Chem. A 2008, 112, 1933–1939. [Google Scholar] [CrossRef]
  85. Mitoraj, M.P.; Michalak, A.; Ziegler, T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
  86. Okuniewski, A.; Rosiak, D.; Chojnacki, J.; Becker, B. Coordination Polymers and Molecular Structures among Complexes of Mercury(II) Halides with Selected 1-Benzoylthioureas. Polyhedron 2015, 90, 47–57. [Google Scholar] [CrossRef]
  87. Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
  88. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  89. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
  90. Axilrod, B.M.; Teller, E. Interaction of the van Der Waals Type Between Three Atoms. J. Chem. Phys. 1943, 11, 299–300. [Google Scholar] [CrossRef]
  91. Muto, Y. Force between Nonpolar Molecules. Proc. Phys. Math. Soc. Jpn. 1943, 17, 629–631. [Google Scholar]
  92. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  93. Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291–309. [Google Scholar] [CrossRef]
  94. Vahtras, O.; Almlöf, J.; Feyereisen, M.W. Integral Approximations for LCAO-SCF Calculations. Chem. Phys. Lett. 1993, 213, 514–518. [Google Scholar] [CrossRef]
  95. Weigend, F.; Kattannek, M.; Ahlrichs, R. Approximated Electron Repulsion Integrals: Cholesky Decomposition versus Resolution of the Identity Methods. J. Chem. Phys. 2009, 130, 164106. [Google Scholar] [CrossRef]
  96. Weigend, F. Hartree–Fock Exchange Fitting Basis Sets for H to Rn. J. Comput. Chem. 2008, 29, 167–175. [Google Scholar] [CrossRef]
  97. Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W. Optimized Accurate Auxiliary Basis Sets for RI-MP2 and RI-CC2 Calculations for the Atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
  98. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO 7.0; 2018. [Google Scholar]
  99. te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
  100. Baerends, E.J.; Ziegler, T.; Atkins, A.J.; Autschbach, J.; Baseggio, O.; Bashford, D.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerrigter, P.M.; et al. ADF; 2021. [Google Scholar]
  101. Van Lenthe, E.; Baerends, E.J. Optimized Slater-Type Basis Sets for the Elements 1-118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
  102. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  103. Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [Green Version]
Inorganics 11 00129 g001 550
Figure 1. Schematic representation of the dominant orbital interactions in the heavier group 14 tetrylidyne complexes and Fischer-type carbyne complexes using charged, closed-shell fragments (a) or neutral fragments in the doublet state (b); dominant orbital interactions in the Schrock-type alkylidyne complexes using neutral, open-shell fragments in the quartet state (c).
Figure 1. Schematic representation of the dominant orbital interactions in the heavier group 14 tetrylidyne complexes and Fischer-type carbyne complexes using charged, closed-shell fragments (a) or neutral fragments in the doublet state (b); dominant orbital interactions in the Schrock-type alkylidyne complexes using neutral, open-shell fragments in the quartet state (c).
Inorganics 11 00129 g001
Inorganics 11 00129 sch001 550
Scheme 1. Examples for heavier tetrylidyne complexes of group 4, 5, 8, and 9 metals obtained by our group. Eind = 1,1,3,3,5,5,7,7-octaethyl-s-hydrindacene-4-yl, ArMes = 2,6-dimesitylphenyl, dmpe = 1,2-bis(dimethylphosphino)ethane, Dipp = 2,6-di-iso-propylphenyl, and Mes* = 2,4,6-tert-butylphenyl.
Scheme 1. Examples for heavier tetrylidyne complexes of group 4, 5, 8, and 9 metals obtained by our group. Eind = 1,1,3,3,5,5,7,7-octaethyl-s-hydrindacene-4-yl, ArMes = 2,6-dimesitylphenyl, dmpe = 1,2-bis(dimethylphosphino)ethane, Dipp = 2,6-di-iso-propylphenyl, and Mes* = 2,4,6-tert-butylphenyl.
Inorganics 11 00129 sch001
Inorganics 11 00129 sch002 550
Scheme 2. Two-step synthesis of the group 10 metal tetrylidyne complexes [(PMe3)3M≡ER][B(ArF)4] developed by our group (M = Ni, Pt; L = PMe3, Ga(C5(CH3)5); E = Si, Ge, Sn; X = Cl, Br; R = Tbb, ArMes; ArF = C6H3-3,5-(CF3)2).
Scheme 2. Two-step synthesis of the group 10 metal tetrylidyne complexes [(PMe3)3M≡ER][B(ArF)4] developed by our group (M = Ni, Pt; L = PMe3, Ga(C5(CH3)5); E = Si, Ge, Sn; X = Cl, Br; R = Tbb, ArMes; ArF = C6H3-3,5-(CF3)2).
Inorganics 11 00129 sch002
Inorganics 11 00129 g002 550
Figure 2. M−E−C1 angle of the minimum structures plotted for every system. The connecting lines have no physical meaning and are only drawn to visualize the trends.
Figure 2. M−E−C1 angle of the minimum structures plotted for every system. The connecting lines have no physical meaning and are only drawn to visualize the trends.
Inorganics 11 00129 g002
Inorganics 11 00129 sch003 550
Scheme 3. Classification of the compounds assessed throughout this study: R = ArMes, Tbb. The hatched complexes also exhibit characteristics of the metallotetrylene type.
Scheme 3. Classification of the compounds assessed throughout this study: R = ArMes, Tbb. The hatched complexes also exhibit characteristics of the metallotetrylene type.
Inorganics 11 00129 sch003
Inorganics 11 00129 sch004 550
Scheme 4. Lewis representation of the M≡E-bond in B-Ge and B-Sn using the tetrylidyne resonance form B-E-a and the allenic resonance form B-E-b; the encircled charges in the resonance form are formal charges.
Scheme 4. Lewis representation of the M≡E-bond in B-Ge and B-Sn using the tetrylidyne resonance form B-E-a and the allenic resonance form B-E-b; the encircled charges in the resonance form are formal charges.
Inorganics 11 00129 sch004
Inorganics 11 00129 g003 550
Figure 3. Selected molecular orbitals and their respective orbital energies of NiSiArMes. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2.
Figure 3. Selected molecular orbitals and their respective orbital energies of NiSiArMes. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2.
Inorganics 11 00129 g003
Inorganics 11 00129 g004 550
Figure 4. Selected molecular orbitals and their respective orbital energies of PtPbArMes. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2.
Figure 4. Selected molecular orbitals and their respective orbital energies of PtPbArMes. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2.
Inorganics 11 00129 g004
Inorganics 11 00129 g005 550
Figure 5. Pipek−Mezey-localized molecular orbitals of NiSiArMes, their assigned orbital type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity, and the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system is applied as seen in Figure 3.
Figure 5. Pipek−Mezey-localized molecular orbitals of NiSiArMes, their assigned orbital type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity, and the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system is applied as seen in Figure 3.
Inorganics 11 00129 g005
Inorganics 11 00129 g006a 550Inorganics 11 00129 g006b 550
Figure 6. Pipek−Mezey-localized molecular orbitals of PtPbArMes, their assigned orbital type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system was applied as shown in Figure 3.
Figure 6. Pipek−Mezey-localized molecular orbitals of PtPbArMes, their assigned orbital type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system was applied as shown in Figure 3.
Inorganics 11 00129 g006aInorganics 11 00129 g006b
Inorganics 11 00129 sch005 550
Scheme 5. Qualitative MO interaction diagram depicting the bonding situations of (a) the tetrylidyne complex (similar to the diagram for L3M≡CR of P. Hofmann [80]) and (b) the metallotetrylene case.
Scheme 5. Qualitative MO interaction diagram depicting the bonding situations of (a) the tetrylidyne complex (similar to the diagram for L3M≡CR of P. Hofmann [80]) and (b) the metallotetrylene case.
Inorganics 11 00129 sch005
Inorganics 11 00129 g007 550
Figure 7. Selected canonical MOs of B-Ge, their respective orbital energies, and the type of bond they represent. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system was applied as shown in Figure 3.
Figure 7. Selected canonical MOs of B-Ge, their respective orbital energies, and the type of bond they represent. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system was applied as shown in Figure 3.
Inorganics 11 00129 g007
Inorganics 11 00129 g008 550
Figure 8. Selected Pipek−Mezey-localized molecular orbitals of B-Ge, their attributed bond type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system was applied as shown in Figure 3.
Figure 8. Selected Pipek−Mezey-localized molecular orbitals of B-Ge, their attributed bond type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2. The same coordinate system was applied as shown in Figure 3.
Inorganics 11 00129 g008
Inorganics 11 00129 g009 550
Figure 9. Plots of the BCEs (left) and BDEs (right) of the [L3MER]+ complexes (M = Ni–Pt; L = PMe3; E = C – Pb; R = ArMes, Tbb (Si)). Energies corresponding to the cleavage into ML3 + ER+ fragments are marked in blue; energies corresponding to the cleavage into ML3+ + ER fragments are marked in yellow. The connecting lines have no physical meaning and are only drawn to visualize the trends.
Figure 9. Plots of the BCEs (left) and BDEs (right) of the [L3MER]+ complexes (M = Ni–Pt; L = PMe3; E = C – Pb; R = ArMes, Tbb (Si)). Energies corresponding to the cleavage into ML3 + ER+ fragments are marked in blue; energies corresponding to the cleavage into ML3+ + ER fragments are marked in yellow. The connecting lines have no physical meaning and are only drawn to visualize the trends.
Inorganics 11 00129 g009
Inorganics 11 00129 g010 550
Figure 10. Calculated charges in e for the M atoms (x, blue), the E atoms (◼, yellow), the ML3 units (●, grey), and the ER (▲, red) units in the complex cations [L3MEArMes]+derived from natural population analysis (NPA) at the level I theory. The connecting lines have no physical meaning and are only drawn to visualize the trends.
Figure 10. Calculated charges in e for the M atoms (x, blue), the E atoms (◼, yellow), the ML3 units (●, grey), and the ER (▲, red) units in the complex cations [L3MEArMes]+derived from natural population analysis (NPA) at the level I theory. The connecting lines have no physical meaning and are only drawn to visualize the trends.
Inorganics 11 00129 g010
Inorganics 11 00129 g011a 550Inorganics 11 00129 g011b 550
Figure 11. Isosurface plots (isosurface value = 0.002 e Bohr−3) of deformation densities (Δρn) in e Bohr−3 of complementary NOCVs (ψ−n and ψ+n) of NiSiTbb (top), NiGeArMes (middle, split into α- and β-spin derived deformation densities), and PtPbArMes (bottom), given with their respective eigenvalues (ν−n and ν+n). Regions of charge depletion (Δρn < 0 e Bohr−3) are shown in red, and regions of charge accumulation (Δρn > 0 e Bohr−3) are shown in grey. Canonical fragment MOs are given in order to relate the respective NOCV interactions to the fragment orbital interactions. The canonical fragment MOs are not directly related to the NOCVs and were obtained through visual comparison of the NOCVs with the fragment MOs. Level of theory: B97-D3 (BJ)/TZ2P//I. The same coordinate system was applied as shown in Figure 3.
Figure 11. Isosurface plots (isosurface value = 0.002 e Bohr−3) of deformation densities (Δρn) in e Bohr−3 of complementary NOCVs (ψ−n and ψ+n) of NiSiTbb (top), NiGeArMes (middle, split into α- and β-spin derived deformation densities), and PtPbArMes (bottom), given with their respective eigenvalues (ν−n and ν+n). Regions of charge depletion (Δρn < 0 e Bohr−3) are shown in red, and regions of charge accumulation (Δρn > 0 e Bohr−3) are shown in grey. Canonical fragment MOs are given in order to relate the respective NOCV interactions to the fragment orbital interactions. The canonical fragment MOs are not directly related to the NOCVs and were obtained through visual comparison of the NOCVs with the fragment MOs. Level of theory: B97-D3 (BJ)/TZ2P//I. The same coordinate system was applied as shown in Figure 3.
Inorganics 11 00129 g011aInorganics 11 00129 g011b
Inorganics 11 00129 g012 550
Figure 12. Schematic representation of the bonding situation found in the herein studied [L3MER]+ complexes (L = PMe3).
Figure 12. Schematic representation of the bonding situation found in the herein studied [L3MER]+ complexes (L = PMe3).
Inorganics 11 00129 g012
Inorganics 11 00129 g013 550
Figure 13. PES scans (theory level I) of the M−E−C bond angle for E = Si (top left (R = Tbb); top right R = ArMes)), E = Ge (middle left), E = Sn (middle right), and E = Pb (bottom). The connecting lines have no physical meaning and are given only to visualize the trends. The thicker dots represent confirmed minimum structures for the respective compound. No minimum structure could be obtained for the isomers of NiSiTbb and NiSiArMes.
Figure 13. PES scans (theory level I) of the M−E−C bond angle for E = Si (top left (R = Tbb); top right R = ArMes)), E = Ge (middle left), E = Sn (middle right), and E = Pb (bottom). The connecting lines have no physical meaning and are given only to visualize the trends. The thicker dots represent confirmed minimum structures for the respective compound. No minimum structure could be obtained for the isomers of NiSiTbb and NiSiArMes.
Inorganics 11 00129 g013
Inorganics 11 00129 g014 550
Figure 14. Minimum gas-phase structure of PtPbArMes-2. Hydrogen atoms are omitted for clarity.
Figure 14. Minimum gas-phase structure of PtPbArMes-2. Hydrogen atoms are omitted for clarity.
Inorganics 11 00129 g014
Inorganics 11 00129 g015 550
Figure 15. Pipek−Mezey-localized molecular orbitals of PtPbArMes-2, their attributed bond type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2.
Figure 15. Pipek−Mezey-localized molecular orbitals of PtPbArMes-2, their attributed bond type, and corresponding Mulliken populations. Hydrogen atoms are omitted for clarity; the isosurface value was set to 0.04 e1/2 Bohr−3/2.
Inorganics 11 00129 g015
Inorganics 11 00129 g016 550
Figure 16. Isosurface plots (isosurface value = 0.002 e Bohr−3) of deformation densities (Δρn) in e Bohr−3 of complementary NOCVs (ψ−n and ψ+n) of PtPbArMes-2 given with the respective eigenvalues (ν−n and ν+n). Regions of charge depletion (Δρn < 0 e Bohr−3) are shown in red, and regions of charge accumulation (Δρn > 0 e Bohr−3) are shown in grey. Level of theory: B97-D3 (BJ)/TZ2P//I.
Figure 16. Isosurface plots (isosurface value = 0.002 e Bohr−3) of deformation densities (Δρn) in e Bohr−3 of complementary NOCVs (ψ−n and ψ+n) of PtPbArMes-2 given with the respective eigenvalues (ν−n and ν+n). Regions of charge depletion (Δρn < 0 e Bohr−3) are shown in red, and regions of charge accumulation (Δρn > 0 e Bohr−3) are shown in grey. Level of theory: B97-D3 (BJ)/TZ2P//I.
Inorganics 11 00129 g016
Table
Table 1. Selected calculated bonding parameters of the group 10 tetrylidyne complex cations [(PMe3)3MER]+ (MER: M = Ni, Pd, Pt; E = C, Si, Ge, Sn, Pb; R = ArMes, Tbb (Si)) at the B97-D3 (BJ)-ATM/def2-TZVP level of theory (0 K, gas phase). Experimental bonding parameters of MERexp were obtained from sc-XRD data at 100–123 K [52]. For NiGeArMesexp and PtGeArMesexp, the bonding parameters of the two independent complex cations found in the unit cell are listed. The experimental bonding parameters of B-Eexp were taken from ref. [53]. Bond lengths and angles are given in picometers and degrees, respectively.
Table 1. Selected calculated bonding parameters of the group 10 tetrylidyne complex cations [(PMe3)3MER]+ (MER: M = Ni, Pd, Pt; E = C, Si, Ge, Sn, Pb; R = ArMes, Tbb (Si)) at the B97-D3 (BJ)-ATM/def2-TZVP level of theory (0 K, gas phase). Experimental bonding parameters of MERexp were obtained from sc-XRD data at 100–123 K [52]. For NiGeArMesexp and PtGeArMesexp, the bonding parameters of the two independent complex cations found in the unit cell are listed. The experimental bonding parameters of B-Eexp were taken from ref. [53]. Bond lengths and angles are given in picometers and degrees, respectively.
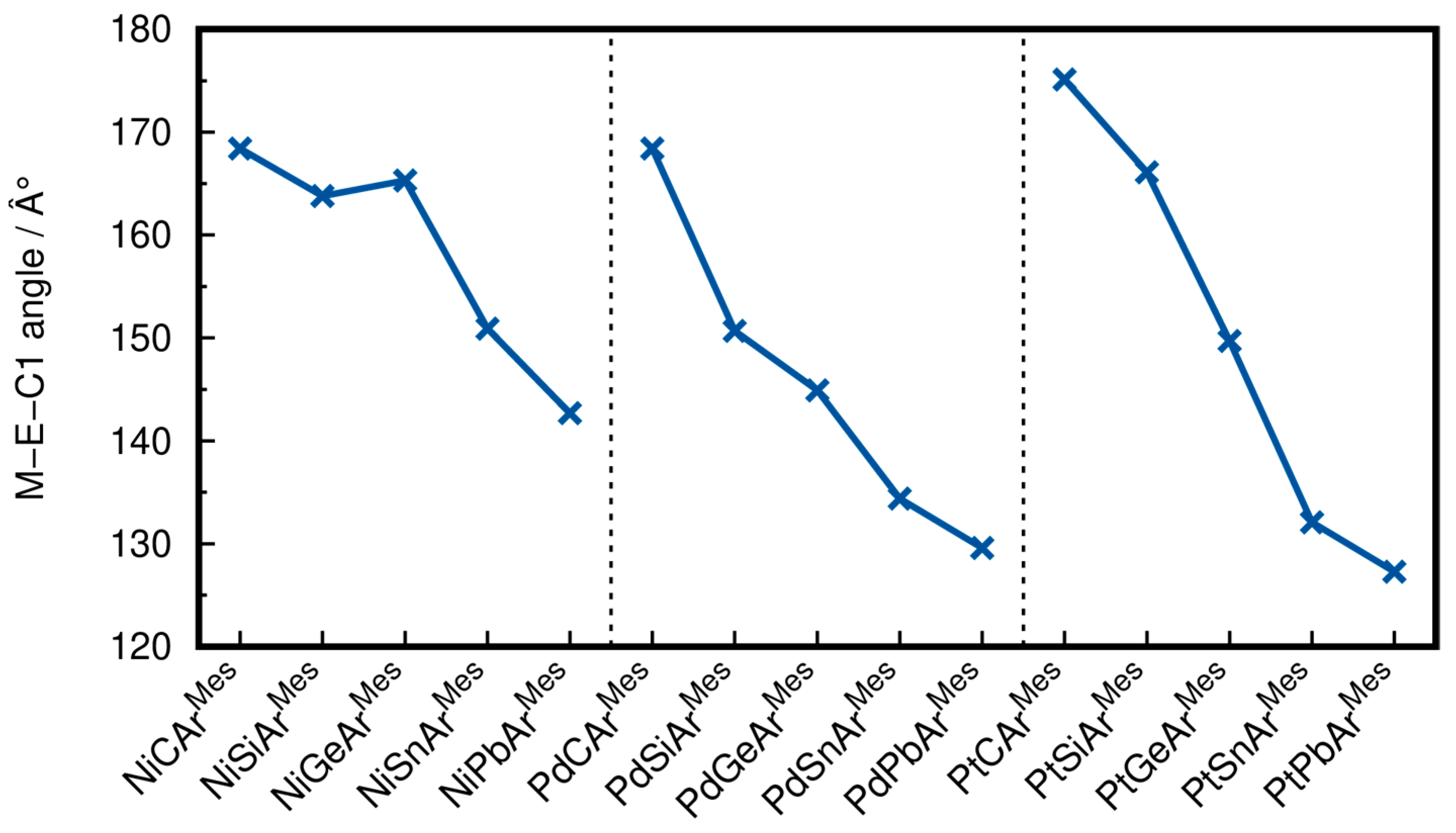
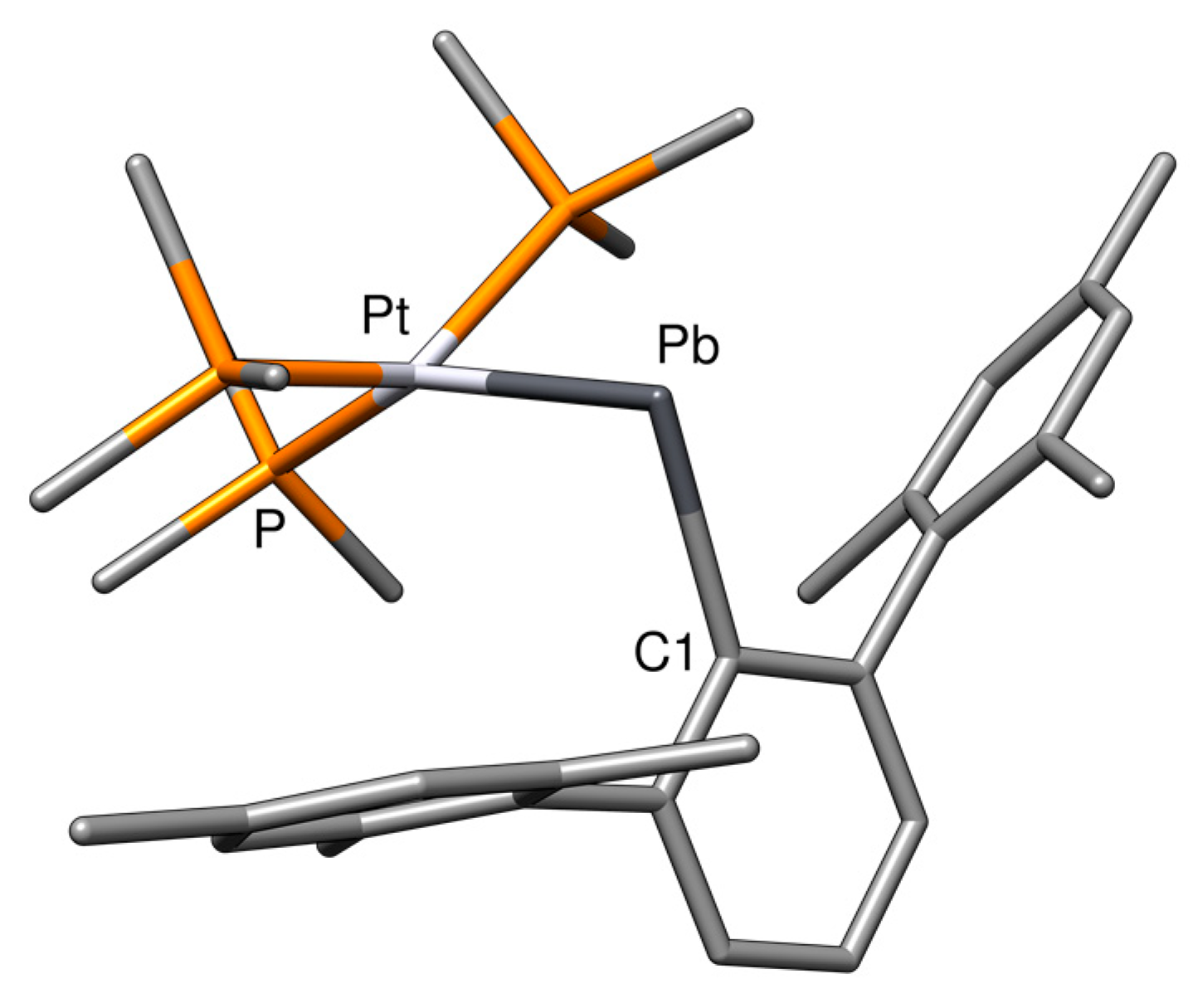
CompoundM−EE−C1M−E−C1
NiCArMes169.1141.3168.4
NiSiTbb204.5184.0167.2
NiSiTbbexp203.11(7)183.8(2)172.40(8)
NiSiArMes204.2186.6163.8
NiGeArMes213.3197.1165.3
NiGeArMesexp210.40(6)194.6(4)164.9(1)
210.20(6)195.0(4)166.5(1)
NiSnArMes235.1219.4150.9
NiSnArMesexp228.08(9)214.0(5)165.1(2)
NiPbArMes244.9229.7142.7
PdCArMes182.0140.9168.4
PdSiTbb215.1184.0163.1
PdSiArMes216.1187.6150.7
PdGeArMes227.9199.5144.9
PdSnArMes251.6222.9134.4
PdPbArMes263.1232.4129.6
PtCArMes179.9141.2175.1
PtSiTbb215.8183.8168.1
PtSiTbbexp213.43(7)184.2(3)173.83(9)
PtSiArMes215.7186.3166.1
PtGeArMes228.4198.9149.7
PtGeArMesexp222.42(7)194.7(7)161.8(2)
222.69(8)195.2(7)163.3(2)
PtSnArMes255.1223.9132.1
PtPbArMes267.7233.1127.3
compoundNi−EE−NNi−E−N
B-Ge218.3186.4173.4
B-Geexp215.9(1)185.3(2)175.9(1)
B-Sn239.6209.1167.8
B-Snexp235.5(1)206.6(6)173.6(2)
Table
Table 2. Calculated BCEs and BDEs in kJ·mol−1 at theory level II of the M−E bonds of the [L3MER]+ complexes to give the ML3 + ER+ and ML3+ + ER fragment combinations (M = Ni–Pt; L = PMe3; E = C–Pb; R = ArMes, Tbb (Si)). BCEs and BDEs of the energetically favorable fragmentation scheme are highlighted in bold.
Table 2. Calculated BCEs and BDEs in kJ·mol−1 at theory level II of the M−E bonds of the [L3MER]+ complexes to give the ML3 + ER+ and ML3+ + ER fragment combinations (M = Ni–Pt; L = PMe3; E = C–Pb; R = ArMes, Tbb (Si)). BCEs and BDEs of the energetically favorable fragmentation scheme are highlighted in bold.
BCEBDE
CompoundML3 + ER+ML3+ + ERML3 + ER+ML3+ + ER
NiCArMes718.6544.3521.8461.6
NiSiTbb470.4427.9402.5377.5
NiSiArMes491.5421.4392.3368.9
NiGeArMes459.3387.7365.0340.0
NiSnArMes383.9346.0316.9304.5
NiPbArMes342.7328.6291.7285.6
PdCArMes625.1469.7404.2340.1
PdSiTbb415.3395.0333.0304.1
PdSiArMes427.4387.9322.5295.3
PdGeArMes383.2349.2289.4260.5
PdSnArMes321.9319.5253.6237.3
PdPbArMes293.3309.0240.4230.4
PtCArMes799.3618.3486.0411.3
PtSiTbb504.0462.5373.5334.0
PtSiArMes520.3450.2362.1324.1
PtGeArMes444.0386.3314.5274.9
PtSnArMes354.6332.6274.1247.2
PtPbArMes313.5307.8251.1230.5
Table
Table 3. Calculated charges in e for the M and E atoms and the ML3 and ER units in the complex cations [L3MER]+ obtained from natural population analysis (NPA) on the theory I level.
Table 3. Calculated charges in e for the M and E atoms and the ML3 and ER units in the complex cations [L3MER]+ obtained from natural population analysis (NPA) on the theory I level.
CompoundMEML3ER
NiCArMes+0.35−0.13+1.18−0.18
NiSiTbb±0.00+0.76+0.62+0.38
NiSiArMes±0.00+0.78+0.67+0.33
NiGeArMes+0.05+0.66+0.59+0.41
NiSnArMes−0.09+1.05+0.48+0.52
NiPbArMes−0.09+1.07+0.46+0.54
PdCArMes+0.31−0.15+1.18−0.18
PdSiTbb−0.03+0.73+0.66+0.34
PdSiArMes−0.03+0.75+0.71+0.29
PdGeArMes−0.01+0.65+0.71+0.29
PdSnArMes−0.15+0.98+0.56+0.44
PdPbArMes−0.17+1.02+0.53+0.47
PtCArMes+0.35−0.24+1.28−0.28
PtSiTbb−0.02+0.65+0.71+0.29
PtSiArMes−0.02+0.68+0.75+0.25
PtGeArMes±0.00+0.58+0.76+0.24
PtSnArMes−0.19+0.96+0.67+0.33
PtPbArMes−0.21+1.00+0.55+0.45
Table
Table 4. Orbital interaction energies ΔEorb in kJ·mol−1 between the ML3 and ER+ fragments in their electronic singlet (s) states and the fragments ML3+ and ER in their electronic doublet (d) states. Values calculated on the B97-D3 (BJ)/TZ2P//I level of theory. The preferred fragment combination is given in bold.
Table 4. Orbital interaction energies ΔEorb in kJ·mol−1 between the ML3 and ER+ fragments in their electronic singlet (s) states and the fragments ML3+ and ER in their electronic doublet (d) states. Values calculated on the B97-D3 (BJ)/TZ2P//I level of theory. The preferred fragment combination is given in bold.
ΔEorb
CompoundML3 (s) + ER+ (s)ML3+ (d) + ER (d)
NiCArMes−848.6−645.3
NiSiTbb−498.1−522.8
NiSiArMes−521.9−486.2
NiGeArMes−461.1−443.5
NiSnArMes−372.7−377.6
NiPbArMes−331.9−370.1
PdCArMes−828.7−671.7
PdSiTbb−472.0−493.8
PdSiArMes−496.5−494.5
PdGeArMes−426.8−428.1
PdSnArMes−334.8−366.9
PdPbArMes−291.1−345.8
PtCArMes−1072.2−903.3
PtSiTbb−585.8−635.1
PtSiArMes−606.9−573.8
PtGeArMes−510.8−499.1
PtSnArMes−380.4−401.8
PtPbArMes−319.6−362.4
Table
Table 5. Key properties of isomers PtPbArMes and PtPbArMes-2. Electronic energies, bond lengths, and angles are given in kJ·mol−1, pm, and deg, respectively.
Table 5. Key properties of isomers PtPbArMes and PtPbArMes-2. Electronic energies, bond lengths, and angles are given in kJ·mol−1, pm, and deg, respectively.
CompoundΔErelM−EE−C1M−E−C1
PtPbArMes+28.5267.7233.1127.3
PtPbArMes-20.0281.9233.794.3
Table
Table 6. Orbital interaction energies ΔEorb in kJ·mol−1 between the fragments ML3 and ER+ in their electronic singlet states of the isomers of PtPbArMes. Values calculated at the B97-D3 (BJ)/TZ2P//I level of theory.
Table 6. Orbital interaction energies ΔEorb in kJ·mol−1 between the fragments ML3 and ER+ in their electronic singlet states of the isomers of PtPbArMes. Values calculated at the B97-D3 (BJ)/TZ2P//I level of theory.
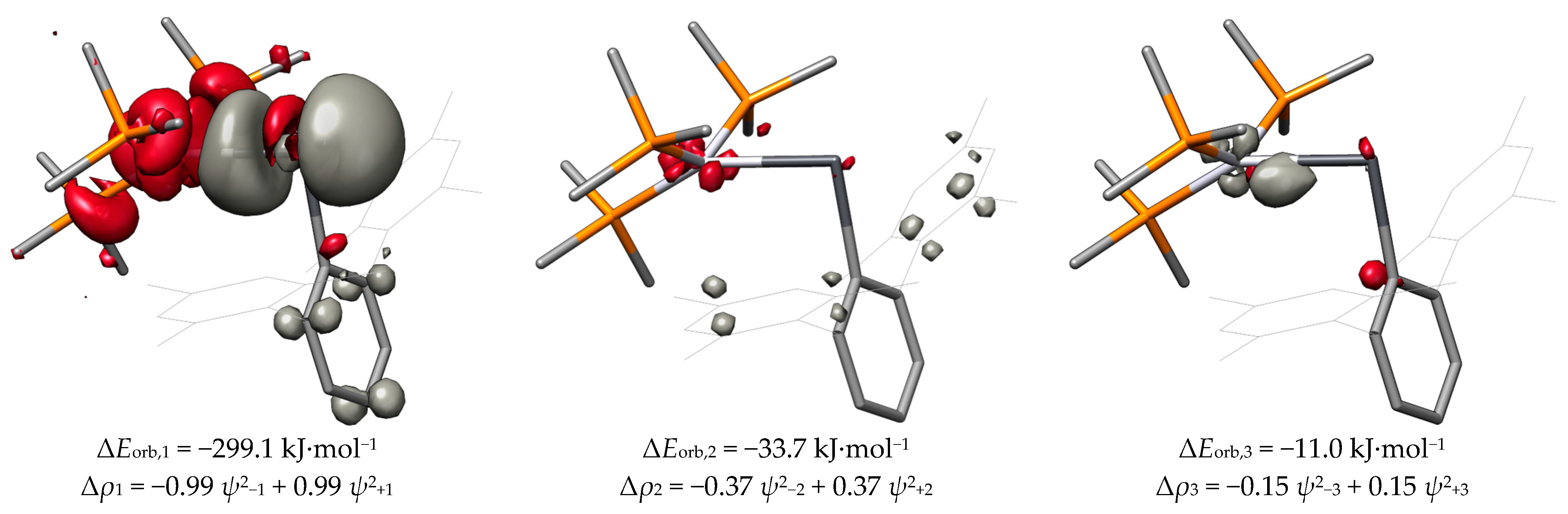
CompoundΔEorb,1ΔEorb,2ΔEorb,3ΔEorb
PtPbArMes−180.1−74.7−26.8−319.6
PtPbArMes-2−299.1−33.7−11.0−386.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Maurer, L.R.; Rump, J.; Filippou, A.C. The Electronic Nature of Cationic Group 10 Ylidyne Complexes. Inorganics 2023, 11, 129. https://doi.org/10.3390/inorganics11030129

AMA Style

Maurer LR, Rump J, Filippou AC. The Electronic Nature of Cationic Group 10 Ylidyne Complexes. Inorganics. 2023; 11(3):129. https://doi.org/10.3390/inorganics11030129

Chicago/Turabian Style

Maurer, Leonard R., Jens Rump, and Alexander C. Filippou. 2023. "The Electronic Nature of Cationic Group 10 Ylidyne Complexes" Inorganics 11, no. 3: 129. https://doi.org/10.3390/inorganics11030129

APA Style

Maurer, L. R., Rump, J., & Filippou, A. C. (2023). The Electronic Nature of Cationic Group 10 Ylidyne Complexes. Inorganics, 11(3), 129. https://doi.org/10.3390/inorganics11030129

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop