Revealing the Minimum Energy Pathways for Formamide Hydrogenation Reactions in the Presence of Platinum and Platinum–Vanadium Clusters: A Quantum Chemical DFT/Nudged Elastic Band Study
Abstract
:1. Introduction
2. Results and Discussion
2.1. Modelling of the Formamide Hydrogenation Reaction in the Absence of a Catalyst
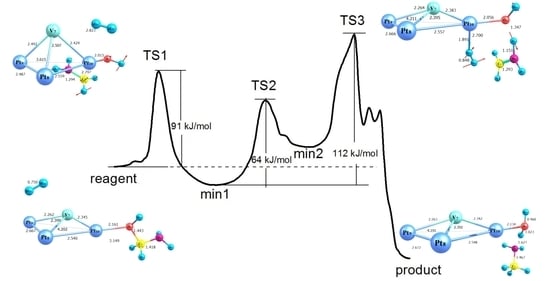
2.2. Modelling of the Formamide Hydrogenation Reaction in the Presence of Pt4 Clusters
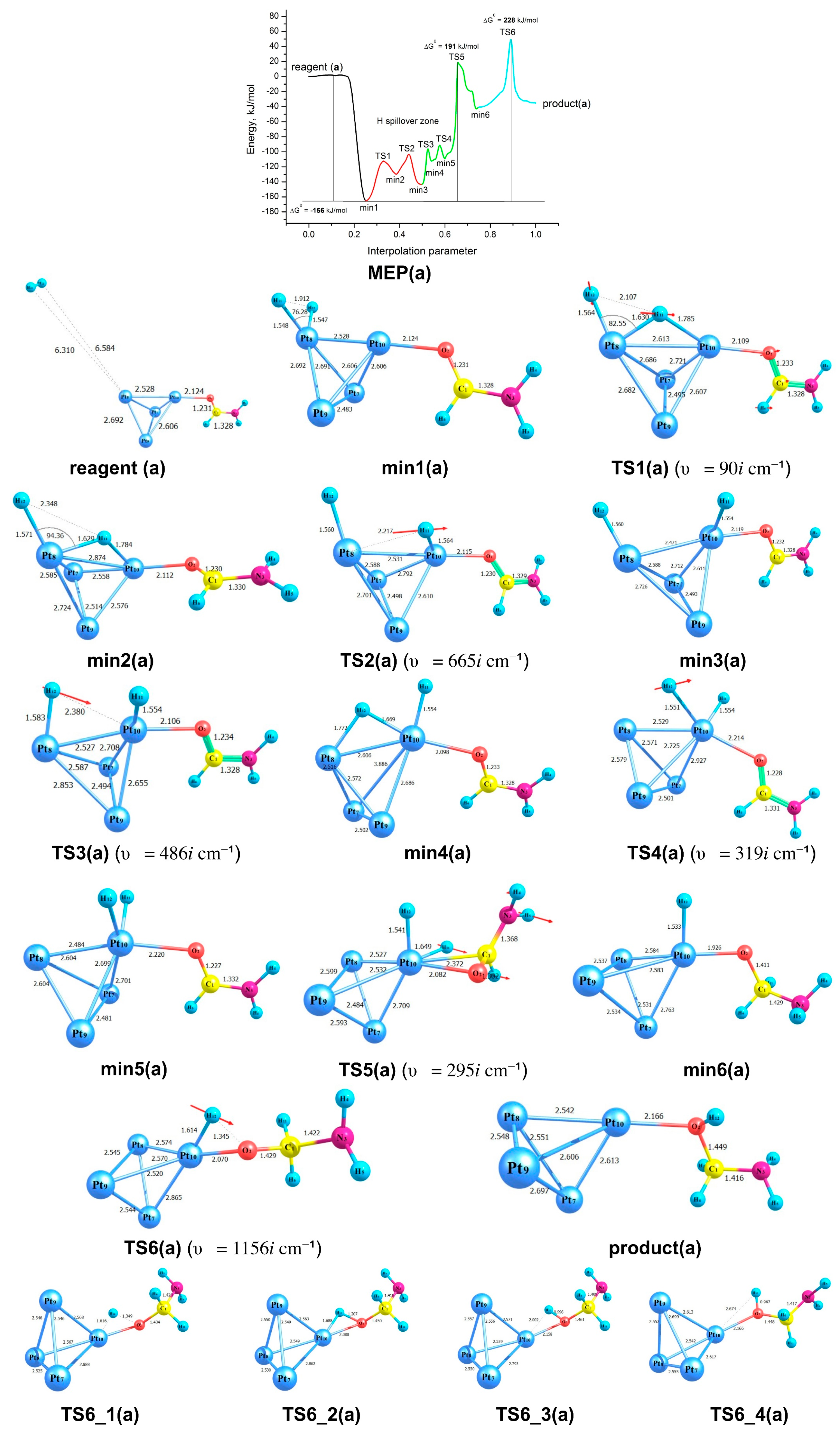
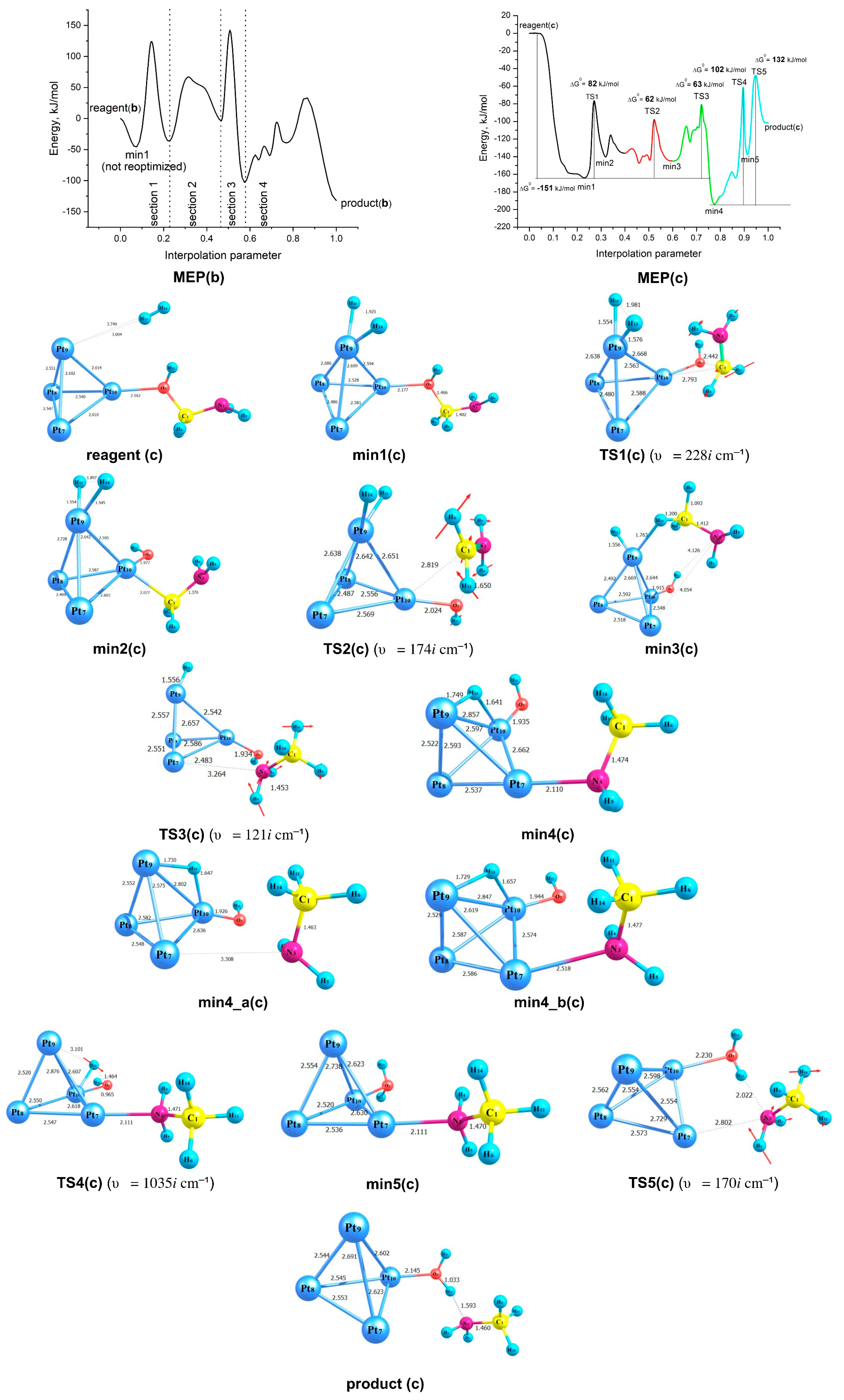
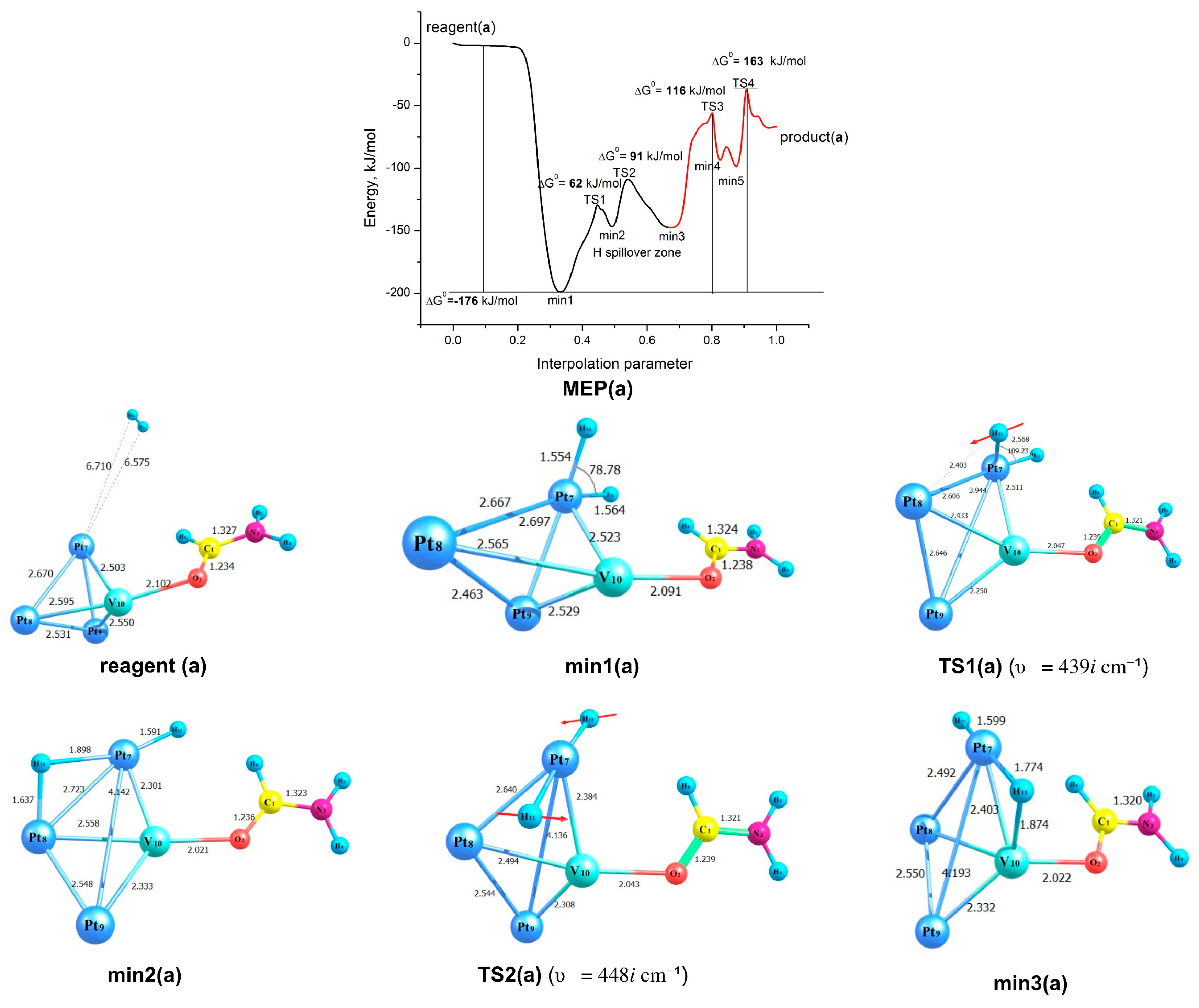
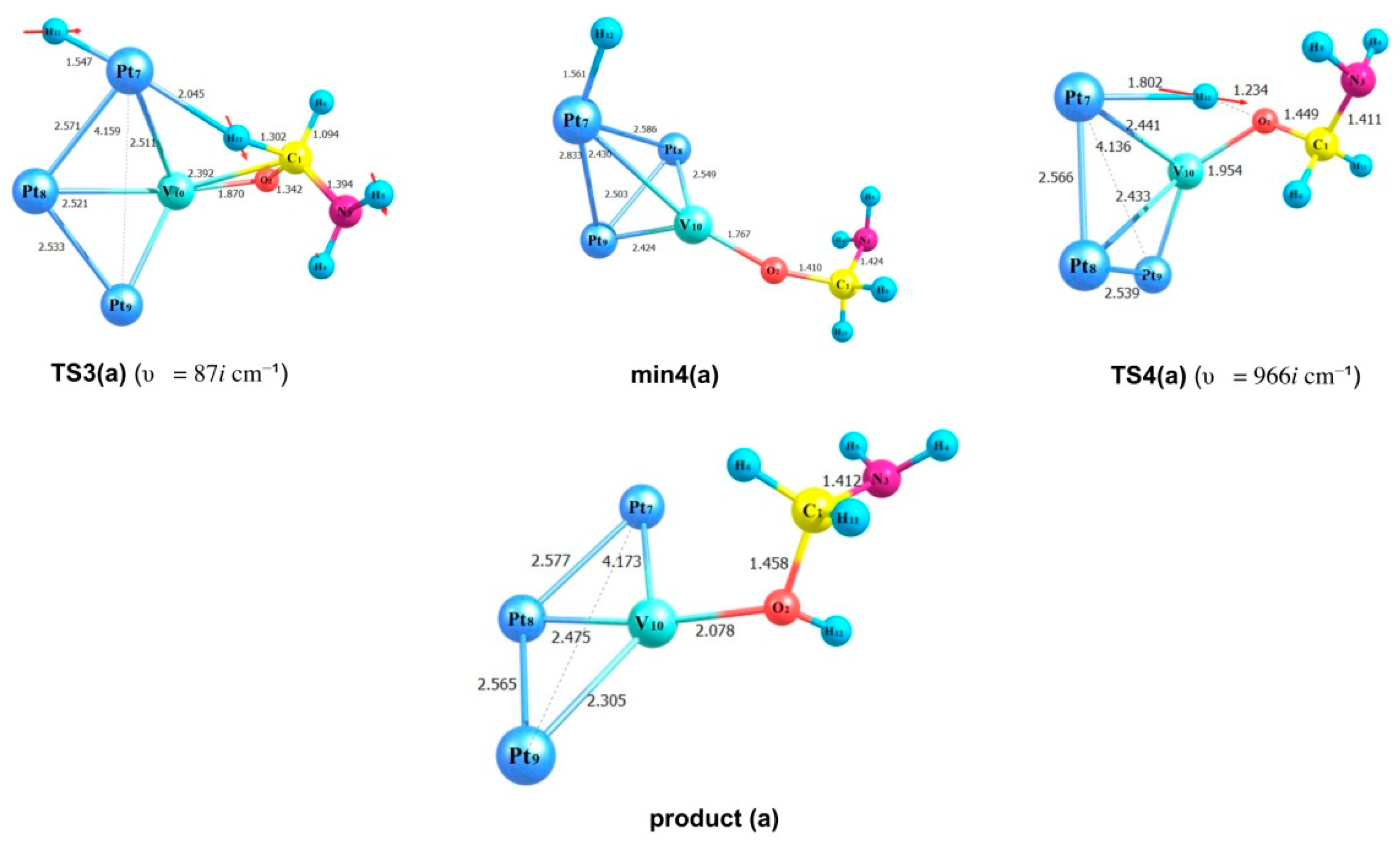
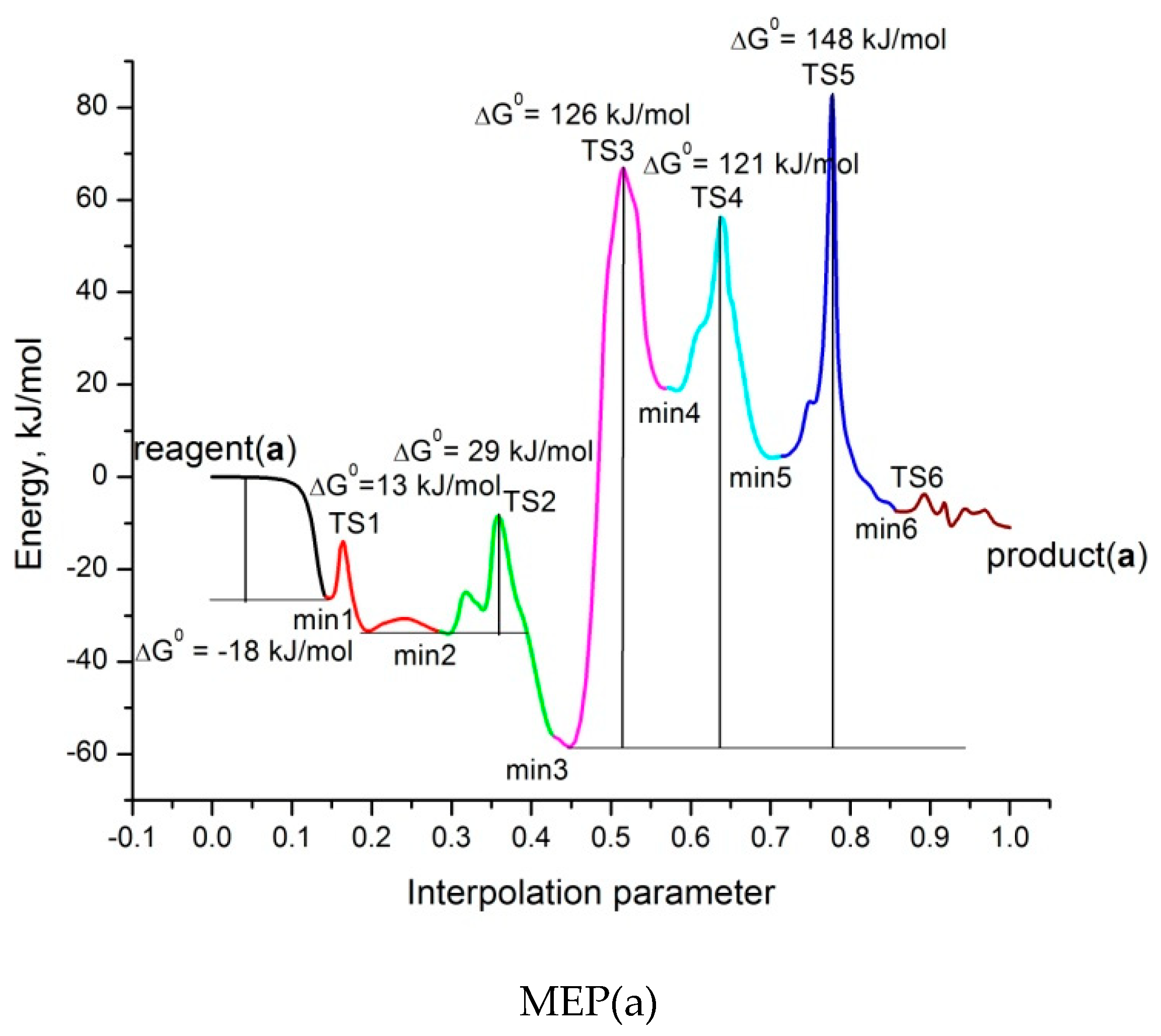
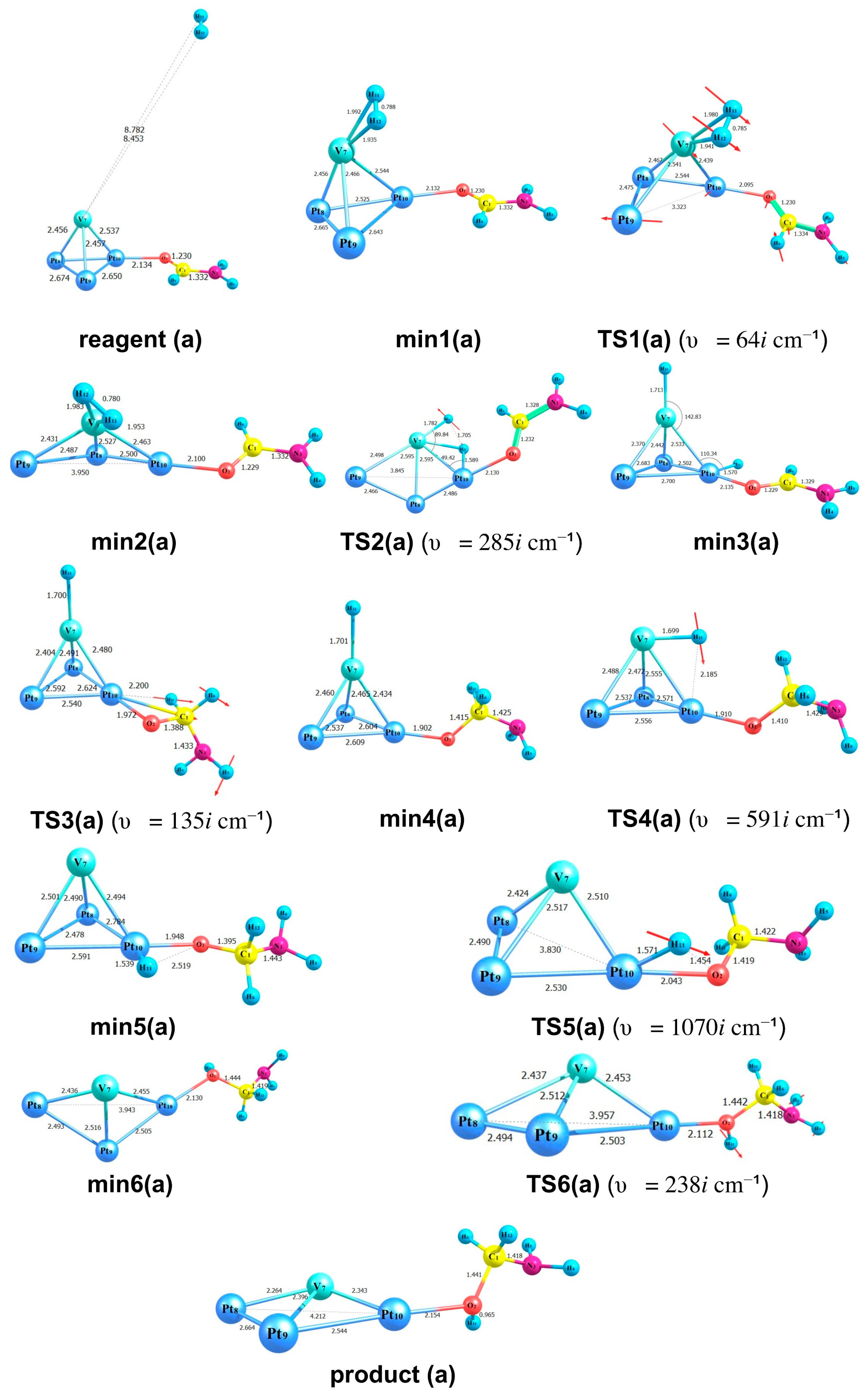
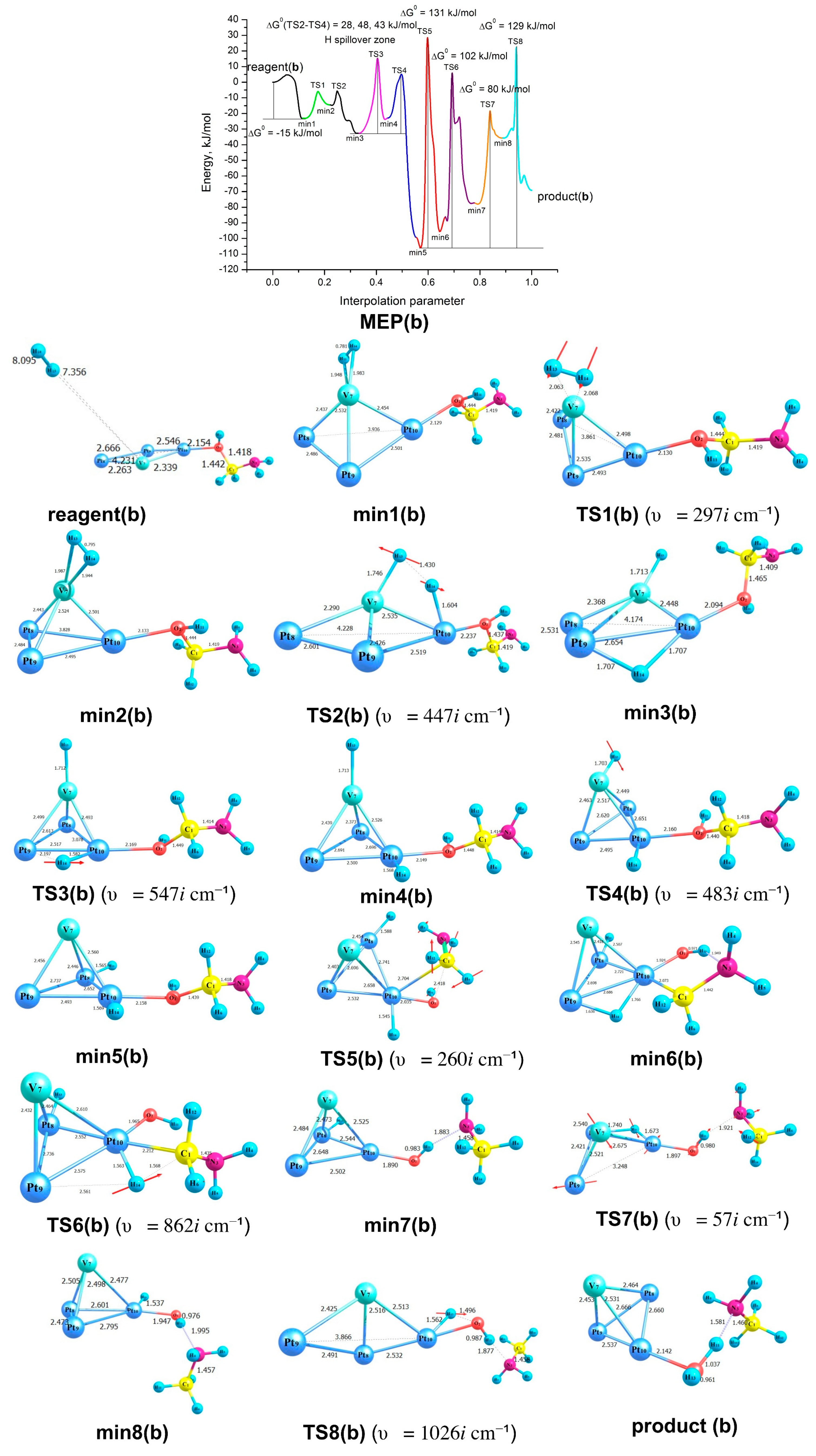
2.3. Modelling of the Formamide Hydrogenation Reaction in the Presence of Pt3V Clusters
3. Details of Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Sun, H.; Wu, L.; Deetz, J.D. Extracting the mechanisms and kinetic models of complex reactions from atomistic simulation data. J. Comput. Chem. 2019, 40, 1586–1592. [Google Scholar] [CrossRef]
- Morgante, P.; Peverati, R. The devil in the details: A tutorial review on some undervalued aspects of density functional theory calculations. Int. J. Quantum Chem. 2020, 120, e26332. [Google Scholar] [CrossRef]
- Chun, H.-J.; Zeng, Z.; Greeley, J. DFT Insights into NO Electrochemical Reduction: A Case Study of Pt(211) and Cu(211) Surfaces. ACS Catal. 2022, 12, 1394–1402. [Google Scholar] [CrossRef]
- Yang, B.; Mendez-Arroyo, J.; May, C.; Yao, J.; Ess, D.H. Transition-State Analysis Reveals Unexpected Coordination-Specific Reactivity That Drives Alkene Dimerization by Sulfated Metal–Organic Frameworks. J. Phys. Chem. C 2023, 127, 8539–8546. [Google Scholar] [CrossRef]
- Kostyukovich, A.Y.; Gordeev, E.G.; Ananikov, V.P. A computational mapping of the R–NHC coupling pathway—The key process in the evolution of Pd/NHC catalytic systems. Mendeleev Commun. 2022, 32, 571–575. [Google Scholar] [CrossRef]
- Schwartz, S.D. Perspective: Path Sampling Methods Applied to Enzymatic Catalysis. J. Chem. Theory Comput. 2022, 18, 6397–6406. [Google Scholar] [CrossRef]
- Du, J.; Sun, X.; Chen, J.; Jiang, G. A Theoretical Study on Small Iridium Clusters: Structural Evolution, Electronic and Magnetic Properties, and Reactivity Predictors. J. Phys. Chem. A 2010, 114, 12825–12833. [Google Scholar] [CrossRef]
- Nikiforov, A.A.; Dubrov, E.N.; Blinou, D.O.; Gurzhiy, V.V.; Selyutin, A.A.; Klyukin, I.N.; Zhdanov, A.P.; Minkovich, A.E.; Panina, N.S.; Eremin, A.V. Penta- and dinuclear carboxylate nickel(II) complexes with pyrazole-based ligands: Syntheses, magnetic properties and DFT calculations. Polyhedron 2021, 195, 114971. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, C.; Zhang, Y.; Cheng, C.; Yang, Z.; Hermansson, K. Regulation of CO oxidation with Pd additives on Nb2CO2 MXene. Int. J. Hydrogen Energy 2021, 46, 8477–8485. [Google Scholar] [CrossRef]
- Zhang, Y.; Chu, B.-S.; Yu, H.-L.; Li, K.; Wang, W.-H.; Yang, W. Molecular dynamics simulations of the initial oxidation process on ferritic Fe–Cr alloy surfaces. RSC Adv. 2022, 12, 9501–9511. [Google Scholar] [CrossRef]
- van der Hoeven, J.E.S.; Jelic, J.; Olthof, L.A.; Totarella, G.; Van Dijk-moes, R.J.A.; Krafft, J.; Louis, C.; Studt, F.; Van Blaaderen, A.; Jongh, P.E. De Unlocking synergy in bimetallic catalysts by core—Shell design. Nat. Mater. 2021, 20, 1216–1220. [Google Scholar] [CrossRef]
- Popov, A.A.; Shubin, Y.V.; Bauman, Y.I.; Plyusnin, P.E.; Mishakov, I.V.; Sharafutdinov, M.R.; Maksimovskiy, E.A.; Korenev, S.V.; Vedyagin, A.A. Preparation of porous Co-Pt alloys for catalytic synthesis of carbon nanofibers. Nanotechnology 2020, 31, 495604. [Google Scholar] [CrossRef]
- Melnikov, D.; Stytsenko, V.; Saveleva, E.; Kotelev, M.; Lyubimenko, V.; Ivanov, E.; Glotov, A.; Vinokurov, V. Selective Hydrogenation of Acetylene over Pd-Mn/Al2O3 Catalysts. Catalysts 2020, 10, 624. [Google Scholar] [CrossRef]
- Zavelev, D.E.; Zhidomirov, G.M.; Tsodikov, M.V. Theoretical Study of Deoxygenation of Esters on Small Pt–Sn Intermetallic Clusters. Kinet. Catal. 2020, 61, 1–39. [Google Scholar] [CrossRef]
- Damte, J.Y.; Zhu, Z.; Lin, P.; Yeh, C.; Jiang, J. B, N-co-doped graphene-supported Ir and Pt clusters for methane activation and C─C coupling: A density functional theory study. J. Comput. Chem. 2020, 41, 194–202. [Google Scholar] [CrossRef]
- Li, K.; An, H.; Yan, P.; Yang, C.; Xiao, T.; Wang, J.; Zhou, S. Hydrogenation of Toluene to Methyl Cyclohexane over PtRh Bimetallic Nanoparticle-Encaged Hollow Mesoporous Silica Catalytic Nanoreactors. ACS Omega 2021, 6, 5846–5855. [Google Scholar] [CrossRef]
- Dadayan, A.K.; Borisov, Y.A.; Zolotarev, Y.A.; Myasoedov, N.F. Modeling Hydrogen Spillover on Oxide Catalytic Centers. Russ. J. Phys. Chem. A 2021, 95, 944–948. [Google Scholar] [CrossRef]
- Deng, Q.; Li, X.; Gao, R.; Wang, J.; Zeng, Z.; Zou, J.; Deng, S.; Tsang, S.C.E. Hydrogen-Catalyzed Acid Transformation for the Hydration of Alkenes and Epoxy Alkanes over Co–N Frustrated Lewis Pair Surfaces. J. Am. Chem. Soc. 2021, 143, 21294–21301. [Google Scholar] [CrossRef]
- Ferrante, F.; Prestianni, A.; Bertini, M.; Duca, D. H2 transformations on graphene supported palladium cluster: Dft-md simulations and neb calculations. Catalysts 2020, 10, 1306. [Google Scholar] [CrossRef]
- Rungnim, C.; Faungnawakij, K.; Sano, N.; Kungwan, N.; Namuangruk, S. Hydrogen storage performance of platinum supported carbon nanohorns: A DFT study of reaction mechanisms, thermodynamics, and kinetics. Int. J. Hydrogen Energy 2018, 43, 23336–23345. [Google Scholar] [CrossRef]
- Liu, L.; Lou, H.; Chen, M. Selective hydrogenation of furfural over Pt based and Pd based bimetallic catalysts supported on modified multiwalled carbon nanotubes (MWNT). Appl. Catal. A Gen. 2018, 550, 1–10. [Google Scholar] [CrossRef]
- Su, J.; Shi, W.; Liu, X.; Zhang, L.; Cheng, S.; Zhang, Y.; Botton, G.A.; Zhang, B. Probing the performance of structurally controlled platinum-cobalt bimetallic catalysts for selective hydrogenation of cinnamaldehyde. J. Catal. 2020, 388, 164–170. [Google Scholar] [CrossRef]
- Zavelev, D.E.; Zhidomirov, G.M.; Tsodikov, M.V. Theoretical Study of Interaction between Hydrogen and Small Pt–Sn Intermetallic Clusters. Kinet. Catal. 2018, 59, 405–417. [Google Scholar] [CrossRef]
- Subramani, M.; Arumugam, D.; Ramasamy, S. Revealing the interfacial phenomenon of metal-hydride formation and spillover effect on C48H16 sheet by platinum metal catalyst (Pt (n = 1–4)) for hydrogen storage enhancement. Int. J. Hydrogen Energy 2023, 48, 4016–4034. [Google Scholar] [CrossRef]
- Szarek, P.; Urakami, K.; Zhou, C.; Cheng, H.; Tachibana, A. On reversible bonding of hydrogen molecules on platinum clusters. J. Chem. Phys. 2009, 130, 084111. [Google Scholar] [CrossRef]
- Xiong, M.; Gao, Z.; Qin, Y. Spillover in Heterogeneous Catalysis: New Insights and Opportunities. ACS Catal. 2021, 11, 3159–3172. [Google Scholar] [CrossRef]
- Sihag, A.; Xie, Z.L.; Thang, H.V.; Kuo, C.L.; Tseng, F.G.; Dyer, M.S.; Chen, H.Y.T. DFT Insights into Comparative Hydrogen Adsorption and Hydrogen Spillover Mechanisms of Pt4/Graphene and Pt4/Anatase (101) Surfaces. J. Phys. Chem. C 2019, 123, 25618–25627. [Google Scholar] [CrossRef]
- Guo, J.; Li, X.-D.; Cheng, X.; Liu, H.; Li, S.; Chen, G. The theoretical study of the bimetallic Ni/Pd, Ni/Pt and Pt/Pd catalysts for hydrogen spillover on penta-graphene. Int. J. Hydrogen Energy 2018, 43, 19121–19129. [Google Scholar] [CrossRef]
- Yang, G.; Akhade, S.A.; Chen, X.; Liu, Y.; Lee, M.; Glezakou, V.; Rousseau, R.; Lercher, J.A. The Nature of Hydrogen Adsorption on Platinum in the Aqueous Phase. Angew. Chem. Int. Ed. 2019, 58, 3527–3532. [Google Scholar] [CrossRef]
- Christmann, K. Interaction of hydrogen with solid surfaces. Surf. Sci. Rep. 1988, 9, 1–163. [Google Scholar] [CrossRef]
- Ruppert, A.M.; Weinberg, K.; Palkovits, R. Hydrogenolysis goes bio: From carbohydrates and sugar alcohols to platform chemicals. Angew. Chem.-Int. Ed. 2012, 51, 2564–2601. [Google Scholar] [CrossRef] [PubMed]
- Rozanov, V.V.; Krylov, O.V. Hydrogen spillover in heterogeneous catalysis. Russ. Chem. Rev. 1997, 66, 107–119. [Google Scholar] [CrossRef]
- Shen, H.; Li, H.; Yang, Z.; Li, C. Magic of hydrogen spillover: Understanding and application. Green Energy Environ. 2022, 7, 1161–1198. [Google Scholar] [CrossRef]
- Matsura, V.A.; Panina, N.S.; Potekhin, V.V.; Ukraintsev, V.B.; Khokhryakov, K.A.; Platonov, V.V.; Tatsenko, O.M.; Panin, A.I. A Quantum-Chemical Study of Dissociation of H2 Molecule on Palladium Clusters. Russ. J. Gen. Chem. 2004, 74, 975–979. [Google Scholar] [CrossRef]
- Panina, N.S.; Buslaeva, T.M.; Fischer, A.I. Activation of H2 molecules on platinum and platinum-vanadium clusters: Quantum-chemical DFT modeling. Kinet. Catal. 2023, 64, 588–602 . [Google Scholar]
- Ásgeirsson, V.; Birgisson, B.O.; Bjornsson, R.; Becker, U.; Neese, F.; Riplinger, C.; Jónsson, H. Nudged Elastic Band Method for Molecular Reactions Using Energy-Weighted Springs Combined with Eigenvector Following. J. Chem. Theory Comput. 2021, 17, 4929–4945. [Google Scholar] [CrossRef]
- Häfner, M.; Bredow, T. Hydrogenation of CO and CO2 Catalyzed by Potassium Chloride F Centers. J. Phys. Chem. C 2022, 126, 9713–9723. [Google Scholar] [CrossRef]
- Mitsuta, Y.; Asada, T. Curvature-weighted nudged elastic band method using the Riemann curvature. J. Comput. Chem. 2023, 44, 662–669. [Google Scholar] [CrossRef]
- Bende, A.; Farcaş, A.A. Intermolecular-Type Conical Intersections in Benzene Dimer. Int. J. Mol. Sci. 2023, 24, 2906. [Google Scholar] [CrossRef]
- Nikiforov, A.; Panina, N.; Blinou, D.; Gurzhiy, V.; Nashchekina, J.; Korzhikova-Vlakh, E.; Eremin, A.; Stepanova, M. Ring-Opening Polymerization of rac-Lactide Catalyzed by Octahedral Nickel Carboxylate Complexes. Catalysts 2023, 13, 304. [Google Scholar] [CrossRef]
- Mitsudome, T.; Miyagawa, K.; Maeno, Z.; Mizugaki, T.; Jitsukawa, K.; Yamasaki, J.; Kitagawa, Y.; Kaneda, K. Mild Hydrogenation of Amides to Amines over a Platinum-Vanadium Bimetallic Catalyst. Angew. Chem. 2017, 129, 9509–9513. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Zhang, W.; Luo, M. A Convenient and General Reduction of Amides to Amines with Low-Valent Titanium. Adv. Synth. Catal. 2013, 355, 2775–2780. [Google Scholar] [CrossRef]
- Ke, D.; Zhou, S. General Construction of Amine via Reduction of N=X (X = C, O, H) Bonds Mediated by Supported Nickel Boride Nanoclusters. Int. J. Mol. Sci. 2022, 23, 9337. [Google Scholar] [CrossRef] [PubMed]
- Núñez Magro, A.A.; Eastham, G.R.; Cole-Hamilton, D.J. The synthesis of amines by the homogeneous hydrogenation of secondary and primary amides. Chem. Commun. 2007, 30, 3154–3156. [Google Scholar] [CrossRef] [PubMed]
- Pennetier, A.; Hernandez, W.Y.; Kusema, B.T.; Streiff, S. Efficient hydrogenation of aliphatic amides to amines over vanadium-modified rhodium supported catalyst. Appl. Catal. A Gen. 2021, 624, 118301. [Google Scholar] [CrossRef]
- Fesik, E.V.; Buslaeva, T.M.; Arkhipushkin, I.A. Reaction of [Pt(NH3)4]Cl2 with NH4VO3 in an Alkaline Solution at 190 °C in Autoclave. Russ. J. Gen. Chem. 2020, 90, 2147–2151. [Google Scholar] [CrossRef]
- Corbel, G.; Topić, M.; Gibaud, A.; Lang, C.I. Selective dry oxidation of the ordered Pt–11.1at.% V alloy surface evidenced by in situ temperature-controlled X-ray diffraction. J. Alloys Compd. 2011, 509, 6532–6538. [Google Scholar] [CrossRef]
- Waterstrat, R.M. The vanadium-platinum constitution diagram. Metall. Trans. 1973, 4, 455–466. [Google Scholar] [CrossRef]
- Maldonado, A.; Schubert, K. Crystal Structure. Investigation in Some Alloy Systems Homologous and Quasihomologous to T5-T10. Z. Met. 1964, 55, 619–626. [Google Scholar]
- Luo, Y.-R. Comprehensive Handbook of Chemical Bond Energies; CRC Press: Boca Raton, FL, USA, 2007; ISBN 9780429128684. [Google Scholar]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F. ORCA Manual, Version 5.0.1. Max Planck Institute for Coal Research: Mülheim, Germany, 2021. [Google Scholar]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Debefve, L.; Pollock, C. Systematic assessment of DFT methods for geometry optimization of mononuclear platinum-containing complexes. Phys. Chem. Chem. Phys. 2021, 23, 24780–24788. [Google Scholar] [CrossRef]
- Schlegel, H.B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
- Chemcraft—Graphical Software for Visualization of Quantum Chemistry Computations. Available online: https://www.chemcraftprog.com (accessed on 15 September 2023).
- Elber, R.; Karplus, M. A method for determining reaction paths in large molecules: Application to myoglobin. Chem. Phys. Lett. 1987, 139, 375–380. [Google Scholar] [CrossRef]
- Czerminski, R.; Elber, R. Self-avoiding walk between two fixed points as a tool to calculate reaction paths in large molecular systems. Int. J. Quantum Chem. 1990, 38, 167–185. [Google Scholar] [CrossRef]
- Gillian, R.E.; Wilson, K.R.J. Shadowing, rare events, and rubber bands. A variational Verlet algorithm for molecular dynamics. Chem. Phys. 1992, 97, 1757–1772. [Google Scholar] [CrossRef]



| Reactions | ΔG0 Stage I | ΔG0 Stage II |
|---|---|---|
| (1) {2H2 + OC(H)NH2} | 289 (TS1) | 292 (TS2) |
| (2) {2H2 + Pt3Pt─OC(H)NH2} | 228 (TS6) | 132 (TS5) |
| (3a) {2H2 + Pt3V─OC(H)NH2} | 163 (TS4) | 209 (TS3) |
| (3b) {2H2 + VPt2Pt─OC(H)NH2} | 148 (TS5) | 131(TS5), 129(TS8) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panina, N.S.; Klyukin, I.N.; Buslaeva, T.M.; Fischer, A.I. Revealing the Minimum Energy Pathways for Formamide Hydrogenation Reactions in the Presence of Platinum and Platinum–Vanadium Clusters: A Quantum Chemical DFT/Nudged Elastic Band Study. Inorganics 2023, 11, 384. https://doi.org/10.3390/inorganics11100384
Panina NS, Klyukin IN, Buslaeva TM, Fischer AI. Revealing the Minimum Energy Pathways for Formamide Hydrogenation Reactions in the Presence of Platinum and Platinum–Vanadium Clusters: A Quantum Chemical DFT/Nudged Elastic Band Study. Inorganics. 2023; 11(10):384. https://doi.org/10.3390/inorganics11100384
Chicago/Turabian StylePanina, Natalia S., Ilya N. Klyukin, Tatyana M. Buslaeva, and Andrei I. Fischer. 2023. "Revealing the Minimum Energy Pathways for Formamide Hydrogenation Reactions in the Presence of Platinum and Platinum–Vanadium Clusters: A Quantum Chemical DFT/Nudged Elastic Band Study" Inorganics 11, no. 10: 384. https://doi.org/10.3390/inorganics11100384
APA StylePanina, N. S., Klyukin, I. N., Buslaeva, T. M., & Fischer, A. I. (2023). Revealing the Minimum Energy Pathways for Formamide Hydrogenation Reactions in the Presence of Platinum and Platinum–Vanadium Clusters: A Quantum Chemical DFT/Nudged Elastic Band Study. Inorganics, 11(10), 384. https://doi.org/10.3390/inorganics11100384