Cu2Zn(Sn1−xSix)Se4: Structural Characterization, Vibrational and Physical Properties of CZTSe-Derivatives
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. Powder X-ray Diffraction Measurements
2.3. SEM-EDS Analysis
2.4. Raman Scattering Measurements
2.5. Diffuse Reflectance Measurements
2.6. Electrical Properties
3. Results and Discussion
3.1. X-ray Powder Diffraction and Compositional Characterization
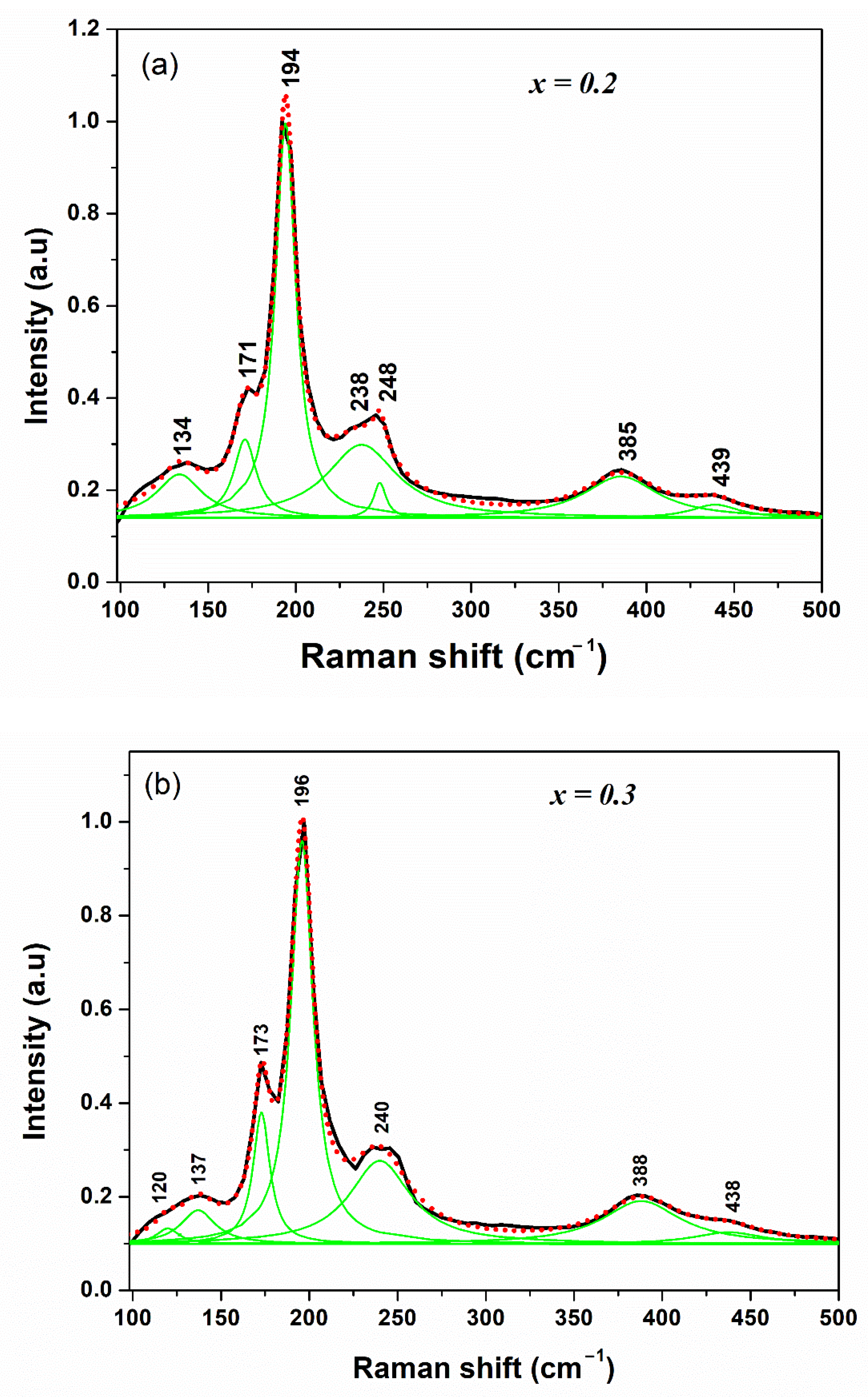
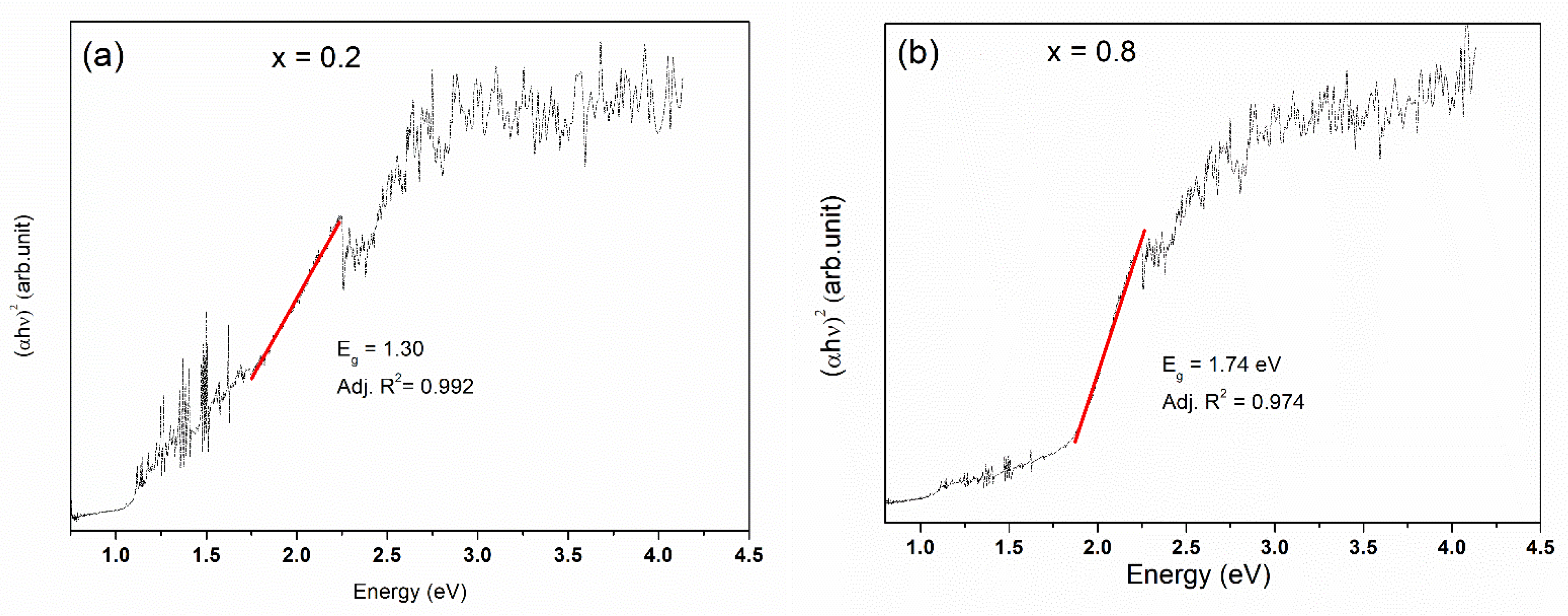
3.2. Raman Analysis and Diffuse Reflectance Measurements
3.3. Electrical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, J.; Ingole, S. Tailoring the surface morphology of Cu2ZnSnS4 thin films for photovoltaic application. Mater. Sci. Semicond. Process. 2019, 93, 173–181. [Google Scholar] [CrossRef]
- Sun, K.; Yan, C.; Liu, F.; Huang, J.; Zhou, F.; Stride, J.A.; Green, M.; Hao, X. Over 9% Efficient Kesterite Cu2ZnSnS4 Solar Cell Fabricated by Using Zn1–xCdxS Buffer Layer. Adv. Energy Mater. 2016, 6, 1600046. [Google Scholar] [CrossRef]
- Ford, G.M.; Guo, Q.; Agrawal, R.; Hillhouse, H.W. Earth abundant element Cu2Zn(Sn1−xGex)S4 nanocrystals for tunable band gap solar cells: 6.8% Efficient device fabrication. Chem. Mater. 2011, 23, 2626–2629. [Google Scholar] [CrossRef]
- Hamdi, M.; Lafond, A.; Guillot-deudon, C.; Hlel, F.; Gargouri, M.; Jobic, S. Crystal chemistry and optical investigations of the Cu2Zn(Sn,Si)S4 series for photovoltaic applications. J. Solid State Chem. 2014, 220, 232–237. [Google Scholar] [CrossRef]
- Ramkumar, S.P.; Gillet, Y.; Miglio, A.; van Setten, M.J.; Gonze, X.; Rignanese, G.-M. First-principles investigation of the structural, dynamical, and dielectric properties of kesterite, stannite, and PMCA phases of Cu2ZnSnS4. Phys. Rev. B 2016, 94, 224302. [Google Scholar] [CrossRef]
- Lu, X.; Zhuang, Z.; Peng, Q.; Li, Y. Wurtzite Cu2ZnSnS4 nanocrystals: A novel quaternary semiconductor. Chem. Commun. 2011, 47, 3141–3143. [Google Scholar] [CrossRef]
- Paier, J.; Asahi, R.; Nagoya, A.; Kresse, G. Cu2ZnSnS4 as a potential photovoltaic material: A hybrid Hartree-Fock density functional theory study. Phys. Rev. B 2009, 79, 115126. [Google Scholar] [CrossRef]
- Park, J.; Yoo, H.; Karade, V.; Gour, K.S.; Choi, E.; Kim, M.; Hao, X.; Shin, S.J.; Kim, J.; Shim, H.; et al. Investigation of low intensity light performances of kesterite CZTSe, CZTSSe, and CZTS thin film solar cells for indoor applications. J. Mater. Chem. A 2020, 8, 14538–14544. [Google Scholar] [CrossRef]
- Tseberlidis, G.; Trifiletti, V.; Vitiello, E.; Husien, A.H.; Frioni, L.; Da Lisca, M.; Alvarez, J.; Acciarri, M.; Binetti, S.O. Band-Gap Tuning Induced by Germanium Introduction in Solution-Processed Kesterite Thin Films. ACS Omega 2022, 7, 23445–23456. [Google Scholar] [CrossRef]
- Kumar, J.; Ingole, S. Optical phonons in pentanary compound (AgxCu1−x)2ZnSnS4 semiconductor: A raman study. J. Alloys Compd. 2021, 865, 158113. [Google Scholar] [CrossRef]
- Guc, M.; Izquierdo-Roca, V.; Pérez Rodríguez, A.; Gurieva, G.; Levcenko, S.; Schorr, S.; Arushanov, E. Raman spectra of wurtzstannite quaternary compounds. Phys. Status Solidi C 2013, 10, 1075–1078. [Google Scholar] [CrossRef]
- Scragg, J.J.S.; Choubrac, L.; Lafond, A.; Ericson, T.; Platzer-Björkman, C. A low-temperature order-disorder transition in Cu2ZnSnS4 thin films. Appl. Phys. Lett. 2014, 104, 41911. [Google Scholar] [CrossRef]
- Kuo, D.-H.; Wubet, W. Mg dopant in Cu2ZnSnSe4: An n-type former and a promoter of electrical mobility up to 120 cm2 V−1 s−1. J. Solid State Chem. 2014, 215, 122–127. [Google Scholar] [CrossRef]
- Kuo, D.-H.; Tsega, M. Electrical conduction and mobility enhancement in p-type In-doped Cu2ZnSnSe4 bulks. Jpn. J. Appl. Phys. 2014, 53, 35801. [Google Scholar] [CrossRef]
- Vishwakarma, M.; Varandani, D.; Shivaprasad, S.M.; Mehta, B.R. Structural, optical, electrical properties and energy band diagram of Cu2ZnSiS4 thin films. Sol. Energy Mater. Sol. Cells 2018, 174, 577–583. [Google Scholar] [CrossRef]
- Schleich, D.M.; Wold, A. Optical and electrical properties of quarternary chalcogenides. Mater. Res. Bull. 1977, 12, 111–114. [Google Scholar] [CrossRef]
- Kuo, D.-H.; Tsega, M. Hole mobility enhancement of Cu-deficient Cu1.75Zn(Sn1−xAlx)Se4 bulks. J. Solid State Chem. 2013, 206, 134–138. [Google Scholar] [CrossRef]
- Cancino-Gordillo, F.E.; Cab, J.V.; Pal, U. Structure and transport behavior of hydrothermally grown phase pure Cu2ZnSn1−xGexS4 (x = 0.0, 0.3) nanoparticles. Appl. Surf. Sci. 2022, 571, 151261. [Google Scholar] [CrossRef]
- Chen, J.; Li, W.; Yan, C.; Huang, S.; Hao, X. Studies of compositional dependent Cu2Zn(GexSn1−x)S4 thin films prepared by sulfurizing sputtered metallic precursors. J. Alloys Compd. 2015, 621, 154–161. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, S.; Xiang, Y. Solvothermal synthesis of Cu2Zn(Sn1−xGex)S4 and Cu2(Sn1−xGex)S3 nanoparticles with tunable band gap energies. J. Alloys Compd. 2015, 640, 75–81. [Google Scholar] [CrossRef]
- Syrbu, N.N.; Zalamai, V.; Guc, M.; Levcenko, S.; Dorogan, A.; Arushanov, E. Birefringence of Cu2ZnSiSe4 single crystals. J. Alloys Compd. 2015, 635, 188–193. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Gürel, T.; Sevik, C.; Çağın, T. Characterization of vibrational and mechanical properties of quaternary compounds Cu2ZnSnS4 and Cu2ZnSnSe4 in kesterite and stannite structures. Phys. Rev. B 2011, 84, 205201. [Google Scholar] [CrossRef]
- Fontané, X.; Izquierdo-Roca, V.; Saucedo, E.; Schorr, S.; Yukhymchuk, V.O.; Valakh, M.Y.; Pérez-Rodríguez, A.; Morante, J.R. Vibrational properties of stannite and kesterite type compounds: Raman scattering analysis of Cu2(Fe,Zn)SnS4. J. Alloys Compd. 2012, 539, 190–194. [Google Scholar] [CrossRef]
- Levcenco, S.; Dumcenco, D.O.; Wang, Y.P.; Wu, J.D.; Huang, Y.S.; Arushanov, E.; Tezlevan, V.; Tiong, K.K. Photoluminescence and Raman scattering characterization of Cu2ZnSiQ4 (Q = S, Se) single crystals. Opt. Mater. 2012, 34, 1072–1076. [Google Scholar] [CrossRef]
- Tauc, J.; Menth, A. States in the gap. J. Non. Cryst. Solids 1972, 8–10, 569–585. [Google Scholar] [CrossRef]
- Moris, S.; Manríquez, V.; Barahona, P.; Galdámez, A.; Valencia-Gálvez, P.; Galdamez, A.; Manriquez, V.; Valencia-Galvez, P. Electrical and optical properties of p-type Ag0.3Cu0.7InQ2 chalcopyrite semiconductors. Lett. Chalcogenide 2018, 15, 615–623. [Google Scholar]
- Ahn, S.; Jung, S.; Gwak, J.; Cho, A.; Shin, K.; Yoon, K.; Park, D.; Cheong, H.; Yun, J.H. Determination of band gap energy (Eg) of Cu2ZnSnSe4 thin films: On the discrepancies of reported band gap values. Appl. Phys. Lett. 2010, 97, 21905. [Google Scholar] [CrossRef]
- Altosaar, M.; Raudoja, J.; Timmo, K.; Danilson, M.; Grossberg, M.; Krustok, J.; Mellikov, E. Cu2Zn1–x Cdx Sn(Se1–ySy)4 solid solutions as absorber materials for solar cells. Phys. Status Solidi A 2008, 205, 167–170. [Google Scholar] [CrossRef]
- Levcenco, S.; Dumcenco, D.; Huang, Y.S.; Arushanov, E.; Tezlevan, V.; Tiong, K.K.; Du, C.H. Absorption-edge anisotropy of Cu2ZnSiQ4 (Q = S, Se) quaternary compound semiconductors. J. Alloys Compd. 2011, 509, 4924–4928. [Google Scholar] [CrossRef]
- Levcenco, S.; Dumcenco, D.; Huang, Y.S.; Arushanov, E.; Tezlevan, V.; Tiong, K.K.; Du, C.H. Polarization-dependent electrolyte electroreflectance study of Cu2ZnSiS4 and Cu2ZnSiSe4 single crystals. J. Alloys Compd. 2011, 509, 7105–7108. [Google Scholar] [CrossRef]
- Chen, S.; Gong, X.G.; Walsh, A.; Wei, S.-H. Electronic structure and stability of quaternary chalcogenide semiconductors derived from cation cross-substitution of II-VI and I-III-VI2 compounds. Phys. Rev. B 2009, 79, 165211. [Google Scholar] [CrossRef]
- Chen, S.; Walsh, A.; Gong, X.-G.; Wei, S.-H. Classification of Lattice Defects in the Kesterite Cu2ZnSnS4 and Cu2ZnSnSe4 Earth-Abundant Solar Cell Absorbers. Adv. Mater. 2013, 25, 1522–1539. [Google Scholar] [CrossRef]
- Tsega, M.; Kuo, D.-H. The performance of the donor and acceptor doping in the Cu-rich Cu2ZnSnSe4 bulks with different Zn/Sn ratios. Solid State Commun. 2013, 164, 42–46. [Google Scholar] [CrossRef]
- Saragih, A.D.; Wubet, W.; Abdullah, H.; Abay, A.K.; Kuo, D.-H. Characterization of Ag-doped Cu2ZnSnSe4 bulks material and their application as thin film semiconductor in solar cells. Mater. Sci. Eng. B 2017, 225, 45–53. [Google Scholar] [CrossRef]
- Kuo, D.-H.; Wubet, W. Mg dopant in Cu2SnSe3: An n-type former and a promoter of electrical mobility up to 387 cm2 V−1 s−1. J. Solid State Chem. 2014, 218, 44–49. [Google Scholar] [CrossRef]
- Hamdi, M.; Chrif, B.; Lafond, A.; Louati, B.; Guillot-Deudon, C.; Hlel, F. Electrical properties of Cu2Zn(Sn1−xSix)S4 (x = 0.1, x = 0.4) compounds for absorber materials in solar-cells. J. Alloys Compd. 2015, 643, 129–136. [Google Scholar] [CrossRef]
- Tsega, M.; Kuo, D.-H. Defects and Its Effects on Properties of Cu-Deficient Cu2ZnSnSe4 Bulks with Different Zn/Sn Ratios. Appl. Phys. Express 2012, 5, 91201. [Google Scholar] [CrossRef]
- Chen, S.; Yang, J.-H.; Gong, X.G.; Walsh, A.; Wei, S.-H. Intrinsic point defects and complexes in the quaternary kesterite semiconductor Cu2ZnSnS4. Phys. Rev. B 2010, 81, 245204. [Google Scholar] [CrossRef]
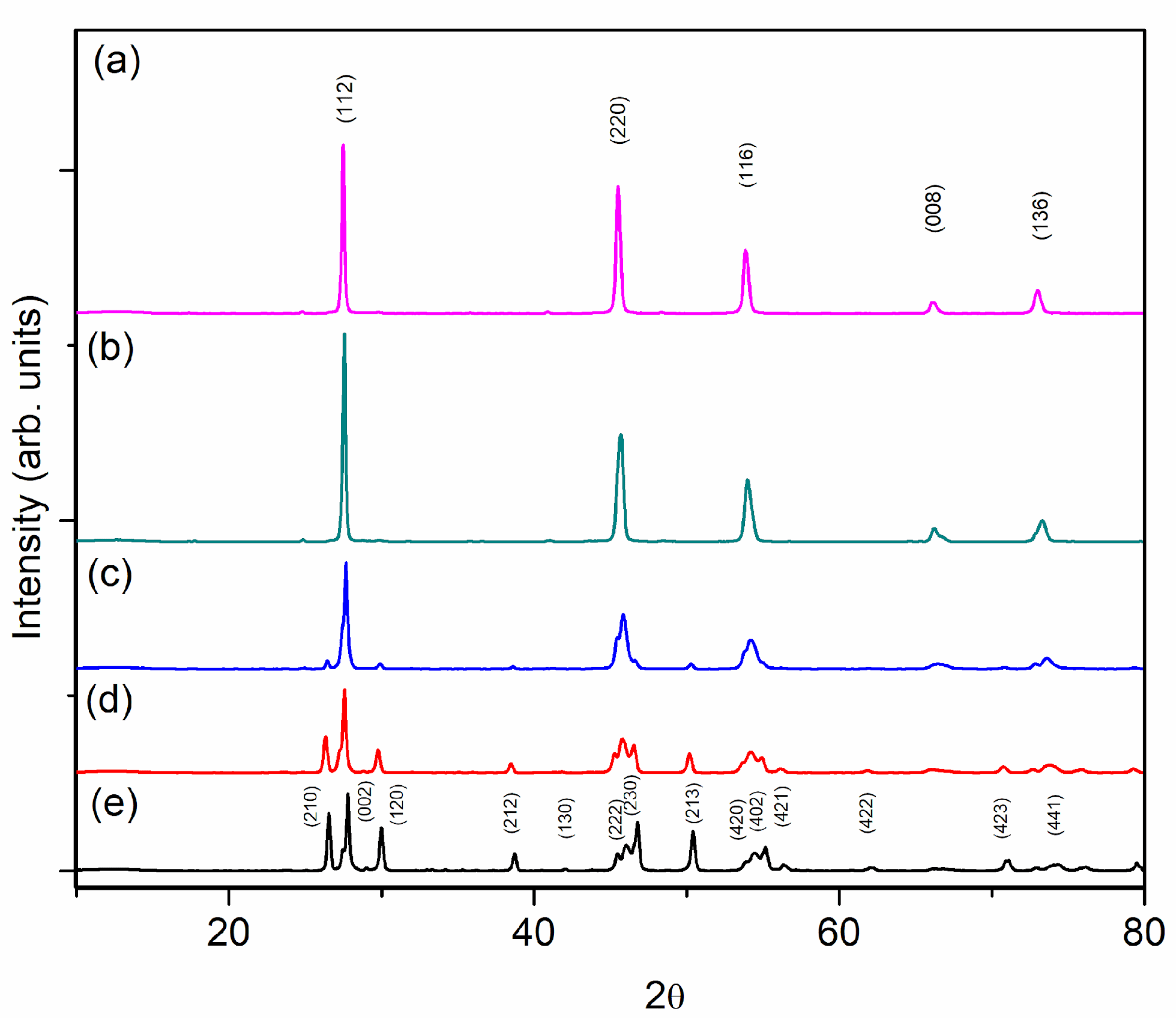
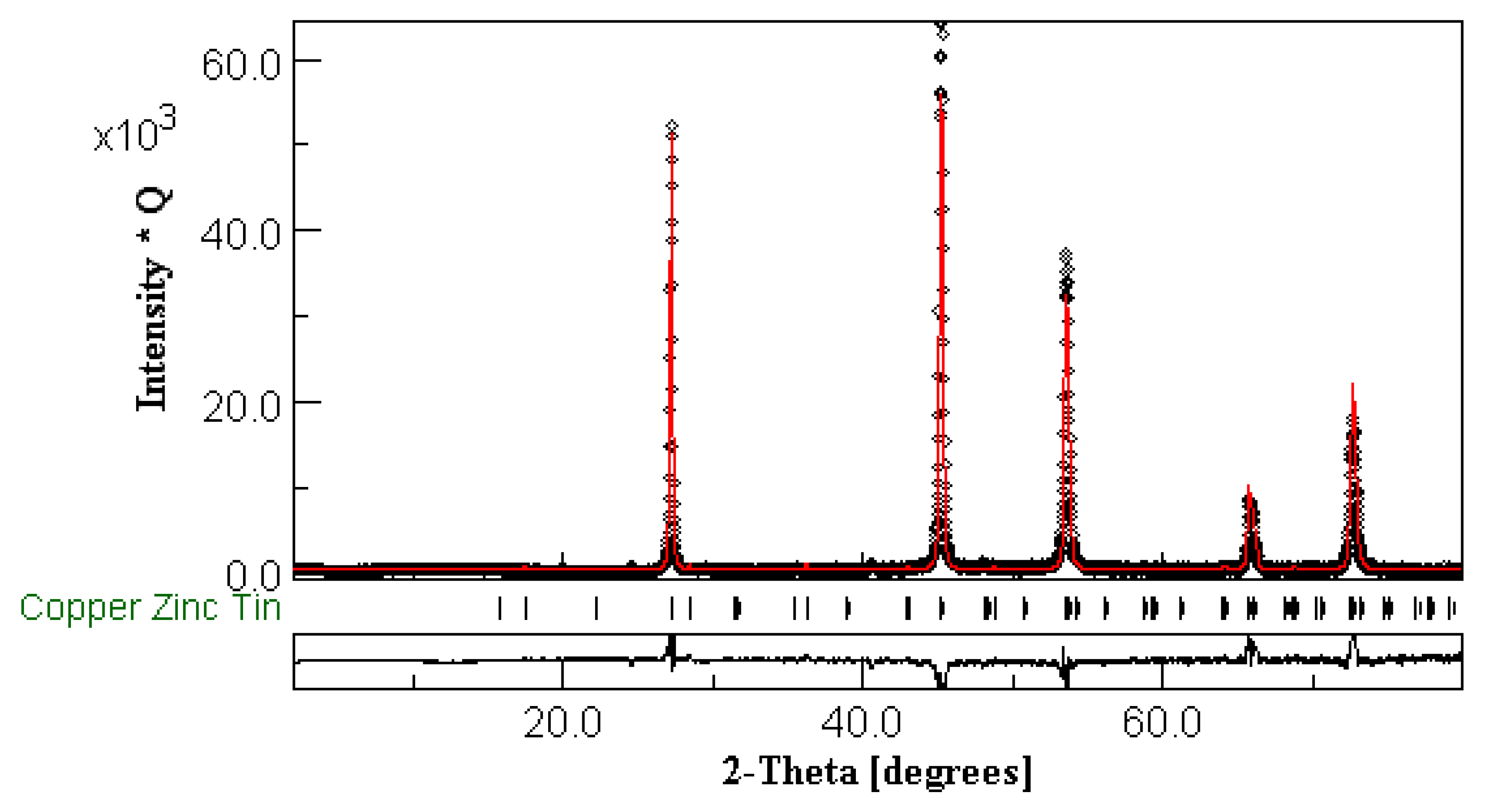


| Composition | Cell Parameters (Å) | Volume (Å3) | %Stannite I42m | %Wurtz-Stannite |
|---|---|---|---|---|
| Cu2ZnSn0.8Si0.2Se4 | a = b = 5.6751(3) c = 11.2991(9) | 363.907(2) | 100.0 | 0 |
| Cu2ZnSn0.7Si0.3Se4 | a = b = 5.6651(4) c = 11.1837(9) | 358.922(2) | 100.0 | 0 |
| Cu2ZnSn0.5Si0.5Se4 | a = b = 5.6515(9) c = 11.1837(3) | 357.201(3) | 85.12 | 14.88 |
| Cu2ZnSn0.3Si0.7Se4 | a = 7.8378(8) b = 6.7498(7) c = 6.4682(6) | 342.191(3) | 45.35 | 54.65 |
| Cu2ZnSn0.2Si0.8Se4 | a = 7.8382(6) b = 6.7480(5) c = 6.4666(4) | 342.033(1) | 29.25 | 70.75 |
| Sample | Mass (%) | Experimental | ||||
|---|---|---|---|---|---|---|
| Cu | Zn | Sn | Si | Se | ||
| Cu2ZnSn0.8Si0.2Se4 | 20.2 | 9.92 | 14.9 | 0.75 | 57.9 | Cu1.9Zn0.92Sn0.77Si0.17Se4.5 |
| Cu2ZnSn0.7Si0.3Se4 | 21.1 | 10.7 | 13.3 | 1.21 | 58.1 | Cu2.0Zn0.99Sn0.68Si0.26Se4.5 |
| Cu2ZnSn0.5Si0.5Se4 | 23.3 | 12.6 | 9.84 | 2.24 | 51.9 | Cu2.1Zn1.1Sn0.48Si0.46Se3.8 |
| Cu2ZnSn0.3Si0.7Se4 | 24.7 | 11.1 | 2.86 | 7.26 | 54.1 | Cu2.2Zn1.0Sn0.25Si0.65Se4.8 |
| Cu2ZnSn0.2Si0.8Se4 | 24.3 | 12.36 | 3.81 | 3.84 | 55.7 | Cu2.1Zn1.1Sn0.18Si0.75Se3.9 |
| Mode | Cu2Zn(Sn1−xSix)Se4 | Cu2ZnSnSe4 | |
|---|---|---|---|
| x = 0.2 | x = 0.3 | Ref. [23] | |
| E | --- | 120 | 160.9 |
| B2 | 134 | 137 | 163.1 |
| A1 | 171 | 173 | 180.0 |
| 194 | 196 | 194.6 | |
| B2 | 238 | 240 | 233.0 |
| 248 | 240.3 | ||
| 385 | 388 | 353.7 | |
| 439 | 438 | --- | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valencia-Gálvez, P.; Barahona, P.; Galdámez, A.; Moris, S. Cu2Zn(Sn1−xSix)Se4: Structural Characterization, Vibrational and Physical Properties of CZTSe-Derivatives. Inorganics 2023, 11, 7. https://doi.org/10.3390/inorganics11010007
Valencia-Gálvez P, Barahona P, Galdámez A, Moris S. Cu2Zn(Sn1−xSix)Se4: Structural Characterization, Vibrational and Physical Properties of CZTSe-Derivatives. Inorganics. 2023; 11(1):7. https://doi.org/10.3390/inorganics11010007
Chicago/Turabian StyleValencia-Gálvez, Paulina, Patricia Barahona, Antonio Galdámez, and Silvana Moris. 2023. "Cu2Zn(Sn1−xSix)Se4: Structural Characterization, Vibrational and Physical Properties of CZTSe-Derivatives" Inorganics 11, no. 1: 7. https://doi.org/10.3390/inorganics11010007
APA StyleValencia-Gálvez, P., Barahona, P., Galdámez, A., & Moris, S. (2023). Cu2Zn(Sn1−xSix)Se4: Structural Characterization, Vibrational and Physical Properties of CZTSe-Derivatives. Inorganics, 11(1), 7. https://doi.org/10.3390/inorganics11010007






