The Role of the Bridge in Single-Ion Magnet Behaviour: Reinvestigation of Cobalt(II) Succinate and Fumarate Coordination Polymers with Nicotinamide
Abstract
:1. Introduction
2. Results
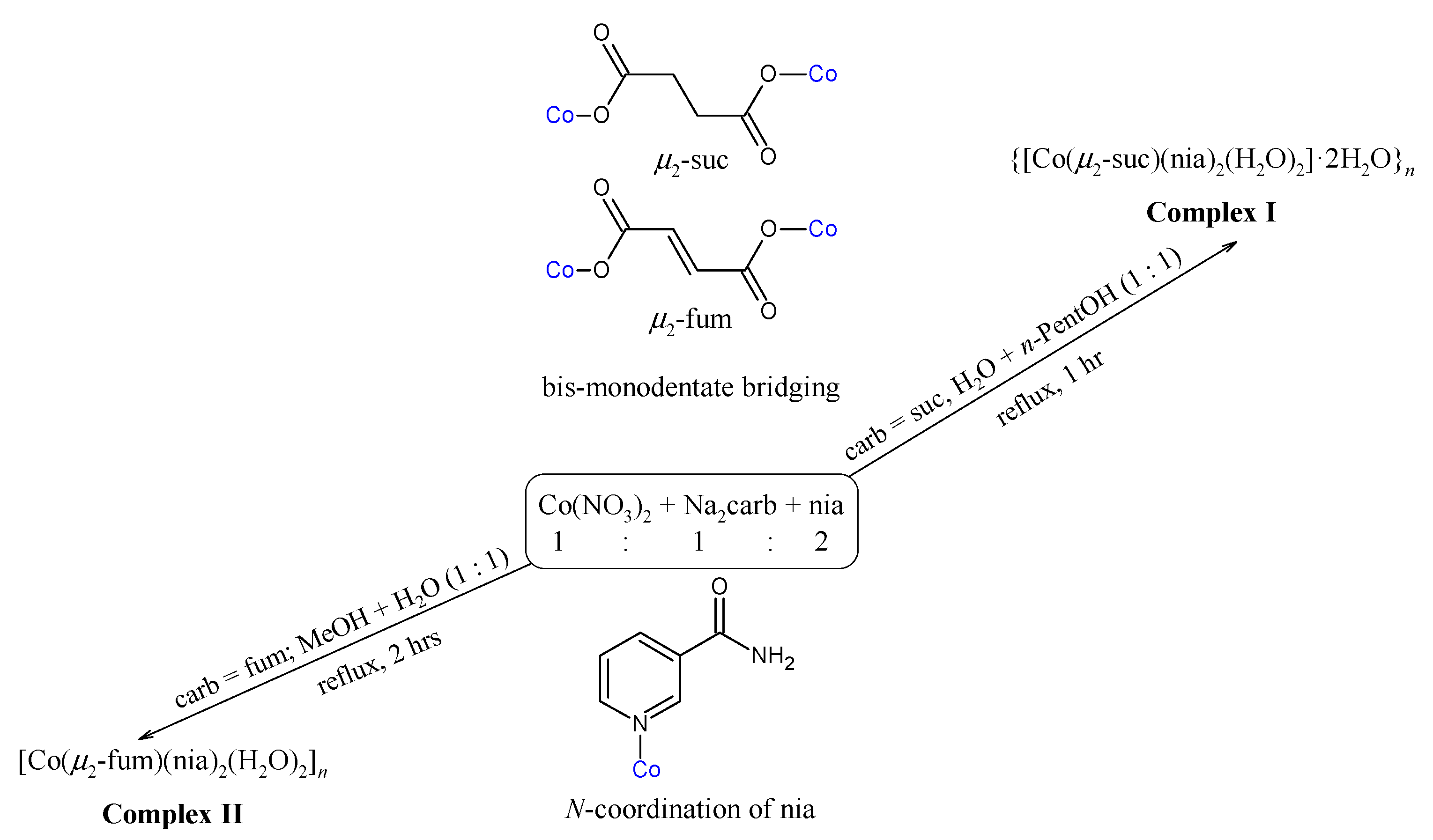
2.1. Syntheses and Characterization
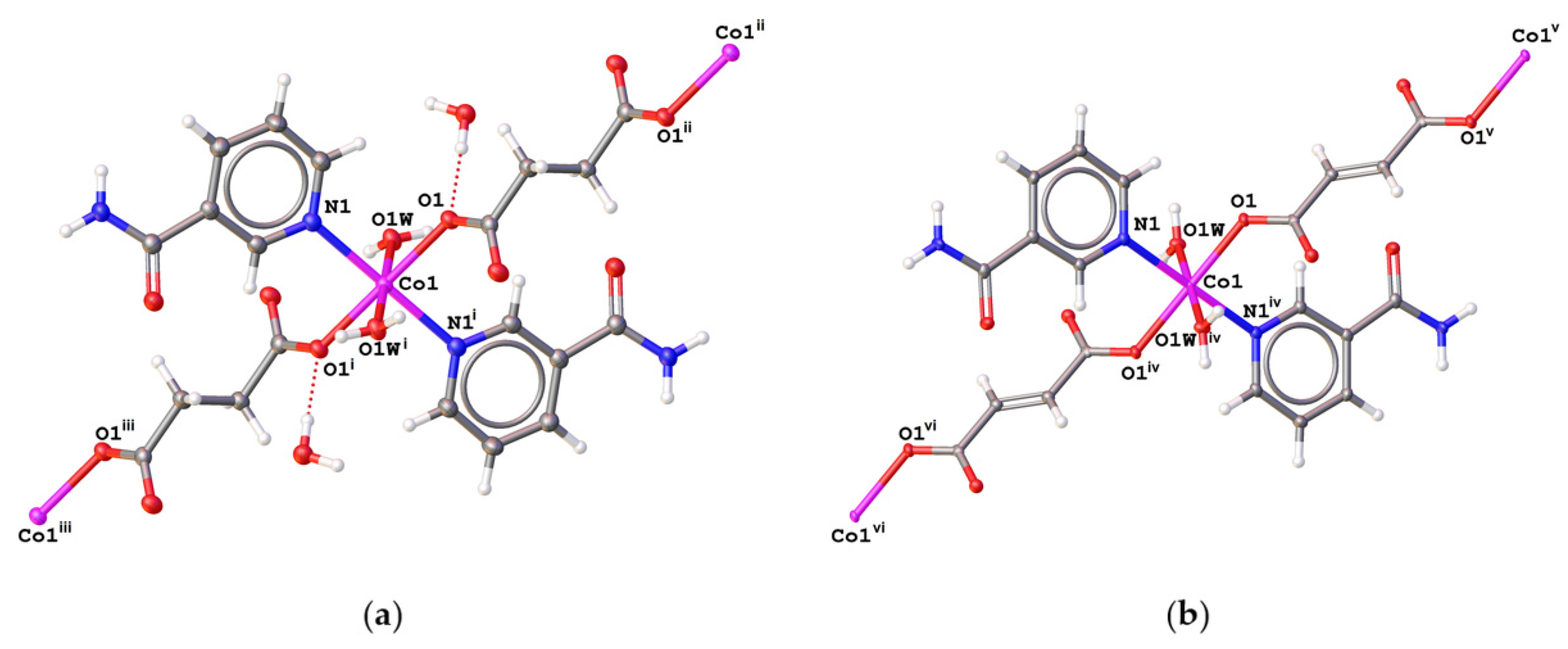
2.2. Description of the Structures
2.2.1. Hirshfeld Surface Analysis
2.2.2. X-ray Powder Diffraction
2.3. Spectral Characterization
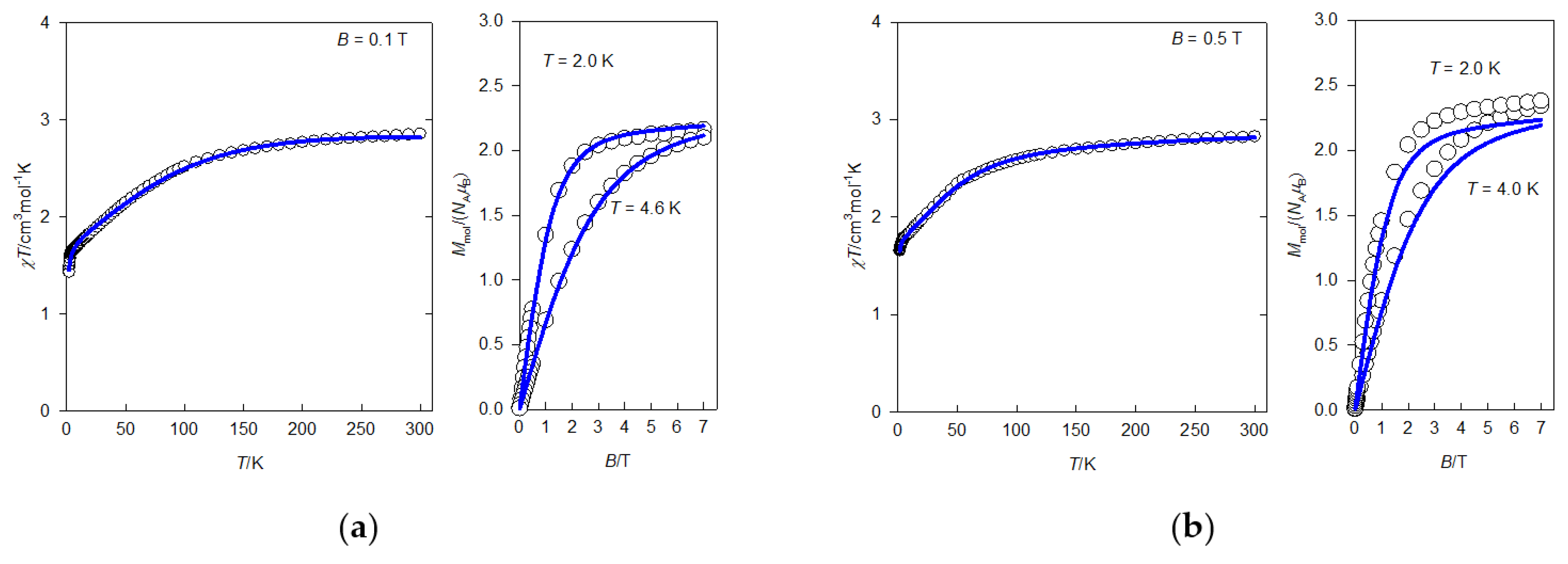
2.4. Static Magnetic Properties
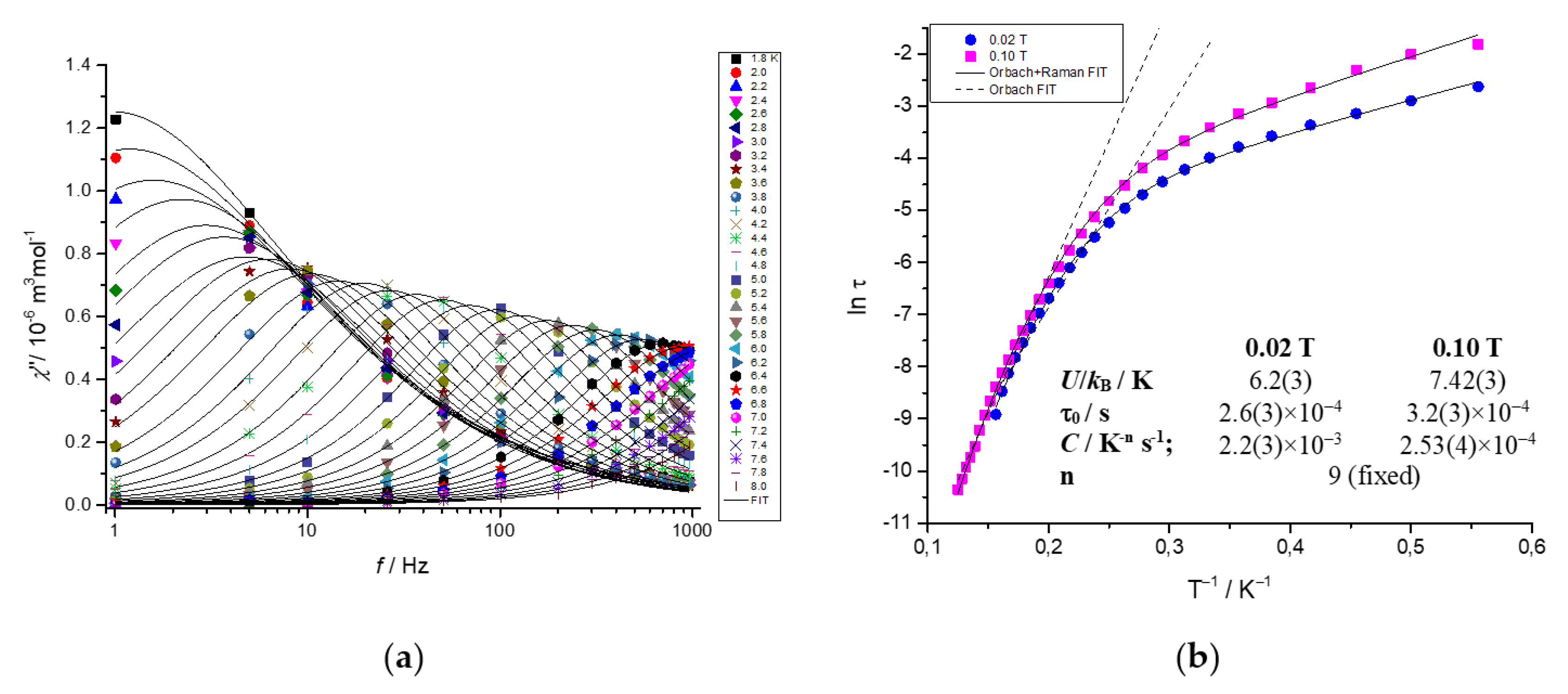
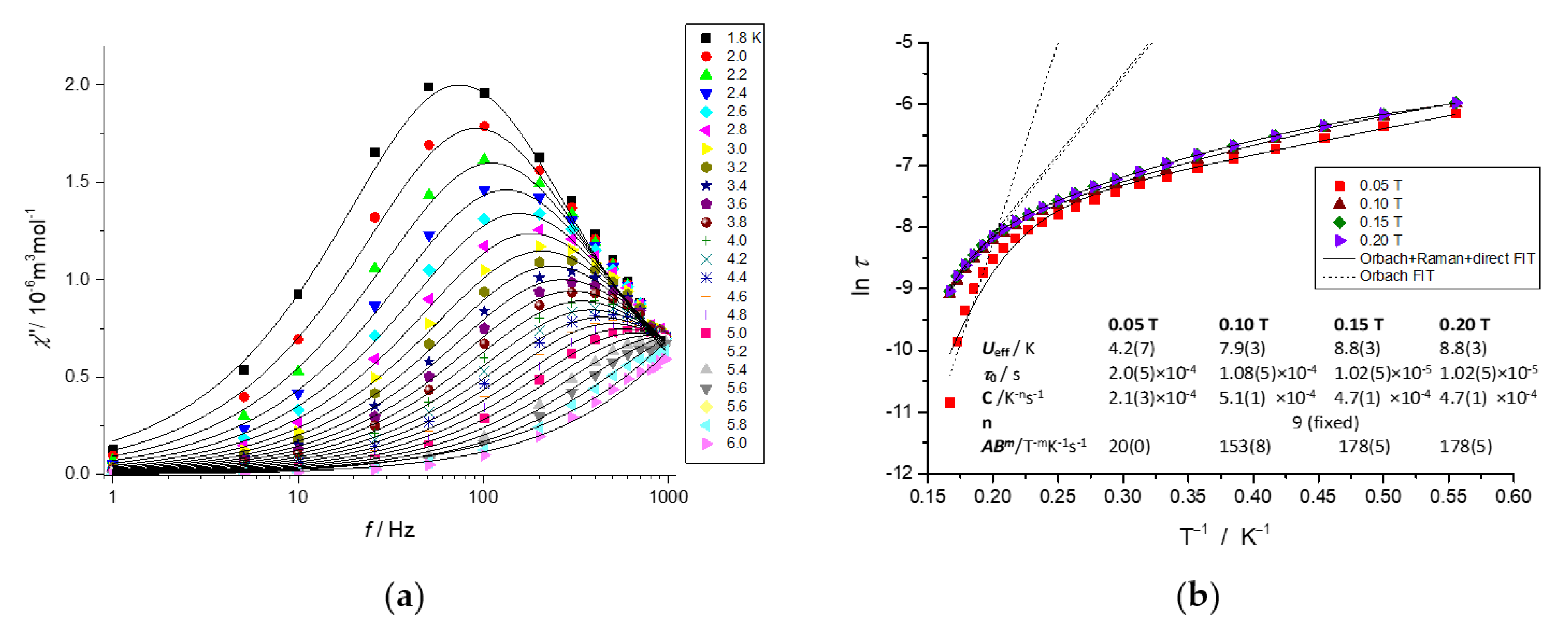
2.5. Dynamic Magnetic Properties
3. Materials and Methods
3.1. Chemical Reagents
3.2. Syntheses of the Complexes
3.2.1. Synthesis of {[Co(μ2-suc)(nia)2(H2O)2]·2H2O}n (Complex I)
- (a)
- From nicotinamide (nia)
- (b)
- From N-(hydroxylmethyl)nicotinamide (hmnia)
3.2.2. Synthesis of [Co(μ2-fum)(nia)2(H2O)2]n (Complex II)
3.3. Analysis and Physical Measurements
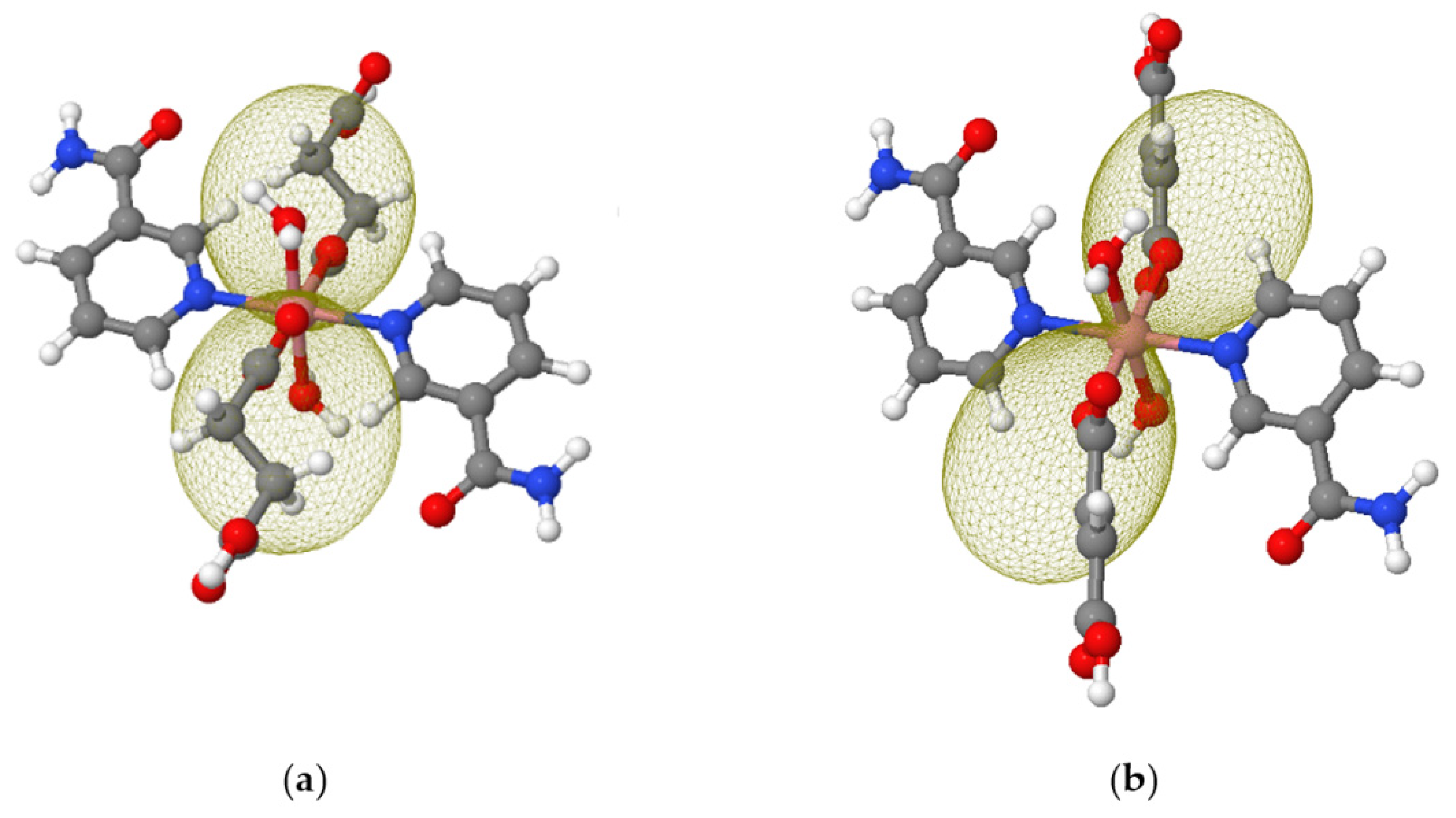
3.4. Computational Details
3.5. Crystal Structure Determination
Hirshfeld Surface Analysis
3.6. Powder X-ray Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.-C.; Li, J.-R.; Lv, X.-L.; Zhang, Y.-Q.; Guo, G. Photocatalytic organic pollutants degradation in metal-organic frameworks. Energy Environ. Sci. 2014, 7, 2831–2867. [Google Scholar] [CrossRef]
- Lee, J.; Farha, O.K.; Roberts, J.; Scheidt, K.A.; Nguyen, S.T.; Hupp, J.T. Metal-organic framework materials as catalysts. Chem. Soc. Rev. 2009, 38, 1450–1459. [Google Scholar] [CrossRef] [PubMed]
- Reinsch, H.; van der Veen, M.A.; Gil, B.; Marszalek, B.; Verbiest, T.; de Vos, D.; Stock, N. Sctructures, Sorption Characteristics, and Nonlinear Optical Properties of a New Series of Highly Stable Aluminum MOFs. Chem. Mater. 2013, 25, 17–26. [Google Scholar] [CrossRef]
- Khan, S.; Masum, A.A.; Giri, P.; Islam, M.; Harms, K.; Chattopadhyay, S. Chirality-Induced Variation In Interaction of Two Similar Copper(II) Coordination Polymers with Calf Thymus DNA: Exploration of Their Antimicrobial Activity and Cytotoxicity. Chem. Select. 2018, 3, 7112–7122. [Google Scholar] [CrossRef]
- Li, J.-R.; Kruppler, R.J.; Zhou, H.-C. Selective gas adsorption and separation in metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, X.; Liang, J.; Huang, Y.; Li, H.; Lin, Z.; Cao, R. Water-Stable Anionic Metal-Organic Framework for Highly Selective Separation of Methane from Natural Gas and Pyrolysis Gas. ACS Appl. Mater. Interfaces 2016, 8, 9777–9781. [Google Scholar] [CrossRef]
- Wilmer, C.E.; Farha, O.K.; Yildimir, T.; Eryazici, I.; Krungleviciute, V.; Sarjeant, A.A.; Snurr, R.Q.; Hupp, J.T. Gram-scale, high-yield synthesis of a robust metal-organic framework for storing methane and other gases. Energy Environ. Sci. 2013, 6, 1158–1163. [Google Scholar] [CrossRef]
- Beauvais, L.G.; Shores, M.P.; Long, J.R. Cyano-Bridged Re6Q8 (Q = S, Se) Cluster-Cobalt(II) Framework Materials: Versatile Solid Chemical Sensors. J. Am. Chem. Soc. 2000, 122, 2763–2772. [Google Scholar] [CrossRef]
- Jianghua, H.; Jihong, Y.; Yuetao, Z.; Qinhe, P.; Ruren, X. Synthesis, Structure, and Luminescent Property of a Heterometallic Metal−Organic Framework Constructed from Rod-Shaped Secondary Building Blocks. Inorg. Chem. 2005, 44, 9279–9289. [Google Scholar]
- Kahn, O. Chemistry and Physics of Supramolecular Magnetic Materials. Acc. Chem. Res. 2000, 33, 647–657. [Google Scholar] [CrossRef]
- Marinho, M.V.; Marques, L.F.; Diniz, R.; Stumpf, H.O.; do Canto Visentin, L.; Yoshida, M.I.; Machado, F.C.; Llorent, F.; Julve, M. Solvothermal synthesis, crystal structure and magnetic properties of homometallic Co(II) and Cu(II) chains with double di(4-pyridyl)sulfide as bridges. Polyhedron 2012, 45, 1–8. [Google Scholar] [CrossRef]
- Zheng, Y.Z.; Evangelisti, M.; Winpenny, R.E.P. Co-Gd phosphonate complexes as magnetic refrigerants. Chem. Sci. 2011, 2, 99–102. [Google Scholar] [CrossRef]
- James, S.L. Metal-organic frameworks. Chem. Soc. Rev. 2003, 32, 276–288. [Google Scholar]
- Natarajan, R.; Sevitha, G.; Dominiak, P.; Wozniak, K.; Moorthy, J.N. Corundum, Diamond, and PtS Metal–Organic Frameworks with a Difference: Self-Assembly of a Unique Pair of 3-Connecting D2d-Symmetric 3,3′,5,5′-Tetrakis(4-pyridyl)bimesityl. Angew. Chem. Int. Ed. 2005, 44, 2115–2119. [Google Scholar]
- Xue, Y.-H.; Liu, Y.; Xu, D.-J. catena-Poly[[diaquabis(1H-benzimidazole-κN3)cobalt(II)]-μ-succinato-κO]. Acta Cryst. 2003, E59, m944–m946. [Google Scholar] [CrossRef]
- Zhang, J.; Kang, Y.; Zhang, R.-B.; Li, Z.-J.; Cheng, J.-K.; Yao, Y.-G. A twisting chiral ‘dense’ 75.9 net, incorporating a helical sub-structure. CrystEngComm 2005, 7, 177–178. [Google Scholar]
- Duangthonyou, T.; Jirakulpattana, S.; Phakawatchai, C.; Kurmoo, M.; Siripaisarnpipat, S. Comparison of crystal structures and magnetic properties of two Co(II) complexes containing different dicarboxylic acid ligands. Polyhedron 2010, 29, 1156. [Google Scholar] [CrossRef]
- Bora, S.J.; Das, B.K. Synthesis and properties of a few 1-D cobaltous fumarates. J. Solid State Chem. 2012, 192, 93–101. [Google Scholar]
- Brezovan, M.; Kuchtanin, V.; Moncoľ, J.; Pavlik, J.; Dlháň, Ľ.; Segľa, P. Four novel cobalt(II) succinate coordination polymers with N-heterocyclic ligands: Crystal structures, spectral properties, magnetism and computational study. Chem. Pap. 2020, 74, 3741–3753. [Google Scholar]
- Beatty, A.M. Hydrogen bonded networks of coordination complexes. CrystEngComm 2001, 3, 243–255. [Google Scholar]
- Beatty, A.M. Open-framework coordination complexes from hydrogen-bonded networks: Toward host/guest complexes. Coord. Chem. Rev. 2003, 246, 131–143. [Google Scholar] [CrossRef]
- Moncoľ, J.; Kuchtanin, V.; Polakovičová, P.; Mrozinski, J.; Kalinska, B.; Koman, M.; Padělková, Z.; Segľa, P.; Melník, M. Study of copper(II) thiophenecarboxylate complexes with nicotinamide. Polyhedron 2012, 45, 94–102. [Google Scholar] [CrossRef]
- Puchoňová, M.; Maroszová, J.; Mazúr, M.; Valigura, D.; Moncol, J. Structures with different supramolecular interactions and spectral properties of monomeric, dimeric and polymeric benzoatocopper(II) complexes. Polyhedron 2021, 197, 115050. [Google Scholar] [CrossRef]
- Ganzhorn, M.; Wernsdorfer, W. Molecular Magnets; Bartolome, J., Luis, F., Fernandez, J.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 319–364. [Google Scholar]
- Boča, R.; Rajnák, C.; Moncol, J.; Titiš, J.; Valigura, D. Breaking the Magic Border of One Second for Slow Magnetic Relaxation of Cobalt-Based Single Ion Magnets. Inorg. Chem. 2018, 57, 14314–14321. [Google Scholar] [CrossRef] [PubMed]
- Clérac, R.; Miyasaka, H.; Yamashita, M.; Coulon, C. Evidence for Single-Chain Magnetic Behavior in a Mn(III)-N(II) Chain Designed with High Spin Magnetic Units: A Route to High Temperature Metastable Magnets. J. Am. Chem. Soc. 2002, 124, 12837–12844. [Google Scholar] [CrossRef]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The Rise of 3-d Single-Ion Magnets in Molecular Magnetism: Towards Materials from Molecules. Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef]
- Jiménez, J.-R.; Xy, B.; El Said, H.; Li, Y.; von Bardeleben, J.; Chamoreau, L.-M.; Lescouëzec, R.; Shova, S.; Visinescu, S.; Alexandru, M.-G.; et al. Field-induced single ion magnet behaviour of discrete and one-dimensional complexes containing [bis(1-methylimidazol-2-yl)ketone]-cobalt(II) building units. Dalton Trans. 2021, 50, 16353–16363. [Google Scholar] [CrossRef]
- Chilton, N.E. Molecular Magnetism. Annu. Rev. Mater. Res. 2022, 52, 79–101. [Google Scholar] [CrossRef]
- Sarkar, A.; Dey, S.; Rajaraman, G. Role of Coordination Number and Geometry in Controlling the Magnetic Anisotropy in FeII, CoII and NiII Single-Ion Magnets. Chem. Eur. J. 2020, 26, 14036–14058. [Google Scholar] [CrossRef]
- Perlepe, P.S.; Maniaki, D.; Pilichos, E.; Katsoulakou, E.; Perlepes, S.P. Smart Ligands for Efficient 3d-, 4d- and 5d-Metal Single-Molecule Magnets and Single-Ion Magnets. Inorganics 2020, 8, 39. [Google Scholar] [CrossRef]
- Váhovská, L.; Vitushkina, S.; Potočňák, I.; Trávníček, Z.; Herchel, R. Effect of linear and non-linear pseudohalides on the structural and magnetic properties of Co(II) hexacoordinate single-molecule magnets. Dalton Trans. 2018, 47, 1498–1512. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.-H.; Zhang, Y.-Q.; Chen, X.-T.; Wang, Z.; Xue, Z.-L. Magnetic anisotropy and slow magnetic relaxation processes of cobalt(II)-pseudohalide complexes. Dalton Trans. 2019, 48, 10743–10752. [Google Scholar] [CrossRef]
- Vallejo, J.; Castro, I.; Ruiz-García, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef]
- Ding, Z.-Y.; Meng, Y.-S.; Xiao, Y.; Zhang, Y.-Q.; Zhu, Y.-Y.; Gao, S. Probing the influence of molecular symmetry on magnetic anisotropy of octahedral cobalt(II) complexes. Inorg. Chem. Front. 2017, 4, 1909–1916. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Yang, L.; Yuan, C.; Zhang, Y.-Q.; Song, Y. Magnetic Anisotropy from Trigonal Prismatic to Trigonal Antiprismatic Co(II) Complexes: Experimental Observation and Theoretical Prediction. Inorg. Chem. 2018, 57, 3903–3912. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhou, J.; Cui, H.-H.; Yuan, A.-H.; Wang, Z.; Zhang, Y.-Q.; Ouyang, Z.-W.; Song, Y. Slow magnetic relaxation influenced by change of symmetry ideal Ci to D3d in cobalt(II)-based single-ion magnets. Dalton Trans. 2018, 47, 2506–2510. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Herchel, R.; Trávníček, Z. Two polymorphic Co(II) field-induced single-ion magnets with enormous angular distortion from the ideal octahedron. Dalton Trans. 2018, 47, 1614–1623. [Google Scholar] [CrossRef] [Green Version]
- Nemec, I.; Fellner, O.I.; Indruchová, B.; Herchel, R. Trigonally Distorted Hexacoordinate Co(II) Single-Ion Magnets. Materials 2022, 15, 1064. [Google Scholar] [CrossRef]
- Landart-Gereka, A.; Quesada-Moreno, M.M.; Díaz-Ortega, I.; Nojiri, H.; Ozerov, M.; Krzystek, J.; Palacios, M.A.; Colacio, E. Large easy-axis magnetic anisotropy in a series of trigonal prismatic mononuclear cobalt(II) complexes with zero-field hidden single-molecule magnet behaviour: The important role of the distortion of the coordination sphere and intermolecular interactions in the slow relaxation. Inorg. Chem. Front. 2022, 9, 2810–2831. [Google Scholar]
- Roy, S.; Oyarzabal, I.; Vallejo, J.; Cano, J.; Colacio, E.; Bauza, A.; Frontera, A.; Kirillov, A.M.; Drew, M.G.B.; Das, S. Two Polymorphic Forms of a Six-Coordinate Mononuclear Cobalt(II) Complex with Easy-Plane Anisotropy: Structural Features, Theoretical Calculations, and Field-Induced Slow Relaxation of the Magnetization. Inorg. Chem. 2016, 55, 8502–8513. [Google Scholar] [CrossRef]
- Peng, G.; Qian, Y.-F.; Wang, Z.-W.; Chen, Y.; Yadav, T.; Fink, K.; Ren, X.-M. Tuning the Coordination Geometry and Magnetic Relaxation of Co(II) Single-Ion Magnets by Varying the Ligand Substitutions. Cryst. Growth Des. 2021, 21, 1035–1044. [Google Scholar] [CrossRef]
- Rajnák, C.; Titiš, J.; Moncol, J.; Boča, R. Effect of the distant substituent on the slow magnetic relaxation of the mononuclear Co(II) complex with pincer-type ligands. Dalton Trans. 2020, 49, 4206–4210. [Google Scholar] [CrossRef] [PubMed]
- Woods, T.J.; Ballesteros-Rivas, M.F.; Gómez-Coca, S.; Ruiz, E.; Dunbar, K.R. Relaxation Dynamics of Identical Trigonal Bipyramidal Cobalt Molecules with Different Local Symmetries and Packing Arrangements: Magnetostructural Correlations and ab inito Calculations. J. Am. Chem. Soc. 2016, 138, 16407–16416. [Google Scholar] [CrossRef] [PubMed]
- de Campos, N.R.; Simosono, C.A.; Landre Rosa, I.M.; da Silva, R.M.R.; Doriguetto, A.C.; do Pim, W.D.; Gomes Simões, T.R.; Valdo, A.K.S.M.; Martins, F.T.; Sarmiento, C.V.; et al. Building-up host–guest helicate motifs and chains: A magneto-structural study of new field-induced cobalt-based single-ion magnets. Dalton Trans. 2021, 50, 10707–10728. [Google Scholar] [CrossRef]
- Demir, S.; Yilmaz, V.T.; Yilmaz, F.; Buyukgungor, O. One-Dimensional Cobalt(II) and Zinc(II) Succinato Coordination Polymers with Nicotinamide: Synthesis, Structural, Spectroscopic, Fluorescent and Thermal Properties. J. Inorg. Organomet. Polym. 2009, 19, 342–347. [Google Scholar] [CrossRef]
- Kansız, S.; Dege, N. Synthesis, crystallographic structure, DFT calculations and Hirshfeld surface analysis of a fumarate bridged Co(II) coordination polymer. J. Mol. Struct. 2018, 1173, 42–51. [Google Scholar] [CrossRef]
- Masárová, P.; Mazúr, M.; Segl’a, P.; Moncol, J. Supramolecular assembled networks in crystal structure built up of copper(II) dipicolinates with pyrazine- and pyridinecarboxamides connected through hydrogen bonds. Polyhedron 2018, 149, 25–33. [Google Scholar] [CrossRef]
- Shamuratov, E.B.; Batsanov, A.S.; Struchkov, Y.T.; Yunuskhodzhaev, A.N.; Dusmatov, A.F.; Sabirov, V.K. Structure of Co(II) and Cu(II) complexes with N-(hydroxymethyl)nicotinamide. Russ. J. Coord. Chem. 1990, 16, 1526–1528. [Google Scholar]
- Shamuratov, E.B.; Batsanov, A.S.; Struchkov, Y.T.; Yunuskhodzhaev, A.N. Crystal structures of Ni(II) and Co(II) chloride and nitrate complexes with N-(hydroxymethyl)nicotinamide. Russ. J. Coord. Chem. 1991, 17, 1668–1675. [Google Scholar]
- Chłopicki, S.; Ku, K.; Kalvins, I.; Adrianov, V.; Loza, E. Quaternary Nicotinamide Derivatives as Precursors for Release of MNA. European Patent Organization. Patent EP3505512 A1, 3 July 2019. [Google Scholar]
- Alvarez, S.; Avnir, D.; Llunell, M.; Pinsky, M. Continuous symmetry maps and shape classification. The case of six-coordinated metal compounds. New J. Chem. 2002, 26, 996–1009. [Google Scholar] [CrossRef]
- Alvarez, S. Relationships between Temperature, Magnetic Moment, and Continuous Symmetry Measures in Spin Crossover Complexes. J. Am. Chem. Soc. 2003, 125, 6795–6802. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S. Distortion Pathways of Transition Metal Coordination Polyhedra Induced by Chelating Topology. Chem. Rev. 2015, 115, 13447–13483. [Google Scholar] [CrossRef]
- Kershaw Cook, L.J.; Mohammed, R.; Sherborne, G.; Roberts, T.D.; Alvarez, S.; Halcrow, M.A. Spin state behavior of iron(II)/dipyrazolylpyridine complexes. New insights from crystallographic and solution measurements. Coord. Chem. Rev. 2015, 289–290, 2–12. [Google Scholar] [CrossRef]
- Guionneau, P.; Marchivie, M.; Bravic, G.; Létard, J.-F.; Chasseau, D. Structural Aspects of Spin Crossover. Example of the [FeIILn(NCS)2] Complexes. Top. Curr. Chem. 2004, 234, 97–128. [Google Scholar]
- Halcrow, M.A. Structure:function relationships in molecular spin-crossover complexes. Chem. Soc. Rev. 2011, 40, 4119–4142. [Google Scholar] [CrossRef]
- Bernstein, J.; Davis, R.E.; Shimoni, L.; Chang, N.-L. Patterns in Hydrogen Bonding: Functionality and Graph Set Analysis in Crystals. Angew. Chem. Int. Ed. 1995, 34, 1555–1573. [Google Scholar] [CrossRef]
- Janiak, C. A critical account on π–π stacking in metal complexes with aromatic nitrogen-containing ligands. J. Chem. Soc. Dalton Trans. 2000, 21, 3885–3896. [Google Scholar] [CrossRef]
- Dziewulska-Kułaczkowska, A.; Mazur, L.; Ferenc, W. Thermal, spectroscopic and structural studies of zinc(II) complex with nicotinamide. J. Therm. Anal. Calorim. 2009, 96, 255–260. [Google Scholar] [CrossRef]
- Nakamoto, K. Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part B; Wiley-VCH: Weinheim, Germany, 1997; pp. 384–387. ISBN 9780471743392. [Google Scholar]
- Bando, Y.; Nagakura, S. The electronic structure and electronic spectrum of dichlorodipyridinecobalt(II). Charge-transfer band due to interaction between halide ion and cobalt(II) cation. Inorg. Chem. 1968, 7, 893–897. [Google Scholar] [CrossRef]
- Lever, A.B.P. Inorganic Electronic Spectroscopy; Elsevier: Amsterdam, The Netherlands, 1984; ISBN 0-444-42389-3. [Google Scholar]
- Martin, R.L. Natural Transition Orbitals. J. Chem. Phys. 2003, 118, 4775. [Google Scholar] [CrossRef]
- Palii, A.; Tsukerblatt, B.; Klokishner, S.; Dunbar, K.R.; Clemente-Juan, J.M.; Coronado, E. Beyond the Spin Model: Exchange Coupling in Molecular Magnets with Unquenched Orbital Angular Momenta. Chem. Soc. Rev. 2011, 40, 3130–3156. [Google Scholar] [CrossRef] [PubMed]
- Boča, R. Magnetic Parameters and Magnetic Functions in Mononuclear Complexes Beyond the Spin-Hamiltonian Formalism. In Magnetic Functions Beyond the Spin-Hamiltonian. Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 2006; Volume 117. [Google Scholar] [CrossRef]
- Juráková, J.; Dubnická Midlíková, J.; Hrubý, J.; Kliuikov, A.; Santana, V.T.; Pavlik, J.; Moncoľ, J.; Čižmár, E.; Orlita, M.; Mohelský, I.; et al. Pentacoordinate cobalt(II) single ion magnets with pendant alkyl chains: Shall we go for chloride or bromide? Inorg. Chem. Front. 2022, 9, 1179–1194. [Google Scholar] [CrossRef]
- Singh, A.; Shrivastava, K. Optical-acoustic two-phonon relaxation in spin systems. Phys. Status Solidi B 1979, 95, 273–277. [Google Scholar] [CrossRef]
- Shrivastava, K.N. Theory of Spin–Lattice Relaxation. Phys. Status Solidi B 1983, 117, 437–458. [Google Scholar] [CrossRef]
- Juráková, J.; Šalitroš, I. Co(II) single-ion magnets: Synthesis, structure and magnetic properties. Monatsh. Chem. 2022; in press. [Google Scholar] [CrossRef] [PubMed]
- Zahradníková, E.; Herchel, R.; Šalitroš, I.; Císařová, I.; Drahoš, B. Late first-row transition metal complexes of a 17-membered piperazine-based macrocyclic ligand: Structures and magnetism. Dalton Trans. 2020, 4I9, 9057–9069. [Google Scholar] [CrossRef] [PubMed]
- Brachňaková, B.; Matejová, S.; Moncoľ, J.; Herchel, R.; Pavlik, J.; Moreno-Pineda, E.; Ruben, M.; Šalitroš, I. Stereochemistry of coordination polyhedral vs. single ion magnetism in penta- and hexacoordinated Co(II) complexes with tridentate rigid ligands. Dalton Trans. 2020, 49, 1249–1264. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Tian, D.; Ferrando-Soria, J.; Cano, J.; Yin, L.; Ouyang, Z.; Wang, Z.; Luo, S.; Liu, X.; Pardo, E. Modulation of the magnetic anisotropy of octahedral cobalt(II) single-ion magnets by a fine-tuning of axial coordination microenvironment. Inorg. Chem. Front. 2019, 6, 848–856. [Google Scholar] [CrossRef]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 5.0. WIREs Comput Mol Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Cole-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5651. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Izsák, R.; Neese, F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F.; Kattanneck, M.; Ahlrichs, R. Approximated electron repulsion integrals: Cholesky decomposition versus resolution of the identity methods. J. Chem. Phys. 2009, 130, 164106. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H-Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Grimme, S.; Brandenburg, J.G.; Bannwarth, C.; Hanse, A. Consistent structures and interactions by density functional theory with small atomic orbital basis sets. J. Chem. Phys. 2015, 143, 054107. [Google Scholar] [CrossRef] [PubMed]
- Malmqvist, P.A.; Roos, B.O. The CASSCF state interaction method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Ganyushin, D.; Neese, F. A fully variational spin-orbit coupled complete active space self-consistent field approach: Application to electron paramagnetic resonance g-tensors. J. Chem. Phys. 2013, 138, 104113. [Google Scholar] [CrossRef]
- Neese, F. Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations. J. Chem. Phys. 2005, 122, 034107. [Google Scholar] [CrossRef] [PubMed]
- Stoychev, G.L.; Auer, A.A.; Neese, F. Automatic Generation of Auxiliary Basis Sets. J. Chem. Theory Comput. 2017, 13, 554–562. [Google Scholar] [CrossRef] [PubMed]
- Kožíšková, J.; Hahn, F.; Richter, J.; Kožíšek, J. Comparison of different absorption corrections on the model structure of tetrakis(μ2-acetato)-diaqua-di-copper(II). Acta Chim. Slovaca 2016, 9, 136–140. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Cryst. 2015, A71, 3–8. [Google Scholar] [CrossRef] [Green Version]
- Coppens, P.; Hansen, N.K. Testing aspherical atom refinements on small-molecule data sets. Acta Crystallogr. 1978, A34, 909–921. [Google Scholar]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, C71, 3–8. [Google Scholar]
- Bourhis, L.J.; Dolomanov, O.V.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. The anatomy of a comprehensive constrained, restrained refinement program for the modern computing environment—Olex2 dissected. Acta Cryst. A 2015, A71, 59–75. [Google Scholar] [CrossRef] [PubMed]
- Kleemiss, F.; Dolomanov, O.V.; Bodensteiner, M.; Peyerimhoff, N.; Midgley, L.; Bourhis, L.J.; Genoni, A.; Malaspina, L.A.; Jayatilaka, D.; Spencer, J.L.; et al. Accurate crystal structures and chemical properties from NoSpherA2. Chem. Sci. 2021, 12, 1675–1692. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayalitaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Cryst. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayalitaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Spackman, M.A.; McKinnon, J.J. Fingerprinting intermolecular interactions in molecular crystals. CrystEngComm 2002, 4, 378–392. [Google Scholar] [CrossRef]
- Parkin, A.; Barr, G.; Dong, W.; Gilmore, C.J.; Jayalitaka, D.; McKinnon, J.J.; Spackman, M.A.; Wilson, C.C. Comparing entire crystal structures: Structural genetic fingerprinting. CrystEngComm 2007, 9, 648–652. [Google Scholar] [CrossRef]
- Petříček, V.; Dušek, M.; Palatinus, L.J. The Crystallographic Computing System; Institute of Physics: Praha, Czech Republic, 2006. [Google Scholar]
- Lunghi, A.; Totti, F.; Sanvito, S.; Sessoli, R. Intra-molecular origin of the spin-phonon coupling in slow-relaxing molecular magnets. Chem. Sci. 2017, 8, 6051–6059. [Google Scholar] [CrossRef] [PubMed]
- Lunghi, A.; Sanvito, S. How do phonons relax molecular spins? Sci. Adv. 2019, 5, eaax7163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garlatti, E.; Tesi, L.; Lunghi, A.; Atzori, M.; Voneshen, D.J.; Santini, P.; Sanvito, S.; Guidi, T.; Sessoli, R.; Carretta, S. Unveiling phonons in a molecular qubit with four-dimensional inelastic neutron scattering and density functional theory. Nat. Commun. 2020, 11, 1751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
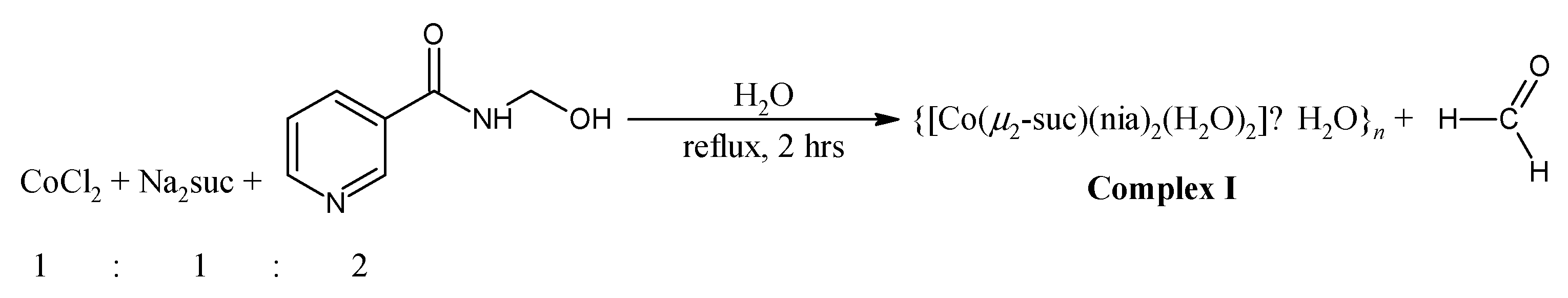
| Complex | λ/cm−1 | σ | Δax/cm−1 | Δrh/cm−1 | zj/cm−1 | R(χT) × R(M) |
|---|---|---|---|---|---|---|
| I | −177.4 | −1.14 | −424.7 | −11.6 | −0.06 | 0.0006 |
| II | −161.5 | −1.39 | −395.1 | −92.1 | 0.007 | 0.0094 |
| λ/cm−1 | Δax/cm−1 | Δrh/cm−1 | |
|---|---|---|---|
| 1 | −175.3 | −522.7 | −151.2 |
| 2 | −175.2 | −425.3 | −128.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brezovan, M.; Juráková, J.; Moncol, J.; Dlháň, Ľ.; Korabik, M.; Šalitroš, I.; Pavlik, J.; Segľa, P. The Role of the Bridge in Single-Ion Magnet Behaviour: Reinvestigation of Cobalt(II) Succinate and Fumarate Coordination Polymers with Nicotinamide. Inorganics 2022, 10, 128. https://doi.org/10.3390/inorganics10090128
Brezovan M, Juráková J, Moncol J, Dlháň Ľ, Korabik M, Šalitroš I, Pavlik J, Segľa P. The Role of the Bridge in Single-Ion Magnet Behaviour: Reinvestigation of Cobalt(II) Succinate and Fumarate Coordination Polymers with Nicotinamide. Inorganics. 2022; 10(9):128. https://doi.org/10.3390/inorganics10090128
Chicago/Turabian StyleBrezovan, Marek, Jana Juráková, Ján Moncol, Ľubor Dlháň, Maria Korabik, Ivan Šalitroš, Ján Pavlik, and Peter Segľa. 2022. "The Role of the Bridge in Single-Ion Magnet Behaviour: Reinvestigation of Cobalt(II) Succinate and Fumarate Coordination Polymers with Nicotinamide" Inorganics 10, no. 9: 128. https://doi.org/10.3390/inorganics10090128
APA StyleBrezovan, M., Juráková, J., Moncol, J., Dlháň, Ľ., Korabik, M., Šalitroš, I., Pavlik, J., & Segľa, P. (2022). The Role of the Bridge in Single-Ion Magnet Behaviour: Reinvestigation of Cobalt(II) Succinate and Fumarate Coordination Polymers with Nicotinamide. Inorganics, 10(9), 128. https://doi.org/10.3390/inorganics10090128







