On the Mechanism of Heterogeneous Water Oxidation Catalysis: A Theoretical Perspective
Abstract
1. Introduction
2. Computational Methodology
- (1)
- The reference potential to be that of NHE is considered when H+ + e− are involved. At standard conditions (U = 0, pH = 0, p = 1 bar, T = 298 K), the reaction *AH → A + H+ + e− is equivalent to *AH → A + 1/2 H2 and ΔG0 = ΔG because the free energy of H+(aq) + e− can be taken equal to that of 1/2 H2;
- (2)
- For the equation, ΔG0 = ΔE + ΔZPE − TΔS, the ΔZPE (zero-point energy) and ΔS are obtained from the vibrational frequency calculations and the standard free energy table. For the atoms and molecules adsorbed to the coordinatively unsaturated sites (CUSs), the S = 0 is considered. The temperature dependence is ignored in the calculations;
- (3)
- Using the ΔGU = −eU, where U is the electrode potential relative to the standard hydrogen electrode, the potential bias is included in the calculation.
- (4)
- pH correction is done using ΔGpH(pH) = −kT ln 10·pH equation.
- (5)
- The energy values of H2O and H2 in the gas phase are used as the reference states. At an equilibrium pressure of 0.035 bar, the entropy of gas phase water occurs at room temperature. The step involving O2, ΔG{2H2O→O2+2H2} = 4.92 eV = EO2 + 2EH2 − 2EH2O + (ΔZPE − TΔS){2H2O→O2+2H2} is considered;
- (6)
- It was considered that the interaction energy is equal to the energy of a hydrogen bond for the interaction of O*, OH*, OOH*, or an empty CUS site. Further, it was found to be negligible in rutile-type oxides [50].
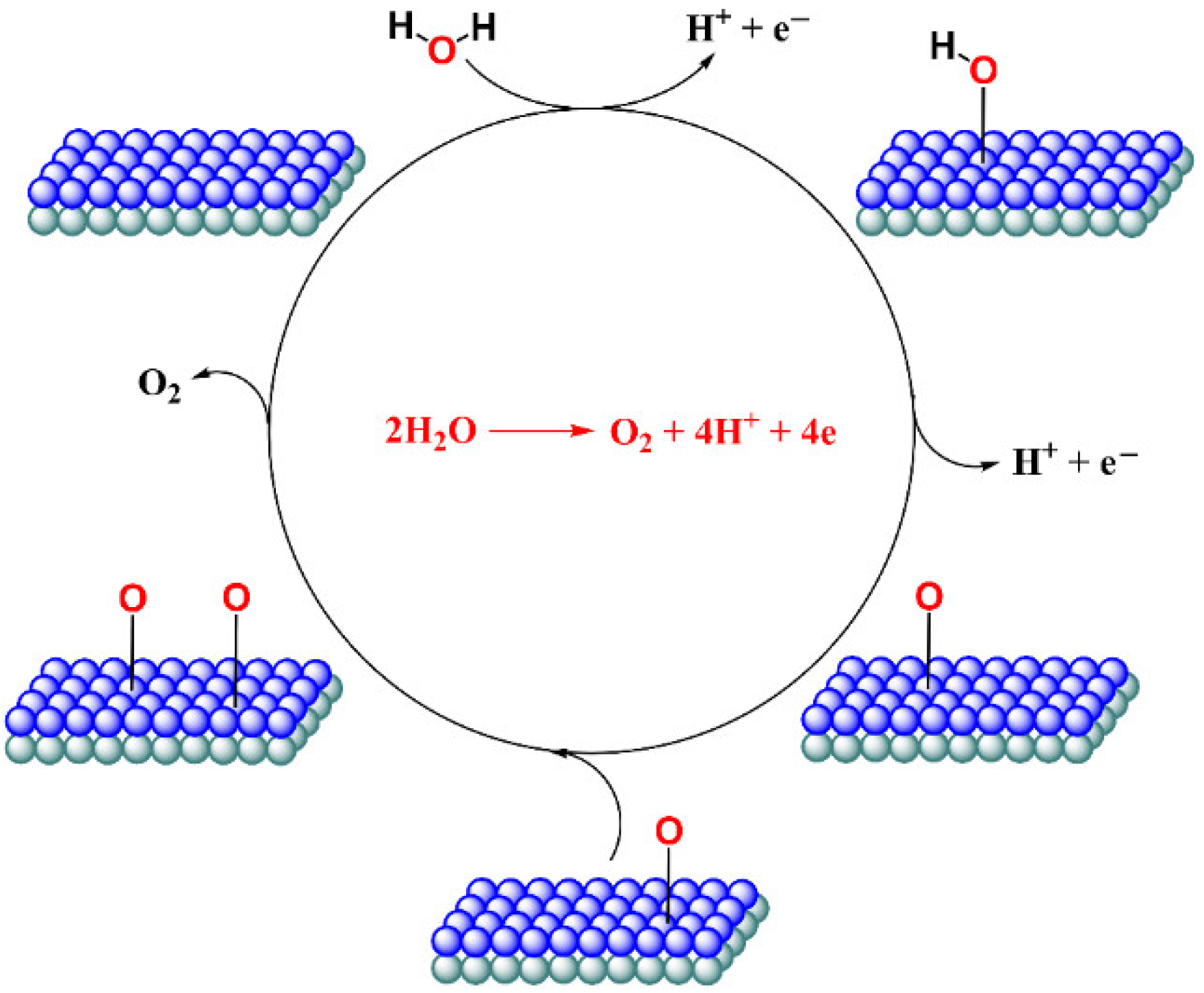
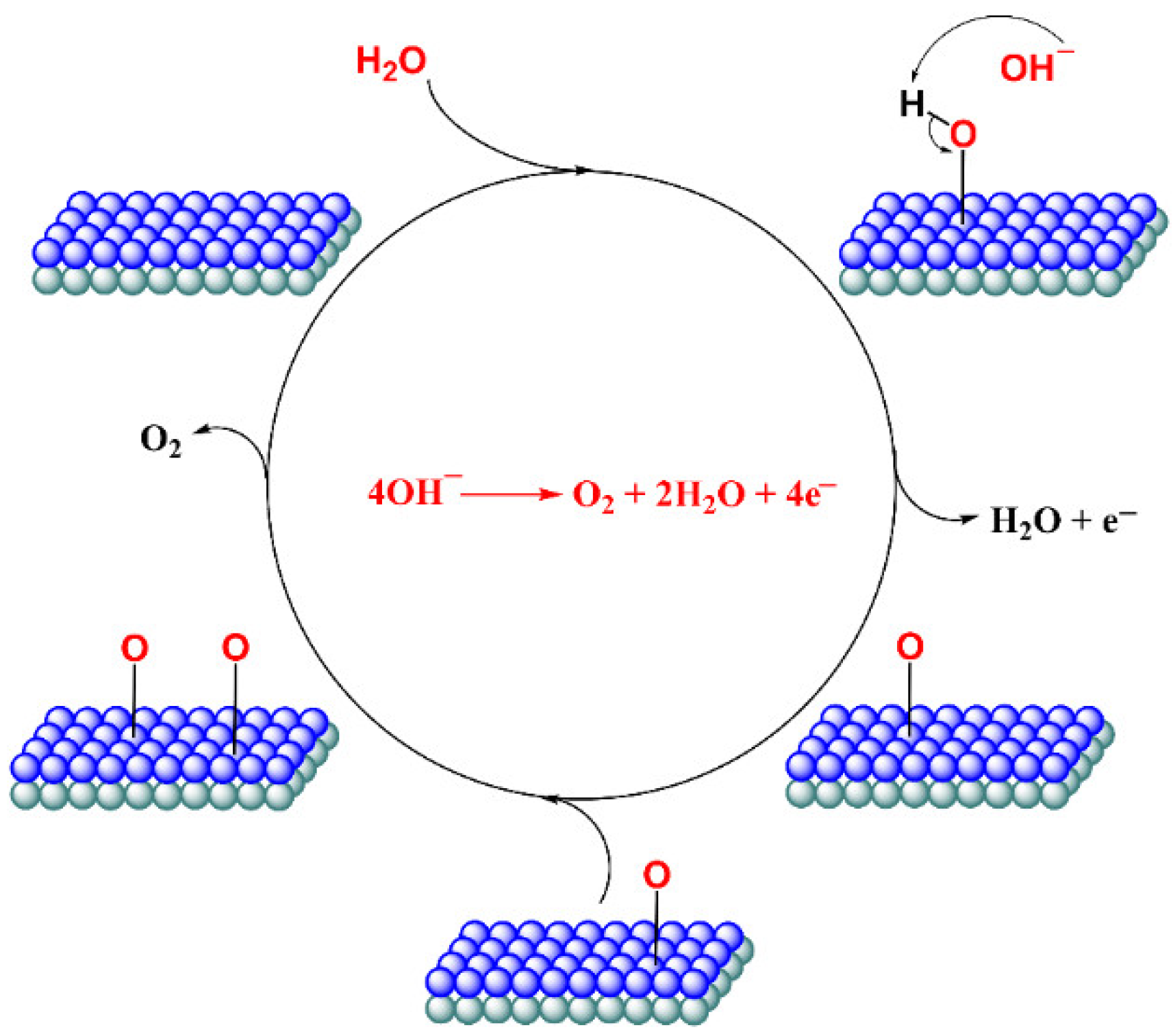
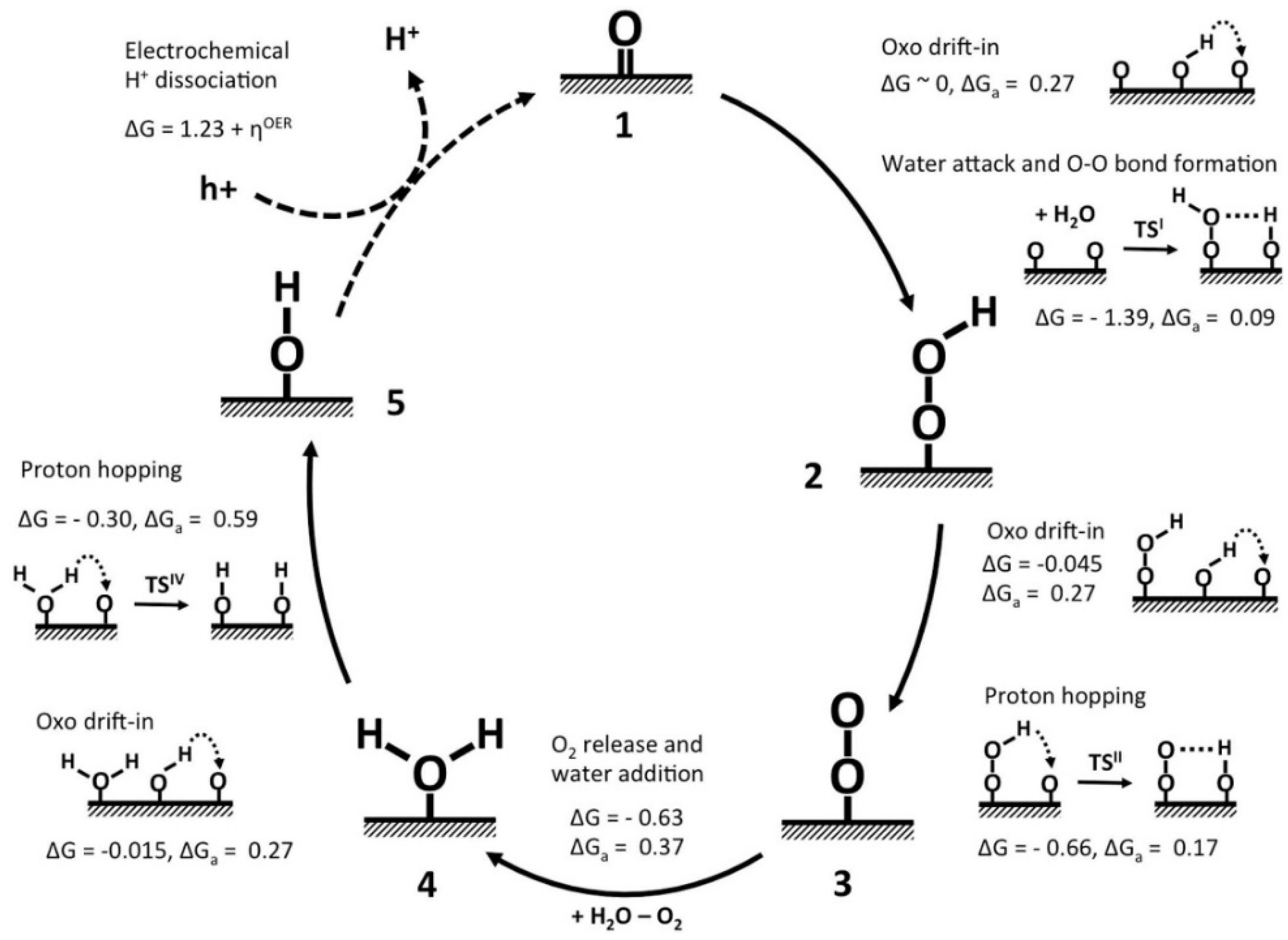
3. Results and Discussion
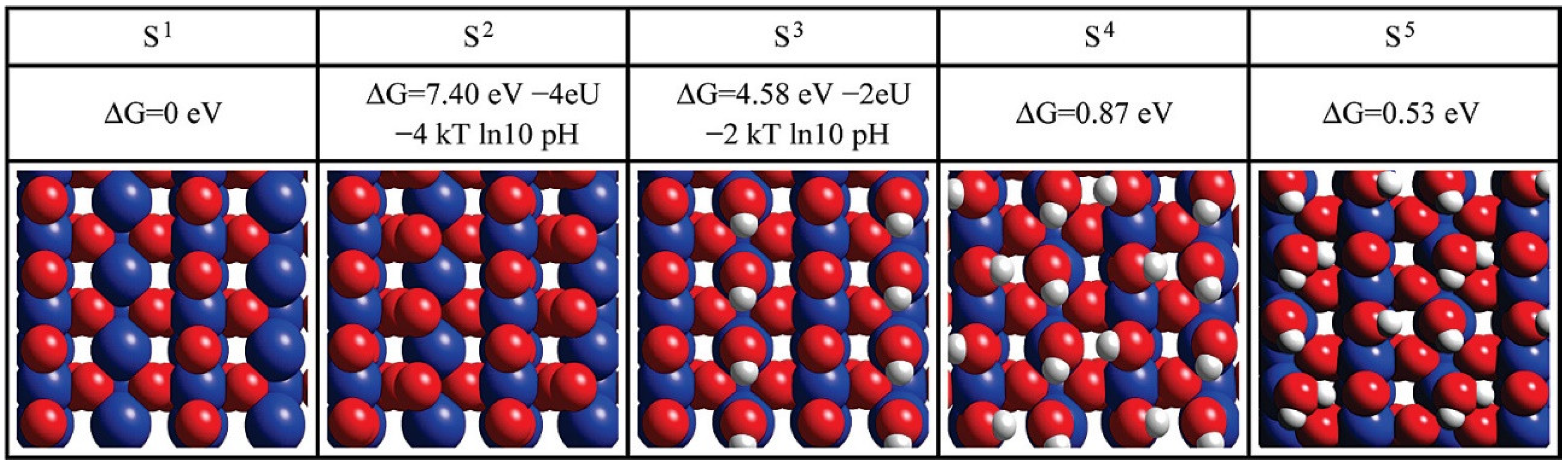
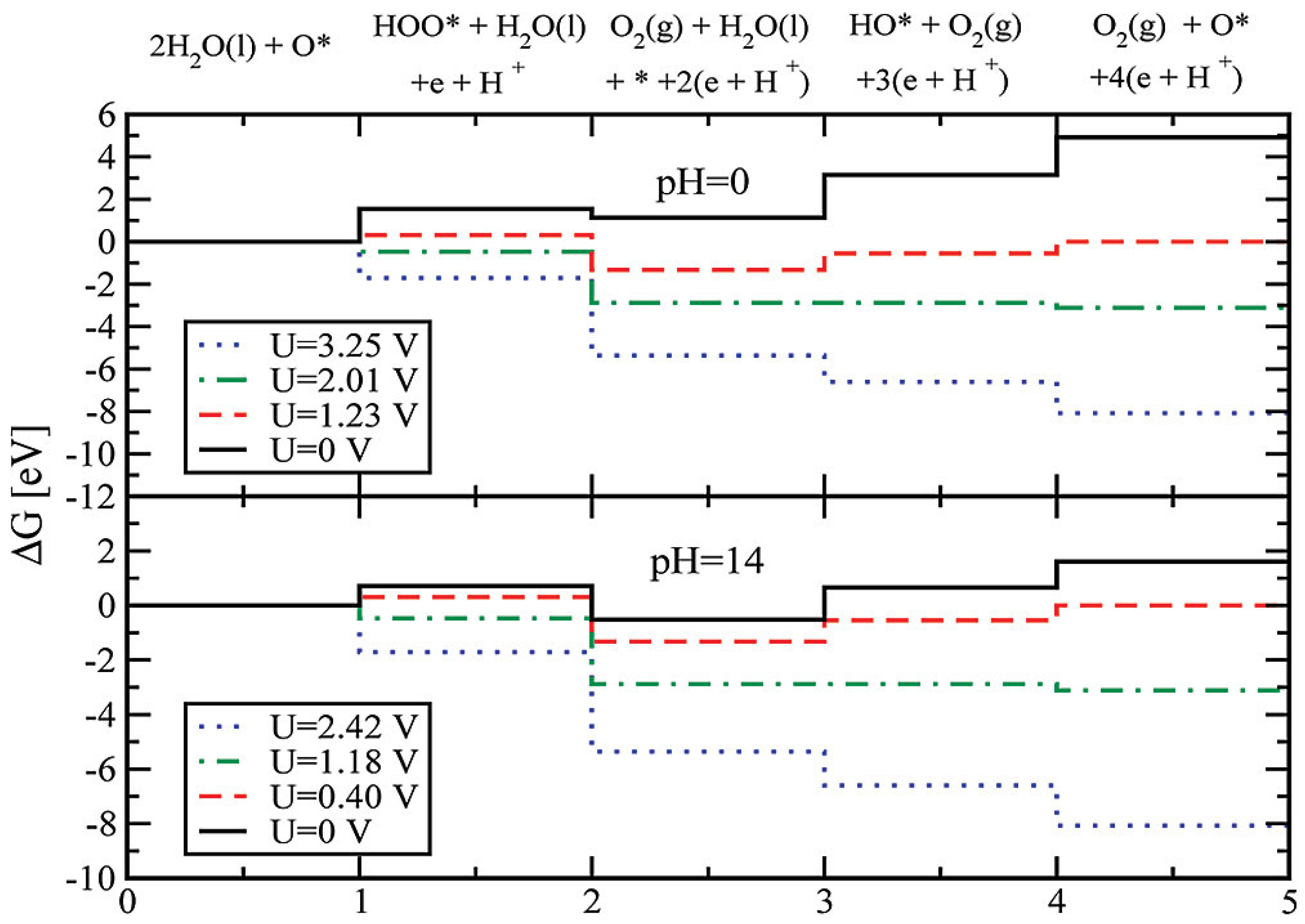
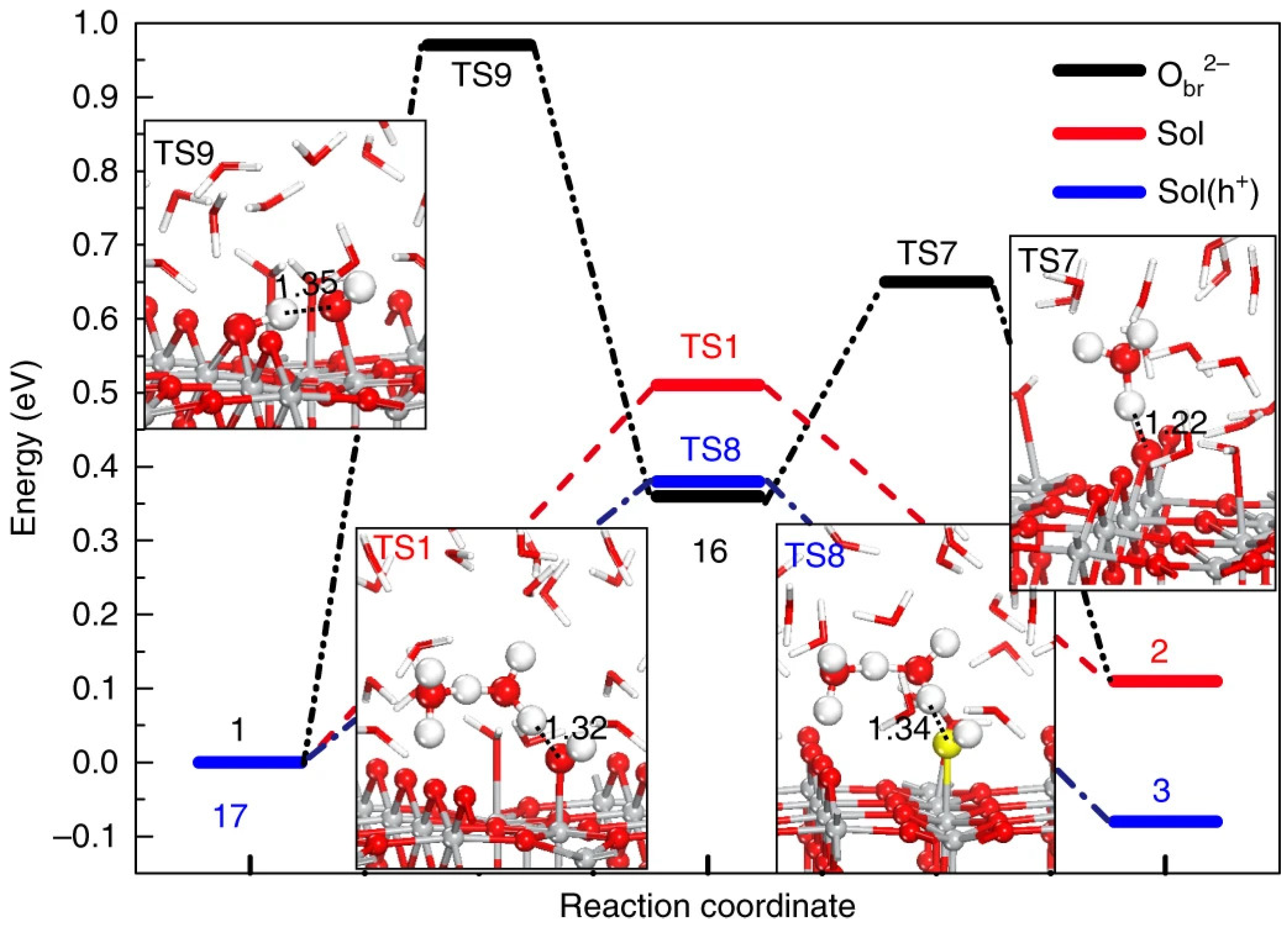
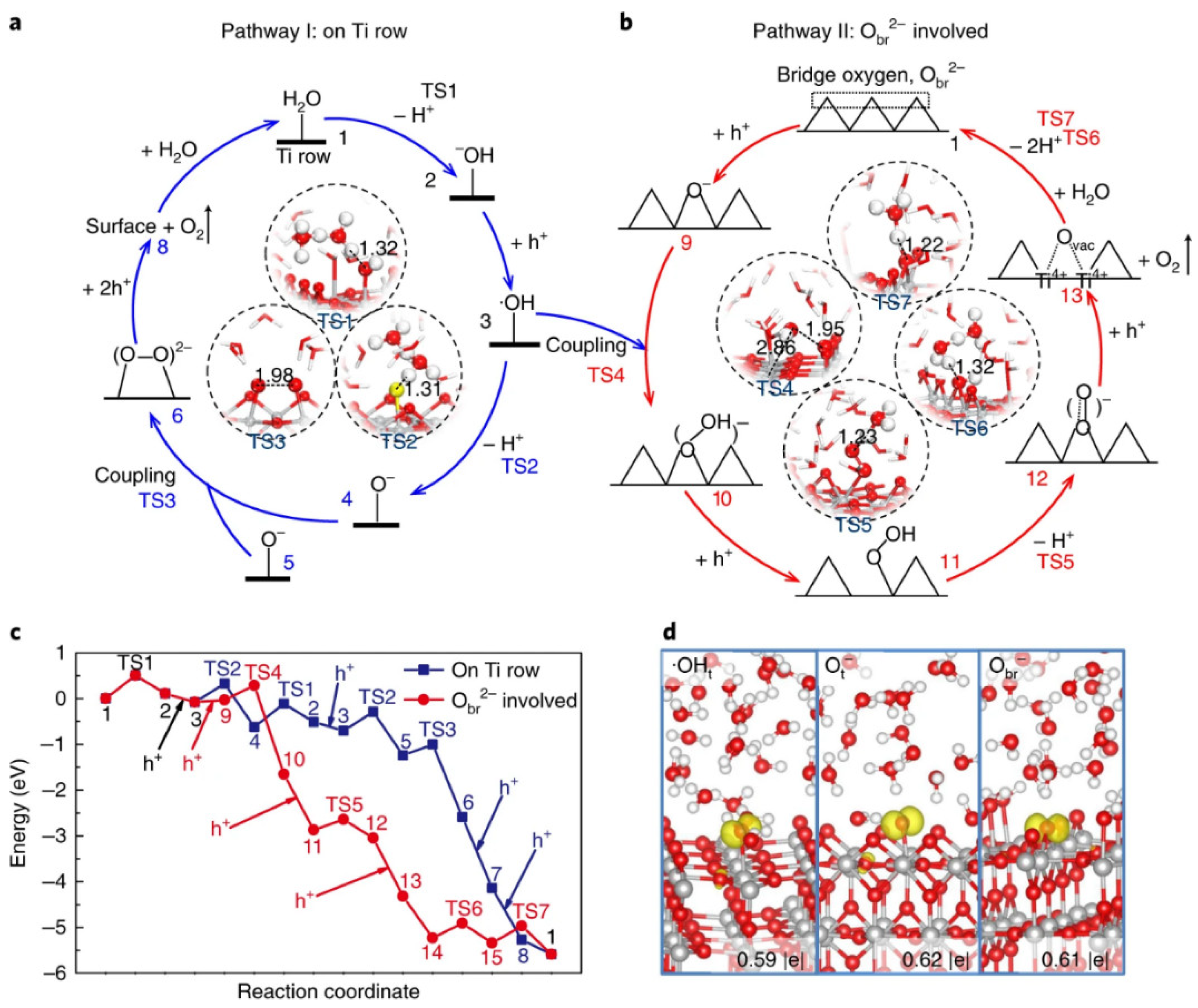
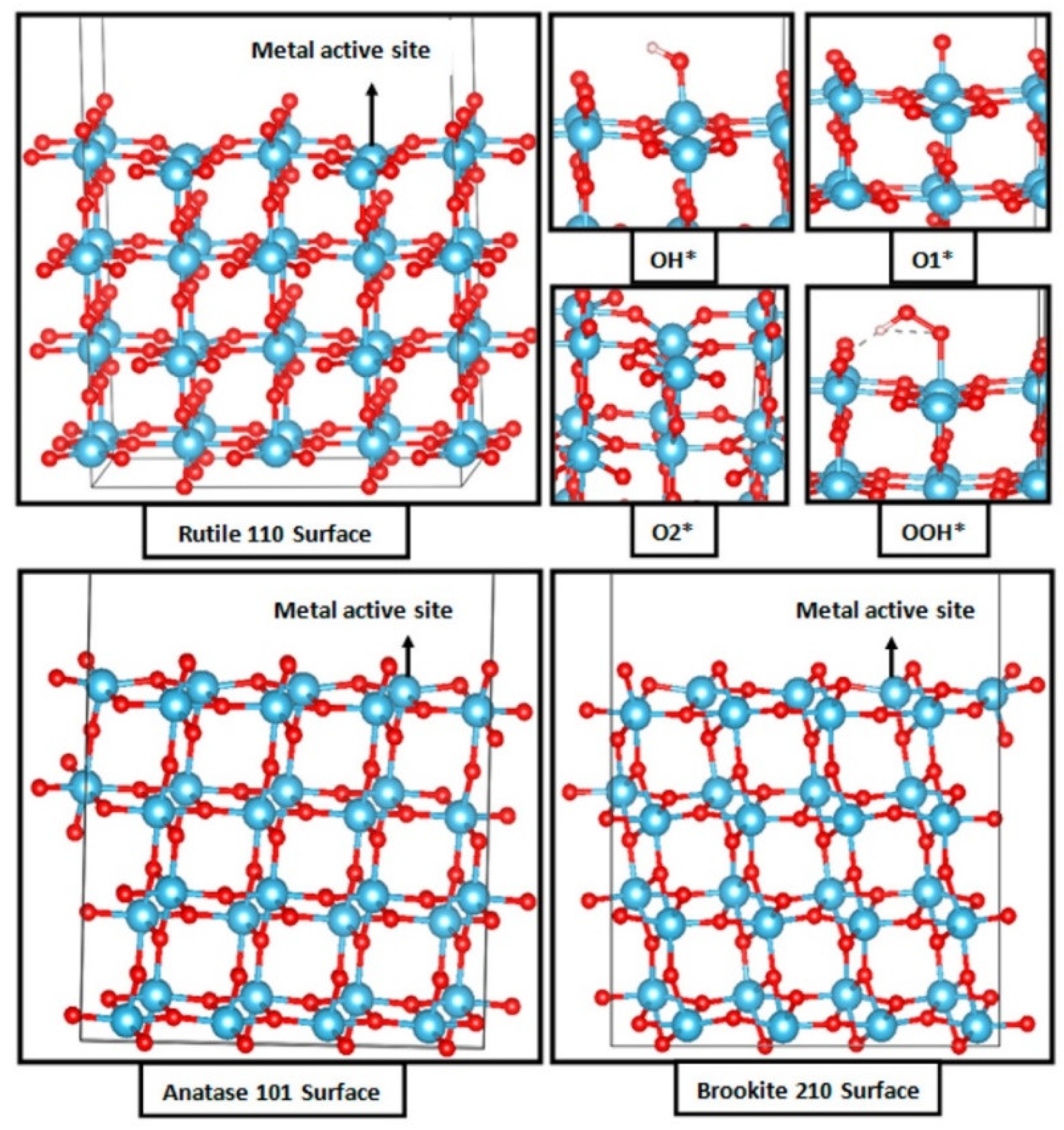
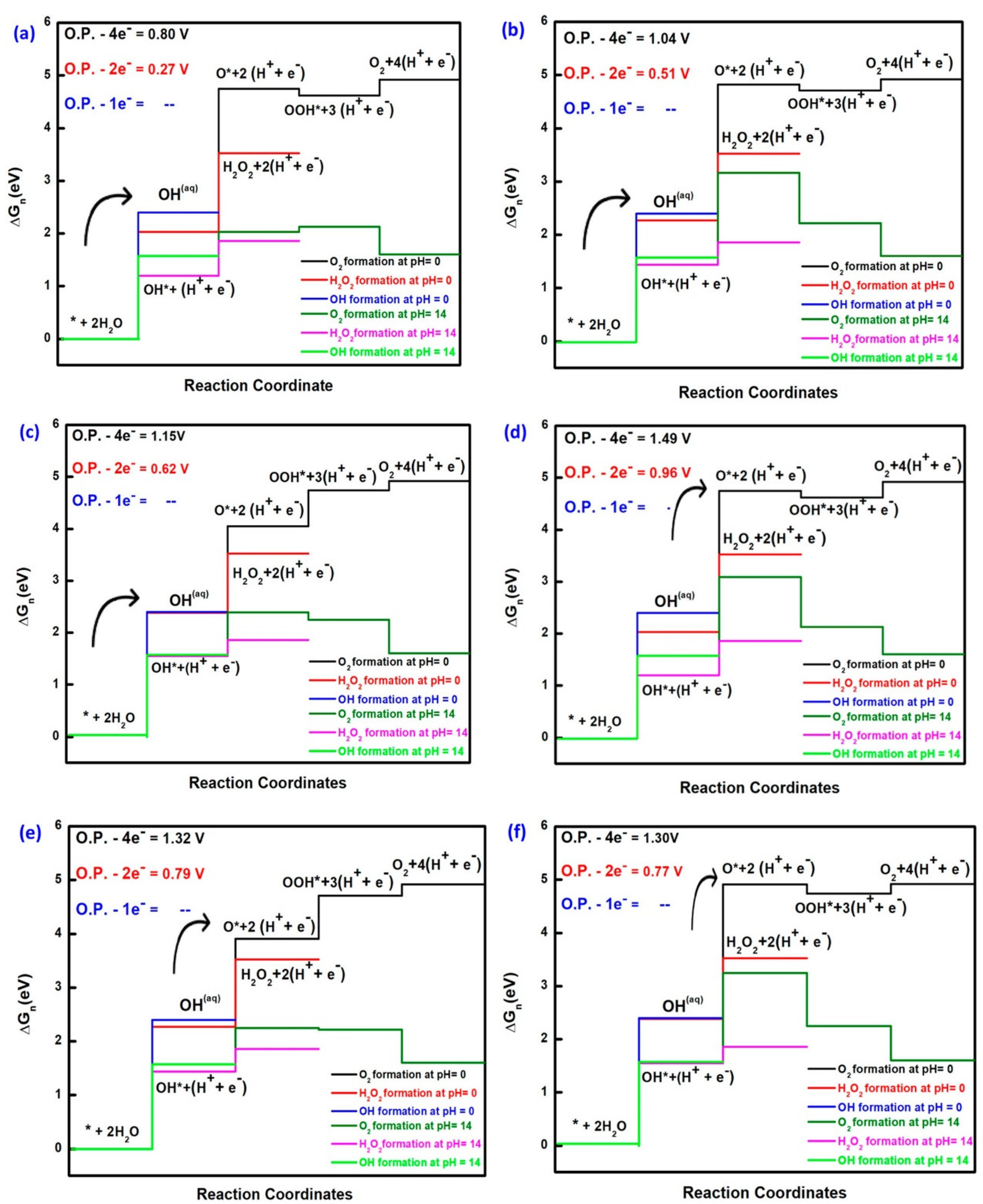
3.1. Titanium Oxide-Based Catalyst
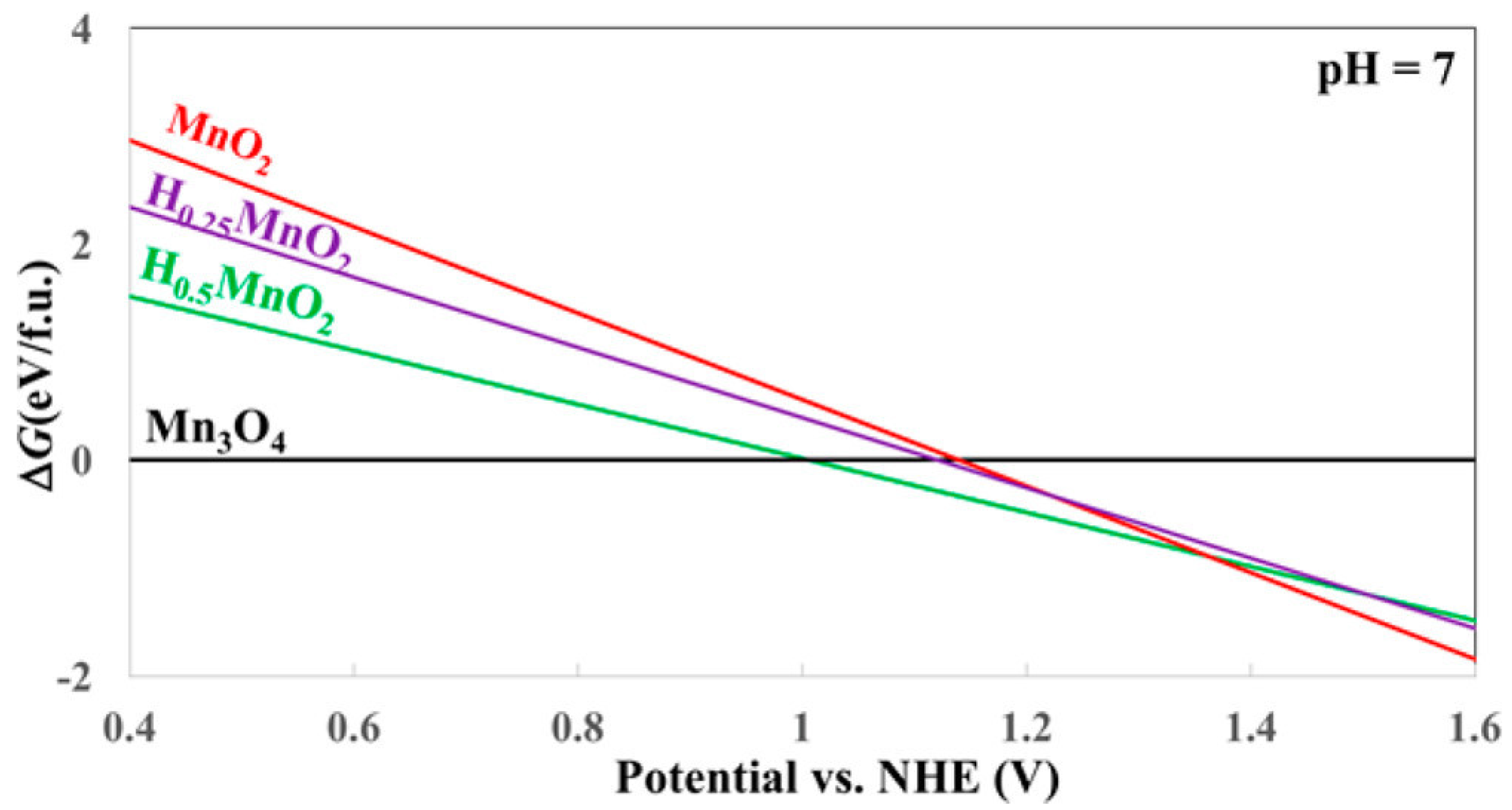
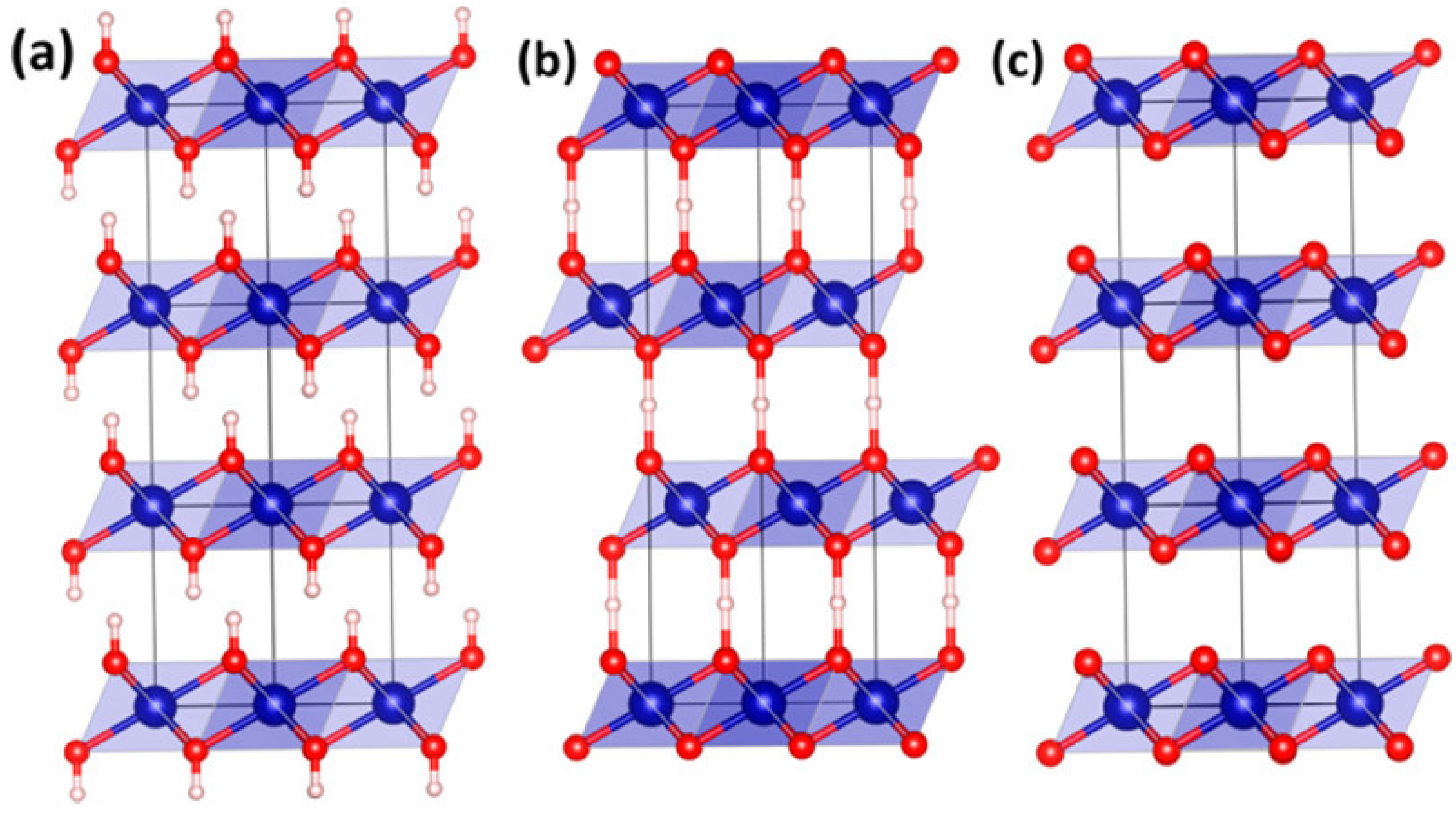
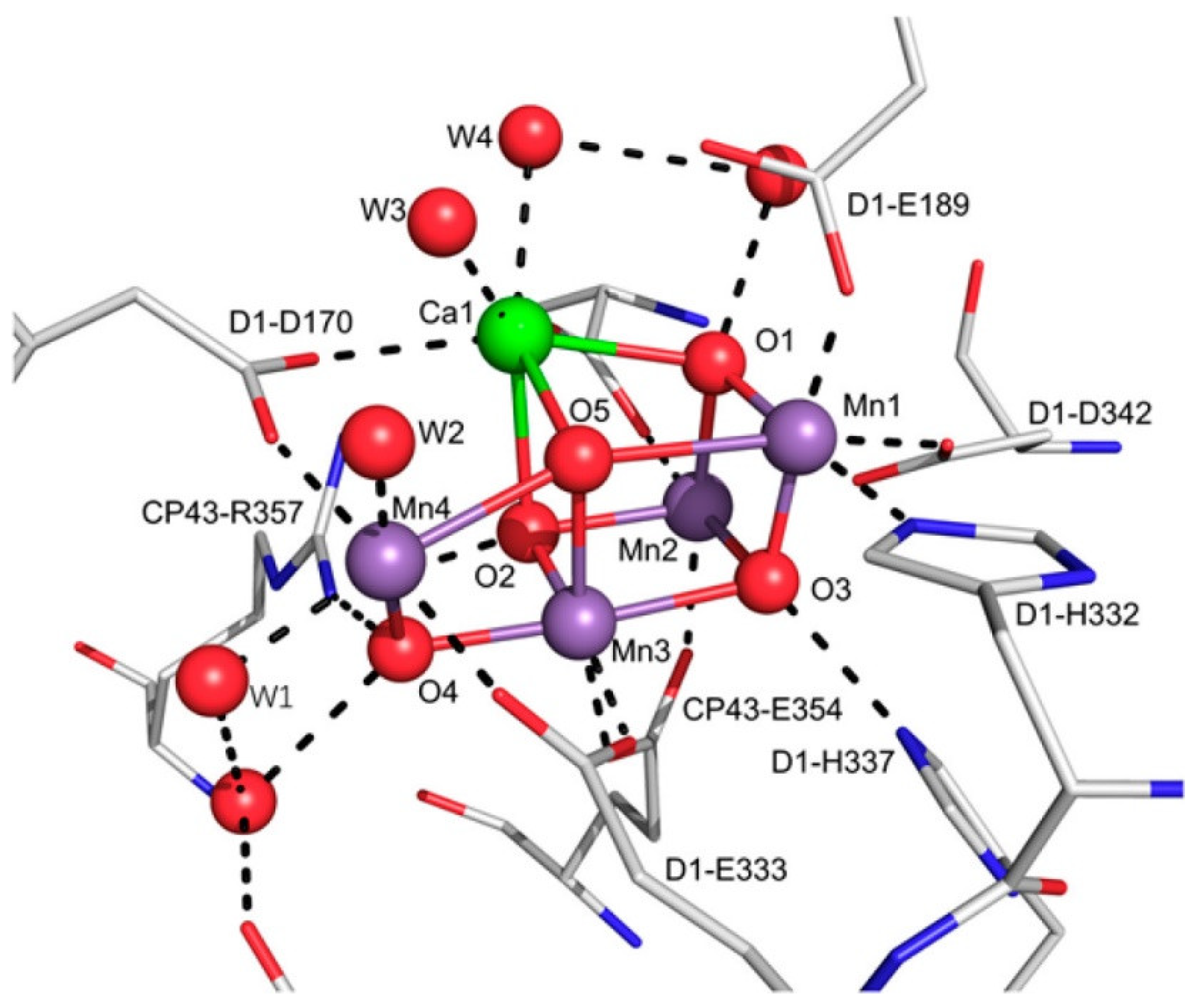
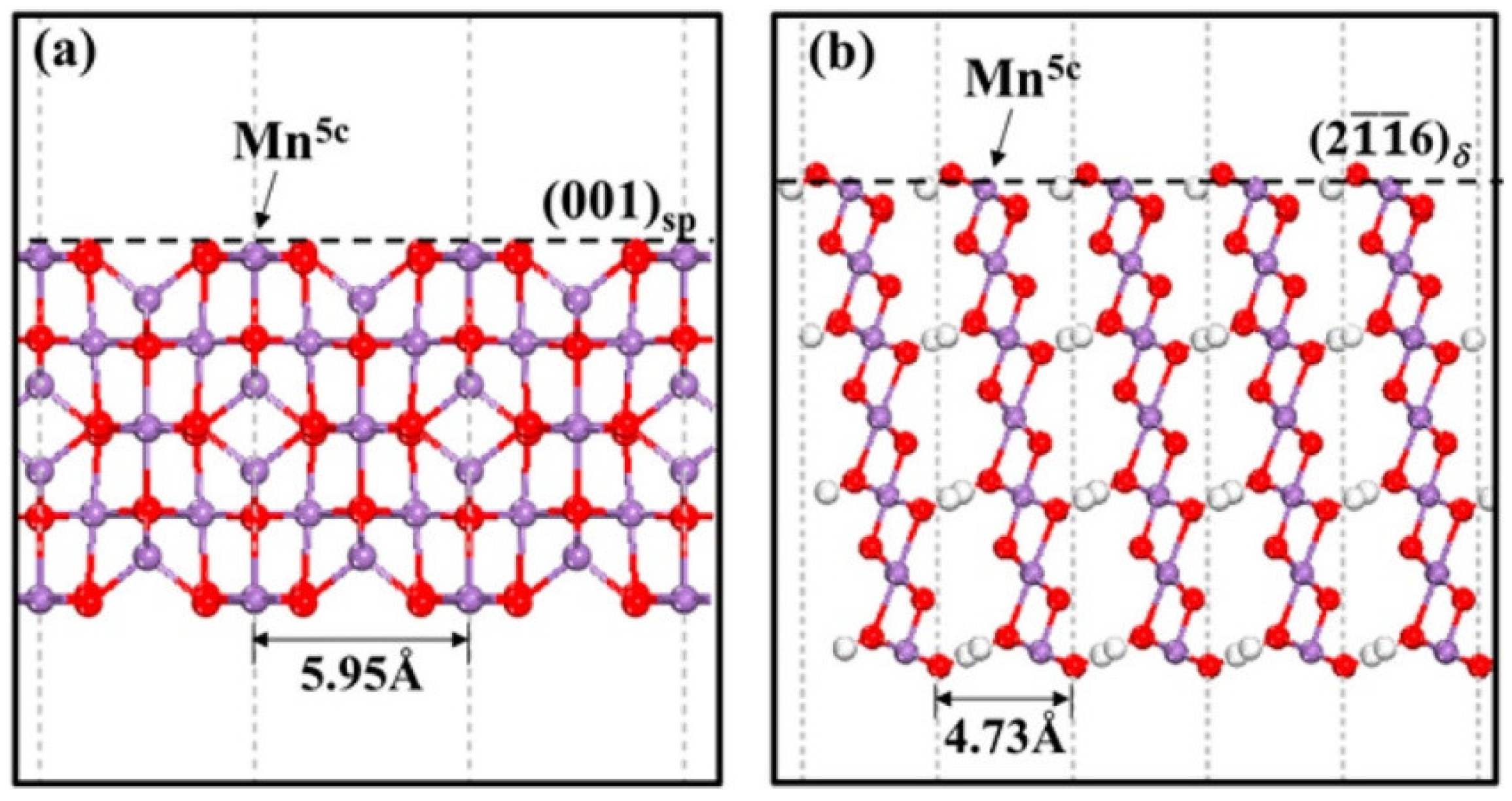
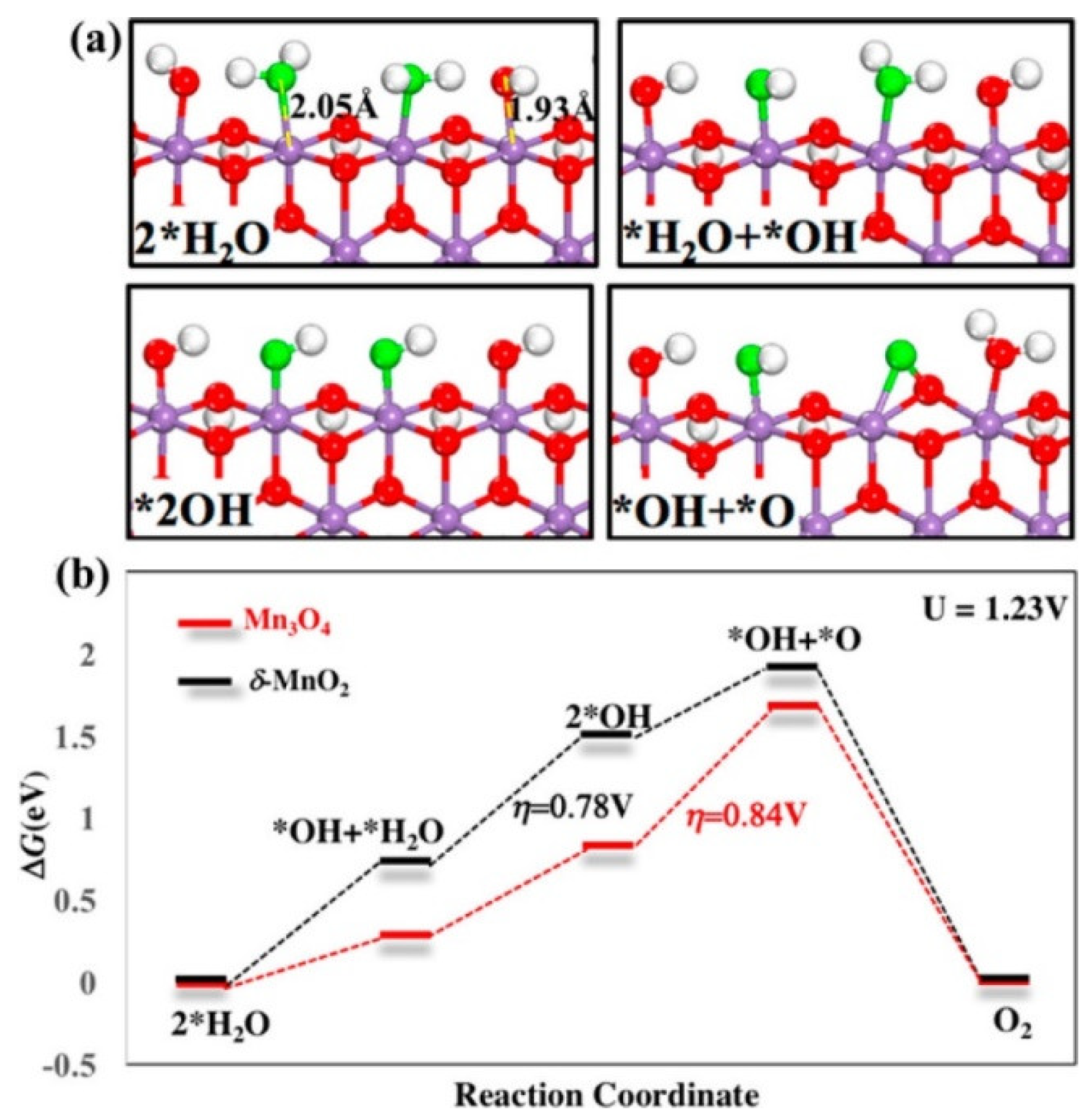
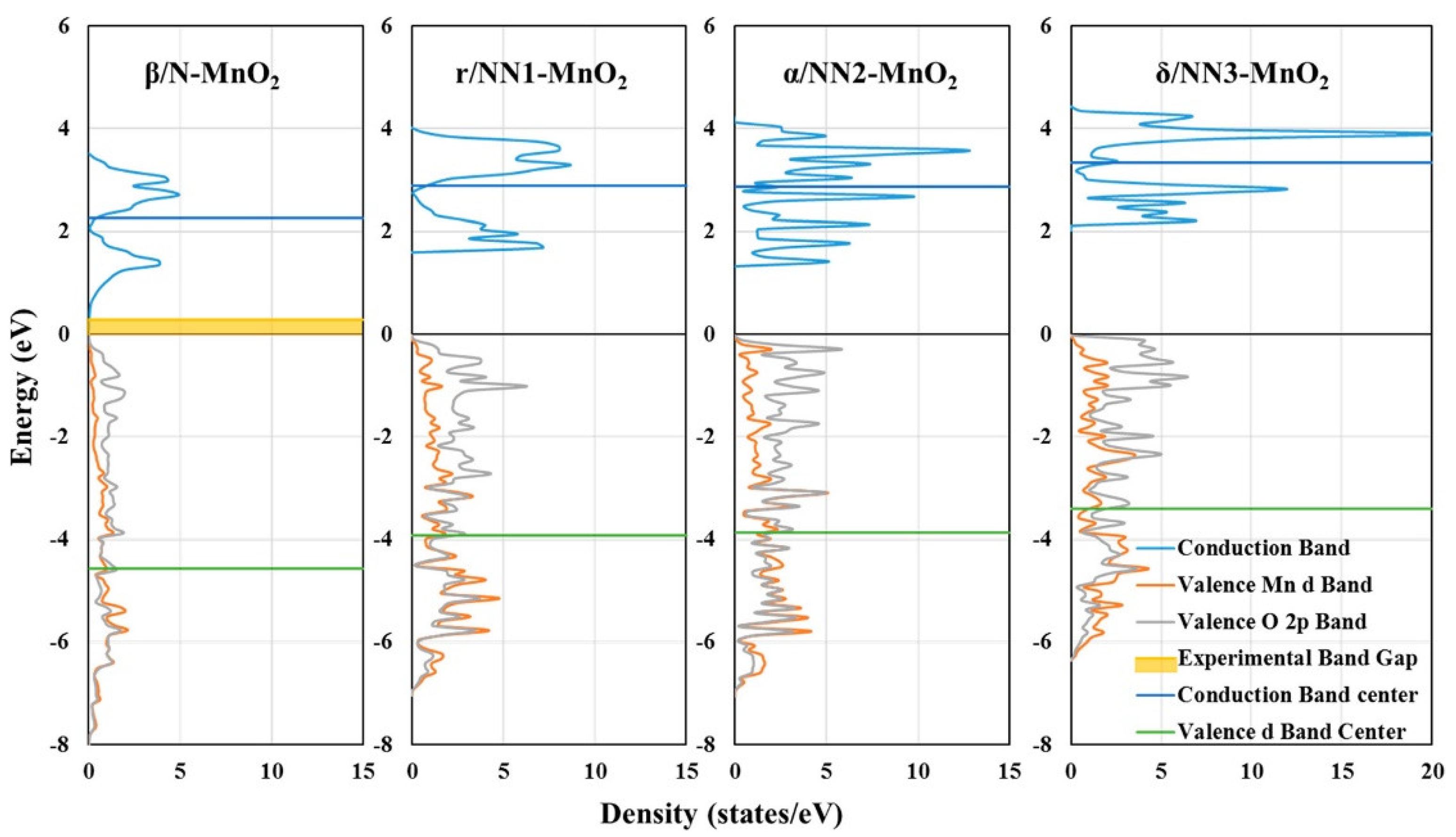
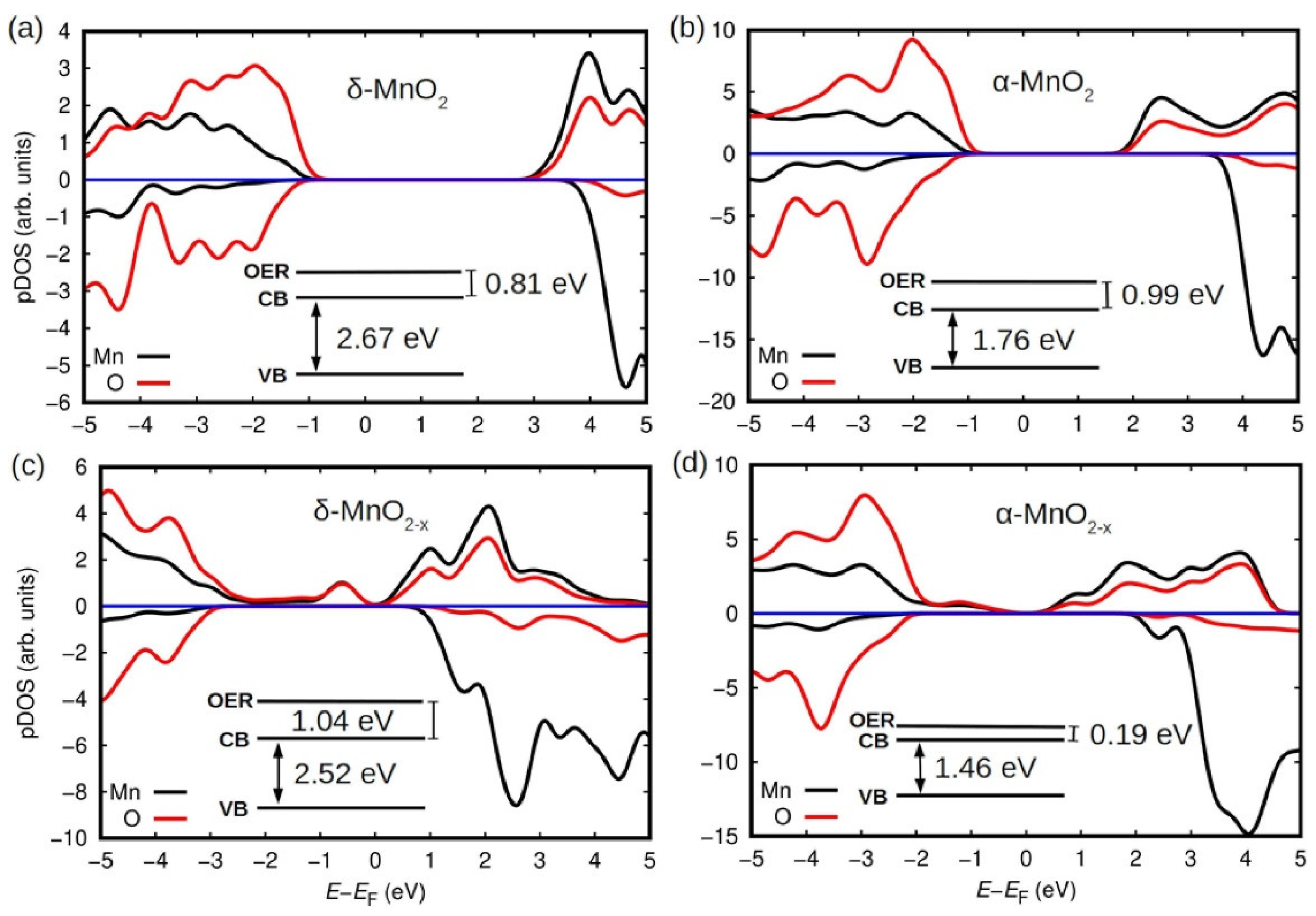
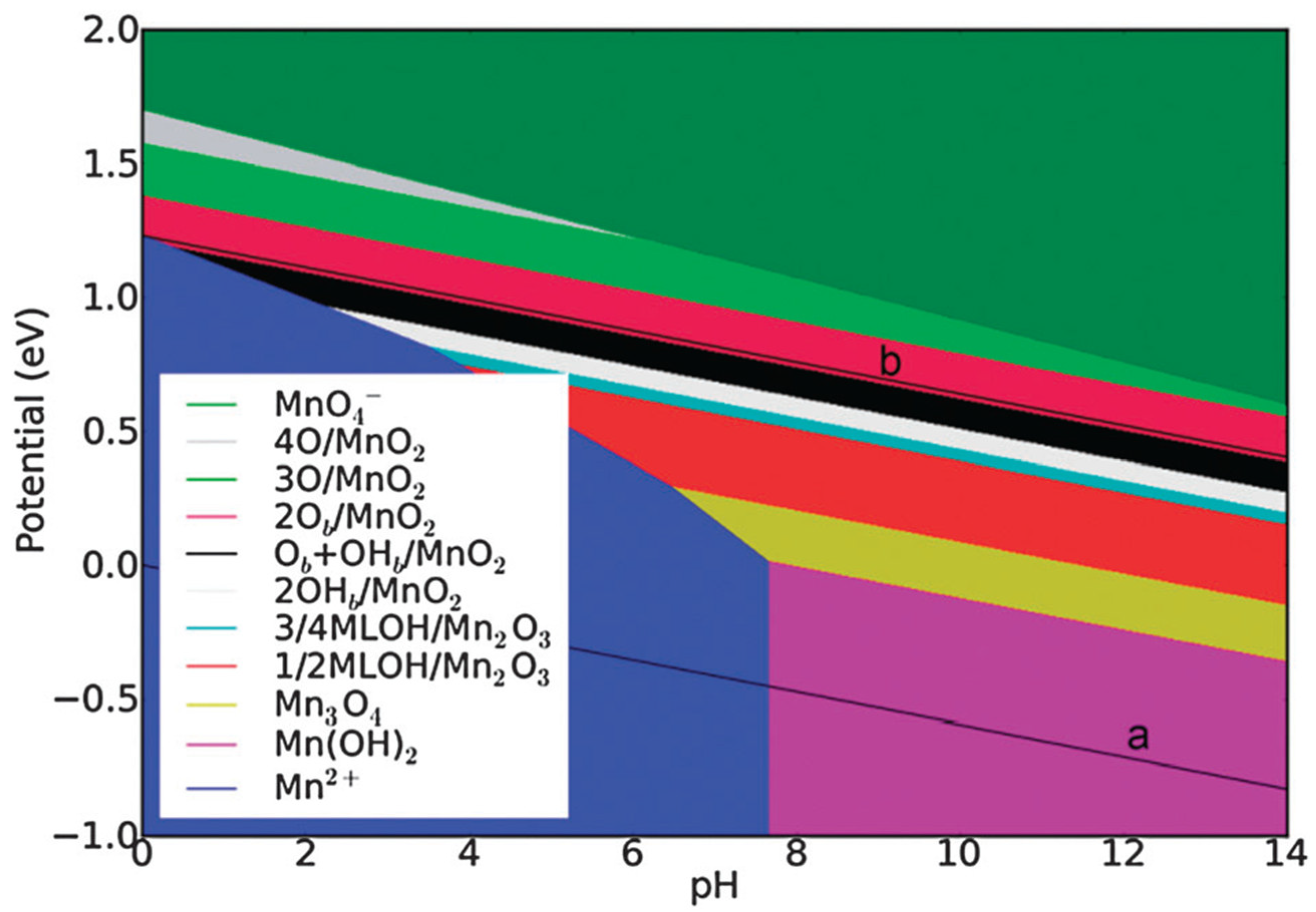
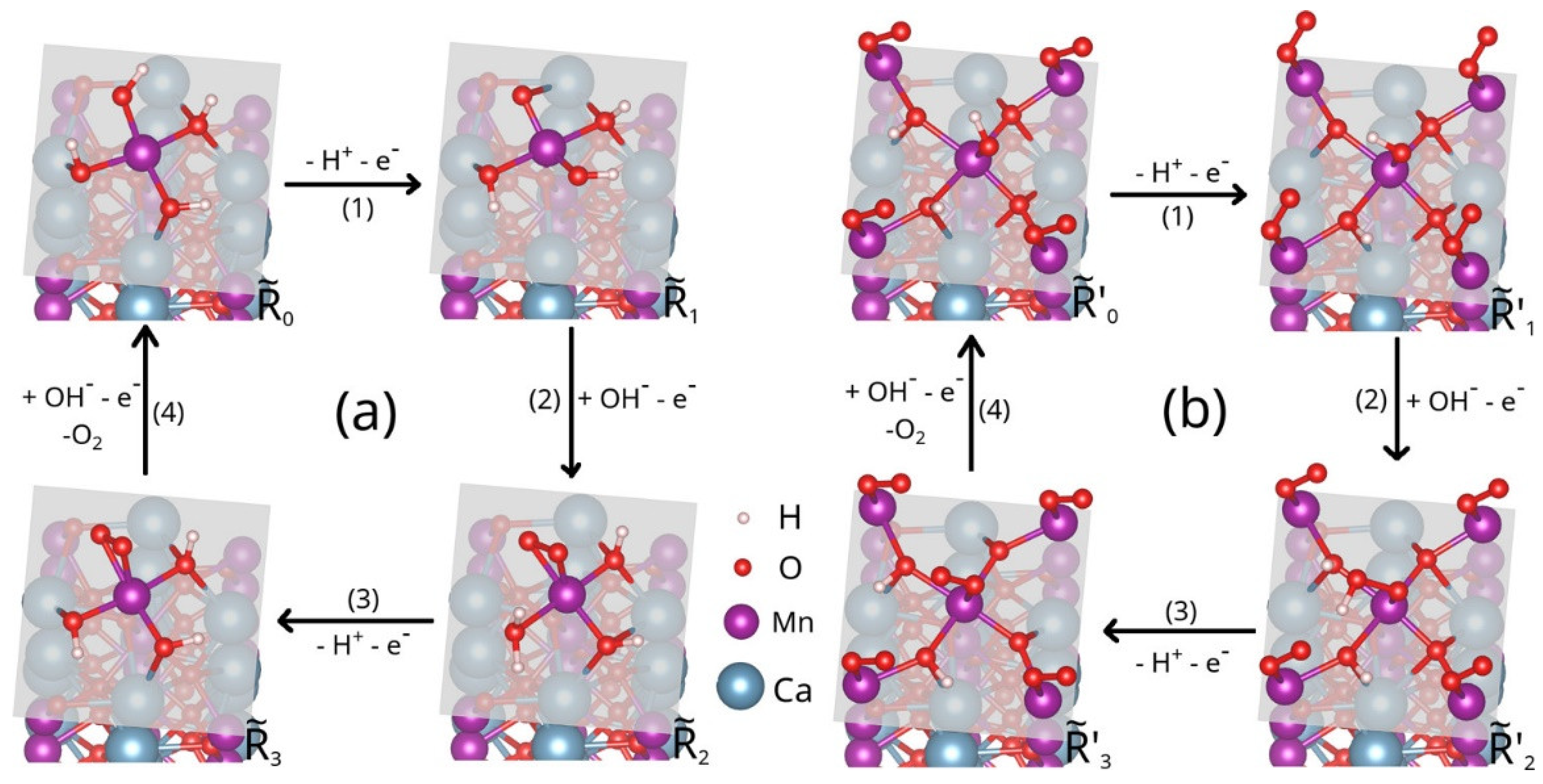
3.2. Manganese Oxide-Based Catalyst
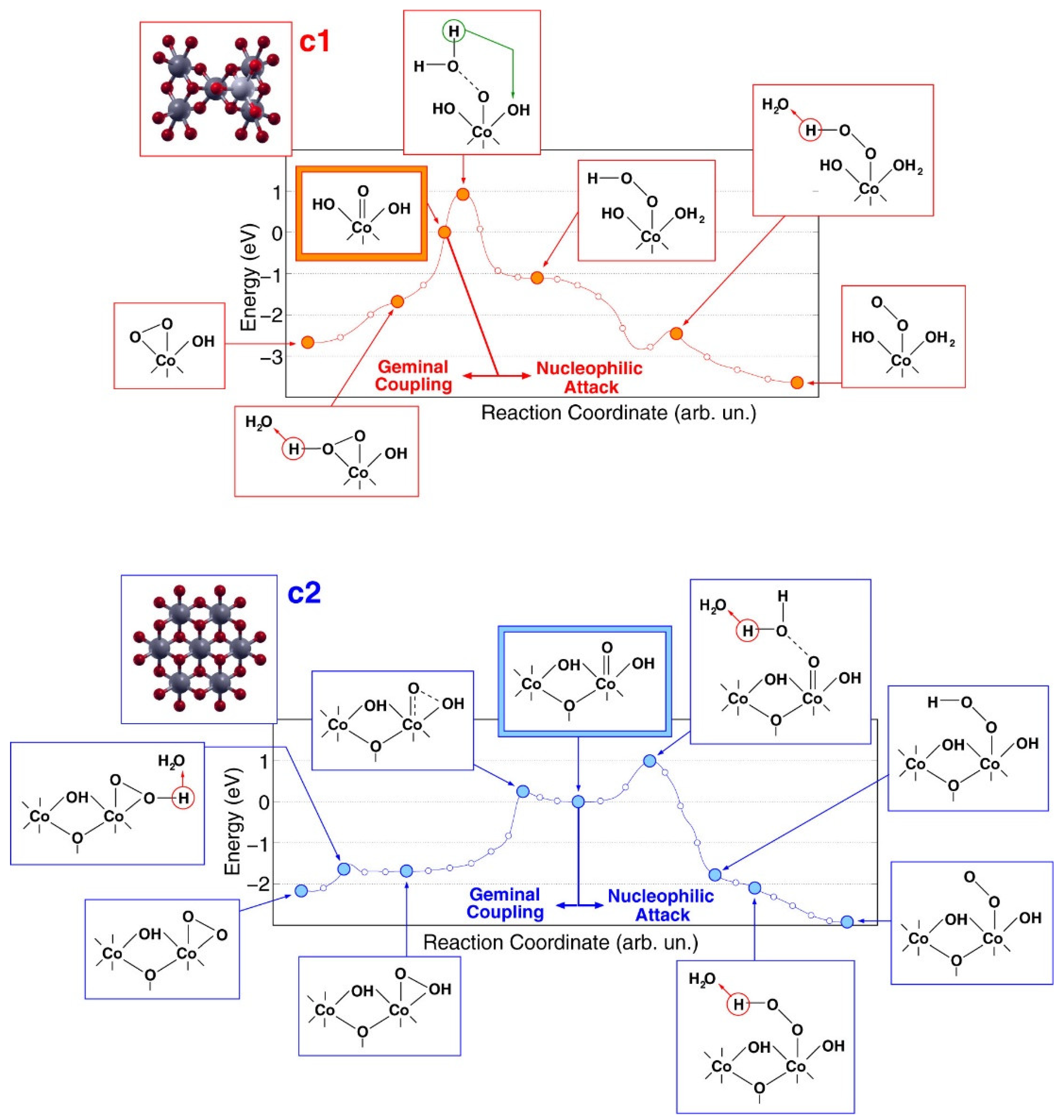
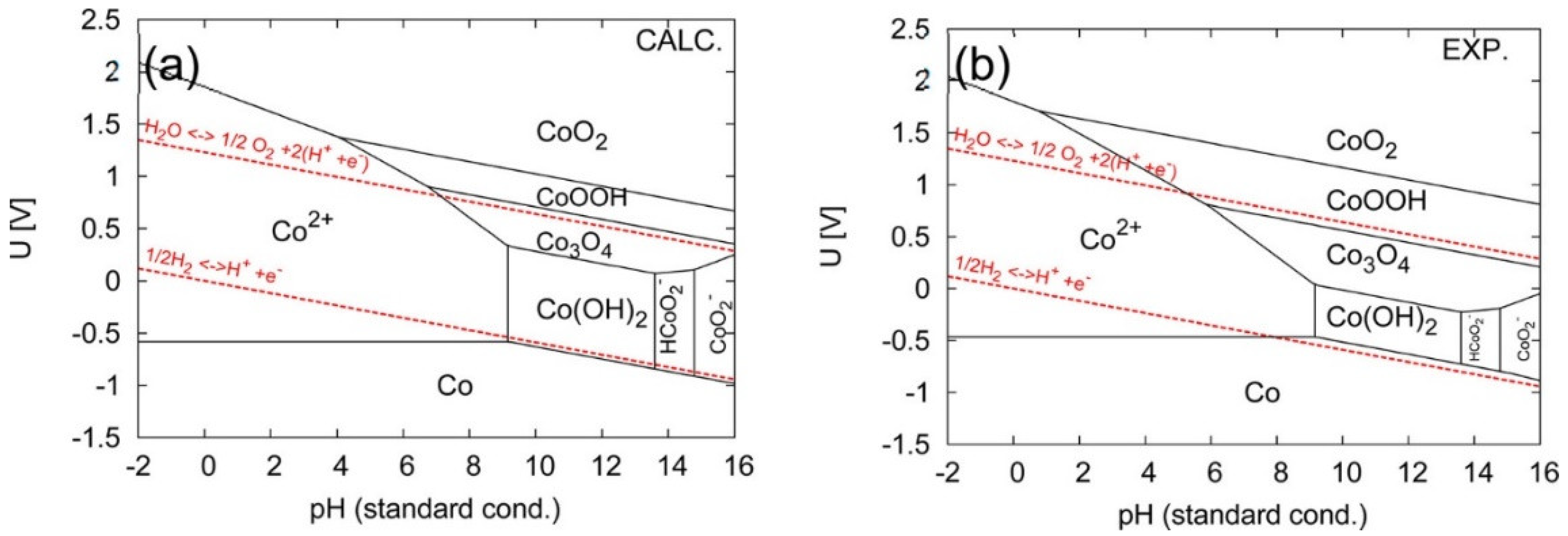
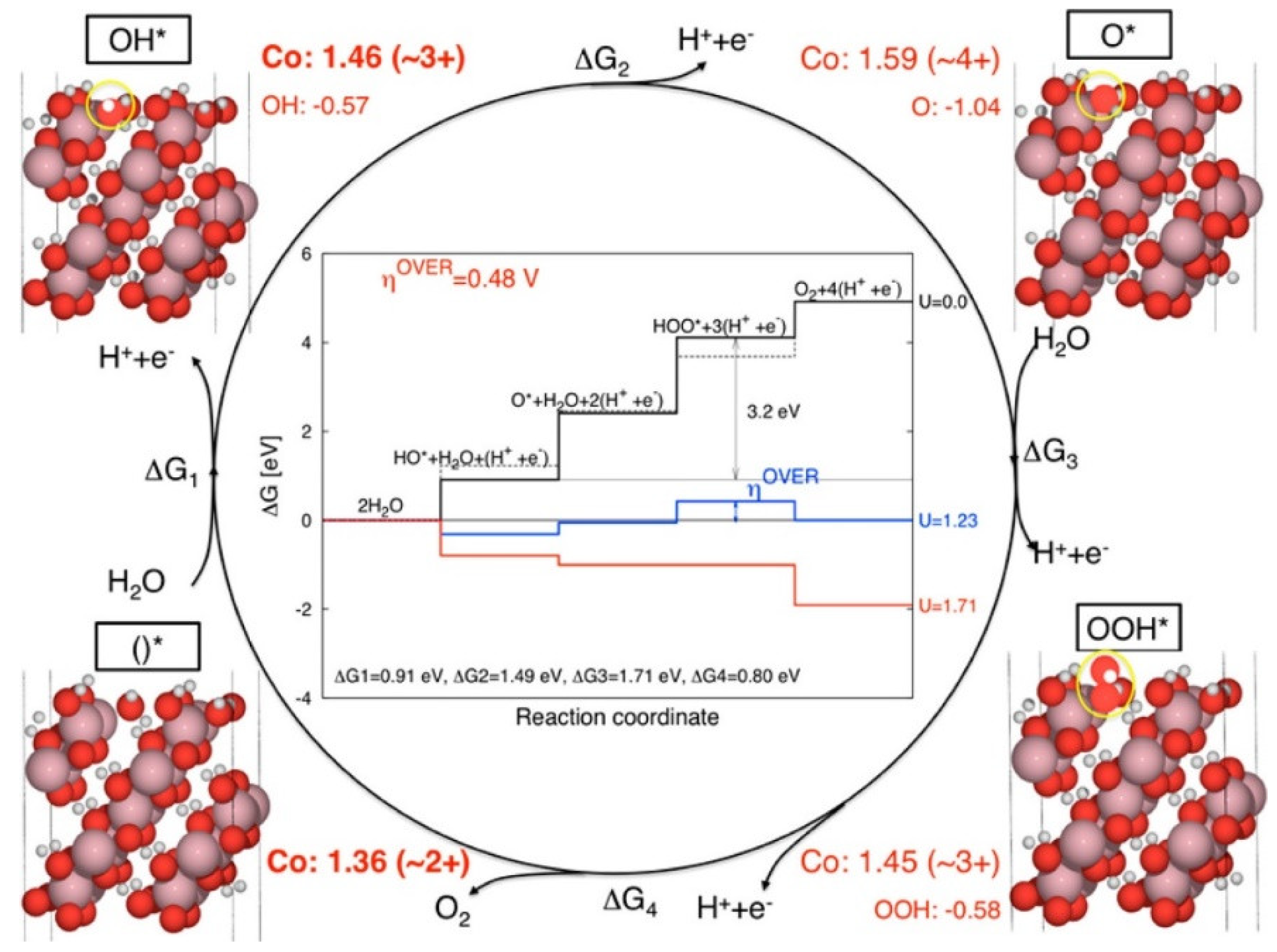
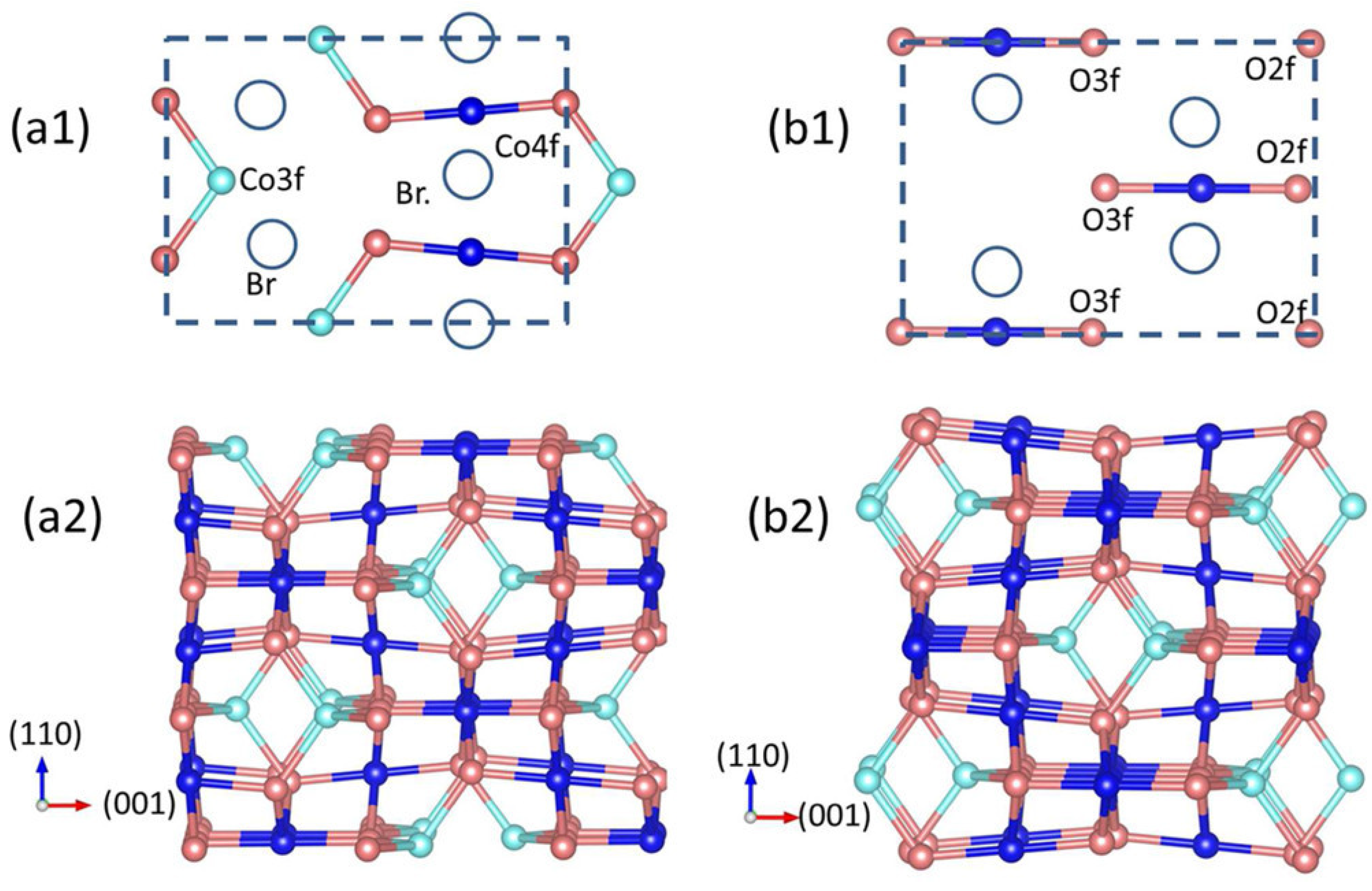
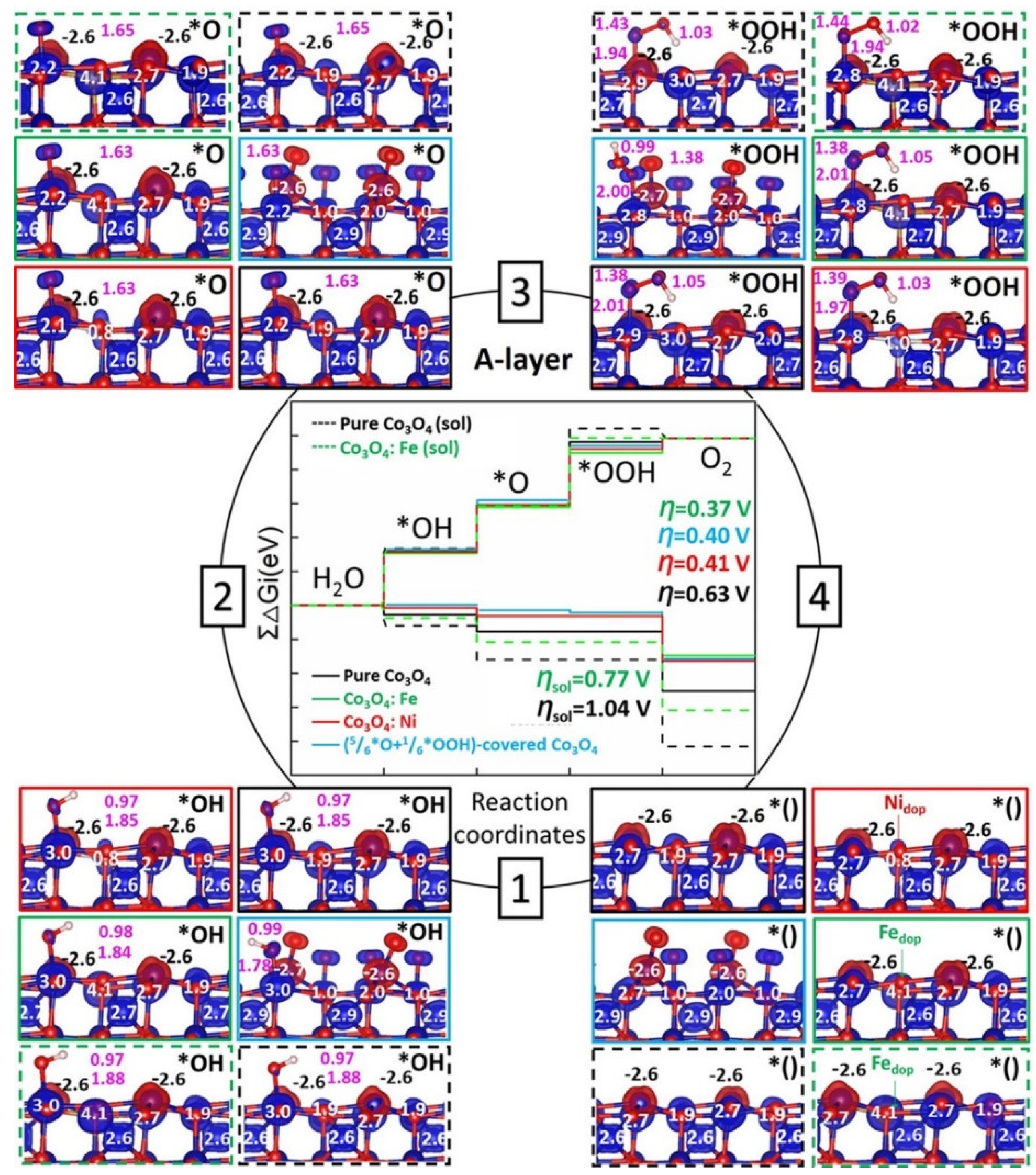
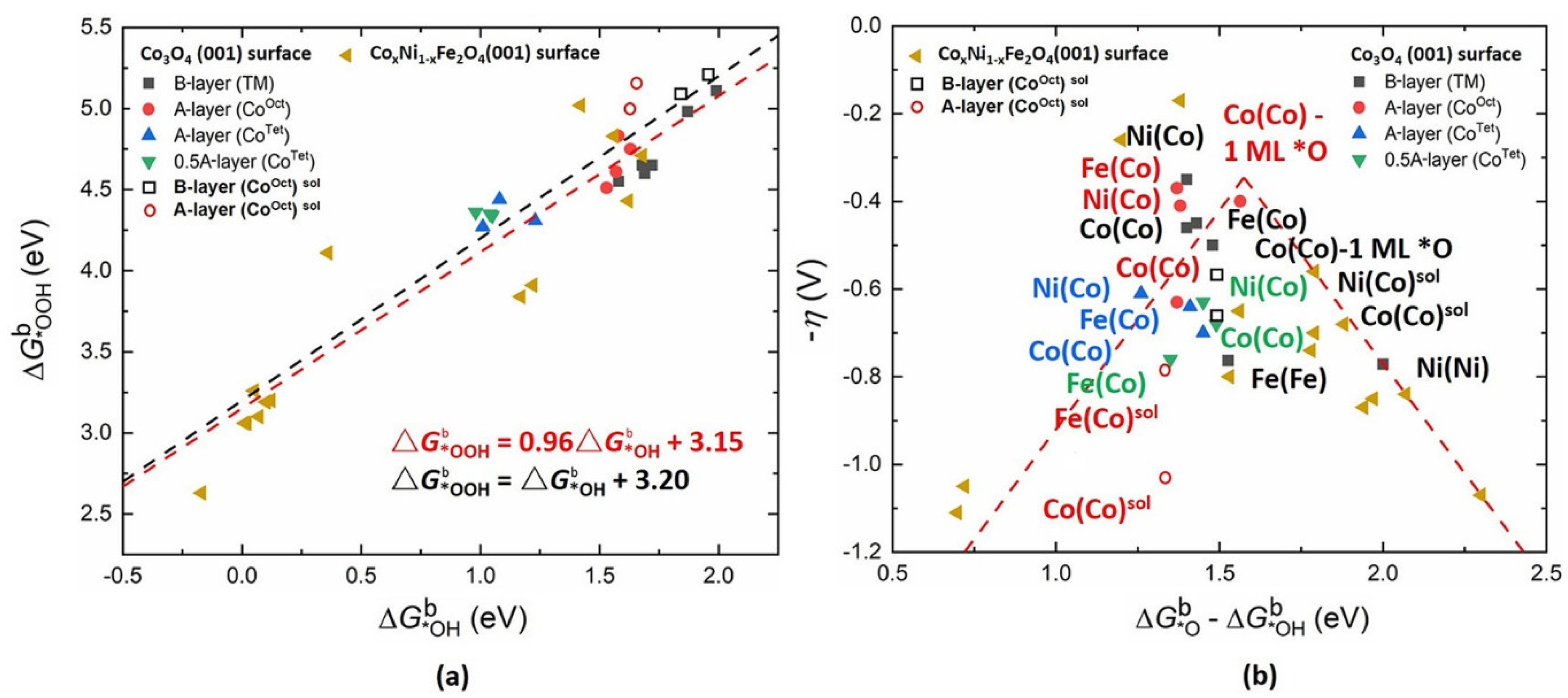
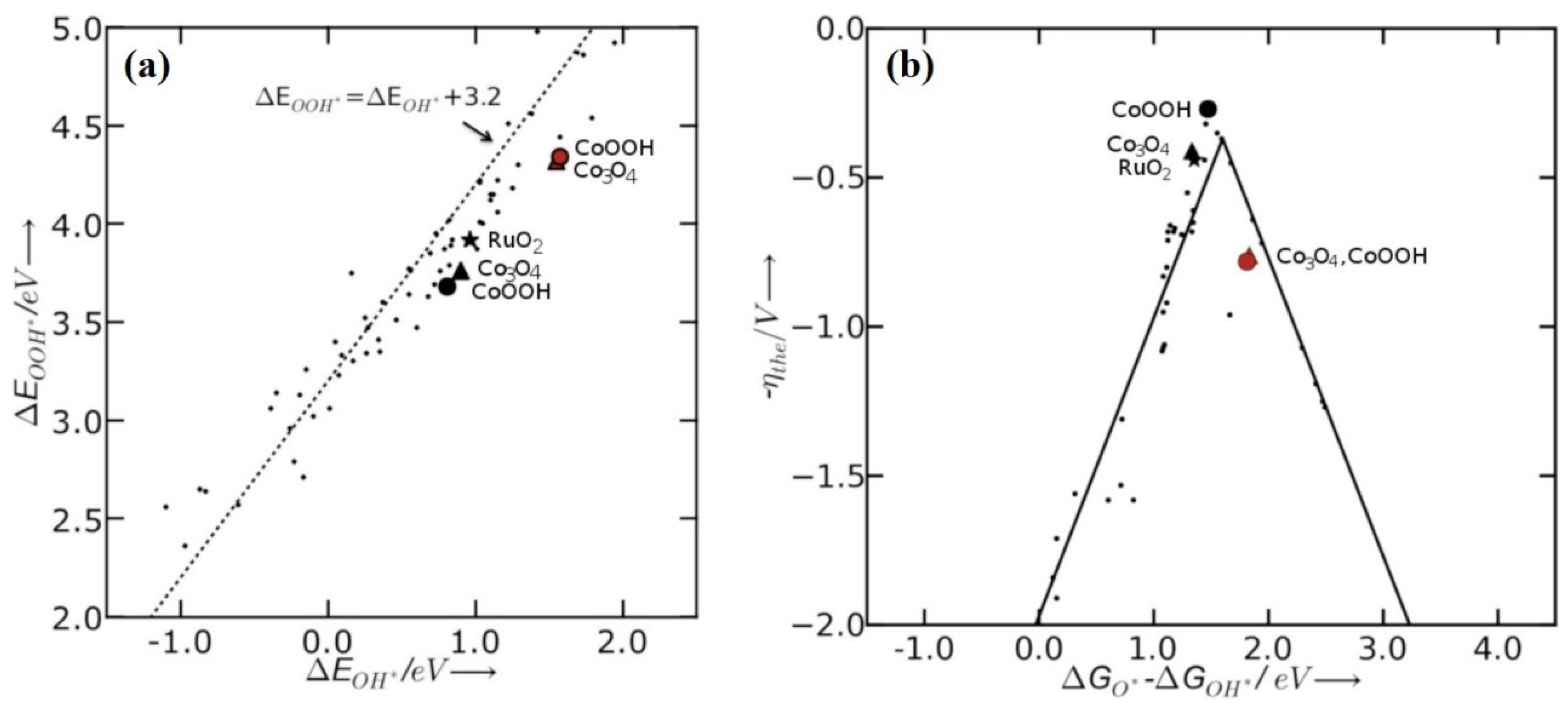
3.3. Cobalt Oxide-Based Catalyst
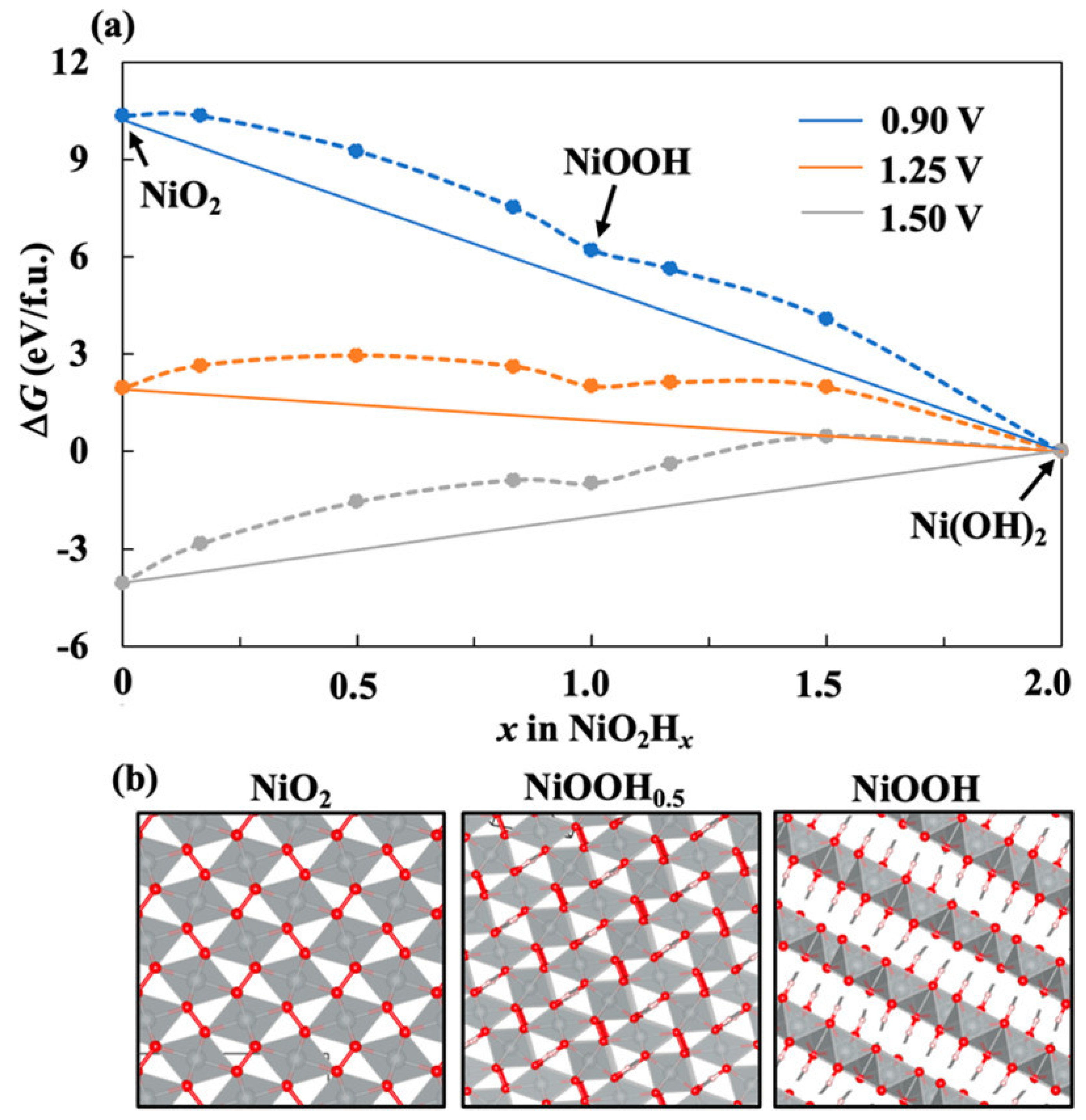
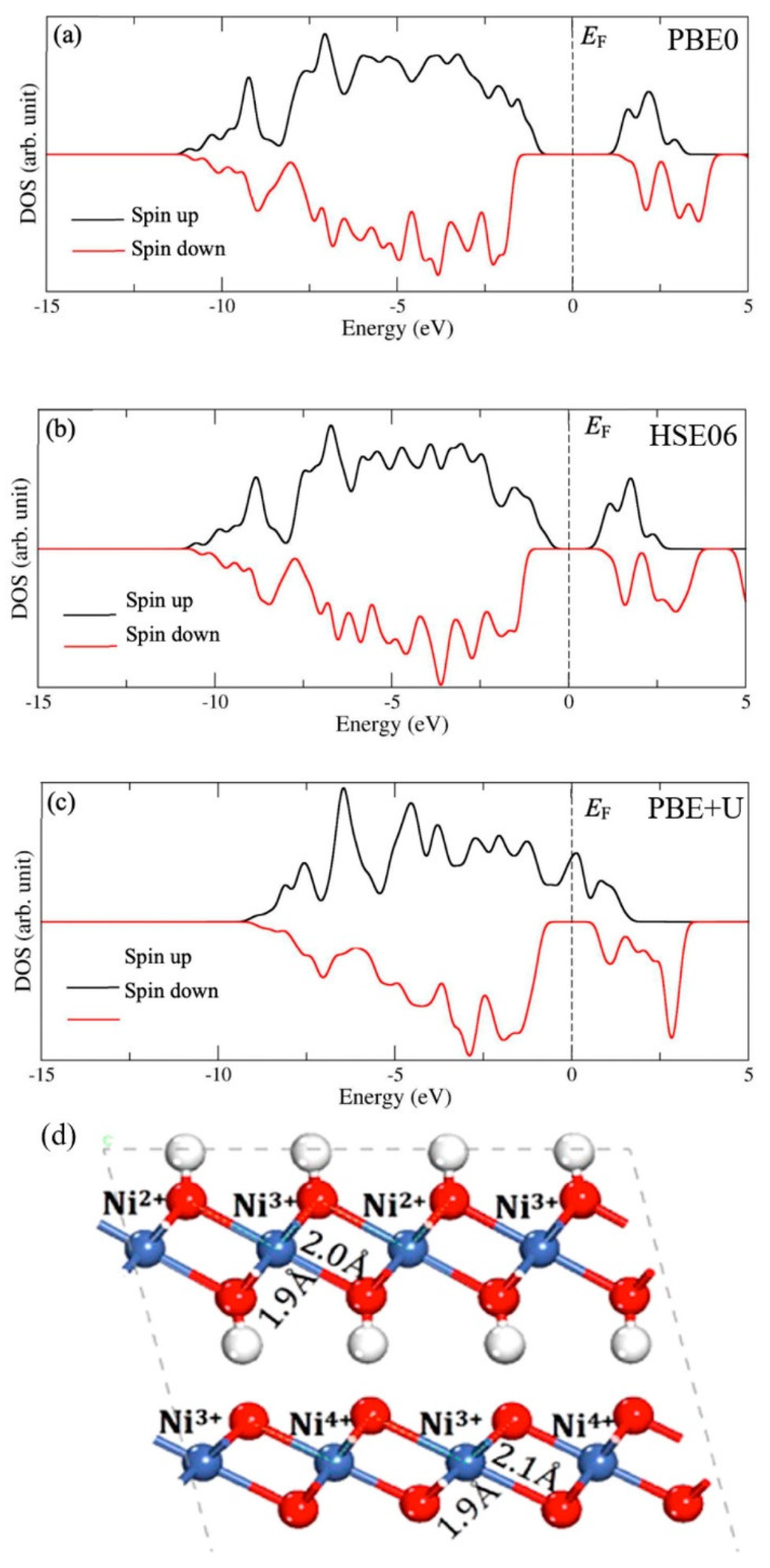
3.4. Nickel Oxide-Based Catalyst
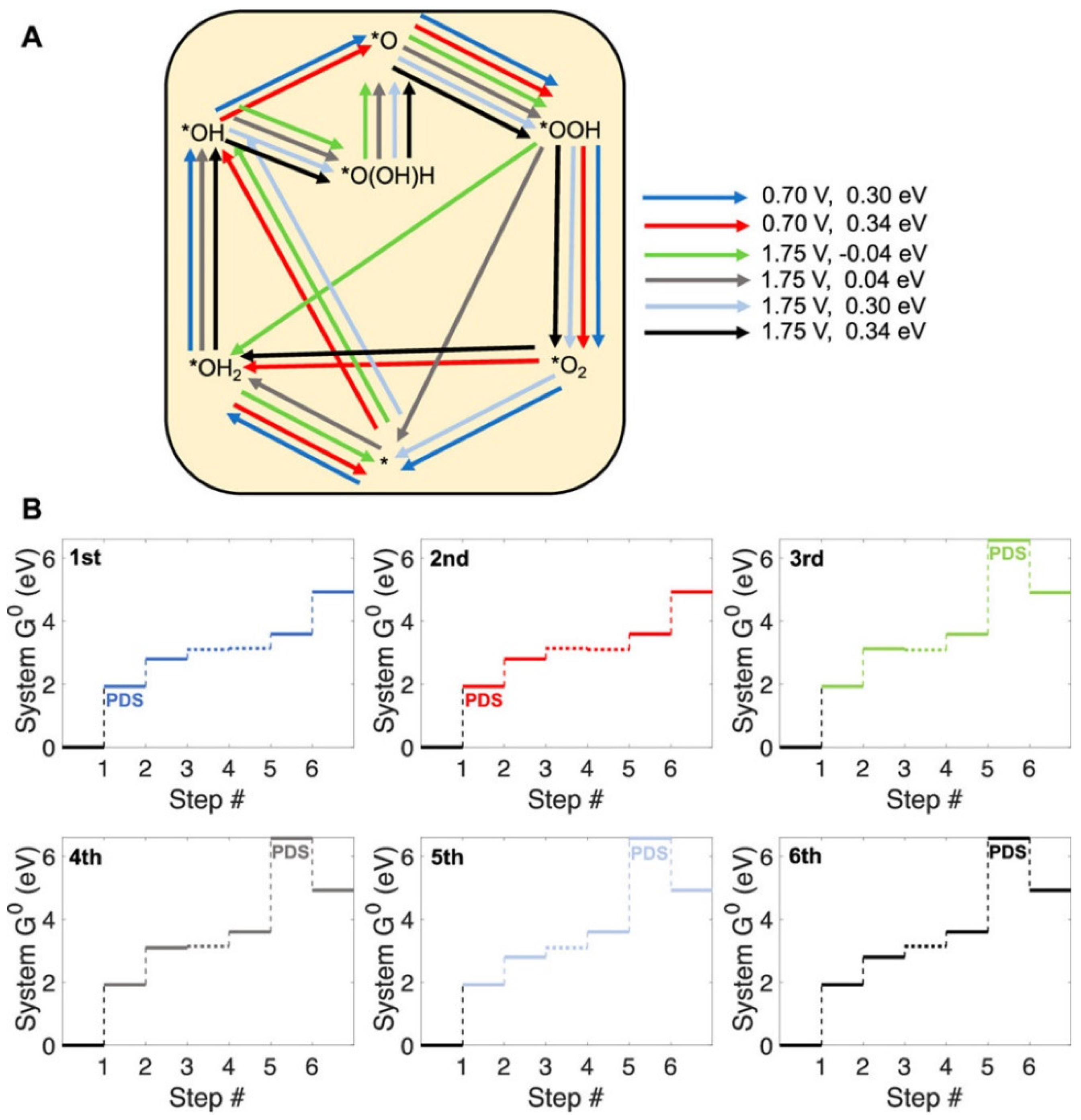
4. Discussion and Summary
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Hunter, B.M.; Gray, H.B.; Müller, A.M. Earth-Abundant Heterogeneous Water Oxidation Catalysts. Chem. Rev. 2016, 116, 14120–14136. [Google Scholar] [CrossRef] [PubMed]
- Man, I.C.; Su, H.; Calle-Vallejo, F.; Hansen, H.A.; Martínez, J.I.; Inoglu, N.G.; Kitchin, J.; Jaramillo, T.F.; Nørskov, J.K.; Rossmeisl, J. Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces. ChemCatChem 2011, 3, 1159–1165. [Google Scholar] [CrossRef]
- Casadevall, C. Heterogenization of Molecular Water Oxidation Catalysts in Electrodes for (Photo)Electrochemical Water Oxidation. Water 2022, 14, 371. [Google Scholar] [CrossRef]
- McEvoy, J.P.; Brudvig, G.W. Water-Splitting Chemistry of Photosystem II. Chem. Rev. 2006, 106, 4455–4483. [Google Scholar] [CrossRef] [PubMed]
- Meyer, T.J.; Huynh, M.H.V.; Thorp, H.H. The possible role of proton-coupled electron transfer (PCET) in water oxidation by photosystem II. Angew. Chem. Int. Ed. 2007, 46, 5284–5304. [Google Scholar] [CrossRef]
- Gagliardi, C.J.; Vannucci, A.K.; Concepcion, J.J.; Chen, Z.; Meyer, T.J. The role of proton coupled electron transfer in water oxidation. Energy Environ. Sci. 2012, 5, 7704. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Inuzuka, R.; Takashima, T.; Hayashi, T.; Hashimoto, K.; Nakamura, R. Regulating proton-coupled electron transfer for efficient water splitting by manganese oxides at neutral pH. Nat. Commun. 2014, 5, 4256. [Google Scholar] [CrossRef]
- Najafpour, M.M.; Renger, G.; Hołyńska, M.; Moghaddam, A.N.; Aro, E.-M.; Carpentier, R.; Nishihara, H.; Eaton-Rye, J.J.; Shen, J.-R.; Allakhverdiev, S.I. Manganese Compounds as Water-Oxidizing Catalysts: From the Natural Water-Oxidizing Complex to Nanosized Manganese Oxide Structures. Chem. Rev. 2016, 116, 2886–2936. [Google Scholar] [CrossRef]
- Weber, F.; Tremblay, J.C.; Bande, A. Proton-Coupled Electron-Transfer Dynamics of Water Oxidation at N-Doped Graphene Oxides. J. Phys. Chem. C 2020, 124, 26688–26698. [Google Scholar] [CrossRef]
- Tyburski, R.; Liu, T.; Glover, S.D.; Hammarström, L. Proton-Coupled Electron Transfer Guidelines, Fair and Square. J. Am. Chem. Soc. 2021, 143, 560–576. [Google Scholar] [CrossRef]
- Parent, A.R.; Nakazono, T.; Tsubonouchi, Y.; Taira, N.; Sakai, K. Mechanisms of Water Oxidation Using Ruthenium, Cobalt, Copper, and Iron Molecular Catalysts, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2019; Volume 74. [Google Scholar]
- Gonçalves, J.M.; Matias, T.A.; Toledo, K.C.F.; Araki, K. Electrocatalytic materials design for oxygen evolution reaction. Adv. Inorg. Chem. 2019, 74, 241–303. [Google Scholar] [CrossRef]
- Najafpour, M.M.; Heidari, S.; Balaghi, S.E.; Hołyńska, M.; Sadr, M.H.; Soltani, B.; Khatamian, M.; Larkum, A.W.; Allakhverdiev, S.I. Proposed mechanisms for water oxidation by Photosystem II and nanosized manganese oxides. Biochim. Biophys. Acta. Bioenerg. 2017, 1858, 156–174. [Google Scholar] [CrossRef]
- Maayan, G.; Gluz, N.; Christou, G. A bioinspired soluble manganese cluster as a water oxidation electrocatalyst with low overpotential. Nat. Catal. 2018, 1, 48–54. [Google Scholar] [CrossRef]
- Pla, J.J.; Garcia-Bosch, I.; Costas, M.; Gómez, L.; Fillol, J.L.; Codolà, Z. Efficient water oxidation catalysts based on readily available iron coordination complexes. Nat. Chem. 2011, 3, 807–813. [Google Scholar] [CrossRef]
- Panda, C.; Debgupta, J.; Díaz, D.D.; Singh, K.K.; Gupta, S.S.; Dhar, B.B. Homogeneous photochemical water oxidation by biuret-modified Fe-TAML: Evidence of FeV(O) intermediate. J. Am. Chem. Soc. 2014, 136, 12273–12282. [Google Scholar] [CrossRef]
- Ellis, W.C.; McDaniel, N.D.; Bernhard, S.; Collins, T.J. Fast water oxidation using Iron. J. Am. Chem. Soc. 2010, 132, 10990–10991. [Google Scholar] [CrossRef]
- Dogutan, D.K.; McGuire, R.; Nocera, D.G. Electocatalytic water oxidation by cobalt(III) hangman β-octafluoro corroles. J. Am. Chem. Soc. 2011, 133, 9178–9180. [Google Scholar] [CrossRef]
- Wang, D.; Ghirlanda, G.; Allen, J.P. Water oxidation by a nickel-glycine catalyst. J. Am. Chem. Soc. 2014, 136, 10198–10201. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, M.T.; Hou, C.; Ke, Z.F.; Lu, T.B. Homogeneous electrocatalytic water oxidation at neutral pH by a robust macrocyclic nickel(II) complex. Angew. Chemie. Int. Ed. 2014, 53, 13042–13048. [Google Scholar] [CrossRef]
- Bagheri, R.; Singh, J.P.; Chae, K.H.; Feizi, H.; Jagličić, Z.; Najafpour, M.M.; Song, Z. A nickel(ii) complex under water-oxidation reaction: What is the true catalyst? Dalt. Trans. 2018, 48, 547–557. [Google Scholar] [CrossRef]
- Barnett, S.M.; Goldberg, K.I.; Mayer, J.M. A soluble copper-bipyridine water-oxidation electrocatalyst. Nat. Chem. 2012, 4, 498–502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.-T.; Chen, Z.; Kang, P.; Meyer, T.J. Electrocatalytic Water Oxidation with a Copper(II) Polypeptide Complex. J. Am. Chem. Soc. 2013, 135, 2048–2051. [Google Scholar] [CrossRef] [PubMed]
- Coggins, M.K.; Zhang, M.T.; Chen, Z.; Song, N.; Meyer, T.J. Single-Site Copper(II) Water Oxidation Electrocatalysis: Rate Enhancements with HPO42- as a Proton Acceptor at pH 8. Angew. Chemie. Int. Ed. 2014, 53, 12226–12230. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, W.; Liu, Y.; Lai, W.; Zhang, Z.; Cao, R.; Han, Y. Low overpotential water oxidation at neutral pH catalyzed by a copper(ii) porphyrin. Chem. Sci. 2019, 10, 2613–2622. [Google Scholar] [CrossRef]
- Gerlach, D.L.; Bhagan, S.; Cruce, A.A.; Burks, D.B.; Nieto, I.; Truong, H.T.; Kelley, S.P.; Herbst-Gervasoni, C.J.; Jernigan, K.L.; Bowman, M.K.; et al. Studies of the pathways open to copper water oxidation catalysts containing proximal hydroxy groups during basic electrocatalysis. Inorg. Chem. 2014, 53, 12689–12698. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, C.; Liu, S.; Wang, J.L.; Lin, W. A biomimetic copper water oxidation catalyst with low overpotential. J. Am. Chem. Soc. 2014, 136, 273–281. [Google Scholar] [CrossRef]
- Garrido-Barros, P.; Funes-Ardoiz, I.; Drouet, S.; Benet-Buchholz, J.; Maseras, F.; Llobet, A. Redox non-innocent ligand controls water oxidation overpotential in a new family of mononuclear cu-based efficient catalysts. J. Am. Chem. Soc. 2015, 137, 6758–6761. [Google Scholar] [CrossRef]
- Prevedello, A.; Bazzan, I.; Dalle Carbonare, N.; Giuliani, A.; Bhardwaj, S.; Africh, C.; Cepek, C.; Argazzi, R.; Bonchio, M.; Caramori, S.; et al. Heterogeneous and Homogeneous Routes in Water Oxidation Catalysis Starting from CuII Complexes with Tetraaza Macrocyclic Ligands. Chem. An Asian J. 2016, 11, 1281–1287. [Google Scholar] [CrossRef]
- Terao, R.; Nakazono, T.; Parent, A.R.; Sakai, K. Photochemical Water Oxidation Catalyzed by a Water-Soluble Copper Phthalocyanine Complex. Chempluschem 2016, 81, 1064–1067. [Google Scholar] [CrossRef]
- Winikoff, S.G.; Cramer, C.J. Mechanistic analysis of water oxidation catalyzed by mononuclear copper in aqueous bicarbonate solutions. Catal. Sci. Technol. 2014, 4, 2484–2489. [Google Scholar] [CrossRef]
- Sander, A.C.; Maji, S.; Francàs, L.; Böhnisch, T.; Dechert, S.; Llobet, A.; Meyer, F. Highly efficient binuclear ruthenium catalyst for water oxidation. ChemSusChem 2015, 8, 1697–1702. [Google Scholar] [CrossRef]
- Concepcion, J.J.; Jurss, J.W.; Templeton, J.L.; Meyer, T.J. Mediator-assisted water oxidation by the ruthenium ‘“ blue dimer ”’ cis, cis- [(bpy) 2 (H 2 O) RuORu (OH 2) (bpy) 2 ] 4. PNAS 2008, 2, 2–5. [Google Scholar] [CrossRef]
- Patra, S.G.; Mondal, T.; Sathiyan, K.; Mizrahi, A.; Kornweitz, H.; Meyerstein, D. Na3[Ru2(µ-CO3)4] as a Homogeneous Catalyst for Water Oxidation; HCO3− as a Co-Catalyst. Catalysts 2021, 11, 281. [Google Scholar] [CrossRef]
- Mavrokefalos, C.; Patzke, G. Water Oxidation Catalysts: The Quest for New Oxide-Based Materials. Inorganics 2019, 7, 29. [Google Scholar] [CrossRef]
- Mizrahi, A.; Maimon, E.; Cohen, H.; Kornweitz, H.; Zilbermann, I.; Meyerstein, D. Mechanistic Studies on the Role of [Cu II (CO 3) n ] 2−2 n as a Water Oxidation Catalyst: Carbonate as a Non-Innocent Ligand. Chem. A Eur. J. 2018, 24, 1088–1096. [Google Scholar] [CrossRef]
- Burke, M.S.; Enman, L.J.; Batchellor, A.S.; Zou, S.; Boettcher, S.W. Oxygen Evolution Reaction Electrocatalysis on Transition Metal Oxides and (Oxy)hydroxides: Activity Trends and Design Principles. Chem. Mater. 2015, 27, 7549–7558. [Google Scholar] [CrossRef]
- Dau, H.; Limberg, C.; Reier, T.; Risch, M.; Roggan, S.; Strasser, P. The Mechanism of Water Oxidation: From Electrolysis via Homogeneous to Biological Catalysis. ChemCatChem 2010, 2, 724–761. [Google Scholar] [CrossRef]
- Leng, Y.; Chen, G.; Mendoza, A.J.; Tighe, T.B.; Hickner, M.A.; Wang, C.-Y. Solid-State Water Electrolysis with an Alkaline Membrane. J. Am. Chem. Soc. 2012, 134, 9054–9057. [Google Scholar] [CrossRef]
- Mauritz, K.A.; Moore, R.B. State of understanding of Nafion. Chem. Rev. 2004, 104, 4535–4585. [Google Scholar] [CrossRef]
- Frame, F.A.; Townsend, T.K.; Chamousis, R.L.; Sabio, E.M.; Dittrich, T.; Browning, N.D.; Osterloh, F.E. Photocatalytic water oxidation with nonsensitized IrO2 nanocrystals under visible and UV light. J. Am. Chem. Soc. 2011, 133, 7264–7267. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Dudarev, S.; Botton, G. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B Condens. Matter Mater. Phys. 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- Valdés, Á.; Qu, Z.-W.; Kroes, G.-J.; Rossmeisl, J.; Nørskov, J.K. Oxidation and Photo-Oxidation of Water on TiO 2 Surface. J. Phys. Chem. C 2008, 112, 9872–9879. [Google Scholar] [CrossRef]
- Rossmeisl, J.; Qu, Z.-W.; Zhu, H.; Kroes, G.-J.; Nørskov, J.K. Electrolysis of water on oxide surfaces. J. Electroanal. Chem. 2007, 607, 83–89. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Smith, J.M.; Jones, S.P.; White, L.D. Rapid Communication. Gastroenterology 1977, 72, 193. [Google Scholar] [CrossRef]
- Atomic Simulation Environment. Available online: https://wiki.fysik.dtu.dk/ase/ (accessed on 1 September 2022).
- Wang, D.; Sheng, T.; Chen, J.; Wang, H.-F.; Hu, P. Identifying the key obstacle in photocatalytic oxygen evolution on rutile TiO2. Nat. Catal. 2018, 1, 291–299. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous- semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Malik, A.S.; Liu, T.; Dupuis, M.; Li, R.; Li, C. Water Oxidation on TiO 2: A Comparative DFT Study of 1e–, 2e–, and 4e–Processes on Rutile, Anatase, and Brookite. J. Phys. Chem. C 2020, 124, 8094–8100. [Google Scholar] [CrossRef]
- Li, Y.F.; Zhu, S.C.; Liu, Z.P. Reaction Network of Layer-to-Tunnel Transition of MnO2. J. Am. Chem. Soc. 2016, 138, 5371–5379. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z. Active Site Revealed for Water Oxidation on Electrochemically Induced δ-MnO 2: Role of Spinel-to-Layer Phase Transition. J. Am. Chem. Soc. 2018, 140, 1783–1792. [Google Scholar] [CrossRef]
- Fattebert, J.L.; Gygi, F. Linear-scaling first-principles molecular dynamics with plane-waves accuracy. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 1–5. [Google Scholar] [CrossRef]
- Zhao, W.N.; Liu, Z.P. Mechanism and active site of photocatalytic water splitting on titania in aqueous surroundings. Chem. Sci. 2014, 5, 2256–2264. [Google Scholar] [CrossRef]
- Fang, Y.H.; Liu, Z.P. Mechanism and tafel lines of electro-oxidation of water to oxygen on RuO2(110). J. Am. Chem. Soc. 2010, 132, 18214–18222. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhou, Z.; Hu, L.; Tian, R.; Wang, Y.; Arandiyan, H.; Chen, F.; Li, M.; Wan, T.; Han, Z.; et al. A facile approach to tailor electrocatalytic properties of MnO2 through tuning phase transition, surface morphology and band structure. Chem. Eng. J. 2022, 438, 135561. [Google Scholar] [CrossRef]
- Mattioli, G.; Giannozzi, P.; Bonapasta, A.A.; Guidoni, L. Reaction Pathways for Oxygen Evolution Promoted by Cobalt Catalyst. J. Am. Chem. Soc. 2013, 135, 15353–15363. [Google Scholar] [CrossRef] [PubMed]
- Car, R.; Parrinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Bajdich, M.; García-Mota, M.; Vojvodic, A.; Nørskov, J.K.; Bell, A.T. Theoretical Investigation of the Activity of Cobalt Oxides for the Electrochemical Oxidation of Water. J. Am. Chem. Soc. 2013, 135, 13521–13530. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, X.W.; Huo, C.F.; Guo, W.P.; Cao, D.B.; Peng, Q.; Dearden, A.; Gonze, X.; Yang, Y.; Wang, J.; et al. When Density Functional Approximations Meet Iron Oxides. J. Chem. Theory Comput. 2016, 12, 5132–5144. [Google Scholar] [CrossRef]
- Conway, B.E.; Liu, T.C. Characterization of electrocatalysis in the oxygen evolution reaction at platinum by evaluation of behavior of surface intermediate states at the oxide film. Langmuir 1990, 6, 268–276. [Google Scholar] [CrossRef]
- Birss, V.I.; Damjanovic, A.; Hudson, P.G. Oxygen Evolution at Platinum Electrodes in Alkaline Solutions: II. Mechanism of the Reaction. J. Electrochem. Soc. 1986, 133, 1621–1625. [Google Scholar] [CrossRef]
- Liao, P.; Keith, J.A.; Carter, E.A. Water oxidation on pure and doped hematite (0001) surfaces: Prediction of Co and Ni as effective dopants for electrocatalysis. J. Am. Chem. Soc. 2012, 134, 13296–13309. [Google Scholar] [CrossRef]
- Vald́s, Á.; Kroes, G.J. First principles study of the photo-oxidation of water on tungsten trioxide (WO3). J. Chem. Phys. 2009, 130, 114701. [Google Scholar] [CrossRef]
- Rossmeisl, J.; Logadottir, A.; Nørskov, J.K. Electrolysis of water on (oxidized) metal surfaces. Chem. Phys. 2005, 319, 178–184. [Google Scholar] [CrossRef]
- Mom, R.V.; Cheng, J.; Koper, M.T.M.; Sprik, M. Modeling the Oxygen Evolution Reaction on Metal Oxides: The Infuence of Unrestricted DFT Calculations. J. Phys. Chem. C 2014, 118, 4095–4102. [Google Scholar] [CrossRef]
- Koper, M.T.M. Thermodynamic theory of multi-electron transfer reactions: Implications for electrocatalysis. J. Electroanal. Chem. 2011, 660, 254–260. [Google Scholar] [CrossRef]
- Helali, Z.; Markovits, A.; Minot, C.; Abderrabba, M. First-row transition metal atoms adsorption on rutile TiO 2(110) surface. Struct. Chem. 2012, 23, 1309–1321. [Google Scholar] [CrossRef]
- Sousa, C.; Tosoni, S.; Illas, F. Theoretical approaches to excited-state-related phenomena in oxide surfaces. Chem. Rev. 2013, 113, 4456–4495. [Google Scholar] [CrossRef]
- Rao, R.R.; Kolb, M.J.; Halck, N.B.; Pedersen, A.F.; Mehta, A.; You, H.; Stoerzinger, K.A.; Feng, Z.; Hansen, H.A.; Zhou, H.; et al. Towards identifying the active sites on RuO2(110) in catalyzing oxygen evolution. Energy Environ. Sci. 2017, 10, 2626–2637. [Google Scholar] [CrossRef]
- Rao, R.R.; Kolb, M.J.; Giordano, L.; Pedersen, A.F.; Katayama, Y.; Hwang, J.; Mehta, A.; You, H.; Lunger, J.R.; Zhou, H.; et al. Operando identification of site-dependent water oxidation activity on ruthenium dioxide single-crystal surfaces. Nat. Catal. 2020, 3, 516–525. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T.; Logadottir, A.; Kitchin, J.R.; Chen, J.G.; Pandelov, S.; Stimming, U. Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc. 2005, 152, J23. [Google Scholar] [CrossRef]
- Liberto, G.D.; Cipriano, L.A.; Pacchioni, G. Role of Dihydride and Dihydrogen Complexes in Hydrogen Evolution Reaction on Single-Atom Catalysts. J. Am. Chem. Soc. 2021, 143, 20431–20441. [Google Scholar] [CrossRef]
- Cipriano, L.A.; Di Liberto, G.; Pacchioni, G. Superoxo and Peroxo Complexes on Single-Atom Catalysts: Impact on the Oxygen Evolution Reaction. ACS Catal. 2022, 12, 11682–11691. [Google Scholar] [CrossRef]
- Zhong, L.; Li, S. Unconventional Oxygen Reduction Reaction Mechanism and Scaling Relation on Single-Atom Catalysts. ACS Catal. 2020, 10, 4313–4318. [Google Scholar] [CrossRef]
- Fujishima, A.; Honda, K. Electrochemical Photolysis of Water at a Semiconductor Electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, R.; Okamura, T.; Ohashi, N.; Imanishi, A. Molecular Mechanisms of Photoinduced Oxygen Evolution, PL Emission, and Surface Roughening at Atomically Smooth Solutions. J. Am. Chem. Soc. 2005, 2, 431–432. [Google Scholar]
- Mattioli, G.; Filippone, F.; Bonapasta, A.A. Reaction Intermediates in the Photoreduction of Oxygen Molecules at the (101) TiO 2 (Anatase) Surface. J. Am. Chem. Soc. 2006, 2, 13772–13780. [Google Scholar] [CrossRef] [PubMed]
- Bak, T.; Nowotny, J.; Rekas, M.; Sorrell, C. Photo-electrochemical hydrogen generation from water using solar energy. Materials-related aspects. Int. J. Hydrogen Energy 2002, 27, 991–1022. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.-P.; Liu, L.; Gao, W. Mechanism and Activity of Photocatalytic Oxygen Evolution on Titania Anatase in Aqueous Surroundings. J. Am. Chem. Soc. 2010, 132, 13008–13015. [Google Scholar] [CrossRef]
- Hayes, D.; Hadt, R.G.; Emery, J.D.; Cordones, A.A.; Martinson, A.B.F.; Shelby, M.L.; Fransted, K.A.; Dahlberg, P.D.; Hong, J.; Zhang, X.; et al. Electronic and nuclear contributions to time-resolved optical and X-ray absorption spectra of hematite and insights into photoelectrochemical performance. Energy Environ. Sci. 2016, 9, 3754–3769. [Google Scholar] [CrossRef]
- Soares, M.R.S.; Gonçalves, R.H.; Nogueira, I.C.; Bettini, J.; Chiquito, A.J.; Leite, E.R. Understanding the fundamental electrical and photoelectrochemical behavior of a hematite photoanode. Phys. Chem. Chem. Phys. 2016, 18, 21780–21788. [Google Scholar] [CrossRef]
- Tamirat, A.G.; Rick, J.; Dubale, A.A.; Su, W.N.; Hwang, B.J. Using hematite for photoelectrochemical water splitting: A review of current progress and challenges. Nanoscale Horiz. 2016, 1, 243–267. [Google Scholar] [CrossRef]
- Zandi, O.; Hamann, T.W. The potential versus current state of water splitting with hematite. Phys. Chem. Chem. Phys. 2015, 17, 22485–22503. [Google Scholar] [CrossRef]
- Dias, P.; Vilanova, A.; Lopes, T.; Andrade, L.; Mendes, A. Extremely stable bare hematite photoanode for solar water splitting. Nano Energy 2016, 23, 70–79. [Google Scholar] [CrossRef]
- Barroso, M.; Pendlebury, S.R.; Cowan, A.J.; Durrant, J.R. Charge carrier trapping, recombination and transfer in hematite (α-Fe2O3) water splitting photoanodes. Chem. Sci. 2013, 4, 2724–2734. [Google Scholar] [CrossRef]
- Neufeld, O.; Toroker, M.C. Play the heavy: An effective mass study for α-Fe2O3 and corundum oxides. J. Chem. Phys. 2016, 144, 1–8. [Google Scholar] [CrossRef]
- Iordanova, N.; Dupuis, M.; Rosso, K.M. Charge transport in metal oxides: A theoretical study of hematite α-Fe2O3. J. Chem. Phys. 2005, 122, 144305. [Google Scholar] [CrossRef]
- Dotan, H.; Kfir, O.; Sharlin, E.; Blank, O.; Gross, M.; Dumchin, I.; Ankonina, G.; Rothschild, A. Resonant light trapping in ultrathin films for water splitting. Nat. Mater. 2013, 12, 158–164. [Google Scholar] [CrossRef]
- Warren, S.C.; Voïtchovsky, K.; Dotan, H.; Leroy, C.M.; Cornuz, M.; Stellacci, F.; Hébert, C.; Rothschild, A.; Grätzel, M. Identifying champion nanostructures for solar water-splitting. Nat. Mater. 2013, 12, 842–849. [Google Scholar] [CrossRef]
- Boudoire, F.; Toth, R.; Heier, J.; Braun, A.; Constable, E.C. Hematite nanostructuring using electrohydrodynamic lithography. Appl. Surf. Sci. 2014, 305, 62–66. [Google Scholar] [CrossRef]
- Townsend, T.K.; Sabio, E.M.; Browning, N.D.; Osterloh, F.E. Photocatalytic water oxidation with suspended alpha-Fe 2O 3 particles-effects of nanoscaling. Energy Environ. Sci. 2011, 4, 4270–4275. [Google Scholar] [CrossRef]
- Dahan, M.H.; Caspary Toroker, M. Water Oxidation Catalysis with Fe 2 O 3 Constrained at the Nanoscale. J. Phys. Chem. C 2017, 121, 6120–6125. [Google Scholar] [CrossRef]
- Teusch, T.; Klüner, T. Understanding the Water Splitting Mechanism on WO3(001)—A Theoretical Approach. J. Phys. Chem. C 2019, 123, 28233–28240. [Google Scholar] [CrossRef]
- Umena, Y.; Kawakami, K.; Shen, J.-R.; Kamiya, N. Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 Å. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Dismukes, G.C.; Brimblecombe, R.; Felton, G.A.N.; Pryadun, R.S.; Sheats, J.E.; Spiccia, L.; Swiegers, G.F. Development of Bioinspired Mn 4 O 4 −Cubane Water Oxidation Catalysts: Lessons from Photosynthesis. Acc. Chem. Res. 2009, 42, 1935–1943. [Google Scholar] [CrossRef] [PubMed]
- Huynh, M.; Shi, C.; Billinge, S.J.L.; Nocera, D.G. Nature of Activated Manganese Oxide for Oxygen Evolution. J. Am. Chem. Soc. 2015, 137, 14887–14904. [Google Scholar] [CrossRef] [PubMed]
- Post, J.E. Manganese oxide minerals: Crystal structures and economic and environmental significance. Proc. Natl. Acad. Sci. USA 1999, 96, 3447–3454. [Google Scholar] [CrossRef] [PubMed]
- Suib, S.L. Porous Manganese Sieves and Octahedral Layered Materials. Acc. Chem. Res. 2008, 41, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Kitchaev, D.A.; Dacek, S.T.; Sun, W.; Ceder, G. Thermodynamics of Phase Selection in MnO2 Framework Structures through Alkali Intercalation and Hydration. J. Am. Chem. Soc. 2017, 139, 2672–2681. [Google Scholar] [CrossRef]
- Devaraj, S.; Munichandraiah, N. Effect of crystallographic structure of MnO2 on its electrochemical capacitance properties. J. Phys. Chem. C 2008, 112, 4406–4417. [Google Scholar] [CrossRef]
- Najafpour, M.M.; Ehrenberg, T.; Wiechen, M.; Kurz, P. Calcium Manganese(III) Oxides (CaMn 2 O 4 ⋅ x H 2 O) as Biomimetic Oxygen-Evolving Catalysts. Angew. Chemie Int. Ed. 2010, 49, 2233–2237. [Google Scholar] [CrossRef]
- Park, S.; Lee, Y.H.; Choi, S.; Seo, H.; Lee, M.Y.; Balamurugan, M.; Nam, K.T. Manganese oxide-based heterogeneous electrocatalysts for water oxidation. Energy Environ. Sci. 2020, 13, 2310–2340. [Google Scholar] [CrossRef]
- Cho, G.; Park, Y.; Hong, Y.K.; Ha, D.H. Ion exchange: An advanced synthetic method for complex nanoparticles. Nano Converg. 2019, 6, 1–17. [Google Scholar] [CrossRef]
- Meng, Y.; Song, W.; Huang, H.; Ren, Z.; Chen, S.-Y.; Suib, S.L. Structure–Property Relationship of Bifunctional MnO 2 Nanostructures: Highly Efficient, Ultra-Stable Electrochemical Water Oxidation and Oxygen Reduction Reaction Catalysts Identified in Alkaline Media. J. Am. Chem. Soc. 2014, 136, 11452–11464. [Google Scholar] [CrossRef]
- Gorlin, Y.; Chung, C.J.; Nordlund, D.; Clemens, B.M.; Jaramillo, T.F. Mn3O4 Supported on glassy carbon: An active non-precious metal catalyst for the oxygen reduction reaction. ACS Catal. 2012, 2, 2687–2694. [Google Scholar] [CrossRef]
- Gorlin, Y.; Chung, C.-J.; Benck, J.D.; Nordlund, D.; Seitz, L.; Weng, T.-C.; Sokaras, D.; Clemens, B.M.; Jaramillo, T.F. Understanding Interactions between Manganese Oxide and Gold That Lead to Enhanced Activity for Electrocatalytic Water Oxidation. J. Am. Chem. Soc. 2014, 136, 4920–4926. [Google Scholar] [CrossRef]
- Kim, S.; Nam, K.W.; Lee, S.; Cho, W.; Kim, J.-S.; Kim, B.G.; Oshima, Y.; Kim, J.-S.; Doo, S.-G.; Chang, H.; et al. Direct Observation of an Anomalous Spinel-to-Layered Phase Transition Mediated by Crystal Water Intercalation. Angew. Chemie Int. Ed. 2015, 54, 15094–15099. [Google Scholar] [CrossRef]
- Seitz, L.C.; Hersbach, T.J.P.; Nordlund, D.; Jaramillo, T.F. Enhancement Effect of Noble Metals on Manganese Oxide for the Oxygen Evolution Reaction. J. Phys. Chem. Lett. 2015, 6, 4178–4183. [Google Scholar] [CrossRef]
- Bergmann, A.; Zaharieva, I.; Dau, H.; Strasser, P. Electrochemical water splitting by layered and 3D cross-linked manganese oxides: Correlating structural motifs and catalytic activity. Energy Environ. Sci. 2013, 6, 2745. [Google Scholar] [CrossRef]
- Pokhrel, R.; Goetz, M.K.; Shaner, S.E.; Wu, X.; Stahl, S.S. The “Best Catalyst” for Water Oxidation Depends on the Oxidation Method Employed: A Case Study of Manganese Oxides. J. Am. Chem. Soc. 2015, 137, 8384–8387. [Google Scholar] [CrossRef]
- Gorlin, Y.; Jaramillo, T.F. A bifunctional nonprecious metal catalyst for oxygen reduction and water oxidation. J. Am. Chem. Soc. 2010, 132, 13612–13614. [Google Scholar] [CrossRef]
- Robinson, D.M.; Go, Y.B.; Mui, M.; Gardner, G.; Zhang, Z.; Mastrogiovanni, D.; Garfunkel, E.; Li, J.; Greenblatt, M.; Dismukes, G.C. Photochemical Water Oxidation by Crystalline Polymorphs of Manganese Oxides: Structural Requirements for Catalysis. J. Am. Chem. Soc. 2013, 135, 3494–3501. [Google Scholar] [CrossRef]
- Mette, K.; Bergmann, A.; Tessonnier, J.P.; Hävecker, M.; Yao, L.; Ressler, T.; Schlögl, R.; Strasser, P.; Behrens, M. Nanostructured Manganese Oxide Supported on Carbon Nanotubes for Electrocatalytic Water Splitting. ChemCatChem 2012, 4, 851–862. [Google Scholar] [CrossRef]
- Boppana, V.B.R.; Jiao, F. Nanostructured MnO2: An efficient and robust water oxidation catalyst. Chem. Commun. 2011, 47, 8973–8975. [Google Scholar] [CrossRef] [PubMed]
- Indra, A.; Menezes, P.W.; Zaharieva, I.; Baktash, E.; Pfrommer, J.; Schwarze, M.; Dau, H.; Driess, M. Active Mixed-Valent MnO x Water Oxidation Catalysts through Partial Oxidation (Corrosion) of Nanostructured MnO Particles. Angew. Chemie Int. Ed. 2013, 52, 13206–13210. [Google Scholar] [CrossRef] [PubMed]
- Fekete, M.; Hocking, R.K.; Chang, S.L.Y.; Italiano, C.; Patti, A.F.; Arena, F.; Spiccia, L. Highly active screen-printed electrocatalysts for water oxidation based on β-manganese oxide. Energy Environ. Sci. 2013, 6, 2222–2232. [Google Scholar] [CrossRef]
- Gorlin, Y.; Lassalle-Kaiser, B.; Benck, J.D.; Gul, S.; Webb, S.M.; Yachandra, V.K.; Yano, J.; Jaramillo, T.F. In situ X-ray absorption spectroscopy investigation of a bifunctional manganese oxide catalyst with high activity for electrochemical water oxidation and oxygen reduction. J. Am. Chem. Soc. 2013, 135, 8525–8534. [Google Scholar] [CrossRef] [PubMed]
- Lian, S.; Browne, M.P.; Domínguez, C.; Stamatin, S.N.; Nolan, H.; Duesberg, G.S.; Lyons, M.E.G.; Fonda, E.; Colavita, P.E. Template-free synthesis of mesoporous manganese oxides with catalytic activity in the oxygen evolution reaction. Sustain. Energy Fuels 2017, 1, 780–788. [Google Scholar] [CrossRef]
- Smith, P.F.; Deibert, B.J.; Kaushik, S.; Gardner, G.; Hwang, S.; Wang, H.; Al-Sharab, J.F.; Garfunkel, E.; Fabris, L.; Li, J.; et al. Coordination Geometry and Oxidation State Requirements of Corner-Sharing MnO6 Octahedra for Water Oxidation Catalysis: An Investigation of Manganite (γ-MnOOH). ACS Catal. 2016, 6, 2089–2099. [Google Scholar] [CrossRef]
- Gupta, P.K.; Bhandari, A.; Saha, S.; Bhattacharya, J.; Pala, R.G.S. Modulating Oxygen Evolution Reactivity in MnO 2 through Polymorphic Engineering. J. Phys. Chem. C 2019, 123, 22345–22357. [Google Scholar] [CrossRef]
- Tao, H.B.; Fang, L.; Chen, J.; Yang, H.B.; Gao, J.; Miao, J.; Chen, S.; Liu, B. Identification of Surface Reactivity Descriptor for Transition Metal Oxides in Oxygen Evolution Reaction. J. Am. Chem. Soc. 2016, 138, 9978–9985. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Zhang, B.; Cheng, F.; Ruan, Y.; Ji, X.; Xu, K.; Chen, C.; Miao, L.; Jiang, J. Stabilizing the oxygen vacancies and promoting water-oxidation kinetics in cobalt oxides by lower valence-state doping. Nano Energy 2018, 53, 144–151. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, L.; Zhao, B.; Chen, H.; Liu, X.; Zhao, R.; Wang, X.; Liu, J.; Chen, Y.; Liu, M. Improving the Activity for Oxygen Evolution Reaction by Tailoring Oxygen Defects in Double Perovskite Oxides. Adv. Funct. Mater. 2019, 29, 1901783. [Google Scholar] [CrossRef]
- Selvakumar, K.; Senthil Kumar, S.M.; Thangamuthu, R.; Kruthika, G.; Murugan, P. Development of shape-engineered α-MnO 2 materials as bi-functional catalysts for oxygen evolution reaction and oxygen reduction reaction in alkaline medium. Int. J. Hydrog. Energy 2014, 39, 21024–21036. [Google Scholar] [CrossRef]
- Tompsett, D.A.; Parker, S.C.; Islam, M.S. Surface properties of α-MnO2: Relevance to catalytic and supercapacitor behaviour. J. Mater. Chem. A 2014, 2, 15509–15518. [Google Scholar] [CrossRef]
- Su, H.-Y.; Gorlin, Y.; Man, I.C.; Calle-Vallejo, F.; Nørskov, J.K.; Jaramillo, T.F.; Rossmeisl, J. Identifying active surface phases for metal oxide electrocatalysts: A study of manganese oxide bi-functional catalysts for oxygen reduction and water oxidation catalysis. Phys. Chem. Chem. Phys. 2012, 14, 14010. [Google Scholar] [CrossRef]
- Rong, X.; Kolpak, A.M. Ab initio approach for prediction of oxide surface structure, stoichiometry, and electrocatalytic activity in aqueous solution. J. Phys. Chem. Lett. 2015, 6, 1785–1789. [Google Scholar] [CrossRef]
- Rong, X.; Parolin, J.; Kolpak, A.M. A Fundamental Relationship between Reaction Mechanism and Stability in Metal Oxide Catalysts for Oxygen Evolution. ACS Catal. 2016, 6, 1153–1158. [Google Scholar] [CrossRef]
- Martirez, J.M.P.; Kim, S.; Morales, E.H.; Diroll, B.T.; Cargnello, M.; Gordon, T.R.; Murray, C.B.; Bonnell, D.A.; Rappe, A.M. Synergistic oxygen evolving activity of a TiO2-rich reconstructed SrTiO3(001) surface. J. Am. Chem. Soc. 2015, 137, 2939–2947. [Google Scholar] [CrossRef]
- Qiu, T.; Tu, B.; Saldana-Greco, D.; Rappe, A.M. Ab Initio Simulation Explains the Enhancement of Catalytic Oxygen Evolution on CaMnO 3. ACS Catal. 2018, 8, 2218–2224. [Google Scholar] [CrossRef]
- Du, J.; Zhang, T.; Cheng, F.; Chu, W.; Wu, Z.; Chen, J. Nonstoichiometric Perovskite CaMnO 3−δ for Oxygen Electrocatalysis with High Activity. Inorg. Chem. 2014, 53, 9106–9114. [Google Scholar] [CrossRef]
- Brunschwig, B.S.; Chou, M.H.; Creutz, C.; Ghosh, P.; Sutin, N. Mechanisms of water oxidation to oxygen: Cobalt(IV) as an intermediate in the aquocobalt(II)-catalyzed reaction. J. Am. Chem. Soc. 1983, 105, 4832–4833. [Google Scholar] [CrossRef]
- Jiao, F.; Frei, H. Nanostructured Cobalt Oxide Clusters in Mesoporous Silica as Efficient Oxygen-Evolving Catalysts. Angew. Chemie Int. Ed. 2009, 48, 1841–1844. [Google Scholar] [CrossRef] [PubMed]
- Artero, V.; Chavarot-Kerlidou, M.; Fontecave, M. Splitting water with cobalt. Angew. Chemie Int. Ed. 2011, 50, 7238–7266. [Google Scholar] [CrossRef] [PubMed]
- Lutterman, D.A.; Surendranath, Y.; Nocera, D.G. A Self-Healing Oxygen-Evolving Catalyst. J. Am. Chem. Soc. 2009, 131, 3838–3839. [Google Scholar] [CrossRef] [PubMed]
- Kanan, M.W.; Surendranath, Y.; Nocera, D.G. Cobalt–phosphate oxygen-evolving compound. Chem. Soc. Rev. 2009, 38, 109–114. [Google Scholar] [CrossRef] [PubMed]
- Kanan, M.W.; Nocera, D.G. In situ formation of an oxygen-evolving catalyst in neutral water containing phosphate and Co2+. Science (80-.). 2008, 321, 1072–1075. [Google Scholar] [CrossRef]
- Patra, S.G.; Illés, E.; Mizrahi, A.; Meyerstein, D. Cobalt Carbonate as an Electrocatalyst for Water Oxidation. Chem. A Eur. J. 2020, 26, 711–720. [Google Scholar] [CrossRef]
- Patra, S.G.; Mizrahi, A.; Meyerstein, D. The Role of Carbonate in Catalytic Oxidations. Acc. Chem. Res. 2020, 53, 2189–2200. [Google Scholar] [CrossRef]
- Surendranath, Y.; Dincǎ, M.; Nocera, D.G. Electrolyte-dependent electrosynthesis and activity of cobalt-based water oxidation catalysts. J. Am. Chem. Soc. 2009, 131, 2615–2620. [Google Scholar] [CrossRef]
- Grewe, T.; Deng, X.; Weidenthaler, C.; Schüth, F.; Tüysüz, H. Design of ordered mesoporous composite materials and their electrocatalytic activities for water oxidation. Chem. Mater. 2013, 25, 4926–4935. [Google Scholar] [CrossRef]
- Higashi, M.; Domen, K.; Abe, R. Highly stable water splitting on oxynitride TaON photoanode system under visible light irradiation. J. Am. Chem. Soc. 2012, 134, 6968–6971. [Google Scholar] [CrossRef]
- Rosen, J.; Hutchings, G.S.; Jiao, F. Ordered mesoporous cobalt oxide as highly efficient oxygen evolution catalyst. J. Am. Chem. Soc. 2013, 135, 4516–4521. [Google Scholar] [CrossRef]
- Grewe, T.; Deng, X.; Tüysüz, H. Influence of Fe doping on structure and water oxidation activity of nanocast Co3O4. Chem. Mater. 2014, 26, 3162–3168. [Google Scholar] [CrossRef]
- Deng, X.; Tüysüz, H. Cobalt-oxide-based materials as water oxidation catalyst: Recent progress and challenges. ACS Catal. 2014, 4, 3701–3714. [Google Scholar] [CrossRef]
- McAlpin, J.G.; Surendranath, Y.; Dincã, M.; Stich, T.A.; Stoian, S.A.; Casey, W.H.; Nocera, D.G.; Britt, R.D. EPR evidence for Co(IV) species produced during water oxidation at neutral pH. J. Am. Chem. Soc. 2010, 132, 6882–6883. [Google Scholar] [CrossRef]
- Wang, L.P.; Voorhis, T.V. Direct-coupling O2 bond forming a pathway in cobalt oxide water oxidation catalysts. J. Phys. Chem. Lett. 2011, 2, 2200–2204. [Google Scholar] [CrossRef]
- Li, X.; Siegbahn, P.E.M. Water oxidation mechanism for synthetic Co-oxides with small nuclearity. J. Am. Chem. Soc. 2013, 135, 13804–13813. [Google Scholar] [CrossRef]
- Amtawong, J.; Nguyen, A.I.; Tilley, T.D. Mechanistic Aspects of Cobalt-Oxo Cubane Clusters in Oxidation Chemistry. J. Am. Chem. Soc. 2022, 144, 1475–1492. [Google Scholar] [CrossRef]
- Fernando, A.; Aikens, C.M. Reaction pathways for water oxidation to molecular oxygen mediated by model cobalt oxide dimer and cubane catalysts. J. Phys. Chem. C 2015, 119, 11072–11085. [Google Scholar] [CrossRef]
- Chen, J.; Selloni, A. Water Adsorption and Oxidation at the CO3O4 (110) Surface. J. Phys. Chem. Lett. 2012, 3, 2808–2814. [Google Scholar] [CrossRef]
- Pham, H.H.; Cheng, M.-J.; Frei, H.; Wang, L.-W. Surface Proton Hopping and Fast-Kinetics Pathway of Water Oxidation on CO3O4 (001) Surface. ACS Catal. 2016, 6, 5610–5617. [Google Scholar] [CrossRef]
- Moysiadou, A.; Lee, S.; Hsu, C.; Chen, H.M.; Hu, X. Mechanism of Oxygen Evolution Catalyzed by Cobalt Oxyhydroxide: Cobalt Superoxide Species as a Key Intermediate and Dioxygen Release as a Rate-Determining Step. J. Am. Chem. Soc. 2020, 142, 11901–11914. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Gu, S.; Wang, Y.; Liang, C.; Yu, Y.; Han, L.; Zheng, S.; Zhang, N.; Liu, X.; Zhou, J.; et al. Spontaneous Delithiation under Operando Condition Triggers Formation of an Amorphous Active Layer in Spinel Cobalt Oxides Electrocatalyst toward Oxygen Evolution. ACS Catal. 2019, 9, 7389–7397. [Google Scholar] [CrossRef]
- Peng, Y.; Hajiyani, H.; Pentcheva, R. In fl uence of Fe and Ni Doping on the OER Performance at the CO3O4 (001) Surface: Insights from DFT+ U Calculations. ACS Catal. 2021, 4, 5601–5613. [Google Scholar] [CrossRef]
- Hajiyani, H.; Pentcheva, R. Surface Termination and Composition Control of Activity of the COxNi1-xFe2O4 (001) Surface for Water Oxidation: Insights from DFT+ U Calculations. ACS Catal. 2018, 8, 11773–11782. [Google Scholar] [CrossRef]
- Kaptagay, G.A.; Inerbaev, T.M.; Mastrikov, Y.A.; Kotomin, E.A.; Akilbekov, A.T. Water interaction with perfect and fluorine-doped CO3O4 (100) surface. Solid State Ion. 2015, 277, 77–82. [Google Scholar] [CrossRef]
- Faculty, S.; Singh, N. 2010—CO3O4 and Co- Based Spinel Oxides Bifunctional Oxygen Electrodes—Unknown.pdf. Int. J. Electrochem. Sci. Int. J. Electrochem. Sci. 2010, 5, 556–577. [Google Scholar]
- Matsumoto, Y.; Sato, E. Electrocatalytic properties of transition metal oxides for oxygen evolution reaction. Mater. Chem. Phys. 1986, 14, 397–426. [Google Scholar] [CrossRef]
- García-Mota, M.; Bajdich, M.; Viswanathan, V.; Vojvodic, A.; Bell, A.T.; Nørskov, J.K. Importance of Correlation in Determining Electrocatalytic Oxygen Evolution Activity on Cobalt Oxides. J. Phys. Chem. C 2012, 116, 21077–21082. [Google Scholar] [CrossRef]
- Menezes, P.W.; Indra, A.; Bergmann, A.; Chernev, P. Uncovering the prominent role of metal ions in octahedral versus tetrahedral sites of cobalt—Zinc oxide catalysts for e ffi cient oxidation of water †. J. Mater. Chem. A 2016, 4, 10014–10022. [Google Scholar] [CrossRef]
- Wang, H.; Hung, S.; Chen, H.-Y.; Chan, T.; Chen, H.M.; Liu, B. In Operando Identification of Geometrical-Site-Dependent Water Oxidation Activity of Spinel Co 3 O 4. J. Am. Chem. Soc. 2016, 138, 36–39. [Google Scholar] [CrossRef]
- Plaisance, C.P.; van Santen, R.A. Structure Sensitivity of the Oxygen Evolution Reaction Catalyzed by Cobalt(II,III) Oxide. J. Am. Chem. Soc. 2015, 137, 14660–14672. [Google Scholar] [CrossRef]
- Wang, X.; Ouyang, T.; Wang, L.; Zhong, J.; Ma, T.; Liu, Z. Redox-Inert Fe 3+ Ions in Octahedral Sites of Co-Fe Spinel Oxides with Enhanced Oxygen Catalytic Activity for Rechargeable Zinc–Air Batteries. Angew. Chemie Int. Ed. 2019, 58, 13291–13296. [Google Scholar] [CrossRef]
- Li, Y.; Hasin, P.; Wu, Y. NixCo3−xO4 Nanowire Arrays for Electrocatalytic Oxygen Evolution. Adv. Mater. 2010, 22, 1926–1929. [Google Scholar] [CrossRef]
- Wu, X.; Scott, K. CuxCo3−xO4 (0 ≤x < 1) nanoparticles for oxygen evolution in high performance alkaline exchange membrane water electrolysers. J. Mater. Chem. 2011, 21, 12344. [Google Scholar] [CrossRef]
- Nikolov, I.; Darkaoui, R.; Zhecheva, E.; Stoyanova, R.; Dimitrov, N.; Vitanov, T. Electrocatalytic activity of spinel related cobalties MxCo3−xO4 (M = Li, Ni, Cu) in the oxygen evolution reaction. J. Electroanal. Chem. 1997, 429, 157–168. [Google Scholar] [CrossRef]
- Xiao, C.; Lu, X.; Zhao, C. A simple and reliable method for determining the delamination degree of nitrate and glycine intercalated LDHs in formamide. Chem. Commun. 2014, 50, 10122–10125. [Google Scholar] [CrossRef]
- Lambert, T.N.; Vigil, J.A.; White, S.E.; Davis, D.J.; Limmer, S.J.; Burton, P.D.; Coker, E.N.; Beechem, T.E.; Brumbach, M.T. Electrodeposited NixCo3-xO4 nanostructured films as bifunctional oxygen electrocatalysts. Chem. Commun. 2015, 51, 9511–9514. [Google Scholar] [CrossRef]
- Bothra, P.; Pati, S.K. Activity of Water Oxidation on Pure and (Fe, Ni, and Cu)-Substituted CO3O4. ACS Energy Lett. 2016, 1, 858–862. [Google Scholar] [CrossRef]
- Zasada, F.; Piskorz, W.; Sojka, Z. Cobalt Spinel at Various Redox Conditions: DFT+U Investigations into the Structure and Surface Thermodynamics of the (100) Facet. J. Phys. Chem. C 2015, 119, 19180–19191. [Google Scholar] [CrossRef]
- Zasada, F.; Piskorz, W.; Cristol, S.; Paul, J.F.; Kotarba, A.; Sojka, Z. Periodic density functional theory and atomistic thermodynamic studies of cobalt spinel nanocrystals in wet environment: Molecular interpretation of water adsorption equilibria. J. Phys. Chem. C 2010, 114, 22245–22253. [Google Scholar] [CrossRef]
- Gao, L.; Cui, X.; Sewell, C.D.; Li, J.; Lin, Z. Recent advances in activating surface reconstruction for the high-efficiency oxygen evolution reaction. Chem. Soc. Rev. 2021, 50, 8428–8469. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; He, Q.; Zhang, Y.; Song, L. Structural Self-Reconstruction of Catalysts in Electrocatalysis. Acc. Chem. Res. 2018, 51, 2968–2977. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, A.; Roldan Cuenya, B. Operando Insights into Nanoparticle Transformations during Catalysis. ACS Catal. 2019, 9, 10020–10043. [Google Scholar] [CrossRef]
- He, D.; Song, X.; Li, W.; Tang, C.; Liu, J.; Ke, Z.; Jiang, C.; Xiao, X. Active Electron Density Modulation of Co 3 O 4 -Based Catalysts Enhances their Oxygen Evolution Performance. Angew. Chemie Int. Ed. 2020, 59, 6929–6935. [Google Scholar] [CrossRef] [PubMed]
- Selcuk, S.; Selloni, A. DFT+U study of the surface structure and stability of Co3O4(110): Dependence on U. J. Phys. Chem. C 2015, 119, 9973–9976. [Google Scholar] [CrossRef]
- Zhang, B.; Zheng, X.; Voznyy, O.; Comin, R.; Bajdich, M.; García-Melchor, M.; Han, L.; Xu, J.; Liu, M.; Zheng, L.; et al. Homogeneously dispersed multimetal oxygen-evolving catalysts. Science 2016, 352, 333–337. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Y.; Dong, J.; He, C.T.; Yin, H.; An, P.; Zhao, K.; Zhang, X.; Gao, C.; Zhang, L.; et al. Ultrathin metal-organic framework nanosheets for electrocatalytic oxygen evolution. Nat. Energy 2016, 1, 1–10. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Zhang, B.; Wan, H.; Li, Z.; Ji, X.; Xu, K.; Chen, C.; Zha, D.; Miao, L.; et al. Synergistic effect of two actions sites on cobalt oxides towards electrochemical water-oxidation. Nano. Energy 2017, 42, 98–105. [Google Scholar] [CrossRef]
- Curutchet, A.; Colinet, P.; Michel, C.; Steinmann, S.N.; Bahers, T.L. Two-sites are better than one: Revisiting the OER mechanism on CoOOH by DFT with electrode polarization. Phys. Chem. Chem. Phys. 2020, 22, 7031–7038. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, T.; Wen, H.; Ni, Z.; He, Y.; Guo, R.; You, J.; Liu, X. The latest development of CoOOH two-dimensional materials used as OER catalysts. Chem. Commun. 2020, 56, 15387–15405. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Yan, Y.; Mei, B.; Qi, R.; He, T.; Wang, Z.; Fang, W.; Zaman, S.; Su, Y.; Ding, S.; et al. Local spin-state tuning of cobalt-iron selenide nanoframes for the boosted oxygen evolution. Energy Environ. Sci. 2021, 14, 365–373. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, S.; Yang, H.; Xi, S.; Gracia, J.; Xu, Z.J. Spin-Related Electron Transfer and Orbital Interactions in Oxygen Electrocatalysis. Adv. Mater. 2020, 32, 2003297. [Google Scholar] [CrossRef]
- Suntivich, J.; May, K.J.; Gasteiger, H.A.; Goodenough, J.B.; Shao-Horn, Y. A perovskite oxide optimized for oxygen evolution catalysis from molecular orbital principles. Science 2011, 334, 1383–1385. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Q.; Wang, Y.; Yang, Z.; Fan, X.; Liu, L.M.; Guo, L. Achieving delafossite analog by in situ electrochemical self-reconstruction as an oxygen-evolving catalyst. Proc. Natl. Acad. Sci. USA 2020, 117, 21906–21913. [Google Scholar] [CrossRef]
- Huang, J.; Chen, J.; Yao, T.; He, J.; Jiang, S.; Sun, Z.; Liu, Q.; Cheng, W.; Hu, F.; Jiang, Y.; et al. CoOOH Nanosheets with High Mass Activity for Water Oxidation. Angew. Chem. 2015, 127, 8846–8851. [Google Scholar] [CrossRef]
- Li, F.; Ai, H.; Liu, D.; Lo, K.H.; Pan, H. An enhanced oxygen evolution reaction on 2D CoOOH: Via strain engineering: An insightful view from spin state transition. J. Mater. Chem. A 2021, 9, 17749–17759. [Google Scholar] [CrossRef]
- Chen, J.; Selloni, A. First principles study of cobalt (Hydr)oxides under electrochemical conditions. J. Phys. Chem. C 2013, 117, 20002–20006. [Google Scholar] [CrossRef]
- Wang, X.; Luo, H.; Yang, H.; Sebastian, P.J.; Gamboa, S.A. Oxygen catalytic evolution reaction on nickel hydroxide electrode modified by electroless cobalt coating. Int. J. Hydrog. Energy 2004, 29, 967–972. [Google Scholar] [CrossRef]
- De Chialvo, M.R.G.; Chialvo, A.C. Oxygen evolution reaction on thick hydrous nickel oxide electrodes. Electrochim. Acta 1988, 33, 825–830. [Google Scholar] [CrossRef]
- Briggs, G.W.D.; Jones, E.; Wynne-Jones, W.F.K. The nickel oxide electrode. Part 1. Trans. Faraday Soc. 1955, 51, 1433. [Google Scholar] [CrossRef]
- Oshitani, M.; Sasaki, Y.; Takashima, K. Development of a nickel electrode having stable performance at various charge and discharge rates over a wide temperature range. J. Power Sources 1984, 12, 219–231. [Google Scholar] [CrossRef]
- Hermet, P.; Gourrier, L.; Bantignies, J.L.; Ravot, D.; Michel, T.; Deabate, S.; Boulet, P.; Henn, F. Dielectric, magnetic, and phonon properties of nickel hydroxide. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 1–10. [Google Scholar] [CrossRef]
- Lyons, M.E.G.; Brandon, M.P. The oxygen evolution reaction on passive oxide covered transition metal electrodes in aqueous alkaline solution. Part 1-Nickel. Int. J. Electrochem. Sci. 2008, 3, 1386–1424. [Google Scholar]
- Bediako, D.K.; Lassalle-Kaiser, B.; Surendranath, Y.; Yano, J.; Yachandra, V.K.; Nocera, D.G. Structure–Activity Correlations in a Nickel–Borate Oxygen Evolution Catalyst. J. Am. Chem. Soc. 2012, 134, 6801–6809. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.F.; Selloni, A. Mosaic texture and double c-Axis periodicity of β-NiOOH: Insights from first-principles and genetic algorithm calculations. J. Phys. Chem. Lett. 2014, 5, 3981–3985. [Google Scholar] [CrossRef] [PubMed]
- Martirez, J.M.P.; Carter, E.A. Effects of the Aqueous Environment on the Stability and Chemistry of β-NiOOH Surfaces. Chem. Mater. 2018, 30, 5205–5219. [Google Scholar] [CrossRef]
- Oliva, P.; Leonardi, J.; Laurent, J.F.; Delmas, C.; Braconnier, J.J.; Figlarz, M.; Fievet, F.; Guibert, A. de Review of the structure and the electrochemistry of nickel hydroxides and oxy-hydroxides. J. Power Sources 1982, 8, 229–255. [Google Scholar] [CrossRef]
- Li, Y.-F.; Li, J.-L.; Liu, Z.-P. Structure and Catalysis of NiOOH: Recent Advances on Atomic Simulation. J. Phys. Chem. C 2021, 125, 27033–27045. [Google Scholar] [CrossRef]
- Li, L.F.; Li, Y.F.; Liu, Z.P. Oxygen Evolution Activity on NiOOH Catalysts: Four-Coordinated Ni Cation as the Active Site and the Hydroperoxide Mechanism. ACS Catal. 2020, 10, 2581–2590. [Google Scholar] [CrossRef]
- Zaffran, J.; Toroker, M.C. Benchmarking Density Functional Theory Based Methods to Model NiOOH Material Properties: Hubbard and van der Waals Corrections vs Hybrid Functionals. J. Chem. Theory Comput. 2016, 12, 3807–3812. [Google Scholar] [CrossRef]
- Rajan, A.G.; Martirez, J.M.P.; Carter, E.A. Facet-Independent Oxygen Evolution Activity of Pure β-NiOOH: Different Chemistries Leading to Similar Overpotentials. J. Am. Chem. Soc. 2020, 142, 3600–3612. [Google Scholar] [CrossRef]
- Tkalych, A.J.; Zhuang, H.L.; Carter, E.A. A Density Functional + U Assessment of Oxygen Evolution Reaction Mechanisms on β-NiOOH. ACS Catal. 2017, 7, 5329–5339. [Google Scholar] [CrossRef]
- Tkalych, A.J.; Martirez, J.M.P.; Carter, E.A. Effect of transition-metal-ion dopants on the oxygen evolution reaction on NiOOH(0001). Phys. Chem. Chem. Phys. 2018, 20, 19525–19531. [Google Scholar] [CrossRef]
- Rajan, A.G.; Carter, E.A. Discovering Competing Electrocatalytic Mechanisms and Their Overpotentials: Automated Enumeration of Oxygen Evolution Pathways. J. Phys. Chem. C 2020, 124, 24883–24898. [Google Scholar] [CrossRef]
- Kumar, M.; Piccinin, S.; Srinivasan, V. Direct and indirect role of Fe doping in NiOOH monolayer for water oxidation catalysis**. ChemPhysChem 2022, 23, e202200085. [Google Scholar] [CrossRef]
- Li, Y.F.; Selloni, A. Mechanism and activity of water oxidation on selected surfaces of pure and Fe-Doped NiOx. ACS Catal. 2014, 4, 1148–1153. [Google Scholar] [CrossRef]
- Martirez, J.M.P.; Carter, E.A. Unraveling Oxygen Evolution on Iron-Doped β-Nickel Oxyhydroxide: The Key Role of Highly Active Molecular-like Sites. J. Am. Chem. Soc. 2019, 141, 693–705. [Google Scholar] [CrossRef]
- Xiao, H.; Shin, H.; Goddard, W.A. Synergy between Fe and Ni in the optimal performance of (Ni,Fe)OOH catalysts for the oxygen evolution reaction. Proc. Natl. Acad. Sci. USA 2018, 115, 5872–5877. [Google Scholar] [CrossRef]
- Klaus, S.; Cai, Y.; Louie, M.W.; Trotochaud, L.; Bell, A.T. Effects of Fe Electrolyte Impurities on Ni(OH) 2/NiOOH Structure and Oxygen Evolution Activity. J. Phys. Chem. C 2015, 119, 7243–7254. [Google Scholar] [CrossRef]
- Diaz-Morales, O.; Ferrus-Suspedra, D.; Koper, M.T.M. The importance of nickel oxyhydroxide deprotonation on its activity towards electrochemical water oxidation. Chem. Sci. 2016, 7, 2639–2645. [Google Scholar] [CrossRef]
- Bediako, D.K.; Surendranath, Y.; Nocera, D.G. Mechanistic Studies of the Oxygen Evolution Reaction Mediated by a Nickel–Borate Thin Film Electrocatalyst. J. Am. Chem. Soc. 2013, 135, 3662–3674. [Google Scholar] [CrossRef] [PubMed]
- Dincă, M.; Surendranath, Y.; Nocera, D.G. Nickel-borate oxygen-evolving catalyst that functions under benign conditions. Proc. Natl. Acad. Sci. USA 2010, 107, 10337–10341. [Google Scholar] [CrossRef] [PubMed]
- Risch, M.; Klingan, K.; Heidkamp, J.; Ehrenberg, D.; Chernev, P.; Zaharieva, I.; Dau, H. Nickel-oxido structure of a water-oxidizing catalyst film. Chem. Commun. 2011, 47, 11912–11914. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, M.; Mitsutomi, Y.; Mineo, T.; Nagasaka, M.; Yuzawa, H.; Kosugi, N.; Kondoh, H. Direct Observation of Active Nickel Oxide Cluster in Nickel-Borate Electrocatalyst for Water Oxidation by in Situ O K-Edge X-ray Absorption Spectroscopy. J. Phys. Chem. C 2015, 119, 19279–19286. [Google Scholar] [CrossRef]
- Trotochaud, L.; Young, S.L.; Ranney, J.K.; Boettcher, S.W. Nickel-Iron oxyhydroxide oxygen-evolution electrocatalysts: The role of intentional and incidental iron incorporation. J. Am. Chem. Soc. 2014, 136, 6744–6753. [Google Scholar] [CrossRef] [PubMed]
- Fidelsky, V.; Toroker, M.C. Enhanced Water Oxidation Catalysis of Nickel Oxyhydroxide through the Addition of Vacancies. J. Phys. Chem. C 2016, 120, 25405–25410. [Google Scholar] [CrossRef]
- Dionigi, F.; Zeng, Z.; Sinev, I.; Merzdorf, T.; Deshpande, S.; Lopez, M.B.; Kunze, S.; Zegkinoglou, I.; Sarodnik, H.; Fan, D.; et al. In-situ structure and catalytic mechanism of NiFe and CoFe layered double hydroxides during oxygen evolution. Nat. Commun. 2020, 11, 2522. [Google Scholar] [CrossRef]
- Szalay, P.G.; Müller, T.; Gidofalvi, G.; Lischka, H.; Shepard, R. Multiconfiguration Self-Consistent Field and Multireference Configuration Interaction Methods and Applications. Chem. Rev. 2012, 112, 108–181. [Google Scholar] [CrossRef]
- Akimov, A.V.; Neukirch, A.J.; Prezhdo, O.V. Theoretical Insights into Photoinduced Charge Transfer and Catalysis at Oxide Interfaces. Chem. Rev. 2013, 113, 4496–4565. [Google Scholar] [CrossRef]
- Austin, B.M.; Zubarev, D.Y.; Lester, W.A. Quantum Monte Carlo and Related Approaches. Chem. Rev. 2012, 112, 263–288. [Google Scholar] [CrossRef]
- Pacchioni, G. Modeling doped and defective oxides in catalysis with density functional theory methods: Room for improvements. J. Chem. Phys. 2008, 128, 182505. [Google Scholar] [CrossRef]
- Getsoian, A.; Zhai, Z.; Bell, A.T. Band-Gap Energy as a Descriptor of Catalytic Activity for Propene Oxidation over Mixed Metal Oxide Catalysts. J. Am. Chem. Soc. 2014, 136, 13684–13697. [Google Scholar] [CrossRef]
- Metiu, H. Preface to Special Topic: A Survey of Some New Developments in Heterogeneous Catalysis. J. Chem. Phys. 2008, 128, 182501. [Google Scholar] [CrossRef]
- Brown, J.J.; Page, A.J. Reaction pathways in the solid state and the Hubbard U correction. J. Chem. Phys. 2021, 154, 124121. [Google Scholar] [CrossRef]
- Tolba, S.A.; Gameel, K.M.; Ali, B.A.; Almossalami, H.A.; Allam, N.K. The DFT+U: Approaches, Accuracy, and Applications. In Density Functional Calculations—Recent Progresses of Theory and Application; Yang, G., Ed.; IntechOpen: London, UK, 2018. [Google Scholar]
- Yang, X.; Wang, Y.; Li, C.M.; Wang, D. Mechanisms of water oxidation on heterogeneous catalyst surfaces. Nano Res. 2021, 14, 3446–3457. [Google Scholar] [CrossRef]





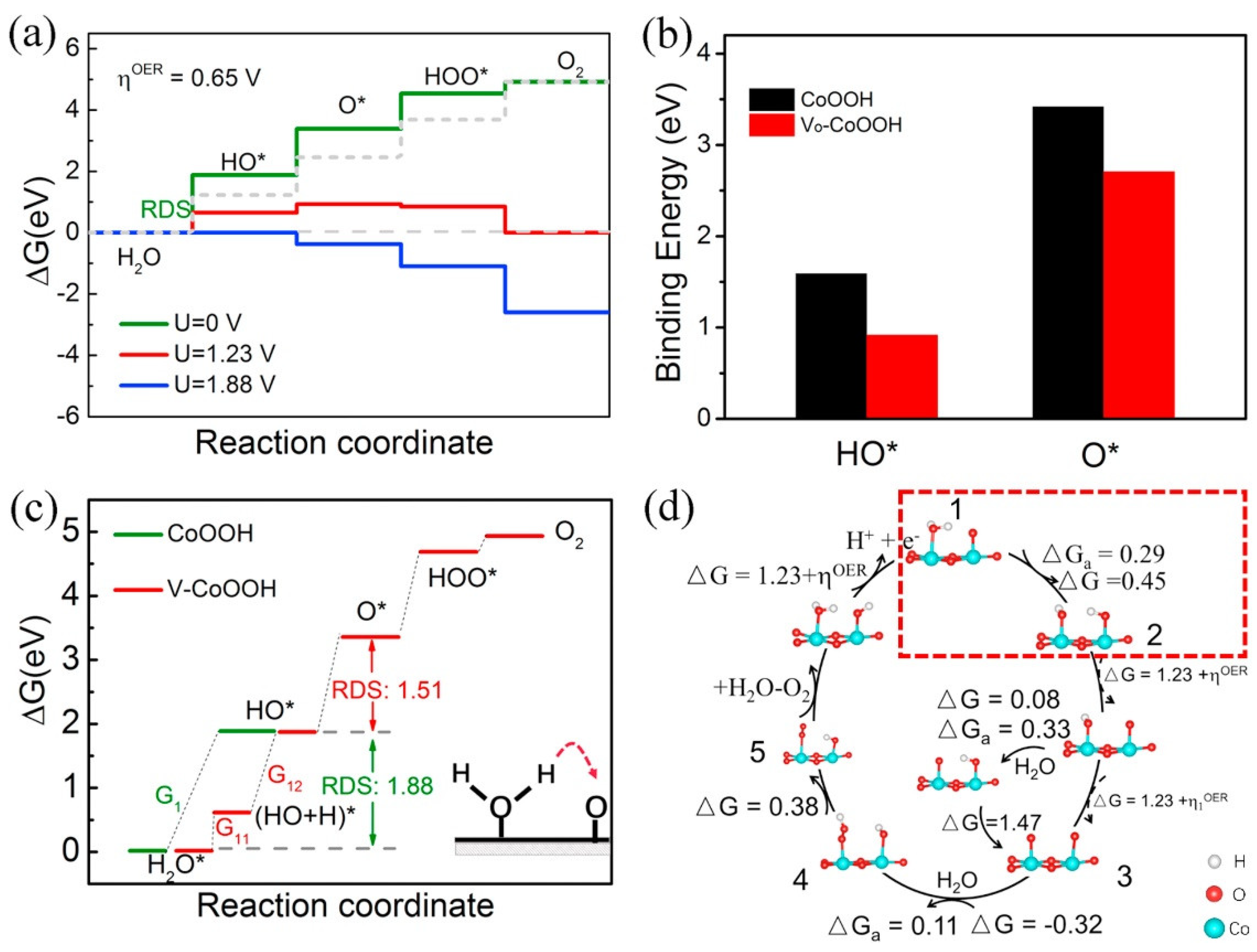
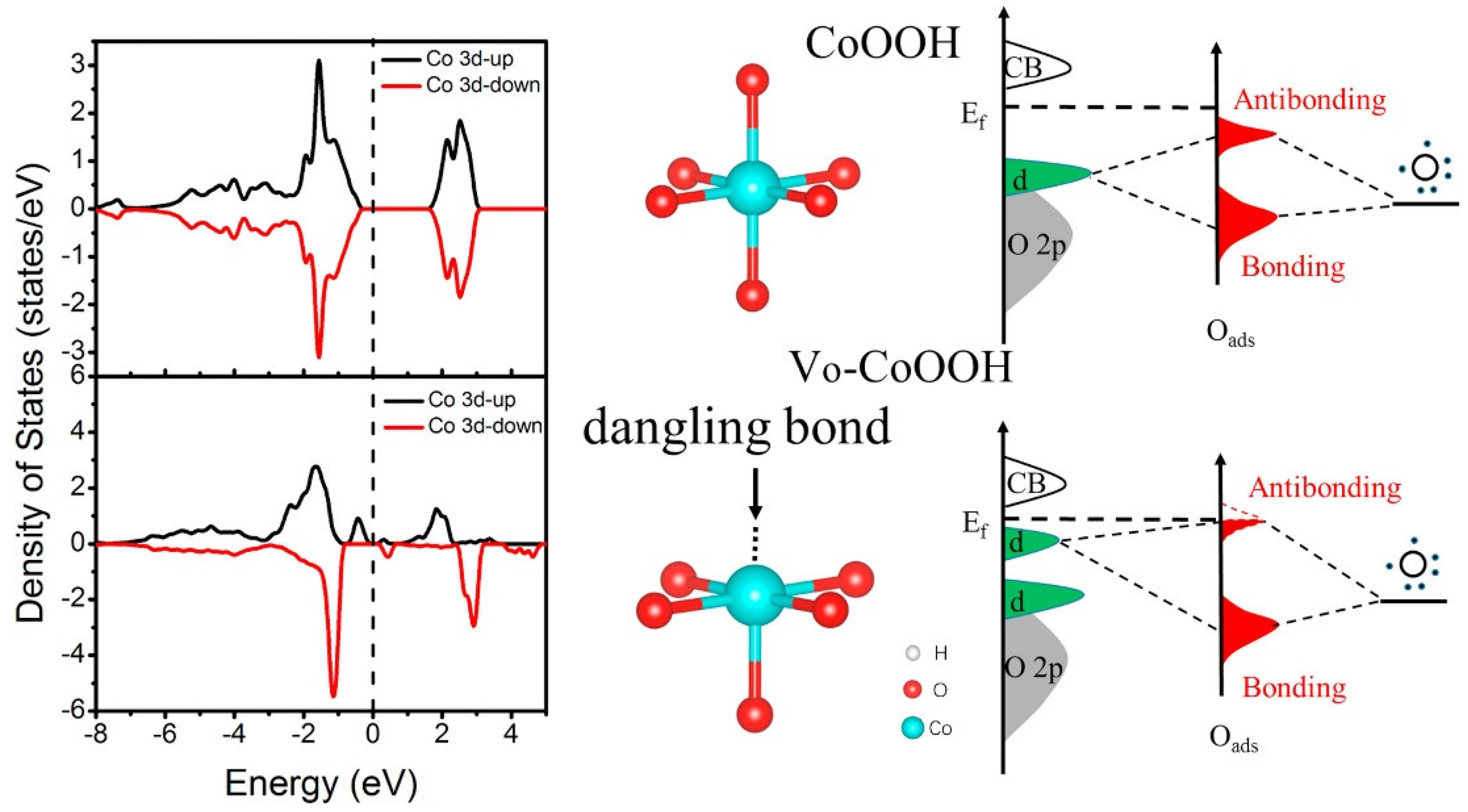
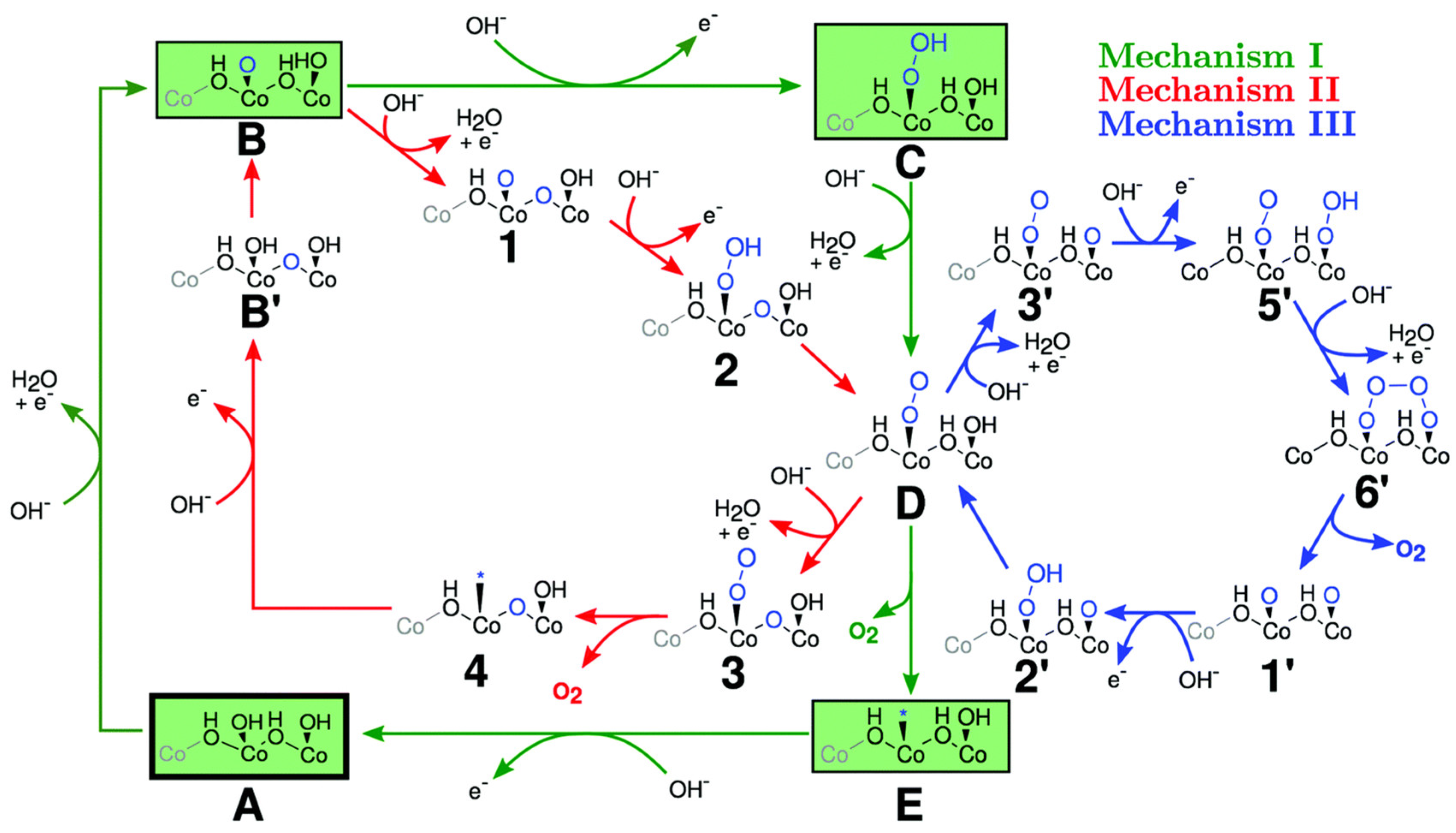
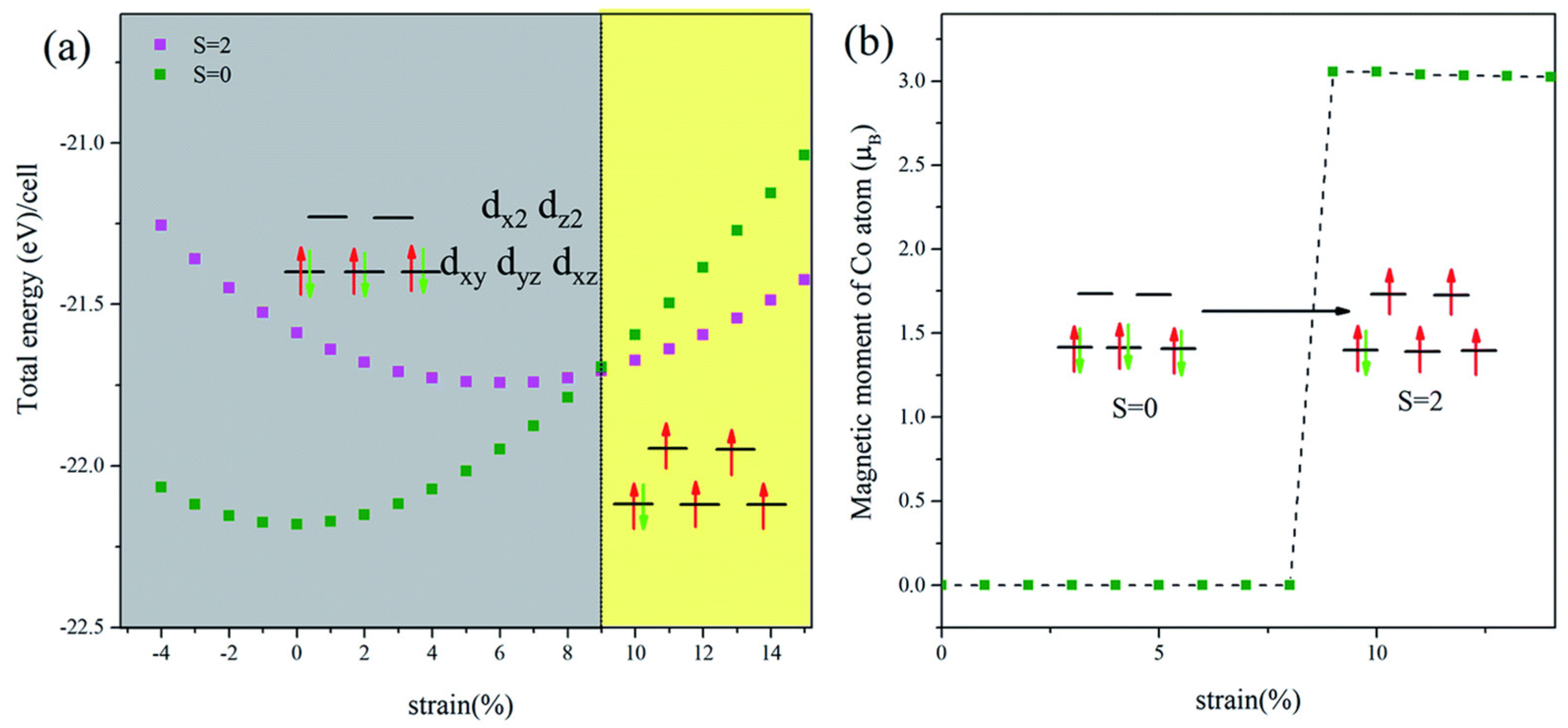

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patra, S.G.; Meyerstein, D. On the Mechanism of Heterogeneous Water Oxidation Catalysis: A Theoretical Perspective. Inorganics 2022, 10, 182. https://doi.org/10.3390/inorganics10110182
Patra SG, Meyerstein D. On the Mechanism of Heterogeneous Water Oxidation Catalysis: A Theoretical Perspective. Inorganics. 2022; 10(11):182. https://doi.org/10.3390/inorganics10110182
Chicago/Turabian StylePatra, Shanti Gopal, and Dan Meyerstein. 2022. "On the Mechanism of Heterogeneous Water Oxidation Catalysis: A Theoretical Perspective" Inorganics 10, no. 11: 182. https://doi.org/10.3390/inorganics10110182
APA StylePatra, S. G., & Meyerstein, D. (2022). On the Mechanism of Heterogeneous Water Oxidation Catalysis: A Theoretical Perspective. Inorganics, 10(11), 182. https://doi.org/10.3390/inorganics10110182







