Abstract
An attempt was made, using computational methods, to understand whether the intermolecular interactions in the dimers of molybdenum dichalcogenides MoCh2 (Ch = chalcogen, element of group 16, especially S, Se and Te) and similar mixed-chalcogenide derivatives resemble the room temperature experimentally observed interactions in the interfacial regions of molybdenites and their other mixed-chalcogen derivatives. To this end, MP2(Full)/def2-TVZPPD level electronic structure calculations on nine dimer systems, including (MoCh2)2 and (MoChCh′2)2 (Ch, Ch′ = S, Se and Te), were carried out not only to demonstrate the energetic stability of these systems in the gas phase, but also to reproduce the intermolecular geometrical properties that resemble the interfacial geometries of 2D layered MoCh2 systems reported in the crystalline phase. Among the six DFT functionals (single and double hybrids) benchmarked against MP2(full), it was found that the double hybrid functional B2PLYPD3 has some ability to reproduce the intermolecular geometries and binding energies. The intermolecular geometries and binding energies of all nine dimers are discussed, together with the charge density topological aspects of the chemical bonding interactions that emerge from the application of the quantum theory of atoms in molecules (QTAIM), the isosurface topology of the reduced density gradient noncovalent index, interaction region indicator and independent gradient model (IGM) approaches. While the electrostatic surface potential model fails to explain the origin of the S···S interaction in the (MoS2)2 dimer, we show that the intermolecular bonding interactions in all nine dimers examined are a result of hyperconjugative charge transfer delocalizations between the lone-pair on (Ch/Ch′) and/or the π-orbitals of a Mo–Ch/Ch′ bond of one monomer and the dπ* anti-bonding orbitals of the same Mo–Ch/Ch′ bond in the second monomer during dimer formation, and vice versa. The HOMO–LUMO gaps calculated with the MN12-L functional were 0.9, 1.0, and 1.1 eV for MoTe2, MoSe2 and MoS2, respectively, which match very well with the solid-state theoretical (SCAN-rVV10)/experimental band gaps of 0.75/0.88, 0.90/1.09 and 0.93/1.23 eV of the corresponding systems, respectively. We observed that the gas phase dimers examined are perhaps prototypical for a basic understanding of the interfacial/inter-layer interactions in molybdenum-based dichalcogenides and their derivatives.
1. Introduction
Transition metal dichalcogenides (TMDCs or TMDs), MCh2 (M = a transition metal; Ch = a chalcogen, an element of group 16) are a special class of exotic 2D layered materials well known to the chemistry and physics community for decades [1,2,3,4]. Formally, in MCh2, the metal cation is in its +4-oxidation state, and the chalcogenide anion carries a −2 charge. They exist in poly-phases, viz. 2H, 1H, 1T, 1T′, 1T″, 3R, etc. [5,6,7], depending on the number of layers, their structure (space groups) and local coordination environments involved [8]. For instance, 2H is a double layer with a hexagonal lattice; 1T refers to a single layer with a trigonal prismatic lattice; and 3R refers to a triple layer structure with a rhombohedral lattice. Many of the TMDCs have also been identified as phase-change materials under certain conditions, and hence their metallic, or insulating, or semiconducting or superconducting character changes. For instance, Chen and coworkers reported the successful growth on bilayer graphene of a quasi-freestanding WSe2 single layer with 1T′ structure that does not exist in the bulk form [9]. A bandgap of 129 meV was observed in the 1T′ layer and an in-gap edge state was located near the layer boundary. The observed gap diminished with doping by Rb adsorption, ultimately leading to an insulator–semimetal transition. Some TMDCs have also displayed metal-to-semiconductor [10,11,12] and metal-to-insulator [13,14,15] phase transition behavior.
Renewed interest in TMDCs occurred, probably after 2012 [16], when it was found that monolayers of these materials displayed reasonable bandgaps, a necessary condition for their application in photovoltaics, as photo-catalysts for water splitting [17,18,19] and other optoelectronic applications [20] such as flexible electronics [21,22], and the properties of these monolayers are different to those of the bulk materials [22,23,24,25,26]. For instance, it was observed that the bandgap transition energy of MoS2 changes from indirect (1.2 eV) to direct (1.8 eV) passing from bulk to a monolayer [26]. Changes in the optoelectronic properties of TMDCs were noted with a distinct photoluminescence (PL) between monolayer (1L), bilayer (2L), quadrilayer (4L) and hexalayer (6L) samples of MoS2 [27,28]. Semiconducting MCh2 materials, with M = Mo, W and Ch = S, Se, Te, possess an advantage over graphene in that they exhibit appropriate bandgaps necessary for applications in the opto-electronic devices, among others. Similar views have been provided in other studies as well [29,30,31,32].
Some MCh2 compounds have been identified as topological excitonic insulators (as observed in a distorted phase of MoS2) [33], semi-metallic, metallic, ferromagnetic (viz. 2H-VS2/-VSe2/-VTe2/-CrTe2/-NbS2/-TaS2/1T-TaTe2) [1,34], anti-ferromagnetic materials (1T-CrS2/-CrSe2/-VTe2), semiconductors (2H-MoS2/-MoSe2/-MoTe2/-WS2/-WSe2) [34,35] or superconductors (viz. 2H-MS2/-MSe2/-MTe2, 2H-NbS2, 2H-MTe2, 2H-WS2/-WTe2/1T′-WSe2) [1,36,37]. Another important feature of these compounds is that strain engineering can change their structural, electronic and optical properties insofar as the direct-to-indirect bandgap transition has been observed upon application of tensile strain [38].
However, a basic understanding of the nature of interlayer bonding in TMDCs is still lacking. Therefore, this study focusses on the MoCh2 (Mo = S, Se, Te) series, among the most intensely studied 2D systems, both experimentally [6,39,40,41,42] and theoretically [34,43,44,45,46]. As mentioned above, they have been observed in several phases, with different level of stacking between the layers. The most stable of these is probably the room temperature phase, the 2H-phase [6,40,47]. The crystal structure of 2H-MoS2, known since 1983 [48], is naturally occurring molybdenite.
Scheme 1 shows the unit-cell structures of the 2H-MoCh2 series, and the nature of the arrangement of atomic domains in each monolayer responsible for the cell. When expanded, each of the supercells will produce a bilayer arrangement, yet each monolayer comprises three sub-layers (two of them are formed by the bonded S-atoms and the other is formed by the metal). The monolayers in an expanded bilayer system are separated by a physical gap. This gap has been referred to as a “van der Waals” gap [49,50,51]. In other words, it has been assumed that the physical rigidity of the TMDCs is driven by “van der Waals forces” [16,52]. While the intralayer Mo–Ch bonding is often assumed to be strongly covalent [53,54], the interlayer bonding is presumed to be weak, as it arises from van der Waals forces and the binding energy between two layers is negligibly small (e.g., 3.77 meV in GeSe2 [55]). It seems from the close proximity of the two layers in the crystal structures (Scheme 1) that the stability of the interfacial region is driven by an extensive array of chalcogen centered Ch···Ch noncovalent interactions. Whether these are a result of the so-called Type-I or Type-II chalcogen bonding [56,57] is unknown. A chalcogen bond is formed when there is evidence of a net attractive interaction between an electrophilic region associated with a chalcogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity [58]. A Type-I or Type-II topology of a bonding interaction in chemical systems emerges when the angle of interaction θ is such that 90° < θ (∠R–Ch···A) < 140° or 140° < θ (∠R–Ch···A) < 180°, respectively, where R is the remainder part of the molecular entity and A is an acceptor [56,59,60] (and a negative site [61,62,63,64]). This topology of bonding is applicable to any noncovalent interaction regardless of its type (hydrogen bond, halogen bond, chalcogen bond, pnictogen bond etc.).
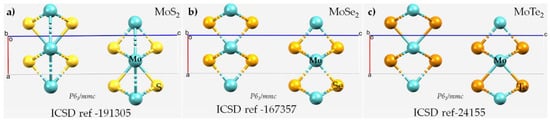
Scheme 1.
The unit-cells of (a) 2H-MoS2, (b) 2H-MoSe2 and (c) 2H-MoTe2. The Inorganic Crystal Structure Database reference codes (ICSD ref) and the space group are shown for each case. Table 1 summarizes the details of the lattice properties.
We report here results of our theoretical investigation of nine dimers, MoCh2 (Ch = Se, Te), and their mixed chalcogenide analogues. We did not examine the conformational space associated with each of these dimers; that requires an extensive study—currently in progress—which will be reported elsewhere. Rather, we focused exploration on a specific conformation that resembles the chemical bonding environment observed in the interfacial region of the 2H-phase of MoCh2. Because transition metals, as well as heavy atom chalcogens, are involved, we have employed a few effective core potential (ECP) basis sets with increasing size to examine their effect on the intermolecular geometry, binding energy and polarity. The second-order Møller–Plesset perturbation method (MP2) was chosen [65], together with the treatment of all-electron correlated effects. As mentioned above, the main motivation for this study was to examine whether gas phase calculations on the simplest (MoCh2)2 dimers and the mixed dichalcogenide derivatives are adequate in any way to delineate the Type-I and quasi-linear Type-II bonding features between the metal bonded chalcogenides that have been observed in the crystalline phase (Scheme 1). A second motivation was to examine whether the quasi-linear inter-layer interactions are indeed a consequence of attraction between a positive site on a bonded chalcogenide in a given layer and a negative site on the same atom in another interacting layer, producing counterintuitive “homo” bonding. Can the often-invoked electrostatic potential on the surfaces of the isolated MoCh2 monomeric units allow us to describe the physical realities associated with the intermolecular bonding in (MoCh2)2 dimers, and can this be applied as a rationalization of similar effects observed in the crystalline phase? We applied the quantum theory of atoms in molecules (QTAIM) [66], interaction region indicator (IRI) [67], independent gradient model (IGM) [68,69] and reduced density gradient (RDG) [70] approaches to the dimers to examine the nature of the intermolecular bonding responsible for the formation of the (MoCh2)2 dimers. Finally, we examined the binding energy of these dimers using a standard supramolecular procedure, as well as the origin of orbital interactions between the interacting monomers using second-order hyperconjugative analysis [71], and we provide our opinion on whether the inter-layer/inter-facial interactions in molybdenum dichalcogenides should be called simply “van der Waals forces”, or whether they are “weak chalcogen bonding interactions”.
2. Computational Details and Model Systems
The geometries of all nine of the (MoCh2)2 and (MoChCh′)2 dimers mentioned above were energy minimized with MP2(Full), followed by the Hessian second derivative energy calculations. The dimer geometries reported are all transition state structures at the level of the theory applied. We selected this method since the interest in MP2 is increasing in the DFT community [72] because of the promising level of accuracy of double-hybrid functionals [73]. The ECP basis set def2-TZVPPD was utilized, obtained from the EMSL basis set exchange library [74]. The Gaussian 16 code was used [75].
The molecular electrostatic surface potentials (MESP) of the three monomers MoCh2 (Ch = S, Se, Te) were computed to examine the nature of their electrostatic surfaces. The 0.0015 a.u. isoelectron density envelope was utilized, on which the electrostatic potential was computed. We chose the non-relativistic segmented Gaussian-type basis set, Sapporo-TZP-Diffuse, which is appropriate for all-electron calculations [76]. We focused on a selected number of extrema of the potential, the so-called the local minimum and the local potential maxima (VS,max and VS,min, respectively), on the electrostatic surfaces of the three isolated MoCh2 monomers to identity regions that can act as Lewis acids and Lewis bases. In particular, when the sign of VS,max or VS,min is positive (VS,max or VS,min > 0), we treat them as representatives of Lewis acids; and when the sign of the VS,max or VS,min is negative (VS,max or VS,min < 0), we treat them as representatives of Lewis bases [61]. If a specific Lewis base on a monomer is centered towards a specific Lewis acid at the equilibrium configuration of an (MoCh2)2 or (MoChCh′)2 dimer, this permitted us to determine whether Coulomb forces are holding the two monomers together at equilibrium. While doing so, we were mindful that the MESP model is incapable of providing the energy of an intermolecular interaction. It does not provide information on the nature of the surface extrema on precisely the same locations on the monomers at the equilibrium geometry of the dimer; the local extrema on the isolated monomers may have been annihilated during the formation of the dimers. It would be misleading to correlate the binding energy of the dimers with the positive or negative potential on the isolated monomeric systems that are interacting with each other, as has sometimes been done [77,78,79]. This would be misleading because both the positive and negative potentials on the two isolated monomers interacting with each other are already affected by the electric field produced by each of them [80]; electrostatic polarization has already played its role during the dimer formation, and hence the sign and magnitude of the minimum and maximum of potentials found on the interacting sites in isolated monomers have at that point already been annihilated in the dimer configuration at equilibrium.
Nevertheless, the QTAIM is uniquely unified. It not only provides a molecular graph of the chemical system examined, but also indicates the bond critical points of charge density between a pair of two bonded atomic basins, and many other related topological properties. These include, for example, the Laplacian of the charge density; the kinetic, potential and total energy densities; and the ellipticity. These properties have been utilized to provide insight into the ionic, covalent or mixed bonding character of a large number of chemical compounds (see, for example, [56,81]). The second-order perturbative estimates of donor–acceptor interactions were calculated using the NBO, v. 3.1 [82] as implemented in Gaussian 16.
The reduced density gradient (RDG) noncovalent index (NCI) approach is similar, in some aspects, to the QTAIM approach, but it accounts for the reduced gradient of the charge density around the bond critical point region [70,83,84,85]. The NCI index is based on the normalized and dimensionless RDG s, which is given by , where ρ(r) is the charge density and ∇ρ is the gradient of the charge density. When the gradient of the charge density vanishes at any point r, s vanishes at that point [85,86]. This is what happens at the bond critical point within the framework of the QTAIM, where ∇ρ = 0 and hence s = 0. The RDG is capable of detecting interactions when the bond critical point centered topological feature is lacking in chemical systems (e.g., 1,n-alkanediols), a conclusion that was arrived at by Kjaergaard and coworkers [87]. Regions in space where (closed-shell) noncovalent interactions occur feature low values of ρ(r), ∇ρ and s, and regions of space where s and ρ have low and high values, respectively, and signify shared interactions (viz. covalent bonds). The isosurfaces of the RDG at low densities allow one to visualize the position and nature of covalent interactions in 3D space [87]. However, it is worth noting that the limitation of the RDG-NCI approach is that the isosurfaces in the inter- and intra-molecular bonding regions in large systems can be very noisy, causing some difficulty in identifying the actual sites that cause the interaction between them. To overcome this, several theoretical approaches similar to the RDG have been proposed more recently that allow one to overcome the noisy RDG isosurface features in large chemical systems. One of them is the real space function called the interaction region indicator (IRI) [67], which is a slight modification of the RDG, yet its results are comparable with the QTAIM’s topological analysis of charge density. The other function is the independent gradient model (IGM), proposed some time ago [68], that can be performed both on the computed wavefunctions and pro-molecular densities on specific regions of interest. These two computational approaches have an advantage over the RDG-NCI in that one can locally characterize an interaction between two atomic basins, ignoring other interactions that are not of focus of interest. We employed all these approaches to examine whether or not they provide similar insight into the nature of the intermolecular bonding interactions in the (MoCh2)2 and (MoChCh′)2 dimers. Post-processing codes, such as AIMAll [88], Multiwfn [89] and VMD 1.9.3 [90], and Gaussview 5.0 [91] software were used for the calculation, visualization, drawing and analysis of the electronic structure results obtained using Gaussian 16 [92].
For the purpose of comparison, we also relaxed the bulk (double-layer) geometries of the MoCh2 (Ch = S, Se, Te) crystals investigated. We employed the strongly constrained and appropriately normed (SCAN) meta-generalized gradient approximation necessary for short- and intermediate-range interactions [93], together with the long-range vdW interaction from rVV10, the revised Vydrov–van Voorhis non-local correlation functional [94], implemented in the Vienna Ab initio Simulation Package (VASP) [95,96]. The incorporation of the latter is presumably essential given that MoCh2 are layered crystal systems, and the presence of van der Waals interaction determines the interlayer distance and spacing. The band structures of the corresponding systems were also computed at the same level of theory. A 5 × 5 × 2 k-point grid, together with the projector augmented-wave (PAW) pseudopotential plane-wave method [97] as implemented in VASP was used for geometry relaxation. The (non-SCF) band structures were calculated using the SCF wavefunctions evaluated using a relatively dense k-point mesh of 10 × 10 × 2, adopting the Gaussian smearing protocol. An energy cutoff of 520 eV was used for the plane wave regardless of the nature of the calculations involved, together with a cutoff of 10−8 eV for the energy convergence and 10−2 eV/Å for the convergence of forces. The linear mixing parameter for the density mixing between each electronic step (AMIX), the linear mixing parameter for the magnetization density (AMIX_MAG), cutoff wave vector for Kerker mixing scheme (BMIX) [98] and cutoff wave vector for the Kerker mixing scheme for the magnetization density (BMIX_MAG), were set to 0.2, 0.00001, 0.8 and 0.00001, respectively. The aspherical contributions from the gradient corrections inside the PAW spheres were included.
3. Results and Discussion
3.1. Interfacial Geometry of the 2H-MoCh2 Crystals and Comparison with Theory
The nature of the bonding modes between the Mo bonded chalcogenides feasible in the interfacial region between the layers of MoCh2 are illustrated in Figure 1. These represent the 1 × 4 × 1 structures that were constructed using the unit-cells of 2H-MoS2 [99], 2H-MoSe2 [100] and 2H-MoTe2 [101]. As can be seen from the interfacial region, each bonded chalcogenide in each layer was linked noncovalently with three other similar sites in other layers, forming three Mo–Ch···Ch interlayer interactions. This conclusion was arrived at based on the analysis of the interfacial Ch···Ch bond lengths and Mo–Ch···Ch angles and comparing them with those reported in the chalcogen bonding literature [62]. For instance, it was shown that the strength of a R–Ch···A interaction (A = negative site that accepts a noncovalent bond) increases as the electronegativity of Ch decreases; i.e., the strength of the interaction increases in the order Ch = (O) < S < Se < Te [102]. Of course, this energetic preference of chalcogen bond formation is consistent with the increasing polarizability and decreasing electronegativity of the chalcogen atoms from O down to Te in the chalcogen series [103]. Chalcogen bonds have been found to be less directional than the R–X···A (X = Cl, Br, I) halogen bonds, for which ∠R–X···A > 170°, with the angle of interaction varying between 80° and 170° [62]. This angular flexibility of covalently bound chalcogen atoms in forming chalcogen bonds with negative sites results in the formation of both directional and non-directional (bent-shaped) interactions [104].
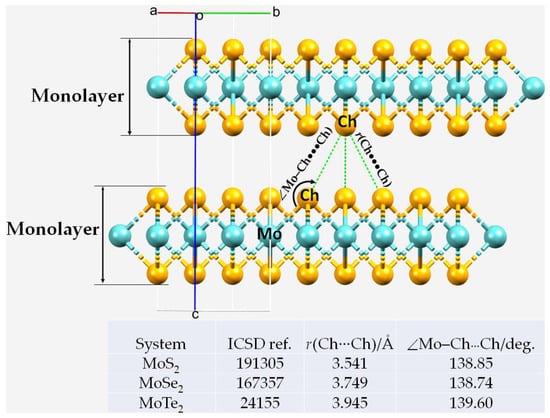
Figure 1.
Nature of interfacial bonding interactions between the Mo-bonded chalcogenides in the 1 × 4 × 1 supercell structures of bilayer MoCh2 (Ch = S, Se, Te). The inset (bottom) summarizes ICSD ref. codes of unit-cells of the three MoCh2 crystals, including the interfacial bond lengths and bond angles (experimental) corresponding to the Ch···Ch interactions.
The Mo–S···S bond distances between the layers were all equivalent in the 2H-MoS2 crystal, with r(S···S) = 3.541 Å and ∠Mo–S···S = 138.9°. These structural features were not very different to those associated with the Mo–Se···Se and Mo–Te···Te contacts found in the 2H-MoSe2 and 2H-MoS2 crystals, respectively. For instance, the r(Ch···Ch) (∠Mo–Ch···Ch) values were 3.749 Å (38.7°) and 3.945 Å (139.6°) for 2H-MoSe2 and 2H-MoTe2, respectively. The difference in bond lengths was clearly a consequence of the difference in the van der Waals radii of the three chalcogens in question (rvdW(S) (Bondi) = 1.80 Å; rvdW(Se) = 1.90 Å; rvdW(Te) = 2.0 Å) [105]. It may therefore be reasonable to conclude that since r(S···S) in 2H-MoS2 < r(Se···Se) in 2H-MoSe2 < r(Te···Te) in 2H-MoTe2, the strength of the interaction decreased in this series, assuming an inverse relationship between the bond length and bond strength. We discuss this further below.
The unit cell of the MoCh2 bulk has the space group P63/mmc, which contains six atoms (two Mo and four Ch atoms, two formula units). The crystal structure is determined by the lattice constants a = b and c, together with the internal displacement parameters, and this feature was reproduced with the level of theory used. Table 1 compares the calculated lattice properties with those reported experimentally. In all cases, an excellent agreement was found. Differences between them were at most 0.01 Å in a = b, and less than 0.251 Å in c. There was a marginal difference between the computed and experimental lattice volumes and the lattice density, which is often found [106,107]. The calculated interlayer bond distances r(Ch···Ch) (and bond angles ∠Mo–Ch···Ch) were 3.612 Å (138.77°), 3.786 Å (139.24°) and 4.053 Å (139.58°) for 2H-MoS2, 2H-MoSe2 and 2H-MoTe2, respectively. These results show that an increase in the size of the chalcogen atom in MoCh2 caused an elongation of the interfacial distances between the monolayers of the bilayer system. Concomitant with this is that the angle of contact also increased as the MoCh2 system became heavier. The calculated trend observed in the interfacial Ch···Ch distances was in good agreement with the experimental values (cf. Figure 1).

Table 1.
Comparison of SCAN-rVV10 computed lattice properties with those reported experimentally for bulk 2H-MoCh2 (Ch = S, Se, Te). Experimental values are given in parentheses in each second line entry.
Table 1.
Comparison of SCAN-rVV10 computed lattice properties with those reported experimentally for bulk 2H-MoCh2 (Ch = S, Se, Te). Experimental values are given in parentheses in each second line entry.
| System | Symmetry | Space Group | a = b | c | α = β | γ | V | ρ |
|---|---|---|---|---|---|---|---|---|
| MoS2 | Hexagonal | P63/mmc | 3.168 | 12.466 | 90 | 120 | 108.38 | 4.91 |
| (3.169) | (12.324) | (90) | (120) | (107.18) | (4.96) | |||
| MoSe2 | Hexagonal | P63/mmc | 3.296 | 13.181 | 90 | 120 | 124.02 | 6.80 |
| (3.29) | (12.93) | (90) | (120) | (121.21) | (6.96) | |||
| MoTe2 | Hexagonal | P63/mmc | 3.508 | 14.197 | 90 | 120 | 151.31 | 7.71 |
| (3.518) | (13.974) | (90) | (120) | (149.79) | (7.786) |
The properties include the lattice constants (a, b and c in Å; α, β and γ in deg), cell volume (V/Å3) and cell density (ρ/gcm−3). The Crystallographic Information File (CIF) for each of the three systems relaxed with SCAN-rVV10 can be found in the Supplementary Materials.
3.2. The Molecular Electrostatic Surface Potential
In order to understand the bonding modes in the interfacial regions of each of the three TMDCs in the crystalline phase, as well as the strength of the three types of chalcogen-centered noncovalent interactions, we computed their monomer and dimer properties.
The 0.0015 a.u. isoelectron density envelope mapped MESP graphs for the three monomers of (a) MoS2, (b) MoSe2 and (c) MoTe2 are shown in Figure 2. From the values of the local-most extrema of the potential VS,max and VS,min, it is clear that the metal centers opposite to the bonds were strongly positive (VS,max 112.3, 103.7 and 107. 6 kcal mol−1 for MoS2, MoSe2 and MoTe2, respectively). On the other hand, the axial and lateral portions of the metal bonded Ch atoms were not all negative for all Ch sites, except MoS2 (VS,min values −9.3, −7.1 and −10.7, for MoS2, MoSe2 and MoTe2, respectively; and VS,max values –0.5, +2.8 and 11.9 kcal mol−1 on S, Se and Te along the Mo–S, Mo–Se and Mo–Te bond extensions, respectively). These values indicate that the character of the p-type σ-hole on S in MoS2 was negative, that those of Se and Te in MoSe2 and MoTe2 were positive, and that the strength of the σ-hole on the bonded chalcogen atoms increased in the series from MoS2 through MoSe2 to MoTe2. The positive regions lay far off on the Mo–Ch bond extensions.
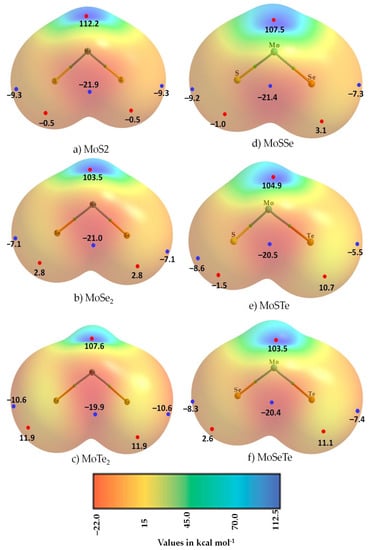
Figure 2.
MP2(Full)/Sapporo-TZP-Diffuse computed electrostatic potential surfaces of the six MoCh2 and MoChCh′2 (Ch, Ch′ = S, Se, Te) monomers. The 0.0015 a.u. isodensity envelope was used, on which the electrostatic potential was computed. The tiny red and blue circles represent the VS,max and VS,min, respectively.
The junction region between the Ch atoms in the monomers was found to be very negative. In all three cases, the charge density profile on the surface of the metal-bonded Ch atoms was anisotropic. This specific nature of potential may explain why the metal-bonded Ch atom in a given MoCh2 monomeric unit (Ch = Se, Te) was involved in an attractive engagement with the equivalent atom in a second monomer to form a dimer when they were in close proximity, as shown in Figure 3.
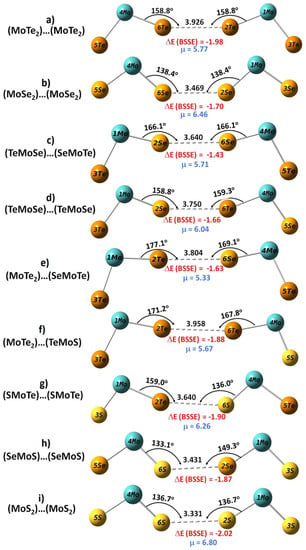
Figure 3.
MP2(Full)/def2-TZVPPD computed energy-minimized geometries of (MoCh2)2 (Ch = Se, Te) and (MoChCh′)2 (Ch, Ch′ = S, Se, Te) dimers. Intermolecular bond distances, r(Ch···Ch), and bond angles, ∠Mo–Ch···Ch, are in Å and degrees, respectively. The basis set superposition error corrected binding energies (ΔE(BSSE)/kcal mol−1) and overall dipole moments (μ/D) of the dimers are shown. Table S2 of the Supplementary Materials lists the relaxed redundant internal coordinates of all the nine dimers.
Because the surface of S in MoS2 is entirely negative, VS,max < 0 and VS,min < 0, the dimer (MoS2)2 may not form in the gas phase. It may then be understood that the effect of packing in the solid state plays a structure-determining role in stabilizing a layered material for the MoS2 system in 2D. Although the molecular electrostatic model fails to provide any insight into the intermolecular chemistry of (MoS2)2, it does suggest that when MoS2 entities are in close proximity, their electric fields polarize each other, leading to the induction of positive and negative sites on the surfaces of metal-bound sulfur; they then attract each other, as demonstrated for some dimers of chloromethane [108,109,110,111,112]. That two positive (or negative) sites on the same or different molecular entities attract each other to form complex systems is not a new finding, and such observations have been noted for a number of dimers in the gas phase [113,114,115,116]. Many Type-I interactions observed in the solid state may also fall into this category of intermolecular bonding, in which the engagement is a result of attraction between sites of dissimilar charge densities [113,114].
Our MESP calculations of the other three molybdenum mixed dichalcogenides, MoChCh′, are summarized in Figure 2c–e. In all cases, the charge density on the surface of each chalcogen atom was anisotropic. In MoSSe and MoSTe (Figure 2c,d, respectively), the bonded S atom was entirely negative, and the heavier chalcogen atoms had both positive and negative regions of electrostatic potential. In the case of MoSeTe, shown in Figure 2f, each of the two chalcogen atoms featured positive and negative regions on their electrostatic surfaces; they should therefore have been capable of acting as Lewis acids and bases towards their interacting partners to drive any attractive engagement between them.
3.3. Intermolecular Geometry of Dimers
We now address whether the intermolecular bonding interactions in the (MoCh2)2 (Ch = S, Se, Te) dimers can serve as prototypes to rationalize similar interactions in the same systems in the solid state. We believe they probably can. This becomes evident when comparing the intermolecular geometries of the (MoTe2)2, (MoSe2)2 and (MoTeS)2 dimers shown in Figure 3a,b,i, respectively, with that summarized in Figure 1 for the corresponding crystal systems. The gas-phase predicted S···S and Se···Se intermolecular distances of 3.331 and 3.469 Å in (MoS2)2 and (MoSe2)2, respectively, were 0.210 and 0.280 Å shorter than the corresponding distances of 3.541 and 3.749 Å observed in the solid-state structure. The angles of interaction were very similar: ∠Mo–S···S = 137.7° and ∠Mo–Se···Se = 138.4° in the gas-phase (Figure 3b); ∠Mo–S···S = 138.9° and ∠Mo–Se···Se = 138.7° in the solid state (Figure 1). In the case of the (MoTe2)2 dimer, the r(Te···Te) (and ∠Mo–Te···Te) were 3.926 Å (and 158.8°) and 3.945 Å (and 139.6°) in the gas- and crystalline-phases, respectively; the intermolecular interaction distance was reproduced well, but the angle of interaction was significantly overestimated by MP2(Full). These results enabled us to conclude that the intermolecular Ch···Ch bonding interactions in the (MoCh2)2 (Ch = Se, Te) dimers may be a prototype for understanding the geometrical aspects of the interfacial regions of the same systems in the crystalline phase.
The Te···Te, Se···Se, Te···Se and Se···S contacts in the mixed-chalcogenide dimers in Figure 3c–h lay between 3.431 and 3.958 Å (also see Table S1). The angles of interaction in these mixed chalcogenide systems were quasi-linear, except for the (SMoTe)···(SMoTe) dimer. Since the electrostatic potentials on the surfaces of the interacting chalcogenide sites in the mixed dimers were dissimilar, the Coulombic interaction between the interacting monomers seems to have played an important role in determining the directionality. These results also lead to a view that the mixed molybdenum dichalcogenide systems should exist and display similar interlayer bonding environments in the crystalline phase. In fact, some mixed dichalcogenide systems have already been investigated experimentally. Janus NbTeSe is a magnetic semiconductor, with an indirect bandgap of 1.478 eV with excellent optical absorption capability in the near infra-red region, whereas MoTeSe and WTeSe monolayers are direct band-gap semiconductors with a bandgap of ~1.85 eV [117]. Bera and coworkers reported a 2H-like structure of MoSSe and examined the chemical ordering and pressure-induced isostructural and electronic transitions in the crystal [118]. The r(Se···S) and ∠Mo–Se···S in the MoSSe crystal were 3.330 Å and 142.51° in the high-pressure experimental geometry, respectively, and were probably comparable with those of 3.431 Å and 133.1°, respectively, computed in the gas phase (Figure 3h). The underlying angular difference between the two phases is not very surprising since our gas phase calculations did not involve an application of any external agency, viz. pressure.
We note that MP2(Full) failed to provide a reasonable ∠Mo–Te…Te for the (MoTe2)2 dimer. Because of this, and assuming it could be a computational artifact associated either with the basis set or the correlated method, we reoptimized the three (MoCh2)2 (Ch = S, Se, Te) dimers to see if this was indeed the case, with DFT and double hybrids, where the latter combined the exact HF exchange with an MP2-like correlation to a DFT calculation. Our further investigation included six DFT functionals, viz., MN12-L [119], MN15 [120], M06-2X [121], MN15-L [122], ωB97XD [123] and PW6B95 [124], and one double hybrid, B2PLYPD3 [73] (D3 in the latter accounts for Grimme’s D3BJ dispersion [124,125]). These methods have often been applied to explore the physical chemistry of noncovalent interactions [126,127], including chalcogen bonding in chemical systems [128,129,130].
Our results are summarized in Table 2. The data lead to a view that all the DFT functionals and the double hybrid provide a reasonable configuration of all three dimers. Among the computational methods selected, M06-2X provided the best intermolecular geometry for the (MoTe2)2 dimer (r(Te···Te) (and ∠Mo–Te···Te) = 3.972 Å (and 139.3°)); MP2(Full) and B2PLYPD3 provided the best intermolecular geometry for the (MoSe2)2 and (MoS2)2 dimers—all compared to the solid-state geometries shown in Figure 1. Whereas the DFT predicted bond distances were overestimated for most dimers, B2PLYPD3 systematically underestimated the Ch···Ch bond distances of all the three (MoCh2)2 (Ch = S, Se, Te) dimers. Regardless of the dimer examined and the computational method employed, all were found to be polar, as evidenced by the dipole moment μ (see Figure 3 and Table 2).

Table 2.
MP2(Full) and DFT/def2-TZVPPD computed Ch···Ch bond distances (r(Ch···Ch)/Å), Mo–Ch···Ch bond angles (∠Mo–Ch···Ch/deg), dipole moments (μ/Debye), uncorrected and BSSE corrected binding energies (ΔE and ΔE(BSSE) in kcal mol−1, respectively) of (MoCh2)2 (Ch = S, Se, Te) dimers.
3.4. Energy Stability
We now focus our attention on the stability of the Ch···Ch interaction found in each dimer and rationalize whether can they be regarded as van der Waals, or weakly bound, or medium strength interactions.
As discussed previously, especially in the area of noncovalent chemistry [131,132,133], interactions with binding energies below −1.0 kcal mol−1 are van der Waals interactions and are dispersive by nature. In such cases, the role of Coulombic contributions that arise, for example, from permanent dipole–dipole or point charge–dipole interactions, are negligibly small. Weakly bound interactions are those with binding energies between −1.0 and −4.0 kcal mol−1, and medium-strength interactions have interaction energies roughly between −4.0 and −15.0 kcal mol−1 [131,132,133,134]. We calculated the uncorrected and BSSE-corrected binding energies using Equations (1) and (2), respectively, where ET refers to the total electronic energy of monomer/dimer and E(BSSE) refers to the error in the energy due to basis set superposition and is the spurious stabilization of the supermolecular system with respect to isolated species [135]:
It is evident from the results shown in Supplementary Materials Tables S1 and S2 that the MP2(Full) level uncorrected binding energies were relatively large for all the dimers examined. Based on this, one would characterize the interactions in the dimers as weak to medium strength. After accounting for the error in energy due to the effect of basis set superposition obtained using the counterpoise method [136] (post-Hartree Fock methods have a tendency to overestimate BSSE), the ΔE values for all the dimers were not below the energy range usually referred to as van der Waals interactions (vide supra). Based on the ΔE(BSSE) values of the highest levels of theory applied (Supplementary Materials Tables S1 and S2), all the dimers can be regarded as “weakly chalcogen bonded” systems. It is worth pointing out that all the six DFT methods underestimated the complexation energies of the dimers compared to MP2(Full), the largest being with PW6B95. Depending on the extent of exchange and correlation in a given functional, the BSSE corrected binding energies were determined to be either positive or negative; this is understandable given that electron–electron correlation effects are not well accounted for by these functionals [137].
ΔE = ET (dimer) − ET (monomer1) − ET (monomer2)
ΔE(BSSE) = ΔE + E(BSSE)
By contrast, the B2PLYPD3 gave ΔE(BSSE) for the (MoCh2)2 (Ch = S, Se, Te) dimers that were slightly smaller than those of the MP2(Full) for the former two systems. The double hybrid recognized the (MoS2)2 dimer as being of the van der Waals type, with ΔE(BSSE) = −1.08 kcal mol−1, but (MoCh2)2 (Ch = Se, Te) as weakly bound. Moreover, all the computation methods suggested that an increase in the Ch···Ch intermolecular distance passing from (MoS2)2 through (MoSe2)2 to (MoTe2)2 results in a concomitant increase in the BSSE corrected binding energy. This was not the case with MP2(Full) given that it predicted (MoS2)2 to be stronger than (MoSe2)2, which was probably the effect of a spuriously large BSSE computed with this method. Nevertheless, our results in Table 2 show that chalcogen-centered noncovalent bonding interactions should not be viewed as emerging predominantly from the electrostatically driven Coulombic interaction; they represent dispersive interactions that play a very crucial role in stabilizing them. This view may be in agreement with Bickelhaupt and coworkers, who suggested that the bonding character of chalcogen bonds stems from strong HOMO−LUMO interactions [138], which is at odds with the view that chalcogen bonding is predominantly electrostatically driven.
From Supplementary Materials Tables S1 and S2, it can be seen that the MP2(Full) level uncorrected binding energies were relatively large for all the dimers examined. Based on this, one would characterize the interactions in the dimers as weak to medium strength. After accounting for the error in energy due to the effect of basis set superposition obtained using the counterpoise method [136] (post-Hartree Fock methods have a tendency to overestimate BSSE) the ΔE values for all the dimers were not below the energy range usually referred to as van der Waals interactions (vide supra). Based on the ΔE(BSSE) values of the highest levels of theory applied (Supplementary Materials Tables S1 and S2), all the dimers can be regarded as “weakly chalcogen bonded” systems. It is worth pointing out that all the six DFT methods underestimated the complexation energies of the dimers compared to MP2(Full), the largest having been with PW6B95.
3.5. Isosurface and Bond Path Topological Properties of Charge Density
Although intermolecular distances and binding energies are good indicators of bonding interactions in complexes, we applied several charge-density-based approaches to confirm the presence of intermolecular interactions in the nine dimers examined. For instance, the MP2/def2-TZVPPD computed sign(λ2) × ρ vs. IRI, sign(λ2) × ρ vs. RDG, and sign(λ2) × ρ vs. IGM-based δgintra/intra plots for the (TeMoSe)···(TeMoSe) dimer are shown in Figure 4. They all indicate that the sign of the second eigenvalue of the Hessian matrix of the charge density, λ2, was negative. Since λ2 < 0 in the intermolecular and intramolecular bonding regions, it signifies the possibility of a bonding interaction, which may be of either shared or closed-shell character. Both van der Waals interactions and non-covalent interactions (e.g., hydrogen bonds) showed negatives value of λ2 at the critical point (with λ2 ≃ 0 for van der Waals interactions) [139]. The charge density in this region, where λ2 < 0, was very small for Te···Se contacts, and was larger for the coordination bonds between Mo and Ch (Ch = Te, Se). This was evident in the sign(λ2) × ρ vs. IRI, and sign(λ2) × ρ vs. IGM-based δg plots, where the two spikes appeared in the regions −0.13 a.u. < sign(λ2) × ρ < −0.15 a.u. and −0.105 a.u. < sign(λ2) × ρ < −0.125 a.u. corresponding to the Mo–Se and Mo–Te bonds, respectively. The Te···Se interaction showed up at sign(λ2) × ρ ≈ −0.01 a.u., indicating the presence of a weakly bound interaction. All these features were present in the corresponding plots of the remaining eight (MoCh2)2 and (MoChCh′2)2 dimers (spike-based plots are not shown, but isosurface plots are depicted in Figure 5).
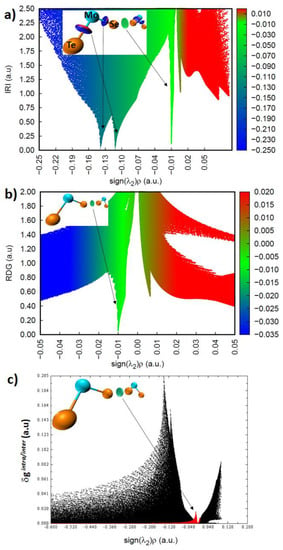
Figure 4.
MP2(Full)/def2-TZVPPD computed (a) sign(λ2) × ρ vs. IRI, (b) sign(λ2) × ρ vs. RDG, and (c) sign(λ2) × ρ vs. IGM-based δgintra/intra plots for the (TeMoSe)···(TeMoSe) dimer. The inset in each plot represents the ball-and-stick model of the dimer with an isosurface in the intermolecular region between the bonded atomic basins. The isosurfaces correspond to isovalues of 1.1, 0.4 and 0.008 a.u. with IRI, RDG and IGM-based approaches, respectively.
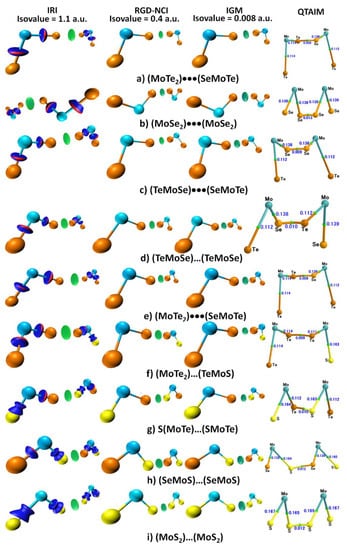
Figure 5.
MP2(Full)/def2-TZVPPD computed IRI, RDG and IGM-based isosurfaceplots between bonded atomic basins for all the nine dimers examined. Isosurfaces representing the presence of noncovalent interactions are colored red/blue/green. Included are the QTAIM molecular graphs, with ρb (a.u.) at bcps.
The QTAIM-based molecular graphs, as well as the IRI, RDG and IGM-based NCI plots for all nine dimers are shown in Figure 5. Based on the conceptual framework of QTAIM, one might expect that the presence of an intermolecular interaction between two atomic entities in a molecular entity should be reflected as a bond critical point (bcp) in the bonding region with a small charge density, and that the Laplacian of the charge density (∇2ρb) should be positive. Indeed, a bcp was found between the intermolecularly bonded Ch atomic basins, with ρb close to 0.01 a.u. (Figure 5). We found ∇2ρb at the Ch…Ch bcps to be +0.021 a.u. (MoTe2···MoTe2, Figure 5a), +0.029 a.u. (MoSe2···MoSe2, Figure 5b), +0.024 a.u. (TeMoSe···SeMoTe, Figure 5c), +0.022 a.u. (TeMoSe···TeMoSe, Figure 5d), +0.021 a.u. (MoTe2···SeMoTe, Figure 5e) 0.018 a.u. (MoTe2···TeMoS, Figure 5f), +0.024 (SMoTe···SMoTe, Figure 5g), +0.030 a.u. (SeMoS···SeMoS, Figure 5h) and +0.033 a.u. (MoS2···MoS2, Figure 5i). The charge density and the Laplacian of the charge density values were small and positive, indicative of closed-shell interactions. The bcp topology was consistent with the IRI-, RDG- and IGM-based isosurface plots in which the bonding region between the chalcogen atoms in each dimer was accompanied by a single circular volume (isosurface), colored green/light-blue, in agreement with the sign(λ2) × ρ vs. IRI, sign(λ2) × ρ vs. RDG, and sign(λ2) × ρ vs. IGM-based δgintra/intra plots shown in Figure 4. We note that each approach had its own specific isovalue for the isosurface plot, and hence the color of these changes from greenish to light-blueish.
Some studies emphasized the presence of van der Waals gaps between layers of, among others, the 2H and 3R phases of 2D crystals [41,49,140]. This gap is driven by van der Waals forces and is suitable for exfoliation and intercalation [141,142]. This concept has been established in the area of layered transition metal mono-, di- and tri-chalcogenides [47,49,50,143,144]. As shown in Figure 6 for the 2H phase of MoS2, different authors recognized van der Waals gaps in 2D materials in different ways. There is no general consensus about the exact nature and position of the gap. We argue that there is no gap between the two chalcogen-bonded metal layers, but instead voids. These exist between the chalcogenides in the interfacial/interlayer region in a multilayer system in 2D. The monolayers of a multi-layer system are driven by van der Waals type or “weak” interlayer forces, in which Ch atoms are chemically bonded to each other. The occurrence of a specific type of force between the layer depends on the nature of the transition metal chalcogenide system. The intercalation between the layers of the TMDCs can modify the interfacial geometry of TMDCs (increasing the distance between two consecutive monolayers), and hence tune the electronic and optical properties for possible applications [50]. However, as noted in several studies, intercalation of the foreign species (for example, Li) results in the loss of the pristine semiconducting properties of MoCh2 due to structural changes in the host materials by way of an expansion in the interlayer spacing and a concomitant weakening of the weak forces in the interlayer region [28,141]. Similar observations have been made about other metal chalcogenide systems [143].
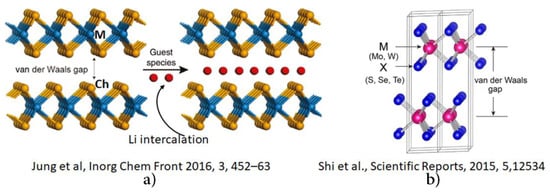
Figure 6.
Examples showing the van der Waals gap in 2H-MCh2 layered crystals, as reported in two different studies. The figure on (a) is reproduced from [49], with permission from the Royal Society of Chemistry, which shows a van der Waals gap and Li intercalation between the two chalcogenide monolayers of 2H-MCh2. The figure on (b) illustrates the same van der Waals gap reported by Shi et al. (Sci. Rep. 2015, 5, 12534), yet persisting between the two metal layers of MCh2, in which, the sole importance of the two chalcogenide layers responsible for the so-called van der Waals gap shown in (a) was completely ignored.
In order to understand whether there is a gap between the monolayers in the MoCh2 crystals, we examined the extent of overlapping between the Ch atoms responsible for the geometries of the dimers that resemble the interfacial geometry of the crystalline phase. To this end, we calculated the mutual penetration distance between the Ch···Ch atom-atom pair within the QTAIM framework. This, by definition, should be the difference between the intermolecular distance and twice the van der Waals radius of the Ch atom; the larger the mutual penetration distance, the stronger would be the strength of the interaction. For this, we calculated the non-bonded radius of each Ch atom in the Ch···Ch pair, responsible for the (MoCh2)2 (Ch = S, Se, Te) dimers shown in Figure 3. We considered these three systems since MoCh2 (Ch = S, Se, Te) have been intensely studied in the crystalline phase. Regardless of whether it is in the solid state, or in the gas phase, the non-bonded radius of an atom in molecules within the framework of the QTAIM was the shortest distance between its nucleus and the 0.001 a.u. isodensity envelope [113,145]. Our B2PLYPD3 calculation produced values of 2.133, 2.235 and 2.409 Å for the non-bonded radii of S, Se and Te in the (MoCh2)2 dimers, respectively. Twice these values are 4.266, 4.470 and 4.818, respectively; these are about 0.779, 0.920, and 1.086 Å larger than the Ch···Ch bond distances of 3.487, 3.550, and 3.732 Å for (MoS2)2, (MoSe2)2, and (MoTe2)2, respectively. This suggests that there is no gap between the two Ch layers of two consecutive monolayers of the bilayer MoCh2 systems.
3.6. Nature of Second-Order Hyper-Conjugative Charge Transfer Delocalization between the Monomers in the (MoCh2)2 and (MoChCh′2)2 (Ch, Ch′ = S, Se and Te) Dimer Geometries
Since the MESP model failed to provide correct insight into the nature of the relationship between the interacting sites, especially for the (MoS2)2 dimer, and why two sites that are completely negative attract each other, we examined the second-order perturbative estimates of donor–acceptor (bond–antibond) interaction energies to identify all possible dominant interactions existing between “filled” (donor) Lewis-type natural bond orbitals (NBOs) and “empty” (acceptor) non-Lewis NBOs. Given that these interactions involve the donation of electron density from the localized NBOs of the idealized Lewis structure into the empty non-Lewis orbitals, they are referred to as “delocalization” corrections to the zeroth-order natural Lewis structure [146,147,148]. For each donor NBO (i) and acceptor NBO (j), the stabilization energy E(2) associated with delocalization (“2e-stabilization”) i → j is estimated by Equation (3), where qi is the donor orbital occupancy, εi and εj are diagonal elements (orbital energies) and F(i,j) is the off-diagonal NBO Fock matrix element:
The stabilization energy E(2) associated with each important hyperconjugative charge transfer delocalization is summarized in Table 3. The data show that each dimer was a result of a charge transfer delocalization from unit 1 (Mo1Ch2Ch3) to unit 2 (Mo4Ch5Ch6) at their equilibrium geometries and vice versa, meaning that back donation of charge density is an important aspect of all the chalcogen-bonded dimers. The charge transfer occurred from a lone-pair type orbital, LP, centered on the interacting Ch atom of a given monomer to the anti-bonding type dπ orbital (BD*) of the Mo–Ch bond of the second monomer involved in an intermolecular bonding interaction. Sometimes these interactions behaved as primary or secondary interactions, depending on the angular orientation between the monomers in the dimers. One such interaction, for instance, in the case of the (MoSe2)···(MoSe2) dimer, was from the BD(3)Mo1–Se2 to BD*(3)Mo4– Se6, with E(2) = 1.06 kcal mol−1 (Table 3). In addition, another such charge transfer interaction, common in most of the dimers, occurred between the BD(3) Mo–Ch to the Rydberg type empty orbital RY*. These observations may be consistent with the nature of band extrema states of solid state systems that were demonstrated originating from a linear combination of Mo-(d) and Ch-(p) orbitals and are sensitive to the interlayer interactions [149]. Since most dimers are a result of a number of hyperconjugative interactions between the monomers, and E(2) associated with each of them is weak, it is reasonable to conclude that the stability of the weakly Ch···Ch chalcogen bonded interactions in most of the (MoCh2)2 and (MoChCh′2)2 (Ch′ = S, Se and Te) dimers was a consequence of their cumulative effect. The charge transfer between interacting units in the MoCh2 systems in the solid state has been demonstrated previously [150].

Table 3.
RHF/Sapporo-TZP//MP2(Full)/def2-TZVPPD computed second-order hyper-conjugative charge transfer delocalization energies, E(2), between the interacting monomers at the energy-minimized geometries of the (MoCh2)2 and (MoChCh′2)2 (Ch′ = S, Se and Te) dimers.
3.7. The Electronic Band Structures of Bulk MoCh2(Ch = S, Se, Te)
We have computed the HOMO and LUMO energies of the (MoS2)2, (MoSe2)2 and (MoTe2)2 dimers, where HOMO and LUMO represent the highest occupied molecular orbital and the lowest unoccupied molecular orbital, respectively. While all the computational methods resulted in large values for the gap energy between the HOMO and LUMO, this was not the case with the MN12-L functional. It gave energy gaps of 1.1, 1.0 and 0.9 eV for the (MoS2)2, (MoSe2)2, and (MoTe2)2 dimers, respectively, which match reasonably well with the solid-state experimental band gap transition energies of 1.23, 1.09 and 0.88 eV for the MoS2, MoSe2 and MoTe2 crystals, respectively [34,35].
The SCAN-rVV10 computed band structures of bulk MoCh2(Ch = S, Se, Te) are shown in Figure 7. In all cases, an indirect bandgap transition between the valence band maximum (VBM) located at Γ and the conduction band minimum (CBM) located between K-Γ was found, a result which is in agreement with previous studies reported using DFT and higher-level calculations [32,151]. Although the SCF-level bandgap transition energies for MoCh2 were close to their corresponding experimental values, the non-SCF bandgaps were all underestimated (see Table 4). Despite this difference, the trend in the SCAN-rVV10-based bandgap energies across the three membered series is consistent with the experiment [34,35]. Our calculation suggests that both the Mo and S atoms contribute toward the formation of the VBM and CBM. In particular, it suggests that the 4d orbital of the Mo site contributes significantly both to the VBM and CBM, as does the np orbital of Ch (n = 3, 4 and 5 for S, Se and Te, respectively), although the 4d orbital contribution of Mo would be significant compared to that of the np orbital of S. For instance, the normalized contributions of the 4d(np) orbital of Mo(Ch) were 72.9 (20.9), 66.1 (27.9) and 58.5% (34.8%) for the VBM of MoS2, MoSe2 and MoTe2, respectively. The corresponding contributions for the CBM were 78.7% (18.7%), 77% (18.4%) and 75.6% (19.1%) for the three systems, respectively. That the 4p and np orbitals, respectively, of Mo and S collectively play a decisive role in determining the bandgap properties of MoCh2 systems is consistent with previous studies [107,152,153]. It is worth noting that the large contributions of Mo(4d) have emerged mainly from the 4dxy, 4dx2−y2 and 4dz2 orbitals, as has been noted by others [154] and that both the VBM and CBM show a significant metallic character.
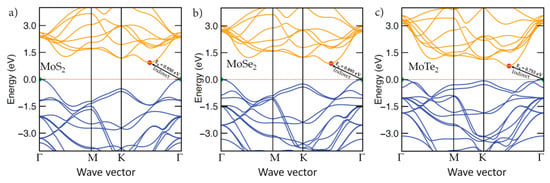
Figure 7.
Comparison of the electronic band structures of bulk 2H-MoCh2 (Ch = S, Se, Te), obtained using SCAN-rVV10: (a) MoS2, (b) MoSe2, (c) MoTe2. The CBM and VBM band edges are marked by tiny circles in red and green, respectively. Bandgap values, Eg, are indicated. The Fermi-level is referenced at 0.0 eV and is marked by a dotted line in red. The high-symmetry points along the wave vector axis considered were similar to that expected of the 2D layered 2H-MoCh2 systems. The nature of bandgap transition did not change when high-symmetry points expected of bulks were used (see Figure S1 of Supplementary Materials).

Table 4.
Comparison computed bandgaps and HOMO–LUMO gap (eV) with experiment for MoCh2 (Ch = S, Se, Te) systems.
4. Conclusions
Using theoretical methods, we examined the intermolecular bonding properties of nine (MoCh2)2 and (MoChCh′2)2 (Ch, Ch′ = S, Se and Te) dimers as models to provide insight into the bent and quasi-linear nature of the Ch···Ch and Ch···Ch′ interactions observed in the crystalline phase. Our calculations indicate that the bent nature of the Te···Te bond observed in the crystalline phase of MoTe2 may not be traced in the gas phase with MP2(Full), which may be a failure of the correlated method, and is not very surprising [155,156]. However, this was not the case for the two other systems, (MoSe2)2 and (MoTe2)2, for which MP2(Full) successfully predicted the nanoscale properties of these two systems, as well as the (SeMoS)···(SeMoS) dimer. We found that none of the computational approaches employed was fully adequate to reveal accurately a variety of properties of the (MoCh2)2 and (MoChCh′2)2 (Ch, Ch′ = S, Se and Te) dimers that resemble the corresponding properties reported in the solid state. This is understandable given that each method has advantages and disadvantages compared to the others in revealing a particular property of a given chemical system [127,129,157].
From a set of DFT and double hybrids examined, it was found that not a single one of them could accurately reproduce the interfacial inter-layer geometries of the widely exploited MoCh2 (Ch = S, Se, Te) systems. Although M06-2X was able to reproduce with some reasonable accuracy the interlayer geometry of the MoTe2 crystal, it somehow failed to do so in the cases of the other two crystal systems MoCh2 (Ch = S, Se). Comparing the performance of all the DFT functionals, double hybrids and MP2(Full), we conclude that MP2(Full) and B3LYPD3 are the best performers in delineating the geometric aspects of the (MoCh2)2 (Ch = S, Se, Te) dimer systems. These are prototypes for rationalizing the nature of the interfacial (or interlayer) Ch···Ch and Ch···Ch′ interactions observed in the crystalline phase of the corresponding crystal systems.
The MP2(Full) and B2PLYPD3 binding energies calculated for most of the dimer systems allowed us to demonstrate that the Ch···Ch interactions revealed are not of the van der Waals type, but rather fall into the “weak bonding regime”. All the DFT functionals, regardless of whether or not the effect of dispersion is considered (viz. ωB97XD), have underestimated the binding energies, which is not surprising, since dispersion is not adequately incorporated into most of them. Given that “union is strength”, it is clear that the union of a large number of weakly bonded Ch···Ch and/or Ch···Ch′ interactions in the interfacial regions between layers plays a significant role, not only in stabilizing the layered 2D systems, but also in assisting in determining their functional properties for application in optoelectronics. In particular, we have observed that the bulk bandgap correlates well with the inter-layer spacing for several well-studied metal dichalcogenide systems, which we will report elsewhere.
The application of the QTAIM, IRI, IGM and RGD-based topological charge density studies have enabled us to identify and quantify the Ch···Ch and Ch···Ch′ intermolecular interactions in the nine (MoCh2)2 and (MoChCh′2)2 (Ch, Ch′ = S, Se and Te) dimers. Similarly, as discussed in previous studies [113,114,158,159], we found that the MESP model did not work well in rationalizing quantitatively why the most negative sites (as on S in an isolated MoS2 monomer) attracted the same site in another of the same molecule to form the (MoS2)2 dimer in the gas phase. By contrast, and using the results of second-order perturbative estimates of the donor–acceptor interactions in the NBO basis, we have shown that significant charge transfer hyperconjugative interactions between the interacting subunits occurred that drove the formation of the nine (MoCh2)2 and (MoChCh′2)2 (Ch, Ch′ = S, Se and Te) dimers examined.
Supplementary Materials
The following supporting materials can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics10010011/s1. These include Tables S1 and S2 and Figure S1. The first includes MP2(Full)/def2-TZVPPD computed uncorrected and BSSE corrected binding energies (h and ΔE(BSSE) in kcal mol−1, respectively) and chalcogen···chalcogen (r(Ch···Ch)) bond distances of the nine dimers of Figure 3. Table S2 includes the Gaussian 16 relaxed geometries (redundant internal coordinates) of all the nine dimers. It also includes the cifs of SCAN-rVV10 relaxed geometries of the three bulk systems MoCh2 (Ch = S, Te, Se) obtained using VASP, as well as the Mol2 files of all the fully-relaxed nine dimers obtained using Gaussian 16. Figure S1 includes the atom/orbital-projected band structures of all the three bulk systems MoCh2 (Ch = S, Te, Se).
Author Contributions
Conceptualization, project design, and project administration, P.R.V.; formal analysis and investigation, P.R.V. and A.V.; discussion—P.R.V., H.M.M., A.V. and K.Y; Supervision, P.R.V.; writing—original draft, P.R.V. and A.V.; writing—review and editing, P.R.V., H.M.M., A.V. and K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This research did not report any data.
Acknowledgments
This work was entirely conducted using the various computation and laboratory facilities provided by the University of Tokyo. P.R.V. is currently affiliated with the University of the Witwatersrand (SA). A.V. is currently affiliated with AIST, Tsukuba 305-8560, Japan. K.Y. is currently affiliated with Kyoto University, ESICB, Kyoto, 615-8245, Japan. H.M.M. thanks the National Research Foundation, Pretoria, South Africa, and the University of the Witwatersrand for funding.
Conflicts of Interest
The authors declare no conflict of interest. The funders had absolutely no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Jana, M.K.; Rao, C.N.R. Two-dimensional inorganic analogues of graphene: Transition metal dichalcogenides. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Colen, J.; Liu, J.; Nguyen, M.C.; Chern, G.-W.; Louca, D. Elastic and electronic tuning of magnetoresistance in MoTe 2. Sci. Adv. 2017, 3, eaao4949. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-R.; Cheng, W.-H.; Richter, M.H.; DuChene, J.S.; Peterson, E.A.; Went, C.M.; Al Balushi, Z.Y.; Jariwala, D.; Neaton, J.B.; Chen, L.-C.; et al. Band Edge Tailoring in Few-Layer Two-Dimensional Molybdenum Sulfide/Selenide Alloys. J. Phys. Chem. C 2020, 124, 22893–22902. [Google Scholar] [CrossRef]
- Sokolikova, M.S.; Sherrell, P.C.; Palczynski, P.; Bemmer, V.L.; Mattevi, C. Direct solution-phase synthesis of 1T’ WSe2 nanosheets. Nat. Commun. 2019, 10, 712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, W.; Pan, J.; Fang, Y.; Che, X.; Wang, D.; Bu, K.; Huang, F. Metastable MoS2: Crystal Structure, Electronic Band Structure, Synthetic Approach and Intriguing Physical Properties. Chem. Eur. J. 2018, 24, 15942–15954. [Google Scholar] [CrossRef] [PubMed]
- Duerloo, K.-A.N.; Li, Y.; Reed, E.J. Structural phase transitions in two-dimensional Mo- and W-dichalcogenide monolayers. Nat. Commun. 2014, 5, 4214. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhu, H. Two-dimensional MoS2: Properties, preparation, and applications. J. Materiomics 2015, 1, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Pai, W.W.; Chan, Y.H.; Sun, W.L.; Xu, C.Z.; Lin, D.S.; Chou, M.Y.; Fedorov, A.V.; Chiang, T.C. Large quantum-spin-Hall gap in single-layer 1T′ WSe2. Nat. Commun. 2018, 9, 2003. [Google Scholar] [CrossRef]
- Li, Y.; Duerloo, K.-A.N.; Wauson, K.; Reed, E.J. Structural semiconductor-to-semimetal phase transition in two-dimensional materials induced by electrostatic gating. Nat. Commun. 2016, 7, 10671. [Google Scholar] [CrossRef]
- Qian, Z.; Jiao, L.; Xie, L. Phase Engineering of Two-Dimensional Transition Metal Dichalcogenides. Chin. J. Chem. 2020, 38, 753–760. [Google Scholar] [CrossRef]
- Yu, P.; Lin, J.; Sun, L.; Le, Q.L.; Yu, X.; Gao, G.; Hsu, C.-H.; Wu, D.; Chang, T.-R.; Zeng, Q.; et al. Metal–Semiconductor Phase-Transition in WSe2(1-x)Te2x Monolayer. Adv. Mater. 2017, 29, 1603991. [Google Scholar] [CrossRef]
- Morales-Durán, N.; MacDonald, A.H.; Potasz, P. Metal-insulator transition in transition metal dichalcogenide heterobilayer moiré superlattices. Phys. Rev. B 2021, 103, L241110. [Google Scholar] [CrossRef]
- Shimazu, Y.; Arai, K.; Iwabuchi, T. Metal–insulator transition in a transition metal dichalcogenide: Dependence on metal contacts. J. Phys. Conf. Ser. 2018, 969, 012105. [Google Scholar] [CrossRef]
- Choe, D.-H.; Sung, H.-J.; Chang, K.J. Understanding topological phase transition in monolayer transition metal dichalcogenides. Phys. Rev. B 2016, 93, 125109. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.-R.; Lin, H.; Jeng, H.-T.; Bansil, A. Thickness dependence of spin polarization and electronic structure of ultra-thin films of MoS2 and related transition-metal dichalcogenides. Sci. Rep. 2014, 4, 6270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhuang, H.L.; Hennig, R.G. Theoretical perspective of photocatalytic properties of single-layer SnS2. Phys. Rev. B 2013, 88, 115314. [Google Scholar] [CrossRef]
- Singh, N.; Jabbour, G.; Schwingenschlögl, U. Optical and photocatalytic properties of two-dimensional MoS2. Eur. Phys. J. B 2012, 85, 392. [Google Scholar] [CrossRef]
- Kang, J.; Tongay, S.; Zhou, J.; Li, J.; Wu, J. Band offsets and heterostructures of two-dimensional semiconductors. Appl. Phys. Lett. 2013, 102, 012111. [Google Scholar] [CrossRef] [Green Version]
- Fiori, G.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerjee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768–779. [Google Scholar] [CrossRef] [PubMed]
- Bhimanapati, G.R.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent Advances in Two-Dimensional Materials beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Bonaccorso, F.; Fal’ko, V.; Novoselov, K.S.; Roche, S.; Bøggild, P.; Borini, S.; Koppens, F.H.L.; Palermo, V.; Pugno, N.; et al. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 2015, 7, 4598–4810. [Google Scholar] [CrossRef] [Green Version]
- Lu, N.; Li, Z.; Yang, J. Electronic Structure Engineering via On-Plane Chemical Functionalization: A Comparison Study on Two-Dimensional Polysilane and Graphane. J. Phys. Chem. C 2009, 113, 16741–16746. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Zhao, Y.; Lu, N.; Kan, E.; Zeng, X.C.; Wu, X.; Yang, J. Tunable Magnetism in a Nonmetal-Substituted ZnO Monolayer: A First-Principles Study. J. Phys Chem. C 2012, 116, 11336–11342. [Google Scholar] [CrossRef]
- Dai, J.; Wu, X.; Yang, J.; Zeng, X.C. Unusual Metallic Microporous Boron Nitride Networks. J. Phys. Chem. Lett. 2013, 4, 3484–3488. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef]
- Eda, G.; Yamaguchi, H.; Voiry, D.; Fujita, T.; Chen, M.; Chhowalla, M. Photoluminescence from Chemically Exfoliated MoS2. Nano Lett. 2011, 11, 5111–5116. [Google Scholar] [CrossRef]
- Johari, P.; Shenoy, V.B. Tuning the Electronic Properties of Semiconducting Transition Metal Dichalcogenides by Applying Mechanical Strains. ACS Nano 2012, 6, 5449–5456. [Google Scholar] [CrossRef] [PubMed]
- Naik, M.H.; Jain, M. Origin of layer dependence in band structures of two-dimensional materials. Phys. Rev. B 2017, 95, 165125. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.; Long, M.; Li, X.; Zhang, Q.; Xu, H.; Chan, K.S. Effects of van der Waals interaction and electric field on the electronic structure of bilayer MoS2. J. Phys. Cond. Matt. 2014, 26, 405302. [Google Scholar] [CrossRef] [PubMed]
- Zahid, F.; Liu, L.; Zhu, Y.; Wang, J.; Guo, H. A generic tight-binding model for monolayer, bilayer and bulk MoS2. AIP Adv. 2013, 3, 052111. [Google Scholar] [CrossRef] [Green Version]
- Varsano, D.; Palummo, M.; Molinari, E.; Rontani, M. A monolayer transition-metal dichalcogenide as a topological excitonic insulator. Nat. Nanotechol. 2020, 15, 367–372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bastos, C.M.O.; Besse, R.; Da Silva, J.L.F.; Sipahi, G.M. Ab initio investigation of structural stability and exfoliation energies in transition metal dichalcogenides based on Ti-, V-, and Mo-group elements. Phys. Rev. Mater. 2019, 3, 044002. [Google Scholar] [CrossRef] [Green Version]
- Kam, K.K.; Parkinson, B.A. Detailed photocurrent spectroscopy of the semiconducting group VIB transition metal dichalcogenides. J. Phys. Chem. 1982, 86, 463–467. [Google Scholar] [CrossRef]
- Hamill, A.; Heischmidt, B.; Sohn, E.; Shaffer, D.; Tsai, K.-T.; Zhang, X.; Xi, X.; Suslov, A.; Berger, H.; Forró, L.; et al. Two-fold symmetric superconductivity in few-layer NbSe2. Nat. Phys. 2021, 17, 949–954. [Google Scholar] [CrossRef]
- Cho, C.-w.; Lyu, J.; Han, T.; Ng, C.Y.; Gao, Y.; Li, G.; Huang, M.; Wang, N.; Schmalian, J.; Lortz, R. Distinct Nodal and Nematic Superconducting Phases in the 2D Ising Superconductor NbSe2. 2020. Available online: https://arxiv.org/abs/2003.12467 (accessed on 6 November 2021).
- Guo, H.; Lu, N.; Wang, L.; Wu, X.; Zeng, X.C. Tuning Electronic and Magnetic Properties of Early Transition-Metal Dichalcogenides via Tensile Strain. J. Phys. Chem. C 2014, 118, 7242–7249. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Qian, X.; Li, J. Phase transitions in 2D materials. Nat. Rev. Mater. 2021, 6, 829–846. [Google Scholar] [CrossRef]
- Cheng, P.; Sun, K.; Hu, Y.H. Mechanically-induced reverse phase transformation of MoS2 from stable 2H to metastable 1T and its memristive behavior. RSC Adv. 2016, 6, 65691–65697. [Google Scholar] [CrossRef]
- Xia, J.; Wang, J.; Chao, D.; Chen, Z.; Liu, Z.; Kuo, J.-L.; Yan, J.; Shen, Z.X. Phase evolution of lithium intercalation dynamics in 2H-MoS2. Nanoscale 2017, 9, 7533–7540. [Google Scholar] [CrossRef]
- Sánchez-Montejo, E.; Santana, G.; Domínguez, A.; Huerta, L.; Hamui, L.; López-López, M.; Limborço, H.; Matinaga, F.M.; da Silva, M.I.N.; de Oliveira, A.G.; et al. Phase stability in MoTe2 prepared by low temperature Mo tellurization using close space isothermal Te annealing. Mater. Chem. Phys. 2017, 198, 317–323. [Google Scholar] [CrossRef]
- Kansara, S.; Gupta, S.K.; Sonvane, Y. Effect of strain engineering on 2D dichalcogenides transition metal: A DFT study. Comput. Mater. Sci. 2018, 141, 235–242. [Google Scholar] [CrossRef]
- Roldán, R.; López-Sancho, M.P.; Guinea, F.; Cappelluti, E.; Silva-Guillén, J.A.; Ordejón, P. Momentum dependence of spin–orbit interaction effects in single-layer and multi-layer transition metal dichalcogenides. 2D Mater. 2014, 1, 034003. [Google Scholar] [CrossRef] [Green Version]
- Babar, V.; Vovusha, H.; Schwingenschlögl, U. Density Functional Theory Analysis of Gas Adsorption on Monolayer and Few Layer Transition Metal Dichalcogenides: Implications for Sensing. ACS Appl. Nano Mater. 2019, 2, 6076–6080. [Google Scholar] [CrossRef]
- García, Á.M.; del Corro, E.; Kalbac, M.; Frank, O. Tuning the electronic properties of monolayer and bilayer transition metal dichalcogenide compounds under direct out-of-plane compression. Phys. Chem. Chem. Phys. 2017, 19, 13333–13340. [Google Scholar] [CrossRef] [PubMed]
- Palencia-Ruiz, S.; Uzio, D.; Legens, C.; Laurenti, D.; Afanasiev, P. Stability and catalytic properties of 1T-MoS2 obtained via solvothermal synthesis. Appl. Catal. A Gen. 2021, 626, 118355. [Google Scholar] [CrossRef]
- Schönfeld, B.; Huang, J.J.; Moss, S.C. Anisotropic mean-square displacements (MSD) in single-crystals of 2H- and 3R-MoS2. Acta Crystallogr. Sect. B Struct. Sci. 1983, 39, 404–407. [Google Scholar] [CrossRef]
- Jung, Y.; Zhou, Y.; Cha, J.J. Intercalation in two-dimensional transition metal chalcogenides. Inorg. Chem. Front. 2016, 3, 452–463. [Google Scholar] [CrossRef]
- Jing, Y.; Liu, B.; Zhu, X.; Ouyang, F.; Sun, J.; Zhou, Y. Tunable electronic structure of two-dimensional transition metal chalcogenides for optoelectronic applications. Nanophotonics 2020, 9, 1675–1694. [Google Scholar] [CrossRef]
- Zhu, W.; Low, T.; Wang, H.; Ye, P.; Duan, X. Nanoscale electronic devices based on transition metal dichalcogenides. 2D Mater. 2019, 6, 032004. [Google Scholar] [CrossRef]
- Fukuda, M.; Zhang, J.; Lee, Y.-T.; Ozaki, T. A structure map for AB2 type 2D materials using high-throughput DFT calculations. Mater. Adv. 2021, 2, 4392–4413. [Google Scholar] [CrossRef]
- Yang, L.; Cui, X.; Zhang, J.; Wang, K.; Shen, M.; Zeng, S.; Dayeh, S.A.; Feng, L.; Xiang, B. Lattice strain effects on the optical properties of MoS2 nanosheets. Sci. Rep. 2014, 4, 5649. [Google Scholar] [CrossRef] [PubMed]
- Kulichenko, M.; Boldyrev, A.I. σ-Aromaticity in the MoS2 Monolayer. J. Phys. Chem. C 2020, 124, 6267–6273. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Liu, S.-C.; Li, Z.; Sun, Z.; Hu, C.; Xue, D.-J.; Zhang, G.; Hu, J.-S. Weak Interlayer Interaction in 2D Anisotropic GeSe2. Sci. Adv. 2019, 6, 1801810. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; MacDougall, P.J. The chalcogen bond: Can it be formed by oxygen? Phys. Chem. Chem. Phys. 2019, 21, 19969–19986. [Google Scholar] [CrossRef]
- Varadwaj, P.R. Does Oxygen Feature Chalcogen Bonding? Molecules 2019, 24, 3166. [Google Scholar] [CrossRef] [Green Version]
- Aakeroy, C.B.; Bryce, D.L.; Desiraju, R.G.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the chalcogen bond (IUPAC Recommendations 2019). Pure Appl. Chem. 2019, 91, 1889–1892. [Google Scholar] [CrossRef]
- Decato, D.A.; John, E.A.; Berryman, O.B. Halogen Bonding: An Introduction. In Halogen Bonding in Solution; Huber, S., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA.: Bochum, Germany, 2021. [Google Scholar]
- Wang, W.; Zhu, H.; Feng, L.; Yu, Q.; Hao, J.; Zhu, R.; Wang, Y. Dual Chalcogen–Chalcogen Bonding Catalysis. J. Am. Chem Soc. 2020, 142, 3117–3124. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Bauzá Riera, A.; Quiñonero Santiago, D.; Deyà Serra, P.M.; Frontera Beccaria, A. Halogen bonding versus chalcogen and pnicogen bonding: A combined Cambridge structural database and theoretical study. CrystEngComm 2013, 15, 3137–3144. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Metrangolo, P.; Resnati, G. Type II halogen···halogen contacts are halogen bonds. IUCrJ 2014, 1, 5–7. [Google Scholar] [CrossRef]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. A direct MP2 gradient method. Chem. Phys. Lett. 1990, 166, 275–280. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Lu, T.; Chen, Q. Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions. Chem. Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Lefebvre, C.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations. ChemPhysChem 2018, 19, 724–735. [Google Scholar] [CrossRef]
- Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Hénon, E. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density. Phys. Chem. Chem. Phys. 2017, 19, 17928–17936. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Dixit, A.; Claudot, J.; Lebègue, S.; Rocca, D. Communication: A novel implementation to compute MP2 correlation energies without basis set superposition errors and complete basis set extrapolation. J. Chem. Phys. 2017, 146, 211102. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [Green Version]
- Pritchard, B.P.; Altarawy, D.; Didier, B.T.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Rev. C.01; Gaussian, Inc.: Wallinford, CT, USA, 2016. [Google Scholar]
- Noro, T.; Sekiya, M.; Koga, T. Segmented contracted basis sets for atoms H through Xe: Sapporo-(DK)-nZP sets (n = D., T., Q). Theor. Chem. Acc. 2012, 131, 1124. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Solimannejad, M. Revealing substitution effects on the strength and nature of halogen-hydride interactions: A theoretical study. J. Mol. Model. 2013, 19, 3767–3777. [Google Scholar] [CrossRef]
- Han, N.; Zeng, Y.; Li, X.; Zheng, S.; Meng, L. Enhancing Effects of Electron-Withdrawing Groups and Metallic Ions on Halogen Bonding in the YC6F4X···C2H8N2 (X = Cl, Br, I.; Y = F, CN, NO2, LiNC+, NaNC+) Complex. J. Phys. Chem. A 2013, 117, 12959–12968. [Google Scholar] [CrossRef]
- Zhang, L.; Li, D. Theoretical studies on how to tune the π-hole pnicogen bonds by substitution and cooperative effects. Int. J. Quant. Chem. 2021, 121, e26531. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. Can Counter-Intuitive Halogen Bonding Be Coulombic? ChemPhysChem 2021, 22, 1201–1207. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.Y. Significant evidence of C···O and C···C long-range contacts in several heterodimeric complexes of CO with CH3-X, should one refer to them as carbon and dicarbon bonds! Phys. Chem. Chem. Phys. 2014, 16, 17238–17252. [Google Scholar] [CrossRef]
- Glendening, E.E.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO (Natural Bond Orbital); Gaussian Inc.: Pittsburg, PA, USA, 2004. [Google Scholar]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comp. 2011, 7, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Contreras-García, J.; Yang, W.; Johnson, E.R. Analysis of Hydrogen-Bond Interaction Potentials from the Electron Density: Integration of Noncovalent Interaction Regions. J. Phys. Chem. A 2011, 115, 12983–12990. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otero-de-la-Roza, A.; Johnson, E.R.; Contreras-García, J. Revealing non-covalent interactions in solids: NCI plots revisited. Phys. Chem. Chem. Phys. 2012, 14, 12165–12172. [Google Scholar] [CrossRef] [PubMed]
- Boto, R.A.; Contreras-García, J.; Tierny, J.; Piquemal, J.-P. Interpretation of the reduced density gradient. Mol. Phys. 2016, 114, 1406–1414. [Google Scholar] [CrossRef] [Green Version]
- Lane, J.R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B.J.; Kjaergaard, H.G. Are Bond Critical Points Really Critical for Hydrogen Bonding? J. Chem. Theory Comput. 2013, 9, 3263–3266. [Google Scholar] [CrossRef] [PubMed]
- Keith, T.A.; Gristmill Software, T.K.; Overland Park, K.S. AIMAll (Version 19.10.12); Overland Park, KS, USA. Available online: http://aim.tkgristmill.com (accessed on 6 November 2021).
- Lu, T.; Chen, F. A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD - Visual Molecular Dynamics. J. Molec. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.; Millam, J. GaussView, 5.0.9; Semichem, Inc.: Shawnee Mission, KS, USA, 2007. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Yang, Z.-H.; Perdew, J.P.; Sun, J. Versatile van der Waals Density Functional Based on a Meta-Generalized Gradient Approximation. Phys. Rev. X 2016, 6, 041005. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kerker, G.P. Efficient iteration scheme for self-consistent pseudopotential calculations. Phys. Rev. B 1981, 23, 3082–3084. [Google Scholar] [CrossRef]
- Lee, C.; Hong, J.; Lee, W.R.; Kim, D.Y.; Shim, J.H. Density functional theory investigation of the electronic structure and thermoelectric properties of layered MoS2, MoSe2 and their mixed-layer compound. J. Solid State Chem. 2014, 211, 113–119. [Google Scholar] [CrossRef]
- Evans, B.L.; Hazelwood, R.A. Optical and structural properties of MoSe2. Phys. Status Solidi (A) 1971, 4, 181–192. [Google Scholar] [CrossRef]
- Knop, O.; MacDonald, R.D. Chalkogenides of the Transition elements: III. Molybdenum Ditelluride. Can. J. Chem. 1961, 39, 897–904. [Google Scholar] [CrossRef] [Green Version]
- Franconetti, A.; Quiñonero, D.; Frontera, A.; Resnati, G. Unexpected chalcogen bonds in tetravalent sulfur compounds. Phys. Chem. Chem. Phys. 2019, 21, 11313–11319. [Google Scholar] [CrossRef] [PubMed]
- Zierkiewicz, W.; Michalczyk, M.; Wysokiński, R.; Scheiner, S. On the ability of pnicogen atoms to engage in both σ and π-hole complexes. Heterodimers of ZF2C6H5 (Z = P, As, Sb, Bi) and NH3. J. Mol. Model. 2019, 25, 152. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; An, X.L.; Li, Q.Z. Se···N Chalcogen Bond and Se···X Halogen Bond Involving F2C=Se: Influence of Hybridization, Substitution, and Cooperativity. J. Phys Chem. A 2015, 119, 3518–3527. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S. A cartography of the van der Waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kadantsev, E.S.; Hawrylak, P. Electronic structure of a single MoS2 monolayer. Solid State Commun. 2012, 152, 909–913. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Halogen bonding interaction of chloromethane withseveral nitrogen donating molecules: Addressing thenature of the chlorine surface σ-hole. Phys. Chem. Chem. Phys. 2014, 16, 19573–19589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Does Chlorine in CH3Cl Behave as a Genuine Halogen Bond Donor? Crystals 2020, 10, 146. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The s-hole revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Hobza, P. Investigations into the Nature of Halogen Bonding Including Symmetry Adapted Perturbation Theory Analyses. J. Chem. Theory Comput. 2008, 4, 232–242. [Google Scholar] [CrossRef]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions? Molecules 2019, 24, 379. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Can Combined Electrostatic and Polarization Effects Alone Explain the F···F Negative-Negative Bonding in Simple Fluoro-Substituted Benzene Derivatives? A First-Principles Perspective. Computation 2018, 6, 51. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Nature of halogen-centered intermolecular interactions in crystal growth and design: Fluorine-centered interactions in dimers in crystalline hexafluoropropylene as a prototype. J. Comp. Chem. 2019, 40, 1836–1860. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Do surfaces of positive electrostatic potential on different halogen derivatives in molecules attract? like attracting like! J. Comput. Chem. 2018, 39, 343–350. [Google Scholar] [CrossRef]
- Yang, X.; Banerjee, A.; Ahuja, R. Structural Insight of the Frailty of 2D Janus NbSeTe as an Active Photocatalyst. ChemCatChem 2020, 12, 6013–6023. [Google Scholar] [CrossRef]
- Bera, A.; Singh, A.; Sorb, Y.A.; Jenjeti, R.N.; Muthu, D.V.S.; Sampath, S.; Narayana, C.; Waghmare, U.V.; Sood, A.K. Chemical ordering and pressure-induced isostructural and electronic transitions in MoSSe crystal. Phys. Rev. B 2020, 102, 014103. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. An improved and broadly accurate local approximation to the exchange–correlation density functional: The MN12-L functional for electronic structure calculations in chemistry and physics. Phys. Chem. Chem. Phys. 2012, 14, 13171–13174. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Yu, H.S.; He, X.; Truhlar, D.G. MN15-L: A New Local Exchange-Correlation Functional for Kohn–Sham Density Functional Theory with Broad Accuracy for Atoms, Molecules, and Solids. J. Chem. Theory Comp. 2016, 12, 1280–1293. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comp. 2011, 7, 291–309. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Uchimaru, T. Accuracy of intermolecular interaction energies, particularly those of hetero-atom containing molecules obtained by DFT calculations with Grimme’s D2, D3 and D3BJ dispersion corrections. Phys. Chem. Chem. Phys. 2020, 22, 22508–22519. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. How Accurate Are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Composed of Main-Group Elements? J. Chem. Theory Comp. 2016, 12, 4303–4325. [Google Scholar] [CrossRef] [Green Version]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef] [Green Version]
- Mehta, N.; Fellowes, T.; White, J.M.; Goerigk, L. CHAL336 Benchmark Set: How Well Do Quantum-Chemical Methods Describe Chalcogen-Bonding Interactions? J. Chem. Theory Comp. 2021, 17, 2783–2806. [Google Scholar] [CrossRef]
- Venkataramanan, N.S. Electronic structure, stability, and cooperativity of chalcogen bonding in sulfur dioxide and hydrated sulfur dioxide clusters: A DFT study and wave functional analysis. Struct. Chem. 2021, 1–15. [Google Scholar] [CrossRef]
- Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond. In Structural Chemistry and Biology; Oxford University Press: Oxford, UK, 2001; Volume 19. [Google Scholar]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Hybrid organic-inorganic CH3NH3PbI3perovskite building blocks: Revealing ultra-strong hydrogen bonding and mulliken inner complexes and their implications in materials design. J. Comput. Chem. 2017, 38, 2802–2818. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Very strong chalcogen bonding: Is oxygen in molecules capable of forming it? A First-Principles Perspective. Authorea 2020. [Google Scholar] [CrossRef]
- Crespo-Otero, R.; Montero, L.A.; Stohrer, W.-D.; de la Vega, J.M.G. Basis set superposition error in MP2 and density-functional theory: A case of methane-nitric oxide association. J. Chem. Phys. 2005, 123, 134107. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Kristensen, K.; Høyvik, I.-M.; Jansik, B.; Jørgensen, P.; Kjærgaard, T.; Reine, S.; Jakowski, J. MP2 energy and density for large molecular systems with internal error control using the Divide-Expand-Consolidate scheme. Phys. Chem. Chem. Phys. 2012, 14, 15706–15714. [Google Scholar] [CrossRef]
- De Azevedo Santos, L.; van der Lubbe, S.C.C.; Hamlin, T.A.; Ramalho, T.C.; Matthias Bickelhaupt, F. A Quantitative Molecular Orbital Perspective of the Chalcogen Bond. ChemistryOpen 2021, 10, 391–401. [Google Scholar] [CrossRef]
- Narth, C.; Maroun, Z.; Boto, R.A.; Chaudret, R.; Bonnet, M.-L.; Piquemal, J.-P.; Contreras-García, J. A Complete NCI Perspective: From New Bonds to Reactivity. In Applications of Topological Methods in Molecular Chemistry; Esmail, A., Remi, C., Christine, L., Bernard, S., Eds.; Springer: Cham, Switzerland, 2016; Volume 22, pp. 491–527. [Google Scholar]
- Xiong, F.; Wang, H.; Liu, X.; Sun, J.; Brongersma, M.; Pop, E.; Cui, Y. Li Intercalation in MoS2: In Situ Observation of Its Dynamics and Tuning Optical and Electrical Properties. Nano Lett. 2015, 15, 6777–6784. [Google Scholar] [CrossRef]
- Zhang, Q.; Mei, L.; Cao, X.; Tang, Y.; Zeng, Z. Intercalation and exfoliation chemistries of transition metal dichalcogenides. J. Mat. Chem. A 2020, 8, 15417–15444. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, H.; Dong, S.; Liu, Y.; Tai Nai, C.; Suk Shin, H.; Young Jeong, H.; Liu, B.; Ping Loh, K. High yield exfoliation of two-dimensional chalcogenides using sodium naphthalenide. Nat. Commun. 2014, 5, 2995. [Google Scholar] [CrossRef]
- Eremeev, S.V.; Vergniory, M.G.; Menshchikova, T.V.; Shaposhnikov, A.A.; Chulkov, E.V. The effect of van der Waal’s gap expansions on the surface electronic structure of layered topological insulators. New J. Phys. 2012, 14, 113030. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, X.; Wang, T.; Li, W.; Wang, X.; Chang, S.; Li, Y.; Zhao, M.; Dai, X. Band structure engineering in a MoS2/PbI2 van der Waals heterostructure via an external electric field. Phys. Chem. Chem. Phys. 2016, 18, 28466–28473. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Resonance Delocalization Corrections. In Discovering Chemistry with Natural Bond Orbitals; Weinhold, F., Landis, C.R., Eds.; Wiley: Hoboken, NJ, USA, 2012; pp. 92–134. [Google Scholar] [CrossRef]
- Weinhold, F. Natural bond orbital analysis: A critical overview of relationships to alternative bonding perspectives. J. Comp. Chem. 2012, 33, 2363–2379. [Google Scholar] [CrossRef]
- Weinhold, F.; Glendening, E.D. NBO 6.0: Natural Bond Orbital Analysis Programs. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar]
- Banerjee, S.; Park, J.; Hwang, C.S.; Choi, J.-H.; Lee, S.-C.; Pati, S.K. Regulation of transport properties by polytypism: A computational study on bilayer MoS2. Phys. Chem. Chem. Phys. 2017, 19, 21282–21286. [Google Scholar] [CrossRef]
- Pike, N.A.; Van Troeye, B.; Dewandre, A.; Petretto, G.; Gonze, X.; Rignanese, G.-M.; Verstraete, M.J. Origin of the counterintuitive dynamic charge in the transition metal dichalcogenides. Phys. Rev. B 2017, 95, 201106. [Google Scholar] [CrossRef] [Green Version]
- Wickramaratne, D.; Zahid, F.; Lake, R.K. Electronic and thermoelectric properties of few-layer transition metal dichalcogenides. J. Chem. Phys. 2014, 140, 124710. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Wang, Z.; Li, Z.; Fu, Y.Q. Origin of Structural Transformation in Mono- and Bi-Layered Molybdenum Disulfide. Sci. Rep. 2016, 6, 26666. [Google Scholar] [CrossRef] [PubMed]
- Todorova, T.; Alexiev, V.; Prins, R.; Weber, T. Ab initio study of 2H-MoS2 using Hay and Wadt effective core pseudo-potentials for modelling the (100) surface structure. Phys. Chem. Chem. Phys. 2004, 6, 3023–3030. [Google Scholar] [CrossRef]
- Naumis, G.G. Electronic Properties of Two-Dimensional Materials. In Synthesis, Modeling, and Characterization of 2D Materials, and Their Heterostructures; Yang, E.-H., Datta, D., Ding, J., Hader, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 77–109. [Google Scholar]
- Ravichandran, L.; Banik, S. Investigation of the Failure of the MP2 Method to Describe the Out-of-Plane Bending Motions of Carbon–Carbon Double-Bonded Molecules: The Role of Atomic Orbitals. J. Phys. Chem. A 2021, 125, 9298–9317. [Google Scholar] [CrossRef] [PubMed]
- Ahlber, P. Structure and Dynamics of C9H9+ Ions: An Experimental and Theoretical Comparison. In Stable Carbocation Chemistry; Surya Prakash, G.K., Schleyer, P.V.R., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Smith, D.G.A.; Burns, L.A.; Patkowski, K.; Sherrill, C.D. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016, 7, 2197–2203. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. Revealing Factors Influencing the Fluorine-Centered Non-Covalent Interactions in Some Fluorine-substituted Molecular Complexes: Insights from First-Principles Studies. ChemPhysChem 2018, 19, 1486–1499. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Jin, B.-Y. Can an entirely negative fluorine in a molecule, viz. perfluorobenzene, interact attractively with the entirely negative site (s) on another molecule (s)? Like liking like! RSC Adv. 2016, 6, 19098–19110. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).