Gain Saturation Modified Quantum Noise Effect on Preparing a Continuous-Variable Entanglement
Abstract
:1. Introduction
2. System
3. Method
4. Results
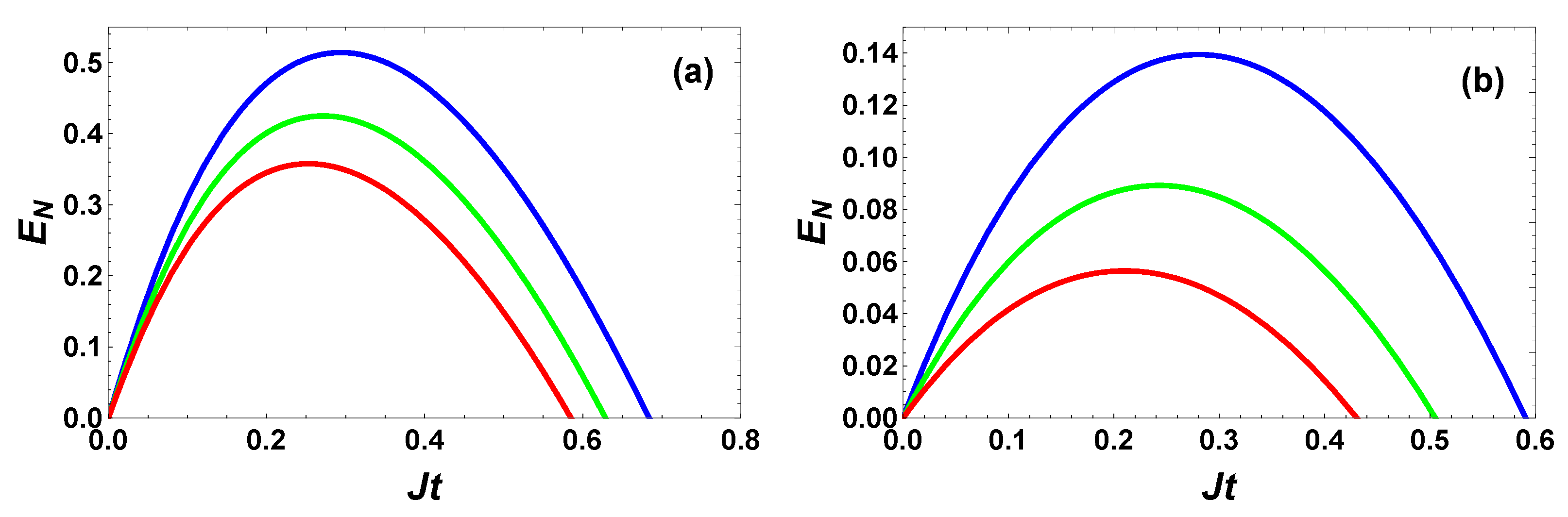
4.1. Entanglement Evolution without Gain Saturation
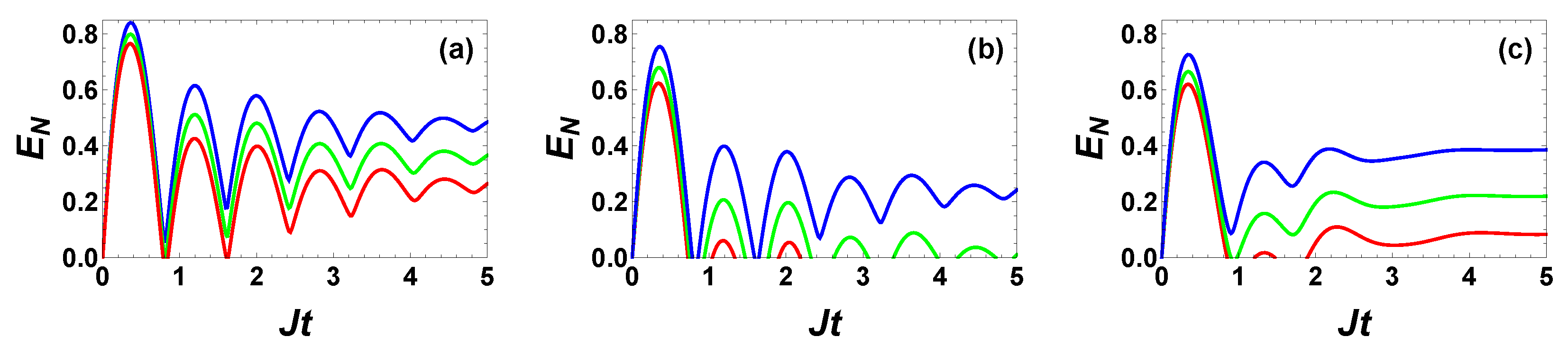
4.2. Special Role of Gain Saturation
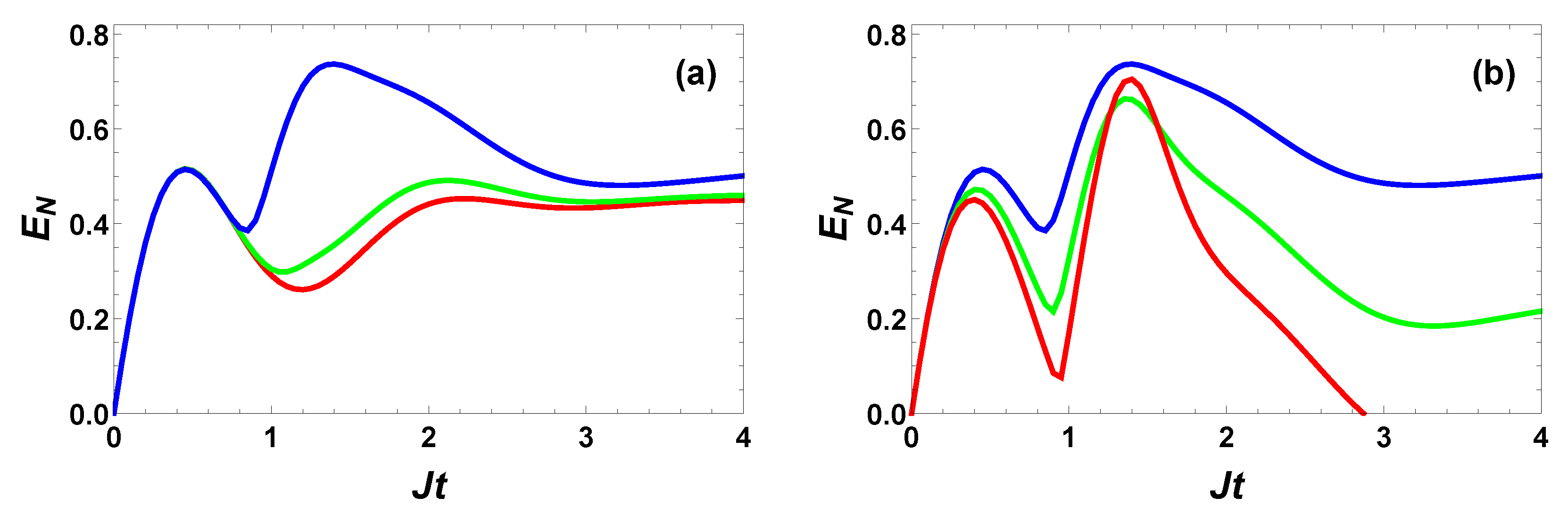
4.3. Entanglement Generation with Coherent Drive
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135. [Google Scholar] [CrossRef]
- Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Bergou, J.A. A general approach to physical realization of unambiguous quantum-state discrimination. Phys. Lett. A 2006, 356, 306–311. [Google Scholar] [CrossRef]
- Genovese, M.; Traina, P. Review on qudits production and their application to quantum communication and studies on local realism. Adv. Sci. Lett. 2008, 1, 153–160. [Google Scholar] [CrossRef]
- Piani, M.; Pitkanen, D.; Kaltenbaek, R.; Lütkenhaus, N. Linear-optics realization of channels for single-photon multimode qudits. Phys. Rev. A 2011, 84, 032304. [Google Scholar] [CrossRef]
- Tischler, N.; Rockstuhl, C.; Slowik, K. Quantum optical realization of arbitrary linear transformations allowing for loss and gain. Phys. Rev. X 2018, 8, 021017. [Google Scholar] [CrossRef]
- Singh, J.; Goyal, S.K. Implementation of discrete positive operator valued measures on linear optical systems using cosine-sine decomposition. Phys. Rev. Res. 2022, 4, 013007. [Google Scholar] [CrossRef]
- Gardiner, C.W.; Zoller, P. Quantum Noise; Springer: Berlin, Germany, 2010. [Google Scholar]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical PT-symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef]
- Klaiman, S.; Günther, U.; Moiseyev, N. Visualization of Branch Points in PT-Symmetric Waveguides. Phys. Rev. Lett. 2008, 101, 080402. [Google Scholar] [CrossRef]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of PT-Symmetry Breaking in Complex Optical Potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef] [Green Version]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, S.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Wen, J.; Jiang, X.; Jiang, L.; Xiao, M. Parity-time symmetry in optical microcavity systems. J. Phys. B 2018, 51, 222001. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- He, B.; Yang, L.; Zhang, Z.; Xiao, M. Cyclic permutation-time symmetric structure with coupled gain–loss microcavities. Phys. Rev. A 2015, 91, 033830. [Google Scholar] [CrossRef]
- Wu, R.B.; Zheng, Y.; Chen, Q.M.; Liu, Y.X. Synthesizing exceptional points with three resonators. Phys. Rev. A 2018, 98, 033817. [Google Scholar] [CrossRef]
- Jin, L. Flat band induced by the interplay of synthetic magnetic flux and non-Hermiticity. Phys. Rev. A 2019, 99, 033810. [Google Scholar] [CrossRef]
- Wang, P.; Jin, L.; Song, Z. Non-Hermitian phase transitionand eigenstate localization induced by asymmetric coupling. Phys. Rev. A 2019, 99, 062112. [Google Scholar] [CrossRef]
- Hassan, A.U.; Hodaei, H.; Miri, M.A.; Khajavikhan, M.; Christodoulides, D.N. Nonlinear reversal of the PT-symmetric phase transition in a system of coupled semiconductor microring resonators. Phys. Rev. A 2015, 92, 063807. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, X.; Hua, S.; Yang, C.; Wen, J.; Jiang, L.; Li, G.; Wang, G.; Xiao, M. Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat. Photonics 2018, 2014, 524–529. [Google Scholar] [CrossRef]
- Wen, J.; Jiang, X.; Zhang, M.; Jiang, L.; Hua, S.; Wu, H.; Yang, C.; Xiao, M. Modeling of On-Chip Optical Nonreciprocity with an Active Microcavity. Photonics 2015, 2, 498–508. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, C.; Wu, H.; Hua, S.; Chang, L.; Ding, Y.; Hua, Q.; Xiao, M. On-Chip Optical Nonreciprocity Using an Active Microcavity. Sci. Rep. 2016, 6, 38972. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Yang, L.; Jiang, X.; Xiao, M. Transmission Nonreciprocity in a Mutually Coupled Circulating Structure. Phys. Rev. Lett. 2018, 120, 203904. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Xie, Y.F.; He, B.; Lin, Q. Ultra-high optical nonreciprocity with a coupled triple-resonator structure. New J. Phys. 2021, 23, 023010. [Google Scholar] [CrossRef]
- Vashahri-Ghamsari, S.; He, B.; Xiao, M. Continuous-variable entanglement generation using a hybrid PT-symmetric system. Phys. Rev. A 2017, 96, 033806. [Google Scholar] [CrossRef]
- Vashahri-Ghamsari, S.; He, B.; Xiao, M. Effects of gain saturation on the quantum properties of light in a non-Hermitian gain–loss coupler. Phys. Rev. A 2019, 99, 023819. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Sudden Death of Entanglement. Science 2009, 323, 598–601. [Google Scholar] [CrossRef]
- Stahlhofen, A.A.; Nimtz, G. Evanescent modes are virtual photons. EPL (Europhys. Lett.) 2006, 76, 189. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Xiong, C.D.; He, B. Alternative perspective on photonic tunneling. Phys. Rev. A 2007, 75, 013813. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; He, B.; Xiao, M. Entangling two macroscopic mechanical resonators at high temperature. Phys. Rev. Appl. 2020, 13, 034030. [Google Scholar] [CrossRef]
- Becker, P.C.; Olsson, N.A.; Simpson, J.R. Erbium-Doped Amplifiers: Fundamentals and Technology; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Silfvast, W.T. Laser Fundamentals; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Agarwal, G. Quantum Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Weedbrook, C.; Pirandola, S.; Garcia-Patron, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 1621. [Google Scholar] [CrossRef]
- He, B.; Yan, S.B.; Wang, J.; Xiao, M. Quantum noise effects with Kerr-nonlinearity enhancement in coupled gain–loss waveguides. Phys. Rev. A 2015, 91, 053832. [Google Scholar] [CrossRef]
- Girardin, F.; Guekos, G.; Houbavlis, A. Gain recovery of bulk semiconductor optical amplifiers. IEEE Photonics Technol. Lett. 1998, 10, 784. [Google Scholar] [CrossRef]
- Hessler, T.P.; Selbmann, P.E.; Pleumeekers, J.L.; Dupertuis, M.A.; Deveaud, B.; Schreieck, R.; Emery, J.Y.; Dagens, B. Propagation effects on the ultrafast cross-gain modulation in semiconductor optical amplifiers. Opt. Commun. 2005, 248, 267. [Google Scholar] [CrossRef]
- Li, X.; Adams, M.J.; Alexandropoulos, D.; Lealman, I.F. Gain recovery in semiconductor optical amplifiers. Opt. Commun. 2008, 281, 3466. [Google Scholar] [CrossRef]
- Kominis, Y.; Kovanis, V.; Bountis, T. Controllable asymmetric phase-locked states of the fundamental active photonic dimer. Phys. Rev. A 2017, 96, 043836. [Google Scholar] [CrossRef]
- Xu, C.; Hayenga, W.E.; Hodaei, H.; Christodoulides, D.N.; Khajavikhan, M.; LiKamWa, P. Enhanced modulation characteristics in broken symmetric coupled microring lasers. Opt. Express 2020, 28, 19608. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vashahri-Ghamsari, S.; He, B. Gain Saturation Modified Quantum Noise Effect on Preparing a Continuous-Variable Entanglement. Photonics 2022, 9, 620. https://doi.org/10.3390/photonics9090620
Vashahri-Ghamsari S, He B. Gain Saturation Modified Quantum Noise Effect on Preparing a Continuous-Variable Entanglement. Photonics. 2022; 9(9):620. https://doi.org/10.3390/photonics9090620
Chicago/Turabian StyleVashahri-Ghamsari, Saeid, and Bing He. 2022. "Gain Saturation Modified Quantum Noise Effect on Preparing a Continuous-Variable Entanglement" Photonics 9, no. 9: 620. https://doi.org/10.3390/photonics9090620
APA StyleVashahri-Ghamsari, S., & He, B. (2022). Gain Saturation Modified Quantum Noise Effect on Preparing a Continuous-Variable Entanglement. Photonics, 9(9), 620. https://doi.org/10.3390/photonics9090620





