Orbital Angular Momentum of Superpositions of Optical Vortices Perturbed by a Sector Aperture

Abstract

In optical communications, it is desirable to know some quantities describing a light field, which are conserved on propagation or resistant to some distortions. Typically, optical vortex beams are characterized by their orbital angular momentum (OAM) and/or topological charge (TC). Here, we show analytically that the OAM of a single rotationally symmetric optical vortex is not affected by an arbitrary-shape aperture or by other amplitude perturbations. For a superposition of two or several optical vortices (with different TCs), we studied what happens to its OAM when it is distorted by a hard-edge sector aperture. We discovered several cases when such perturbation does not violate the OAM of the whole superposition. The first case is when the incident beam consists of two vortices of the same power. The second case is when the aperture half-angle equals π multiplied by an integer number and divided by the difference between the topological charges. For more than two incident beams, this angle equals π multiplied by an integer number and divided by the greatest common divisor of all possible differences between the topological charges. We also show that such a sector aperture also conserves the orthogonality between the complex amplitudes of the constituent vortex beams. For two incident vortex beams with real-valued radial envelopes of the complex amplitudes, the OAM is also conserved, when there is a ±π/2 phase delay between the beams. When two beams with the same power pass through a binary radial grating, their total OAM is also conserved. We hope that these findings could be useful for optical communications since they allow for the identification of incoming optical signals by their OAM by registering only part of the light field within a sector aperture, thus reducing the cost of the receiving devices.

1. Introduction

Structured light, with its arbitrarily tailoring structure and multiple degrees of freedom, has attracted wide attention [1,2]. One of the remarkable properties of some structured light beams is their self-healing, i.e., their ability to reconstruct themselves after passing through obstacles. Interest in this phenomenon has continued from the pioneering work [3] to the present day. Among recent works, we can mention, for instance, [4,5]. In [4], the field’s modal content was studied as a predictor or indicator of the self-healing ability of coherent structured light beams. It was shown that the fidelity between the obstructed and unobstructed beams’ modal spectra allows for the estimation of how likely it is that the beam will self-heal after an arbitrary obstacle. As an example, the superiority of the self-healing properties of Laguerre–Gaussian over Bessel–Gaussian beams was experimentally demonstrated. In [5], the self-healing of a partially obstructed beam was analyzed by representing it by two orthogonal field components—an attenuated copy of the unobstructed beam and a pure distortion field. It was discovered that the self-healing reaches a limit degree at the far field, and that certain relatively small phase obstructions may produce total damage on the beam. In [6], the possibility of vortex beam generation was studied by incomplete computer generated holograms, imitating digital micromirror devices with random dead pixels. It was observed that such distorted beams are less intense, but maintain their transverse intensity profiles, and that their topological charge is not affected.

When studying the resistance of various beams to perturbations, two opposite cases can be considered. The first one is when the obstacle is small compared to the beam width. Another case occurs, when only a small portion of the beam cross-section remains. The second case does not necessarily mean that the beam was distorted by a large obstacle. A similar problem occurs when there is a need to obtain the beam properties by analyzing only a small part of the beam cross-section. For instance, on propagation, beams with a larger TC diverge more strongly, and it becomes impractical to register the whole intensity ring. The authors of [7] address this problem of orbital angular momentum (OAM) modes demultiplexing by using only the partial aperture receiving scheme. As a partial case of the problem studied in [7], the demultiplexing of the OAM modes was studied earlier by using a partial angular receiving aperture [8] with the shape of a truncated sector (large-radius sector minus small-radius sector). Another work, studying how the sector aperture affects the beam is the paper by Volyar, A.V. et al. [9]. In [9], sector perturbations of vortex beams in the form of a hard-edged aperture were investigated both theoretically and experimentally. Transformations of the vortex spectra, OAM, and the informational entropy of the perturbed beam were measured. It was found that relatively small angular sector perturbations have almost no effect on the OAM, although the informational entropy rapidly increases due to the birth of new optical vortices caused by diffraction at the diaphragm edges. At small sector angles, the OAM rapidly decreases due to the uncertainty principle between the OAM and the sector angle. However, in [9], the incident beam was a single cylindrically symmetric optical vortex. To the best of our knowledge, it is unknown yet how the sector aperture affects the OAM of a superposition of optical vortices. There is a theoretical work that analytically investigated the diffraction of a light field by a sector aperture in the Fresnel zone [10]. However, the OAM was not studied.

In this paper, we studied what happens to the OAM when, instead of one cylindrically symmetric vortex, a superposition of such vortices is truncated by a sector aperture. We show that the normalized-to-power OAM is conserved in some specific cases. We note that at small sector angles, the uncertainty principle between the aperture angle and the OAM takes place [11,12]. In the current work, we did not consider this effect, and supposed that the sector angle was large enough so that both this angle and the OAM could be exactly determined.

The results of this work can find application in optical data transmission since they allow for the identification of incoming optical signals by their OAM by registering only part of the light field within a sector aperture.

2. Normalized Orbital Angular Momentum of a Rotationally Symmetric Vortex Beam Passed through an Arbitrary-Shape Aperture

Throughout the paper, we suppose that a paraxial light beam propagates along the optical axis z and that its transverse complex amplitude distribution is E(r, φ, z), with (r, φ) being the transverse polar coordinates. For a paraxial beam, transverse components of the OAM vector are usually neglected, and only the longitudinal component J_z can be notable. Orbital angular momentum J_z and the power W of a paraxial beam are given by the following formulae [13]:

$$J_z=\mathrm{Im}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{E}^{*}\left(r,\phi ,z\right)\frac{\partial }{\partial \phi }E\left(r,\phi ,z\right)rdrd\phi }},$$

(1)

$$W={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\left|E\left(r,\phi ,z\right)\right|}^{2}rdrd\phi }}.$$

(2)

We note that the left parts are constant, whereas the right parts depend on the propagation distance z. Actually, calculation for an arbitrary z yields the same values. This means that the power and the OAM should conserve their values on propagation in free space. This is actually always the case since if some function E(r, φ, z) is a solution of the Helmholtz equation ${\partial }^{2}E/\partial {\phi }^2+r^{-1}\partial E/\partial \phi +r^{-2}{\partial }^{2}E/\partial {\phi }^2+{\partial }^{2}E/\partial z^2=0$ (in the paraxial limits), then the functions E^* and ∂E/∂φ are also solutions of these equations and the dot product of two arbitrary solutions (Equations (1) and (2) are the dot products) conserves its value on propagation in free space. Only some element can distort the beam power and OAM, and here, in this work, we considered apertures as such elements.

If we represent the complex amplitude via the intensity I and phase Ψ:

$$E\left(r,\phi ,z\right)=\sqrt{I\left(r,\phi ,z\right)}\exp \left[i\mathsf{\Psi }\left(r,\phi ,z\right)\right],$$

(3)

then the OAM and the power can be rewritten as

$$J_z={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}I\left(r,\phi ,z\right)\frac{\partial }{\partial \phi }\mathsf{\Psi }\left(r,\phi ,z\right)rdrd\phi }},$$

(4)

$$W={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}I\left(r,\phi ,z\right)rdrd\phi }}.$$

(5)

Equations (4) and (5) indicate that if the angular derivative of the field phase is a constant that is independent of the polar coordinates r and φ, like is the case for the rotationally symmetric optical vortices, then any amplitude perturbation does not affect the normalized OAM, i.e., the OAM divided by the power. Indeed, if ∂Ψ/∂φ = n and if we perturb the amplitude so that the intensity distribution becomes I_pert(r, φ, z), instead of I(r, φ, z), the normalized OAM reads as

$$\frac{J_z}{W}=\left[{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{I}_{\mathrm{pert}}\left(r,\phi ,z\right)nrdrd\phi }}\right]·{\left[{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{I}_{\mathrm{pert}}\left(r,\phi ,z\right)rdrd\phi }}\right]}^{-1}=n.$$

(6)

In particular, when an optical vortex passes through an arbitrary-shape aperture, its transverse shape becomes distorted, and its topological charge also can change, but the normalized OAM is conserved.

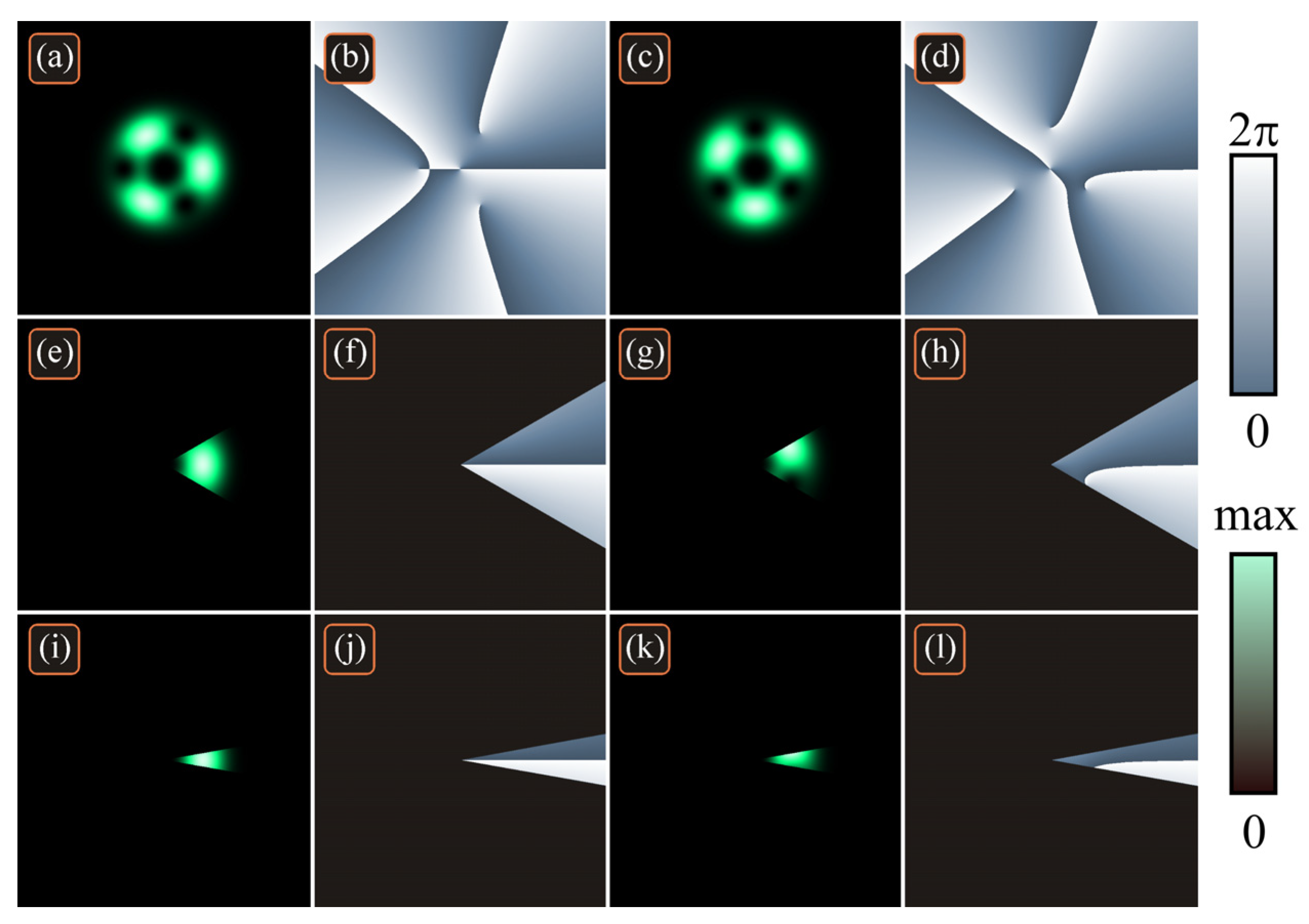
As an example, Figure 1 illustrates a Laguerre–Gaussian beam truncated or not truncated by an elliptic aperture. Intensity and phase distributions in the initial plane are shown in Figure 1a,b. Complex amplitude in the initial plane is given by

$$\begin{array}{c}E\left(r,\phi ,z=0\right)={\left(\frac{\sqrt{2}r}{w_0}\right)}^n{L}_p^n\left(\frac{2r^2}{w_0^2}\right)\exp \left(-\frac{r^2}{w_0^2}+in\phi \right)\\ \times \mathrm{rect}\left[{\left(r\cos \phi -x_0\right)}^2/a_x^2+{\left(r\sin \phi -y_0\right)}^2/a_y^2\right],\end{array}$$

(7)

where w₀ is the waist radius of the Gaussian beam, n is the vortex topological charge, p is the radial mode index, a_x and a_y are the horizontal and vertical radii of the elliptic aperture, (x₀, y₀) are Cartesian coordinates of the ellipse center, rect() is the aperture function [rect(ξ) = 1 at |ξ| ≤ 1 and rect(ξ) = 0 at |ξ| > 1], and $L_p^n$ is the associated Laguerre polynomial.

Figure 1c–j show the beam after propagation in space when it is not truncated (Figure 1c,d) in the waist plane or truncated (Figure 1e–j) by an elliptic aperture with three different locations. The following parameters were used: wavelength λ = 532 nm, waist radius w₀ = 0.5 mm, topological charge n = 5, radial index p = 2 (i.e., the beam contains three light rings), horizontal and vertical radii of the elliptic aperture a_x = 0.5 mm and a_y = 1 mm, position of the ellipse center y₀ = 0 and x₀ = 0.25 mm (vortex is within the aperture, Figure 1e,f), x₀ = 0.5 mm (vortex is on the aperture edge, Figure 1g,h), x₀ = 0.25 mm (vortex is outside the aperture, Figure 1i,j), propagation distance z = 2z₀ (z₀ = k$w_0^2$/2 is the Rayleigh distance), illustrated area |x|, |y| ≤ R with R = 3.3 mm (initial plane, Figure 1a,b), R = 5 mm (untruncated beam, Figure 1c,d), and R = 6.7 mm (untruncated beam, Figure 1c–j).

As seen in Figure 1, the aperture damages the beam significantly, its shape is distorted, and only an outer ring is recognizable. Instead of the single fifth-order vortex in the center, as in Figure 1d, truncation leads to a large amount of peripheral vortices, so that it is hard to compute the topological charge. Its computation by using M.V. Berry’s formula

$$TC=\frac{1}{2\pi }\underset{r\to \infty }{\lim }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\partial }{\partial \phi }\left[\arg E\left(r,\phi ,z\right)\right]d\phi }$$

(8)

over a ring with the radius 7.5 mm yields the following values: 3 (Figure 1e,f), 0 (Figure 1g,h), and 3 (Figure 1i,j), whereas we expected other values: 5 (since the entire vortex is within the aperture), 2 or 3 (since the vortex is on the aperture edge), and 0 (since the vortex is outside the edge). This mismatch is due to the numerous peripheral vortices, which are outside the computed distributions of the complex amplitude.

Nevertheless, the computed normalized OAM values J_z/W are almost the same for the untruncated and all truncated beams: 4.99 (Figure 1c,d), 4.87 (Figure 1e,f), 4.88 (Figure 1g,h), and 4.78 (Figure 1i,j). In the initial plane, the OAM values of these beams are even close to 5: 5.00 (for the beam from Figure 1c,d), and 4.99 (for the beams from Figure 1e–j).

3. Normalized Orbital Angular Momentum of a Superposition of Two Vortex Beams Passed through a Sector Aperture

If two cylindrically symmetric optical vortices pass through a sector aperture placed in the initial plane (z = 0), then the complex amplitude behind the aperture reads as

$$E\left(r,\phi ,0\right)=\left[C_1{E}_1\left(r,\phi ,0\right)+C_2{E}_2\left(r,\phi ,0\right)\right]\mathrm{rect}\left(\phi /\alpha \right),$$

(9)

where (r, φ) are the polar coordinates in the initial plane, C₁ and C₂ are the superposition coefficients, α is the half-angle of the sector aperture, and E₁(r,φ,0) and E₂(r,φ,0) are the complex amplitudes of two coaxial optical vortices with the different topological charges n and m, but the same energy:

$$E_1\left(r,\phi ,0\right)=W_1^{-1/2}{A}_1\left(r\right)\exp \left(in\phi \right),E_2\left(r,\phi ,0\right)=W_2^{-1/2}{A}_2\left(r\right)\exp \left(im\phi \right),$$

(10)

with W₁, W₂ being the factors making the energies of the beams E₁ and E₂ equal:

$$W_{1,2}=2\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|A_{1,2}\left(r\right)\right|}^{2}rdr}.$$

(11)

Now, we derive the normalized-to-power OAM of the beam (9).

Substituting the complex amplitude (9), we get the beam power (Appendix A):

$$W={\left|C_1\right|}^2\frac{\alpha }{\pi }+{\left|C_2\right|}^2\frac{\alpha }{\pi }+\frac{\left|C_1{C}_2\right|}{\sqrt{W_1{W}_2}}\frac{4}{n-m}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left|A_1\left(r\right)\right|\left|A_2\left(r\right)\right|\chi \left(r\right)rdr},$$

(12)

with

$$\chi \left(r\right)=\sin \left[\left(n-m\right)\alpha \right]\cos \left[\arg C_1-\arg C_2+\arg A_1\left(r\right)-\arg A_2\left(r\right)\right].$$

(13)

Substitution of the complex amplitude (9) into Equation (4) yields the OAM (Appendix A):

$$J_z=n{\left|C_1\right|}^2\frac{\alpha }{\pi }+m{\left|C_2\right|}^2\frac{\alpha }{\pi }+2\frac{n+m}{n-m}\frac{\left|C_1{C}_2\right|}{\sqrt{W_1{W}_2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left|A_1\left(r\right)\right|\left|A_2\left(r\right)\right|\chi \left(r\right)rdr}.$$

(14)

Dividing the OAM by the beam power, we get the normalized-to-power OAM of the beam (9):

$$\begin{array}{c}\frac{J_z}{W}=\left[n{\left|C_1\right|}^2\frac{\alpha }{\pi }+m{\left|C_2\right|}^2\frac{\alpha }{\pi }+2\frac{n+m}{n-m}\frac{\left|C_1{C}_2\right|}{\sqrt{W_1{W}_2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left|A_1\left(r\right)\right|\left|A_2\left(r\right)\right|\chi \left(r\right)rdr}\right]\\ \times {\left[{\left|C_1\right|}^2\frac{\alpha }{\pi }+{\left|C_2\right|}^2\frac{\alpha }{\pi }+\frac{4}{n-m}\frac{\left|C_1{C}_2\right|}{\sqrt{W_1{W}_2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left|A_1\left(r\right)\right|\left|A_2\left(r\right)\right|\chi \left(r\right)rdr}\right]}^{-1}.\end{array}$$

(15)

This expression looks huge, but it is drastically simplified in several cases.

4. Superposition of Two Vortex Beams of Equal Energy

If the two incident vortex beams have the same energies, i.e., the superposition coefficients are equal by the absolute value (|C₁| = |C₂|), then Equation (15) reduces to

$$\frac{J_z}{W}=\frac{n+m}{2}.$$

(16)

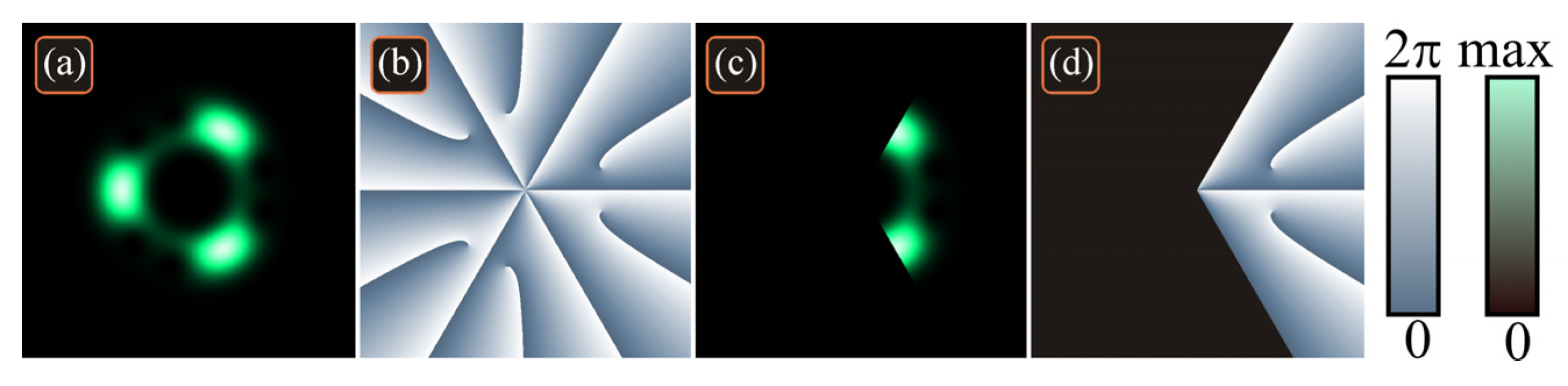
This expression is independent of the aperture half-angle α and, therefore, the aperture does not affect the normalized OAM. For example, Figure 2 shows truncated and not truncated superpositions of two single-ringed LG beams with the same energies, i.e., a light field with the following complex amplitude:

$$E\left(r,\phi ,z=0\right)=\frac{C_1}{\sqrt{W_1}}{\left(\frac{\sqrt{2}r}{w_0}\right)}^n\exp \left(-\frac{r^2}{w_0^2}+in\phi \right)+\frac{C_2}{\sqrt{W_2}}{\left(\frac{\sqrt{2}r}{w_0}\right)}^m\exp \left(-\frac{r^2}{w_0^2}+im\phi \right),$$

(17)

with |C₁| = |C₂| and

$$W_1=\frac{\pi w_0^2}{2}n!,W_2=\frac{\pi w_0^2}{2}m!.$$

(18)

The following parameters were used for computation: wavelength λ = 532 nm, waist radius w₀ = 0.5 mm, topological charges n = 5 and m = 2, half-angle of the sector aperture α = π (first row), α = π/6 (second row), and α = π/18 (third row), superposition coefficients C₁ = C₂ = 1 (first and second columns) and C₁ = 1, C₂ = i (third and fourth columns), and computation area |x|, |y| ≤ R (R = 2.5 mm).

Computation by the general expressions (1) and (2) yields the following values of the normalized OAM: 3.499 (Figure 2a–d), 3.493 (Figure 2e,f), 3.491 (Figure 2g,h), and 3.492 (Figure 2i–l), i.e., in all cases, J_z/W ≈ 3.5. These values are consistent with (16). Thus, we conclude that if the energies of both constituent beams are equal, then the sector aperture cannot violate the normalized-to-power OAM of such a superposition, regardless of the aperture angle.

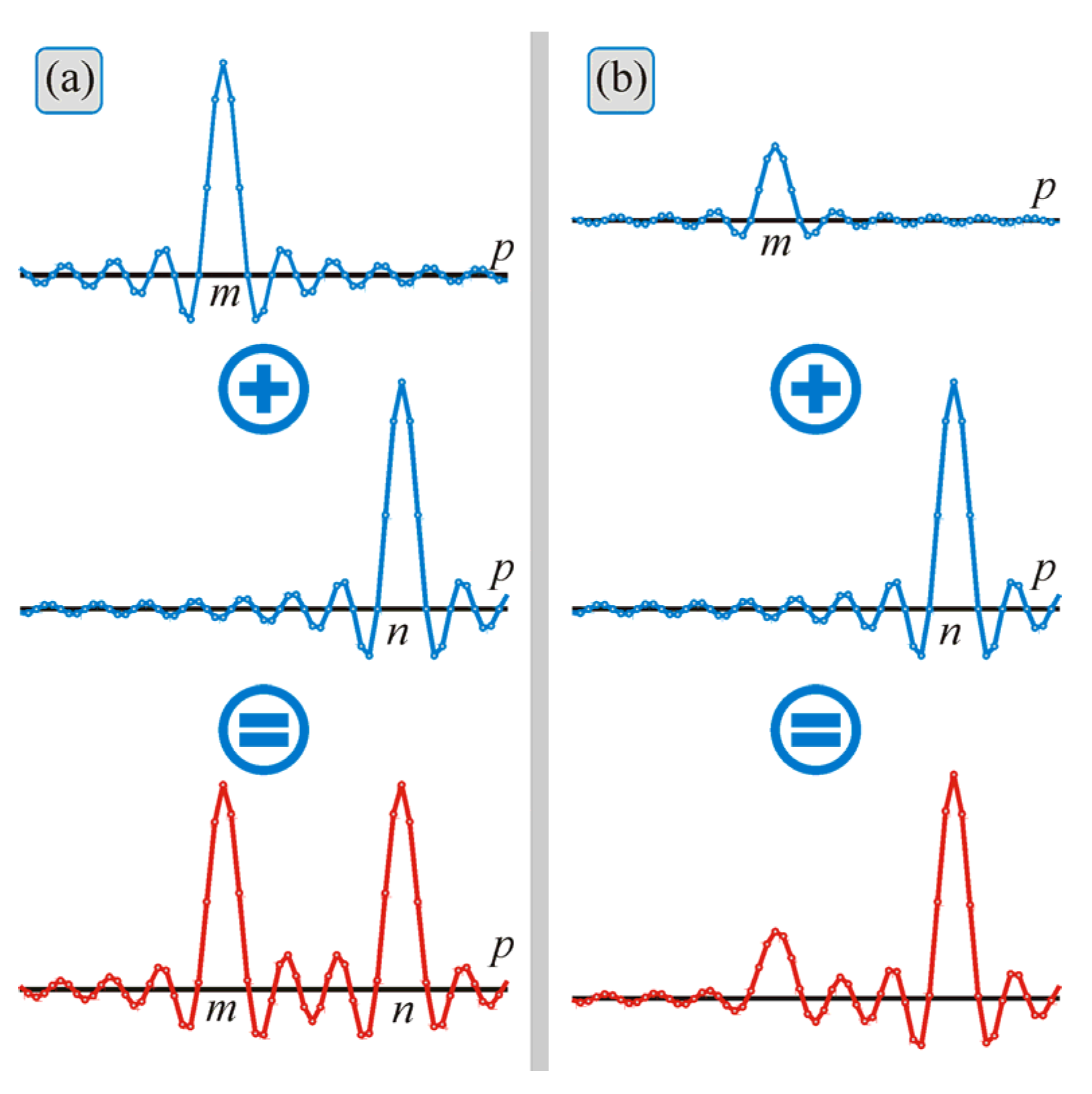
This phenomenon can be roughly described by decomposing the beams into the OAM spectrum. The transmittance function of the sector aperture can be decomposed into a symmetric series of angular harmonics:

$$\mathrm{rect}\left(\frac{\phi }{\alpha }\right)={\displaystyle \sum _{p=-\infty }^{\infty }\frac{\sin \alpha p}{\pi p}{e}^{ip\phi }}.$$

(19)

Therefore, when a single optical vortex passes through such an aperture, it becomes a superposition of an infinite number of optical vortices of all possible integer orders. If the aperture is illuminated by two optical vortex beams, their OAM spectra interact, and, if both beams have equal energies, the resulting OAM spectrum remains symmetric (Figure 3a). However, if the beam energies are different, the resulting OAM spectrum is, in general, asymmetric (Figure 3b). When the OAM spectrum is symmetric, the OAM of such a light field is equal to the average TC in such a spectrum [14], i.e., (m + n)/2.

5. Superposition of Two Vortex Beams with Different Energies

5.1. Conserving the OAM of Two Incident Beams by Choosing the Angle of the Sector Aperture

If two constituent vortex beams of the superposition (9) have different energies, i.e., if the superposition coefficients are not equal to the absolute values (|C₁| ≠ |C₂|), then the normalized OAM of the untruncated beam (i.e. α = π) reads as

$$\frac{J_z}{W}=\frac{n{\left|C_1\right|}^2+m{\left|C_2\right|}^2}{{\left|C_1\right|}^2+{\left|C_2\right|}^2}.$$

(20)

Generally, the sector aperture violates this normalized OAM of the beam (9). Here, we tried to determine some partial cases, when the OAM remains unchanged, despite the aperture. For instance, the OAM (16) can be conserved after the truncation, if the function χ(r) from Equation (13) is zero. This can be achieved by choosing the following half-angle α of the sector aperture:

$$\alpha =\frac{\pi p}{n-m},$$

(21)

with p being an arbitrary integer number.

For example, Figure 4 shows two untruncated and truncated superpositions of two single-ringed LG beams with different energies, i.e., the beam (17) with different values |C₁| and |C₂|. The following parameters were used for computation: wavelength λ = 532 nm, waist radius w₀ = 0.5 mm, topological charges n = 5 and m = 2, half-angle of the sector aperture α = π (Figure 4a–d), α = π/9 (Figure 4e–h), α = π/18 (Figure 4i–l), and α = π/3 (Figure 4m–p), superposition coefficients C₁ = 2^1/2, C₂ = 1 (Figure 4, 1st and 2nd columns) and C₂ = –1 (Figure 4, 3rd and 4th columns), and computation area |x|, |y| ≤ R (R = 2.5 mm). The dark spots in Figure 4g,k seem smaller than those in Figure 4c,o, but this is only because all the images are normalized to their maximal intensity.

According to Equation (20), the theoretical OAM value of the untruncated beam is J_z/W = (5·2 + 2·1)/(2 + 1) = 4. Computation yields the following values of the normalized OAM: 3.999 (Figure 4a–d), 3.801 (Figure 4e,f), 4.682 (Figure 4g,h), 3.764 (Figure 4i,j), 4.999 (Figure 4k,l), 3.998 (Figure 4m,n), and 3.992 (Figure 4o,p).

This indicates that the sector aperture changes the OAM (although not by large values). However, at α = π/3 (condition (21)), the OAM is conserved.

We note that the angle (21) conserves not only the normalized OAM, but conserves also the orthogonality of two vortices (10), i.e., the dot product of their complex amplitudes yields zero if the topological charges are different. Indeed, for an arbitrary angle of the sector aperture, the dot product is (Appendix A)

$$\langle C_1{E}_1\left(r,\phi ,0\right),C_2{E}_2\left(r,\phi ,0\right)\rangle =\frac{C_1^{*}{C}_2}{\sqrt{W_1{W}_2}}\frac{2}{m-n}{\displaystyle \underset{0}{\overset{\infty }{\int }}{A}_1^{*}\left(r\right)A_2\left(r\right)\sin \left[\left(m-n\right)\alpha \right]rdr}.$$

(22)

If the angle α is given by (21), the sine in the integrand is zero.

Thus, since the sector aperture conserves the orthogonality of the constituent beams, diffractive optical elements can be used to determine individual mode values of the distorted superimposed beam. Such techniques for modal decomposition of light fields are described, for instance, in [15,16].

5.2. Generalization for More Than Two Incident Beams

The rule (21) can be generalized for the case of more than two beams in the superposition. If the incident beam contains M beams with the topological charges m_s (s = 1, …, M), then, beyond the aperture, its complex amplitude is given by

$$E\left(r,\phi ,0\right)={\displaystyle \sum _{s=1}^M\frac{C_s}{\sqrt{W_s}}{A}_s\left(r\right)\exp \left(i{m}_s\phi \right)}·\mathrm{rect}\left(\phi /\alpha \right),$$

(23)

with C_s being the superposition coefficients and W_s being the normalizing factors:

$$W_s=2\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|A_s\left(r\right)\right|}^{2}rdr}.$$

(24)

Obtaining the normalized OAM yields an expression, similar to Equation (15), but even more bulky:

$$\begin{array}{c}\frac{J_z}{W}=\left[\frac{\alpha }{\pi }{\displaystyle \sum _{s=1}^M{m}_s{\left|C_s\right|}^2}+2{\displaystyle \sum _{s=2}^M{\displaystyle \sum _{q=1}^{s-1}\frac{\left|C_s\right|\left|C_q\right|}{\sqrt{W_s{W}_q}}\frac{m_q+m_s}{m_q-m_s}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left|A_s\left(r\right)\right|\left|A_q\left(r\right)\right|{\chi }_{sq}\left(r\right)rdr}}}\right]\\ \times {\left[\frac{\alpha }{\pi }{\displaystyle \sum _{s=1}^M{\left|C_s\right|}^2}+{\displaystyle \sum _{s=2}^M{\displaystyle \sum _{q=1}^{s-1}\frac{\left|C_s\right|\left|C_q\right|}{\sqrt{W_s{W}_q}}\frac{4}{m_q-m_s}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left|A_s\left(r\right)\right|\left|A_q\left(r\right)\right|{\chi }_{sq}\left(r\right)rdr}}}\right]}^{-1}\end{array}$$

(25)

with

$${\chi }_{sq}\left(r\right)=\sin \left[\left(m_q-m_s\right)\alpha \right]\cos \left[\arg C_q-\arg C_s+\arg A_q\left(r\right)-\arg A_s\left(r\right)\right].$$

(26)

Unfortunately, if all the beams have the same energy, i.e., |C₁| = |C₂| = … = |C_M|, Equation (25) does not lead to the average OAM, in contrast to the case of two beams (Equation (16)). However, we can make all the functions χ_sq(r) equal to zero. This happens, if, for any s, q = 1, …, M, the following condition holds

$$\alpha =\frac{\pi p_{qs}}{m_q-m_s},$$

(27)

with p_qs being arbitrary integer numbers.

Thus, for the OAM to be conserved, the aperture half-angle should be equal to an integer number of π divided by the greatest common divisor of all the possible differences between the topological charges.

To demonstrate this, Figure 5 shows an untruncated and truncated superposition of three single-ringed LG beams. The following parameters were used for computation: wavelength λ = 532 nm, waist radius of all three beams w₀ = 0.5 mm, topological charges m₁ = 6, m₂ = 9 and m₃ = 12, half-angle of the sector aperture α = π (Figure 5a,b) and α = π/3 (Figure 5c,d), superposition coefficients of the three beams C₁ = 3^1/2, C₂ = –2^1/2, and C₃ = 1, and computation area |x|, |y| ≤ R (R = 2.5 mm).

Similarly to Equation (20), the theoretical OAM value of the untruncated beam is J_z/W = (6·3 + 9·2 + 12·1)/(3 + 2 + 1) = 8. Computation yields the following values of the normalized OAM: 7.999 (Figure 5a,b), and 7.991 (Figure 5c,d). The greatest common divisor of all possible differences between the topological charges 6, 9, and 12, is 3, and, indeed, the OAM is conserved for the aperture with the half-angle π/3.

As in the case of two vortices, we note that, according to Equation (22), the half-angle (27) of the sector aperture also conserves the orthogonality of several optical vortices.

5.3. Distorting the Beam and Conserving the OAM on Propagation in Free Space

If the beam from Figure 5a,b passes through a sector aperture, its shape on propagation is distorted. Figure 6 demonstrates the intensity and phase distributions in the initial plane before the aperture, truncated distributions beyond two apertures with different angles, and after propagation over a Rayleigh distance from these apertures. The following parameters were used for computation: wavelength λ = 532 nm, waist radius of all three beams w₀ = 0.5 mm, topological charges m₁ = 6, m₂ = 9 and m₃ = 12, propagation distance z = z₀ = kw₀²/2, half-angle of the sector aperture α = π/6 (Figure 6c–f) and α = π/3 (Figure 6g–j), and superposition coefficients of the three beams C₁ = 3^1/2, C₂ = –2^1/2, C₃ = 1.

The theoretical value of the initial beam is J_z/W = 8. The OAM values computed by Equations (1) and (2) confirm that the aperture with α = π/6 distorts the OAM (J_z/W ≈ 6.18), whereas the aperture with α = π/3 leaves the OAM almost unchanged (J_z/W ≈ 7.87).

5.4. Orbital Angular Momentum of a Superposition of Two Beams with a ±π/2 Phase Delay

Another example of conserving OAM occurs when two beams have the ±π/2 phase delay (|arg C₁ – arg C₂| = π/2) and if the functions A₁(r) and A₂(r) are real-valued. This is the case, for example, for the Laguerre–Gaussian beams [17] and Bessel–Gaussian beams [18], but not for the hypergeometric-Gaussian beams [19,20], since their Gaussian envelope is real, but the confluent hypergeometric function [21] is complex.

For instance, it can be seen in Figure 4 that a small-angle sector aperture can change the normalized OAM significantly (e.g., Figure 4i–l). Figure 7 depicts similar two superpositions of two LG beams, but with ±π/2 phase delays between them. The following parameters were used for computation: wavelength λ = 532 nm, waist radius w₀ = 0.5 mm, topological charges n = 5 and m = 2, half-angle of the aperture α = π (Figure 7a–d), α = π/9 (Figure 7e–h), α = π/18 (Figure 7i–l), superposition coefficients C₁ = 2^1/2, C₂ = i (Figure 7, 1st and 2nd columns) and C₂ = –i (Figure 7, 3rd and 4th columns), and computation area |x|, |y| ≤ R (R = 2.5 mm).

It can be seen that the untruncated beam (Figure 7a,c) has the same intensity distribution as in Figure 4a,c, but rotated. However, in contrast to Figure 4e–l, the theory predicts that the sector aperture should not violate the normalized OAM, which should remain equal to four. Computation by general expressions (1) and (2) yields the following values of the normalized OAM: 3.999 (Figure 7a–d), 3.992 (Figure 7e–h), and 3.982 (Figure 7i–l), i.e., all values are close to 4. This indicates that ±π/2 phase delay allows the normalized OAM to be conserved.

6. Normalized Orbital Angular Momentum of a Superposition of Two Vortex Beams Passed through a Binary Radial Grating

Radial grating is a symmetric optical element, with its transmittance function being periodic with the azimuthal polar coordinate. For example, amplitude sinusoidal radial gratings can be used for measuring the topological charge of vortex beams [22]. It was also recently proposed for use in generating sub-diffracted Bessel beams [23]. A phase binary radial grating has the following transmittance function:

$$T\left(r,\phi \right)=\mathrm{sgn}\cos \left(p\phi \right)\mathrm{rect}\left(r/R\right),$$

(28)

with R being the grating radius, and p being an integer number defining the azimuthal period. Such a grating can be considered as composed of sector apertures and, therefore, the above theory can be applied for analyzing the normalized OAM of beams passing through the binary radial grating.

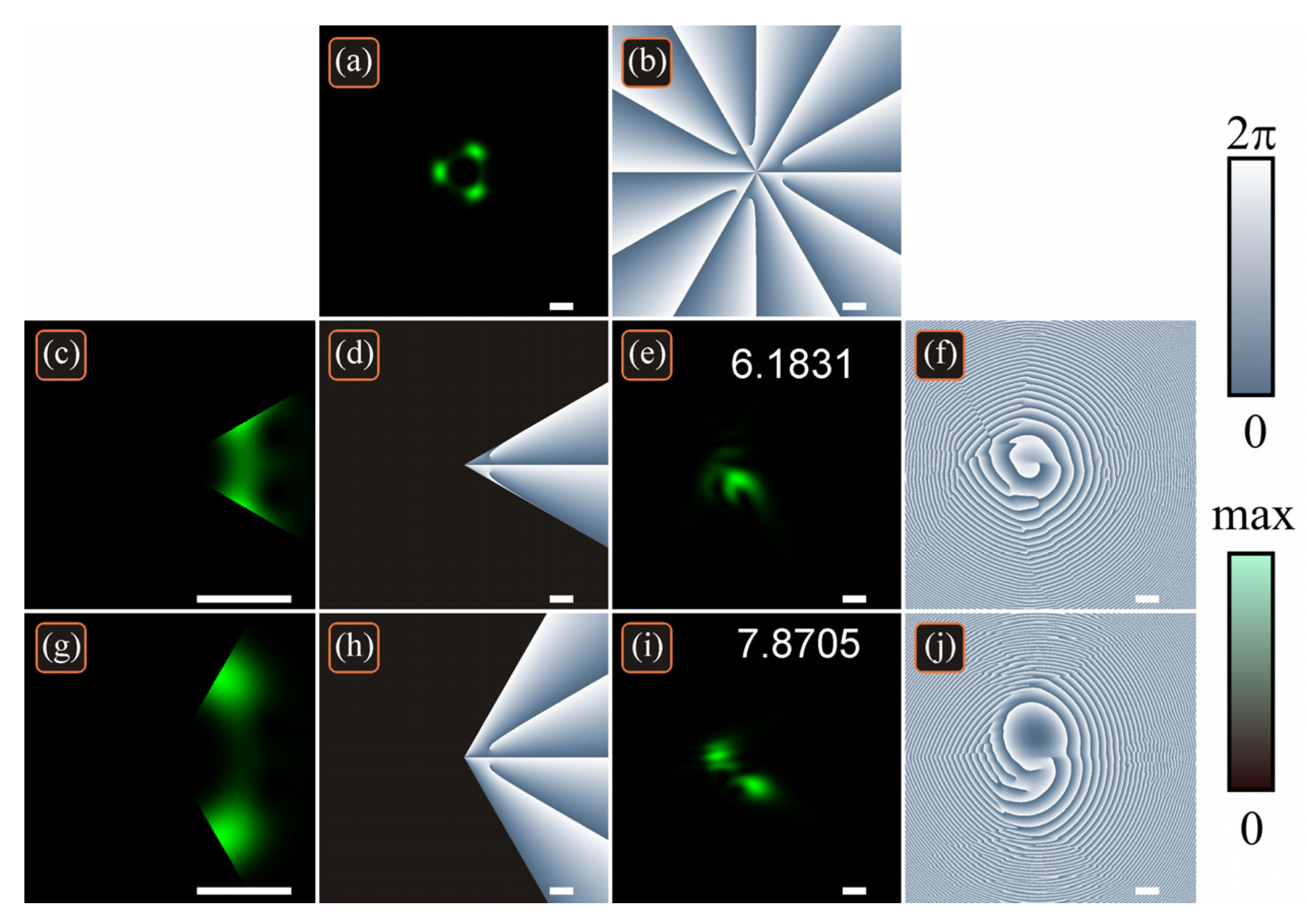
According to (16), if two coaxial vortex beams have the same energy, then, after passing the binary radial grating, its OAM should be conserved. Figure 8 illustrates the intensity and phase of the beam from Figure 2a,b passing through two phase binary radial gratings (with p = 8 and with p = 17). Computation yields the following values of the normalized OAM: 3.487 (Figure 8a,b), and 3.472 (Figure 8a,c), i.e., the values are close to theoretical 3.5.

7. Conclusions

Today, structured light is a hot topic, and significant progress has been achieved in this field, allowing for the tailoring of optical patterns in all their degrees of freedom, from conventional 2D transverse patterns to exotic forms of 3D, 4D, and even higher-dimensional modes of light [24], including vector vortex light fields [25]. Potential applications of such fields include laser machining and fabrication, complex tweezers and multi-particle manipulation, topological photonics, high-capacity encoding and communication, high-dimensional quantum information processing, and others [24]. Using structured light with multiple degrees of freedom will allow for spatial multiplexing to achieve in the future ultrahigh capacity, low error-rate optical communications. For instance, it is demonstrated in [26] that the modal basis of ray-wave geometric beams outperforms the OAM and LG modal basis, in terms of approaching the capacity limit of a free-space optical communication channel.

To use structured light in optical data transmission, it is needed to study how all such structured light beams resist obstacles, e.g., apertures, and whether or not the incoming optical signal can be identified by registering only a portion of the transverse intensity.

Here, in this work, we limited our analysis by a simple case of one or several circularly symmetric scalar vortex beams. We found that when a single rotationally symmetric optical vortex beam is distorted by passing through an arbitrary-shape aperture or by other amplitude perturbations, its normalized OAM remains unaffected and conserves its value. If, however, two or more coaxial optical vortex beams pass through a sector aperture, the normalized OAM of the whole superposition is, in general, changed. However, several cases exist where this OAM is conserved. We found that this happens when both beams have the same power. If the beams are of different power, the OAM is also conserved when the aperture half-angle has a specific value, namely, it is an integer number of π divided by the difference between the topological charges. For more than two incident beams, this angle equals an integer number of π divided by the greatest common divisor of all possible differences between the topological charges. If the radial envelopes of the complex amplitudes of two vortex beams are real-valued, then the OAM is conserved, when there is a ±π/2 phase delay between the beams. When two vortex beams with the same power pass through a binary radial grating, their total OAM is also conserved.

The results of this work can find application in optical data transmission since they allow for the identification of incoming optical signals by their OAM by registering only part of the light field within a sector aperture, thus reducing the cost of the receiving devices. Future research on this topic can study what happens with other quantities that describe the optical vortices and topological charge after passing through a sector aperture.