1. Introduction
Solitons, as localized structures formed in nonlinear systems, are studied in numerous fields such as plasma physics, fluids, Bose–Einstein condensates, and optics [
1,
2,
3,
4]. In the context of optics, the existence of solitons in optical fibers was first theoretically predicted in [
5] and experimentally demonstrated in [
6]. The formation of optical solitons could be interpreted as a result of an interplay between dispersion and nonlinear Kerr effects in conservative systems. It was found that optical solitons can also exist in dissipative systems, where solitons arise from the composite balances between dispersion and nonlinearity as well as gain and loss. Solitons in dissipative systems exhibit distinct dynamics due to the dissipative effects. As typical dissipative systems, mode-locked fiber lasers have been regarded as ideal test beds for the exploration of diverse soliton phenomena such as vector solitons [
7,
8], noise-like pulses [
9,
10], and soliton pulsations [
11,
12]. When the pump power is increased above a given level, mode-locked fiber lasers are prone to emit multiple solitons with equal soliton parameters due to the peak-power-limiting effect [
13]. In addition to its potential applications in all-optical information storage and high-level modulation formats for optical communications [
14,
15], the multi-pulsing operation caused by the peak-power-limiting effect facilitates the exploration of soliton interactions. In mode-locked fiber lasers, soliton interactions could be classified into short- and long-range interactions depending on the soliton separation. The short-range interaction corresponds to direct soliton interaction, which originates from pulse tail overlapping [
16]. The long-range interactions are mediated by various mechanisms such as continuous wave (CW) components, dispersive wave mediation [
17], gain depletion and recovery [
18,
19], as well as fiber acoustic effects [
20]. In addition, Andrianov et al. reported a new mechanism of long-range pulse-to-pulse interaction in a mode-locked fiber laser with an unbalanced Mach–Zehnder interferometer, in which elastic soliton crystals were produced [
21,
22]. Different soliton interaction mechanisms could coexist in the fiber laser cavities. As one of the most fascinating soliton interactions, soliton collisions occur between two or more solitons with different group velocities; these have been extensively investigated in early works. However, the transient dynamics of soliton collisions in ultrafast fiber lasers cannot be experimentally retrieved by conventional instruments, such as oscilloscopes, optical spectral analyzers (OSAs), and autocorrelators, due to their limited scan speed. In recent years, the dispersive Fourier transform (DFT) technique has been developed to overcome the scan-speed limitation, which permits single-shot spectral measurements of ultrashort optical pulses [
23]. By virtue of this technique, diverse soliton dynamics have been observed in fiber lasers, such as soliton buildup [
24], soliton explosions [
25], pulsating solitons [
26], and evolving soliton molecules [
27,
28,
29]. Moreover, the field autocorrelation traces could be obtained by Fourier transform of the corresponding shot-to-shot DFT spectra to probe the internal evolutions of the soliton molecule and soliton triplet [
28,
29]. The powerful DFT technique has also been applied to revealing real-time dynamics of soliton collisions [
30,
31,
32,
33].
In early studies, collisions between a soliton molecule and a soliton singlet were investigated in stretched-pulse fiber lasers [
34,
35,
36,
37]. In some cases, “elastic” collisions were observed using an oscilloscope, and it was numerically demonstrated that the difference in velocities between the soliton molecule and the singlet is the same before and after collision [
34,
35]. Other collision scenarios, such as the soliton fusion, the merging of all colliding solitons into a three-soliton bound state, and recoil of the soliton molecule, were also predicted from the simulations [
35]. In these works, the transient collision dynamics were not revealed experimentally due to the absence of real-time measurement techniques. Very recently, He et al. reported an experimental observation of collisions between soliton molecules in different states and a single soliton in a mode-locked fiber laser using the DFT technique [
38]. By adjusting the pump power, several possible collision outcomes were obtained and the collision processes were analyzed. However, the collision dynamics have not been fully explored. The influence of other cavity parameters (e.g., cavity linear birefringence) on the collision outcomes has not been observed. A variety of other collision scenarios remain to be investigated.
In this paper, we experimentally investigate the real-time dynamics of collisions between a soliton molecule and a soliton singlet in an all-anomalous-dispersion ultrafast fiber laser by virtue of the DFT technique. In the “quasi-elastic” collision regime, a soliton molecule collides repeatedly with a soliton singlet in the cavity. It is found that the soliton molecule keeps its initial state after the collision and the group-velocity difference between the soliton molecule and the singlet is changed. The collision occurs through the bond exchange between the solitons forming the soliton molecule. By slightly tuning the intra-cavity polarization controller, other outcomes of the collision, including the annihilation of a soliton in the soliton molecule as well as the formation of a stable unequally spaced soliton triplet, are also found, and their collision dynamic processes are unveiled. In addition, the collision mechanisms are discussed.
3. Results and Discussion
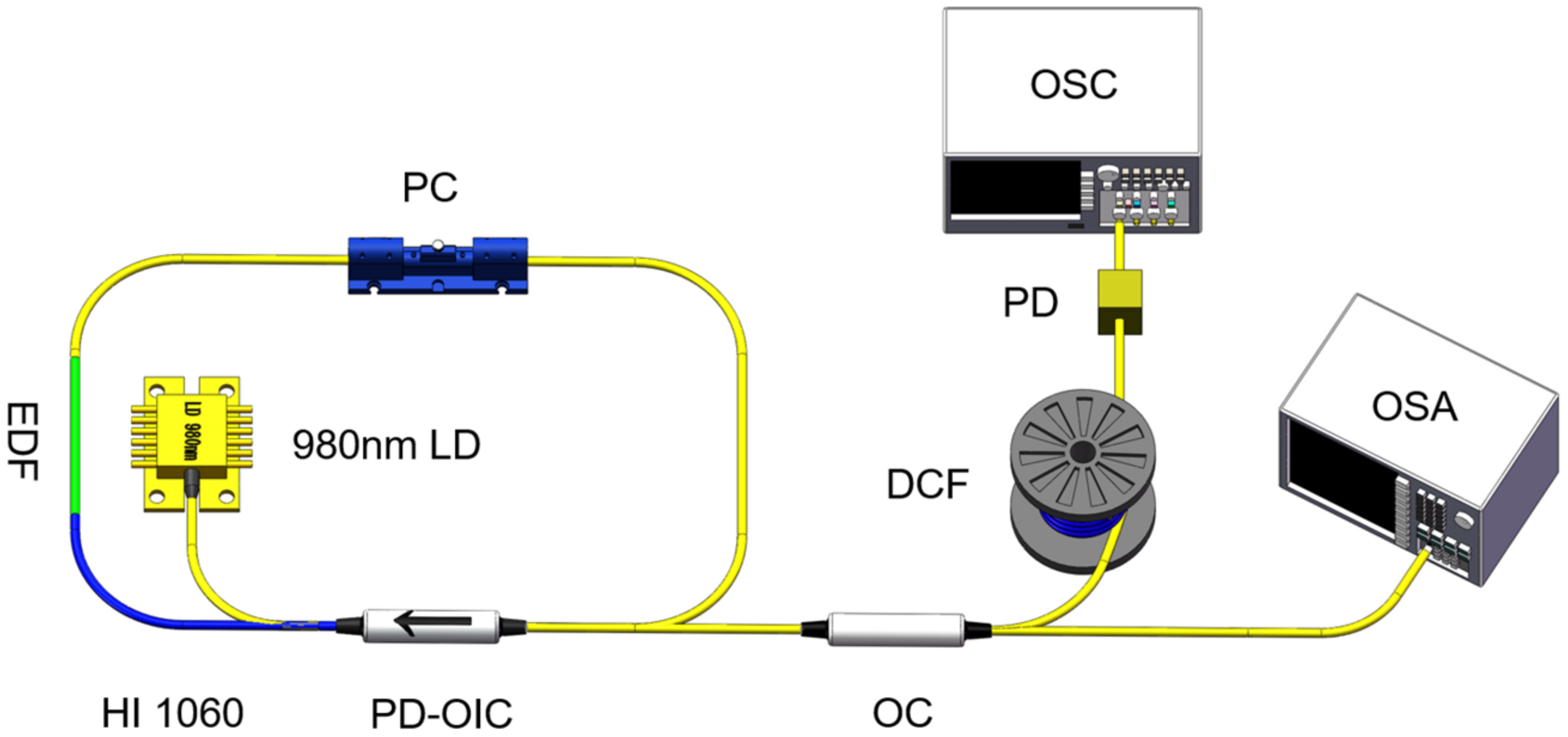
At a pump power of 68 mW, the single-soliton state is obtained by properly tuning the intra-cavity PC.
Figure 2a shows an oscilloscope trace of the mode-locked pulse train. The time interval between adjacent pulses is ~69.7 ns, matching well with the 14 m cavity length. The optical spectrum (black curve) recorded with the OSA is illustrated in
Figure 2b, which is centered at 1571.3 nm with a 3 dB spectral bandwidth of 4.8 nm. The Kelly sidebands in the optical spectrum, corresponding to the dispersive waves [
17], imply that the fiber laser operates in the conventional soliton regime. As presented in the RF spectrum of
Figure 2c, the repetition rate of output pulses is about 14.34 MHz. The signal-to-noise ratio (SNR) is ~60 dB, indicating good mode-locking stability. A measured autocorrelation (AC) trace of output pulses is displayed in the inset of
Figure 2c. The full width at half maximum (FWHM) of the autocorrelation is 955 fs, corresponding to a 620 fs pulse duration fitted by a Sech
2 profile. The time–bandwidth product of the pulses is 0.37, indicating that the pulses are slightly chirped.
Figure 2d maps the single-shot spectra of output pulses measured by the DFT technique, verifying that the laser operates in a stationary single-soliton state. As shown in
Figure 2b, the average (red dashed curve) of the shot-to-shot spectra agrees well with the OSA-measured optical spectrum, which demonstrates the accuracy of our DFT measurement.
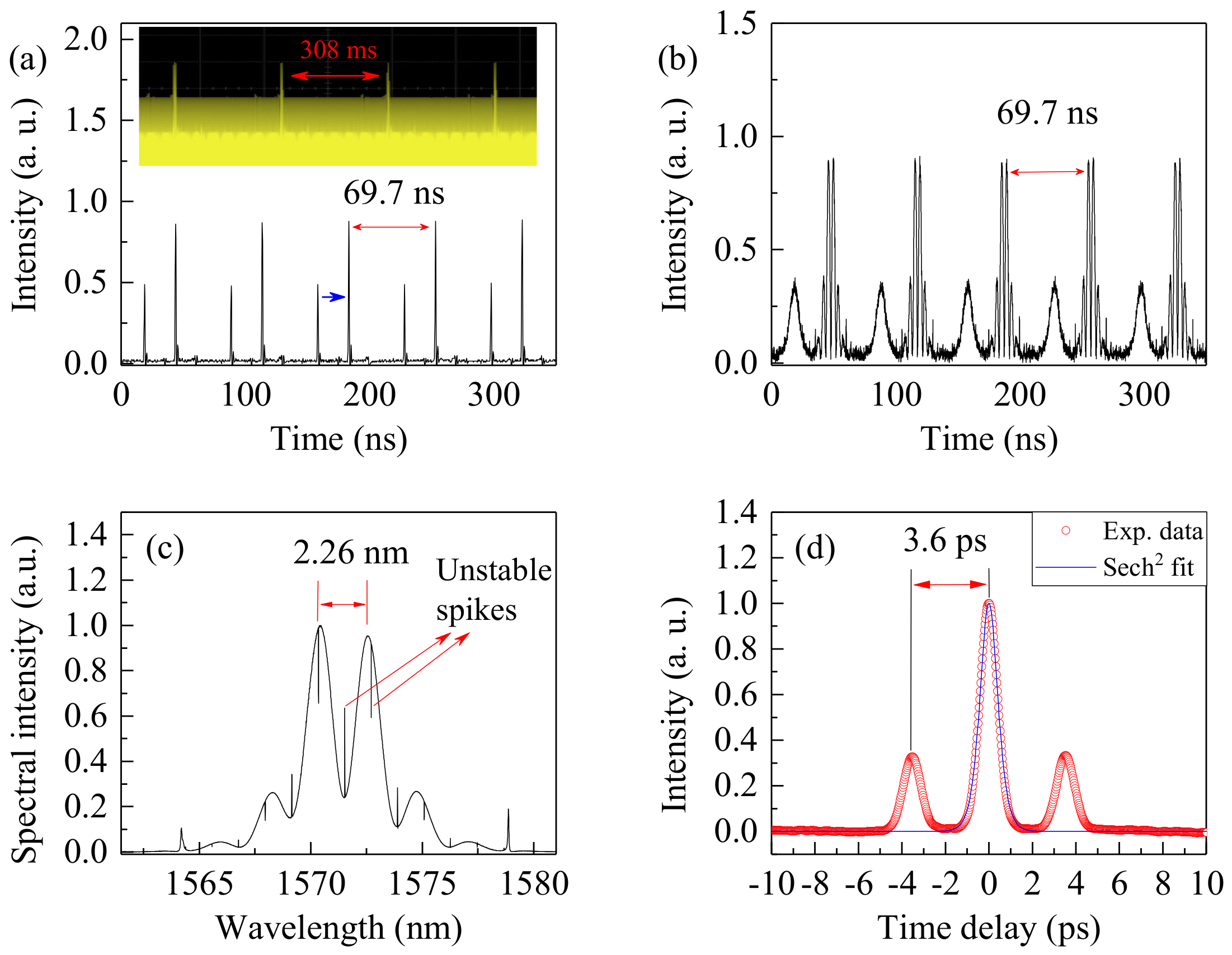
By increasing the pump power to 89 mW, the laser operates in a regime where a soliton molecule and a soliton singlet coexist in the laser cavity with different group velocities. The output pulse train is presented in
Figure 3a, featuring two peaks per cavity roundtrip. The higher peak is twice the other one in intensity. The higher peak represents a soliton molecule while the other corresponds to a soliton singlet. We use the soliton molecule as the trigger signal for the measurements. Therefore, it has a fixed position in the oscilloscope traces. The single soliton ceaselessly moves with respect to the soliton molecule from the left side to the right side on the oscilloscope (the blue arrow in
Figure 3a represents the moving direction), which means that the soliton molecule moves faster than the single soliton in the cavity. The inset of
Figure 3a displays the pulse train with a larger time scale, indicating that the interval between adjacent collision events is about 308 ms. Considering the 14 m cavity length, the group-velocity difference between the doublet and the singlet is about 45.5 m/s, which is much smaller than the soliton group velocity.
Figure 3b shows the corresponding pulse train after the DFT. It consists of soliton-molecule modulated spectra and soliton-singlet spectra, which demonstrates the coexistence of a soliton molecule and a soliton singlet in the laser cavity. The OSA-measured optical spectrum is shown in
Figure 3c, which originates from the incoherent superposition of a soliton-molecule spectrum and a soliton-singlet spectrum. The soliton-molecule spectrum has a spectral modulation period of ~2.26 nm. In addition, the unstable spikes in the OSA-measured spectrum could be attributed to interference fringes induced by transient collisions. It should be mentioned that the soliton-molecule spectrum exhibits an asymmetric feature, which causes a slightly modified gravity center for its spectral intensity. This could provide a group-velocity difference between the soliton molecule and the soliton singlet due to the nonzero cavity dispersion [
35].
Figure 3d exhibits the autocorrelation trace of output pulses, in which three peaks have an intensity ratio of 1:3:1. This implies that the soliton molecule is made of two identical solitons, which have the same pulse duration and intensity as the third moving single soliton. The pulse separation between the two solitons in the soliton molecule is ~3.6 ps, which agrees well with its 2.26 nm spectral modulation period, as shown in
Figure 3c.
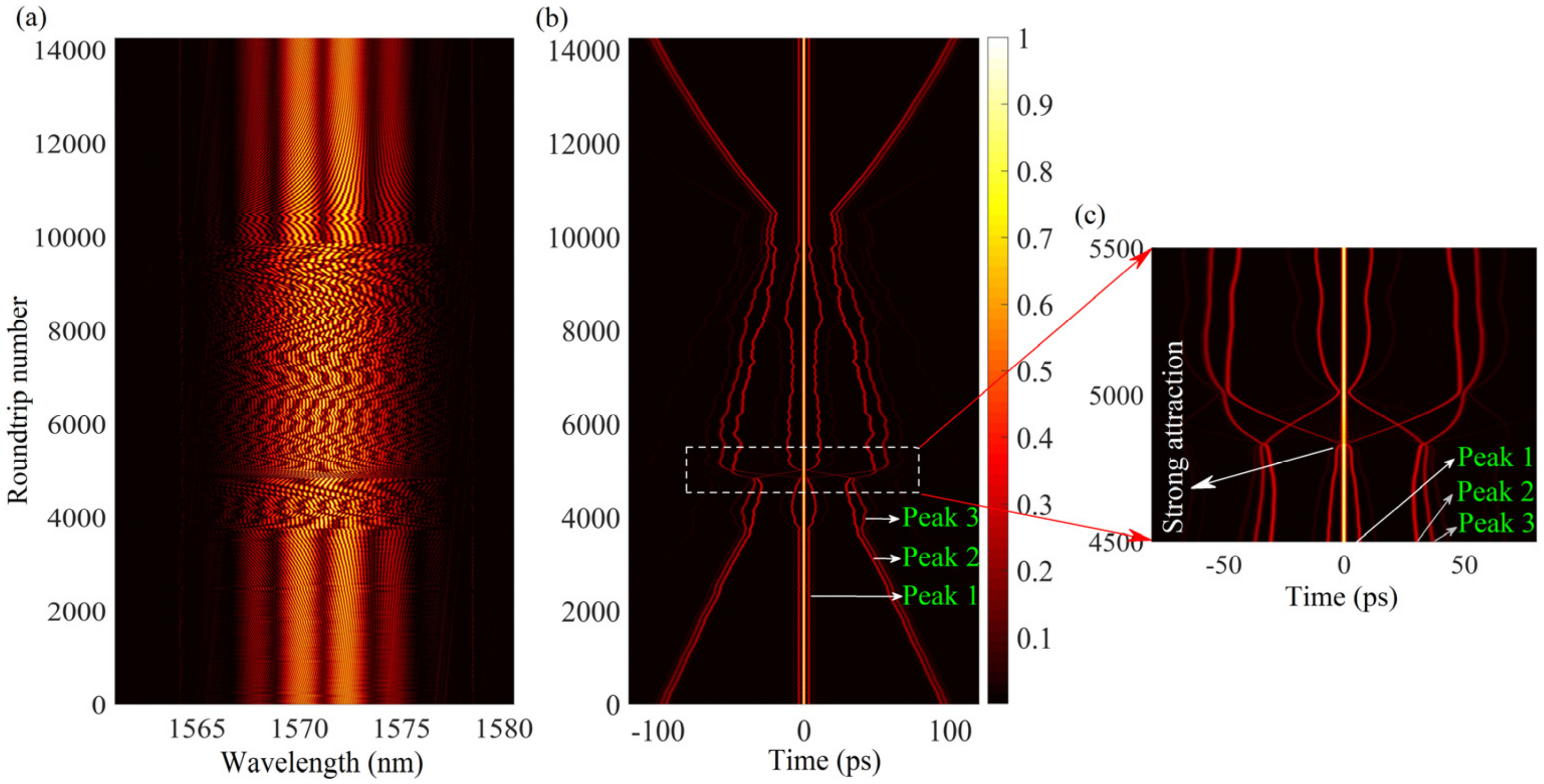
In order to reveal the transient dynamics of a single collision event, we measure the shot-to-shot spectral interferograms over 14,000 roundtrips, as shown in
Figure 4a. The recorded interferograms exhibit three superimposed fringe periodicities, confirming that the collision is a three-soliton coherent interaction. The interference-fringe periodicities in these modulated spectra are determined by the soliton separations [
29]. The calculated shot-to-shot field autocorrelation traces are presented in
Figure 4b, which exhibits the soliton-separation evolution.
Figure 4c depicts the zoom-in plot of the dashed rectangle in
Figure 4b. Seven peaks are symmetrically located on each field autocorrelation trace. As shown in
Figure 4b, we assign the numbers 1, 2, and 3 to the peaks on the right side of the field autocorrelation trace. The position changes of these peaks represent the soliton-separation evolution during the collision process. To better understand the collision dynamics, the separations among the interacting solitons are retrieved. As an example,
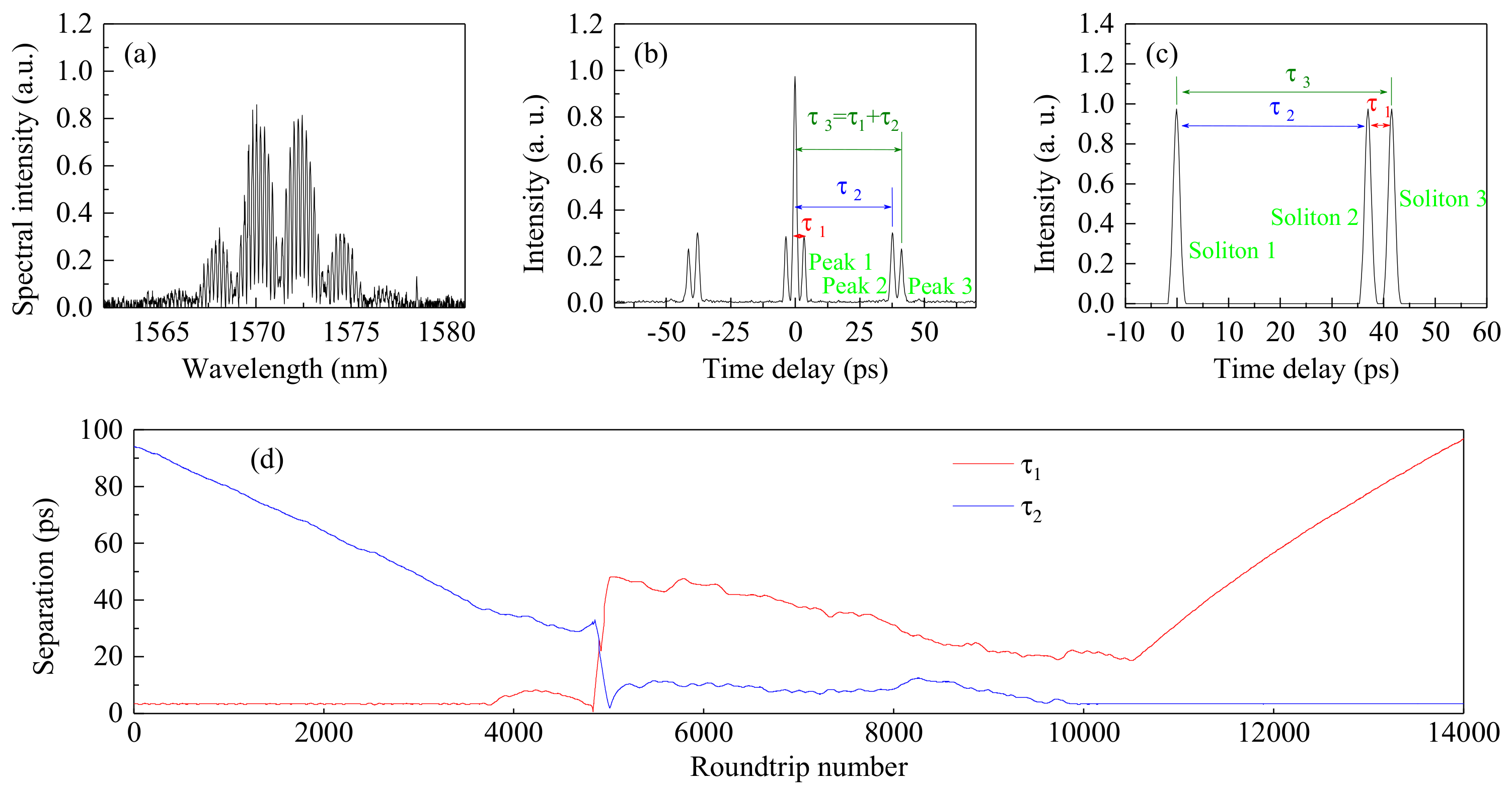
Figure 5a depicts the single-shot spectrum at the roundtrip of 3600, and the calculated field autocorrelation trace is exhibited in
Figure 5b.
Figure 5c displays the corresponding actual soliton distribution deduced by the field autocorrelation trace, where soliton 1 represents the soliton singlet while soliton 2 and soliton 3 constitute the soliton molecule. It can be seen that the separation between the central peak and peak 1 in
Figure 5b is equal to the temporal interval between soliton 2 and soliton 3 in
Figure 5c, which is denoted by τ
1. The separation between the central peak and peak 2 stands for the separation between soliton 1 and soliton 2, labeled as τ
2, and the separation between the central peak and peak 3 corresponds to the separation between soliton 1 and soliton 3, denoted by τ
3.
Figure 5d shows the retrieved soliton-separation evolution of a single collision event. The collision event can be divided into three stages, i.e., approaching, colliding, and being far away.
During the approaching stage from the first roundtrip to the ~3650th roundtrip, the separation between the soliton molecule and the singlet decreases at a constant speed, which can be calculated to be ~15.7 fs/roundtrip from the data in
Figure 5d. When the separation is about 40 ps at the roundtrip of 3650, the approaching speed slows down and the soliton separation in the molecule starts to vary. In the colliding stage from the ~3650th roundtrip to the ~10,800th roundtrip, the shot-to-shot spectral interferograms in
Figure 4a change dramatically, which indicates intensive three-soliton interaction. The interacting solitons experience complicated repulsions and attractions, as shown in
Figure 4b.
Figure 4c depicts that the bond between soliton 2 and soliton 3 is broken and the new bond between soliton 1 and soliton 2 is formed, i.e., the bond exchange between the colliding solitons. The results demonstrate that the soliton singlet does not pass through the soliton molecule but rather bonds with the leading pulse of the soliton molecule to form a new molecule, and the tailing pulse of the initial soliton molecule remains. In addition, a strong attraction between the solitons in the initial soliton molecule is induced by the collision, as shown in
Figure 4c. Due to the strong attraction, the separation between soliton 2 and soliton 3 decreases to a minimum, which leads to pulse tail overlapping. Subsequently, a strong repulsion between soliton 2 and soliton 3 is aroused to break the initial soliton-molecule bond. The repulsion here might be attributed to dissipative factors (e.g., peak-power clamping) in the laser cavity, which prevents two solitons from merging into one with a higher peak power [
40]. After the bond exchange, the newly generated soliton molecule ultimately stabilizes to a two-soliton bound state identical to the initial one. In the being-far-away stage from the ~10,800th roundtrip to the 14,000th roundtrip in
Figure 4b, the new soliton singlet possesses a different group velocity relative to the soliton molecule, leading to endlessly repeated collisions in the laser cavity. The separation between the soliton molecule and the soliton singlet increases at a speed of ~22.1 fs/roundtrip in the being-far-away stage, which is slightly greater than that before the collision. Numerous repeated measurements show that different collision events in this regime have similar dynamic processes.
It should be emphasized that, in this collision scenario, the group-velocity difference between the molecule and the singlet is slightly changed after the collision though the molecule keeps its initial state. Therefore, we refer to this case as a “quasi-elastic” collision. We speculate that the change in the relative speed between the molecule and the singlet mainly originates from the soliton interaction mediated by the dispersive waves. It is known that the dispersive waves could induce a long-range repulsive force on interacting solitons in mode-locked fiber lasers [
40]. The weak repulsive force between the molecule and the singlet could make the approaching speed a little slower and the being-far-away speed a little faster, leading to the relative-speed change. Other origins of soliton interactions, such as pulse tail overlapping, CW component, gain depletion and recovery, as well as acoustic effects, could be neglected in the approaching and being-far-away stages, and the reasons are presented as follows. The direct soliton interaction mediated by pulse tail overlapping only occurs for close solitons, typically separated by a few picoseconds, while the separation between the molecule and the singlet is dozens of picoseconds in the two stages mentioned above. In addition, there is no CW component in the measured optical spectrum. On the other hand, soliton interactions caused by gain depletion and recovery as well as acoustic effects are relatively weak compared to soliton interactions mediated by the dispersive waves [
17]. Further studies to identify the mechanism for the relative-speed change are under way.
By slightly tuning the PC, another collision scenario is observed, where one of the solitons in the soliton molecule is annihilated as a result of the collision.
Figure 6a shows the DFT measured shot-to-shot spectra. An enlargement of the dashed rectangle in
Figure 6a is manifested in
Figure 6b, which indicates that a beating process occurs. The field autocorrelation traces are shown in
Figure 6c.
Figure 6d displays the field autocorrelation traces corresponding to the shot-to-shot spectra in
Figure 6b. The results show that, in the colliding process, one of the solitons in the initial soliton molecule evolves into a weak pulse, and the weak pulse gradually disappears due to the NPR mode-locking mechanism (the weak pulse experiences higher loss) [
41]. The beating process, as shown in
Figure 6b, could be attributed to the appearance of the weak pulse. Subsequently, the remaining pulses are coupled into a new soliton molecule. Finally, the new soliton molecule is stabilized to a molecule identical to the initial soliton molecule. It should be mentioned that, limited by the memory depth of the real-time oscilloscope used, an entire stabilization process of the new soliton molecule cannot be recorded. The stabilized soliton molecule is not presented in
Figure 6c. The collision outcome indicates that the number of colliding solitons is not necessarily conserved since the fiber laser is a dissipative system. In addition, a CW component appears in the OSA-measured spectrum after the annihilation of one soliton, which implies that the excess intracavity energy maintained by the pump power manifests itself as a CW component.
The third collision scenario, where a soliton molecule and a soliton singlet proceed to form a soliton triplet, is observed by further adjusting the PC.
Figure 7a shows the real-time spectral evolution in the collision process. The corresponding field autocorrelation traces are manifested in
Figure 7b, which exhibits the merging of the molecule and the singlet into a three-pulse bound state. Limited by the record length of the oscilloscope, the entire stabilization process of the three-pulse bound state cannot be recorded. We measured the shot-to-shot spectra of the stabilized soliton triplet after the collision, as illustrated in
Figure 7c. The corresponding field autocorrelation traces are shown in
Figure 7d, indicating that the stabilized soliton triplet is unequally spaced. It can be found that the soliton triplet consists of a soliton pair and a single soliton. The two solitons in the soliton pair are tightly bound with a short separation of 3.6 ps, and the pair is further weakly bound with the single soliton over a large separation of ~70 ps. The results demonstrate that different binding strengths could coexist in the soliton triplet.
Pulse collisions between a soliton molecule and a soliton singlet in mode-locked fiber lasers have been numerically investigated within the framework of the complex cubic-quintic Ginzburg–Landau equation [
35]. A variety of collision scenarios, such as the “elastic” collision, the soliton fusion, and the merging of all colliding solitons into a three-soliton bound state, were predicted. The collision outcomes could mainly be attributed to the phase difference between the single soliton and the closest soliton in the molecule. In our experiment, various collision scenarios in an NPR mode-locked fiber laser are observed by tuning the intra-cavity PC. The adjustment of the PC will alter the net-cavity birefringence and further lead to a variation in the transmission curve for the NPR structure [
42]. Consequently, the parameters (e.g., the peak power and the relative phase) of the colliding solitons will be changed. This could influence the nonlinear interactions among the colliding solitons, resulting in various collision outcomes. It should be emphasized that the transient collision dynamics cannot be resolved by oscilloscopes or conventional OSAs. With the help of the DFT technique, transient collision processes, such as the soliton repulsions and attractions, the bond exchange, and the soliton annihilation, are experimentally observed. The results obtained could further enrich the soliton collision dynamics in ultrafast fiber lasers.