Low-Cost 3D-Printed Electromagnetically Driven Large-Area 1-DOF Optical Scanners
Abstract
:1. Introduction
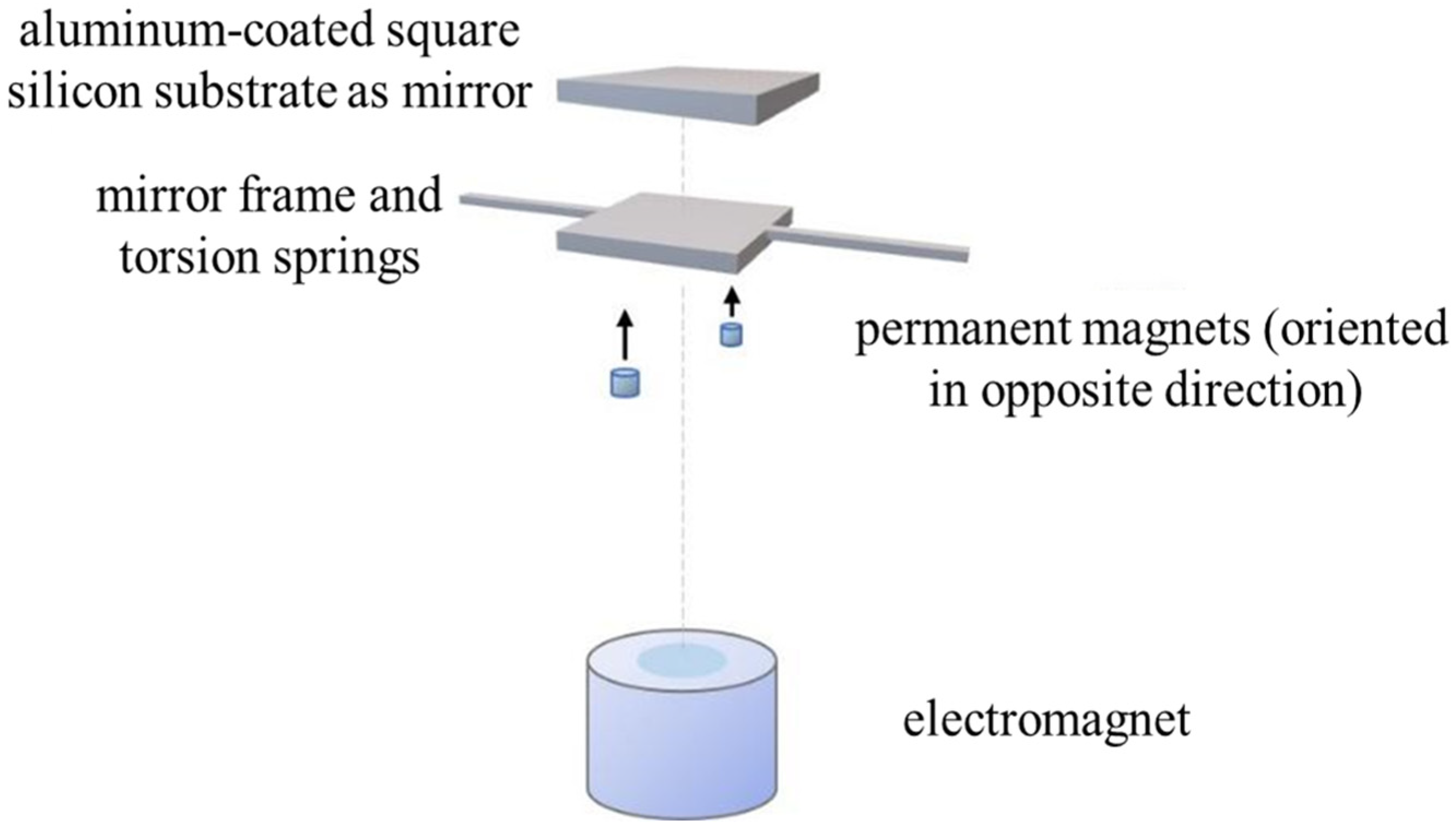
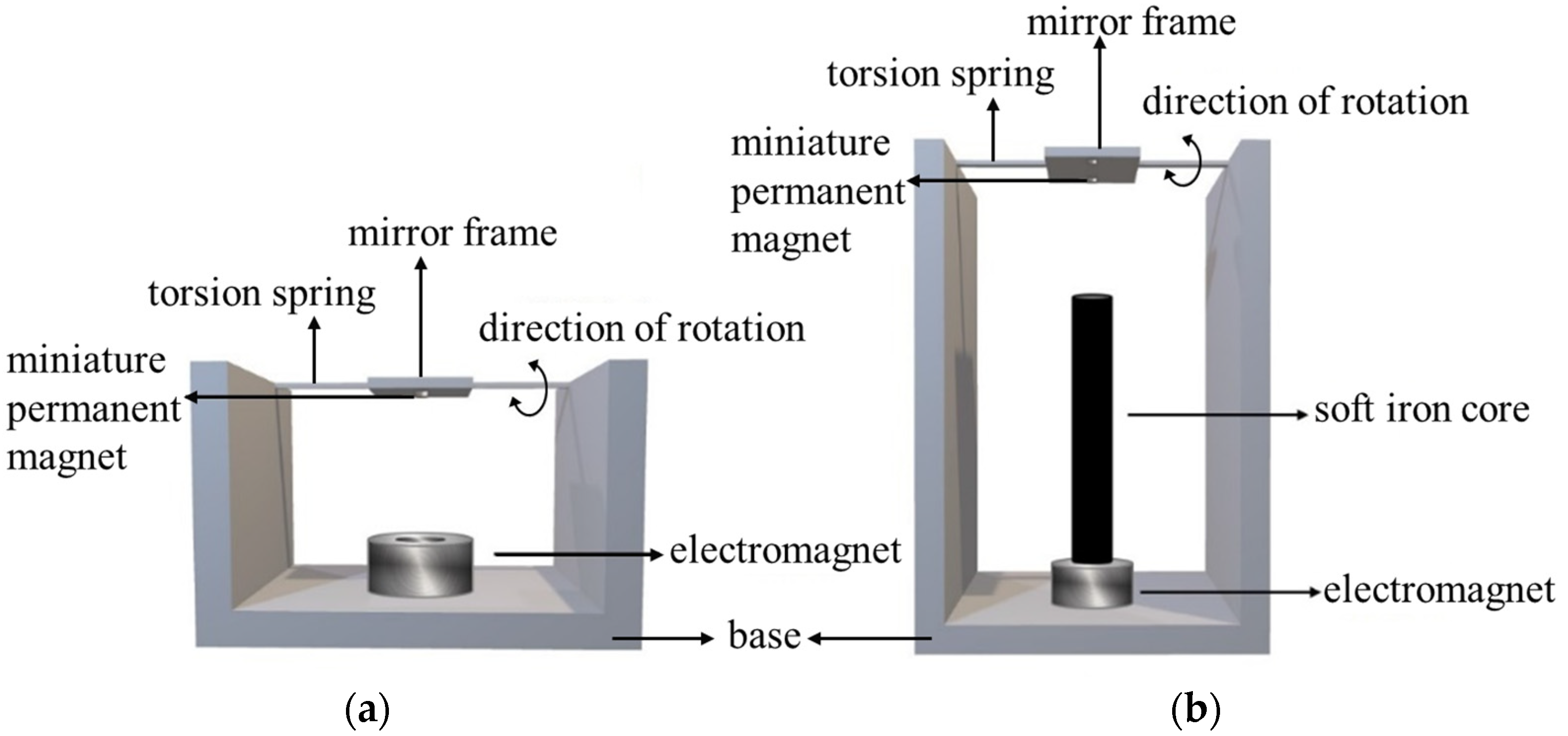
2. Device Design and Fabrication
3. Device Characterization and Results
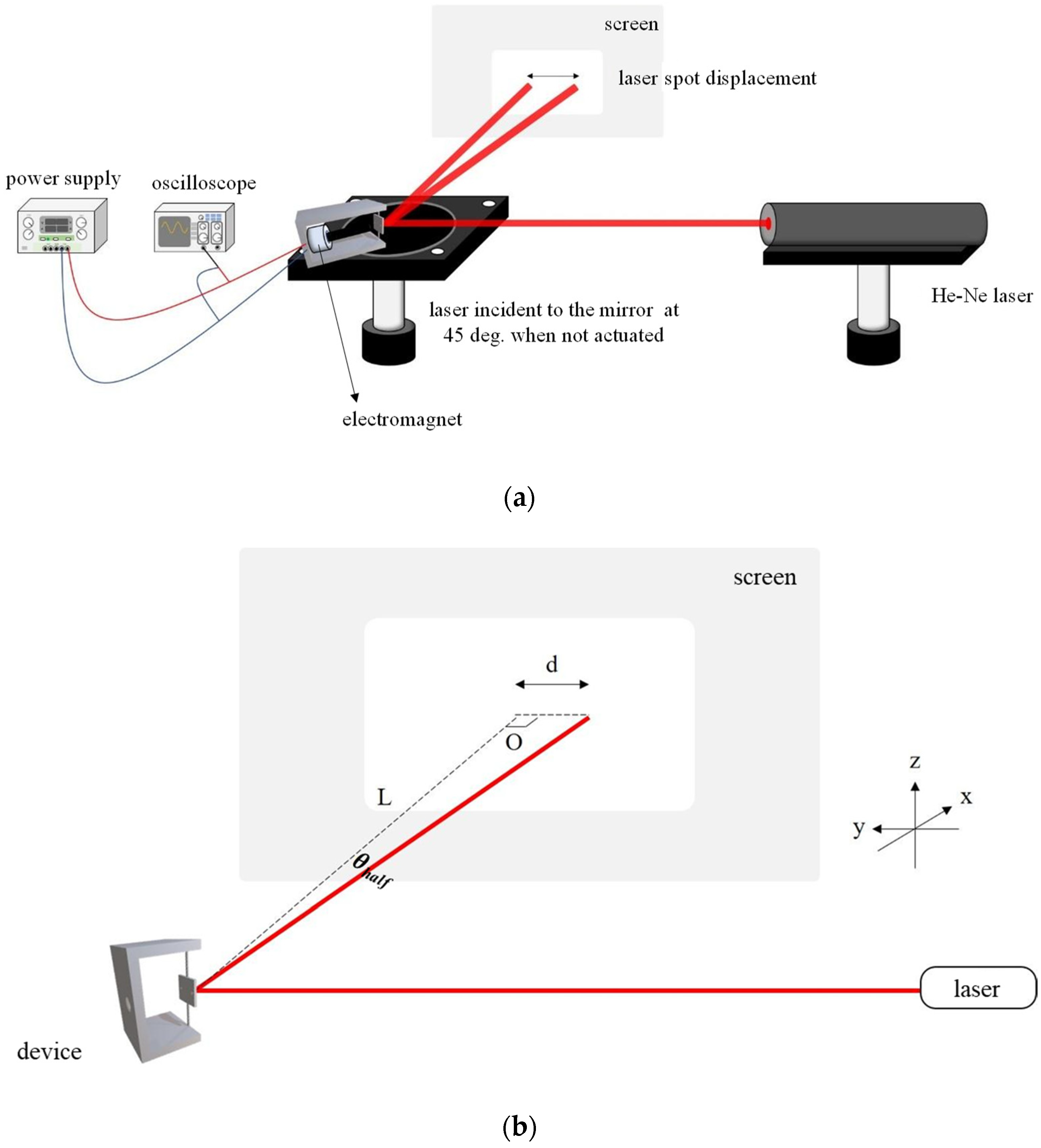
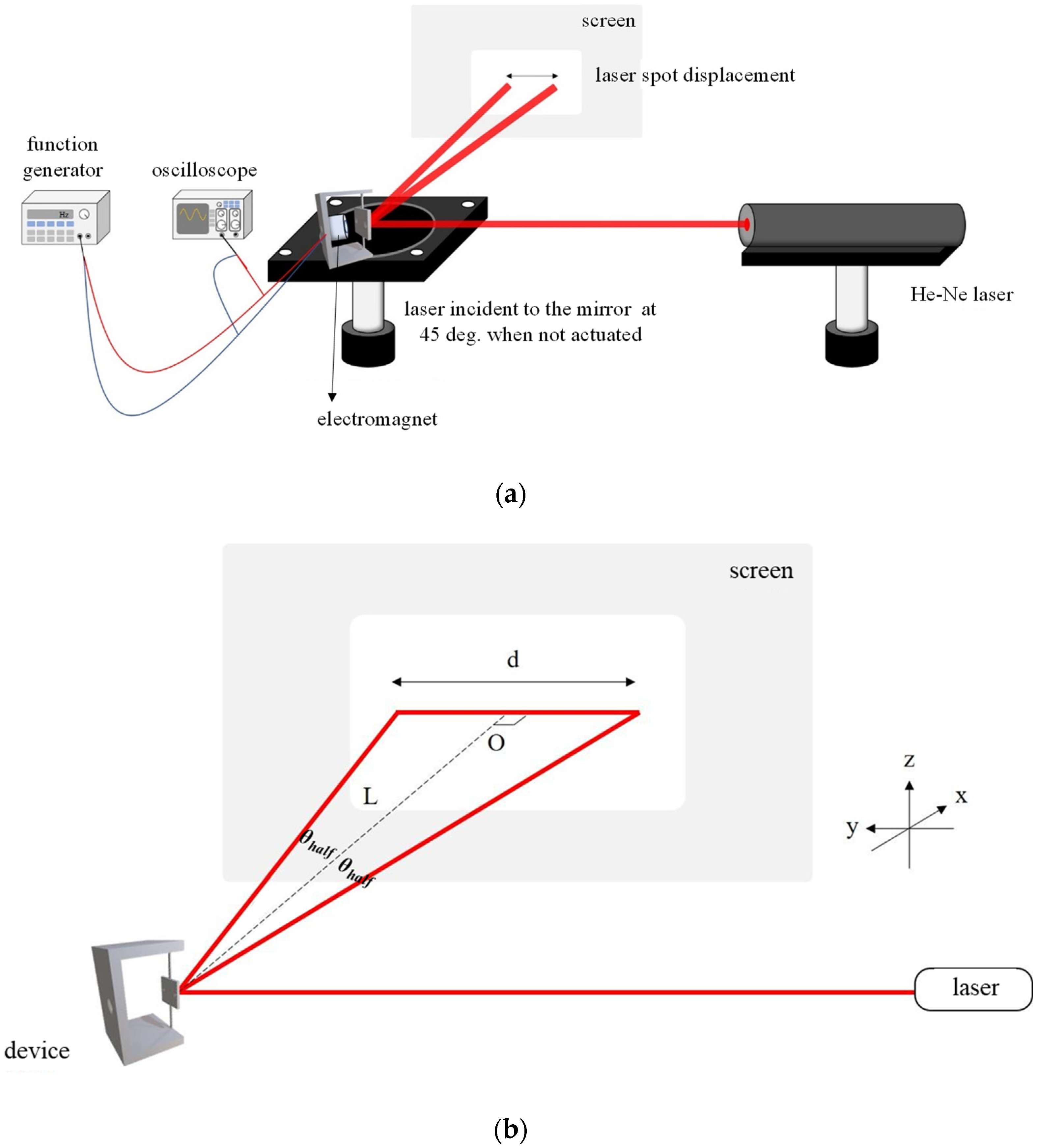
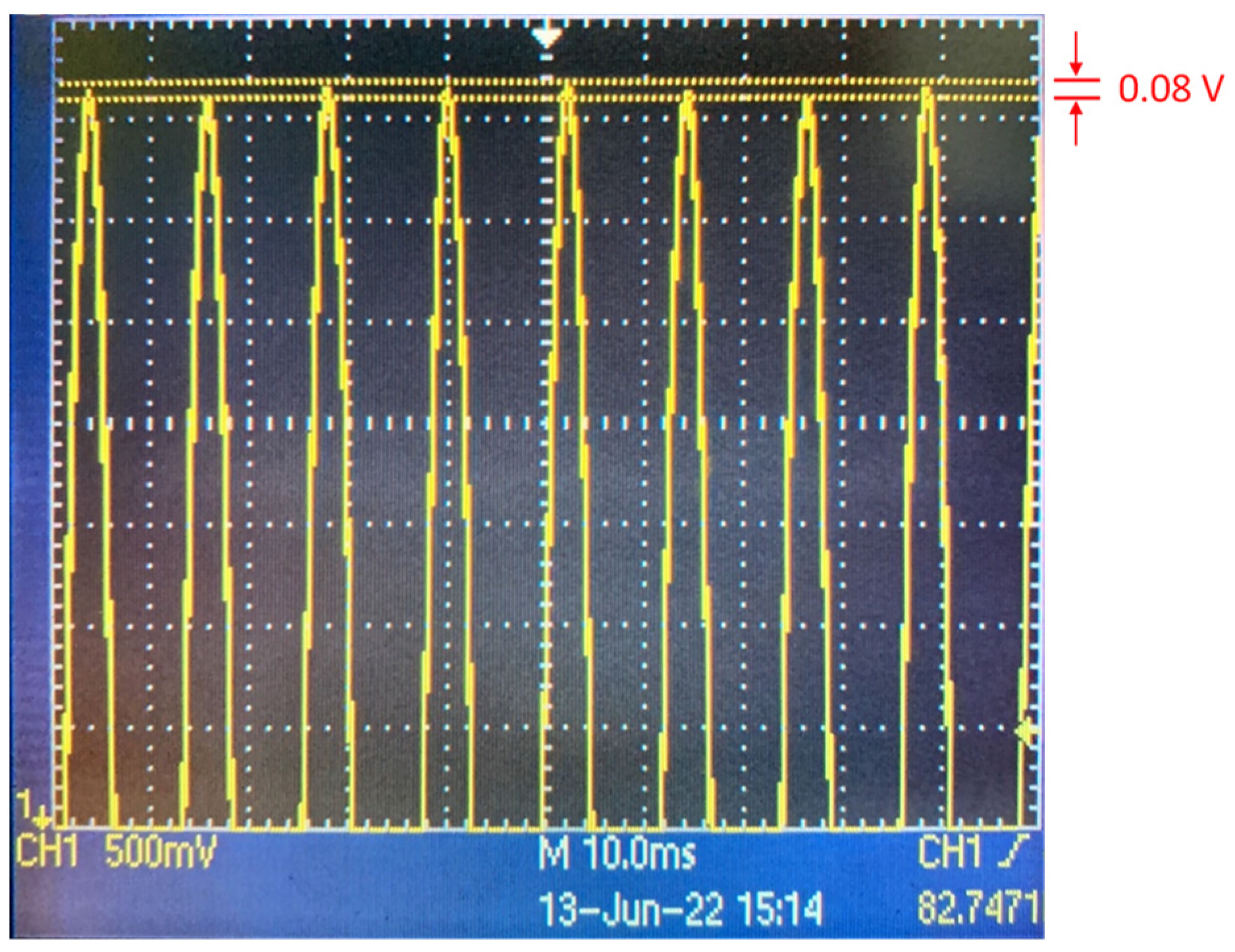
3.1. Experiment Setup and Characterization
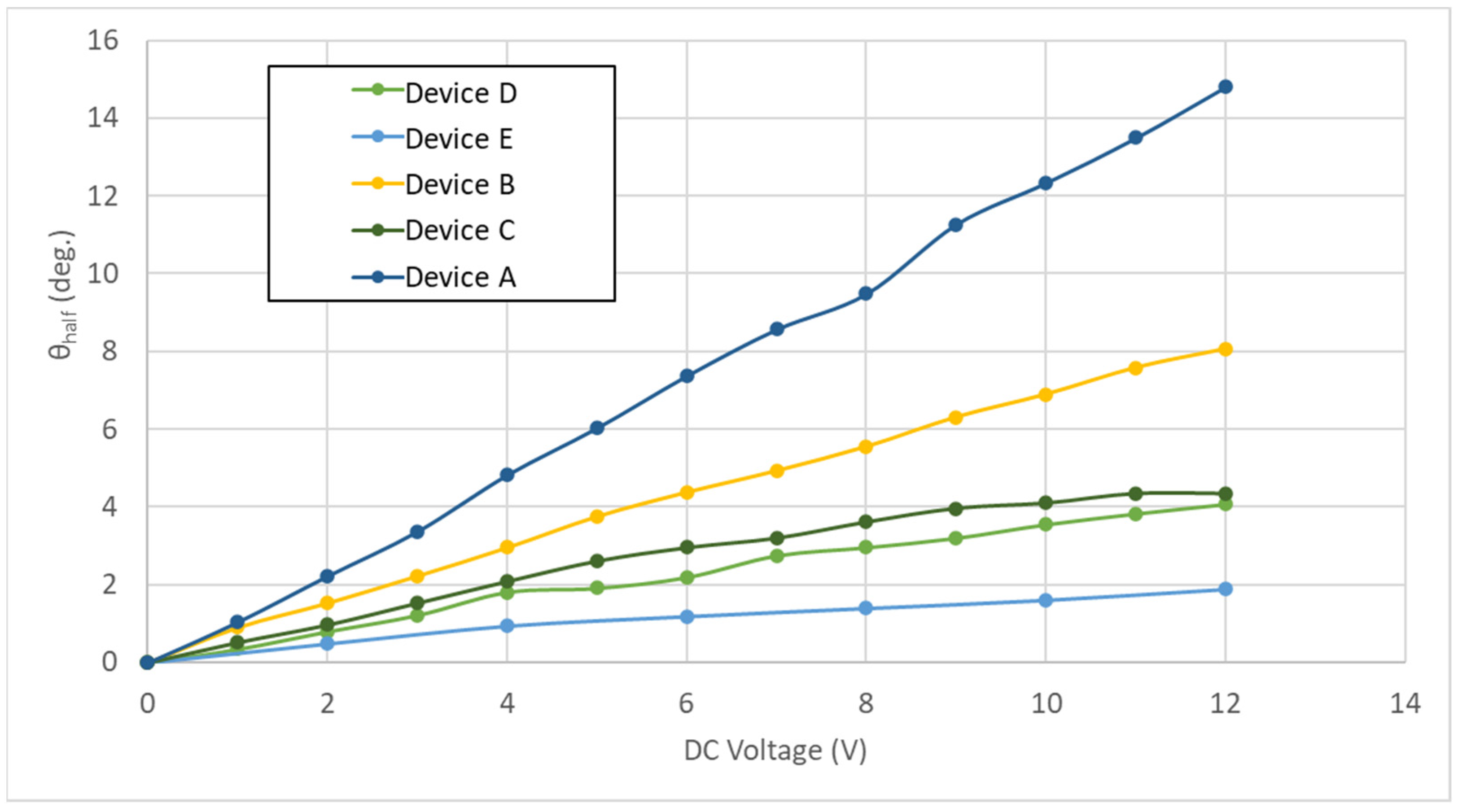
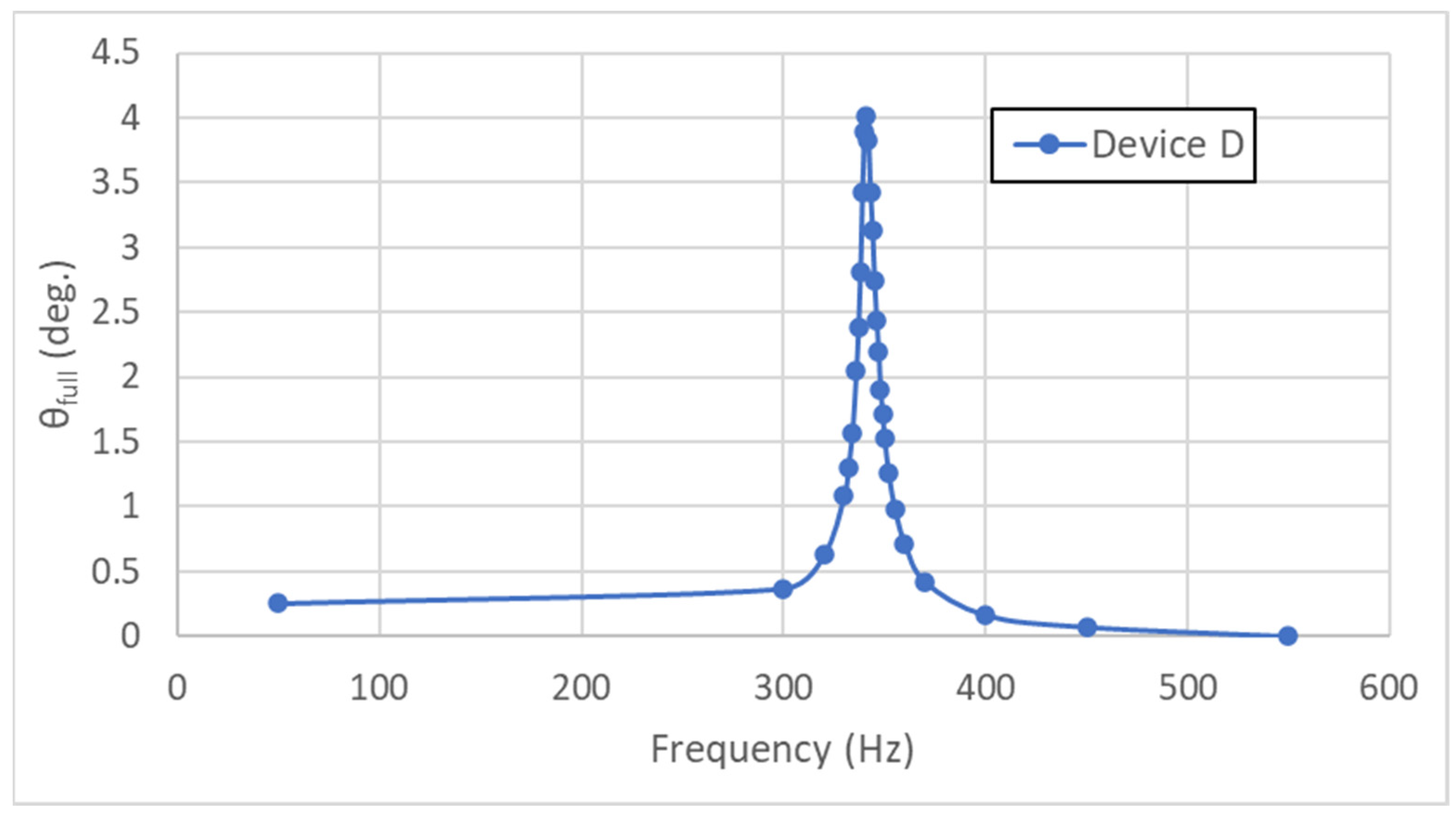
3.2. Experiment Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aylward, R.P. Advances and technologies of galvanometer-based optical scanners. In Proceedings of the SPIE’S International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 18–23 July 1999. [Google Scholar]
- Duma, V.-F. Laser scanners with oscillatory elements: Design and optimization of 1D and 2D scanning functions. Appl. Math. Model. 2018, 67, 456–476. [Google Scholar] [CrossRef]
- Li, Y. Single-mirror beam steering system: Analysis and synthesis of high-order conic-section scan patterns. Appl. Opt. 2008, 47, 386–398. [Google Scholar] [CrossRef] [PubMed]
- Novanta Photonics. 62xxK and 83xxK Series, Galvanometers. Available online: https://novantaphotonics.com/product/62xxk-and-83xxk-series-galvanometers/ (accessed on 22 June 2022).
- Thorlabs. Galvanometers. Available online: https://www.thorlabs.com/navigation.cfm?guide_id=2269 (accessed on 22 June 2022).
- Scanlab. Galvanometer Scanners. Available online: https://www.scanlab.de/en/products/galvanometer-scanners (accessed on 22 June 2022).
- Salimi, M.H.; Villiger, M.; Tabatabaei, N. New Model for Understanding the Relationship between Tissue Composition and Photothermal Optical Coherence Tomography Signals. In Proc. SPIE 11655, Label-Free Biomedical Imaging and Sensing (LBIS) 2021; SPIE Proceedings: Bellingham, WA, USA, 2021. [Google Scholar] [CrossRef]
- Luo, Y.; Arauz, L.J.; Castillo, J.E.; Barton, J.K.; Kostuk, R.K. Parallel optical coherence tomography system. Appl. Opt. 2007, 46, 8291–8297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, M.; Lin, J.; Cheng, Z.; Gan, W. Jitter suppression for resonant galvo based high-throughput laser scanning systems. Opt. Express 2020, 28, 26414–26420. [Google Scholar] [CrossRef]
- Li, Y.; Cui, T.; Li, Q.; Zhang, B.; Bai, Y.; Wang, C. A study of correction method to the pincushion distortion based on dual galvanometer LiDAR scanning system. Optik 2019, 181, 555–561. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Zhuang, X.; Zhou, C.; Fan, B. Development of an Electrostatic Comb-Driven MEMS Scanning Mirror for Two-Dimensional Raster Scanning. Micromachines 2021, 12, 378. [Google Scholar] [CrossRef] [PubMed]
- Strathman, M.; Liu, Y.; Keeler, E.G.; Song, M.; Baran, U.; Xi, J.; Sun, M.T.; Wang, R.; Li, X.; Lin, L.Y. MEMS scanning micromirror for optical coherence tomography. Biomed. Optics Express 2015, 6, 211–224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorecki, C.; Bargiel, S. MEMS Scanning Mirrors for Optical Coherence Tomography. Photonics 2020, 8, 6. [Google Scholar] [CrossRef]
- Yalcinkaya, A.D.; Urey, H.; Brown, D.; Montague, T.; Sprague, R. Two-Axis Electromagnetic Microscanner for High Resolution Displays. J. Microelectromech. Syst. 2006, 15, 786–794. [Google Scholar] [CrossRef]
- Tanguy, Q.A.A.; Gaiffe, O.; Passilly, N.; Cote, J.-M.; Cabodevila, G.; Bargiel, S.; Lutz, P.; Xie, H.; Gorecki, C. Real-time Lissajous imaging with a low-voltage 2-axis MEMS scanner based on electrothermal actuation. Opt. Express 2020, 28, 8512–8527. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, M.; Taguchi, Y. Design and Fabrication of a Kirigami-Inspired Electrothermal MEMS Scanner with Large Dis-placement. Micromachines 2020, 11, 362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senger, F.; Albers, J.; Hofmann, U.; Piechotta, G.; Giese, T.; Heinrich, F.; von Wantoch, T.; Gu-Stoppel, S. A bi-axial vacu-um-packaged piezoelectric MEMS mirror for smart headlights. In MOEMS and Miniaturized Systems XIX; SPIE Proceedings: Bellingham, WA, USA, 2020; Volume 1129305. [Google Scholar]
- Kim, J.; Lee, H.; Kim, B.; Jeon, J.; Yoon, J.; Yoon, E. A high fill-factor micro-mirror stacked on a crossbar torsion spring for electrostatically-actuated two-axis operation in large-scale optical switch. In Proceedings of the Sixteenth Annual International Conference on Micro Electro Mechanical Systems, Kyoto, Japan, 23–23 January 2003. [Google Scholar] [CrossRef]
- Conant, R.A.; Nee, J.T.; Lau, K.Y.; Muller, R.S. A flat high-frequency scanning micromirror. In Proceedings of the Technical Digest 2000 Solid-State Sensor & Actuator Workshop, Hilton Head Island, SC, USA, 4–8 June 2000; pp. 6–9. [Google Scholar]
- Duma, V.-F.; Dimb, A.-L. Exact Scan Patterns of Rotational Risley Prisms Obtained with a Graphical Method: Multi-Parameter Analysis and Design. Appl. Sci. 2021, 11, 8451. [Google Scholar] [CrossRef]
- Li, A.; Yi, W.; Zuo, Q.; Sun, W. Performance characterization of scanning beam steered by tilting double prisms. Opt. Express 2016, 24, 23543. [Google Scholar] [CrossRef]
- Li, Y. Third-order theory of the Risley-prism-based beam steering system. Appl. Opt. 2011, 50, 679–686. [Google Scholar] [CrossRef] [PubMed]
- Urey, H. Torsional MEMS scanner design for high-resolution scanning display systems. In Optical Scanning; SPIE Proceedings: Bellingham, WA, USA, 2002; Volume 4773, pp. 27–38. [Google Scholar] [CrossRef] [Green Version]
- Farah, S.; Anderson, D.G.; Langer, R. Physical and mechanical properties of PLA, and their functions in widespread applications—A comprehensive review. Adv. Drug Delivery Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hayakawa, T.; Watanabe, T.; Senoo, T.; Ishikawa, M. Gain-compensated sinusoidal scanning of a galvanometer mirror in proportional-integral-differential control using the pre-emphasis technique for motion-blur compensation. Appl. Opt. 2016, 55, 5640–5646. [Google Scholar] [CrossRef] [PubMed]
- Carrasco-Zevallos, O.M.; Viehland, C.; Keller, B.; McNabb, R.P.; Kuo, A.N.; Izatt, J.A. Constant linear velocity spiral scanning for near video rate 4D OCT ophthalmic and surgical imaging with isotropic transverse sampling. Biomed. Opt. Express 2018, 9, 5052–5070. [Google Scholar] [CrossRef] [PubMed]
- Hwang, K.; Seo, Y.-H.; Ahn, J.; Kim, P.; Jeong, K.-H. Frequency selection rule for high definition and high frame rate Lissajous scanning. Sci. Rep. 2017, 7, 14075. [Google Scholar] [CrossRef] [PubMed]




| Oblique Top View | Side View | Bottom View (Beneath the Mirror) | |
|---|---|---|---|
| A (Type I) |  | 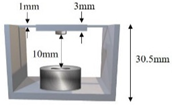 | 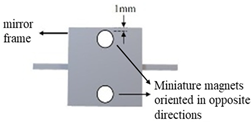 |
| B (Type I) |  |  | 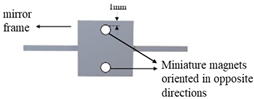 |
| C (Type II) |  |  | 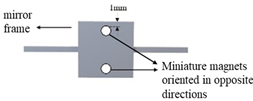 |
| D (Type I) | 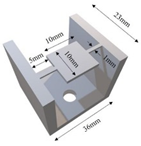 | 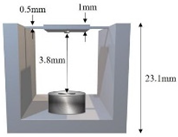 | 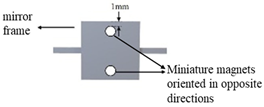 |
| E (Type II) | 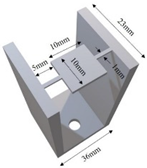 |  | 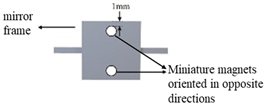 |
| A (Type I) | B (Type I) | C (Type II) | D (Type I) | E (Type II) | |
|---|---|---|---|---|---|
| Mirror frame size (mm3) | 20 × 20 × 3 | 10 × 10 × 1 | 10 × 10 × 1 | 10 × 10 × 1 | 10 × 10 × 1 |
| Torsion spring size (mm3) | 10 × 1.5 × 1 | 10 × 1 × 0.5 | 10 × 1 × 0.5 | 5 × 1 × 0.5 | 5 × 1 × 0.5 |
| Devices | Measured Mirror Frame Thickness (mm) | Measured Spring Size (mm3, Length × Width × Thickness) | Est. Mirror Mass (g) | Est. Torsion Spring Const. (N m/rad) | Est. Bending Spring Const. (N/m) | Predicted Torsional Resonance Freq. (Hz) | Predicted Bending Resonance Freq. (Hz) | Measured Torsional Resonance Freq. (Hz) |
|---|---|---|---|---|---|---|---|---|
| Device A | 2.57 | 9.82 × 1.6 × 0.99 | 2.58 | 3.24 × 10−2 | 4460 | 91.25 | 209.19 | 84 |
| Device B | 1.13 | 9.97 × 1.01 × 0.65 | 0.279 | 5.56 × 10−3 | 761.2 | 243.94 | 263.02 | 229 |
| Device C | 1.12 | 9.83 × 1.1 × 0.62 | 0.278 | 5.76 × 10−3 | 750.6 | 248.66 | 261.77 | 227 |
| Device D | 1.16 | 4.9 × 1.02 × 0.59 | 0.271 | 9.1 × 10−3 | 4844 | 316.42 | 673.05 | 341 |
| Device E | 1.15 | 4.87 × 1.02 × 0.62 | 0.281 | 10.34 × 10−3 | 5724 | 331 | 718.07 | 348 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.-K.; Huang, Y.-N.; Liu, G.-Y.; Tsui, W.-A.; Cheng, Y.-W.; Yeh, P.-H.; Tsai, J.-c. Low-Cost 3D-Printed Electromagnetically Driven Large-Area 1-DOF Optical Scanners. Photonics 2022, 9, 484. https://doi.org/10.3390/photonics9070484
Shen C-K, Huang Y-N, Liu G-Y, Tsui W-A, Cheng Y-W, Yeh P-H, Tsai J-c. Low-Cost 3D-Printed Electromagnetically Driven Large-Area 1-DOF Optical Scanners. Photonics. 2022; 9(7):484. https://doi.org/10.3390/photonics9070484
Chicago/Turabian StyleShen, Ching-Kai, Yu-Nung Huang, Guan-Yang Liu, Wei-An Tsui, Yi-Wen Cheng, Pin-Hung Yeh, and Jui-che Tsai. 2022. "Low-Cost 3D-Printed Electromagnetically Driven Large-Area 1-DOF Optical Scanners" Photonics 9, no. 7: 484. https://doi.org/10.3390/photonics9070484
APA StyleShen, C.-K., Huang, Y.-N., Liu, G.-Y., Tsui, W.-A., Cheng, Y.-W., Yeh, P.-H., & Tsai, J.-c. (2022). Low-Cost 3D-Printed Electromagnetically Driven Large-Area 1-DOF Optical Scanners. Photonics, 9(7), 484. https://doi.org/10.3390/photonics9070484





