Numerical Demonstration of the Transmission of Low Frequency Fluctuation Dynamics Generated by a Semiconductor Laser with Optical Feedback
Abstract
:1. Introduction
2. Materials and Methods
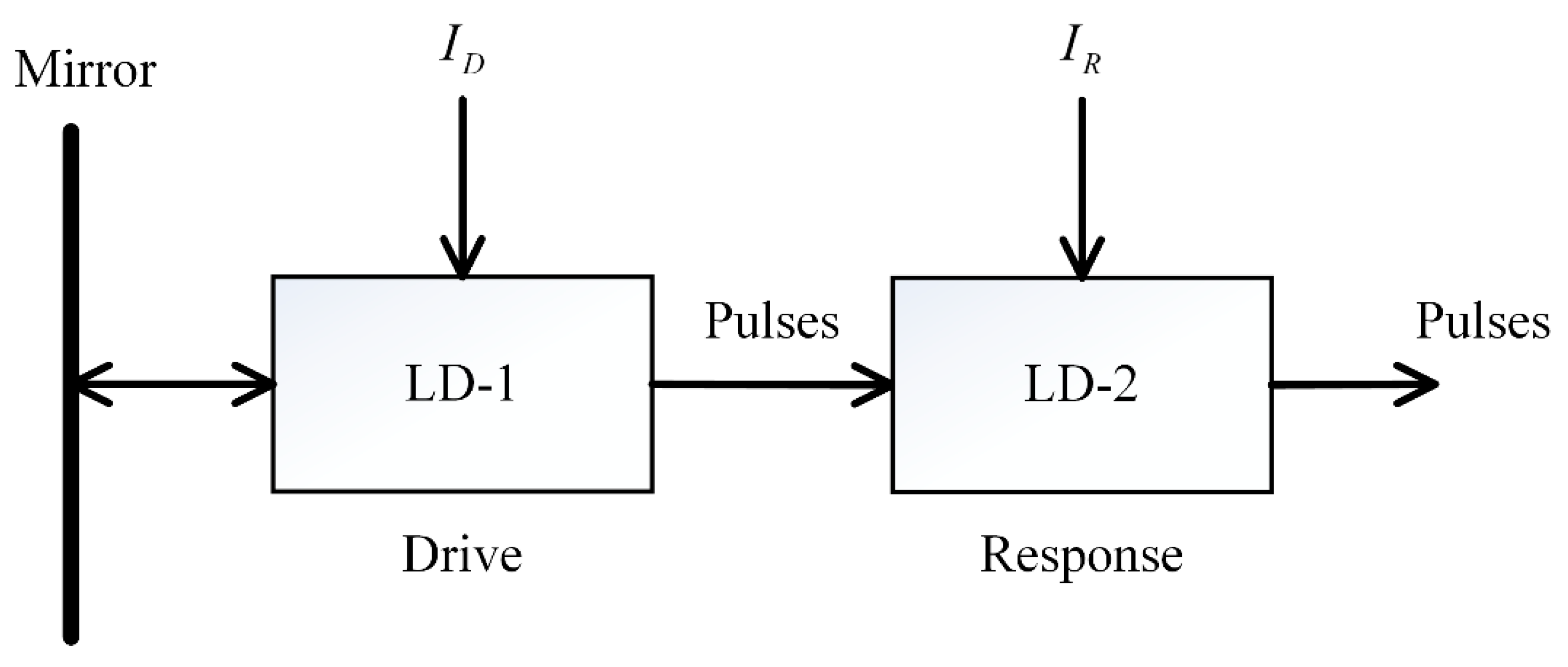
2.1. System Architecture
2.2. Tools
3. Results
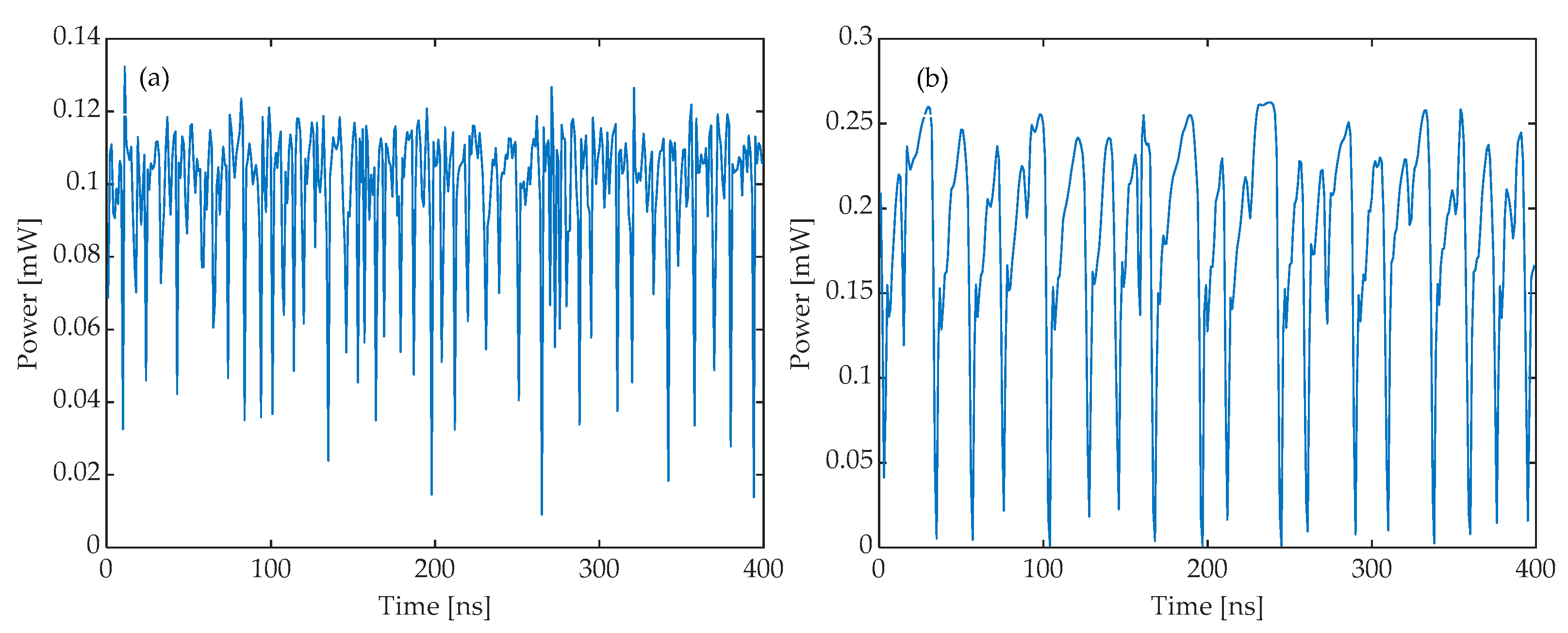
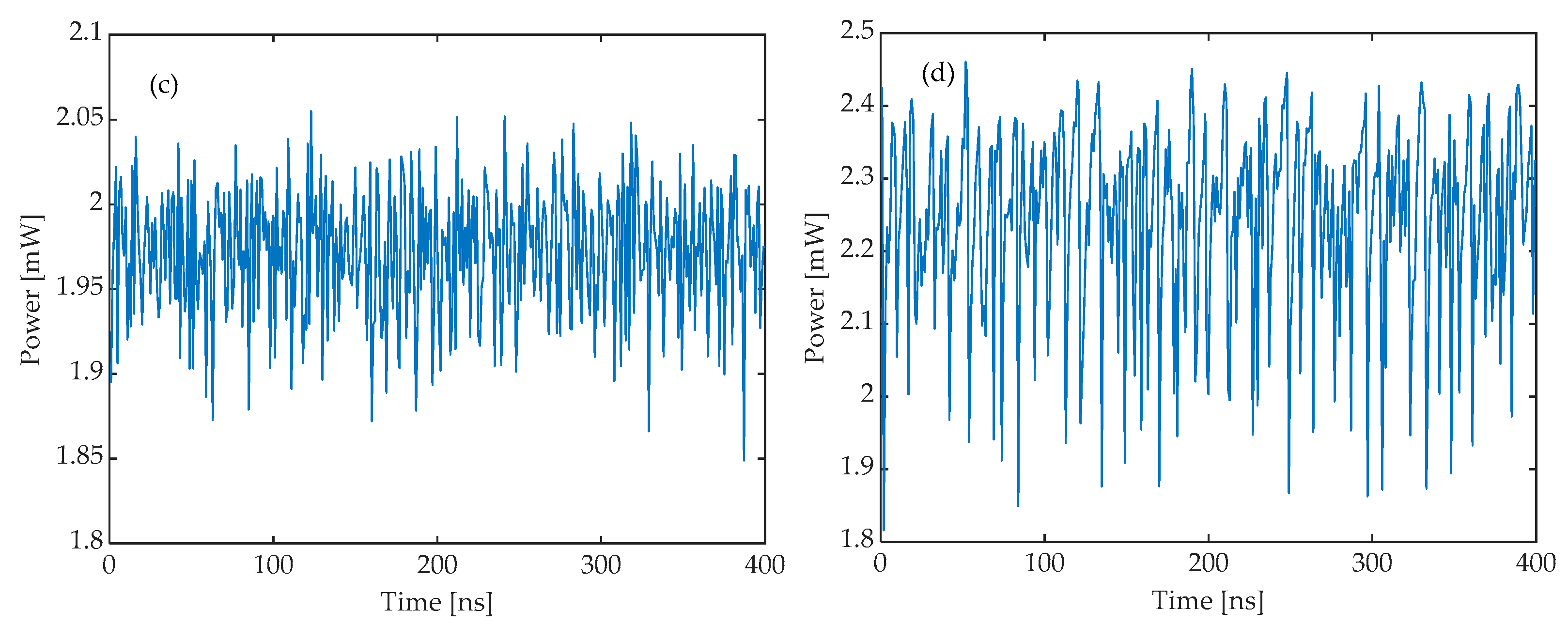
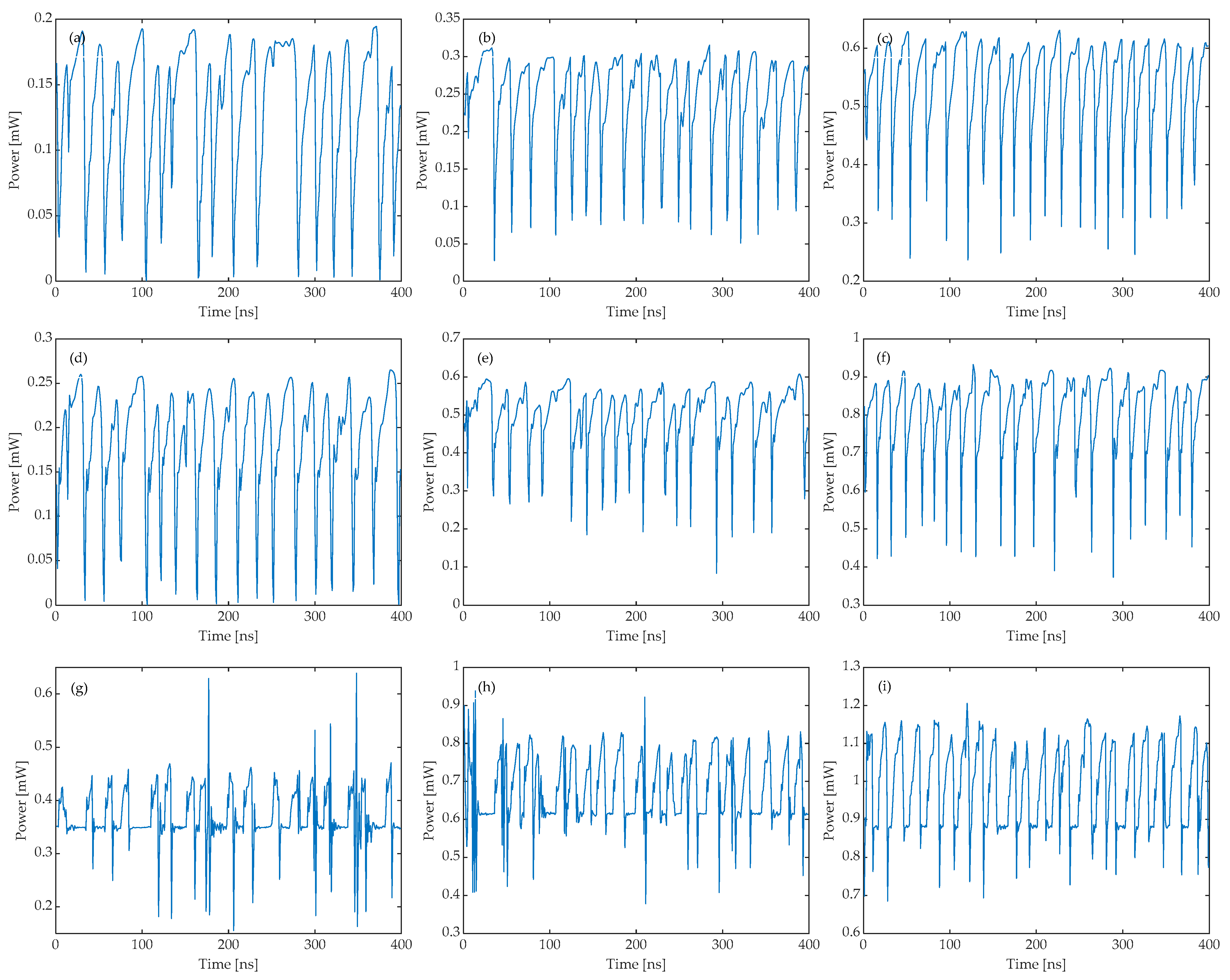
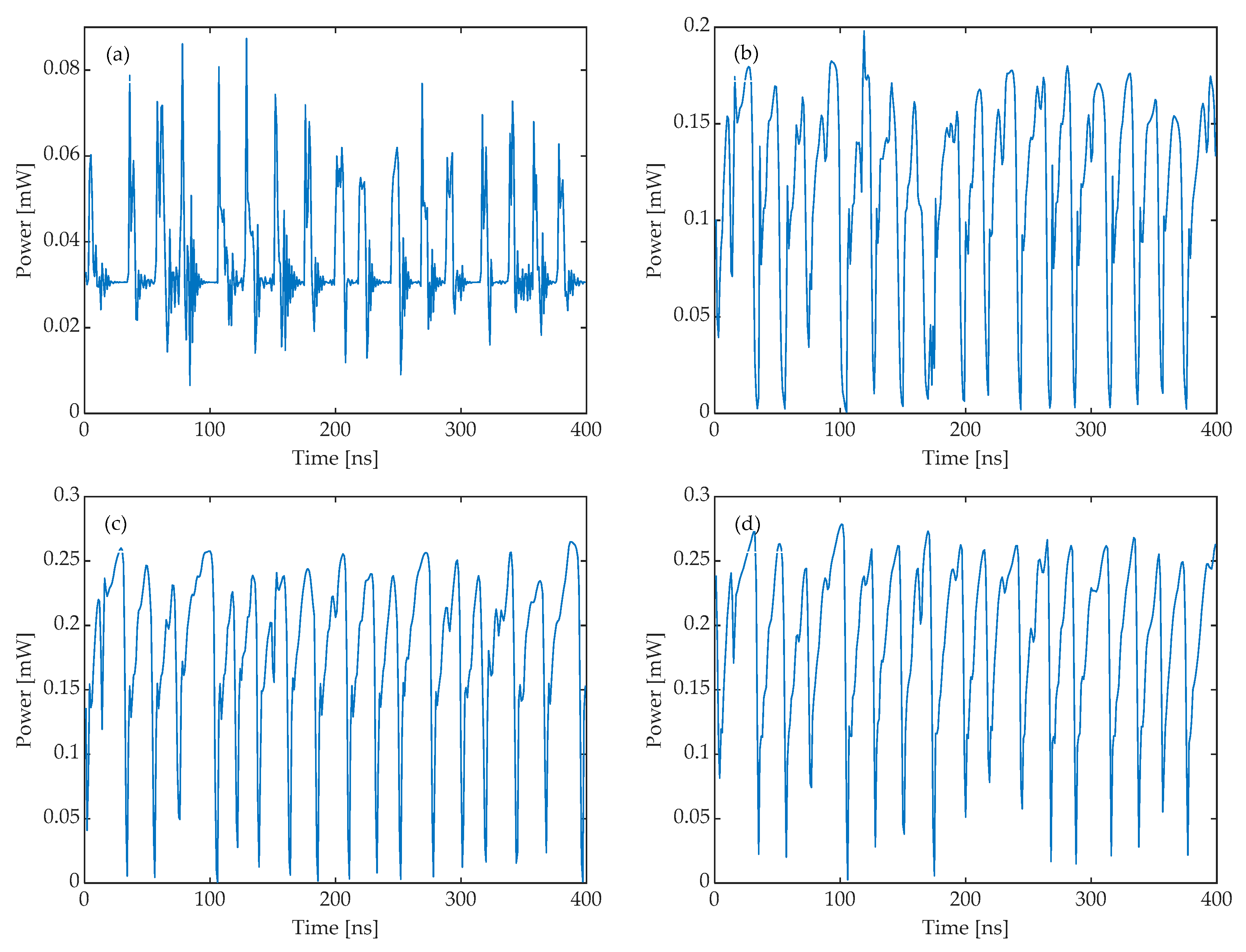
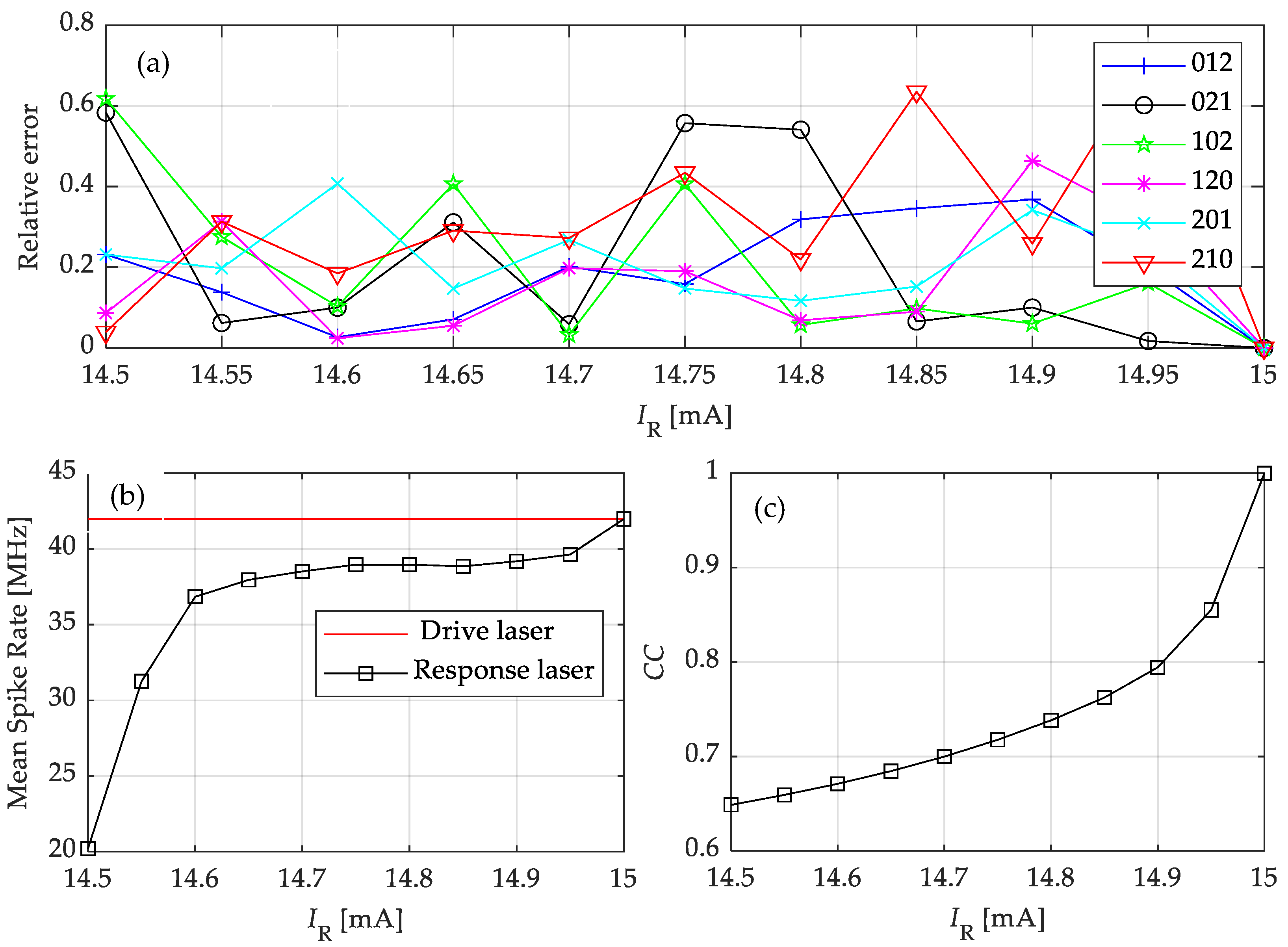
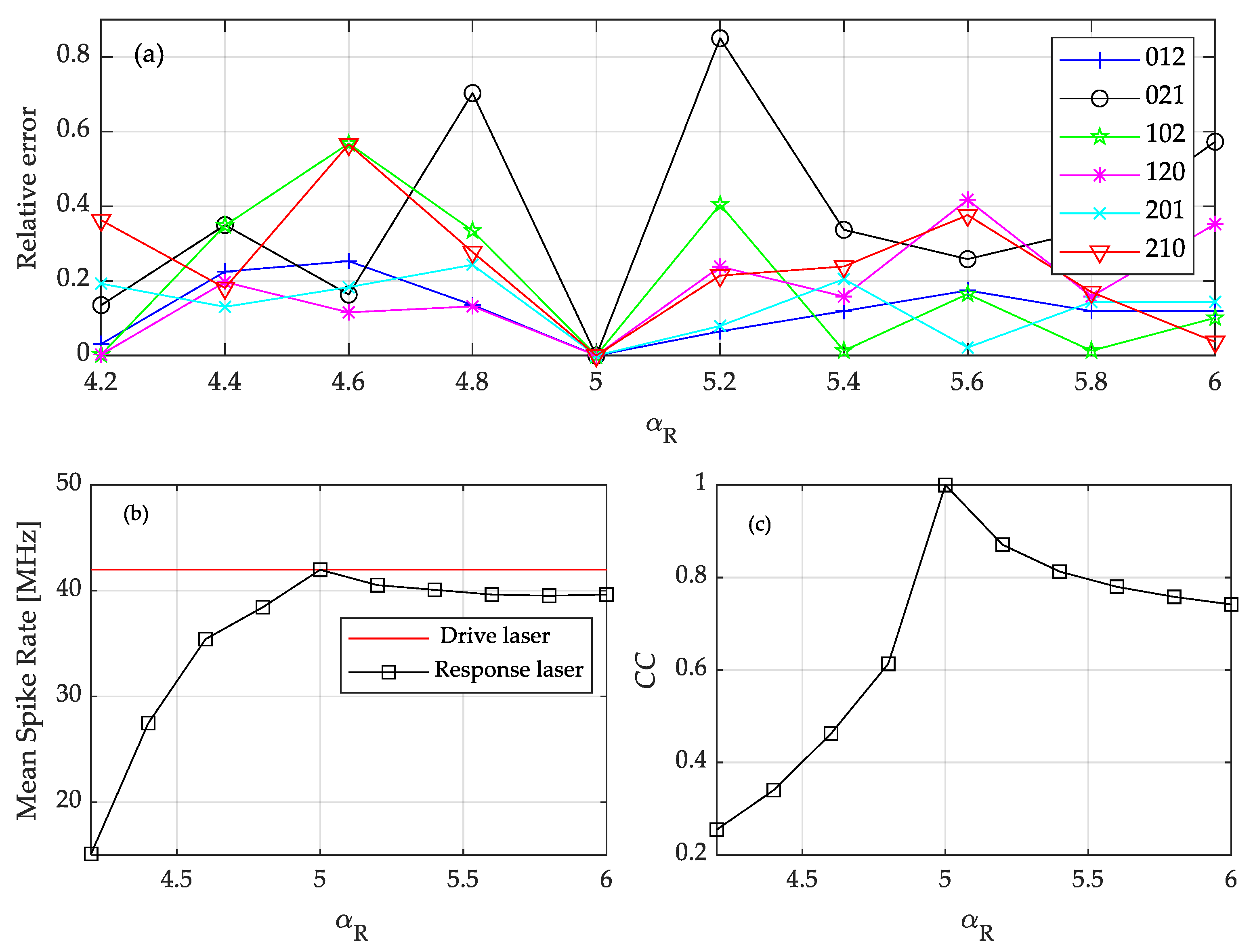
3.1. Effect of System Parameters on the Output of the Response Laser
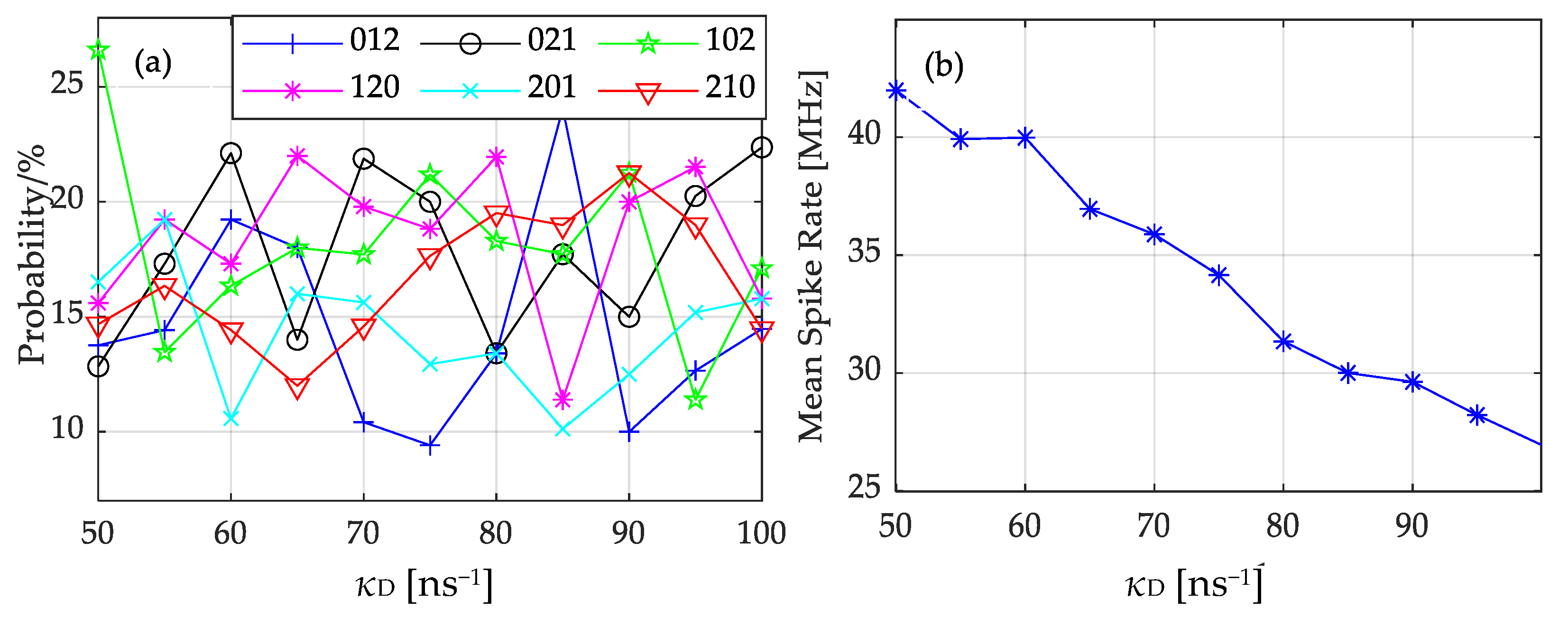
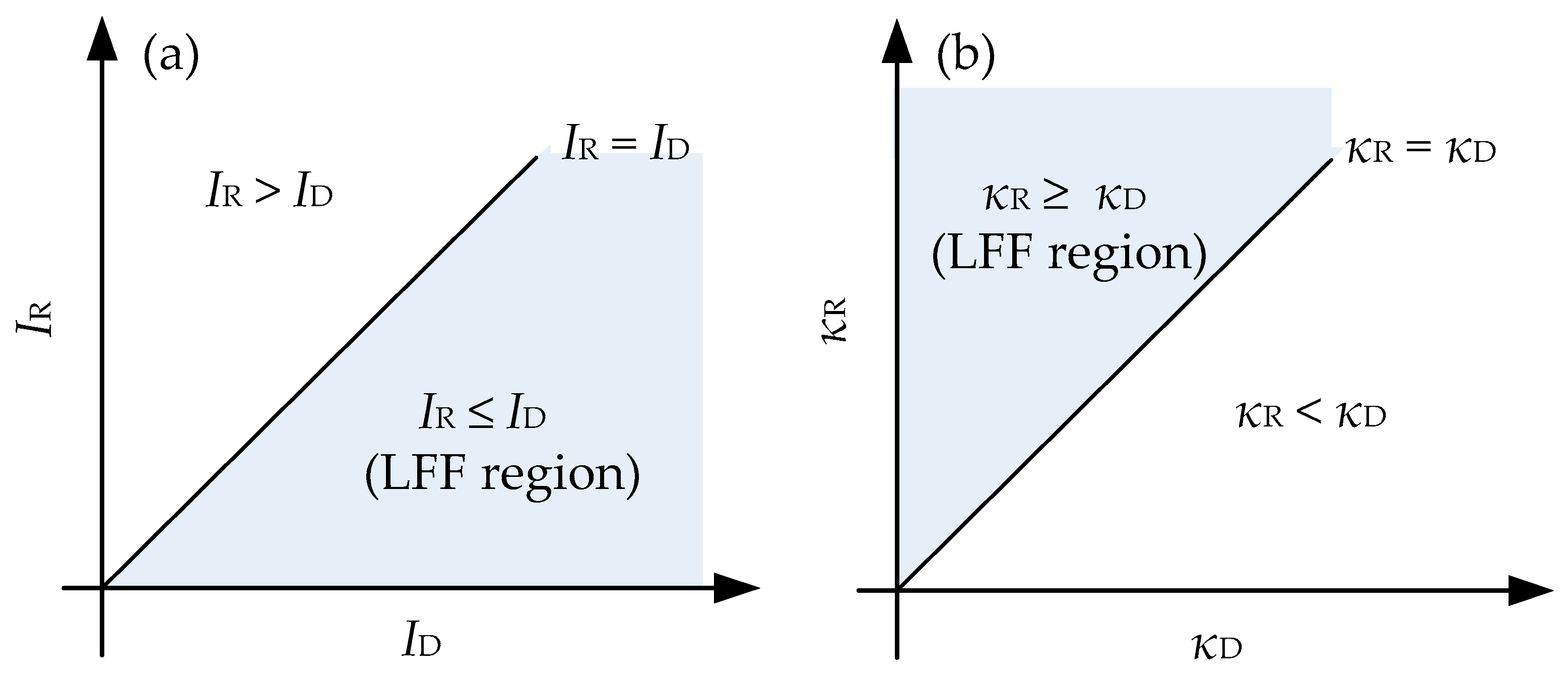
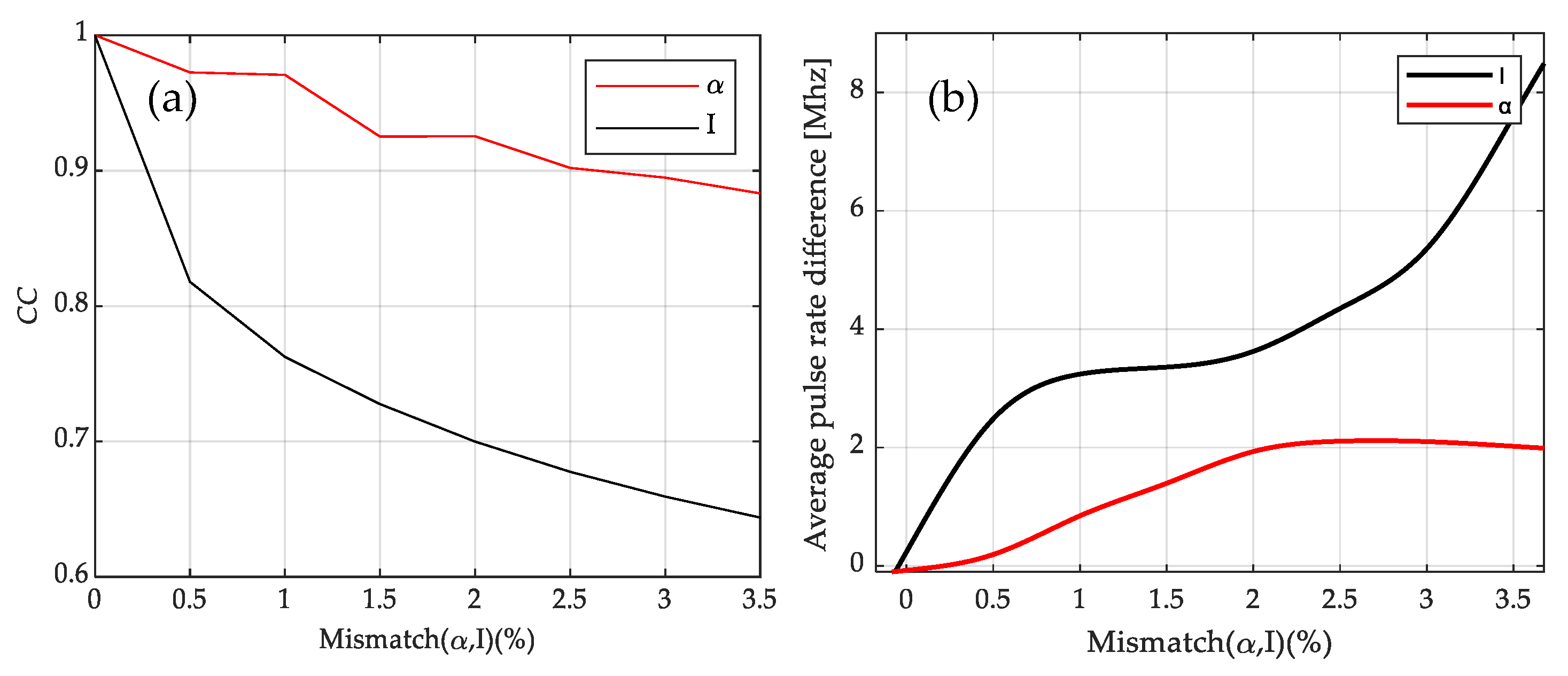
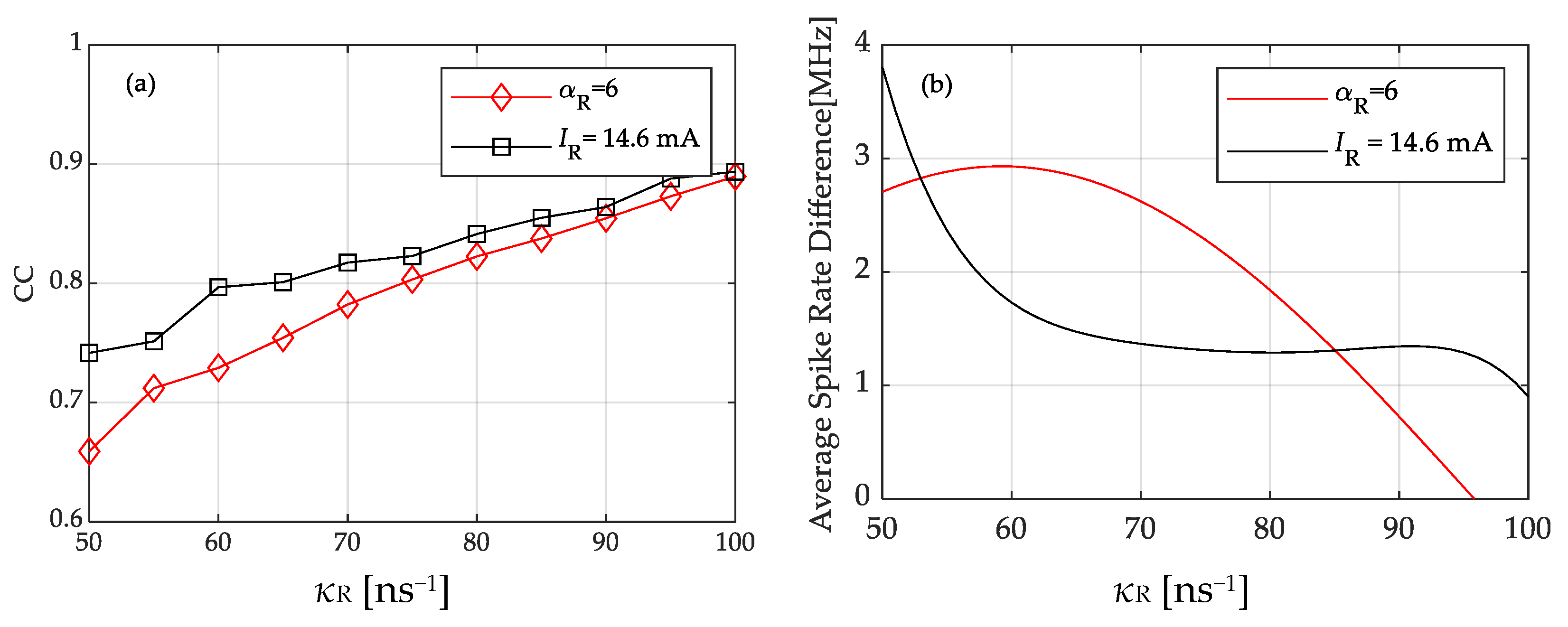
3.2. Influence of System Parameter Mismatch on the Transmission of LFF Waveforms
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, D.Z.; Deng, T.; Zheng, G.L. Manipulation of the complete chaos synchronization in dual-channel encryption system based on polarization-division-multiplexing. Acta Phys. Sin. 2014, 63, 070504. [Google Scholar] [CrossRef]
- Kanter, I.; Aviad, Y.; Reidler, I.; Cohen, E.; Rosenbluh, M. An optical ultrafast random bit generator. Nat. Photonics 2010, 4, 58–61. [Google Scholar] [CrossRef]
- Chen, C.Y.; Cheng, C.H.; Pan, D.K.; Lin, F.Y. Experimental generations and analyses of chaos-modulated pulses for pulsed chaos lidar applications based on gain-switched semiconductor lasers subject to optical feedback. Opt. Express 2018, 26, 20851–20860. [Google Scholar] [CrossRef] [PubMed]
- Rontani, D.; Choi, D.; Chang, C.Y.; Locquet, A.; Citrin, D.S. 6 Compressive sensing with optical chaos. Sci. Rep. 2016, 6, 35206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.; Zhou, P.; Yang, Y.; Chen, T.; Li, N. Time-Delayed Reservoir Computing Based on a Two-Element Phased Laser Array for Image Identification. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
- Bao, X.; Zhao, Q.; Yin, H. A multiple-input multiple-output reservoir computing system subject to optoelectronic feedbacks and mutual coupling. Entropy 2020, 22, 231. [Google Scholar] [CrossRef] [Green Version]
- Tao, J.-Y.; Wu, Z.-M.; Yue, D.-Z.; Tan, X.-S.; Zeng, Q.-Q.; Xia, G.-Q. Performance enhancement of a delay-based Reservoir computing system by using gradient boosting technology. IEEE Access 2020, 8, 151990–151996. [Google Scholar] [CrossRef]
- Fischer, I.; van Tartwijk, G.H.M.; Levine, A.M.; Elsasser, W.; Gobel, E.; Lenstra, D. Fast Pulsing and Chaotic Itinerancy with a Drift in the Coherence Collapse of Semiconductor Lasers. Phys. Rev. Lett. 1996, 76, 220–223. [Google Scholar] [CrossRef] [Green Version]
- Shastri, B.J.; Nahmias, M.A.; Tait, A.N.; Robriguez, A.W.; Wu, B.; Prucnal, P.R. Spike Processing With a Graphene Excitable Laser. Sci. Rep. 2016, 6, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hurtado, A.; Schires, K.; Henning, I.; Adams, M. Investigation of vertical cavity surface emitting laser dynamics for neuromorphic photonic systems. Appl. Phys. Lett. 2012, 100, 103703. [Google Scholar] [CrossRef] [Green Version]
- Deng, T.; Robertson, J.; Hurtado, A. Controlled propagation of spiking dynamics in vertical-cavity surface-emitting lasers: Towards neuromorphic photonic networks. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.Y.; Zhang, H.; Guo, X.X.; Li, J.F.; Wen, A.J.; Pan, W.; Hao, Y. Cascadable neuron-like spiking dynamics in coupled VCSELs subject to orthogonally polarized optical pulse injection. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–7. [Google Scholar] [CrossRef]
- Tait, A.N.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Broadcast and weight: An integrated network for scalable photonic spike processing. J. Lightwave Technol. 2014, 32, 3427–3439. [Google Scholar] [CrossRef]
- Ma, P.Y.; Shastri, B.J.; de Lima, T.F.; Huang, C.; Tait, A.N.; Nahmias, M.A.; Peng, H.T.; Prucnal, P.R. Simultaneous excitatory and inhibitory dynamics in an excitable laser. Opt. Lett. 2018, 43, 3802–3805. [Google Scholar] [CrossRef]
- Robertson, J.; Deng, T.; Javaloyes, J.; Hurtado, A. Controlled inhibition of spiking dynamics in VCSELs for neuromorphic photonics: Theory and experiments. Opt. Lett. 2017, 42, 1560–1563. [Google Scholar] [CrossRef] [Green Version]
- Selmi, F.; Braiv, R.; Beaudoin, G.; Sagnes, I.; Kuszelewicz, R.; Erneux, T.; Barbay, S. Spike latency and response properties of an excitable micropillar laser. Phys. Rev. E 2016, 94, 042219. [Google Scholar] [CrossRef] [Green Version]
- Hurtado, A.; Javaloyes, J. Controllable spiking patterns in long-wavelength vertical cavity surface emitting lasers for neuromorphic photonics systems. Appl. Phys. Lett. 2015, 107, 241103. [Google Scholar] [CrossRef] [Green Version]
- Nahmias, M.A.; Shastri, B.J.; Tait, A.N.; Prucnal, P.R. A leaky integrate-and-fire laser neuron for ultrafast cognitive computing. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1–12. [Google Scholar] [CrossRef]
- Peng, H.T.; Nahmias, M.A.; de Lima, T.F.; Tait, A.N.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 6101715. [Google Scholar] [CrossRef]
- Tiana-Alsina, J.; Quintero-Quiroz, C.; Masoller, C. Comparing the dynamics of periodically forced lasers and neurons. N. J. Phys. 2019, 21, 103039. [Google Scholar] [CrossRef] [Green Version]
- Aragoneses, A.; Rubido, N.; Tiana-Alsina, J.; Torrent, M.; Masoller, C. Distinguishing signatures of determinism and stochasticity in spiking complex systems. Sci. Rep. 2013, 3, 1778. [Google Scholar] [CrossRef] [Green Version]
- Aragoneses, A.; Perrone, S.; Sorrentino, T.; Torrent, M.; Masoller, C. Unveiling the complex organization of recurrent patterns in spiking dynamical systems. Sci. Rep. 2014, 4, 4696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sorrentino, T.; Quintero-Quiroz, C.; Torrent, M.; Masoller, C. Analysis of the spike rate and spike correlations in modulated semiconductor lasers with optical feedback. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 561–567. [Google Scholar] [CrossRef]
- Sorrentino, T.; Quintero-Quiroz, C.; Aragoneses, A.; Torrent, M.; Masoller, C. Effects of periodic forcing on the temporally correlated spikes of a semiconductor laser with feedback. Opt. Express 2015, 23, 5571–5581. [Google Scholar] [CrossRef] [Green Version]
- Tiana-Alsina, J.; Quintero-Quiroz, C.; Panozzo, M.; Torrent, M.; Masoller, C. Experimental study of modulation waveforms for entraining the spikes emitted by a semiconductor laser with optical feedback. Opt. Express 2018, 26, 9298–9309. [Google Scholar] [CrossRef]
- Prucnal, P.R.; Shastri, B.J.; de Lima, T.F.; Nahmias, M.A.; Tait, A.N. Recent progress in semiconductor excitable lasers for photonic spike processing. Adv. Opt. Photonics 2016, 8, 228–299. [Google Scholar] [CrossRef]
- Masoliver, M.; Masoller, C. Sub-threshold signal encoding in coupled FitzHugh-Nagumo neurons. Sci. Rep. 2018, 8, 8276. [Google Scholar] [CrossRef]
- Takiguchi, Y.; Fujino, H.; Ohtsubo, J. Experimental synchronization of chaotic oscillations in externally injected semiconductor lasers in a low-frequency fluctuation regime. Opt. Lett. 1999, 24, 1570–1572. [Google Scholar] [CrossRef] [PubMed]
- Locquet, A.; Masoller, C.; Mirasso, C.R. Synchronization regimes of optical-feedback-induced chaos in unidirectionally coupled semiconductor lasers. Phys. Rev. E 2002, 65, 056205. [Google Scholar] [CrossRef] [Green Version]
| Symbol | Parameter | Value |
|---|---|---|
| G | Gain coefficient | 1.5 × 104 m3/s |
| τn | Carrier lifetime | 2 × 10−9 s |
| τp | Photon lifetime | 2 × 10−12 s |
| N0 | Carrier density at transparency | 1.5 × 108 m−3 |
| ε | Gain saturation coefficient | 0.05 |
| τ | Feedback delay time | 1 × 10−9 s |
| V | Active region volume | 1.5 × 10−16 m3 |
| Serial Number | Word | Relation | Quantity |
|---|---|---|---|
| 1 | 012 | n1 | |
| 2 | 021 | n2 | |
| 3 | 102 | n3 | |
| 4 | 120 | n4 | |
| 5 | 201 | n5 | |
| 6 | 210 | n6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, X.; Qiu, S.; Wu, W. Numerical Demonstration of the Transmission of Low Frequency Fluctuation Dynamics Generated by a Semiconductor Laser with Optical Feedback. Photonics 2022, 9, 483. https://doi.org/10.3390/photonics9070483
Dou X, Qiu S, Wu W. Numerical Demonstration of the Transmission of Low Frequency Fluctuation Dynamics Generated by a Semiconductor Laser with Optical Feedback. Photonics. 2022; 9(7):483. https://doi.org/10.3390/photonics9070483
Chicago/Turabian StyleDou, Xinyu, Shimeng Qiu, and Wanqing Wu. 2022. "Numerical Demonstration of the Transmission of Low Frequency Fluctuation Dynamics Generated by a Semiconductor Laser with Optical Feedback" Photonics 9, no. 7: 483. https://doi.org/10.3390/photonics9070483
APA StyleDou, X., Qiu, S., & Wu, W. (2022). Numerical Demonstration of the Transmission of Low Frequency Fluctuation Dynamics Generated by a Semiconductor Laser with Optical Feedback. Photonics, 9(7), 483. https://doi.org/10.3390/photonics9070483




