Toroidal Dipole Excitation in Metamaterial Perfect Absorber Consisting of Dielectric Nanodisks Quadrumer Clusters and Spacer on Metal Substrate
Abstract
:1. Introduction
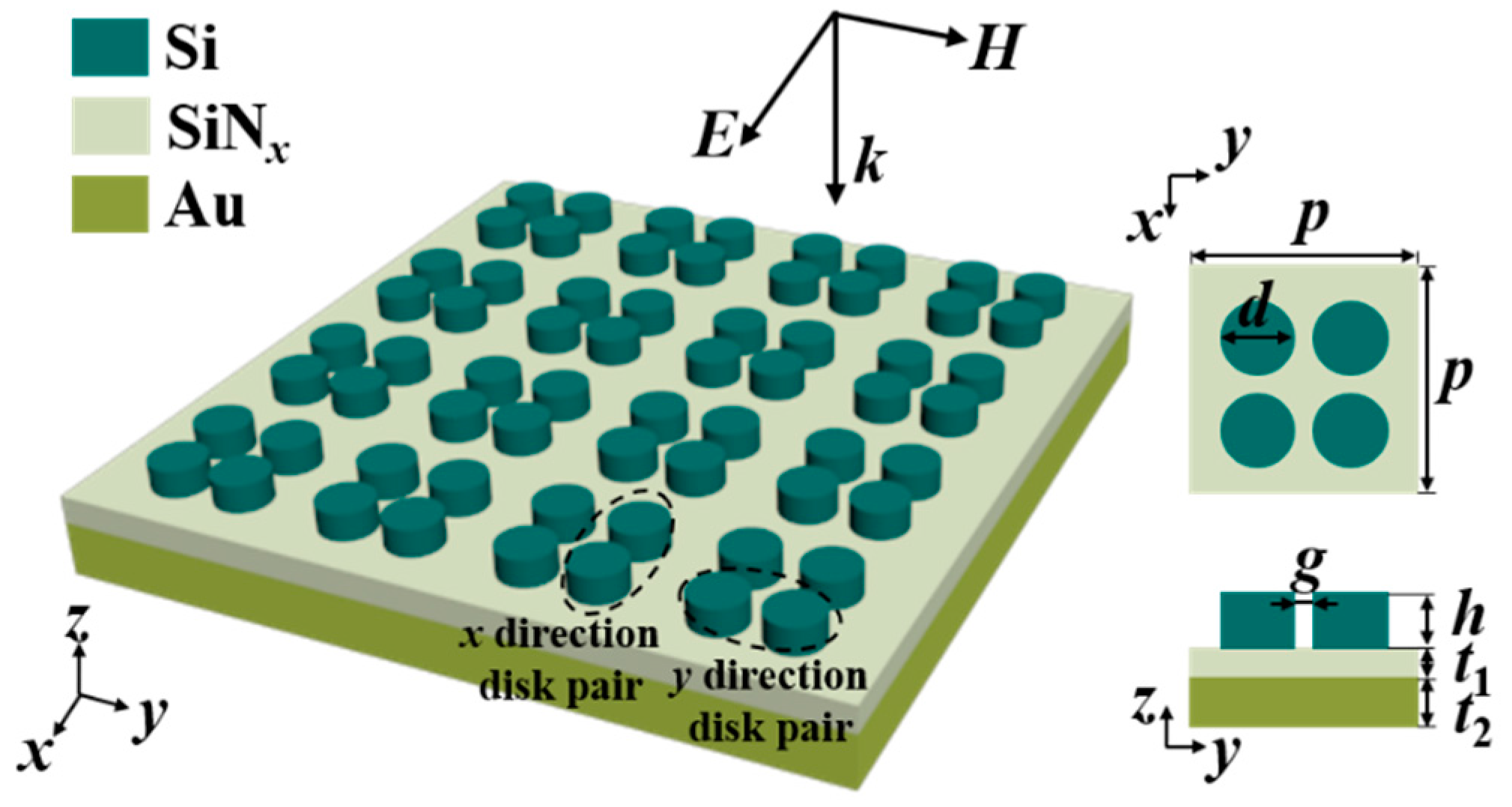
2. Model and Method
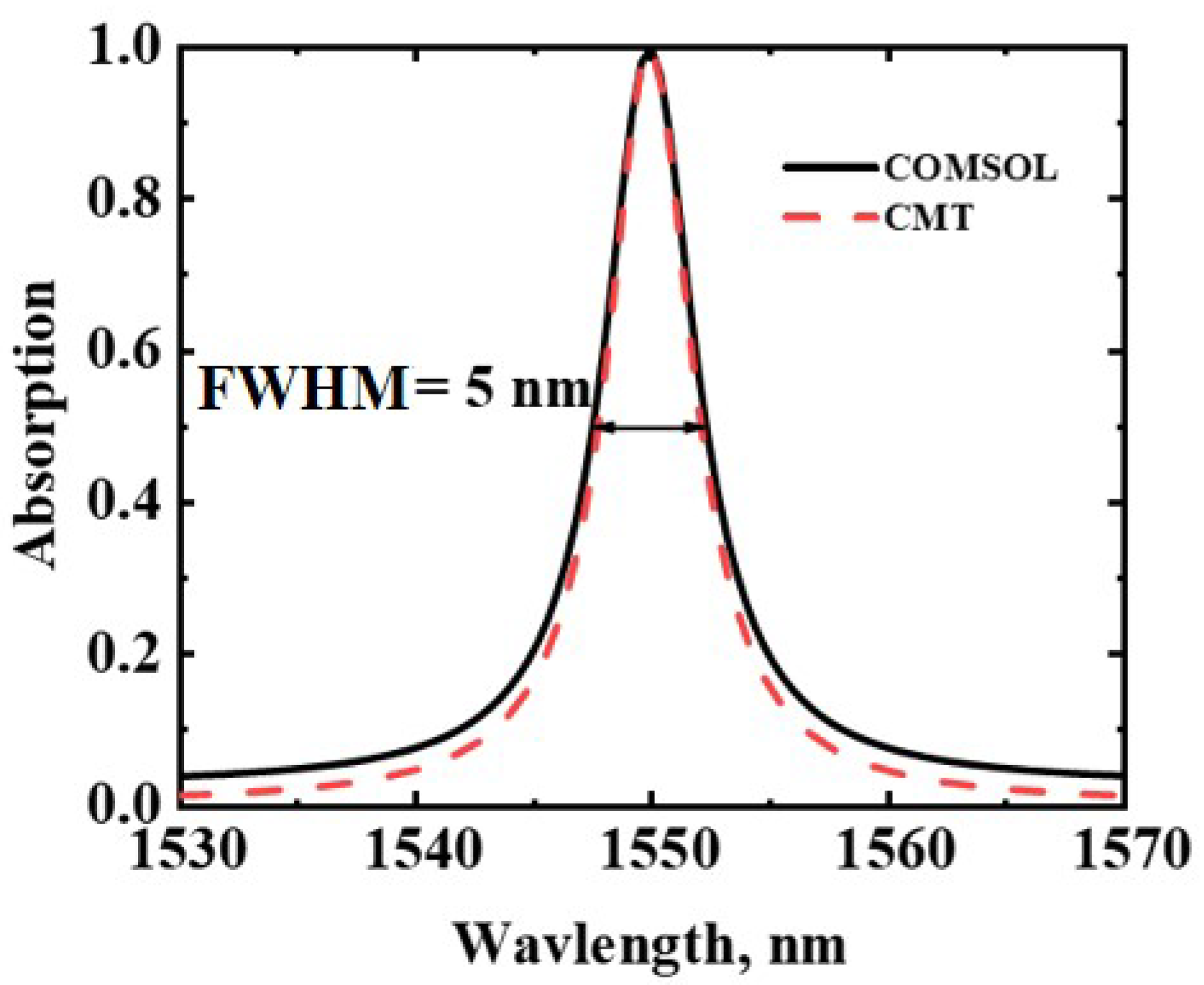
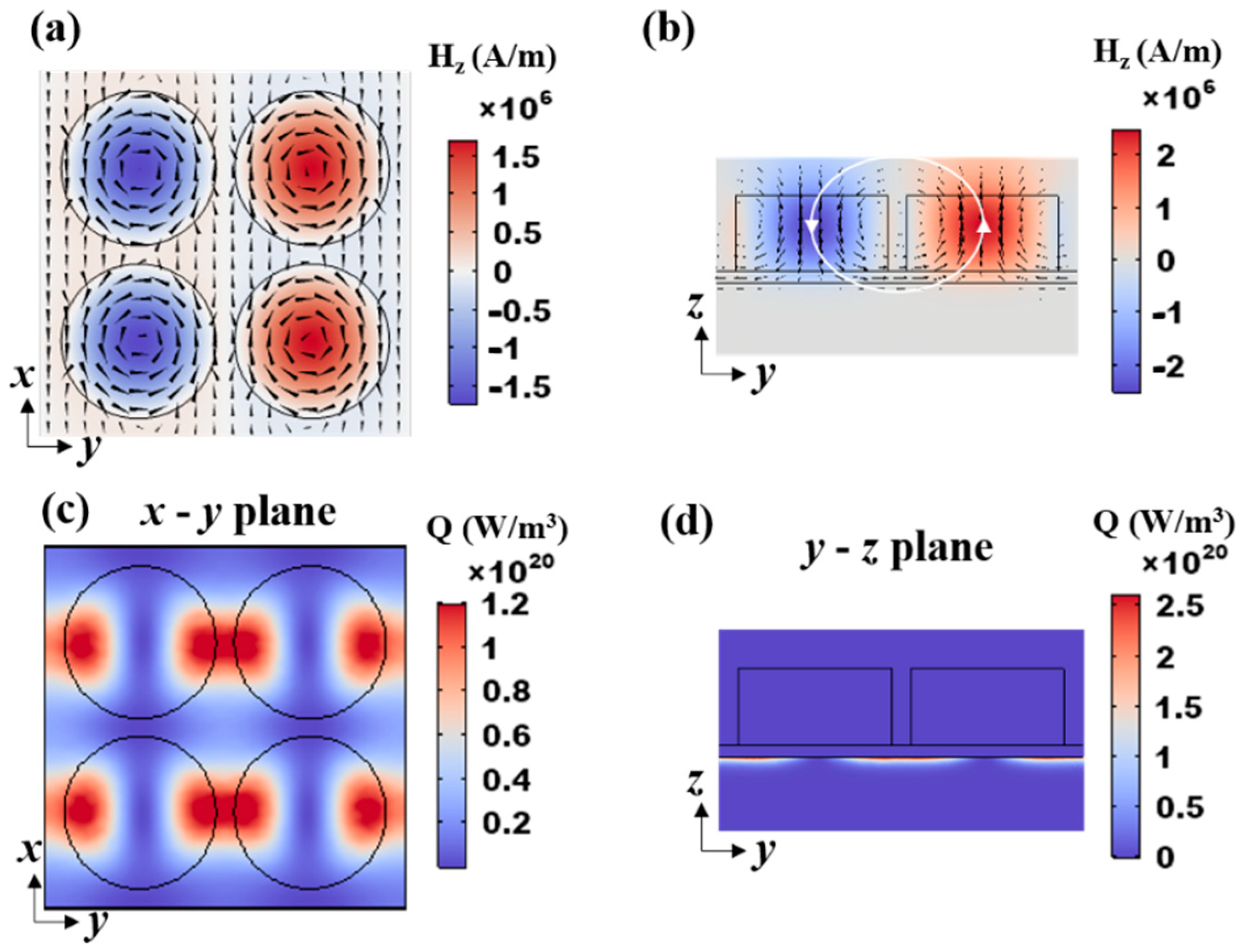
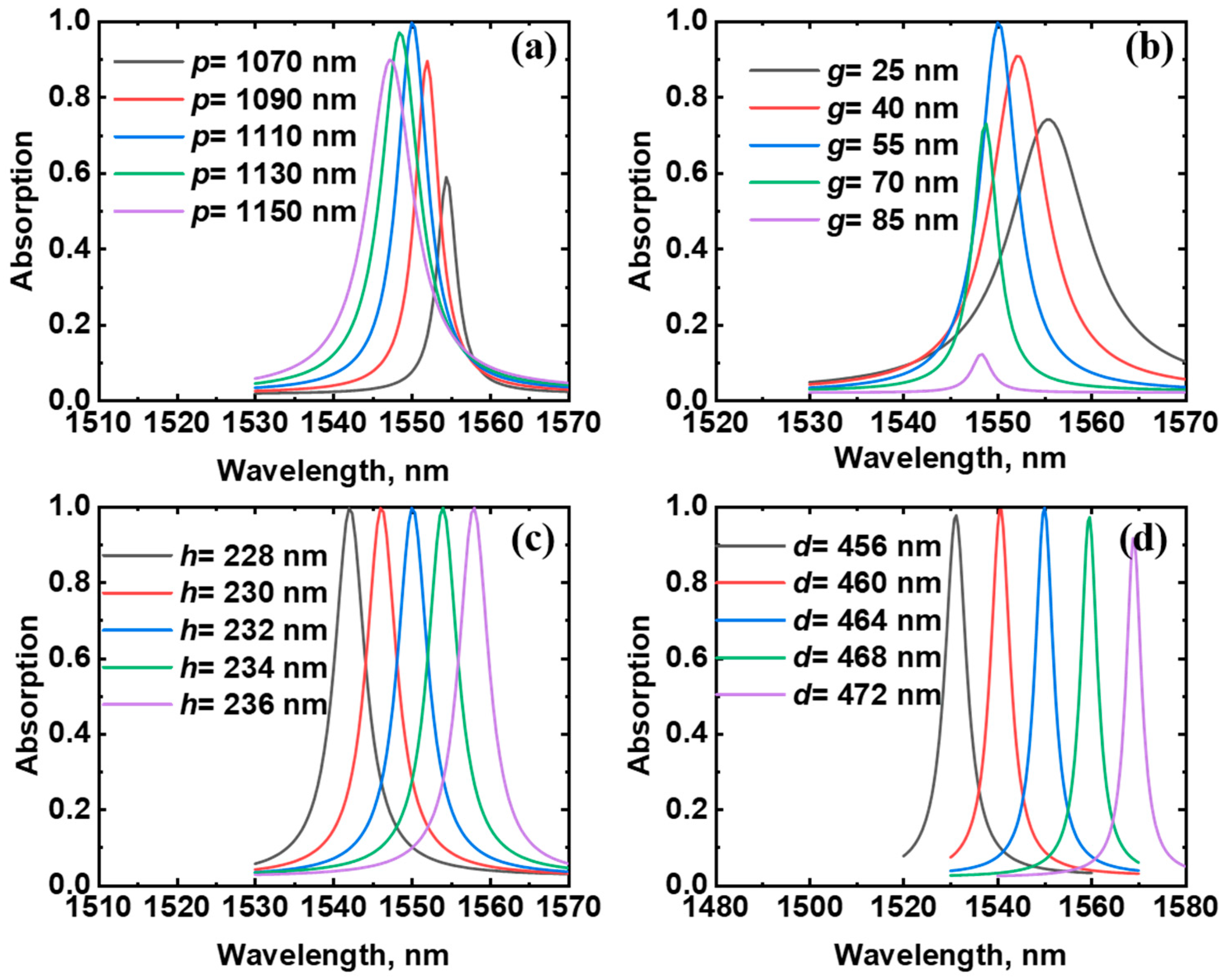
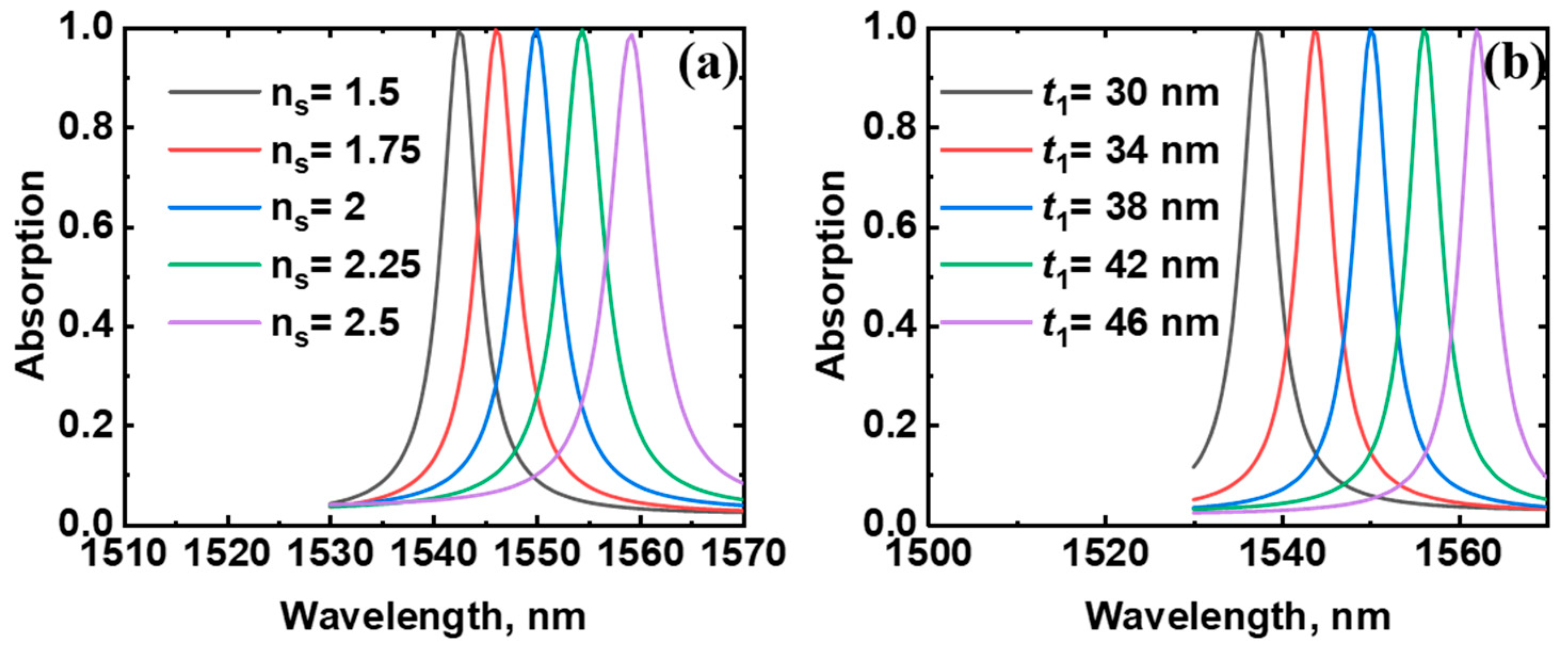
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, Y.; He, Y.; Jin, Y.; Ding, F.; Yang, L.; Ye, Y.; Zhong, S.; Lin, Y.; He, S. Plasmonic and Metamaterial Structures as Electromagnetic Absorbers. Laser Photon. Rev. 2014, 8, 495–520. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-C.; Kort-Kamp, W.J.M.; Nogan, J.; Luk, T.S.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.R.; Sykora, M.; Chen, H.-T. High-Temperature Refractory Metasurfaces for Solar Thermophotovoltaic Energy Harvesting. Nano Lett. 2018, 18, 7665–7673. [Google Scholar] [CrossRef]
- Silva-Oelker, G.; Jerez-Hanckes, C.; Fay, P. High-Temperature Tungsten-Hafnia Optimized Selective Thermal Emitters for Thermophotovoltaic Applications. J. Quant. Spectrosc. Radiat. Transf. 2019, 231, 61–68. [Google Scholar] [CrossRef]
- Kim, J.; Han, K.; Hahn, J.W. Selective Dual-Band Metamaterial Perfect Absorber for Infrared Stealth Technology. Sci. Rep. 2017, 7, 6740. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, H.; He, Z.; Dong, S. All-Metal Frequency-Selective Absorber/Emitter for Laser Stealth and Infrared Stealth. Appl. Opt. 2018, 57, 1757. [Google Scholar] [CrossRef]
- Raman, A.P.; Anoma, M.A.; Zhu, L.; Rephaeli, E.; Fan, S. Passive Radiative Cooling below Ambient Air Temperature under Direct Sunlight. Nature 2014, 515, 540–544. [Google Scholar] [CrossRef]
- Hervé, A.; Drévillon, J.; Ezzahri, Y.; Joulain, K. Radiative Cooling by Tailoring Surfaces with Microstructures: Association of a Grating and a Multi-Layer Structure. J. Quant. Spectrosc. Radiat. Transf. 2018, 221, 155–163. [Google Scholar] [CrossRef]
- Wang, K.; Hu, H.; Lu, S.; Jin, M.; Wang, Y.; He, T. Visible and Near-Infrared Dual-Band Photodetector Based on Gold–Silicon Metamaterial. Appl. Phys. Lett. 2020, 116, 203107. [Google Scholar] [CrossRef]
- Luxmoore, I.J.; Liu, P.Q.; Li, P.; Faist, J.; Nash, G.R. Graphene–Metamaterial Photodetectors for Integrated Infrared Sensing. ACS Photonics 2016, 3, 936–941. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Dănilă, O. Spectroscopic Assessment of a Simple Hybrid Si-Au Cell Metasurface-Based Sensor in the Mid-Infrared Domain. J. Quant. Spectrosc. Radiat. Transf. 2020, 254, 107209. [Google Scholar] [CrossRef]
- Chen, J.; Nie, H.; Tang, C.; Cui, Y.; Yan, B.; Zhang, Z. Highly sensitive refractive-index sensor based on strong magnetic resonance in metamaterials. Appl. Phys. Express 2019, 12, 052015. [Google Scholar] [CrossRef]
- Chen, J.; Peng, C.; Qi, S.; Zhang, Q.; Tang, C.; Shen, X. Photonic Microcavity-Enhanced Magnetic Plasmon Resonance of Metamaterials for Sensing Applications. IEEE Photonics Technol. Lett. 2019, 31, 113–116. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Y.; Zhu, B.; Zhao, J.; Jiang, T. Graphene Based Tunable Metamaterial Absorber and Polarization Modulation in Terahertz Frequency. Opt. Express 2014, 22, 22743. [Google Scholar] [CrossRef]
- Chen, J.; Chen, S.; Gu, P.; Yan, Z.; Tang, C.; Xu, Z.; Liu, B.; Liu, Z. Electrically Modulating and Switching Infrared Absorption of Monolayer Graphene in Metamaterials. Carbon N. Y. 2020, 162, 187–194. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Ha, D.T.; Tung, B.S.; Khuyen, B.X.; Pham, T.S.; Tung, N.T.; Tung, N.H.; Hoa, N.T.; Lam, V.D.; Zheng, H.; Chen, L.; et al. Dual-Band, Polarization-Insensitive, Ultrathin and Flexible Metamaterial Absorber Based on High-Order Magnetic Resonance. Photonics 2021, 8, 574. [Google Scholar] [CrossRef]
- Yang, C.-Y.; Yang, J.-H.; Yang, Z.-Y.; Zhou, Z.-X.; Sun, M.-G.; Babicheva, V.E.; Chen, K.-P. Nonradiating Silicon Nanoantenna Metasurfaces as Narrowband Absorbers. ACS Photonics 2018, 5, 2596–2601. [Google Scholar] [CrossRef]
- Cai, Y.; Huang, Y.; Zhu, K.; Wu, H. Direction-Independent Dual-Band Perfect Absorption Induced by Fundamental Magnetic Polaritons. Opt. Express 2019, 27, A1431. [Google Scholar] [CrossRef]
- Shamkhi, H.K.; Sayanskiy, A.; Valero, A.C.; Kupriianov, A.S.; Kapitanova, P.; Kivshar, Y.S.; Shalin, A.S.; Tuz, V.R. Transparency and Perfect Absorption of All-Dielectric Resonant Metasurfaces Governed by the Transverse Kerker Effect. Phys. Rev. Mater. 2019, 3, 085201. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Koshelev, K.; Zhang, F.; Lin, H.; Lin, S.; Wu, J. Bound States in the Continuum in Anisotropic Plasmonic Metasurfaces. Nano Lett. 2020, 20, 6351–6356. [Google Scholar] [CrossRef]
- Talebi, N.; Guo, S.; van Aken, P.A. Theory and Applications of Toroidal Moments in Electrodynamics: Their Emergence, Characteristics, and Technological Relevance. Nanophotonics 2018, 7, 93–110. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, R. Toroidal Metasurfaces in a 2D Flatland. Rev. Phys. 2020, 5, 100040. [Google Scholar] [CrossRef]
- Kaelberer, T.; Fedotov, V.A.; Papasimakis, N.; Tsai, D.P.; Zheludev, N.I. Toroidal Dipolar Response in a Metamaterial. Science 2010, 330, 1510–1512. [Google Scholar] [CrossRef] [Green Version]
- Stenishchev, I.V.; Basharin, A.A. Toroidal Response in All-Dielectric Metamaterials Based on Water. Sci. Rep. 2017, 7, 9468. [Google Scholar] [CrossRef] [Green Version]
- Marinov, K.; Boardman, A.D.; Fedotov, V.A.; Zheludev, N. Toroidal Metamaterial. New J. Phys. 2007, 9, 324. [Google Scholar] [CrossRef]
- Huang, Y.-W.; Chen, W.T.; Wu, P.C.; Fedotov, V.; Savinov, V.; Ho, Y.Z.; Chau, Y.-F.; Zheludev, N.I.; Tsai, D.P. Design of Plasmonic Toroidal Metamaterials at Optical Frequencies. Opt. Express 2012, 20, 1760. [Google Scholar] [CrossRef] [Green Version]
- Ögüt, B.; Talebi, N.; Vogelgesang, R.; Sigle, W.; Van Aken, P.A. Toroidal Plasmonic Eigenmodes in Oligomer Nanocavities for the Visible. Nano Lett. 2012, 12, 5239. [Google Scholar] [CrossRef]
- Tang, C.; Yan, B.; Wang, Q.; Chen, J.; Yan, Z.; Liu, F.; Chen, N.; Sui, C. Toroidal Dipolar Excitation in Metamaterials Consisting of Metal Nanodisks and a Dielectrc Spacer on Metal Substrate. Sci. Rep. 2017, 7, 582. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Wei, Z.; Li, H.; Chen, H.; Soukoulis, C.M. Low-Loss and High-Q Planar Metamaterial with Toroidal Moment. Phys. Rev. B 2013, 87, 115417. [Google Scholar] [CrossRef] [Green Version]
- Tuz, V.R.; Khardikov, V.V.; Kivshar, Y.S. All-Dielectric Resonant Metasurfaces with a Strong Toroidal Response. ACS Photonics 2018, 5, 1871–1876. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Zhang, Q.; Wang, Y. Dual-Toroidal Dipole Excitation on Permittivity-Asymmetric Dielectric Metasurfaces. Opt. Lett. 2020, 45, 2826–2829. [Google Scholar] [CrossRef]
- Wang, W.; Qi, J. Polarization Sensitive Toroidal Dipole Metasurface for Switch and Magnetic Field Tunability. Appl. Phys. Express 2019, 12, 065004. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Jin, R.; Li, J.; Dong, Z. Toroidal-Dipole Induced Plasmonic Perfect Absorber. J. Phys. D. Appl. Phys. 2017, 50, 485301. [Google Scholar] [CrossRef]
- Li, J.; Zhai, Y.; Li, W.; Cao, Y.; Dong, Z. Perfect Absorption Induced by Plasmon Toriodal Mode for Hot Electron Based NIR Photo-Detection. Appl. Phys. Express 2020, 13, 122003. [Google Scholar] [CrossRef]
- Luo, J.; Lin, Q.; Wang, L.; Xia, S.; Meng, H.; Zhai, X. Ultrasensitive Tunable Terahertz Sensor Based on Five-Band Perfect Absorber with Dirac Semimetal. Opt. Express 2019, 27, 20165. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Z.; Liu, J.; Cheng, J.; Zhou, Y.; Xiao, L.; Chen, K. Ultra-Narrow Band Mid-Infrared Perfect Absorber Based on Hybrid Dielectric Metasurface. Nanomaterials 2019, 9, 1350. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.P.; Basu, S.; Zhang, Z.M. Direct Measurement of Thermal Emission from a Fabry–Perot Cavity Resonator. J. Heat Transf. 2012, 134, 72701–72709. [Google Scholar] [CrossRef]
- Duttagupta, S.; Ma, F.; Hoex, B.; Mueller, T.; Aberle, A.G. Optimised Antireflection Coatings Using Silicon Nitride on Textured Silicon Surfaces Based on Measurements and Multidimensional Modelling. Energy Procedia 2012, 15, 78–83. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.C.; Liao, C.Y.; Savinov, V.; Chung, T.L.; Chen, W.T.; Huang, Y.-W.; Wu, P.R.; Chen, Y.-H.; Liu, A.-Q.; Zheludev, N.I.; et al. Optical Anapole Metamaterial. ACS Nano 2018, 12, 1920–1927. [Google Scholar] [CrossRef] [Green Version]
- Piper, J.R.; Fan, S. Total Absorption in a Graphene Monolayer in the Optical Regime by Critical Coupling with a Photonic Crystal Guided Resonance. ACS Photonics 2014, 1, 347–353. [Google Scholar] [CrossRef]
- Liu, G.-D.; Zhai, X.; Meng, H.-Y.; Lin, Q.; Huang, Y.; Zhao, C.-J.; Wang, L.-L. Dirac Semimetals Based Tunable Narrowband Absorber at Terahertz Frequencies. Opt. Express 2018, 26, 11471. [Google Scholar] [CrossRef]
- Yao, Y.; Kats, M.A.; Genevet, P.; Yu, N.; Song, Y.; Kong, J.; Capasso, F. Broad Electrical Tuning of Graphene-Loaded Plasmonic Antennas. Nano Lett. 2013, 13, 1257–1264. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Shi, D. Perfect Absorption for Monolayer Transition-Metal Dichalcogenides by Critical Coupling. Nanotechnology 2020, 31, 465205. [Google Scholar] [CrossRef]
- Xiang, J.; Xu, Y.; Chen, J.-D.; Lan, S. Tailoring the Spatial Localization of Bound State in the Continuum in Plasmonic-Dielectric Hybrid System. Nanophotonics 2020, 9, 133–142. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Huang, Y.; Zhu, K. Toroidal Dipole Excitation in Metamaterial Perfect Absorber Consisting of Dielectric Nanodisks Quadrumer Clusters and Spacer on Metal Substrate. Photonics 2022, 9, 462. https://doi.org/10.3390/photonics9070462
Cai Y, Huang Y, Zhu K. Toroidal Dipole Excitation in Metamaterial Perfect Absorber Consisting of Dielectric Nanodisks Quadrumer Clusters and Spacer on Metal Substrate. Photonics. 2022; 9(7):462. https://doi.org/10.3390/photonics9070462
Chicago/Turabian StyleCai, Yuepei, Yong Huang, and Keyong Zhu. 2022. "Toroidal Dipole Excitation in Metamaterial Perfect Absorber Consisting of Dielectric Nanodisks Quadrumer Clusters and Spacer on Metal Substrate" Photonics 9, no. 7: 462. https://doi.org/10.3390/photonics9070462
APA StyleCai, Y., Huang, Y., & Zhu, K. (2022). Toroidal Dipole Excitation in Metamaterial Perfect Absorber Consisting of Dielectric Nanodisks Quadrumer Clusters and Spacer on Metal Substrate. Photonics, 9(7), 462. https://doi.org/10.3390/photonics9070462



