Analysis of Combination Frequencies Arising from the Ionization of Gases by Multicolor Femtosecond Pulses

Abstract

Ionization-induced multiwave mixing is attracting much interest nowadays due to the possibility of generating short pulses of secondary radiation over a very wide spectral range, from terahertz to far ultraviolet. This paper presents an analytical method for calculating the amplitudes of arbitrary spectral components of free electron currents arising under the action of multicolor ionizing laser pulses. We show that this method can be used to obtain the dependences of characteristics of a frequency-tunable third harmonic of the intense component of a three-color pulse obtained in an optical parametric generator. The obtained results are in good agreement with quantum mechanical calculations.

1. Introduction

At present, the processes associated with the generation of secondary radiation in gases under the action of ionizing laser pulses are widely studied in connection with the possibility of creating compact sources of frequency-tunable super-broadband coherent radiation in wide ranges of central wavelengths (100–10,000 nm) [1,2,3,4,5]. Within this range, several different subranges can be distinguished, each of which is relevant for different applied areas; as a rule, such ultrashort pulses are in demand for ultra-precise measurements and spectroscopy [6,7], control of various quantum or chemical processes [8,9], biomedical imaging [10], while the possibility of frequency tuning further expands the range of applicability of such sources. This can be done using the frequency tuning of the ionizing pulse components in optical parametric generators [11,12,13]. Recently, the possibility of using multi-color (three or more) pulses instead of traditional two-color ionizing pulses has been increasingly investigated [13,14,15,16]. The solution of optimization problems for such systems is complicated by the fact that the extremely nonlinear nature of ionization-induced multiwave mixing (IMWM) manifests itself in a strong interdependence of the optimal values of each pulse parameter on the values of all others [14,17,18,19].

In this work, we propose a new method for calculating the combination frequencies in the spectrum of the free electron current generated under the action of a multicolor laser pulse. This method does not rely on the smallness of the intensities of any components compared to others, or on a large number of mixing waves, and is also suitable for arbitrary elliptical polarizations of quasimonochromatic components. We show that our results are in good agreement with the solutions of three-dimensional time-dependent Schrödinger equation.

Section 2 of this paper contains a description of the semiclassical approach and the derivation of closed expressions for combination frequencies in the free electron current spectrum. Section 3 presents the results of semiclassical and quantum-mechanical numerical calculations for two- and three-color ionizing pulses with different polarizations of the quasimonochromatic components and the discussion of the obtained results.

2. Analytical Model

In our analytical model, we use the so-called semiclassical approach [2,4,5,14,17,19]. To calculate the current density of free electrons generated by the laser field, we use the system of equations

$$\begin{array}{c}\frac{\partial N}{\partial t}=(N_{\mathrm{m}}-N)w\left(\right|\mathbf{E}\left|\right),\end{array}$$

(1)

$$\begin{array}{c}\frac{\partial \mathbf{j}}{\partial t}=\frac{e^2}{m}N\mathbf{E},\end{array}$$

(2)

with the initial conditions $N(t\to -\infty )=0$, $\mathbf{j}(t\to -\infty )=0$. Here, N is free-electron density, $N_{\mathrm{m}}$ is initial density of neutral particles, $w\left(\right|\mathbf{E}\left|\right)$ is tunneling ionization probability per unit time under the action of electric field $\mathbf{E}$, $\mathbf{j}$ is the free-electron current density, e and m are electron charge and mass.

The electric field is given by

$$\mathbf{E}=f\left(t\right)\sum _{k=1}^l{\mathbf{E}}_k{e}^{i{a}_k{\omega }_{0}t}+c.c.,$$

(3)

where $f\left(t\right)$ is a slow envelope, $a_k$ are some natural numbers, l is the total number of quasimonochromatic components of the pulse, ${\mathbf{E}}_k$ are the complex amplitudes of components with frequencies $a_k{\omega }_0$

$${\mathbf{E}}_k=E_{kx}{e}^{i{\varphi }_{kx}}{\mathbf{x}}_0+E_{ky}{e}^{i{\varphi }_{ky}}{\mathbf{y}}_0,$$

(4)

${\mathbf{x}}_0$ and ${\mathbf{y}}_0$ are unit vectors along X and Y axes, $E_{kx,y}$ and ${\varphi }_{kx,y}$ are the amplitudes of projections and phase shifts. In this case, we do not assume the field as a successive series of harmonics, ${\omega }_0$ has the meaning of the least common divisor of frequencies (or the least common multiple of wavelengths) for example, for a pulse of two components at 800 nm and 1200 nm, such a frequency will correspond to a wavelength of 2400 nm (and such a pulse itself, within the framework of the proposed theory, should be understood as a combination of the second and third harmonics of this fundamental frequency). We do not assume that $a_k$ are small, and the following calculations are also applicable to incommensurate multicolor laser pulses.

Since the carrier of laser field is periodic with a period $2\pi /{\omega }_0$, we can also represent the dependence of the ionization probability on time as a superposition of harmonics of the fundamental frequency:

$$w\left(\right|\mathbf{E}\left(t\right)\left|\right)=\sum w_s{e}^{is{\omega }_{0}t},$$

(5)

where $w_s$ are slow amplitudes. Moreover, the derivative of the free electron current density can also be expanded in a similar series $d\mathbf{j}/dt=\sum d{\mathbf{j}}_s/dt{e}^{is{\omega }_{0}t}$, with coefficients

$$\frac{d{\mathbf{j}}_s}{dt}\approx \frac{e^2}{im{w}_0{\omega }_0}\frac{d\overline{N}}{dt}\sum _{k=1}^l\frac{{\mathbf{E}}_k{w}_{s-a_k}}{s-a_k}+\frac{{\mathbf{E}}_k^{*}{w}_{s+a_k}}{s+a_k},$$

(6)

where $\overline{N}\left(t\right)=N_m[1-exp(-{\int }_{-\infty }^t{w}_0\left(t^{\prime }\right)d{t}^{\prime })]$. These amplitudes of the spectral components of $d\mathbf{j}/dt$ determine the energy spectrum of the secondary radiation generated during the ionization of a gas target. So far, the only unknown quantities in expressions (5) and (6) are the amplitudes $w_s$, the rest of this subsection is devoted to finding their values.

Traditionally, the polynomial dependence of the ionization probability on the strength of the ionizing field is associated with the multiphoton ionization regime. In this paper, we propose the use of the polynomial approximation also for the probability of tunneling ionization, for example, given by the expression [20]

$$w\left(\right|\mathbf{E}\left|\right)=4{\mathrm{\Omega }}_a\frac{E_a}{\left|\mathbf{E}\right|}exp\left(-\frac{2E_a}{3\left|\mathbf{E}\right|}-\frac{12\left|\mathbf{E}\right|}{E_a}\right),$$

(7)

where $E_a$ and ${\mathrm{\Omega }}_a$ are atomic field and frequency. For practical purposes, it is sufficient to carry out such an approximation for a segment limited by the value of $E_{\lim }$, equal to the sum of the amplitudes of all quasi-monochromatic components of the ionizing pulse (since the field strength modulus cannot exceed this sum). The use of polynomial approximation makes it possible, as will be shown below, to express the combination components amplitudes as finite sums of combinations of the ionizing pulse parameters.

There are several different ways to expand a given function on a segment into a polynomial series, for example, using Legendre polynomials that form an orthogonal system on the segment [−1, 1] [21]. Since the argument of w is strictly positive, it is convenient for us to extend it in an even way to the region of negative values. For linearly polarized fields, this corresponds to using the field strength projection E as an argument of this function. The n-th Legendre polynomial is defined by a formula $P_n\left(z\right)=\frac{1}{2^{n}n!}\frac{d^n}{d{z}^n}{(z^2-1)}^n$ (in our case $z=E/E_{\lim }$), and the expansion coefficients for decomposition $w\left(z\right)=\sum {\alpha }_n{P}_n\left(z\right)$ for an arbitrary function can be calculated as ${\alpha }_n=\left({\int }_{-1}^{1}w\left(z\right)P_n\left(z\right)dz\right)/\left({\int }_{-1}^1{P}_n^2\left(z\right)dz\right)$ (since w is a function of the modulus of the field strength, we can use only even polynomials and integrate from 0 to 1). This series converges to the original smooth function at each point, and the remainder term for the final expansion satisfies the condition of the least square deviation from the original function. There are other ways of approximating a given function by a polynomial; we will carry out further reasoning for an arbitrary polynomial, without relying on specific methods of expanding the function. As a suggestion, for simplicity one can use a binomial approximation of the form

$$w_{\mathrm{bin}}\left(E\right)=w\left(E_{\lim }\right)\left((n_0-n_1){(E/E_{\lim })}^{n_1+2}+(n_1+2-n_0){(E/E_{\lim })}^{n_1}\right)/2,$$

(8)

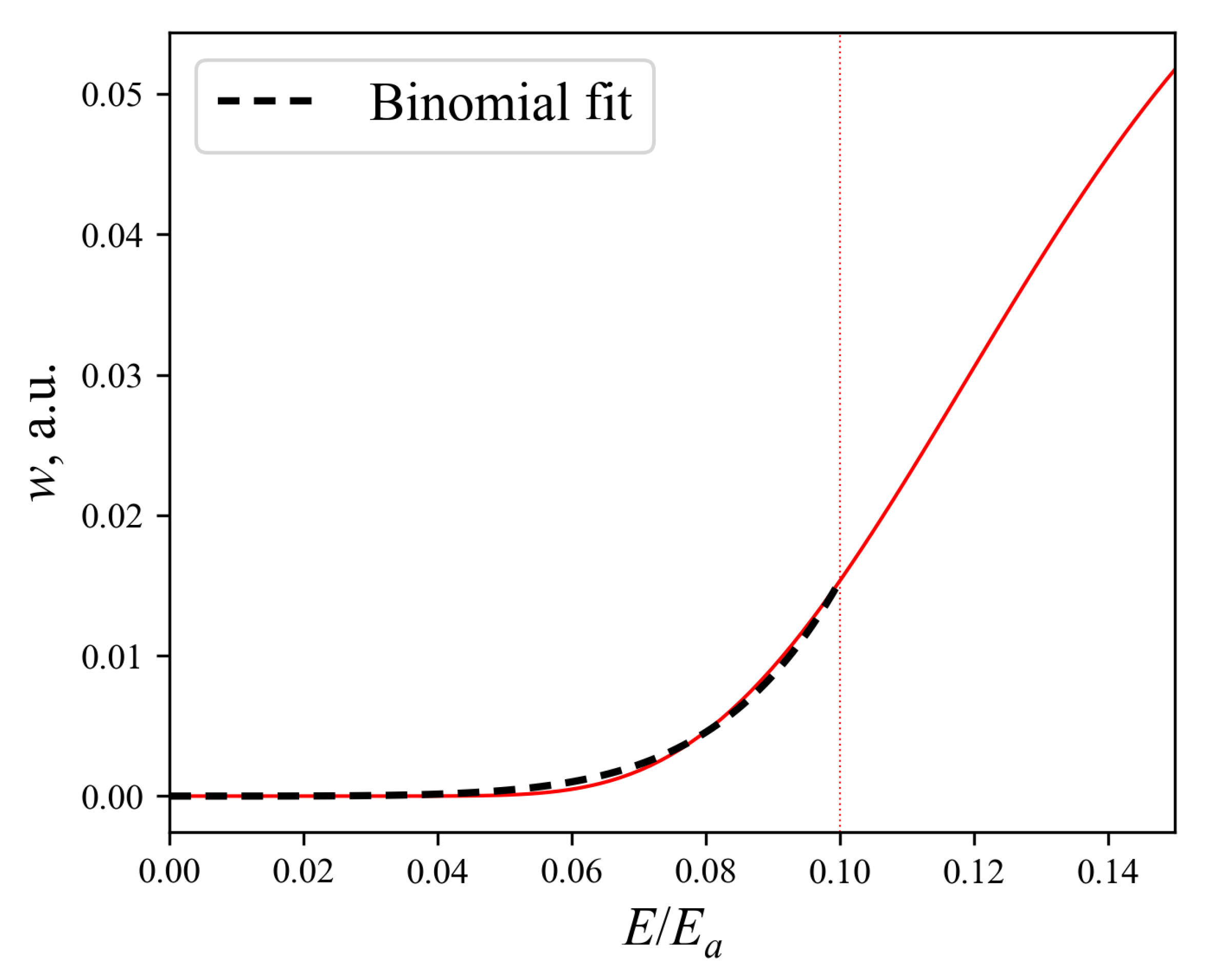
where $n_0=E_{\lim }{w}^{\prime }\left(E_{\lim }\right)/w\left(E_{\lim }\right)$ is the effective exponent of w at the point $E_{\lim }$, and $n_1=2\lfloor n_0/2\rfloor$. The comparison of the original function (7) with this approximation for $E_{\lim }=0.1E_a$ (which for a one-color pulse corresponds to intensity of $3.5\times {10}^{14}$ W/cm²) is shown in the Figure 1. This approximation is convenient primarily because it allows you to reduce the number of necessary calculations to a minimum. However, the error in such a binomial approximation is rather difficult to calculate accurately. On the contrary, when using expansions in Legendre or Chebyshev polynomials, we obtain a guaranteed smallness of the remainder term, from which, due to the linearity of the Fourier transform, follows the smallness of the error in estimating any combination frequency $w_s$.

Let us represent the square of the field modulus (3) in the form

$$\begin{array}{c}{\left|\mathbf{E}\left(t\right)\right|}^2/f^2\left(t\right)={\mathcal{I}}_0+({\displaystyle \sum _k}{\mathcal{I}}_{2a_k}{e}^{i2a_k{\omega }_{0}t}+\\ +{\displaystyle \sum _{n\ne m}}{\mathcal{I}}_{a_n+a_m}{e}^{i(a_n+a_m){\omega }_{0}t}+\sum _{n\ne m}{\mathcal{I}}_{a_n-a_m}{e}^{i(a_n-a_m){\omega }_{0}t}+c.c.),\\ {\mathcal{I}}_0={\displaystyle \sum _k}{\mathbf{E}}_k{\mathbf{E}}_k^{*},\\ {\mathcal{I}}_{2a_k}={\mathbf{E}}_k^2,{\mathcal{I}}_{a_n+a_m}=2{\mathbf{E}}_n{\mathbf{E}}_m,{\mathcal{I}}_{a_n-a_m}=2{\mathbf{E}}_n{\mathbf{E}}_m^{*}.\end{array}$$

(9)

Here, vector multiplication is a scalar product without complex conjugation, $\mathbf{X}\mathbf{Y}=\left(\mathbf{X}{\mathbf{Y}}^{*}\right)$. To calculate the harmonics of an even polynomial function, we use the following. Let us have the product of two Fourier series $(\sum A_s{e}^{ist})(\sum B_s{e}^{ist})=\sum C_s{e}^{ist},$ then $C_s={\sum }_k{A}_k{B}_{s-k}.$ By iterating this procedure, we can obtain an expression for the Fourier components of any even power of the field,

$${\left|\mathbf{E}\left(t\right)\right|}^{2n}/f^{2n}\left(t\right)=\sum {\mathcal{I}}_s^{\left(n\right)}{e}^{is{\omega }_{0}t},$$

(10)

where

$${\mathcal{I}}_s^{\left(n\right)}=\sum _{s_1,s_2,...,s_{n-1}}{\mathcal{I}}_{s_1}{\mathcal{I}}_{s_2}·...·{\mathcal{I}}_{s_{n-1}}{\mathcal{I}}_{s-s_1-s_2-...-s_{n-1}},$$

(11)

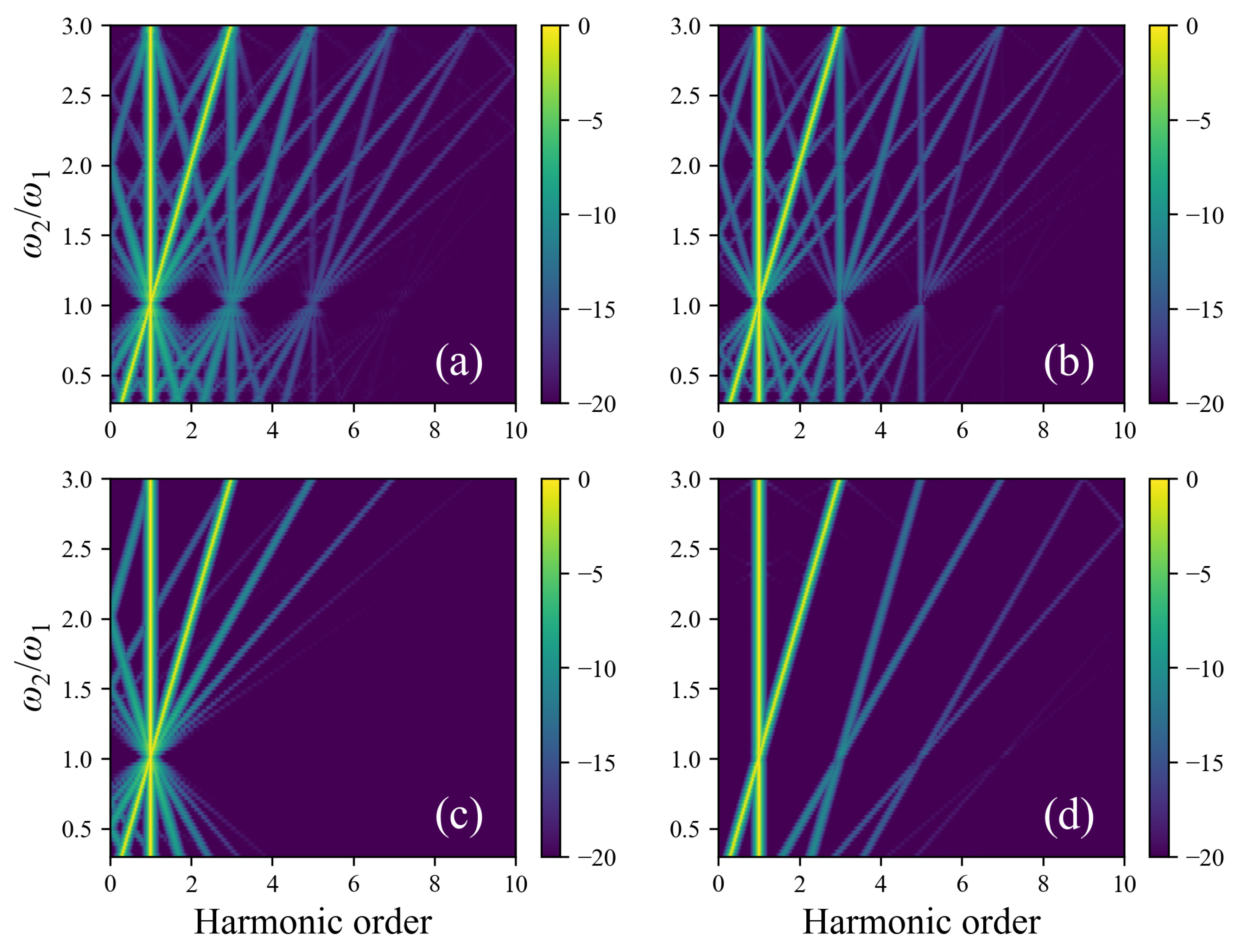
summation should be carried out over all non-zero components of ${\left|\mathbf{E}\left(t\right)\right|}^2$ in the expression (9). In certain cases, some of the terms in Equation (9) vanish, for example, for two circular components, either only the sum frequency remains (for opposite directions of polarization rotation) or only the difference frequency (for codirectional rotation), while for orthogonal linear polarizations, on the contrary, both the sum and difference frequencies vanish (see Figure 2).

Finally, for a polynomial

$$w\left(\right|\mathbf{E}\left(t\right)\left|\right)=\sum _n{\alpha }_n{\left|\mathbf{E}\left(t\right)\right|}^{2n},$$

(12)

we obtain

$$w_s=\sum _n{f}^{2n}\left(t\right){\alpha }_n{\mathcal{I}}_s^{\left(n\right)}.$$

(13)

Substituting (13) into (6) we obtain a closed analytical formula for the pulse shape of an arbitrary combination frequency of the generated secondary radiation.

The obtained analytical expressions, although not always compact, can be used by algorithms for the analytical calculation of the objective function and its derivatives in solving the problems of optimizing the generation of a given combination frequency in the secondary radiation spectrum [22]. The complexity of direct calculations of such optima can be quite large, since each quasi-monochromatic component, even with a given envelope shape, is characterized by a frequency and four more parameters that determine its polarization. In the next section of this work, we consider the simplest illustrative properties of this model, which are observed in the results of numerical calculations.

3. Numerical Calculations and Discussion

The above model may seem complicated to use: iterations in the expressions (6), (11) and (13) look unwieldy. However, in many cases these expressions can be simplified. Figure 2 shows the results of semiclassical calculations of the spectral components of $d\mathbf{j}/dt$ for two-color pulses with fixed intensities and durations of the components with a change in the frequency of one of the components, different subplots correspond to different polarizations of the components. The envelopes of the pulse components in the numerical calculations had Gaussian shapes,

$$f\left(t\right)=exp\left(-\frac{t^{2}ln4}{{\tau }_p^2}\right),$$

(14)

with the pulse FWHM duration ${\tau }_p=$ 50 fs and ${\omega }_1$ corresponding to the wavelength ${\lambda }_1=800$ nm. Ionization probability for a hydrogen atom was given by expression (7).

Collinear linear polarizations, which are most often used in calculations and in the construction of analytical models, give the most complex picture compared to other options. The fact is that the spectrum of the squared modulus of the field of such two-color pulses contains, in addition to the constant component, the doubled frequencies of both components, as well as the difference and sum frequencies, and all their combinations generated by a strongly nonlinear IMWM seem to be diverse. However, even in this case it is quite easy to analyze Figure 2a and understand from what combinations each of the pronounced spectral lines is obtained. At ${\omega }_2/{\omega }_1=1$ (this is simply the one-color field) the spectrum of $d\mathbf{j}/dt$ contains just odd harmonics. In other cases the spectrum contains all the combinations $a{\omega }_1+b{\omega }_2$ where $\left|a\right|+\left|b\right|$ is a small odd natural number, and the bigger this sum, the less efficient is the generation. We note here that setting the field in the form of expression (3) allows us, without additional constructions, to consider the cases of superposition of several channels of multiwave mixing (overlaps of bright straight lines on each of the subplots of Figure 2).

For other polarizations of the components, the analysis becomes much simpler. With orthogonal linear polarizations, the spectrum of ${\left|\mathbf{E}\left(t\right)\right|}^2$ contains only doubled frequencies of both field components, with codirectional circular polarizations only their difference frequency, and with oppositely rotating only the sum frequency. Accordingly, for bicircular pulses there are much fewer combinations of frequencies in $d\mathbf{j}/dt$ spectrum, which can be seen in Figure 2c,d.

In several recent experiments were demonstrated the generation of terahertz radiation under the action of two-color and three-color pulses, consisting of the main field at $\omega$ frequency and one or two additional waves from a parametric light generator, the frequencies of which can be detuned from $\omega /2$ by some small $\Delta \omega$. In this work we theoretically studied another effect for a three-color pulse with the frequencies of additional fields $\omega /2-\Delta \omega$ and $\omega /2+\Delta \omega$, which allows to generate a frequency-tunable third harmonic $3\omega +2\Delta \omega$.

For such a pulse we can use the proposed model to determine the interdependence of $d{\mathbf{j}}_{3\omega +2\Delta \omega }/dt$ on field amplitudes. The smallest order of wave mixing (number of mixing waves) in which the given component appears is 6. If we assign ${\mu }_1=E_{\omega /2+\Delta \omega }/E_{\omega }$ and ${\mu }_2=E_{\omega /2-\Delta \omega }/E_{\omega }$, and set all three phases to zero, we obtain

$$\frac{d{\mathbf{j}}_{3\omega +2\Delta \omega }}{dt}\propto {\mu }_1{\mu }_2\left(\frac{{(1+{\mu }_1)}^2}{\omega +\Delta \omega }+\frac{2+6{\mu }_1^2}{2.5\omega +3\Delta \omega }+\frac{2}{3.5\omega +\Delta \omega }+\frac{2{\mu }_1^2}{2.5\omega +3\Delta \omega }\right)/w_0,$$

(15)

where $w_0\propto (1+{\mu }_1^4+{\mu }_2^4+4[{\mu }_1^2+{\mu }_2^2+{\mu }_1^2{\mu }_2^2])$.

The obtained analytical results were also compared with the numerical solutions of the three-dimensional time-dependent Schrödinger equation (3D TDSE)

$$i\hslash \frac{\partial }{\partial t}\psi (\mathbf{r},t)=\left[-\frac{{\hslash }^2}{2m}{\nabla }^2-e\mathbf{r}\mathbf{E}\left(t\right)+V\left(r\right)\right]\psi (\mathbf{r},t),$$

(16)

where $\psi (\mathbf{t},t)$ is the electron wavefunction, ℏ is the reduced Plank constant, $V\left(r\right)$ is the parent ion potential. The used potential $V\left(r\right)$ for He atom is found based on the density functional theory [23]. The numerical 3D TDSE solution was performed similarly to [23] using expansion of the wavefunction in spherical harmonics with maximum orbital momentum $l_{max}=256$ and with radial boundary at $r_{max}=200r_B$ (where $r_B$ is Bohr radius). The generated radiation is characterized by Fourier spectrum ${\mathbf{a}}_{\omega }=\int \mathbf{a}\left(t\right)e^{i\omega t}dt$ of the atom dipole acceleration $\mathbf{a}\left(t\right)$, which determines the time derivative of the electron current density, $\partial \mathbf{j}/\partial t$:

$$\frac{\partial \mathbf{j}}{\partial t}=e{N}_m\mathbf{a},\mathbf{a}=\frac{e}{m}\left[\mathbf{E}-\langle \psi |\nabla V|\psi \rangle \right].$$

(17)

The semiclassical model uses the ionization probability rate for He atom [20],

$$w_{\mathrm{He}}\left(\right|\mathbf{E}\left|\right)=C_l^2\frac{1}{2k^{2/k-1}}{\left(\frac{2k^3}{\left|\mathbf{E}\right|}\right)}^{2/k-1}exp\left(-\frac{2k^3}{3\left|\mathbf{E}\right|}-\frac{\alpha \left|\mathbf{E}\right|}{I_p{k}^3}\right),$$

(18)

which, for simplicity, is written in the atomic units and where $I_p=0.904$ a.u. is ionization potential of He atom, $k=\sqrt{2I_p}$, $\alpha =7.0$, $C_l=3.13$.

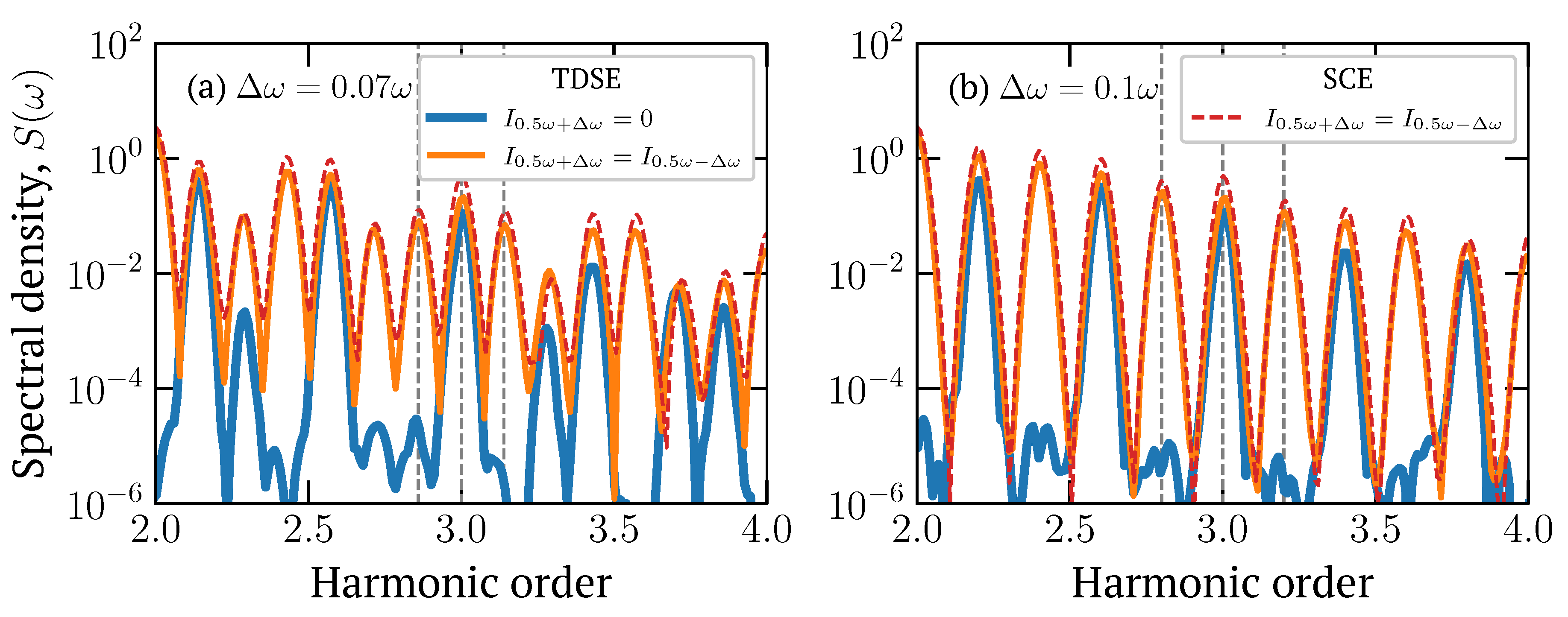
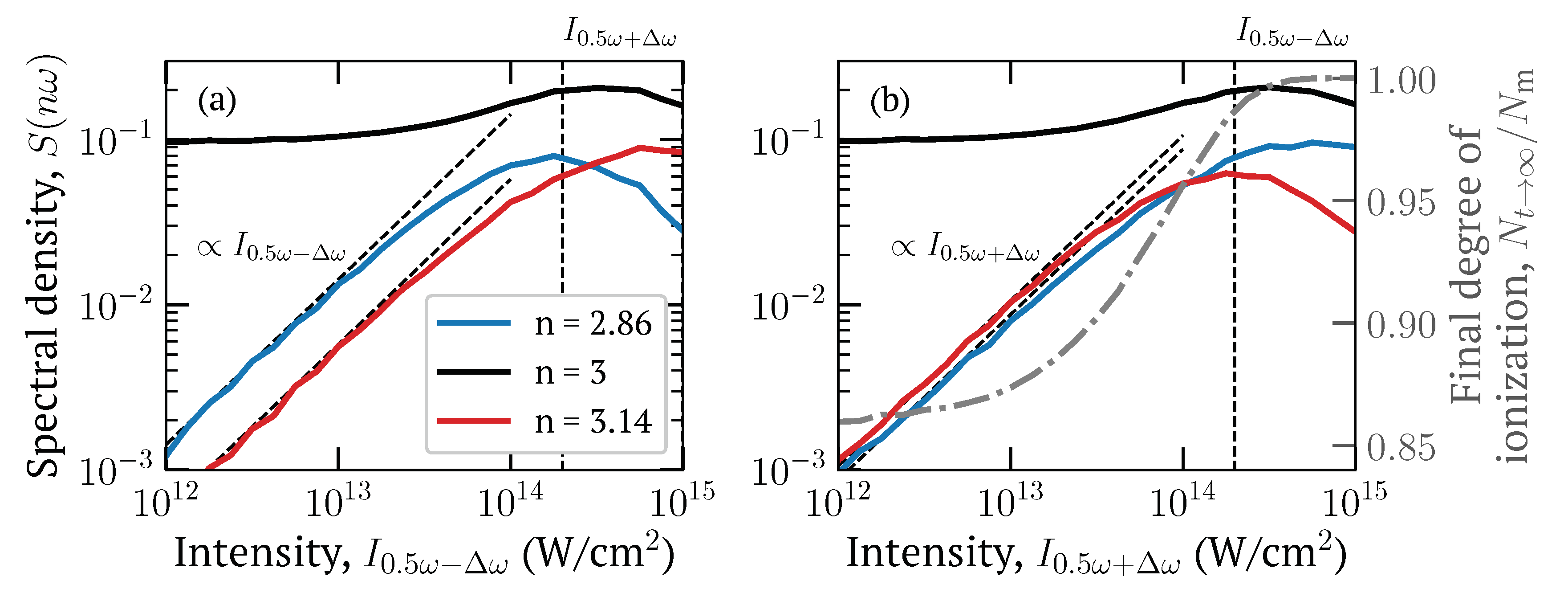
Numerically we have investigated the properties of the combination components $3\omega \pm 2\Delta \omega$, the results are shown on Figure 3 (the spectral density near the third harmonic for pulses with two different values of $\Delta \omega$) and Figure 4 (the dependence of intensities of $3\omega \pm 2\Delta \omega$ on the intensity of one of the components with fixed intensities of two other in a three-color pulse and $\Delta \omega =0.07\omega$). Expression (15) does not correctly describe the entire form of the dependence of $d{\mathbf{j}}_{3\omega +2\Delta \omega }/dt$ on ${\mu }_{1,2}$, since to do this, it is necessary to take into account all the significant higher orders of the IMWM. However, already from it one can see some properties of the generation of a given combination frequency, such as linearity in both amplitudes at low values, and a slight asymmetry: if we put ${\mu }_1={\mu }_2$ and change the sign of $\Delta \omega$, we see that when the intensities of both additional components are equal, the low-frequency satellite of the third harmonic should have a slightly larger amplitude, which is confirmed by both semiclassical and quantum mechanical calculations.

In higher orders there will be different (and more complex) analogous terms in large brackets, but the discussed properties will hold: this component grows linearly and equally with both of additional waves amplitudes, when one of them is small (due to the term ${\mu }_1{\mu }_2$) and then the growth with ${\mu }_1$ becomes slightly faster than with ${\mu }_2$. With the use of such an expression one can analytically solve various optimization problems, such as searching for the maxima of $j_{3\omega +2\Delta \omega }/dt$ under a fixed condition on ${\mu }_1$ and ${\mu }_2$, e.g., fixed total energy.

Another interesting example found by us in numerical calculations is that when several channels are superimposed, which occurs when $\omega$ is a multiple of $\Delta \omega$, the effect of “aligning” the spectral comb occurs (Figure 3b), in our case with a distance between neighboring spectral intensity peaks of $2\Delta \omega =0.2\omega$. Moreover, this happens even if the intensities of the three components are relatively arbitrary, but comparable to each other.

4. Conclusions

We have developed an analytical model for calculating the amplitudes of arbitrary spectral components of free electron currents arising under the action of multicolor ionizing pulses. We show that this method can be used to obtain the dependences of characteristics of a frequency-tunable third harmonic of the intense component of a three-color pulse obtained in an optical parametric generator. Our theoretical conclusions based on the analysis of semiclassical equations for free electron currents are supported by the results of quantum mechanical calculations using time-dependent Schrödinger equation in the framework single-active electron approximation for the helium atom. The proposed model can be useful in designing circuits utilizing multicolor ionizing laser radiation for generating short pulses in a wide frequency range from mid-IR to XUV.