Cooling Effect and Cooling Speed for a Membrane-in-Middle Optomechanical System
Abstract
1. Introduction
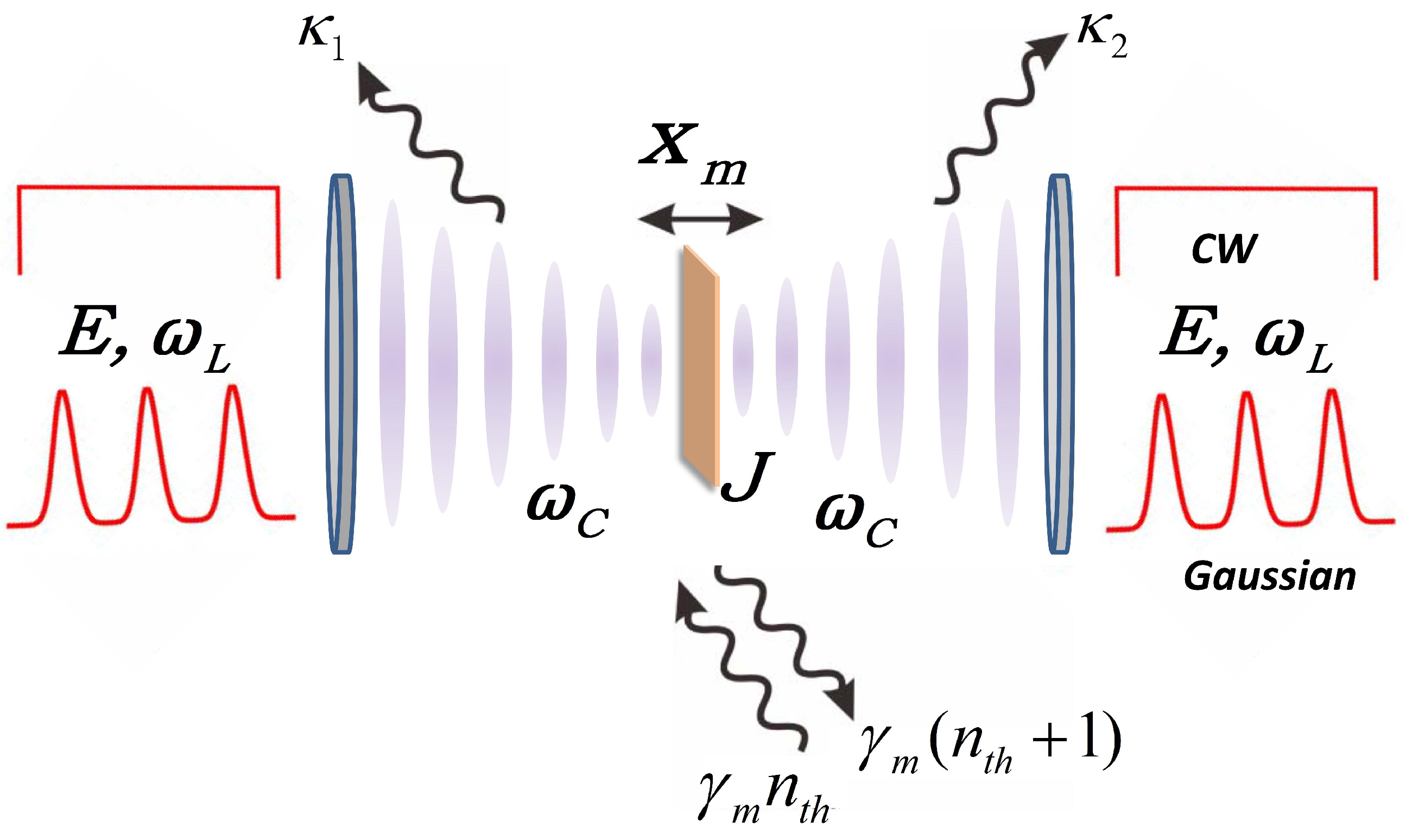
2. Method
3. Results
3.1. Dynamical Evolution of the Thermal Phonon Number
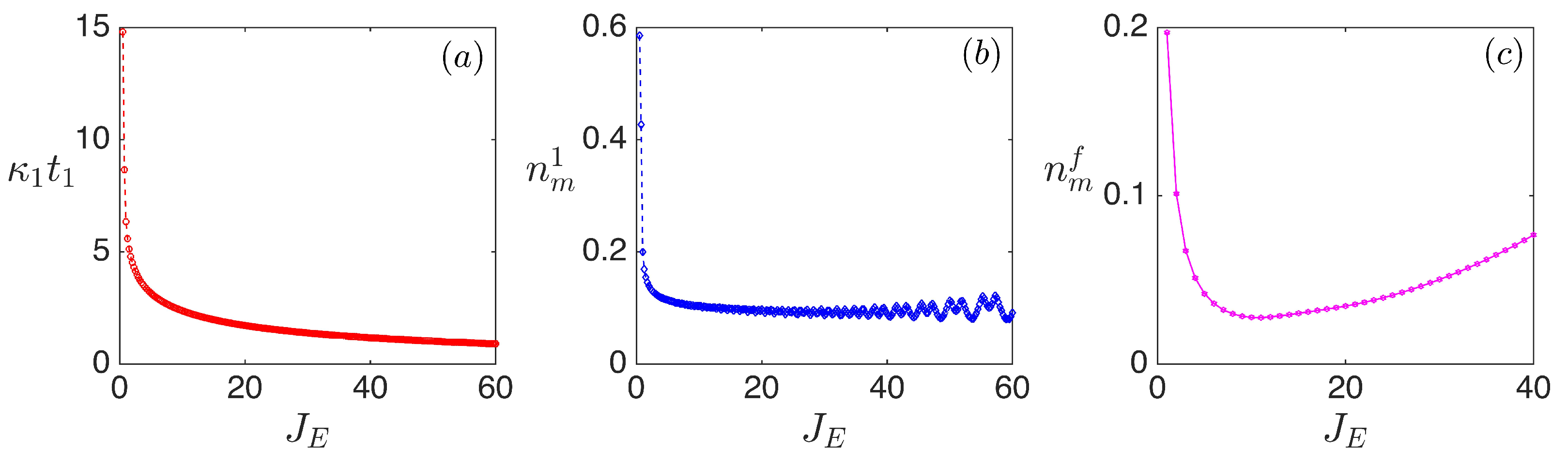
3.2. Determination of the Cooling Result and Cooling Speed
3.3. Effect of the Mechanical Damping Rate
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coleman, P. Introduction to Many-Body Physics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Leggett, A.J.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857–860. [Google Scholar] [CrossRef]
- Leggett, A.J. Testing the limits of quantum mechanics: Motivation, state of play, prospects. J. Phys. Cond. Mat. 2002, 14, R415–R451. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Wilson-Rae, I.; Nooshi, N.; Zwerger, W.; Kippenberg, T.J. Theory of ground state cooling of a mechanical oscillator using dynamical backaction. Phys. Rev. Lett. 2007, 99, 093901. [Google Scholar] [CrossRef] [PubMed]
- Marquardt, F.; Chen, J.P.; Clerk, A.A.; Girvin, S.M. Quantum theory of cavity-assisted sideband cooling of mechanical motion. Phys. Rev. Lett. 2007, 99, 093902. [Google Scholar] [CrossRef]
- Marquardt, F.; Clerk, A.A.; Girvin, S.M. Quantum theory of optomechanical cooling. J. Mod. Opt. 2008, 55, 3329–3338. [Google Scholar] [CrossRef]
- Genes, C.; Vitali, D.; Tombesi, P.; Gigan, S.; Aspelmeyer, M. Ground-state cooling of a micromechanical oscillator: Comparing cold damping and cavity-assisted cooling schemes. Phys. Rev. A 2008, 77, 033804. [Google Scholar] [CrossRef]
- Dantan, A.; Genes, C.; Vitali, D.; Pinard, M. Self-cooling of a movable mirror to the ground state using radiation pressure. Phys. Rev. A 2008, 77, 011804. [Google Scholar] [CrossRef]
- Li, Y.; Wu, L.A.; Wang, Y.D.; Yang, L.P. Nondeterministic ultrafast ground-state cooling of a mechanical resonator. Phys. Rev. B 2011, 84, 094502. [Google Scholar] [CrossRef]
- Wang, X.T.; Vinjanampathy, S.; Strauch, F.W.; Jacobs, K. Ultraefficient cooling of resonators: Beating sideband cooling with quantum control. Phys. Rev. Lett. 2011, 107, 177204. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.C.; Xiao, Y.-F.; Luan, X.; Wong, C.W. Dynamic dissipative cooling of a mechanical resonator in strong coupling optomechanics. Phys. Rev. Lett. 2013, 110, 153606. [Google Scholar] [CrossRef]
- Liu, Y.C.; Hu, Y.W.; Wong, C.W.; Xiao, Y.F. Review of cavity optomechanical cooling. Chin. Phys. B 2013, 22, 114213. [Google Scholar] [CrossRef]
- He, B.; Yang, L.; Lin, Q.; Xiao, M. Radiation pressure cooling as a quantum dynamical process. Phys. Rev. Lett. 2017, 118, 233604. [Google Scholar] [CrossRef]
- Lai, D.G.; Huang, J.F.; Yin, X.L.; Hou, B.P.; Li, W.; Vitali, D.; Nori, F.; Liao, J.Q. Nonreciprocal ground-state cooling of multiple mechanical resonators. Phys. Rev. A 2020, 102, 011502. [Google Scholar] [CrossRef]
- Teufel, J.D.; Harlow, J.W.; Regal, C.A.; Lehnert, K.W. Dynamical backaction of microwave fields on a nanomechanical oscillator. Phys. Rev. Lett. 2008, 101, 197203. [Google Scholar] [CrossRef]
- Gröblacher, S.; Hertzberg, J.B.; Vanner, M.R.; Gigan, S.; Schwab, K.C.; Aspelmeyer, M. Demonstration of an ultracold micro-optomechanical oscillator in a cryogenic cavity. Nat. Phys. 2009, 5, 485–488. [Google Scholar] [CrossRef]
- Schliesser, A.; Arcizet, O.; Riviére, R.; Anetsberger, G.; Kippenberg, T.J. Resolved-sideband cooling and position measurement of a micromechanical oscillator close to the Heisenberg uncertainty limit. Nat. Phys. 2009, 5, 509–514. [Google Scholar] [CrossRef]
- Park, Y.-S.; Wang, H. Resolved-sideband and cryogenic cooling of an optomechanical resonator. Nat. Phys. 2009, 5, 489–493. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef] [PubMed]
- Rocheleau, T.; Ndukum, T.; Macklin, C.; Hertzberg, J.B.; Clerk, A.A.; Schwab, K.C. Preparation and detection of a mechanical resonator near the ground state of motion. Nature 2010, 463, 72–75. [Google Scholar] [CrossRef]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.H.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef]
- Verhagen, E.; Delèglise, S.; Weis, S.; Schliesser, A.; Kippenberg, T.J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 2012, 482, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Peterson, R.W.; Purdy, T.P.; Kampel, N.S.; Andrews, R.W.; Yu, P.-L.; Lehnert, K.W.; Regal, C.A. Laser cooling of a micromechanical membrane to the quantum backaction limit. Phys. Rev. Lett. 2016, 116, 063601. [Google Scholar] [CrossRef]
- Clark, J.B.; Lecocq, F.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature 2017, 541, 191–195. [Google Scholar] [CrossRef]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical Entanglement between a Movable Mirror and a Cavity Field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef] [PubMed]
- Palomaki, T.A.; Teufel, J.D.; Simmonds, R.W.; Lehnert, K.W. Entangling mechanical motion with microwave fields. Science 2013, 342, 710–713. [Google Scholar] [CrossRef]
- Lin, Q.; He, B. Optomechanical entanglement under pulse drive. Opt. Express 2015, 23, 24497. [Google Scholar] [CrossRef]
- Chen, Z.X.; Lin, Q.; He, B.; Lin, Z.Y. Entanglement dynamics in double-cavity optomechanical systems. Opt. Express 2017, 25, 17237. [Google Scholar] [CrossRef]
- Lin, Q.; He, B.; Xiao, M. Entangling two macroscopic mechanical resonators at high temperature. Phys. Rev. Appl. 2020, 13, 034030. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-Based Optical Frequency Combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef]
- Jiang, X.F.; Shao, L.B.; Zhang, S.X.; Yi, X.; Wiersig, J.; Wang, L.; Gong, Q.H.; Lonar, M.; Yang, L.; Xiao, Y.F. Chaos-assisted broadband momentum transformation in optical microresonators. Science 2017, 358, 344–347. [Google Scholar] [CrossRef]
- Lin, Q.; He, B. Highly efficient cooling of mechanical resonator with square pulse drives. Opt. Express 2018, 26, 33830. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.X.; Lin, Q. Cooling the mechanical resonator by Gaussian pulses. Sci. Sin-Phys. Mech. Astron. 2020, 50, 034213. (In Chinese) [Google Scholar]
- Chen, Z.X.; He, B.; Lin, Q. Efficient ground state cooling of a membrane by the combination of continuous-wave field and pulses. J. Phys. B-Atom. Mol. Opt. Phys. 2021, 54, 095502. [Google Scholar] [CrossRef]
- Wang, C.; Lin, Q.; He, B. Breaking the optomechanical cooling limit by two drive fields on a membrane-in-the-middle system. Phys. Rev. A 2019, 99, 023829. [Google Scholar] [CrossRef]
- Zhai, Y.; Chen, Z.X.; Lin, Q. Efficient ground state cooling of a mechanical resonator in a membrane-in-the-middle system by a single drive. J. Phys. B-Atom. Mol. Opt. Phys. 2020, 37, 956–962. [Google Scholar] [CrossRef]
- Meystre, P.; Wright, E.M.; McCullen, J.D.; Vignes, E. Theory of radiation-pressure-driven interferometers. J. Opt. Soc. Am. B 1985, 2, 1830–1840. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Meystre, P. Trapping and cooling a mirror to its quantum mechanical ground state. Phys. Rev. Lett. 2007, 99, 073601. [Google Scholar] [CrossRef] [PubMed]
- Jayich, A.M.; Sankey, J.C.; Zwickl, B.M.; Yang, C.; Thompson, J.D.; Girvin, S.M.; Clerk, A.A.; Marquardt, F.; Harris, J.G.E. Dispersive optomechanics: A membrane inside a cavity. New J. Phys. 2008, 10, 095008. [Google Scholar] [CrossRef]
- Li, Y.; Wu, L.A.; Wang, Z.D. Fast ground-state cooling of mechanical resonators with time-dependent optical cavities. Phys. Rev. A 2011, 83, 043804. [Google Scholar] [CrossRef]
- Karuza, M.; Molinelli, C.; Galassi, M.; Biancofiore, C.; Natali, R.; Tombesi, P.; Di Giuseppe, G.; Vitali, D. Optomechanical sideband cooling of a thin membrane within a cavity. New J. Phys. 2012, 14, 095015. [Google Scholar] [CrossRef][Green Version]
- Guo, Y.J.; Li, K.; Nie, W.J.; Li, Y. Electromagnetically-induced-transparency-like ground-state cooling in a double-cavity optomechanical system. Phys. Rev. A 2014, 90, 053841. [Google Scholar] [CrossRef]
- Liu, Y.C.; Xiao, Y.F.; Luan, X.S.; Gong, Q.H.; Wong, C.W. Coupled cavities for motional ground-state cooling and strong optomechanical coupling. Phys. Rev. A 2015, 91, 033818. [Google Scholar] [CrossRef]
- Piergentili, P.; Catalini, L.; Bawaj, M.; Zippilli, S.; Malossi, N.; Natali, R.; Vitali, D.; Di Giuseppe, G. Two-membrane cavity optomechanics. New J. Phys. 2018, 20, 083024. [Google Scholar] [CrossRef]
- Gardiner, C.W.; Zoller, P. Quantum Noise, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- He, B. Quantum optomechanics beyond linearization. Phys. Rev. A 2012, 85, 063820. [Google Scholar] [CrossRef]
- Lin, Q.; He, B.; Ghobadi, R.; Simon, C. Fully quantum approach to optomechanical entanglement. Phys. Rev. A 2014, 90, 022309. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Lin, Q.; He, B. Cooling Effect and Cooling Speed for a Membrane-in-Middle Optomechanical System. Photonics 2022, 9, 400. https://doi.org/10.3390/photonics9060400
Chen Z, Lin Q, He B. Cooling Effect and Cooling Speed for a Membrane-in-Middle Optomechanical System. Photonics. 2022; 9(6):400. https://doi.org/10.3390/photonics9060400
Chicago/Turabian StyleChen, Zhixin, Qing Lin, and Bing He. 2022. "Cooling Effect and Cooling Speed for a Membrane-in-Middle Optomechanical System" Photonics 9, no. 6: 400. https://doi.org/10.3390/photonics9060400
APA StyleChen, Z., Lin, Q., & He, B. (2022). Cooling Effect and Cooling Speed for a Membrane-in-Middle Optomechanical System. Photonics, 9(6), 400. https://doi.org/10.3390/photonics9060400





