Manipulating Orbital Angular Momentum Entanglement in Three-Dimensional Spiral Nonlinear Photonic Crystals
Abstract
1. Introduction
2. Theory
3. Results
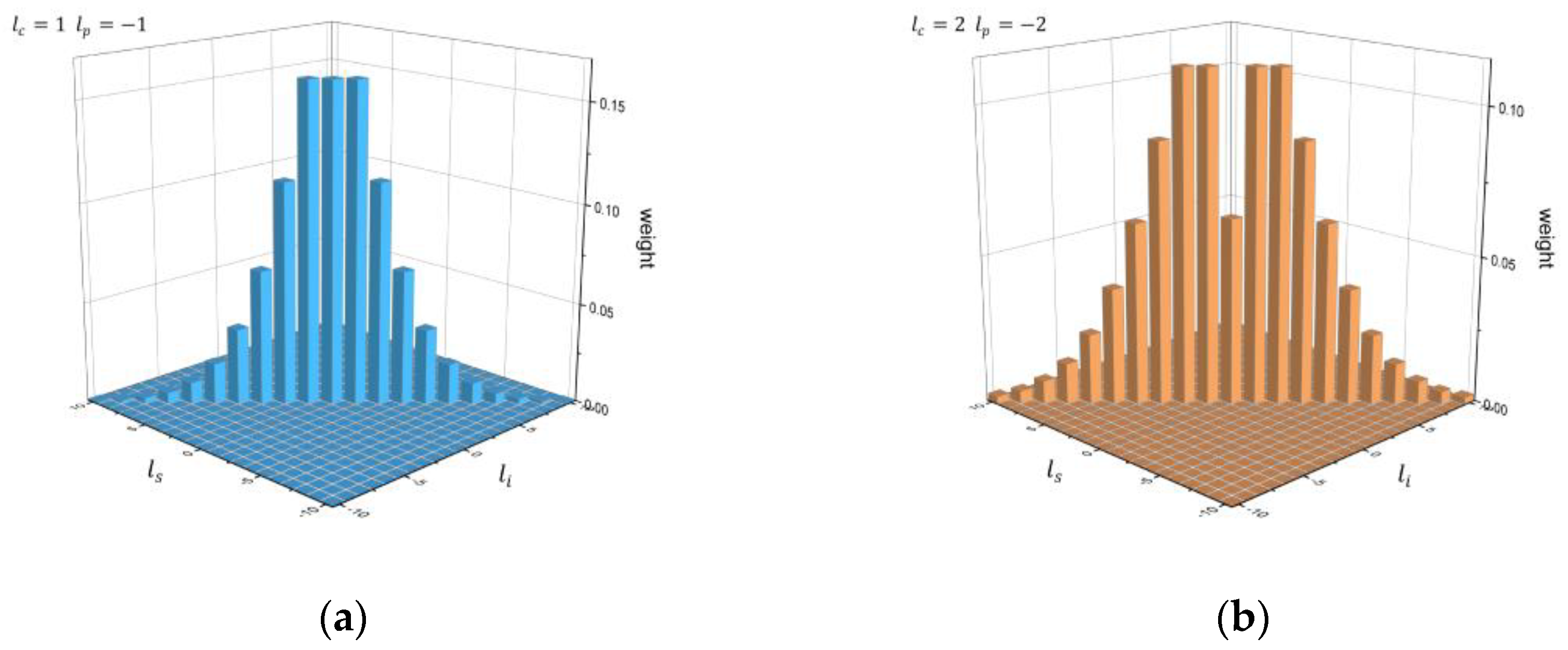
3.1. Two-Photon OAM Correlation in a 3D Spiral NPC Structure
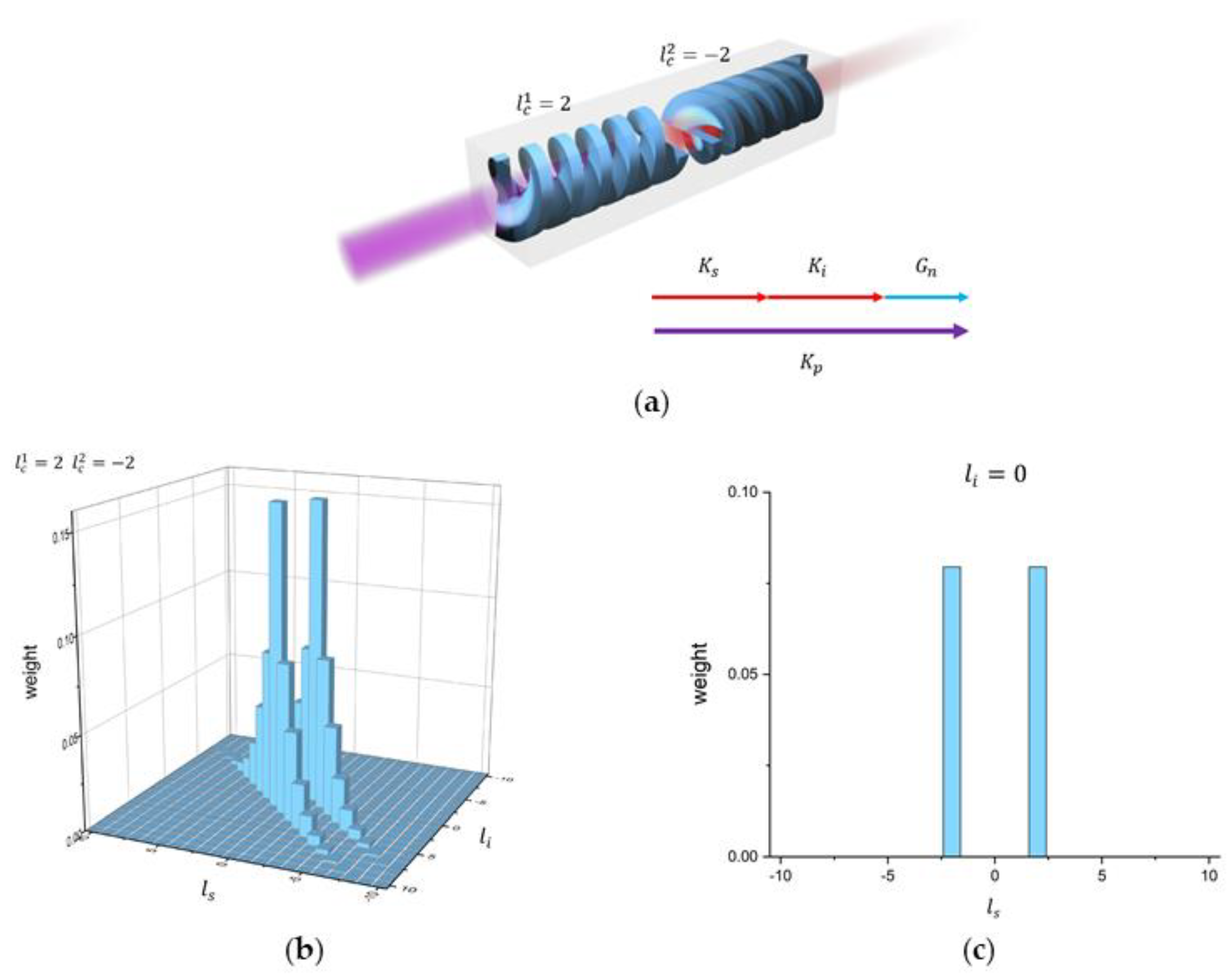
3.2. Two-Photon OAM Correlation from the Cascaded 3D Spiral Structure
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Ou, Z.Y.; Mandel, L. Violation of Bells-Inequality and Classical Probability in a two-Photon Correlation Experiment. Phys. Rev. Lett. 1988, 61, 50–53. [Google Scholar] [CrossRef] [PubMed]
- Shih, Y.H.; Alley, C.O. New Type of Einstein-Podolsky-Rosen-Bohm Experiment Using Pairs of Light Quanta Produced by Optical Parametric Down Conversion. Phys. Rev. Lett. 1988, 61, 2921–2924. [Google Scholar] [CrossRef] [PubMed]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental Quantum Teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Rubin, M.H. Transverse Correlation in Optical Spontaneous Parametric Down-Conversion. Phys. Rev. A 1996, 54, 5349–5360. [Google Scholar] [CrossRef]
- Rubin, M.H.; Klyshko, D.N.; Shih, Y.H.; Sergienko, A.V. Theory of Two-Photon Entanglement in Type-II Optical Parametric Down-Conversion. Phys. Rev. A 1994, 50, 5122–5133. [Google Scholar] [CrossRef]
- Haddadan, F.; Soroosh, M. Low-power all-optical 8-to-3 encoder using photonic crystal-based waveguides. Photonic Netw. Commun. 2019, 37, 83–89. [Google Scholar] [CrossRef]
- Haddadan, F.; Soroosh, M.; Alaei-Sheini, N. Designing an electro-optical encoder based on photonic crystals using the graphene-Al2O3 stacks. Appl. Opt. 2020, 59, 2179–2185. [Google Scholar] [CrossRef]
- Noori, M.; Soroosh, M.; Baghban, H. All-angle self-collimation in two-dimensional square array photonic crystals based on index contrast tailoring. Opt. Eng. 2015, 54, 7111. [Google Scholar] [CrossRef]
- Seraj, Z.; Soroosh, M.; Alaei-Sheini, N. Ultra-compact ultra-fast 1-bit comparator based on a two-dimensional nonlinear photonic crystal structure. Appl. Opt. 2020, 59, 811–816. [Google Scholar] [CrossRef]
- Franson, J.D. Bell Inequality for Position and Time. Phys. Rev. Lett. 1989, 62, 2205–2208. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Mattle, K.; Weinfurter, H.; Zeilinger, A.; Sergienko, A.V.; Shih, Y.H. New High-Intensity Source of Polarization-Entangled Photon Pairs. Phys. Rev. Lett. 1995, 75, 4337–4341. [Google Scholar] [CrossRef] [PubMed]
- Rossi, A.; Vallone, G.; Chiuri, A.; De Martini, F.; Mataloni, P. Multipath Entanglement of Two Photons. Phys. Rev. Lett. 2009, 102, 153902. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital Angular-Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Lei, J.; Romero, J. Quantum Digital Spiral Imaging. Light: Sci. Appl. 2014, 3, E153. [Google Scholar] [CrossRef]
- Torner, L.; Torres, J.P.; Carrasco, S. Digital Spiral Imaging. Opt. Express 2005, 13, 873–881. [Google Scholar] [CrossRef] [PubMed]
- Molina-Terriza, G.; Torres, J.P.; Torner, L. Twisted photons. Nat. Phys. 2007, 3, 305–310. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the Orbital Angular Momentum States of Photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef]
- Vaziri, A.; Pan, J.W.; Jennewein, T.; Weihs, G.; Zeilinger, A. Concentration of Higher Dimensional Entanglement: Qutrits of Photon Orbital Angular Momentum. Phys. Rev. Lett. 2003, 91, 7902. [Google Scholar] [CrossRef]
- Torres, J.P.; Alexandrescu, A.; Torner, L. Quantum Spiral Bandwidth of Entangled Two-Photon States. Phys. Rev. A 2003, 68, 301. [Google Scholar] [CrossRef]
- Walborn, S.P.; De Oliveira, A.N.; Thebaldi, R.S.; Monken, C.H. Entanglement and Conservation of Orbital Angular Momentum in Spontaneous Parametric Down-Conversion. Phys. Rev. A 2004, 69, 3811. [Google Scholar] [CrossRef]
- Kovlakov, E.V.; Straupe, S.S.; Kulik, S.P. Quantum State Engineering with Twisted Photons via Adaptive Shaping of the Pump Beam. Phys. Rev. A 2018, 98, 301. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, Z.; Liu, S.; Li, Y.; Li, Y.; Yang, C.; Xu, Z.; Liu, Z.; Guo, G.; Shi, B. Coherent Manipulation of a Three-Dimensional Maximally Entangled State. Phys. Rev. A 2018, 98, 2316. [Google Scholar] [CrossRef]
- Torres, J.P.; Alexandrescu, A.; Carrasco, S.; Torner, L. Quasi-Phase-Matching Engineering for Spatial Control of Entangled Two-Photon States. Opt. Lett. 2004, 29, 376–378. [Google Scholar] [CrossRef] [PubMed]
- Megidish, E.; Halevy, A.; Eisenberg, H.S.; Ganany-Padowicz, A.; Habshoosh, N.; Arie, A. Compact 2d Nonlinear Photonic Crystal Source of Beamlike Path Entangled Photons. Opt. Express 2013, 21, 6689–6696. [Google Scholar] [CrossRef][Green Version]
- Bloch, N.V.; Shemer, K.; Shapira, A.; Shiloh, R.; Juwiler, I.; Arie, A. Twisting Light by Nonlinear Photonic Crystals. Phys. Rev. Lett. 2012, 108, 3902. [Google Scholar] [CrossRef]
- Lu, L.L.; Xu, P.; Zhong, M.L.; Bai, Y.F.; Zhu, S.N. Orbital Angular Momentum Entanglement via Fork-Poling Nonlinear Photonic Crystals. Opt. Express 2015, 23, 1203–1212. [Google Scholar] [CrossRef]
- Yang, M.; Jie, T.; Zhao-Xian, C.; Fei, X.; Li-Jian, Z.; Yan-Qing, L. Generation of N00N State with Orbital Angular Momentum in a Twisted Nonlinear Photonic Crystal. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 225–230. [Google Scholar] [CrossRef]
- Wei, D.; Wang, C.; Wang, H.; Hu, X.; Wei, D.; Fang, X.; Zhang, Y.; Wu, D.; Hu, Y.; Li, J.; et al. Experimental Demonstration of a Three-Dimensional Lithium Niobate Nonlinear Photonic Crystal. Nat. Photonics 2018, 12, 596–600. [Google Scholar] [CrossRef]
- Xu, T.; Switkowski, K.; Chen, X.; Liu, S.; Koynov, K.; Yu, H.; Zhang, H.; Wang, J.; Sheng, Y.; Krolikowski, W. Three-Dimensional Nonlinear Photonic Crystal in Ferroelectric Barium Calcium Titanate. Nat. Photonics 2018, 12, 591–595. [Google Scholar] [CrossRef]
- Wei, D.; Wang, C.; Xu, X.; Wang, H.; Hu, Y.; Chen, P.; Li, J.; Zhu, Y.; Xin, C.; Hu, X.; et al. Efficient Nonlinear Beam Shaping in Three-Dimensional Lithium Niobate Nonlinear Photonic Crystals. Nat. Commun. 2019, 10, 4193. [Google Scholar] [CrossRef]
- Wang, T.; Chen, P.; Xu, C.; Zhang, Y.; Wei, D.; Hu, X.; Zhao, G.; Xiao, M.; Zhu, S. Periodically Poled Linbo3 Crystals from 1d and 2d to 3d. Sci. China Technol. Sci. 2020, 63, 1110–1126. [Google Scholar] [CrossRef]
- Zhang, Y.; Sheng, Y.; Zhu, S.; Xiao, M.; Krolikowski, W. Nonlinear Photonic Crystals: From 2d to 3d. Optics 2021, 8, 372–381. [Google Scholar] [CrossRef]
- Bahabad, A.; Arie, A. Generation of Optical Vortex Beams by Nonlinear Wave Mixing. Opt. Express 2007, 15, 17619–17624. [Google Scholar] [CrossRef] [PubMed]
- Gong, Y.-X.; Xie, Z.-D.; Xu, P.; Yu, X.-Q.; Xue, P.; Zhu, S.-N. Compact source of narrow-band counterpropagating polarization-entangled photon pairs using a single dual-periodically-poled crystal. Phys. Rev. A 2011, 84, 3825. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Xu, C.; Chen, S.; Chen, P.; Nie, S.; Ke, S.; Wei, D.; Xiao, M.; Zhang, Y. Manipulating Orbital Angular Momentum Entanglement in Three-Dimensional Spiral Nonlinear Photonic Crystals. Photonics 2022, 9, 504. https://doi.org/10.3390/photonics9070504
Yu Q, Xu C, Chen S, Chen P, Nie S, Ke S, Wei D, Xiao M, Zhang Y. Manipulating Orbital Angular Momentum Entanglement in Three-Dimensional Spiral Nonlinear Photonic Crystals. Photonics. 2022; 9(7):504. https://doi.org/10.3390/photonics9070504
Chicago/Turabian StyleYu, Qian, Chuan Xu, Sixin Chen, Pengcheng Chen, Saiwei Nie, Shijie Ke, Dunzhao Wei, Min Xiao, and Yong Zhang. 2022. "Manipulating Orbital Angular Momentum Entanglement in Three-Dimensional Spiral Nonlinear Photonic Crystals" Photonics 9, no. 7: 504. https://doi.org/10.3390/photonics9070504
APA StyleYu, Q., Xu, C., Chen, S., Chen, P., Nie, S., Ke, S., Wei, D., Xiao, M., & Zhang, Y. (2022). Manipulating Orbital Angular Momentum Entanglement in Three-Dimensional Spiral Nonlinear Photonic Crystals. Photonics, 9(7), 504. https://doi.org/10.3390/photonics9070504





