Abstract
Imaging spectrometry plays a significant role in various scientific realms. Although imaging spectrometers based on different schemes have been proposed, the pursuit of compact and high-performance devices is still ongoing. A compact broadband and ultrahigh-resolution imaging spectrometer (CBURIS) is presented, which comprises a microlens array, multiple fiber bundles, a microscope, and a two-dimensional detector array. The principle of the device is to spatially sample and integrate the field information via the front microlens array and then further process with the fiber bundles and imaging system based on the multimode interference theory. From both the theoretical and numerical analysis, this CBURIS design is a superior concept that not only achieves a 0.17° spatial resolution and ultrahigh spectral resolution (resolving power exceeds 2.58 × 106 at 1.55 µm) from the visible to mid-infrared region but also has the advantages of snapshot measurement, thermal stability, and a compact footprint compared with most existing imaging spectrometers.
1. Introduction
The imaging spectrometry technique involves imaging and spectroscopy to reconstruct both spatial and spectral information of a luminous target. Originating from earth remote sensing by Alexander Goetz in the 1980s [1], this implement has been developed for various realms in agriculture monitoring, environmental testing, geographical surveying, and aerial remote sensing [2,3,4,5,6,7,8]. Traditional imaging spectrometers employ a slit or aperture stop to sample the field of view (FOV), and then the spatial elements are further processed with different dispersive elements into a three-dimensional data cube. According to different spectral component detection schemes, imaging spectrometers can be classified into three categories. Color-filter imaging spectrometers [9,10] consist of a tunable filter matrix that is controlled by an external signal to measure monochromatic images at a series of spectral components. This scheme requires an elaborate control of the individual unit and suffers from mechanical disturbance. Although liquid-crystal cells based imaging spectrometers partially mitigate the drawbacks, problems such as temporal retardation, moderate resolution, and heavy acquisition and computations are still unresolved [11,12]. Traditional imaging spectrometers employ a built-in dispersive module such as a grating, a prism, or both to distribute different spectral components onto a calibrated area detector array. Owing to the reverse relationship of spectral resolution and optical path, a delicate design with moderate performance can only be realized within a bulky and high-cost instrument. The interferometric ones need a complicated transformation of the acquired image to retrieve spectral information [13,14,15]. Although recent developments of the Michelson-type and Fabry–Perot interferometers meet the requirement of ultrahigh spectral resolution, their physical size is still large, and their long measurement time makes them unsuitable for real-time applications.
The design of a compact ultrahigh-spectral-resolution imaging spectrometer (CBUSRIS) resolved the above concerns with ultrahigh spectral resolution and quick measurement within a compact footprint but still cannot avoid the complexity of the system assembly and mechanical disturbance [16]. Although the performance of several outstanding imaging spectrometers could be compared with that of commercial ones, a compact device with high spatial resolution, high resolving power, and broad operating bandwidth remains elusive. With the maturity of manufacturing techniques, microlens array integral field spectrometry has contributed an indispensable counterpart [17]. The microlens array replaces the slit or aperture stop of the traditional method and samples the FOV. Meanwhile, modal interference generated inside a multimode medium strongly depends on a certain wavelength, improving the dispersion efficiency within a compact size [18,19]. On this basis, a compact broadband and ultrahigh-resolution imaging spectrometer (CBURIS) based on the multimode interference (MMI) is proposed, which simultaneously achieves high resolving power of >2 × 106 and spatial resolution of ~0.1° across the visible to mid-infrared range within a 600 cm3 footprint, superior to most of its counterparts. Table 1 compares several advanced fiber-based imaging spectrometers, proving that CBURIS is superior to most of its counterparts. Section 2 describes the optical layout of the system. Section 3 explains the operating principle of CBURIS in detail, including coupled-mode theory and MMI theory. Section 4 performs numerical simulation regarding MMI and further demonstrates the operating bandwidth, resolving power, operating mode, and thermal stability, which verifies the feasibility of the device design. The last section discusses the practical advantages and critical parameters and then concludes our work.

Table 1.
The performance of fiber-based imaging spectrometers in recent literature.
2. Optical Layout for the CBURIS
Figure 1a illustrates the layout of the compact broadband and ultrahigh-resolution imaging spectrometer (CBURIS), which consists of a front microlens array (MLA), a bunch of multimode fiber bundles (MMFBs), an optical adhesive, a microscope, and a two-dimensional (2D) detector array. The MLA is horizontally fabricated into a 120° circular curve to obtain an ultra-wide FOV, and the spatial field is roughly divided into multiple smaller angles. One end of each MMFB is circularly superposed with the front focal plane of the microlens, which enables the field angle of the microlens to be subdivided into finer angular resolution (corresponding to a sub-degree spatial resolution of 0.17°), and then assembled beneath an optical adhesive (i.e., a glass slide). The other end of each MMFB could be upwards routed, dispersed into a linear arrangement, and stripped and tapered using the flame-brush technique with a taper length around several millimeters. Owing to the destruction of total internal reflection (TIR), optical signals radiated from the taper are amplified and captured by a 2D detector (e.g., a CCD camera) integrated on top, ensuring every detail of MMI patterns is captured. As the detecting area may not be large enough to cover the whole taper matrix, the imaging combination should precisely scan in the horizontal plane. The graphic structure of MMFB is shown in Figure 1b, and for better illustration, different fibers, i.e., spatial channels, are filled with colors. Thanks to the development of fiber fabrication and mass production, this special treatment could be easily realized by bare fiber-splicing or fiber perform drawing. Fastening them onto the adhesive guarantees the mechanical stability and polarization maintenance of the MMI, which is the significant point of the operating principle. Consequently, the subdivided spatial information can be further processed in the spectral domain, as demonstrated below.
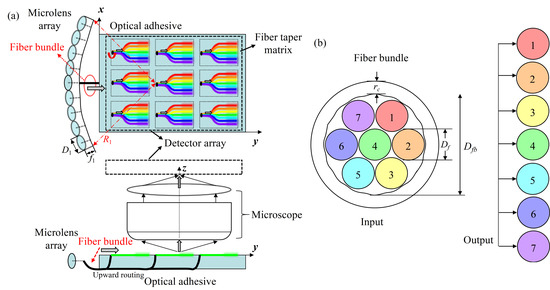
Figure 1.
(a) Optical layout of the CBURIS: optical signals are coupled from the MLA into the MMFBs, and when they reach the tapered region, radiated portions are collected by the 2D detector array integrated above. (b) Schematic diagram of the MMFB, the input ends are bundled into a circular form, while the output ends are spread in line for planar detection.
3. Operating Principles of the CBURIS
3.1. Coupled-Mode Theory from MLA to MMF
Assuming that the MLA is parallel to the optical adhesive in the horizontal plane and the 2D detector array could capture the tapered area. Here, D1 is the aperture size of microlens and φ is the field angle; the number of microlenses in MLA is:
When designing curvature radius R1 of MLA, which determines the lateral size of the device, the aperture size of each microlens can be approximately calculated by:
In practice, the field angle φ of each microlens is much smaller than the maximum acceptance angle of each MMF, while the diameter of MMFB is smaller than microlens, the influence of slight deviation of assembly can be ignored. According to the geometry in Figure 1b and Figure 2a, the characteristic of the lens and MMF can be obtained that:
where Dfb is the diameter of MMFB, composed of the fiber diameter Df and cladding thickness rc, θin is the incident angle to fiber, and f1 is the focal length of each microlens.
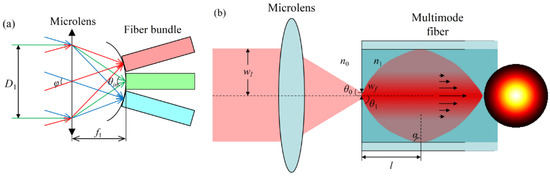
Figure 2.
Equivalent schematic diagram of (a) an MMFB coupled with a microlens in MLA and (b) beam launching condition into a graded-index MMF where the red beam represents the distribution of the intensity.
Compared with the step-index medium, the graded-index fiber provides lower modal dispersion and less bend loss within a broad operating bandwidth. As shown in Figure 2b, a Gaussian beam is launched when the light is coupled to the graded-index MMF [20,21]. NA is the numerical aperture of the fiber, n0 and n1 are the refractive indexes of the air and silica. To satisfy the TIR condition, the critical incident angle θ0 and beam waist wf of the coupled mode could be obtained by:
wl is the beam waist in front of the microlens, Δ represents relative variation of the refractive index. Supposing the beam transmits to z direction, the curvature radius r(z) evolves in the form . Subsequently, as illustrated in Figure 2b, the beam waist arrives at the position of is .
Within the graded-index MMF, the optical field E could be decomposed into three cylindrical polar coordinates r, ϕ, and z, and has the separate forms:
where β is the propagation constant, m and n are the indexes of non-degenerate spatial modes. It is indicated that as the number of modes increases, periodic distributions are introduced by high-order modes. The circular symmetry of MMF authorizes separable field solutions that satisfy Equation (10). The critical parameters are defined as and . Consequently, the fundamental mode E0,0 can be written as: , where w(z) and r(z) are determined by Equation (8) when m = n = 0.
3.2. MMI Theory within the MMF
When a monochromatic light (λ) incidents into a non-adiabatic MMF, multiple transmitted modes are excited with different propagation constants. As the proportion of individual mode greatly relies on the coupling efficiency from different media, each has a variable and unpredicted amplitude or phase, leading to a unique MMI pattern. To describe the fraction of the Gaussian field from each mode, the coupling efficiency is used. The propagation constant βm,n and coupling efficiency χm,n are:
the number of modes is given by . Therefore, the differential of βm,n and λ are:
critically determines the spectral resolution of this MMI-based CBURIS.
It is well-known that normal fibers do not leak out signals because of TIR conditions. Moreover, when it is tapered down by several millimeters length using the bare fiber-splicing technique, this condition is destroyed, and we could capture the MMI pattern via the con-focal setup, as shown in Figure 1a, where the objective magnifies the signal and the lens focus it onto the detector, ensuring to capture every detail of MMI pattern. As it is a vector summation of each individual mode, the radiation loss captured can be expressed as . Every mode propagates with a different βm,n and accumulates optical path difference. The maximum value occurs between the fundamental mode and the highest mode, which we denote . In order for a wavelength shift Δλ to produce a distinct MMI distribution, Δφ(λ) should change π [22], which significantly determines the resolving ability. Although the structure of each MMFB may generate different Δφ(λ) between the MMFs, this could be resolved by an advanced positional calibration method or fiber length compensation (i.e., introducing a corrective phase term for each fiber). The resolving power RP is:
Based on the measurement of the microscopy system, the spatial imaging resolution is usually determined by the maximum value of optical system resolution Ropt and imaging resolution of the detector Rccd. According to the Nyquist–Shannon criterion, the sampling frequency (1/d, d is the pixel size of the detector) should be at least twice the spatial frequency of the MMI pattern. These resolutions are calculated by and , where NAo is numerical aperture of objective, and ς is magnification. The effective area of one taper unit is .
For each MMF, which is a spatial channel of CBURIS, the spectrum information could be retrieved from the MMI patterns using the reconstruction algorithm. To operate as an imaging spectrometer, the detector should record each pattern when λ changes and a corresponding transmission matrix Ti(k) is obtained. Considering the spectral responsivity η(k) of the camera, the relationship between the probe signal’s intensity pattern bi and spectrum s(k) is:
here, the interval of s(k) is spectral resolution Δλ of CBURIS, and k = 1,2,…,m corresponds to the number of spectral channels. Assuming:
and
The discretized formation is modeled as Ax = b. Note that this approximation might underdetermine the reconstruction quality of the continuous spectrum. However, these complex functions create a random basis that recovers the unknown spectrum using compressive sensing [23,24] or least-square methods [25,26]. Here, least-squared-based reconstruction algorithm is chosen to optimize ||Ax−b||2, where ||.||2 denotes the 2-norm. By eliminating the non-physical solutions and solving the problem with a nonlinear optimization algorithm, one could accurately reconstruct the spectrum of any simulated signal.
4. Analysis of the Spectral Performance
4.1. Simulation of MMI Model in Fiber
In order to verify the feasibility of the proposed CBURIS design, the MMI model resulting from multiple excited propagation modes inside the graded-index MMF was numerically simulated. Based on previous results [25], different generated MMI patterns (i.e., intensity distribution) mainly results from different parameters of fiber structure and laser source. As the diameter of the MMF taper decreases from 200 μm to 60 μm along its 4 mm length, it is rational to treat the model straight (the slope is ~0.03%). Due to the different coupling conditions in practical application, χm,n are randomly assigned using a rand function when the optical field within MMF is established. As CBURIS is packaged for a portable scenario, once the modes’ amplitudes and phases are generated, they should be maintained in the follow-up calculation process. The pattern captured from the cross-section is shown in Figure 3a (the x- and y-axis denote the electric field components), and both its grain pattern and spectral dependence agree well with the experimental results [18,19]. To better observe its intensity distribution, fewer modes (~15 modes) at 1.55 μm are shown in the inset. In Figure 3b, an MMI pattern is obtained by a single fiber taper test in the experiment when a calibration wavelength is 637.00 nm. A spatial period is chosen to verify the correctness of the MMI model. In the simulation, we chose 50 transmitted modes, set initial amplitudes, and performed the nonlinear optimization in Matlab with the intensity distribution captured in the experiment. As shown in Figure 3c, the fitting result is perfect, and the higher its order, the smaller its amplitude is. The deviation from experiments mainly results from structure parameters, the number of supported modes, and fabrication imperfection. We then chose this set of amplitudes in the calibration process to perform its characteristics. In Figure 3d, setting ϕ = 0° corresponds to side radiation from the taper, which contains rich spectral features. Multiple spectral channels with fixed spacing form the transmission matrix in the reconstruction algorithm. In our cylindrical model, the periodic beating comes from optical path differences between the fundamental mode and higher modes, and the projection d′ = Δz·ς/N = 2πς/(Δβ·N) must be larger than the pixel size of the camera. Here, for a detector array with d = 9 μm, the number of pixels on projection N is calculated ~200 (ς = 20). The slight beatings could be approximated by many-modes limits Δz′~5Δz/M2, where M is the number of modes supported. In Figure 3e, different values of 200 μm, 400 μm, 600 μm, and 800 μm for Df are chosen, indicating that higher RP could be achieved with a larger Df and wavenumber. The βm,n planes of supported modes with indexes of (m,n) are plotted in Figure 3f, which are uniformly distributed in the dispersive space. Ranging from 600 nm to 2 μm, the unique dispersive points correspond to certain (λ,m,n) that reflects a broadband operation for CBURIS.
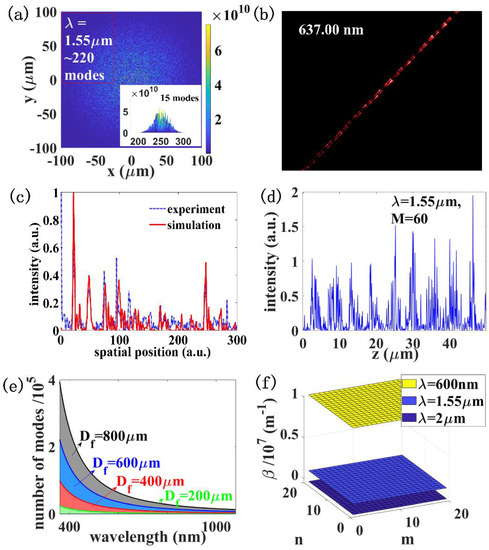
Figure 3.
Simulated MMI pattern obtained from (a) cross-section of the MMF. (b) is the pattern obtained by a single fiber taper test in the experiment, and (c) is using the nonlinear optimization with a spatial period from (b). In (d), simulated MMI pattern from axial place which can be detected and treated as a fingerprint of λ. (e) The plots of M with λ at different Df, indicating a larger core could support more modes in visible region. (f) The dispersive planes of βm,n at three different λ across the operation bandwidth.
The parameters employed in the numerical simulation are summarized in Table 2. In Section 4.3 and Section 4.4, the results are calculated and compared with the theoretical model with proper parameters.

Table 2.
Parameters used in simulation throughout the article.
4.2. Ultra-Wide Bandwidth Calibration
Both the simulation and theoretical results predict that different wavelengths could produce distinguishable MMI patterns within the taper length. Assuming the detector has a relatively flat responsivity η(k) within the bandwidth of interest, a transmission matrix A or T(k) is obtained by scanning λ from 400 nm to 2.2 μm in steps of 10 nm. This matrix not only represents the uniqueness of the device but also contains complete spectral information. In the simulation, we selected a 4 mm long MMF and sampled the MMI profile along the interface of core and cladding. To demonstrate an ultra-wide bandwidth, the inner-product of A or T(k) was calculated and optimized to obtain an uncorrelated spectral profile with a high signal-to-noise ratio. When the value is zero, it means two λ generate two fully different patterns distinguishable by the detector, and one means the range |λ1–λ2| exceeds the operation bandwidth. As shown in Figure 4, the inner-product calculation is conducted across the transparency window of silica, where spectral channels of 600 nm and 2 μm are chosen for clear observation, indicating that as Δλ increases, the correlation sharply decreases within the bandwidth, corresponding to the fingerprint of wavelength. Considering that no individual camera operates within this wide range, we have to institute different detectors according to the signal detected, e.g., silicon for visible to near-infrared and InGaAs for near- to mid-infrared. Benefited from the broad transparency window of MMF and the replacement of the detector with a calibrated spectral response, this figure of merit (FOM) is superior to most of its counterparts.
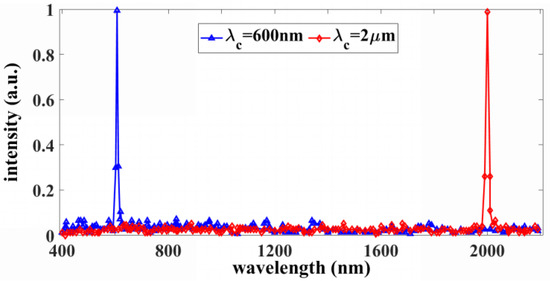
Figure 4.
The inner-products between wavelengths from 400 nm to 2.2 μm decay, showing that no 2 distinguishable channels have the same associated fingerprint.
4.3. Optimization for Ultrahigh Resolving Power
On the basis of the spectroscopy scheme, we precisely detuned the Δλ, captured T(k), and pushed its resolving ability to the limit. In Figure 5a, the spectral correlation C(Δλ,r) = <I(λ,r)I(λ + Δλ,r)>/<I(λ,r)> <I(λ + Δλ,r)> −1 is calculated at a step of 0.12 pm, where I(λ,r) is the MMI profile at position r, as shown in Figure 3b. The FWHM of the curves shows that when the wavelength shifts away from λ, it is possible to distinguish the difference. This value also sets the upper limit for Δλ. The CBURIS performs better in the visible than in the infrared region for the reason that it excites more modes (M = 4–8 × 105), and the imaging resolution (Rres = 200–300 nm) is smaller. To compromise a resolution at 1.55 μm, a similar implement with a 12 nm step was performed in Figure 5b. As 2 closely spaced spectral channels are pushed closer, the inner-product should be lower than 0.5 based on the Rayleigh criterion. The spectral resolution is 0.6 pm [22], which corresponds to a resolving power of RP = 2.58 × 106. Similarly, the RP at 600 nm and 2 μm are 1.00 × 107 and 2.03 × 106, respectively. As illustrated above, the reconstruction procedure is regardless of the wavelength, and in our previous experiments, we succeeded in spectrum reconstructing within the bandwidth [25]. The transparent window centered at 1550 nm is significant in optical communications, which is mainly investigated and discussed.
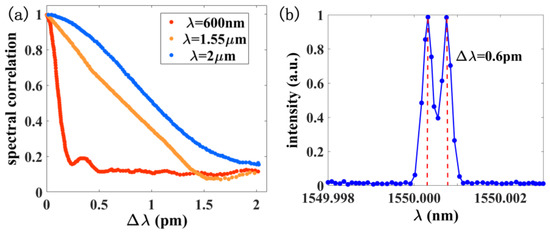
Figure 5.
(a) Spectral correlation function at different λ, showing an FWHM (resolution) around picometer scale; (b) δλ is verified by directly resolving two closely spaced spectral channels using the reconstruction algorithm, sharply peaked λ are clearly resolved at λ = 1.55 μm.
Next, parameters that greatly influence RP are investigated in detail. According to Equation (14), the RP for the spectral range from 400 nm to 2.2 μm is shown in Figure 6a. The MMI theory indicates that the resolving ability decreases with λ, which can be explained by the changing of supported modes in Figure 3c. Meanwhile, to verify the correctness of this evolution, interference profiles were randomly selected at five different positions within the simulation, and the results coincide well with the theoretical model. By repeating this process as we varied L, Df, and NA, one could obtain the dependence of RP on these parameters. Figure 6b plots RP as a function of L for Df = 200 μm and NA = 0.39. RP scales exponentially with L, indicating that the resolving ability can be improved simply by increasing the length. The criterion of choosing L is tricky: when L is short, it is tedious to fix and package into the style as Figure 1a denoted, while when it is long, the CBURIS will be greatly affected by thermal or mechanical perturbations. Next, NA = 0.39 is fixed, and the plot of RP with Df is shown in Figure 6c when L = 0.1 m. RP initially rises but quickly saturates. Increasing Df introduces more modes, but it compresses the spatial pattern to some extent, causing a complicated trade-off process. In Figure 6d, we vary NA from 0.1 to 0.5 while keeping L = 0.1 m and Df = 200 μm and observe a quadratic increment of RP with NA. This analysis is performed on the assumption that Df is small enough, and its effect on the MMI profile can be ignored so that a larger NA is only responsible for more modes and larger RP.
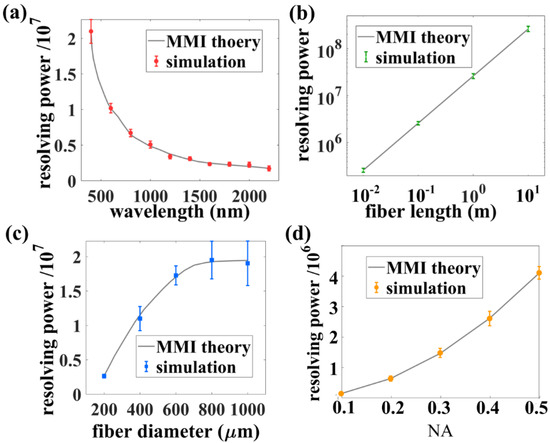
Figure 6.
Theoretical analysis of several important parameters (a) wavelength λ, (b) fiber length L, (c) fiber diameter Df, and (d) numerical aperture NA on RP of the CBURIS. The discrete data with errorbar are calculated from the MMI patterns in numerical simulation, which coincide well with the MMI theory.
4.4. Operating Mode and Thermal Stability
To incorporate the elements and package them together, Figure 7a illustrates the sketch of high spatial resolution. Each microlens in MLA is coupled with an MMFB, and its aperture size φ = 0.5° can be further divided by 3 for 1 MMF (φ′ = 0.17°). The spatial resolution could be improved by substituting with 19 or more fiber cores for a much finer angular resolution. With the tapers arranged in a matrix for compactness, a spatial-to-spatial mapping procedure should be conducted for imaging recovery in real-time. The reason we focused on an individual MMF spectrometer is that it undertakes both spatial and spectral channels for this imaging spectrometer and determines most of its FOMs, i.e., operating bandwidth, RP, spectrum reconstruction, and thermal stability. The operating mode could be realized by a simple spatial-to-spatial mapping algorithm. As illustrated in Figure 7b–d, several precise reconstructions have been conducted in numerical simulation; 3 typical types of spectra, i.e., a broad spectrum with 42 nm bandwidth, 2 broad spectra with a sharp peak, and a sharp valley, are artificially simulated together with their reconstruction results in spatial channels of No.1, 4, and 5, which sufficiently illustrates the ability to detect arbitrary signals. To be noted, as the CBURIS is packaged, both the single-wavelength light for calibration and probed light confront the same coupling condition, making the spectrum reconstruction independent of the exact coupling coefficient and modal distributions. After integrating the photon counts across the spectral range at each spatial channel, the spatial-to-spatial mapping procedure produces a detected image as the CBURIS. From another point of view, when integrating the intensity within a series of infinitesimal ranges centered at λck (k = 1,2,…,m), it functions as a one-dimensional hyperspectral imaging spectrometer.
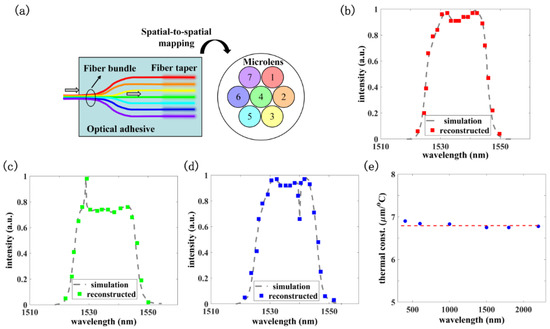
Figure 7.
(a) The operation mode of the high spatial-resolution CBURIS, each MMF works as a spatial channel that marks with a different color. (b–d) Three different channels corresponding to ones in (a) (No.1, 4, and 5) are chosen to illustrate a well-performed reconstruction scheme. (e) The product of Δφ/ΔT and λ at different λ are plotted, which equals a constant.
As mentioned above, mechanical and thermal perturbations are critical limiting factors for applications. Based on the layout, mechanical perturbation primarily results from an out-of-focus MMI pattern, and as tested in experiments [24], the correlation between time-related calibration matrices after improving the image by an automatically optimized software proved the long-term stability of CBURIS. In addition, the temperature perturbations cannot be ignored with this length scale. As ambient temperature varies, the refractive index of fiber core n1 changes due to the thermo-optic effect, n1(T + ΔT) = n1(T)·(1 + 7 × 10−6ΔT), and length L changes due to the thermal expansion, L(T + ΔT) = L(T)·(1 + 5 × 10−7ΔT) [18]. From the theoretical model, these could disturb the coupling efficiency χ, amplitude E, and phase ϕ of the modes, as well as the propagation constant β, leading to a difference in the MMI pattern. Meanwhile, Δϕ is also amplified by L(T + ΔT) at the detecting region; the path difference then becomes:
It has been proven that for small temperature variations, the change of φ is approximately the same for all modes [18,25]. In order to distinguish the patterns under ΔT, the minimal of Δφ(λ) should also be π. For L = 0.1 m, ΔT equals to ~7.2 °C. Shorter MMFBs could improve this FOM and make it robust against the temperature change. According to and , where α1 and α2 are thermal coefficients 7 × 10−6 and 5 × 10−7, respectively. The products of Δφ/ΔT and λ at different λ shown in Figure 7e remain unchanged. This λ·(Δφ/ΔT) can be defined as a thermal constant, which provides a tendency that the CBURIS in the infrared region performs more steadily under a small temperature shift.
5. Discussion and Conclusions
The designed CBURIS has the following advantages. First, it achieves both high spatial and ultrahigh spectral resolution. On the one hand, each MMFB containing multiple optical fibers is coupled with an individual microlens of the MLA, subdividing the field angle 0.5° into smaller ones (<0.1° if possible), which guarantees a high angular resolution. On the other hand, the combination of MMF tapers and a detector pushes CBURIS to obtain an ultrahigh spectral resolution across visible to mid-infrared regions compared to its counterparts, and the RP is improved by at least two orders of magnitude higher [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Secondly, it possesses an ultra-wide FOV in the horizontal plane to meet the wide-angle search requirement since the MLA arranged in a circular arc approaches a straight angle. Thirdly, it can obtain information with a snapshot measurement, superior to most of the existing ones. After recording the spatial and spectral information within an MMI matrix, the hyper-image could be reconstructed by spectrum reconstruction and spatial-to-spatial mapping procedure. The trade-off is the computation time and spectral resolution, which can be adjusted according to practical requirements. Fourthly, the lack of moving parts makes it stable against a variety of external perturbations and reduces deviation during the assembly and adjustment process. Fifthly, as estimated from the layout and theoretical model, the footprint of CBURIS is 600 cm3 (=6 cm × 10 cm × 10 cm). As illustrated in Figure 1a, the number of microlenses is FOV divided by the field angle of a microlens 120°/0.5° = 240, and the chord length of MLA 2R1·sin(FOV/2) = 6 cm determines the size in x direction. When setting Df/2 as the margin between MMF tapers, it can hold 24 transversal units. In y direction, 10 cm length is spacious for 240/24 = 10 longitudinal units. The most tricky part is z direction, considering the imaging components for MMI patterns, they totally consume 15 mm (focal length of lens) + 5 mm (lens thickness) + 63 mm (length of objective) + 2 mm (focal length of objective) = 85 mm. The remaining 1.5 cm is enough for the optical adhesive and area detector array. The focal length of the lens in front of the detector can be ~1.5 cm (Thorlabs LA1540-ML), and one possible choice of the detector has a pixel size of 4.8 μm, and pixel number is 1280 × 1024, from visible to near-infrared. Except for the scanning sketch, the CBURIS could also be realized with an area detector array of several hundred cm2.
There are shortcomings, such as the usage of a number of microlenses and MMFBs will increase the complexity of the system, making the manufacturability elaborate. However, with the development of ultra-precision manufacturing and assembly technologies, the difficulty of manufacturing and assembly will continue to decrease in the future. Another concern is that in practical applications, fabrication imperfections existing in MMF may deteriorate the spectral resolution and consume more time before packaging, which limits its development to some extent. However, for a moderate scenario, it is still superior for high integration detection. Some critical parameters for the CBURIS design are shown in Table 3.

Table 3.
Critical parameters for the CBURIS design.
In conclusion, the principle of a high-performance CBURIS design consisting of an MLA, multiple MMFBs, a microscope, and a 2D detector array integrated on top is presented in detail. Complementary simulations of the MMI generation, correlation, and spectrum reconstruction are also conducted to verify the correctness of the MMI theory. Traditional imaging spectrometry always includes the procedure of spatial or spectral scanning, which requires a large optical path and long acquisition time, and meanwhile, they are only available for stationary conditions. The existing non-scanning frameworks often possess large size and moderate resolution. Benefited from the strong dependence of MMI patterns on wavelength, the CBURIS realizes a wide field of view, ultrahigh spatial resolution, ultra-broad operation bandwidth, ultrahigh spectral resolution, and a small footprint at the same time. Integrated with various functional fiber-based devices, the CBURIS is expected to have an indispensable role in high-performance, real-time, and portable applications.
Author Contributions
Conceptualization, F.M.; methodology, F.M. and Z.L.; software, F.M., P.W. and W.F.; validation, F.M., Z.L. and J.C.; investigation, F.M. and P.W.; resources, F.M. and J.C.; writing—original draft preparation, F.M.; writing—review and editing, F.M., Z.L., P.W. and W.F.; visualization, J.C.; project administration, F.M.; funding acquisition, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 12004265), the Natural Science Foundation of Hebei Province (No. A2020210001), the Youth Talent Support Program of Universities of Hebei Province (No. BJ2021038), and the Development project Fundamental Research Program of Shanxi Province (No. 202103021224203).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on reasonable request from the corresponding author.
Acknowledgments
The authors sincerely thank the anonymous reviewers for their valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging Spectrometry for Earth Remote Sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Pawlowski, M.E.; Cheng, S.; Dwight, J.G.; Stoian, R.I.; Lu, J.; Alexander, D.; Tkaczyk, T.S. Light-guide snapshot imaging spectrometer for remote sensing applications. Opt. Express 2019, 27, 15701–15725. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.; Rajesh, M. Computational multispectral video imaging. J. Opt. Soc. Am. A 2018, 35, 189–199. [Google Scholar]
- Kato, T.; Uchida, M.; Tanaka, Y.; Minoshima, K. One-shot three-dimensional imaging using a two-dimensional spectrometer with a fiber bundle. Opt. Express 2021, 29, 43778–43792. [Google Scholar] [CrossRef]
- Flynn, C.; Stoian, R.I.; Weers, B.D.; Mullet, J.E.; Thomasson, J.A.; Alexander, D.; Tkaczyk, T.S. Ruggedized, field-ready snapshot light-guide-based imaging spectrometer for environmental and remote sensing applications. Opt. Express 2022, 30, 10614–10632. [Google Scholar] [CrossRef]
- Palombi, L.; Raimondi, V. A compact LIF spectrometer for in-field operation in polar environments. Sensors 2021, 21, 1729. [Google Scholar] [CrossRef]
- Uddin, N.; Sheng, Q.; Lee, S.; Reinke, M.L.; Donovan, D.; Shafer, M.; Han, M. Multichannel fiber-optic silicon Fabry-Perot interferometric bolometer system for plasma radiation measurements. Photonics 2021, 8, 344. [Google Scholar] [CrossRef]
- Malara, P.; Giorgini, A.; Avino, S.; Sarno, V.D.; Aiello, R.; Maddaloni, P.; Natale, P.D.; Gagliardi, G. A self-operating broadband spectrometer on a droplet. Nat. Commun. 2020, 11, 2263. [Google Scholar] [CrossRef]
- Korablev, O.I.; Belyaev, D.A.; Dobrolenskiy, Y.S.; Trokhimovskiy, A.Y.; Kalinnikov, Y.K. Acousto-optic tunable filter spectrometers in space missions. Appl. Opt. 2018, 57, C103–C119. [Google Scholar] [CrossRef]
- Sahin, F.E.; Tanguay, A.R. Distortion optimization for wide-angle computational cameras. Opt. Express 2018, 26, 5478–5487. [Google Scholar] [CrossRef]
- Jullien, A.; Pascal, R.; Bortolozzo, U.; Forget, N.; Residori, S. High-resolution hyperspectral imaging with cascaded liquid crystal cells. Optica 2017, 4, 400–405. [Google Scholar] [CrossRef]
- August, I.; Oiknine, Y.; AbuLeil, M.; Stern, A. Miniature compressive ultra-spectral imaging system utilizing a single liquid crystal phase retarder. Sci. Rep. 2016, 6, 23524. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q. Moving corner-cube-mirror interferometer and reflection characteristic of corner-cube mirror. Appl. Opt. 2010, 49, 4088–4095. [Google Scholar] [CrossRef]
- Zucco, M.; Pisani, M.; Caricato, V.; Egidi, A. A hyperspectral imager based on a Fabry-Perot interferometer with dielectric mirrors. Opt. Express 2014, 22, 1824–1834. [Google Scholar] [CrossRef] [PubMed]
- Pisani, M.; Zucco, M. Compact imaging spectrometer combining Fourier transform spectroscopy with a Fabry-Perot interferometer. Opt. Express 2009, 17, 8319–8331. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q. Design study of a compact ultra-wide-angle high-spatial-resolution high-spectral-resolution snapshot imaging spectrometer. Opt. Express 2021, 29, 2893–2908. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, J.; Liu, J.; Feng, S.; Li, X.; Cui, J. Optical design of a prism-grating-based lenslet array integral field spectrometer. Opt. Express 2018, 26, 19456–19469. [Google Scholar] [CrossRef]
- Redding, B.; Alam, M.; Seifert, M.; Cao, H. High-resolution and broadband all-fiber spectrometers. Optica 2014, 1, 175–180. [Google Scholar] [CrossRef]
- Redding, B.; Cao, H. Using a multimode fiber as high-resolution, low-loss spectrometer. Opt. Lett. 2012, 37, 3384–3386. [Google Scholar] [CrossRef]
- Wang, J.; Yan, S.; Ruan, Y.; Xu, F.; Lu, Y. Fiber-optic point-based sensor using specklegram measurement. Sensors 2017, 17, 2429. [Google Scholar] [CrossRef] [Green Version]
- Chanclou, P.; Kaczmarek, C.; Mouzer, G.; Gravey, P.; Thual, M.; Lecollinet, M.A.; Rochard, P. Expanded single-mode fiber using graded index multimode fiber. Opt. Eng. 2004, 43, 1634–1642. [Google Scholar]
- Redding, B.; Popoff, S.M.; Cao, H. All-fiber spectrometer based on speckle pattern reconstruction. Opt. Express 2013, 21, 6584–6600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Yu, Z. Spectral analysis based on compressive sensing in nanophotonic structures. Opt. Express 2014, 22, 25608–25614. [Google Scholar] [CrossRef] [PubMed]
- Redding, B.; Liew, S.F.; Bromberg, Y.; Sarma, B.; Cao, H. Evanescently coupled multimode spiral spectrometer. Optica 2016, 3, 956–962. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Zhao, Y.; Wang, H.; Zhang, Y. High-performance compact spectrometer based on multimode interference in a tapered spiral-shaped waveguide. Opt. Express 2019, 27, 38349–38358. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Z.; Sullivan, M.; Brady, D.; Adibi, A. Multimodal multiplex spectroscopy using photonic crystals. Opt. Express 2003, 11, 2126–2133. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).