Infrared Small Target Detection by Modified Density Peaks Searching and Local Gray Difference

Abstract

Infrared small target detection is a challenging task with important applications in the field of remote sensing. The idea of density peaks searching for infrared small target detection has been proved to be effective. However, if high-brightness clutter is close to the target, the distance from the target pixel to the surrounding density peak will be very small, which easily leads to missing detection. In this paper, a new detection method, named modified density peaks searching and local gray difference (MDPS-LGD), is proposed. First, a local heterogeneity indicator is used as the density to suppress high-brightness clutter, and an iterative search is adopted to improve the efficiency in the process of searching for density peaks. Following this, a local feature descriptor named the local gray difference indicator (LGD) is proposed according to the local features of the target. In order to highlight the target, we extract the core area of the density peak by a random walker (RW) algorithm, and take the maximum response of the minimum gray difference element in the core region as the LGD of the density peak. Finally, targets are extracted using an adaptive threshold. Extensive experimental evaluation results in various real datasets demonstrate that our method outperforms state-of-the-art algorithms in both background suppression and target detection.

1. Introduction

Infrared search and track systems (IRST) have been widely used in early warning, precise guidance, remote sensing and other fields [1]. Due to the large imaging distance, infrared small targets occupy quite a few pixels in the image, which leads to a lack of obvious texture features and shape information. All of these reasons make the detection of infrared small targets very difficult [2,3]. In addition, the targets usually hide under strong noise and complex background clutter, leading to a small signal-to-noise ratio of the image [4]. There is also some target-like interference in the image, such as pixel-sized noises with high brightness (PNHB) [5,6]. These factors greatly increase the difficulty of detection. Therefore, robust infrared small target detection is considered to be an extremely challenging task. In order to detect targets accurately in various backgrounds, a large number of methods have been developed over the past decades [7,8,9,10,11].

Conventional single-frame-based detection methods segment small targets from infrared images using a spatial or frequency filter, such as a top-hat filter [12,13], max-mean/max-median filter [14], wavelet filter [15] or two-dimensional least mean squares (TDLMS) filter [16]. These methods can easily capture targets in simple uniform scenes, but they are sensitive to noise and cannot achieve satisfactory results with complex backgrounds [17,18]. In order to better suppress the noise in complex background, methods based on robust principal component analysis (RPCA) have been proposed, such as an infrared patch-image (IPI) model [19], nonconvex rank approximation minimization joint l_2,1 norm (NRAM) [20] and partial sum of the tensor nuclear norm (PSTNN) [21]. Based on the nonlocal self-correlation property of the infrared image background and the sparsity of small targets [5], these methods transform the infrared small target detection problem into the optimization problem of recovering low-rank and sparse matrices. However, the target image recovered by RPCA-based methods still retains some edge structures, as the strong edge has similar sparse characteristics as the target image.

With the development of human visual system (HVS) theory, many HVS-based methods have been proposed. These methods try to describe local features with different feature descriptors, such as a local contrast measure (LCM) [22], improved LCM (ILCM) [23], multiscale patch-based contrast measure (MPCM) [24] and neighborhood saliency map (NSM) [25]. However, when multiple targets are close to each other, all targets will be missed by these methods. In order to enhance detection performance, methods utilizing both local contrast and gradient features were proposed to distinguish real targets from strong clutter, such as a double-neighborhood gradient (DNGM) [26], fast adaptive masking and scaling with iterative segmentation (FAMSIS) [27] and absolute directional mean difference (ADMD) [28].

In addition, many joint methods that combine HVS features with other techniques were proposed to detect small targets. For example, the methods based on ring top-hat transformation (RTH) exploited contrast information in the top-hat transform through different ring structuring elements [29,30]. Deng et al. [31] designed a multiscale gray difference weighted image entropy (MGDWIE) detector, which used entropy as a weighting function for local contrast. Xia et al. [32] proposed a modified random walks (MRWs) algorithm, which applied the random walker (RW) [33] algorithm in small target detection. Subsequently, Qin et al. [34] proposed a method based on a facet kernel and random walker (FKRW) to segment targets and backgrounds in local images. Qiu et al. [35] proposed a pixel-level local contrast measure (PLLCM) to subdivide small targets and backgrounds at the pixel level by RW. However, the detection performance and running speed of HVS-based methods usually restrict each other; in other words, more time is consumed by more sophisticated feature descriptors. Inspired by the idea of density peak clustering (DPC) [36] in cluster analysis, DPS-GVR [37] takes the pixel intensity as the density and regards the small target as a high-density center point surrounded by a number of low-density points. It searches for the density peaks in the whole image, and then real targets will be identified using sophisticated local features. Compared with other joint methods, DPS-GVR has the advantages of better detection performance and higher computational efficiency. However, the density is defined based on the isolated pixels in DPS-GVR, which ignores the correlation between neighboring pixels. Zhu et al. proposed a local feature-based density peaks searching method (LF-DPS) [38], combined the local tetra pattern (LTrP) and the second-order LTrP to generate the density feature map. Although LF-DPS is adaptable to clutter better compared to DPS-GVR, the calculation of LTrP features consumes more time.

In this paper, we propose a method named modified density peaks searching and local gray difference. First, a modified density peaks searching (MDPS) is applied to select candidate target points from the image. The “concentration effects” are circumvented by the local heterogeneity indicator in MDPS and the algorithm efficiency is improved by iterative search. Subsequently, a local gray difference indicator (LGD) based on the local feature differences between small targets and the background is designed to describe the local contrast of candidate points. Finally, targets are extracted using an adaptive threshold. Note that our method is different from [37,38]; the density is defined based on the isolated pixels in [37], and the LTrP and the second-order LTrP are adopted to generate the density map in [38]. Our method takes the LHI as density. Furthermore, the LGD used to highlight real targets in our method is also different from the fused feature adopted in [38]. The calculation strategy we designed enables our method to run in less time than other methods based on density peaks searching. The main points of this paper can be summarized as follows:

• A local heterogeneity indicator is proposed as a density feature to suppress high-brightness clutter;
• The efficiency of the algorithm is improved by iterative search;
• The LGD is proposed to describe the local contrast of candidate points, which highlights the targets better.

The remainder of this article is organized as follows. Section 2 reviews the density peaks searching algorithm. Section 3 presents the proposed method. Section 4 describes the experimental setup and results. Section 5 summarizes the conclusions.

2. Density Peaks Searching

2.1. Density Peaks Searching

Density peaks searching and maximum-gray region growing (DPS-GVR) is a method for infrared small target detection proposed in [37], which can detect targets with different scales in images effectively. Inspired by density peak clustering [36] (DPC), density peaks searching (DPS) is a novel candidate target-points extraction strategy based on the definition of “density” and “δ-distance” for every pixel point. Using DPS, all pixels are converted to the feature space composed of density ρ and δ-distance. In the ρ–δ space, the density peaks are selected and their corresponding pixels in the original image are taken as candidate target points. A local feature named maximum-gray region growing (GVR) is then used to extract the real target. The density and δ-distance of pixel i are defined as

$${\rho }_i=g_i$$

(1)

$${\delta }_i=\min (d_{ij})$$

(2)

where g_i is the intensity of the pixel i, j is the pixel whose density is larger than ρ_i, and d_ij represents the Euclidean distance between pixel i and j. The δ-distance of the pixel with the highest density is defined as δ_i = max_j(d_ij). When using DPS, pixels with large ρ and δ are considered more likely to be target points. The density peaks clustering index γ for each pixel can be calculated by

$$\gamma =\rho \times \delta$$

(3)

All pixels are sorted in descending order according to γ, and the first n_p pixels are taken as the density peaks, denoted as s₁, s₂, …, s_np. This procedure is called “density peaks searching”.

2.2. Shortcomings of DPS-GVR

DPS can select the candidate targets effectively and has a natural capability of multiscale target detection. However, when the target is dim or close to background clutter with high-brightness (the δ-distance of the target pixel is small), it is possible to miss the target when extracting candidate points, which is called the “concentration effect.” Figure 1 shows a few density peaks extracted by DPS in some representative infrared images. It can be seen that the “concentration effect” makes the δ of target pixel very small, resulting in missing detection.

Density peaks are found by DPS based on image intensity, so it is difficult to apply DPS to infrared images with strong noise, especially for PNHB in infrared images. As PNHB satisfies two characteristics of density peaks, relatively high density and relatively large distance from higher-density pixels, the algorithm tends to regard PNHB as a density peak. When multiple PNHBs exist in the image, DPS will miss the real target.

In those scenes with strong background clutter, the enhancement effect of GVR on the target is not significant. Using the GVR value as a feature to distinguish candidate points may sometimes lead to false detection or missing detection. Therefore, a new feature that can significantly enhance the target is needed. In addition, we found that in the process of calculating δ-distance, the elements in windows of 3 × 3 should be sorted several times, which takes some unnecessary time.

3. Proposed Method

In this section, a method is proposed to improve the existing problems of DPS-GVR. As shown in Figure 2, our method consists of two main stages: extracting candidate targets with modified density peaks searching (MDPS) and distinguishing true targets from candidate targets with a local gray difference (LGD) indicator. The small target detection method based on MDPS-LGD is introduced in detail below.

3.1. Modified Density Peaks Searching

To overcome the shortcomings of DPS, we propose the modified density peaks searching (MDPS). A novel local heterogeneity indicator is employed to improve DPS for better clutter suppression ability, and a fast computation strategy is designed to calculate δ-distance.

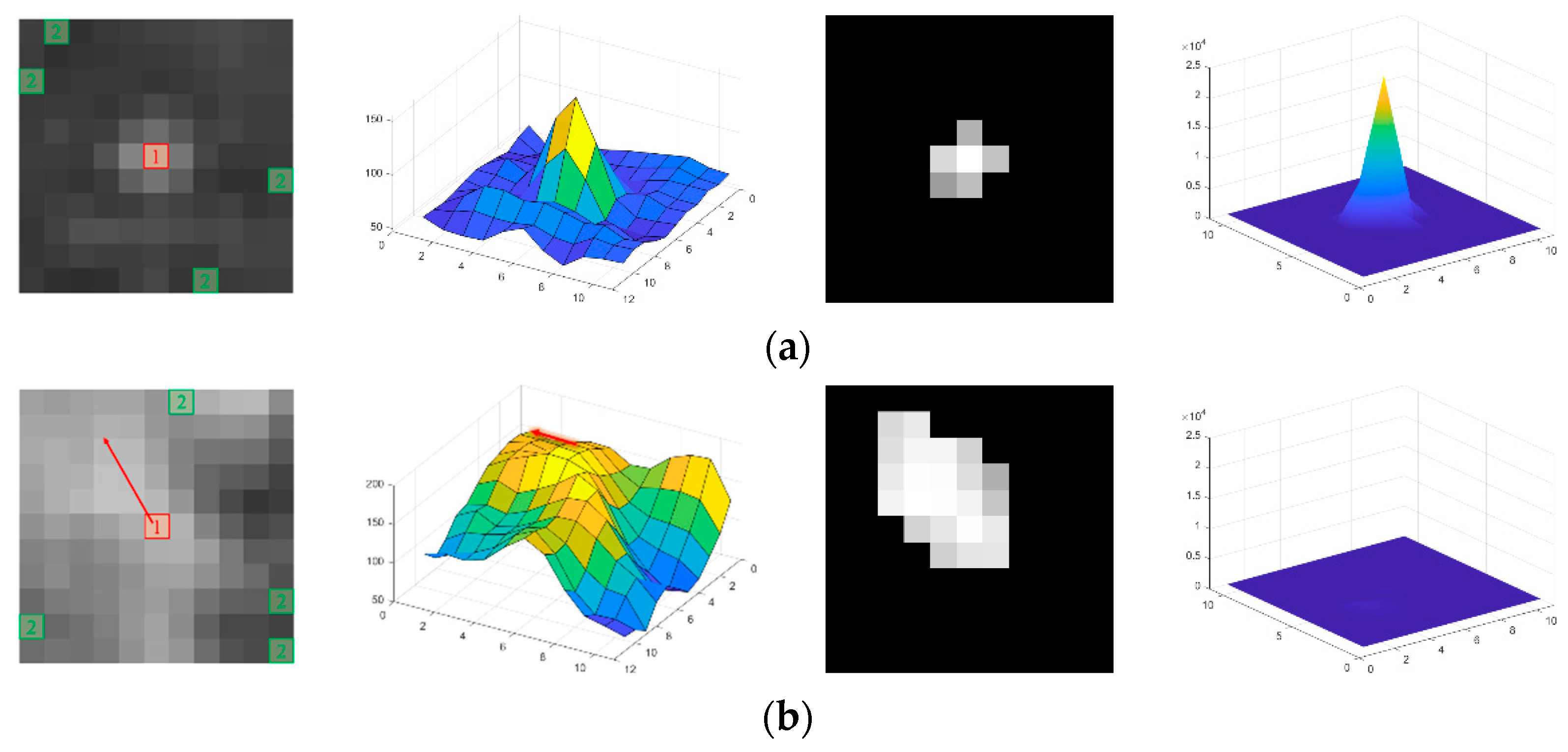
3.1.1. Local Heterogeneity Indicator

The pixel intensity is defined as density in the density peaks searching algorithm. If the intensity of pixel j in clutter is larger than the intensity of target pixel i (that is to say, the distance d_ij between i and j is small), the δ_i will also be small. Therefore, simply defining pixel intensity as density could lead to missing detections. A new definition of density is needed so that bright clutter is suppressed while targets are enhanced. Additionally, since the densities for every pixel in the image need to be calculated, the calculation of density should be fast enough. Infrared small targets usually have different shapes with no obvious texture features. However, they tend to appear as heterogeneous and compact regions when compared with the surrounding background pixels [34,39]. Considering that “heterogeneity” is an important distinction between target pixels and background pixels, we construct a local heterogeneity indicator (LHI) as the density feature. Firstly, a 5 × 5 mean filter is applied to smooth the image and reduce the influence of PNHB. For the smoothed image denoted as g, the local heterogeneity measure of pixel i is defined as

$$I_{LH}(i)=\max \left(g_i-\mathrm{mean}(W\backslash i),0\right)$$

(4)

in which W is a l × l local window centered on i, W\i represents the region in W except the center pixel i, and mean(W\i) represents the mean of elements in W\i. LHI counts the difference between pixel i and its surrounding pixels. For the target pixel, its intensity must be greater than most of the pixels in the local window, and the I_LH will be very large. If i is located at the edge of the high-brightness background or clutter, the intensity of some pixels in the local window is close to the intensity of i, and the others are smaller than i. In this circumstance, the value of the mean (W\i) will be slightly smaller than i. Compared with the case that pixel i is the target pixel, the I_LH will be smaller. If i is located inside the bright background and clutter, mean(W\i) will be close to g_i and I_LH will be close to 0. Thus, LHI can effectively suppress background clutter with high-brightness and enhance target.

In order to verify the effectiveness of LHI, LHI is used to process the local image around the target (purple box) in Figure 1a. As shown in Figure 3, Figure 3a is a 3D schematic diagram of the local image of Figure 1a and Figure 3b shows the processing results. It can be seen that high-brightness clutter is suppressed and the target is enhanced.

Based on the analysis above, we changed the definition of density in the DPS as shown in Equations (5) and (6), where LHI is taken as the density in Equation (5) and γ is calculated in Equation (6). The new peak density searching algorithm is used to detect the target in Figure 1a. As shown in Figure 3d, the target pixel is away from background pixels in ρ–δ space, while background clutter and noise are perfectly suppressed in Figure 3e.

$${\rho }_{LH}=I_{LH}$$

(5)

$$\gamma ={\rho }_{LH}\times \delta$$

(6)

3.1.2. Modified Density Peaks Searching Algorithm

The δ-distance of every pixel needs to be calculated when searching for density peaks, and we found that the elements of 3 × 3 windows are repeatedly sorted in the calculation strategy [37], causing a lot of unnecessary time consumption. We present a new calculation strategy that iteratively scales the image to obtain the δ-distance for every pixel. At each iteration, we sort the density from large to small, and process points with larger density first. In this way, the density map is only sorted once in each iteration, which reduces the computation time effectively. The schematic diagram of the computational strategy is shown in Figure 4a. For the original input density map ρ, the detailed algorithm to calculate the δ-distance is as follows:

Let D⁽¹⁾ = ρ, S⁽¹⁾ = 0, k = 1. The following iterative process is repeated until the size of D^(k) is equal to 1 × 1.

• All of elements in D^(k) are sorted from large to small, and the index of the sorted elements are represented as I_des;
• Traverse I_des, for each element (i, j) in I_des, execute 3, until all elements in the signed matrix S^(k) are 1. Then stop the traversal and execute 4;
• Let S^(k) (i, j) = 1. As shown in Figure 4b, U_{(i, j)} represents an area of 3 × 3 window centered at (i, j) in D^(k), for each point (s, t) in U_{(i, j)}, if S^(k) (s, t) = 0: let S^(k) (s, t) = 1, D^(k) (s, t) = 0, the corresponding points of D^(k) (s, t) and D^(k) (i, j) in ρ are denoted as p and q, respectively. The δ-distance of point p can be calculated by Equation (7)

  $${\delta }_p=d_{pq}^{\rho }$$

  (7)
• Scale D^(k) to half of the original, keep the points larger than 0 in D^(k). Every element in the result D^(k+1) can be calculated by Equation (8); the area represented by V(i, j) is shown in Figure 4b. Define the signed matrix S^(k+1); every element in S^(k+1) can be can be calculated by Equation (9). Then let k = k + 1.

  $$D^{(k+1)}(i,j)=\underset{(s,t)\in V_{(i,j)}}{\max }{D}^{(k)}(s,t)$$

  (8)

  $$S^{(k+1)}(i,j)=\{\begin{array}{cc}1,& \mathrm{if} D^{(k+1)}(i,j)=0\\ 0,& \mathrm{otherwise}\end{array}$$

  (9)

Finally, for the point i in D with the highest density, let δ_i = max_j(d_ij).

We propose an algorithm called modified density peaks searching (MDPS) for candidate target selection in infrared images. LHI is taken as density and the δ-distances of pixels are calculated by iteratively scaling the image in MDPS, as shown in Algorithm 1. According to this flowchart, we can analyze the computational complexity to explain how the designed strategy can improve the efficiency. As mentioned above, the elements of 3 × 3 windows are repeatedly sorted to calculate the δ-distance of the elements in the windows [37]. For a frame with N pixels, the complexity of this process is O(3.1699N). The complexity of traversing the sorted density map in our algorithm is O(N). It can be seen from the complexity that the efficiency of the algorithm is improved through our calculation strategy.

Algorithm 1 Modified Density Peaks Searching.

Input: Infrared image I ϵ ℝw×h

Output: Candidate target pixels set C

1:   Initialize: ρ = 0w×h, δ = 0w×h.

2:   Calculate the density ρ according to Equation (5).

3:   D(1) = ρ, S(1) = 0, k = 1, [m, n] = size(D(1)).

4:   while m > 1 or n > 1

5:      Sort all elements in D(k) in descending order. The index vector of the sorted result is Ides.

6:      for each index (i, j) in Ides do

7:         S(k) (i, j) = 1.

8:         for (s, t) in U(i, j) do

9:            if S(k) (s, t) = 0

10:              S(k) (s, t) =1, D(k) (s, t) = 0, calculate δ by Equation (7)

11:          end if

12:       end for

13:    end for

14:    Generate matrix D(k+1) = 0m/2×n/2, S(k+1) = 0m/2×n/2.

15:    The value of the pixel (i, j) in the D(k+1) is obtained by (8).

16:    The value of the pixel (i, j) in the S(k+1) is obtained by (9).

17:    [m, n] = size(D(k+1)), k = k + 1.

18:  end while

19:  For the last pixel i in D(k), δi = maxj(dij).

20:  Calculate the density peaks clustering index γ according to (6).

21:  Sort all the pixels by γ in descending order.

22:  Output candidate target pixels set C with the first np pixels.

3.2. Local Gray Difference Indicator

In order to choose real targets from candidate targets (density peaks), we designed a feature called the local gray difference indicator (LGD) which is more effective than GVR. First, the local image is segmented using a random walker algorithm [33], and the region closely related to the candidate pixels is extracted, which is called the “core region”. Following this, we constructed a minimum gray difference element (MGDE), and the maximum response of the core region to the MGDE is taken as the LGD of candidate pixels.

Figure 5 shows two local image blocks around the candidate pixels found by the MDPS. Figure 5a,b are two local images containing both target and background, respectively. The candidate pixel selected by MDPS is usually the maximum point of the local image, but there are some differences between the target pixel and the background pixel. As shown in Figure 5a, there are obvious differences between the target area and the surrounding background in all orientations. For the image in Figure 5b, the difference between the central pixel and the surrounding background is small in a certain orientation (see the arrow in Figure 5b), showing consistency in this direction. Therefore, the characteristic of the target area can be used to distinguish the target from the background.

Image segmentation can be realized by using an RW algorithm with a small number of labeled pixels, that is, the probability that an unlabeled pixel belongs to every label is calculated by the RW algorithm. The RW algorithm is able to exploit the characteristics of the target region. Similar to the work in [32,34], we apply RW in the local region which contains d × d pixels and has a center on the candidate pixel. Figure 6a shows the labeling strategy we designed. The candidate pixels are labeled as class 1, and the minimum value points on the four sides (E₁, E₂, E₃ and E₄) of the local region are labeled as class 2. The local image blocks in Figure 5 are segmented using the labeling strategy. In Figure 5a, since the gray value of pixels in the target area are significantly higher than those of the surrounding background pixels, these pixels are labeled as class 1. In Figure 5b, the pixels within the smoothed regions in the local block are labeled as class 1. We refer to the set of points labeled as class 1 as the “core area.” The procedure of calculating the LGD for each candidate pixel is as follows.

Denoting the kth point in candidate target set C as c_k. The RW algorithm is applied to segment the local image block centered on c_k, and A_k represents the core area of this block. As shown in Figure 6b, for every point p in A_k, the local block centered on p is divided into m regions {${\Phi }_p^j$ | j ϵ [1, m] }, where ${\Phi }_p^j$ represents the set of points whose Chebyshev distance from point p is equal to j, as shown in Equation (10).

$${\Phi }_p^j=\left\{q\right|\max (\left|p_x-q_x\right|,\left|p_y-q_y\right|)=j\}$$

(10)

In order to describe the contrast of the pixel p, we construct a vector s ϵ ℝ^m, and each element s_j in s is defined as

$$s_j=\frac{1}{K}{\displaystyle \sum _i^K(g_p-g_i^j})$$

(11)

where $g_i^j$ represents the ith maximal gray value in region ${\Phi }_p^j$, and g_p is the gray value of point p. K represents the number of pixels considered to eliminate the influence of outliers and is set to 2 or 3. s_j describes the minimum gray difference between pixel p and ${\Phi }_p^j$. The minimum gray difference element (MGDE) of p is defined as

$$MGD{E}_p={\{\begin{array}{c}s\cdot \mathrm{abs}(s), \mathrm{if} s\cdot \mathrm{abs}(s)>\left(\frac{g_p}{\tau }\right)\\ 0, \mathrm{otherwise}\end{array}}^2$$

(12)

where abs(·) represents the absolute value of each element in the original vector, and the parameter τ is the background suppression factor. Considering that the intensity of background pixel is lower than the pixel in small target center, the value of τ is chosen to be between 5 and 10. The local gray difference indicator (LGD) of c_k is defined as

$$I_{LGD}^k=\underset{p\in A_k}{\max }(MGD{E}_p)$$

(13)

If c_k is a small target, the MGDE of the central pixel of the target will be large since the brightness of the small target is higher than the neighborhood in all directions, and the $I_{LGD}^k$ will also be large. If c_k is the background pixel, all components of s are close to 0 due to the directional consistency, and the $I_{LGD}^k$ will be small. Considering that the size of small targets in infrared images is usually less than 9 × 9 pixels, the parameter d is set to 11 and m to 5, so that the local block will contain a small target completely. Column 4 of Figure 5 shows the MGDE of the target block and background block. It is clear the MGDE of the target block is significantly higher than background block. The I_LGD of target and background pixel are 24,360 and 751, respectively. Therefore, the features of target and background can be distinguished to identify the real target by using LGD.

To extract effective targets from candidate points, we merge two adjacent candidate points into one, and take the larger I_LGD between them as the LGD of the candidate point. Specifically: for any two candidate points c_i and c_j, if there exists a point p_i ϵ A_i with U_pi ∩ A_i ≠ Ø, remove the candidate point with smaller I_LGD from the candidate points set C.

3.3. Implementation of the Proposed Method

From the discussion above, it can be seen that the LGD of the real target is much larger than the background. Therefore, a simple threshold operation is used to extract the real target, and it can be defined as

$$T=\mathrm{mean}(I_{LGD})+\lambda \ast \mathrm{std}(I_{LGD})$$

(14)

where mean(·) and std(·) represent mean and standard deviation, respectively, and λ is a given parameter. Candidate points whose LGD are greater than the threshold T are selected as detected small targets.

On the basis of the above work, we propose a small target detection method based on MDPS and LGD, as shown in Algorithm 2. MDPS-LGD consists of three main steps: (1) Obtaining the set C of candidate target points by MDPS. (2) Calculating the core area A_k for each candidate target c_k. (3) Extracting the real target through the threshold in Equation (14).

Algorithm 2 The Proposed Detection Method Based on LGD.

Input: Infrared image I ϵ ℝw×h

Output: Detection result

1:   Obtain candidate target pixels set C according to Algorithm 1.

2:   for any ck ϵ C do

3:      Obtain core area Ak by RW algorithm.

4:      for any p ϵ Ak do

5:         Compute the MGDEp according to (12).

6:      end for

7:      Compute the $I_{LGD}^k$ according to (13).

8:   end for

9:   Extract targets from candidate target pixels using adaptive threshold in (14).

4. Experimental Results and Analysis

In this section, we first introduce test datasets, baseline methods for comparison, and evaluation metrics. Then, the anti-noise performance of our method is analyzed. Finally, we test the performance of each method through qualitative and quantitative experiments. All experiments were conducted in MATLAB R2020a on a PC with 4.3 GH Intel i5-10400 processor and 16 GB RAM.

4.1. Experimental Setup

4.1.1. Datasets and Baseline Methods

To demonstrate the effectiveness and robustness of the proposed method, we used four infrared image sequences with different backgrounds, and their details are presented in

Table 1. The details of four real image sequence.

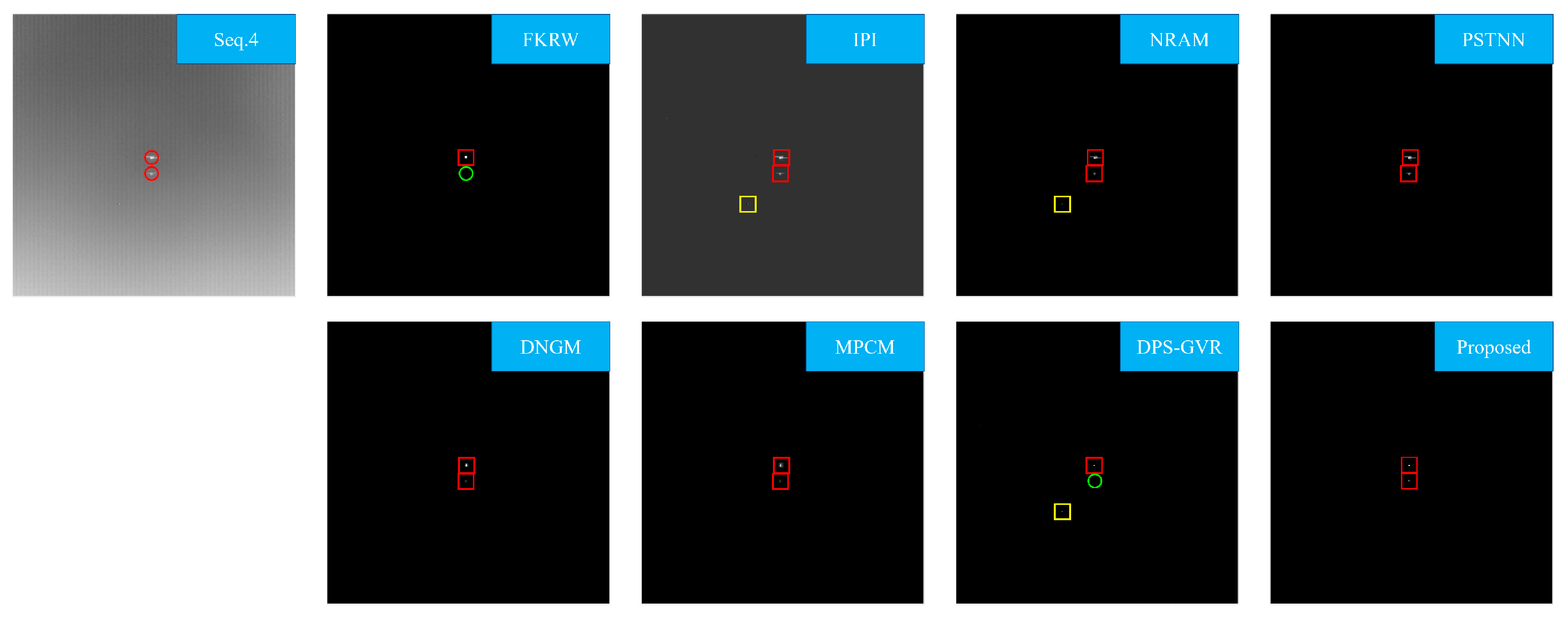
	Frame Number	Frame Size	Targets	Target Size	Background	Clutter Description
Seq.1	100	278 × 360, 128 × 128	141	3 × 3 to 9 × 9	Building, sea, etc.	Heavy noise, salient strong edges
Seq.2	300	256 × 256	300	3 × 3 to 5 × 5	Cloudy sky	Irregular cloud
Seq.3	180	256 × 256	300	6 × 6 to 11 × 11	Sea	Sea-level background with much clutter
Seq.4	100	256 × 256	200	10 × 3, 3 × 2	Sky	Banding noise, PNHB

. Seq.1 consisted of 100 single-frame images, every of them containing one or more targets, complex backgrounds with significant strong edges and sources of interference. Seq.2–4 were sequences containing successive images. Seq.2 contained 300 frames, and each frame had one target whose size was less than 6 × 6. Seq.3 contained 180 frames, and each frame had one target whose size was larger than 6 × 6. In Seq.4, every frame contained two close targets, and there were PNHB and stripe noises in the images. The minimum distance between targets in all frames of the dataset was greater than 10 pixels.

The baseline methods for comparison included both conventional methods including MPCM [24], IPI [19] and NRAM [20] and some state-of-the-art methods including PSTNN [21], DNGM [26], MKRW [34] and DPS-GVR [37]. FKRW is a detection method based on facet kernel filtering and random walker. IPI, NRAM, and PSTN are RPCA-based methods, and MPCM and DNGM are HVS-based multiscale detection methods.

Table 2. Parameter setting of eight methods.

Methods	Parameter Setting
MKRW	K = 4, p = 6, β = 200, window size: 11 × 11
IPI	patch size: 50 × 50, sliding setp:10, $\lambda =1/\sqrt{\max (m,n)}$, ε = 10−7
NRAM	patch size: 50 × 50, sliding setp:10, $\lambda =1/\sqrt{\max (m,n)}$, ε = 10−7, γ = −0.002
PSTNN	patch size: 50 × 50, sliding setp:40, $\lambda =0.6/\sqrt{\min (n_1,n_2)\ast n_3}$, ε = 10−7, γ = −0.002
DNGM	N = 3
MPCM	N = 3, 5, 7, 9, L = 3
DSP-GVR	np = 20, nk = 0.0015 × mn
Proposed	l = 4, d = 11, m = 5, τ = 8

shows all the methods used in the experiments and their parameter settings.

4.1.2. Evaluation Metrics

For a comprehensive comparison, we evaluate the performance of small target detection algorithms from three aspects: image quality, detection accuracy, and running speed. The quality of the enhanced image output by detection algorithms can be quantitatively described with background suppression factor (BSF) and contrast gain (CG) [5]. In general, BSF and CG are defined as follows:

$$\mathrm{BSF}=\frac{{\sigma }_r}{{\sigma }_e}$$

(15)

$$\mathrm{CG}=\frac{{\mathrm{CON}}_e}{{\mathrm{CON}}_r}$$

(16)

where σ_r and σ_e represent the standard deviation of original image and enhanced image, respectively. CON_r and CON_e represent the contrast of original image and enhanced image. Contrast (CON) is defined as

$$\mathrm{CON}=\left|m_t-m_b\right|$$

(17)

where m_t is the average value of the target pixels, m_b is the average value of the background pixels in the neighboring region of the target. The neighboring region is defined as a region that is less than 16 pixels away from the center of the target. By using DPS-GVR, we can get the GVR values of candidate pixels, except the enhanced image. Thus, the GVR of the candidate pixel is used to define the enhanced image during evaluation. Specifically, the enhanced image I_e of DPS-GVR is defined as

$$I_e(i)=\{\begin{array}{c}\mathrm{GVR}(i),i \mathrm{is} \mathrm{candidate} \mathrm{pixel}\\ 0, \mathrm{otherwise}\end{array}$$

(18)

Likewise, MGDE is used to define the enhanced image in our methods. Considering the definition above, only the candidate points in the enhanced image are not equal to 0. In order to evaluate the target enhancement ability of these methods better, we define a new contrast as

$$\mathrm{CON}=\left|M_t-m_b\right|$$

(19)

where M_t represents the maximum value of the target pixels, and we use the contrast defined above to calculate CG. Furthermore, in order to describe the noise intensity in the image, the signal-to-clutter ratio (SCR) of the image is defined as

$$\mathrm{SCR}=\frac{\mathrm{CON}}{\sigma }$$

(20)

where σ represents the standard deviation of image intensities in the neighboring area of target. The detection performance of the algorithm is evaluated by the receiver operating characteristic (ROC) curve. The vertical coordinate of the ROC curve represents the detection probability R_d, and the horizontal coordinate represents the false alarm rate R_f, which are defined as follows:

$$R_d=\frac{\mathrm{number} \mathrm{of} \mathrm{true} \mathrm{detections}}{\mathrm{number} \mathrm{of} \mathrm{total} \mathrm{actual} \mathrm{targets}}$$

(21)

$$R_f=\frac{\mathrm{number} \mathrm{of} \mathrm{false} \mathrm{detections}}{\mathrm{number} \mathrm{of} \mathrm{total} \mathrm{detections}}$$

(22)

The ROC curve shows the trade-off between true detection and false detection. Specifically, the algorithm with the ROC curve closer to the upper left corner has better performance. We calculated the area under the curve (AUC) to quantitatively compare the ROC curves.

4.2. Anti-Noise Performance

As described in Section 3.1, DPS is less robust to noise in images, especially to PNHB. It is necessary to evaluate the method based on the DPS proposed above. We selected four infrared images from Seq.1, and added Gaussian white noise to them; the mean value and the variance of Gaussian white noise were 0 and 0.005, respectively. In Figure 7, the first row shows the original images, the second row shows the images after adding noise, and the processing results of the proposed method are shown in the third row. After adding white Gaussian noise, the targets in the image became indistinguishable. However, the proposed method can enhance the target effectively. We repeated the above experiment 100 times and recorded the average SCR of original images and processed images. The results of the experiment are shown in

Table 3. Average SCR of the images in Figure 7.

	Original Image	Enhanced Image	Nosie-Added Image	Enhanced Image
Figure 7a	2.8262	31.5807	1.7068	27.3232
Figure 7b	6.3872	23.0794	3.4259	22.9246
Figure 7c	5.8426	21.6889	2.8987	21.0840
Figure 7d	7.2077	26.3750	2.1380	24.2110

. It can be seen that the SCR of the images decreases significantly after adding noise. In all four scenes, the SCR of the enhanced images processed by our method are greater than 20, and most of the clutter and noise in the images are suppressed. This shows that our method has a certain degree of anti-noise ability.

4.3. Image Quality

Figure 8 and Figure 9 show the processing results of representative images from four sequences using different methods. We normalized the enhanced images obtained by all methods, and marked correct detections with red boxes and false detections with yellow boxes. It can be seen that all targets are accurately detected by the proposed method, which achieves the best clutter suppression ability and target enhancement effect. In contrast, those baseline methods do not show good performance on the four sequences simultaneously. Among all of those baseline methods, FKRW has the best target enhancement ability, which enhances all targets from Seq.1 and removes clutter completely. However, when using FKRW, a small residual of buildings is still in images from Seq.2, and the dim targets from Seq.4 are missed. IPI suppresses the target hidden at the edge of clouds in Seq.1 (b) incorrectly, and PNHB is not suppressed in the result of Seq.4. NRAM misses the target in Seq.1 (a) and fails to suppress the PNHB of Seq.4. PSTNN successfully enhances all targets, but the strong edges in Seq.1 (b) and Seq.1 (c) remain in the results. The clutter suppression effect of DNGM and MPCM is the worst, especially for the clouds in Seq.1 (a) and Seq.1 (b). Both algorithms have a large amount of clutter residue. DPS-GVR misses the smaller targets in Seq.4, and the PNHB in Seq.4 is not suppressed.

In addition to qualitative evaluations based on different scenes, we further evaluate the detection performance of the proposed method and baseline methods on four sequences using BSF and CG. It is worth noting that the infinite value (INF) for BSF indicates that the background in the image is completely suppressed.

Table 4. Average BSF and CG using different methods on four sequences. The best-obtained results are bolded, and the second-best results are underlined.

		FKRW	IPI	NRAM	PSTNN	DNGM	MPCM	DPS-GVR	Proposed
Seq.1	BSF	311.51	32.41	94.36	28.94	175.11	23.95	42.04	329.79
	INF in BSF	0	5	20	9	0	0	0	14
	CG	5.45	5.25	5.19	5.62	6.92	7.13	5.27	6.49
Seq.2	BSF	639.17	424.56	102.54	36.42	305.86	15.46	41.93	2.17 × 103
	INF in BSF	12	72	127	105	0	0	0	102
	CG	8.45	9.47	10.73	9.83	10.72	11.0361	11.23	11.71
Seq.3	BSF	164.93	561.83	40.72	28.38	320.08	40.71	14.24	421.03
	INF in BSF	38	43	56	93	0	0	0	35
	CG	6.22	5.72	5.06	5.43	6.62	6.62	6.48	6.55
Seq.4	BSF	174.99	65.07	92.15	133.19	559.60	47.60	65.66	5.00 × 103
	INF in BSF	0	0	0	50	0	0	0	76
	CG	3.35	3.11	3.98	4.08	3.28	3.27	2.55	3.81

shows the number of BSF equals INF in the results obtained by every method and the average value of BSF for images without INF; the average value of CG is also given in Table 4. The proposed method achieves the best or second-best results on all four sequences. The background is completely suppressed in Seq.2 for more than 100 images. Due to the presence of PNHB and stripe noise in image of Seq.4, only PSTNN and our method are able to completely suppress the clutter in the image. The clutter in 76 images of Seq.4 is completely suppressed by the proposed method, which shows the robustness of our method with regard to PNHB. It can be concluded that our method outperforms most of the baseline methods with excellent background suppression on test datasets.

4.4. Detection Performance

As an improvement to the density peaks searching, we firstly compared our method with DPS-GVR to verify that our improvement are effective. As shown in Figure 10, regarding the four images are selected from Seq.1, all images have the “concentration effect” described in Section 3.1. DPS-GVR and our method are applied to these four images, respectively. The results show that the targets are all missed by DPS-GVR. However, our method is able to detect targets accurately, which proves the effectiveness of our improved density peaks searching by LHI.

We also use ROC curves to evaluate the detection performance of our method and baseline methods. The ROC curves of the different methods of four sequences are shown in Figure 11. It can be seen that our method achieves the best detection performance on Seq.1, Seq.2 and Seq.3 compared with the baseline methods. In Seq.2 and Seq.3, our method obtains almost perfect curves. It is worth noting that two targets are close to each other in Seq.4, and PNHB is present in all frames from Seq.4. DPS-GVR suffers from the “concentration effect” and detects only one target per image, while our improved method is not affected. In conclusion, the proposed method can achieve ideal detection performance for the four sequences.

4.5. Running Speed

The main computational cost of our method comes from two parts: the calculation of the δ-distance in the MDPS and the solution of RW algorithm. The time complexity of MDPS is O(Nlog₂(N)), where N is the total number of pixels in the image. The RW algorithm is used to segment n_p local blocks with a size of d × d, complexity O(n_pd⁶) and where n_p and d are fixed values. Therefore, the computational complexity of the proposed method is O(Nlog₂(N)). To demonstrate the efficiency of the proposed method, we compare the running time of different methods on the dataset and analyze the computational complexity of the proposed methods.

Table 5. Average running time (s) of different methods.

	FKRW	IPI	NRAM	PSTNN	DNGM	MPCM	DPS-GVR	Proposed
Seq.1	0.1468	3.4239	1.0260	0.1715	2.1835	0.0331	0.3626	0.0840
Seq.2	0.2330	3.4830	1.2912	0.2806	3.1556	0.0724	0.4964	0.1336
Seq.3	0.2270	3.2550	1.2408	0.2696	3.0464	0.0732	0.5332	0.1376
Seq.4	0.1080	3.6193	1.6296	0.1542	3.1383	0.0380	0.5648	0.1322

shows the average running time of different methods on test datasets. It can be seen that the proposed method achieves the second-best results in all four sequences, which is just slower than MPCM. However, the proposed method performs much better than MPCM in any other metric and IPI is the most time-consuming method. The proposed method is much faster than DPS-GVR, which reflects the advantage of MDPS.

5. Conclusions

In this paper, a single-frame infrared small target detection algorithm based on modified density peaks searching and local gray difference is proposed. In order to circumvent the “concentration effect”, we used LHI as density to enhance the target and suppress the influence of PNHB. Subsequently, according to the local feature differences between small target and clutter regions around candidate points, a local gray difference indicator was proposed to highlight targets, and real targets were extracted by an adaptive threshold. We conducted extensive experiments on real test datasets to evaluate the robustness and effectiveness of our method. Experimental results show that, compared to several state-of-the-art methods, our method can suppress various types of background clutter better, with a lower false alarm rate even under complex background conditions. At the same time, the proposed method has a lower time cost than most of the compared methods. In the future, the mean filter can be replaced by an order-statistic filter in the process of constructing LHI to prevent extremely dim targets from being eliminated, and the detection performance can be further improved by combining it with multi-frame based methods. In addition, the speed of detection can be further improved by using parallel computing.