A Simplified Laser System for Atom Interferometry Based on a Free-Space EOM
Abstract
:1. Introduction
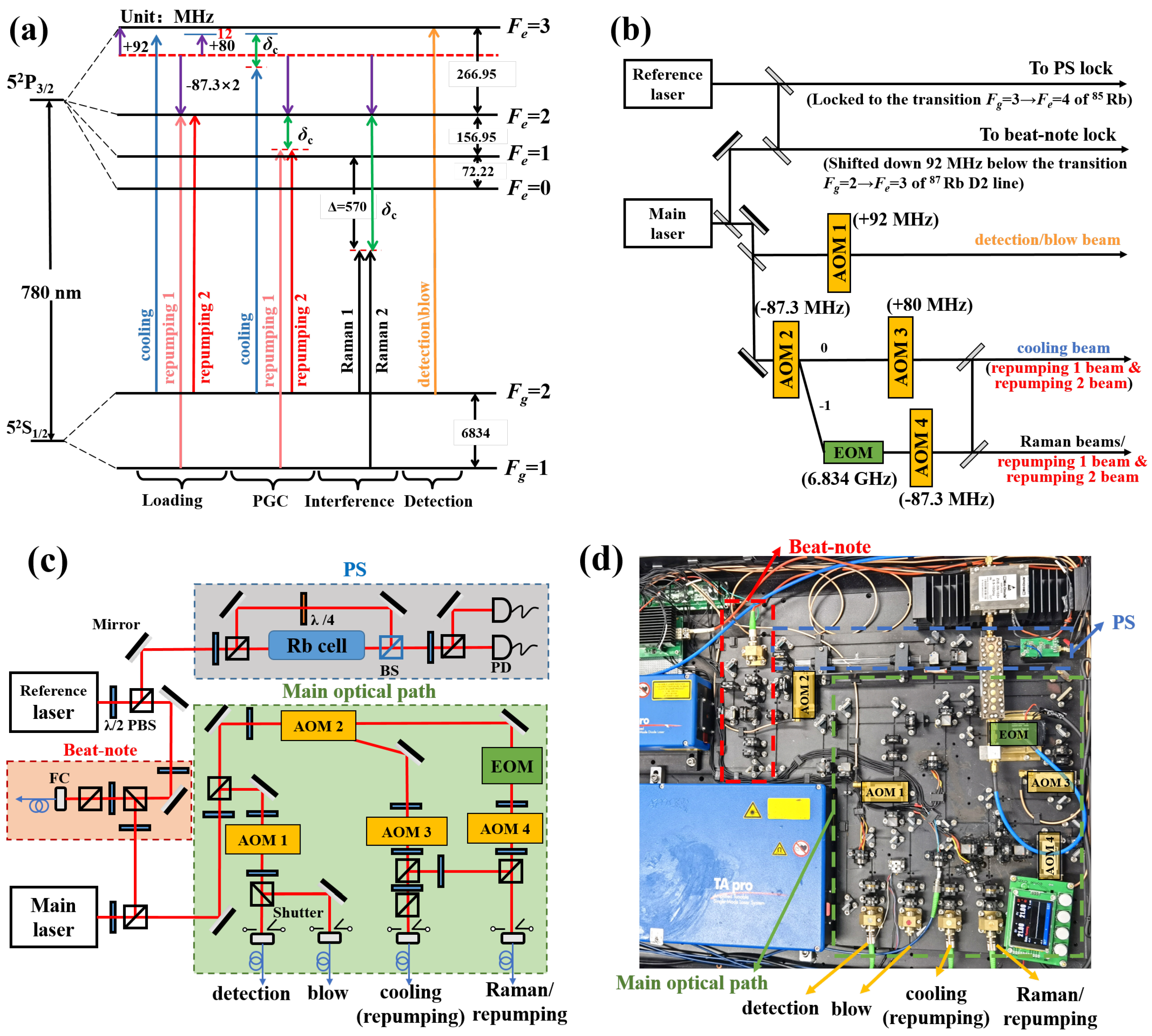
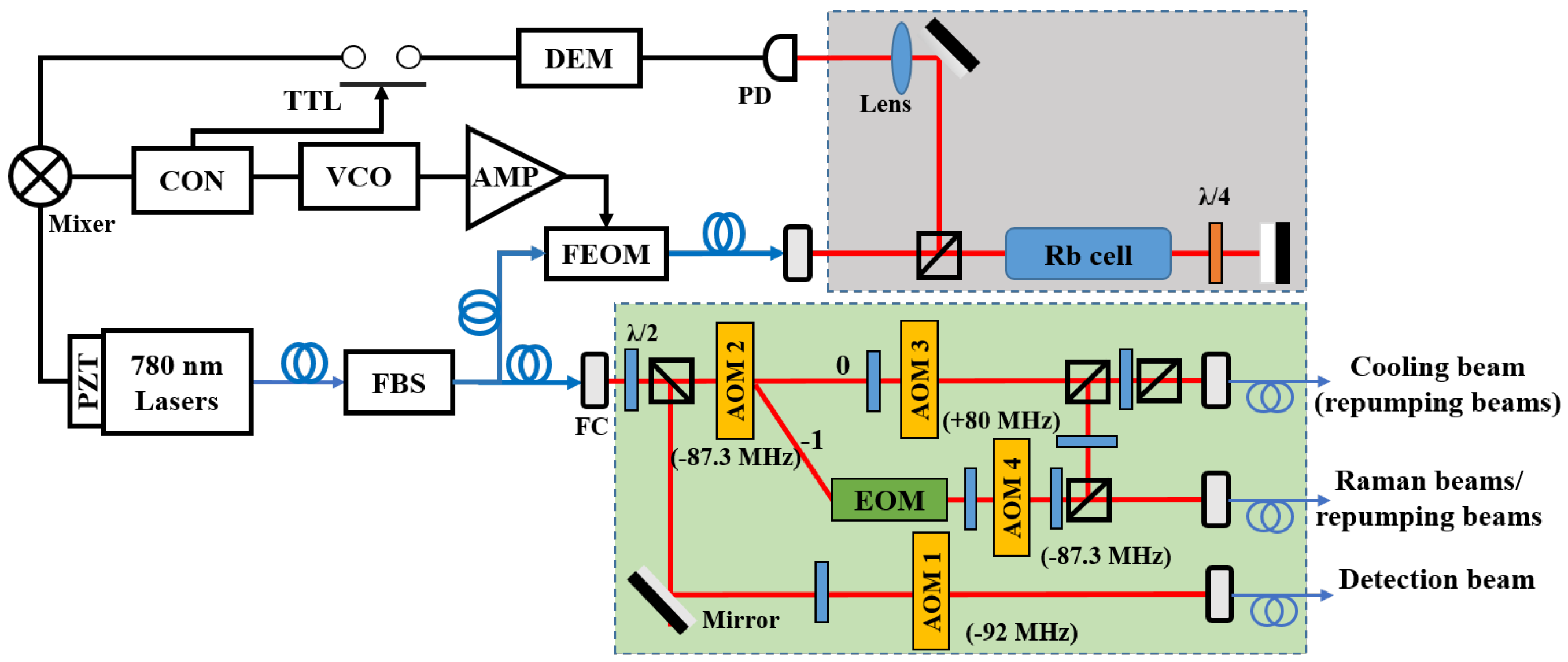
2. The Laser System of Atom Interferometer
3. Theoretical Analysis of the Cooling Caused by the Laser System
4. The Experiment and Results
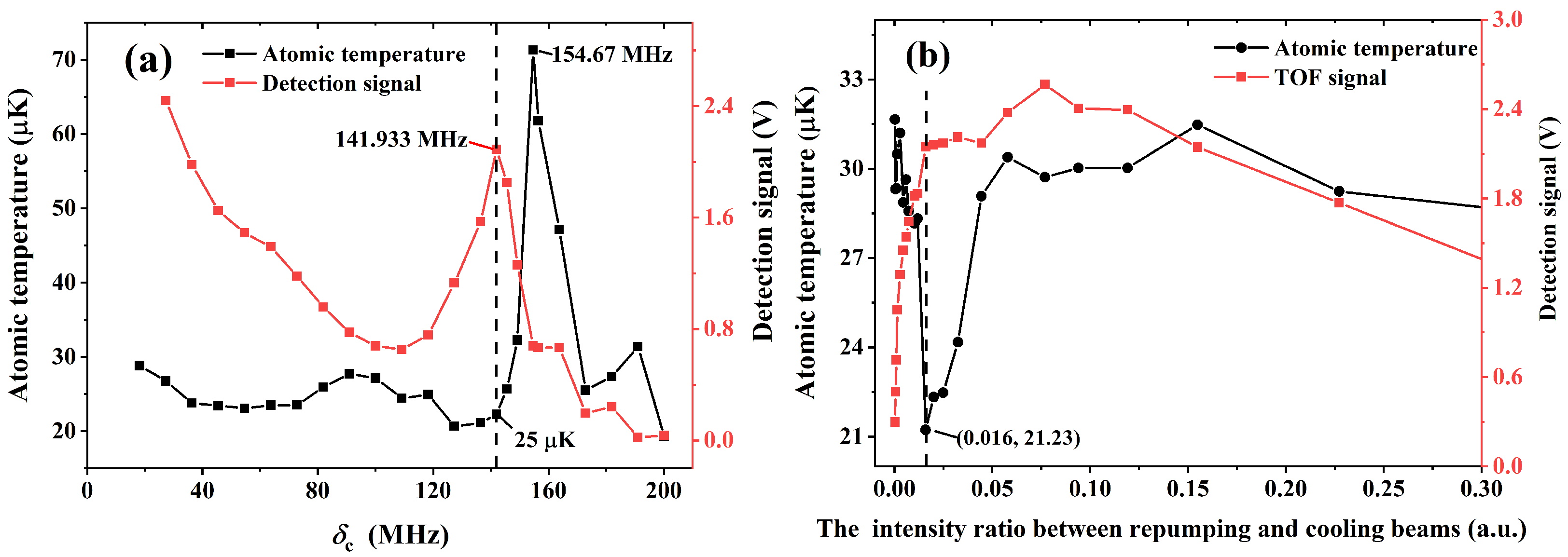
4.1. The Optimization of Laser System Configurations in the PGC Process
4.2. The Atomic Interference Fringes
4.3. The Improvement of This Laser System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kasevich, M.; Chu, S. Atomic interferometry using stimulated Raman transitions. Phys. Rev. Lett. 1991, 67, 181. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lu, X.Y.; Qin, C.G.; Tan, Y.J.; Shao, C.G. Modeling gravitational wave detection with atom interferometry. Class. Quantum Gravity 2021, 38, 145025. [Google Scholar] [CrossRef]
- Kasevich, M.; Chu, S. Measurement of the gravitational acceleration of an atom with a light-pulse atom interferometer. Appl. Phys. B 1992, 54, 321–332. [Google Scholar] [CrossRef]
- Gustavson, T.; Bouyer, P.; Kasevich, M. Precision rotation measurements with an atom interferometer gyroscope. Phys. Rev. Lett. 1997, 78, 2046. [Google Scholar] [CrossRef] [Green Version]
- Dutta, I.; Savoie, D.; Fang, B.; Venon, B.; Alzar, C.G.; Geiger, R.; Landragin, A. Continuous cold-atom inertial sensor with 1 nrad/s rotation stability. Phys. Rev. Lett. 2016, 116, 183003. [Google Scholar] [CrossRef] [Green Version]
- Rosi, G.; Cacciapuoti, L.; Sorrentino, F.; Menchetti, M.; Prevedelli, M.; Tino, G. Measurement of the gravity-field curvature by atom interferometry. Phys. Rev. Lett. 2015, 114, 013001. [Google Scholar] [CrossRef] [Green Version]
- Mcguirk, J.M.; Foster, G.; Fixler, J.; Snadden, M.; Kasevich, M. Sensitive absolute-gravity gradiometry using atom interferometry. Phys. Rev. A 2002, 65, 033608. [Google Scholar] [CrossRef] [Green Version]
- Bertoldi, A.; Lamporesi, G.; Cacciapuoti, L.; De Angelis, M.; Fattori, M.; Petelski, T.; Peters, A.; Prevedelli, M.; Stuhler, J.; Tino, G. Atom interferometry gravity-gradiometer for the determination of the Newtonian gravitational constant G. Eur. Phys. J. D At. Mol. Opt. Plasma Phys. 2006, 40, 271–279. [Google Scholar]
- Weiss, D.; Young, B.; Chu, S. Precision measurement of ℏ/m Cs based on photon recoil using laser-cooled atoms and atomic interferometry. Appl. Phys. B Lasers Opt. 1994, 59, 217–256. [Google Scholar] [CrossRef]
- Bouchendira, R.; Cladé, P.; Guellati-Khélifa, S.; Nez, F.; Biraben, F. New determination of the fine structure constant and test of the quantum electrodynamics. Phys. Rev. Lett. 2011, 106, 080801. [Google Scholar] [CrossRef] [Green Version]
- Parker, R.H.; Yu, C.; Zhong, W.; Estey, B.; Müller, H. Measurement of the fine-structure constant as a test of the Standard Model. Science 2018, 360, 191–195. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, M.; Efremov, M.; Roura, A.; Schleich, W.; DeSavage, S.; Davis, J.; Srinivasan, A.; Narducci, F.; Werner, S.; Rasel, E. T3-Interferometer for atoms. Appl. Phys. B 2017, 123, 102. [Google Scholar] [CrossRef] [Green Version]
- Rozenman, G.G.; Zimmermann, M.; Efremov, M.A.; Schleich, W.P.; Shemer, L.; Arie, A. Amplitude and phase of wave packets in a linear potential. Phys. Rev. Lett. 2019, 122, 124302. [Google Scholar] [CrossRef] [Green Version]
- Amit, O.; Margalit, Y.; Dobkowski, O.; Zhou, Z.; Japha, Y.; Zimmermann, M.; Efremov, M.A.; Narducci, F.A.; Rasel, E.M.; Schleich, W.P.; et al. T3 Stern-Gerlach matter-wave interferometer. Phys. Rev. Lett. 2019, 123, 083601. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.; Sun, Y.; Wang, B.; Xia, W.; Qu, Q.; Xiang, J.; Dong, Z.; Lü, D.; Liu, L. Highly reliable optical system for a rubidium space cold atom clock. Appl. Opt. 2016, 55, 3607–3614. [Google Scholar] [CrossRef]
- Cheinet, P.; Pereira Dos Santos, F.; Petelski, T.; Le Gouët, J.; Kim, J.; Therkildsen, K.; Clairon, A.; Landragin, A. Compact laser system for atom interferometry. Appl. Phys. B 2006, 84, 643–646. [Google Scholar] [CrossRef] [Green Version]
- Merlet, S.; Volodimer, L.; Lours, M.; Pereira Dos Santos, F. A simple laser system for atom interferometry. Appl. Phys. B 2014, 117, 749–754. [Google Scholar] [CrossRef] [Green Version]
- Carraz, O.; Lienhart, F.; Charrière, R.; Cadoret, M.; Zahzam, N.; Bidel, Y.; Bresson, A. Compact and robust laser system for onboard atom interferometry. Appl. Phys. B 2009, 97, 405–411. [Google Scholar] [CrossRef]
- Luo, Q.; Zhang, H.; Zhang, K.; Duan, X.C.; Hu, Z.K.; Chen, L.L.; Zhou, M.K. A compact laser system for a portable atom interferometry gravimeter. Rev. Sci. Instrum. 2019, 90, 043104. [Google Scholar] [CrossRef]
- Feng, Y.; Xue, H.; Wang, X.; Chen, S.; Zhou, Z. Observation of Ramsey fringes using stimulated Raman transitions in a laser-cooled continuous rubidium atomic beam. Appl. Phys. B 2015, 118, 139–144. [Google Scholar] [CrossRef]
- Fang, J.; Hu, J.; Chen, X.; Zhu, H.; Zhou, L.; Zhong, J.; Wang, J.; Zhan, M. Realization of a compact one-seed laser system for atom interferometer-based gravimeters. Opt. Express 2018, 26, 1586–1596. [Google Scholar] [CrossRef]
- Metcalf, H.J.; Van der Straten, P. Laser cooling and trapping of neutral atoms. J. Opt. Soc. Am. B 2003, 20, 887–908. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.C.; Wei, R.; Shi, C.Y.; Wang, Y.Z. Observation of modulation transfer spectroscopy in the deep modulation regime. Chin. Phys. Lett. 2010, 27, 124211. [Google Scholar] [CrossRef]
- Phillips, W.D. Nobel Lecture: Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 1998, 70, 721. [Google Scholar] [CrossRef] [Green Version]
- Cohen-Tannoudji, C.; Phillips, W.D. New mechanisms for laser cooling. Phys. Today 1990, 43, 33–40. [Google Scholar] [CrossRef]
- Steck, D. Rubidium 85 D Line Data, Revision (2.1.5). 2012. Available online: http://steck.us/alkalidata (accessed on 1 February 2022).
- Beattie, S.; Barrett, B.; Weel, M.; Chan, I.; Mok, C.; Cahn, S.; Kumarakrishnan, A. Influence of spontaneous emission on a single-state atom interferometer. Phys. Rev. A 2008, 77, 013610. [Google Scholar] [CrossRef]
- Naskar, S.; Sardar, D.; Deb, B.; Agarwal, G. Suppressing deleterious effects of spontaneous emission in creating bound states in cold atom continuum. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 245204. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Zhao, Y.; Cheng, B.; Zhang, C.; Li, D.; Zhu, D.; Yue, Y.; Li, J.; Zhang, K.; Lin, Q.; et al. A Simplified Laser System for Atom Interferometry Based on a Free-Space EOM. Photonics 2022, 9, 301. https://doi.org/10.3390/photonics9050301
Wu B, Zhao Y, Cheng B, Zhang C, Li D, Zhu D, Yue Y, Li J, Zhang K, Lin Q, et al. A Simplified Laser System for Atom Interferometry Based on a Free-Space EOM. Photonics. 2022; 9(5):301. https://doi.org/10.3390/photonics9050301
Chicago/Turabian StyleWu, Bin, Yingpeng Zhao, Bing Cheng, Can Zhang, Dianrong Li, Dong Zhu, Yazhou Yue, Jun Li, Kaijun Zhang, Qiang Lin, and et al. 2022. "A Simplified Laser System for Atom Interferometry Based on a Free-Space EOM" Photonics 9, no. 5: 301. https://doi.org/10.3390/photonics9050301
APA StyleWu, B., Zhao, Y., Cheng, B., Zhang, C., Li, D., Zhu, D., Yue, Y., Li, J., Zhang, K., Lin, Q., & Weng, K. (2022). A Simplified Laser System for Atom Interferometry Based on a Free-Space EOM. Photonics, 9(5), 301. https://doi.org/10.3390/photonics9050301




