Machine Learning-Based Optical Performance Monitoring for Super-Channel Optical Networks
Abstract
:1. Introduction
- (a)
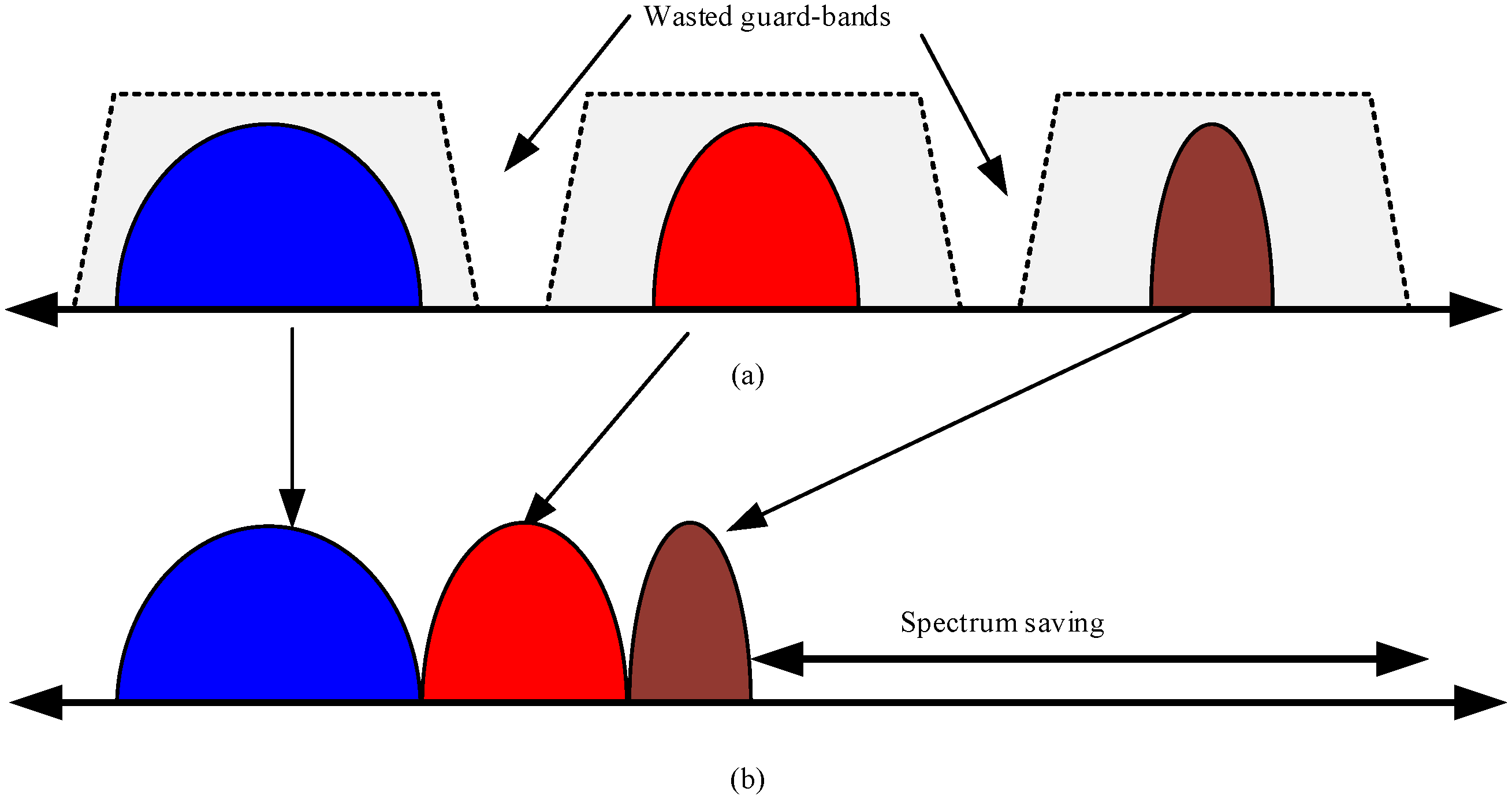
- It is the first in literature, to the best of author’s knowledge, which considers the OPM in super-channel optical networks. In contrast to the conventional WDM networks, super-channel optical networks have an additional impairment arising from subcarrier interference, which makes the OPM a challenging task.
- (b)
- It proposes a novel ML-based OPM scheme using the discrete Fourier transform/discrete cosine transform (DFT/DCT) of in-phase quadrature histogram (IQH) for features extraction and the support vector regressor (SVR) for the estimation of the channel’s impairments. IQH-based OPM for single carrier optical networks was originally proposed in [35]. IQH has also been used for OPM in few mode fiber channels [24]. Here, we consider new features (transformed IQH) for monitoring a new type of channels (super-channel). The advantages of proposed features are two-fold: (i) they provide low feature size compared to the non-transformed IQH features, hence less complexity; and (ii) they show excellent OPM results compared to the non-transformed IQH and to the conventional 1D features (i.e., AAH), as demonstrated in Section 5.
- (c)
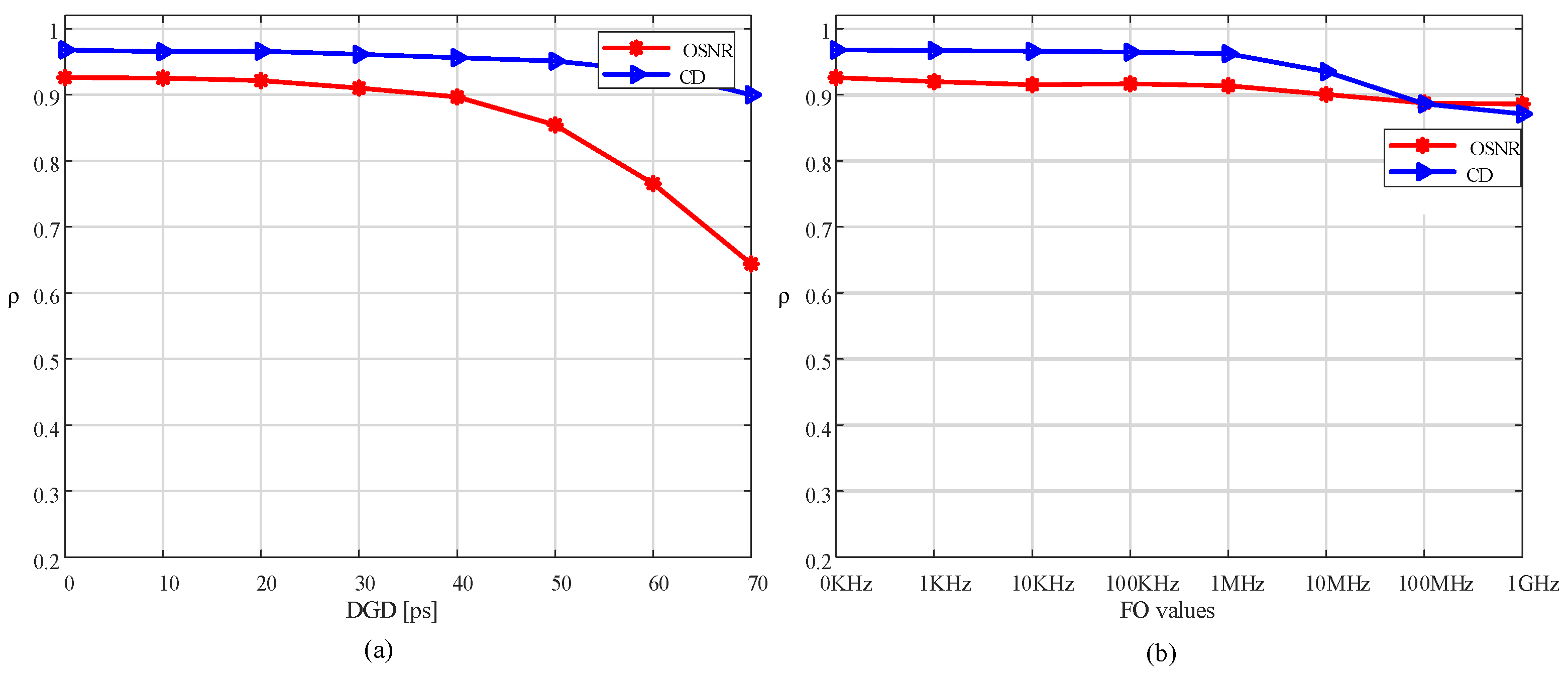
- It evaluates the performance of IQH and transformed IQH features in the presence of different channel impairments. In addition, it investigates the impact of PMD, frequency offset (FO), and utilization of different modulation formats including the DP-QPSK, DP-8QAM, and DP-16QAM, on the monitoring accuracy.
- (d)
- It presents proof-of-concept experimental results for validation purposes.
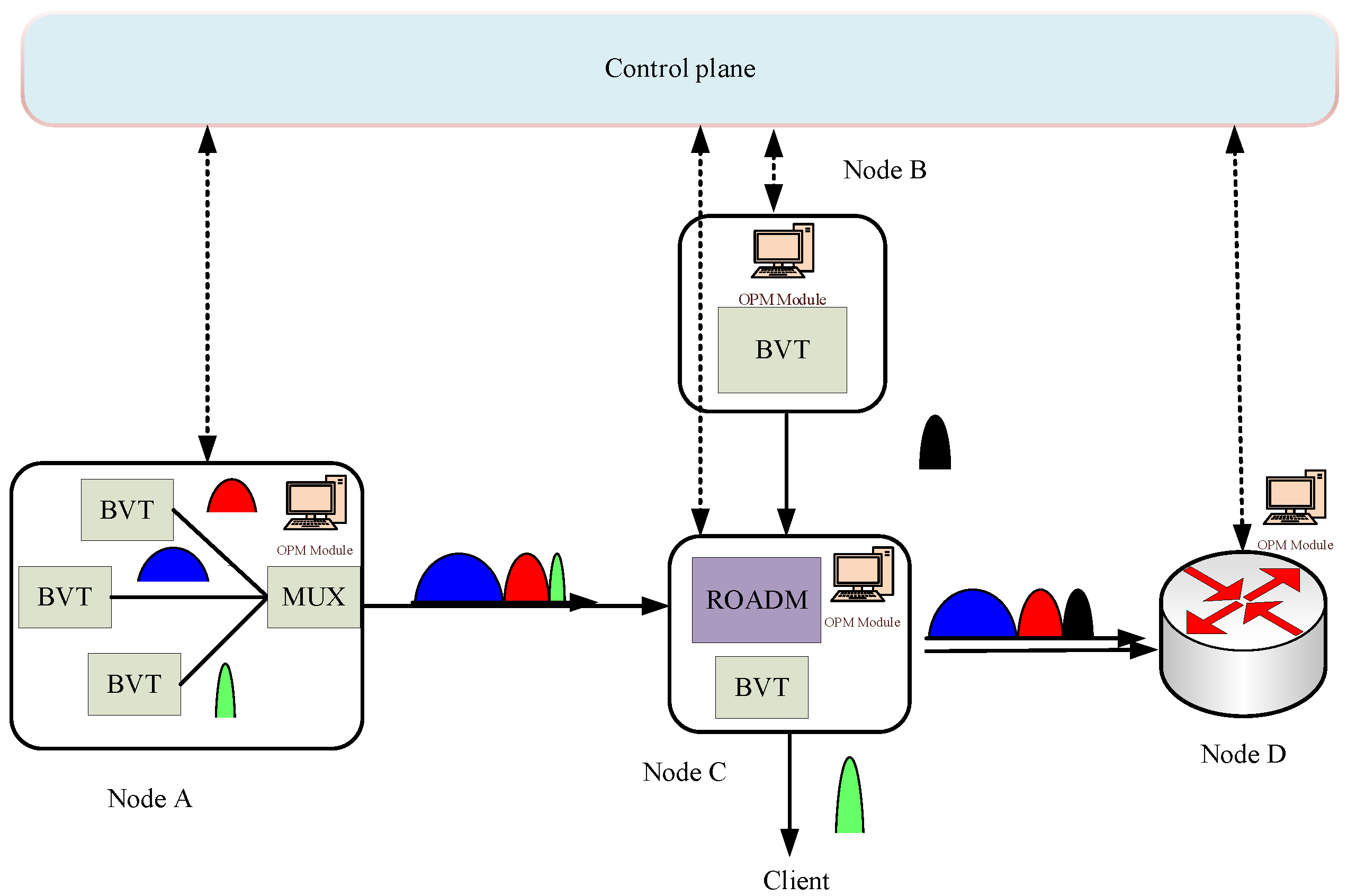
2. Elastic Optical Networks (EONs)
3. Proposed OPM Techniques
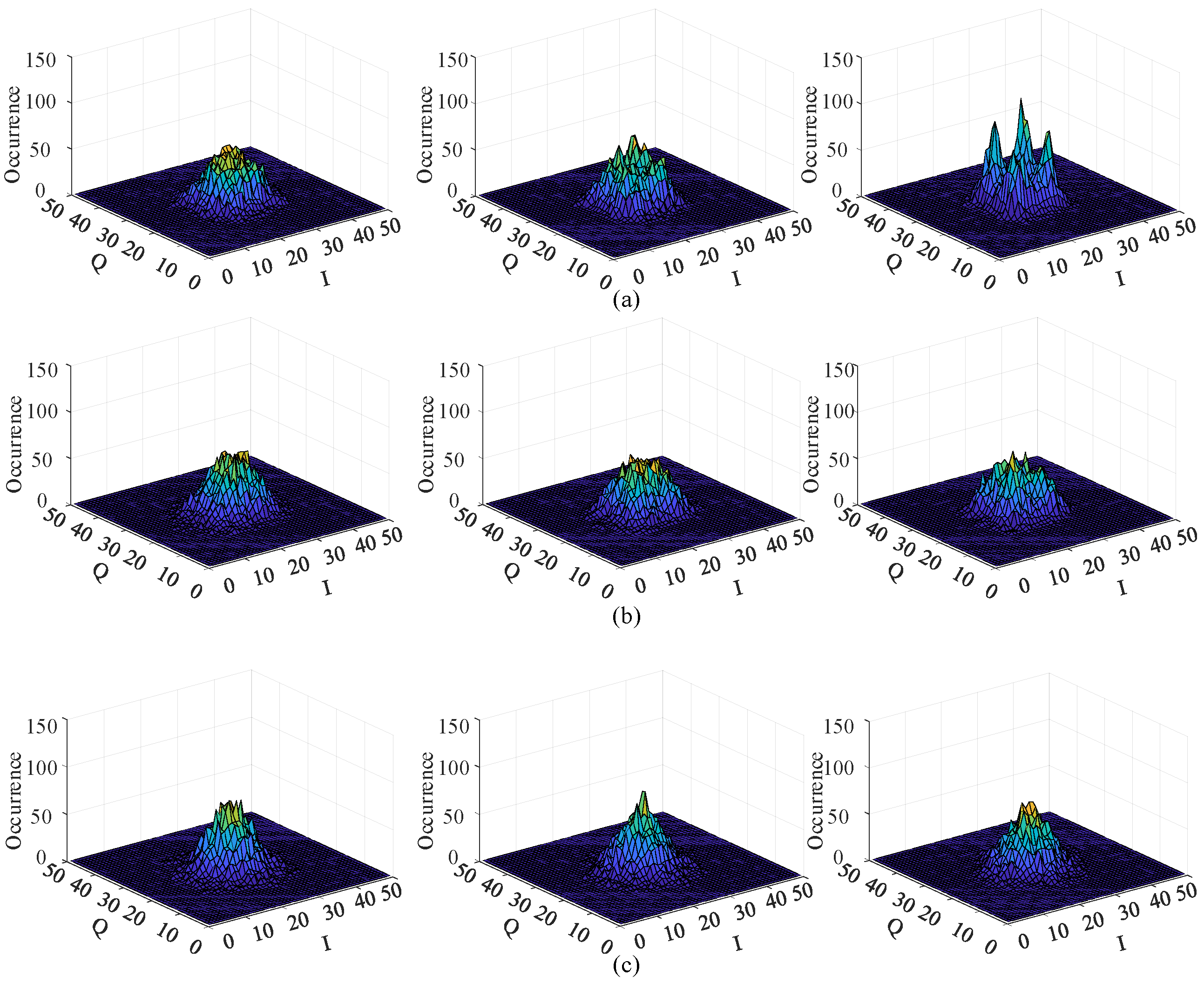
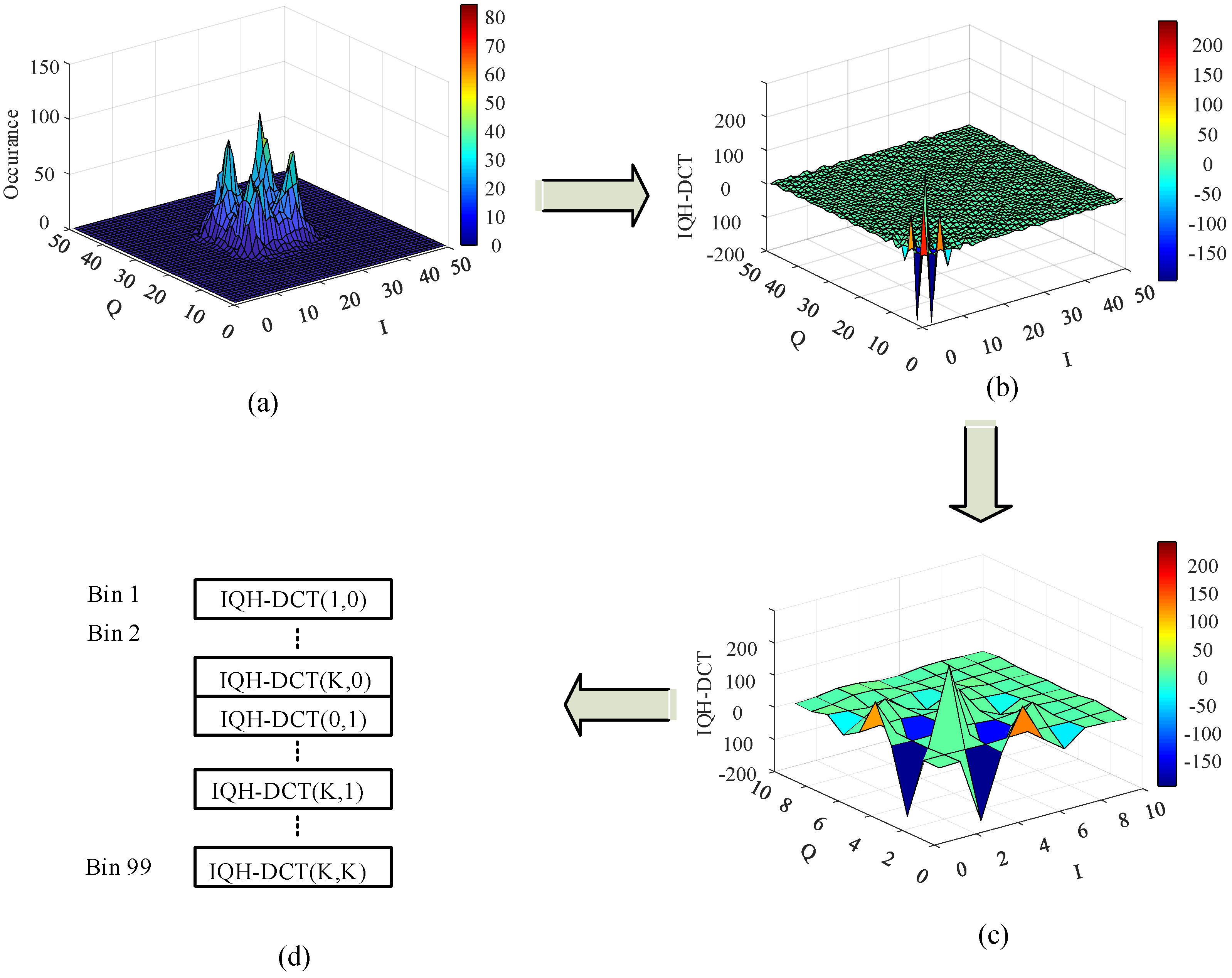
3.1. Transformed IQH Features
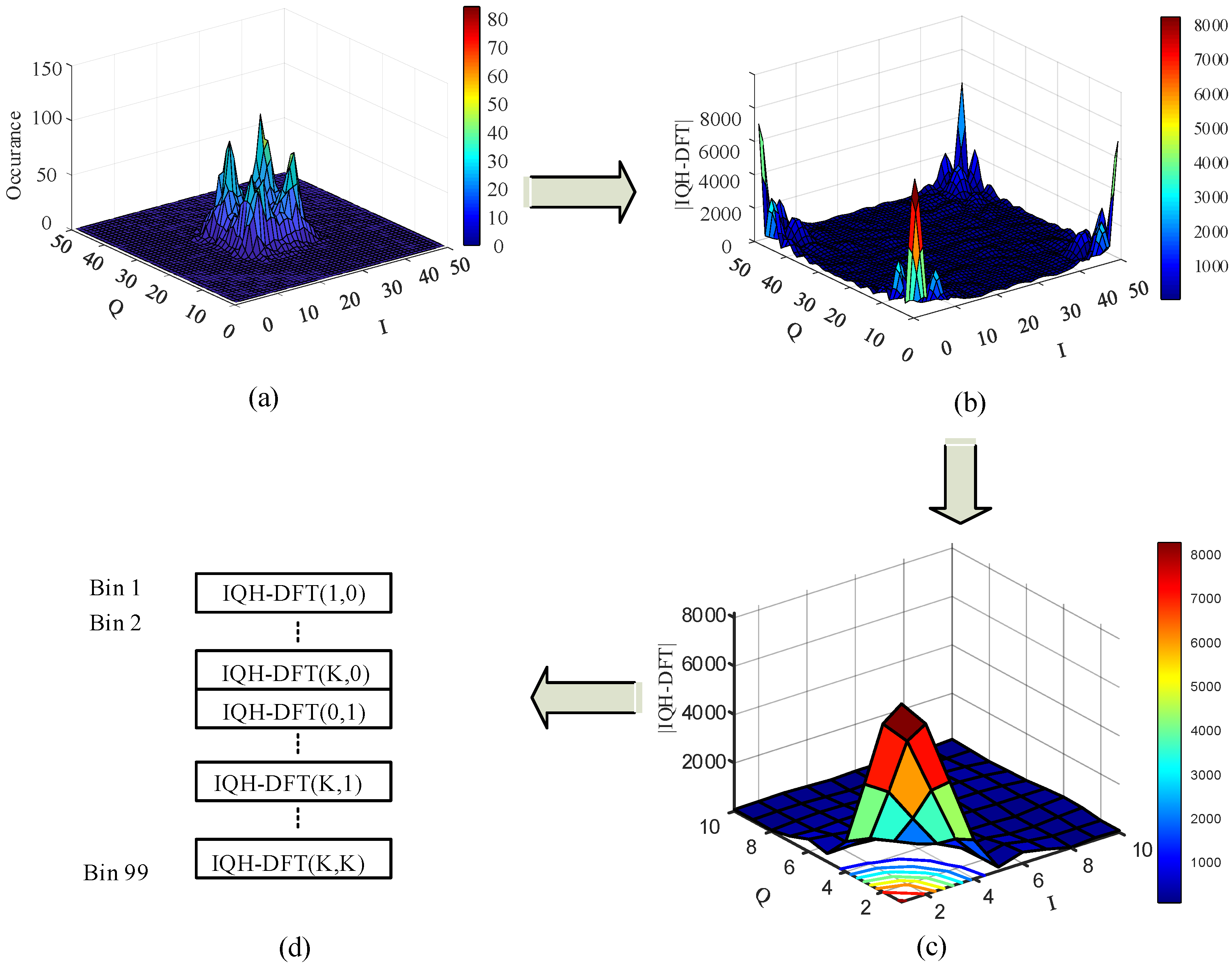
3.1.1. IQH-DFT Features
- (a)
- (b)
- The transformed IQH features are truncated by choosing the value of K as small as possible; see, for example, Figure 5c when K = 10. In the sequel, the value of K that provides the best performance is considered. More details about the selection of value of K will be discussed in Section 5.2.
- (c)
- The truncated frequency domain features are concatenated in the form of a 1D vector after removing the DFT value at the origin (i.e., DC component). The resultant 1D features vector is denoted by V-DFT.
3.1.2. IQH-DCT Features
3.2. Support Vector Regressor
4. Simulation Setup
5. Results and Discussion
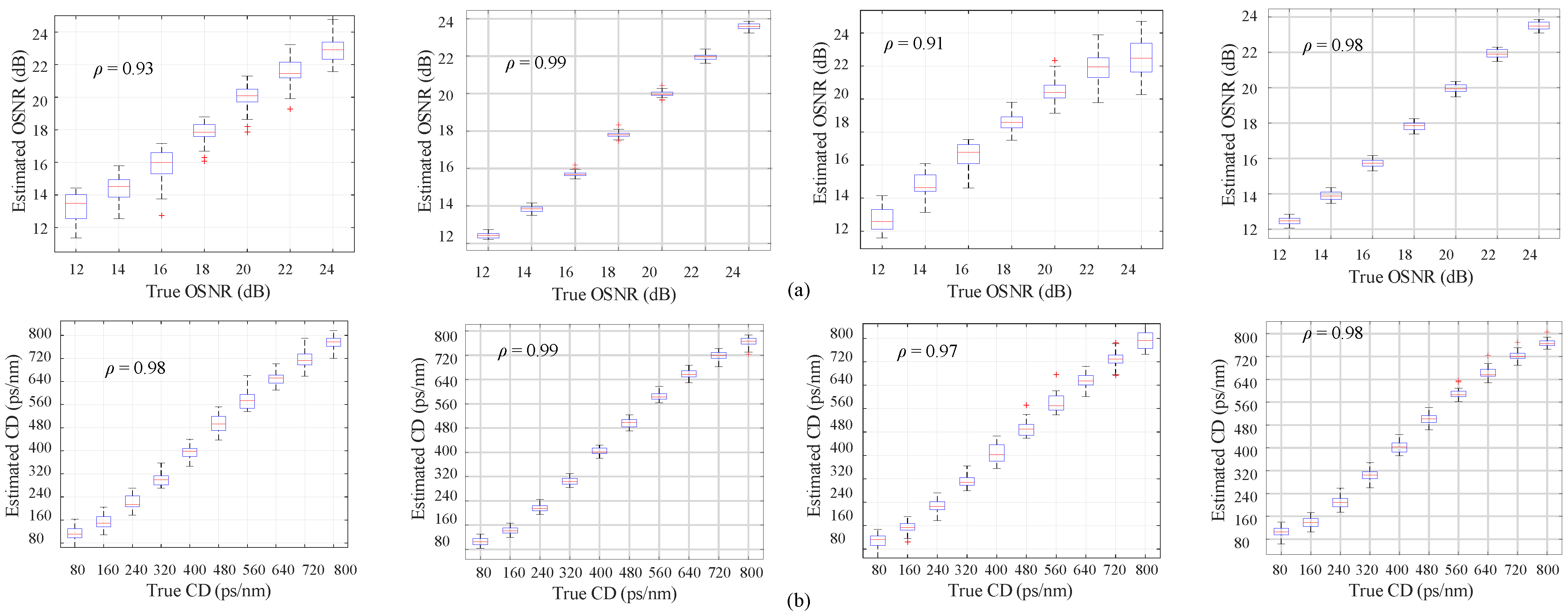
5.1. OPM Using Concatenated IQH Features
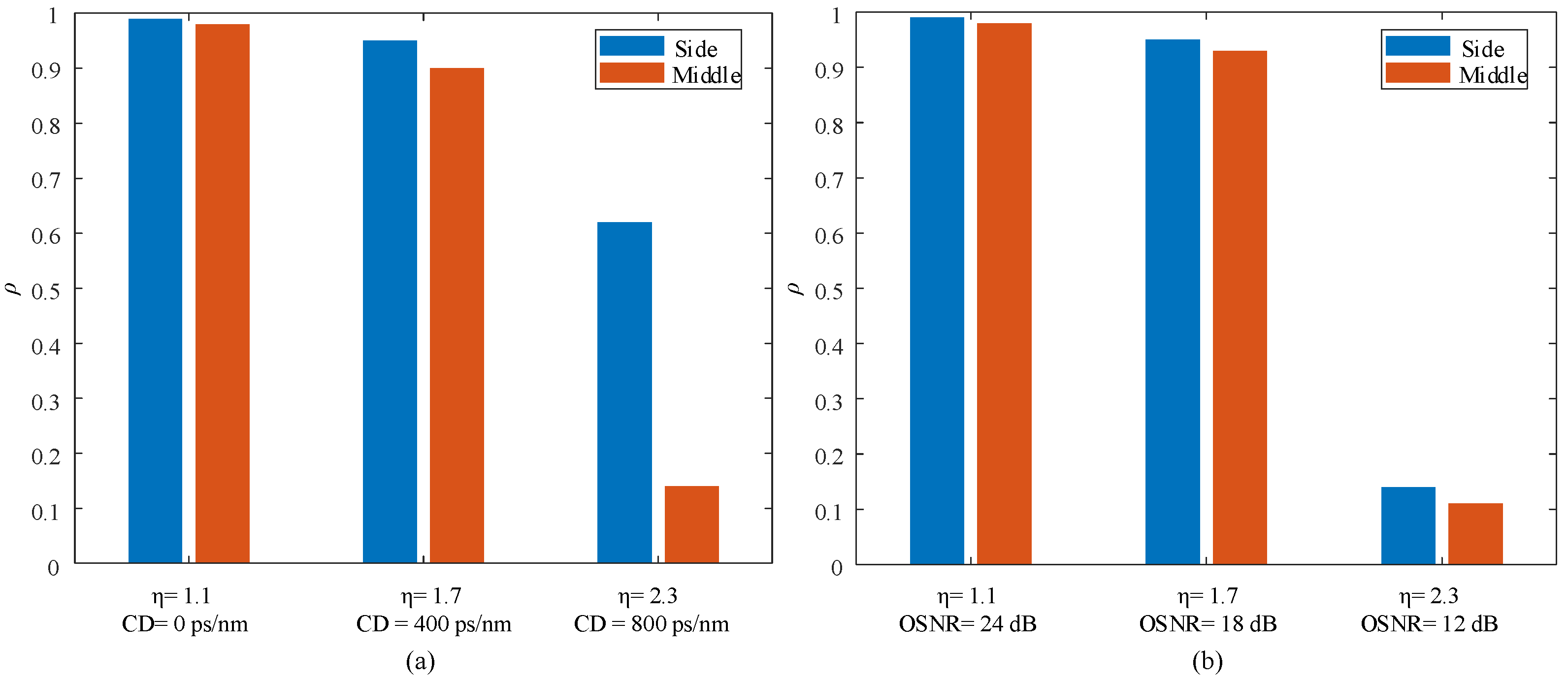
5.2. OPM Using V-DFT and V-DCT Features
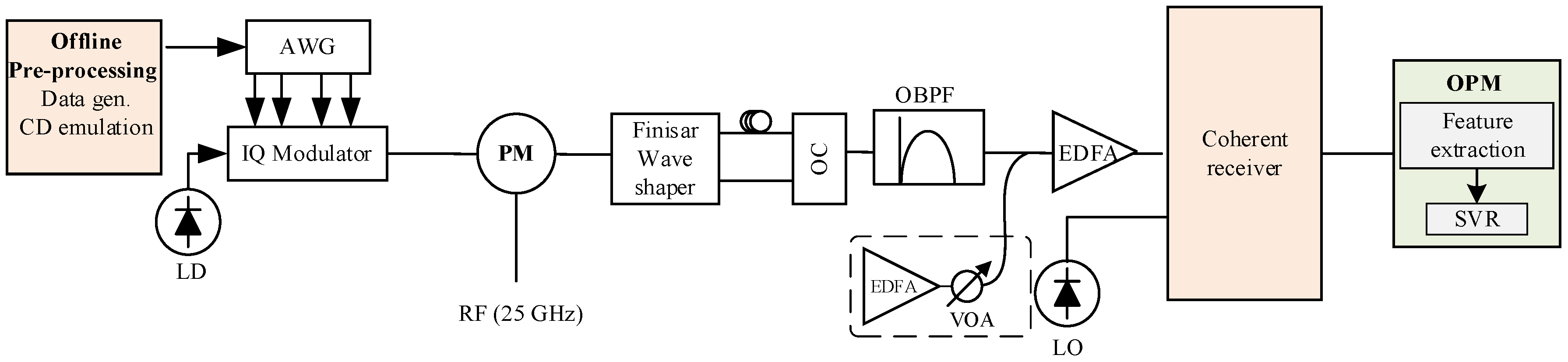
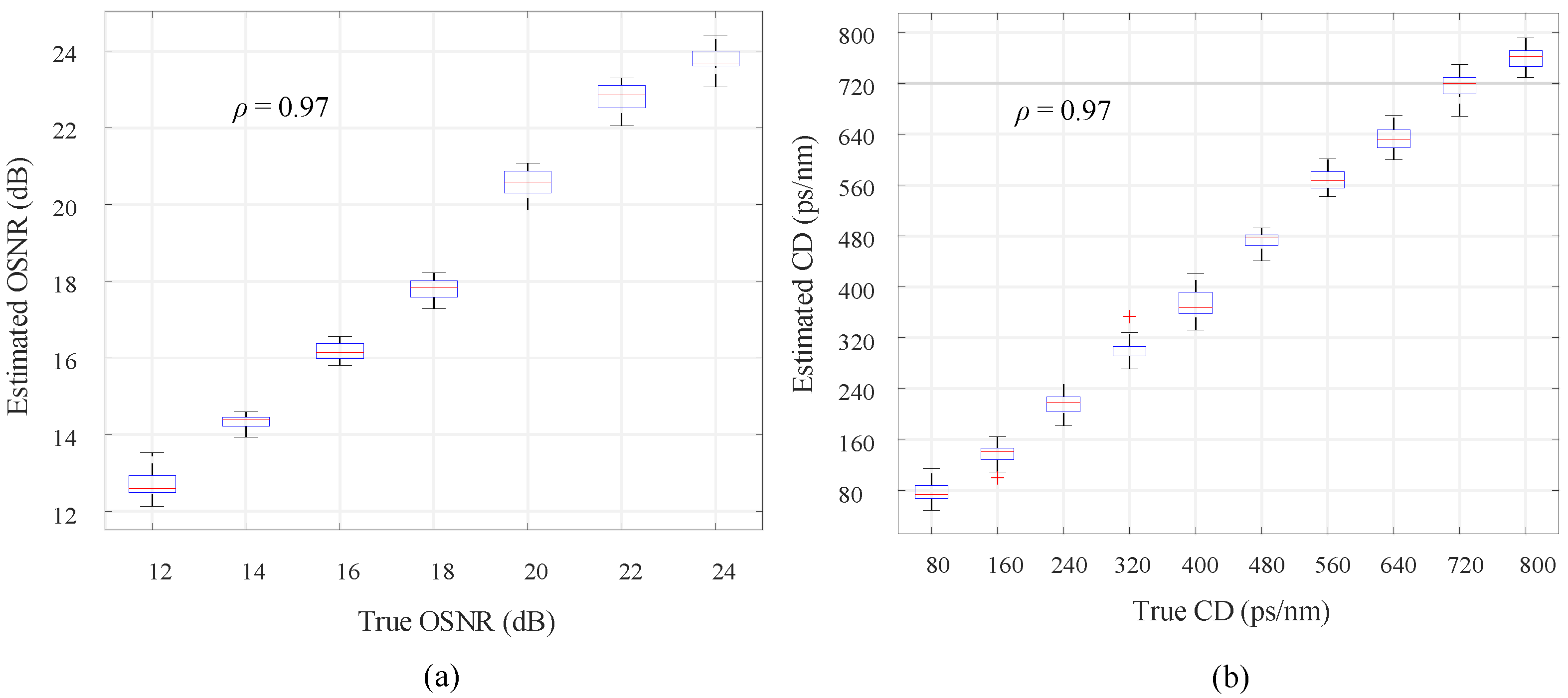
6. Experimental Validation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAH | Asynchronous amplitude histogram |
| ADTS | Asynchronous delay-tap sampling |
| ANN | Artificial neural network |
| ASE | Amplified spontaneous emission |
| BD | Balanced detector |
| BRI | Baud rate identification |
| BVT | Bandwidth-variable transponder |
| CD | Chromatic dispersion |
| DCT | Discrete cosine transform |
| DFT | Discrete Fourier transform |
| DNN | Deep neural network |
| DP | Dual polarization |
| DWDM | Dense wavelength-division multiplexing |
| EON | Elastic optical network |
| FMF | Few mode fiber |
| FO | Frequency offset |
| IoT | Internet of things |
| IQH | In-phase quadrature histogram |
| LO | Local oscillator |
| MFI | Modulation format identification |
| ML | Machine learning |
| MTL | Multi-task learning |
| OBPF | Optical bandpass filter |
| OPM | Optical performance monitoring |
| OSNR | Optical signal-to-noise ratio |
| PBS | Polarization beam splitter |
| PMD | Polarization mode dispersion |
| RBF | Radial basis function |
| ROADM | Reconfigurable optical add-drop multiplexers |
| SMO | Sequential minimal optimization |
| SVR | Support vector regressor |
| TL | Transfer learning |
| VOA | Variable optical attenuator |
References
- Cisco. Cisco Annual Internet Report (2018–2023) White Paper; White Paper; Cisco: San Jose, CA, USA, 2020. [Google Scholar]
- Yin, Y.; Liu, L.; Proietti, R.; Yoo, S.B. Software defined elastic optical networks for cloud computing. IEEE Netw. 2016, 31, 4–10. [Google Scholar] [CrossRef]
- Winzer, P.J.; Neilson, D.T.; Chraplyvy, A.R. Fiber-optic transmission and networking: The previous 20 and the next 20 years. Opt. Express 2018, 26, 24190–24239. [Google Scholar] [CrossRef] [PubMed]
- Gerstel, O.; Jinno, M.; Lord, A.; Yoo, S.B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, s12–s20. [Google Scholar] [CrossRef]
- Chatterjee, B.C.; Oki, E. Elastic Optical Networks: Fundamentals, Design, Control, and Management: Fundamentals, Design, Control, and Management; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Dong, Z.; Khan, F.N.; Sui, Q.; Zhong, K.; Lu, C.; Lau, A.P.T. Optical performance monitoring: A review of current and future technologies. J. Light. Technol. 2015, 34, 525–543. [Google Scholar] [CrossRef]
- Willner, A.E.; Pan, Z.; Yu, C. Optical performance monitoring. In Optical Fiber Telecommunications VB; Elsevier: Amsterdam, The Netherlands, 2008; pp. 233–292. [Google Scholar]
- Wang, D.; Sui, Q.; Li, Z. Toward universal optical performance monitoring for intelligent optical fiber communication networks. IEEE Commun. Mag. 2020, 58, 54–59. [Google Scholar] [CrossRef]
- Wang, D.; Jiang, H.; Liang, G.; Zhan, Q.; Mo, Y.; Sui, Q.; Li, Z. Optical Performance Monitoring of Multiple Parameters in Future Optical Networks. J. Light. Technol. 2021, 39, 3792–3800. [Google Scholar] [CrossRef]
- Suzuki, H.; Takachio, N. Optical signal quality monitor built into WDM linear repeaters using semiconductor arrayed waveguide grating filter monolithically integrated with eight photodiodes. Electron. Lett. 1999, 35, 836–837. [Google Scholar] [CrossRef]
- Lee, J.; Choi, H.; Shin, S.; Chung, Y.C. A review of the polarization-nulling technique for monitoring optical-signal-to-noise ratio in dynamic WDM networks. J. Light. Technol. 2006, 24, 4162–4171. [Google Scholar] [CrossRef]
- Liu, X.; Kao, Y.H.; Chandrasekhar, S.; Kang, I.; Cabot, S.; Buhl, L. OSNR monitoring method for OOK and DPSK based on optical delay interferometer. IEEE Photonics Technol. Lett. 2007, 19, 1172–1174. [Google Scholar] [CrossRef]
- Flood, E.; Guo, W.; Reid, D.; Lynch, M.; Bradley, A.; Barry, L.; Donegan, J. In-band OSNR monitoring using a pair of Michelson fiber interferometers. Opt. Express 2010, 18, 3618–3625. [Google Scholar] [CrossRef]
- Ji, T.; Peng, Y.; Zhu, G. In-band OSNR monitoring from Stokes parameters using support vector regression. IEEE Photonics Technol. Lett. 2019, 31, 385–388. [Google Scholar] [CrossRef]
- Xu, K.; Tsang, H.K.; Lei, G.K.; Chen, Y.M.; Wang, L.; Cheng, Z.; Chen, X.; Shu, C. OSNR monitoring for NRZ-PSK signals using silicon waveguide two-photon absorption. IEEE Photonics J. 2011, 3, 968–974. [Google Scholar] [CrossRef]
- Yu, Q.; Pan, Z.; Yan, L.S.; Willner, A.E. Chromatic dispersion monitoring technique using sideband optical filtering and clock phase-shift detection. J. Light. Technol. 2002, 20, 2267–2271. [Google Scholar]
- Zaidi, A.; Estella-Aguerri, I.; Shamai, S. On the information bottleneck problems: Models, connections, applications and information theoretic views. Entropy 2020, 22, 151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farsad, N.; Yilmaz, H.B.; Eckford, A.; Chae, C.B.; Guo, W. A Comprehensive survey of recent advancements in molecular communication. IEEE Commun. Surv. Tutor. 2016, 18, 1887–1919. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. CSI-Based fingerprinting for indoor localization: A deep learning approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef] [Green Version]
- Aguerri, I.E.; Zaidi, A. Distributed variational representation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 120–138. [Google Scholar] [CrossRef] [Green Version]
- Saif, W.S.; Esmail, M.A.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Machine Learning Techniques for Optical Performance Monitoring and Modulation Format Identification: A Survey. IEEE Commun. Surv. Tutor. 2020, 22, 2839–2882. [Google Scholar] [CrossRef]
- Khan, F.N.; Fan, Q.; Lu, C.; Lau, A.P.T. An optical communication’s perspective on machine learning and its applications. J. Light. Technol. 2019, 37, 493–516. [Google Scholar] [CrossRef]
- Musumeci, F.; Rottondi, C.; Nag, A.; Macaluso, I.; Zibar, D.; Ruffini, M.; Tornatore, M. An overview on application of machine learning techniques in optical networks. IEEE Commun. Surv. Tutor. 2018, 21, 1383–1408. [Google Scholar] [CrossRef] [Green Version]
- Saif, W.S.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Optical Performance Monitoring in Mode Division Multiplexed Optical Networks. J. Light. Technol. 2020, 39, 491–504. [Google Scholar] [CrossRef]
- Khan, F.N.; Lu, C.; Lau, A.P.T. Optical performance monitoring in fiber-optic networks enabled by machine learning techniques. In Proceedings of the Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 7–9 March 2018; pp. 1–3. [Google Scholar]
- Xiang, Q.; Yang, Y.; Zhang, Q.; Yao, Y. Joint and accurate OSNR estimation and modulation format identification scheme using the feature-based ANN. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Mata, J.; de Miguel, I.; Duran, R.J.; Merayo, N.; Singh, S.K.; Jukan, A.; Chamania, M. Artificial intelligence (AI) methods in optical networks: A comprehensive survey. Opt. Switch. Netw. 2018, 28, 43–57. [Google Scholar] [CrossRef]
- Wu, X.; Jargon, J.A.; Skoog, R.A.; Paraschis, L.; Willner, A.E. Applications of artificial neural networks in optical performance monitoring. J. Light. Technol. 2009, 27, 3580–3589. [Google Scholar]
- Shen, T.S.R.; Meng, K.; Lau, A.P.T.; Dong, Z.Y. Optical performance monitoring using artificial neural network trained with asynchronous amplitude histograms. IEEE Photonics Technol. Lett. 2010, 22, 1665–1667. [Google Scholar] [CrossRef]
- Jargon, J.A.; Wu, X.; Willner, A.E. Optical performance monitoring by use of artificial neural networks trained with parameters derived from delay-tap asynchronous sampling. In Proceedings of the 2009 Conference on Optical Fiber Communication, San Diego, CA, USA, 22–26 March 2009; pp. 1–3. [Google Scholar]
- Cheng, Y.; Fu, S.; Tang, M.; Liu, D. Multi-task deep neural network (MT-DNN) enabled optical performance monitoring from directly detected PDM-QAM signals. Opt. Express 2019, 27, 19062–19074. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Huang, Z.; Wu, X.; Yu, C. Cost-Effective Multi-Parameter Optical Performance Monitoring Using Multi-Task Deep Learning With Adaptive ADTP and AAH. J. Light. Technol. 2021, 39, 1733–1741. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, J.; Hu, S.; Zhu, M.; Song, Y.; Qiu, K. Transfer learning assisted deep neural network for OSNR estimation. Opt. Express 2019, 27, 19398–19406. [Google Scholar] [CrossRef]
- Tanimura, T.; Hoshida, T.; Kato, T.; Watanabe, S.; Rasmussen, J.C.; Suzuki, M.; Morikawa, H. Deep learning based OSNR monitoring independent of modulation format, symbol rate and chromatic dispersion. In Proceedings of the 42nd European Conference on Optical Communication (ECOC 2016), Dusseldorf, Germany, 18–22 September 2016; pp. 1–3. [Google Scholar]
- Saif, W.S.; Alshawi, T.; Esmail, M.A.; Ragheb, A.; Alshebeili, S. Separability of histogram based features for optical performance monitoring: An investigation using t-SNE technique. IEEE Photonics J. 2019, 11, 1–12. [Google Scholar] [CrossRef]
- Gonzalez, R.; Woods, R. Digital Image Processing; Pearson: New York, NY, USA, 2018. [Google Scholar]
- Rasheed, M.H.; Salih, O.M.; Siddeq, M.M.; Rodrigues, M.A. Image compression based on 2D Discrete Fourier Transform and matrix minimization algorithm. Array 2020, 6, 100024. [Google Scholar] [CrossRef]
- Jain, A.K. Fundamentals of Digital Image Processing; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Thrane, J.; Wass, J.; Piels, M.; Diniz, J.C.M.; Jones, R.; Zibar, D. Machine Learning Techniques for Optical Performance Monitoring From Directly Detected PDM-QAM Signals. J. Light. Technol. 2017, 35, 868–875. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Dobre, O.A.; Ngatched, T.M.N.; Eldemerdash, Y.A.; Li, C. Joint Modulation Classification and OSNR Estimation Enabled by Support Vector Machine. IEEE Photonics Technol. Lett. 2018, 30, 2127–2130. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Transactions on Neural Networks 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Platt, J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report MSR-TR-98-14, Advances in Kernel Methods—Support Vector Learning; Microsoft: Redmond, WA, USA, 1998. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines: A practical consequence of learning theory. IEEE Intell. Syst. 1998, 13, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Saif, W.S.; Ragheb, A.M.; Nebendahl, B.; Alshawi, T.; Marey, M.; Alshebeili, S.A. Performance Investigation of Modulation Format Identification in Super-Channel Optical Networks. IEEE Photonics J. 2022, 14, 1–10. [Google Scholar] [CrossRef]
- Khan, F.N.; Zhou, Y.; Lau, A.P.T.; Lu, C. Modulation format identification in heterogeneous fiber-optic networks using artificial neural networks. Opt. Express 2012, 20, 12422–12431. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.N.; Zhong, K.; Al-Arashi, W.H.; Yu, C.; Lu, C.; Lau, A.P.T. Modulation format identification in coherent receivers using deep machine learning. IEEE Photonics Technol. Lett. 2016, 28, 1886–1889. [Google Scholar] [CrossRef]
- Khan, F.N.; Zhong, K.; Zhou, X.; Al-Arashi, W.H.; Yu, C.; Lu, C.; Lau, A.P.T. Joint OSNR monitoring and modulation format identification in digital coherent receivers using deep neural networks. Opt. Express 2017, 25, 17767–17776. [Google Scholar] [CrossRef]
- Guesmi, L.; Ragheb, A.M.; Fathallah, H.; Menif, M. Experimental Demonstration of Simultaneous Modulation Format/Symbol Rate Identification and Optical Performance Monitoring for Coherent Optical Systems. J. Light. Technol. 2018, 36, 2230–2239. [Google Scholar] [CrossRef]
- Zhao, Y.; Shi, C.; Wang, D.; Chen, X.; Wang, L.; Yang, T.; Du, J. Low-complexity and nonlinearity-tolerant modulation format identification using random forest. IEEE Photonics Technol. Lett. 2019, 31, 853–856. [Google Scholar] [CrossRef]
- Wan, Z.; Yu, Z.; Shu, L.; Zhao, Y.; Zhang, H.; Xu, K. Intelligent optical performance monitor using multi-task learning based artificial neural network. Opt. Express 2019, 27, 11281–11291. [Google Scholar] [CrossRef] [Green Version]
- Saif, W.S.; Ragheb, A.M.; Seleem, H.E.; Alshawi, T.A.; Alshebeili, S.A. Modulation format identification in mode division multiplexed optical networks. IEEE Access 2019, 7, 156207–156216. [Google Scholar] [CrossRef]
- Kva, T.O. Note on the R2 measure of goodness of fit for nonlinear models. Bull. Psychon. Soc. 1983, 21, 79–80. [Google Scholar]
- Esmail, M.A.; Saif, W.S.; Ragheb, A.M.; Alshebeili, S.A. Free space optic channel monitoring using machine learning. Opt. Express 2021, 29, 10967–10981. [Google Scholar] [CrossRef]
- Tanimura, T.; Hoshida, T.; Kato, T.; Watanabe, S.; Morikawa, H. Convolutional neural network-based optical performance monitoring for optical transport networks. J. Opt. Commun. Netw. 2019, 11, A52–A59. [Google Scholar] [CrossRef]
- Eltaieb, R.A.; Farghal, A.E.A.; Ahmed, H.d.H.; Saif, W.S.; Ragheb, A.; Alshebeili, S.A.; Shalaby, H.M.H.; Abd El-Samie, F.E. Efficient Classification of Optical Modulation Formats Based on Singular Value Decomposition and Radon Transformation. J. Light. Technol. 2020, 38, 619–631. [Google Scholar] [CrossRef]







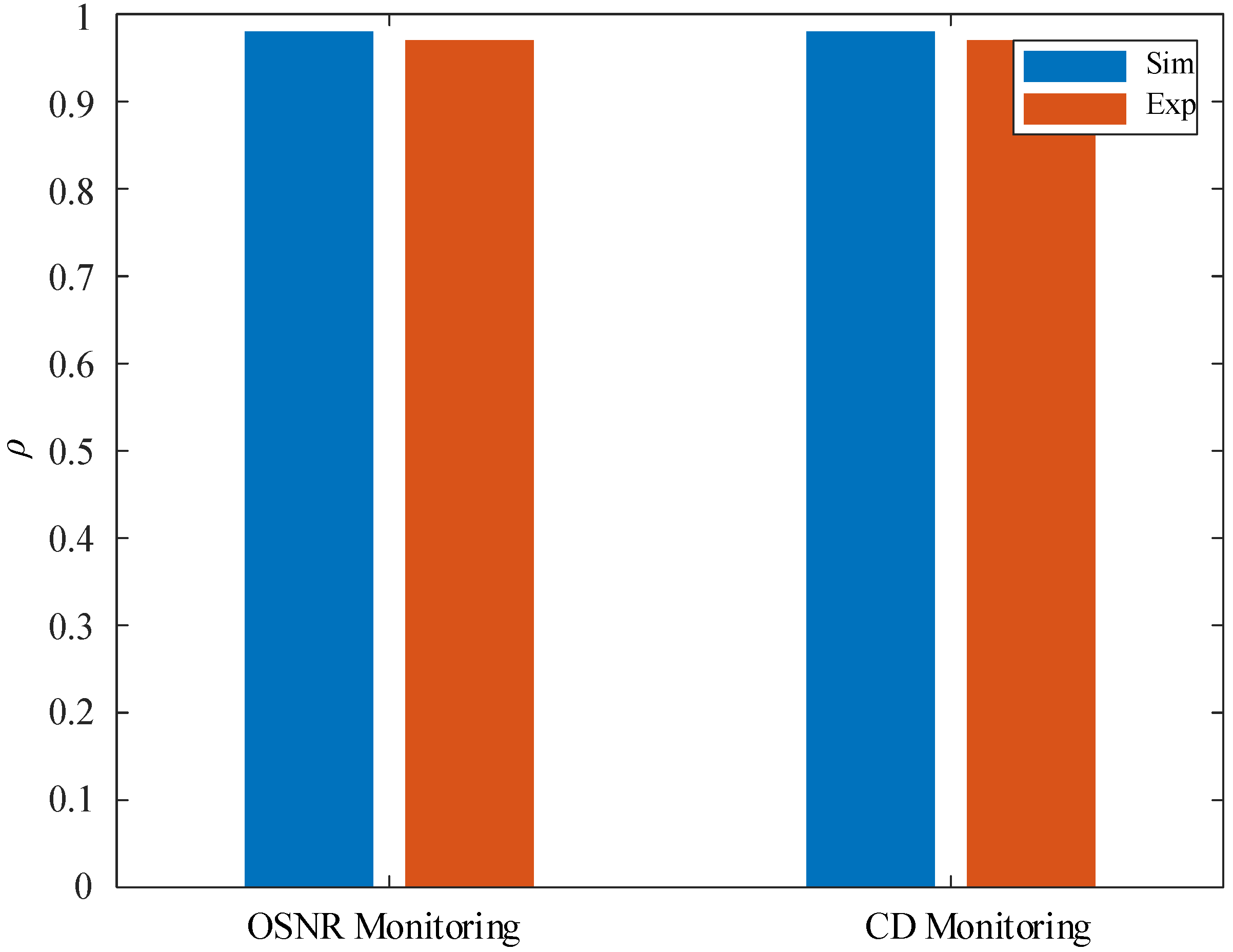
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saif, W.S.; Ragheb, A.M.; Nebendahl, B.; Alshawi, T.; Marey, M.; Alshebeili, S.A. Machine Learning-Based Optical Performance Monitoring for Super-Channel Optical Networks. Photonics 2022, 9, 299. https://doi.org/10.3390/photonics9050299
Saif WS, Ragheb AM, Nebendahl B, Alshawi T, Marey M, Alshebeili SA. Machine Learning-Based Optical Performance Monitoring for Super-Channel Optical Networks. Photonics. 2022; 9(5):299. https://doi.org/10.3390/photonics9050299
Chicago/Turabian StyleSaif, Waddah S., Amr M. Ragheb, Bernd Nebendahl, Tariq Alshawi, Mohamed Marey, and Saleh A. Alshebeili. 2022. "Machine Learning-Based Optical Performance Monitoring for Super-Channel Optical Networks" Photonics 9, no. 5: 299. https://doi.org/10.3390/photonics9050299
APA StyleSaif, W. S., Ragheb, A. M., Nebendahl, B., Alshawi, T., Marey, M., & Alshebeili, S. A. (2022). Machine Learning-Based Optical Performance Monitoring for Super-Channel Optical Networks. Photonics, 9(5), 299. https://doi.org/10.3390/photonics9050299




