Mode Coupling and Steady-State Distribution in Multimode Step-Index Organic Glass-Clad PMMA Fibers
Abstract
:1. Introduction
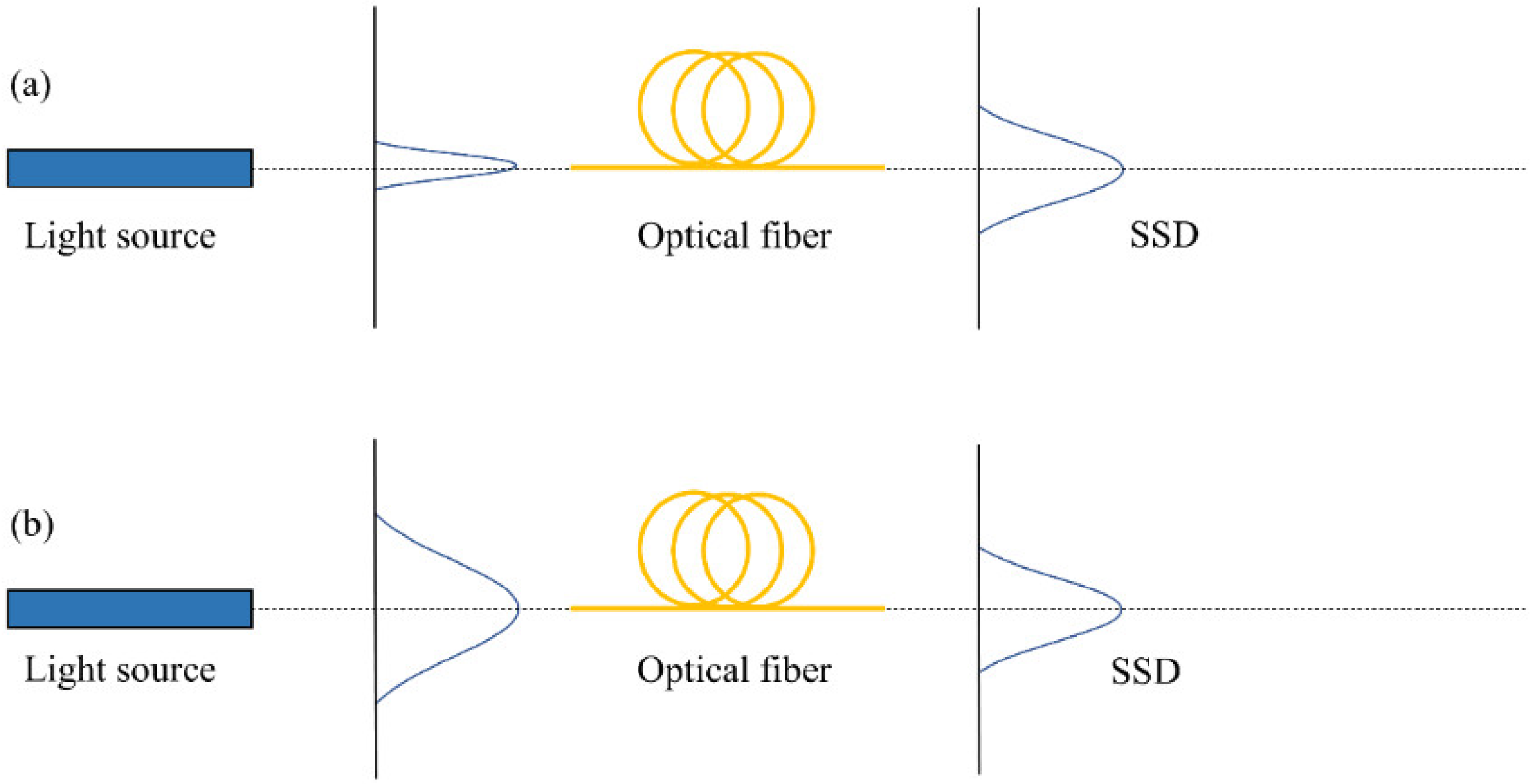
2. Power Flow Equation
3. Method for Calculating Coupling Coefficient D
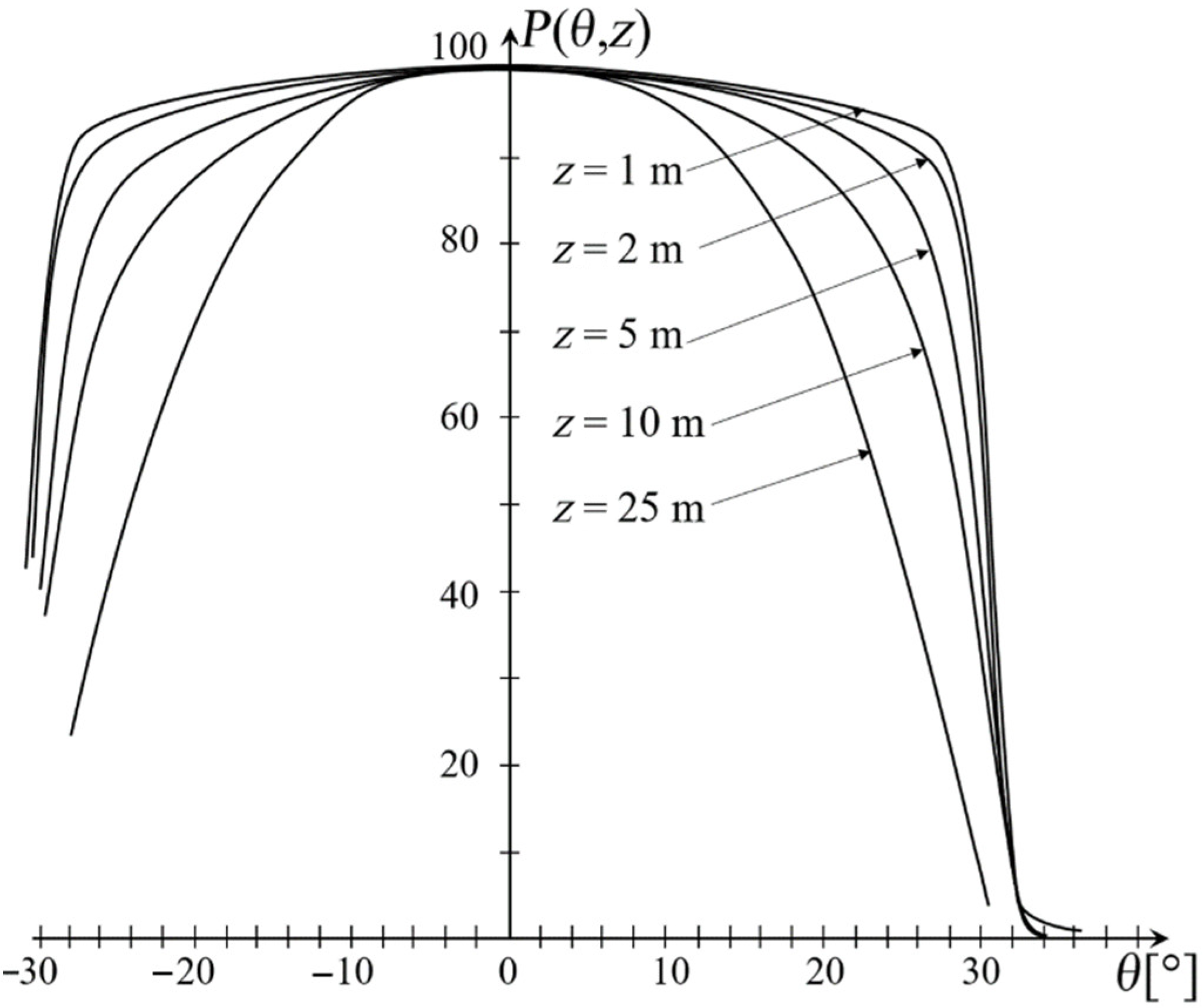
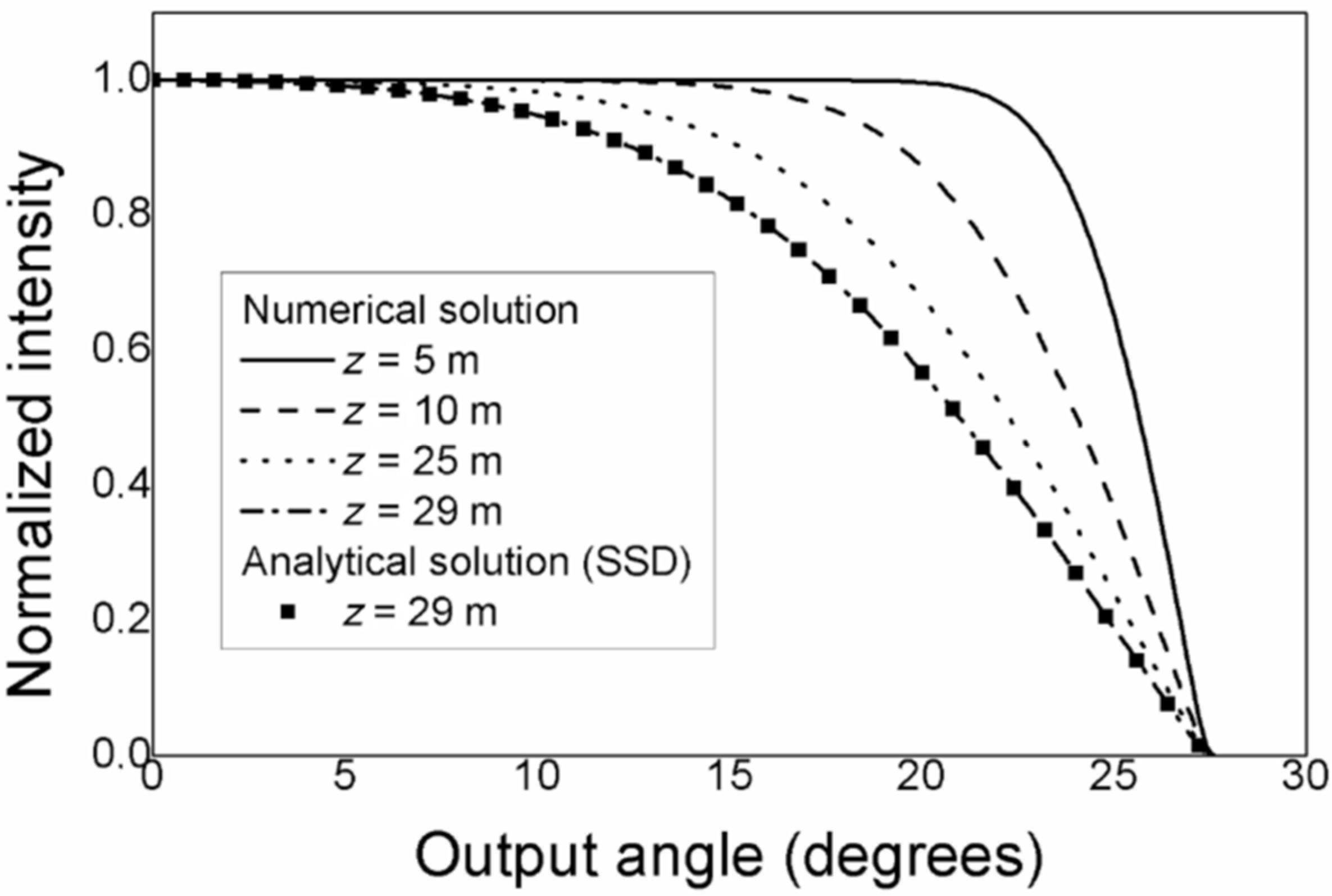
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Yang, C.; Sui, Q.; Wang, H.; Feng, Y.; Liu, W.; Yan, Y.; Li, J.; Yu, C.; Li, Z. Burst-error-propagation suppression for decision-feedback equalizer in field-trial submarine fiber-optic communications. J. Lightwave Technol. 2021, 39, 4601–4606. [Google Scholar] [CrossRef]
- Anuszkiewicz, A.; Kasztelanic, R.; Filipkowski, A.; Stepniewski, G.; Stefaniuk, T.; Siwicki, B.; Pysz, D.; Klimczak, M.; Buczynski, R. Fused silica optical fibers with graded index nanostructured core. Sci. Rep. 2018, 8, 12329. [Google Scholar] [CrossRef] [PubMed]
- Ayesta, I.; Zubia, J.; Arrue, J.; Illarramendi, J.M.A.; Azkune, M. Characterization of chromatic dispersion and refractive index of polymer optical fibers. Polymers 2017, 9, 730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zubía, J.; Durana, G.; Aldabaldetreku, G.; Arrue, J.; Losada, M.A.; Lopez-Higuera, M. New method to calculate mode conversion coefficients in SI multimode optical fibers. J. Lightwave Technol. 2003, 21, 776–781. [Google Scholar] [CrossRef]
- Kobayashi, T.; Blau, W.J.; Tillmann, H.; Horhold, H.-H. Light amplification and lasing in a stilbenoid compound-doped glass-clad polymer optical fiber. IEEE J. Quant. Electron. 2003, 39, 664–672. [Google Scholar] [CrossRef]
- Apolo, J.; Ortega, B.; Almenar, V. Hybrid POF/VLC links based on a single LED for indoor communications. Photonics 2021, 8, 254. [Google Scholar] [CrossRef]
- Garito, A.F.; Wang, J.; Gao, R. Effects of random perturbations in plastic optical fibers. Science 1998, 281, 962–967. [Google Scholar] [CrossRef] [PubMed]
- Leal-Junior, A.; Frizera, A.; Marques, C.; José Pontes, M. Mechanical properties characterization of polymethyl methacrylate polymer optical fibers after thermal and chemical treatments. Opt. Fiber Technol. 2018, 43, 106–111. [Google Scholar] [CrossRef]
- Corrado, A.; Polini, W. Measurement of high flexibility components in composite material by touch probe and force sensing resistors. J. Manuf. Process. 2019, 45, 520–531. [Google Scholar] [CrossRef]
- Hao, M.; Li, H.; Cui, L.; Liu, W.; Fang, B.; Liang, J.; Xie, X.; Wang, D.; Wang, F. Higher photocatalytic removal of organic pollutants using pangolin-like composites made of 3–4 atomic layers of MoS2 nanosheets deposited on tourmaline. Environ. Chem. Lett. 2021, 19, 3573–3582. [Google Scholar] [CrossRef]
- Lustermann, B.; Quandt, B.M.; Ulrich, S.; Spano, F.; Rossi, R.M.; Boese, L.F. Experimental determination and ray-tracing simulation of bending losses in melt-spun polymer optical fibres. Sci. Rep. 2020, 10, 11885. [Google Scholar] [CrossRef] [PubMed]
- Gloge, D. Optical power flow in multimode fibers. Bell Syst. Tech. J. 1972, 51, 1767–1783. [Google Scholar] [CrossRef]
- Gambling, A.; Payne, D.P.; Matsumura, H. Mode conversion coefficients in optical fibers. Appl. Opt. 1975, 14, 1538–1542. [Google Scholar] [CrossRef] [PubMed]
- Savović, S.; Djordjevich, A. Method for calculating the coupling coefficient in step index optical fibers. Appl. Opt. 2007, 46, 1477–1481. [Google Scholar] [CrossRef] [PubMed]
- Dugas, J.; Sotom, M.; Martin, L.; Cariou, J.-M. Accurate characterization of the transmissivity of large diameter multimode optical fibers. Appl. Opt. 1987, 26, 4198–4208. [Google Scholar] [CrossRef] [PubMed]
- Savović, S.; Djordjevich, A. Mode coupling in strained and unstrained step-index plastic optical fibers. Appl. Opt. 2006, 45, 6775–6780. [Google Scholar] [CrossRef] [PubMed]
- Savović, S.; Djordjevich, A. Mode coupling and its influence on space division multiplexing in step-index plastic-clad silica fibers. Opt. Fiber Technol. 2018, 46, 92–197. [Google Scholar] [CrossRef]
- Hurand, S.; Chauny, L.-A.; El-Rabii, H.; Joshi, S.; Yalin, A. Mode coupling and output beam quality of 100–400 μm core silica fibers. Appl. Opt. 2011, 50, 492–499. [Google Scholar] [CrossRef] [PubMed]
- Savović, S.; Drljača, B.; Djordjevich, A. Influence of launch beam distribution on bandwidth in step index plastic optical fibers. Appl. Opt. 2013, 52, 1117–1121. [Google Scholar] [CrossRef] [PubMed]
| SI OGC PMMA Fiber (This Work) | SI PMMA Fiber (Ref. [16]) | SI Plastic-Clad Silica Fiber (Ref. [17]) | SI Silica Fiber (Ref. [18]) | |
|---|---|---|---|---|
| n0 | 1.4877 | 1.492 | 1.457 | 1.457 |
| θc (deg) | 30.4 | 30.0 | 24.0 | 13.5 |
| NA | 0.506 | 0.5 | 0.4 | 0.22 |
| D (rad2/m) | ||||
| zs (m) | 29 | 98 | 1400 | 2470 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savović, S.; Djordjevich, A.; Savović, I.; Min, R. Mode Coupling and Steady-State Distribution in Multimode Step-Index Organic Glass-Clad PMMA Fibers. Photonics 2022, 9, 297. https://doi.org/10.3390/photonics9050297
Savović S, Djordjevich A, Savović I, Min R. Mode Coupling and Steady-State Distribution in Multimode Step-Index Organic Glass-Clad PMMA Fibers. Photonics. 2022; 9(5):297. https://doi.org/10.3390/photonics9050297
Chicago/Turabian StyleSavović, Svetislav, Alexandar Djordjevich, Isidora Savović, and Rui Min. 2022. "Mode Coupling and Steady-State Distribution in Multimode Step-Index Organic Glass-Clad PMMA Fibers" Photonics 9, no. 5: 297. https://doi.org/10.3390/photonics9050297
APA StyleSavović, S., Djordjevich, A., Savović, I., & Min, R. (2022). Mode Coupling and Steady-State Distribution in Multimode Step-Index Organic Glass-Clad PMMA Fibers. Photonics, 9(5), 297. https://doi.org/10.3390/photonics9050297






