Ultra-Sensitive Si-Based Optical Sensor for Nanoparticle-Size Traditional Water Pollutant Detection

Abstract

A low-cost Si-based optical nano-sensor that monitors traditional water pollutants is introduced in this paper. The introduced sensor works in the near-infrared region, 900 nm to 2500 nm spectral range. The proposed structure consists of a Si layer with an optimized thickness of 300 nm on the top of the Al layer acting as a back reflector. On the top of the Si layer, the water pollutants are modeled as nanoparticle materials of different sizes. The finite difference time domain method is utilized to optimize the thicknesses of the Si layer by analyzing the optical light absorption considering different Si layer thicknesses and different pollutant nanoparticles’ sizes. Different interpolation techniques, including polynomials with various degrees and locally weighted smoothing quadratic regression, are used to find the best fitting model representing the simulated data points with goodness of fit analysis. Three features are proposed to identify the water pollutant with its size, peak absorption wavelength, relative amplitude, and a full width at half maximum. The device’s performance in detecting six different pollutants, silver, aluminum, copper, chromium, selenium, and ammonia, is evaluated. Sensitivity, a figure of merit, and a quality factor are used to evaluate the proposed sensor. The obtained maximum sensitivity is 11,300 nm/RIU, FOM of 740, and quality factor of 670.

1. Introduction

Human daily activities have increased water pollution, and water sources deteriorate yearly [1]. Common water pollutants include nitrate (NO₃⁻, and NH₃⁺), fluoride (F⁻), and heavy metals “iron (Fe), Pb (lead), Cd (cadmium), Cr (chromium), Ni (nickel), Zn (zinc), Sb (antimony), As (arsenic), Hg (mercury), etc.” [2]. As the concentration of these pollutants increases, they severely affect human health. This attracts researchers’ attention to develop techniques to monitor and treat water pollutants. There are several techniques used to detect water pollutants. One of the old methods is the separation of pollutants using the chromatography technique. It is a very sensitive method for the detection of pollutants but a very expensive technique and needs complicated tools [3,4]. Furthermore, electrochemical techniques are also used to detect pollutants, especially those that are non-UV-absorbing analytes. This technique detects an electric current in a cell generated by a chemical oxidation or reduction process [5,6]. With the rapid progress in the field of semiconductor optical devices, another technique that depends on fluorescence has been adopted because of its high sensitivity, fast detection, and low cost [7,8]. Additionally, graphene quantum dots with gold plasmonic particles are used in the pollutant detection process using localized surface plasmon resonance (LSPR) interaction between graphene and the plasmonic particles [9,10]. Gold nanoparticles with ZnO nanoparticles on the surface of tapered optical fiber are utilized to detect p-cresol in water. ZnO is a direct bandgap semiconductor material and is used to improve the biocompatibility of the sensor as it helps in binding the enzyme over the sensor [11].

Moreover, silver nanoparticles in optical sensors are used for water pollutant detection by measuring the changes in the peak wavelength and shape of the spectrum curve due to the presence of the pollutants [12]. Silver nanoparticles have a lower cost and higher extinction coefficients than gold nanoparticles. The high molar extinction coefficient of silver nanoparticles leads to improved visibility based on the difference in optical brightness and increased sensitivity of UV-visible spectroscopic detection [13].

Nanostructure-based devices are used as SPR sensors. Si-based sensors that use layers of Si, silver (Ag), and aluminum oxide (Al₂O₃) grating are reported to be a highly sensitive device (sensitivity of 477 nm/RIU, and FOM of 38) in an optical communication band from 1400 to 1550 nm [14]. Additionally, Si nanowire Field Effect Transistor (FET) sensors with gold nanoparticles are reported to have enhanced NH₃-sensing characteristics and long-term reliability [15].

In this work, we introduced a highly sensitive Si-based water pollutant ultra-thin optical nano-sensor that operates in the NIR region, 11,300 nm/RIU. The following sections are organized as follows: first, the sensors’ performance metrics are introduced; second, the proposed sensor for water pollutant detection is presented; and finally, the simulation results, optimizing the sensor design and its performance evaluation, are discussed.

2. Sensor Performance Excellence Indicators and the Proposed Structure

As reported in the literature, the performance indicators for sensor evaluation are the refractive index sensitivity (RIS), full width at half maximum (FWHM), and figure of merit (FOM). The RIS of a sensor is defined in terms of the shift in peak wavelength (∆λ) per the change in the surrounding medium refractive index ‘refractive index (n) unit’ (RIU) [16]. The refractive index sensitivity is given by:

$$RIS=\frac{\mathsf{\Delta }\lambda }{\mathsf{\Delta }n}$$

(1)

Another characterization factor to determine the quality of sensors is the spectral resolution. The resolution is determined by the linewidth and the intensity of the spectral peak and is represented by the FWHM of the spectral peak. A narrow peak helps recognize a peak shift and enhances detection accuracy. Another performance indicator is the figure of merit, which indicates the sensor’s performance by combining sensitivity and FWHM of sensing spectrum [17,18], calculated using Equation (2).

$$FOM=\frac{RIS}{FWHM}$$

(2)

One more parameter is the quality factor (Q-factor) which is defined as the ratio of peak wavelength (λ_max) to the FWHM [16,17,18]. Large Q-factor values represent the high selectivity of the sensor. The quality factor is given by:

$$Q=\frac{{\lambda }_{max}}{FWHM}$$

(3)

The peak wavelength (λ_max) depends on the dielectric of the surrounded medium and relative permittivity of the nanoparticles and is given by:

$${\lambda }_{max}=\frac{P}{n}{\left(\frac{{\epsilon }_P{\epsilon }_m\left({\lambda }_{max}\right)}{{\epsilon }_m+{\epsilon }_P\left({\lambda }_{max}\right)}\right)}^{1/2}$$

(4)

where ε_m is the permittivity of the surrounding medium, ε_P is a plasmonic NP dielectric constant at corresponding λ_max, n is an integer, and P is structural periodicity.

The dielectric permittivity can be expressed by using a multi-oscillator Drude–Lorentz model [19] as given in Equation (5):

$${\epsilon }_{plasmonic}={\epsilon }_{\infty }-\frac{{\omega }_D^2}{{\omega }^2+j\omega {\gamma }_D}-{\displaystyle \sum }_{k=1}^6\frac{{\delta }_k{\omega }_k^2}{{\omega }^2-{\omega }_k^2+2j\omega {\gamma }_k}$$

(5)

where ε_ꝏ is the plasmonic high frequency dielectric permittivity, ω_D and γ_D are the plasma and collision frequencies of the free electrons, δ_k is the amplitude of Lorentz oscillator, ω_k is the resonance angular frequencies and γ_k is the damping constants (k = 1,2,…, 6).

On the other hand, the proposed structure is designed, optimized, and analyzed using an electromagnetic wave solver, Lumerical Finite Difference Time Domain (FDTD) solutions software in the near-infrared region. The proposed model contains a single unit cell parametrized by a Si layer of a varying cross-section area from 1 × 10⁴ nm² to 1 × 10⁶ nm² and thickness, d, optimized to 300 nm. A thick Al layer is used on the bottom of the Si layer, acting as a back reflector and ohmic contact. The back reflector layer is used to enhance light trapping and reflects the transmitted light from the silicon layer to the structure for more light absorption [20,21]. The schematic diagram is shown in Figure 1. The Si layer is the platform for the water pollutants nanoparticle modeled as spherical nanoparticles (NPs) with a radius varying from 50 nm to 500 nm. The spherical shape has some advantages over other shapes as they are highly symmetrical particles with mono-dispersity and synthetic reproducibility. It is reported that the spherical shape gives the best absorption properties [22].

In the simulation of a unit cell, the boundary conditions are considered as a periodic structure in x and y directions, and the layers are perfectly matched in z-direction. A plane wave source with a wavelength band 500–3000 nm is used as a light source, and the minimum mesh size is 0.5 nm in all directions with an offset time of 7.5 fs used for the light source. The absorption of the nanoparticles is measured at different wavelengths. We started the optimization process by adding plasmonic Au NPs on the Si platform layer. Plasmonic NPs such as Au and Ag have shape- and size-dependent optical properties, so they are widely used to fabricate water pollutant sensors [23,24,25]. The absorption spectrum is measured, and accordingly, the Si layer thickness maximizing the absorption is recorded. In the results section, optimizing the layer thickness is detailed. As a result of optimization, the thickness is selected to be 300 nm, and this thickness maximizes the variation in maximum absorption wavelength shift as a function of the particle radius. The sensor’s performance depending on the absorption spectrum peak wavelength, FWHM, and absorption intensity is characterized and illustrated below.

Then, the performance of the designed sensor is studied in detecting other common water pollutants such as Ag, Al, Cu, Cr, Se, and NH₃. Furthermore, the quality indicators, which are sensor sensitivity (RIS), the figure of merit (FOM), and quality factor (Q) are calculated.

The refractive indices of plasmonic NPs used in the simulation are summarized in

Table 1. Plasmonic parameters used for the metallic nanoparticle.

Material	Term	Strength	Plasma Frequency	Resonant Frequency	Damping Frequency
Ag	0	0.8450	1.36884 × 1016	0.000000 × 100	7.29239 × 1013
	1	0.0650	1.36884 × 1016	1.23971 × 1015	5.90380 × 1015
	2	0.1240	1.36884 × 1016	6.80775 × 1015	6.86701 × 1014
	3	0.0110	1.36884 × 1016	1.24351 × 1016	9.87512 × 1013
	4	0.8400	1.36884 × 1016	1.37993 × 1016	1.39163 × 1015
	5	5.6460	1.36884 × 1016	3.08256 × 1016	3.67506 × 1015
Au	0	0.7600	1.37188 × 1016	0.000000 × 100	8.05202 × 1013
	1	0.0240	1.37188 × 1016	6.30488 × 1014	3.66139 × 1014
	2	0.0100	1.37188 × 1016	1.26098 × 1015	5.24141 × 1014
	3	0.0710	1.37188 × 1016	4.51065 × 1015	1.32175 × 1015
	4	0.6010	1.37188 × 1016	6.53885 × 1015	3.78901 × 1015
	5	4.3840	1.37188 × 1016	2.02364 × 1016	3.36362 × 1015
Cu	0	0.5750	1.64535 × 1016	0.000000 × 100	4.55775 × 1013
	1	0.0610	1.64535 × 1016	4.42101 × 1014	5.74276 × 1014
	2	0.1040	1.64535 × 1016	4.49242 × 1015	1.60433 × 1015
	3	0.7230	1.64535 × 1016	8.05202 × 1015	4.88135 × 1015
	4	0.6380	1.64535 × 1016	1.69852 × 1016	6.54037 × 1015
Al	0	0.5230	2.27583 × 1016	0.000000 × 100	7.14047 × 1013
	1	0.2270	2.27583 × 1016	2.46118 × 1014	5.05910 × 1014
	2	0.0500	2.27583 × 1016	2.34572 × 1015	4.74006 × 1014
	3	0.1660	2.27583 × 1016	2.74680 × 1015	2.05251 × 1015
	4	0.0300	2.27583 × 1016	5.27635 × 1015	5.13810 × 1015

[26]. They are calculated using Equation (5). The refractive index of silicon is a function of the wavelength and is characterized by the Aspnes and Studna model [27], while selenium is characterized by Ciesielski et al.’s model [28]. Chromium follows Rakić et al.’s model [29], and NH₃ refractive index is characterized by Clive Cuthbertson and Maude Cuthbertson’s model [30].

3. Results and Discussion

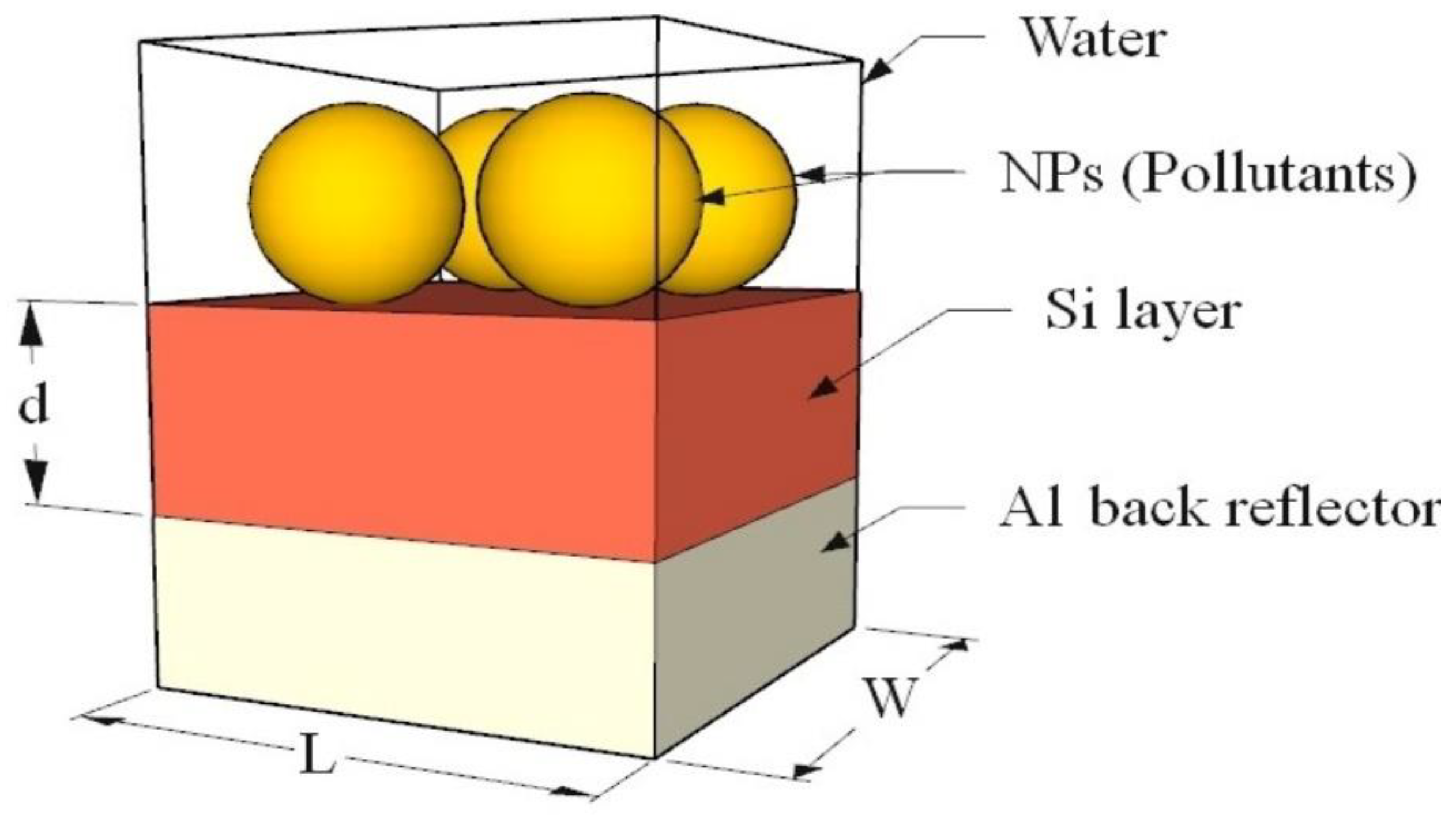
In this section, the optimization of the Si layer thickness is given, then the device’s performance in detecting various water pollutants is evaluated. Furthermore, the ability of the device to detect more than one water pollutant existing simultaneously is discussed.

3.1. Optimizing Si Layer Thickness

The device has been simulated for different thicknesses of the Si layer, $d$, and with different Au NP sizes. The Si layer has been changed from 100 nm to 500 nm in a step of 100 nm, while the Au NP radius, r, takes the following values (50 nm, 100 nm, 200 nm, 300 nm, 400 nm, and 500 nm). In the simulation, it is assumed that the Au spherical NPs are touching each other with no separation between them. The absorption spectrum of the device is measured, and the peak wavelength (λ_max), peak amplitude (I), and the FWHM of the absorption curve have been recorded for each case.

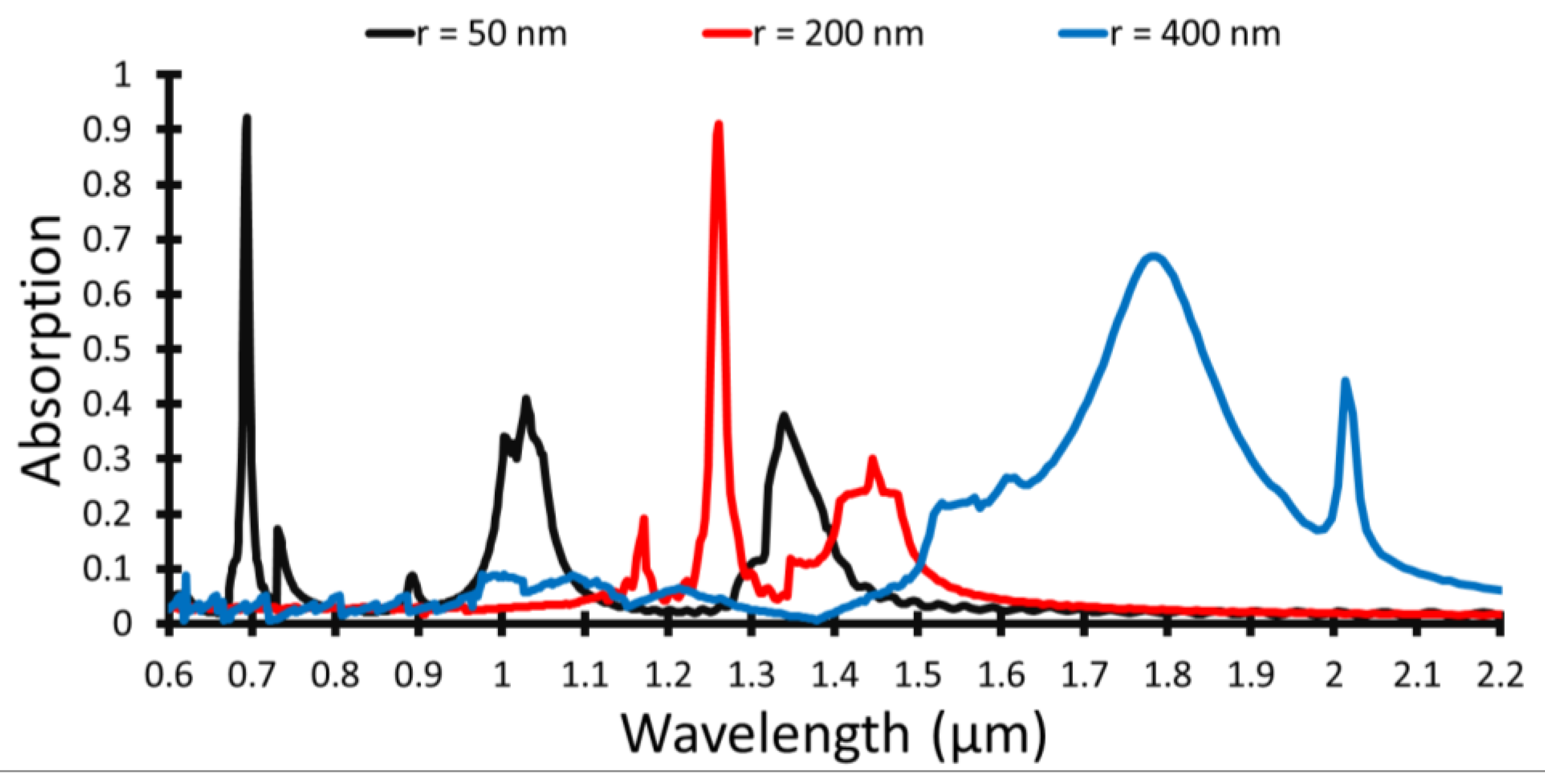
The absorbed light spectrum is shown in Figure 2 with Au NP of radius 50 nm, 200 nm, and 400 nm when the Si layer is 300 nm thick. This is a sample of the measured spectrum where only three full-spectrum curves are selected to display the obtained absorption behavior. The absorption spectral shapes reveal that each NP size has size-dependent absorption characteristics, considering that the NP absorption cross-section depends on the Au NP size. Changing the NP size does not only change the peak wavelength but also changes the FWHM and relative intensity of the absorption spectrum. Figure 3 shows a sample of the absorbed power distribution around the Au NP and in the Si layer for NPs of radius 500 nm at its maximum absorption wavelength (λ_max = 2.1 μm) and at a minimum absorption wavelength. 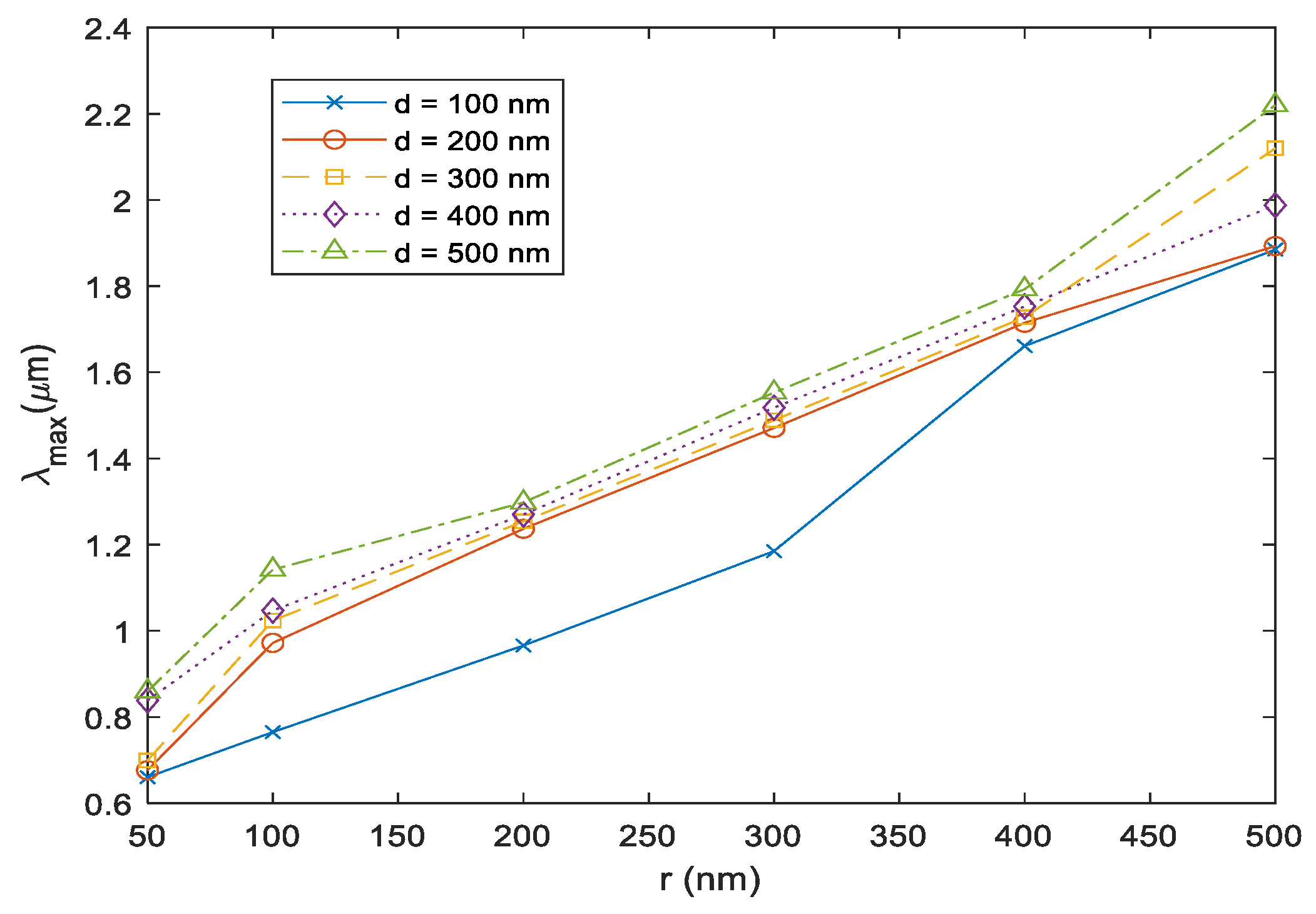It is clear from Figure 3a that the absorption power increases at the resonance wavelength of the Au NP, which increases the overall absorption of the sensor. The peak wavelength variation depending on the Au NP’s size (50 nm, 100 nm, 200 nm, 300 nm, 400 nm, and 500 nm) is shown in Figure 4 for unoptimized Si layer thickness that varies from 100 to 500 nm. The observed absorption peak wavelength (λ_max) is redshifted as the size of the Au NP increases for all Si layer thickness values. This behavior is expected as the resonance wavelength of the Au plasmons is tunable depending on the particle shape, size, and number [31]. When irradiated with electromagnetic waves, the metal NPs oscillate with size-dependent Eigen frequencies. This feature results from the confinement of the electron cloud at the metal-Si layer boundary. Using the Drude–Sommerfeld model of the dielectric function of the NP metal shows that plasmons resonance wavelength shifts to a longer wavelength as the size of the NP increases [32,33]. This NP behavior eventually leads to the size-dependent optical and electronic properties that could be optimized to suit devices applications by varying the nanoparticle size.

The dependence of the FWHM and absorption intensity on the size of the Au NPs and the thickness of the Si layer is shown in

Table 2. FWHM, and peak amplitude for different nanoparticle size, and Si layer thickness.

r (nm)	d = 100 nm		d = 200 nm		d = 300 nm		d = 400 nm		d = 500 nm
	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude
50	16	0.99	18	0.97	10	0.92	30	0.84	26	0.75
100	47	0.93	40	1	36	0.44	31	0.2	35	0.13
200	47	0.82	28	1	39	0.87	26	0.313	40	0.12
300	23	1	19	0.96	55	0.85	29	0.76	50	0.26
400	50	1	38	0.95	170	0.69	30	0.93	37	0.43
500	47	0.96	23	0.91	41	0.98	31	0.8	77	0.26

. The data shows that the shape of the absorption curve varies depending on both the nanoparticle size and the thickness of the Si layer.

For all Si layer thickness values, FWHM and relative intensity seem to be distinct for each particle size, i.e., each particle size has a spectral shape that varies depending on the size. From the obtained data and encouraged by the systematic variation of the peak absorption wavelength, we elected the peak absorption wavelength as the parameter that will be used to optimize the Si layer thickness to maximize the shift in λ_max as a function of the particle radius. This will increase the sensitivity of the sensor to NP size variations.

To optimize the Si layer thickness, an equation governing the peak absorption wavelength as a function of nanoparticle radius and Si layer thickness needs to be generated. Different interpolation techniques are adopted, including polynomials with various degrees and locally weighted smoothing quadratic regression (LOESS) to generate the required equation [34]. These techniques have been utilized to find the best fitting models of the simulated data points shown in Figure 4. The optimum model is selected based on the goodness of fit criterion considering the following statistics:

• Sum of squares due to error (SSE)

SSE measures the deviation in the fitted model as defined by Equation (6):

$$SSE={\displaystyle \sum }_{i=1}^n{w}_i{\left(y_i-{\widehat{y}}_i\right)}^2$$

(6)

where $w_i$ is the weights while $y_i$ and the $\widehat{y}$ are the actual data and the interpolated ones, respectively [35]. A model with good fitting is when SSE is close to 0.

2.

R-Square

The metric indicates how well the fit describes the variability. It is defined as the proportion of the sum of squares of the regression (SSR) and the total sum of squares (SST). SSR is defined as:

$$SSR={\displaystyle \sum }_{i=1}^n{w}_i{\left({\widehat{y}}_i-{\overline{y}}_i\right)}^2$$

(7)

SST is defined as the sum of squares that deviated from the mean and is defined as

$$SST={\displaystyle \sum }_{i=1}^n{w}_i{\left(y_i-{\overline{y}}_i\right)}^2$$

(8)

where SST = SSR + SSE. R-square is defined as:

$$\mathrm{R}-\mathrm{Square}=\frac{SSR}{SST}=1-\frac{SSE}{SST}$$

(9)

R-Square can take values between 0 and 1, with a value close to 1 representing a good fitting model.

3.

Adjusted R-Square

The adjusted R-Square is defined by:

$$\mathrm{Adjusted} \mathrm{R}-\mathrm{Square}=\frac{1-SSE\left(n-1\right)}{v}$$

(10)

where $n$ is defined as the number of response values and $v$ is the residual degrees of freedom defined by the difference between $n$ and the number of fitted coefficients estimated from the response values. The static can take any value between 0 and 1, with a value close to 1 representing a good fitting model.

4.

Root Mean Squared Error (RMSE)

It is defined as the square root of the mean square error (MSR). Again, a model with a value close to zero will represent a good fitting model.

Applying the previously mentioned interpolation techniques, the peak location of the maximum light absorption as a function of Si layer thickness $d$ and the Au NP radius, r, is modeled by a polynomial of degree 5 as given by Equation (11):

$${\lambda }_{max}(d,r)=p_{00}+p_{10}\times d+p_{01}\times r+p_{20}\times d^2+p_{11}\times d\times r+p_{02}\times r^2+p_{30}\times d^3+p_{21}\times d^2\times r+p_{12}\times d\times r^2+p_{03}\times r^3+p_{40}\times d^4+p_{31}\times d^3\times r+p_{22}\times d^2\times r^2+p_{13}\times d\times r^3+p_{04}\times r^4+p_{41}\times d^4\times r+p_{32}\times d^3\times r^2+p_{23}\times d^2\times r^3+p_{14}\times d\times r^4+p_{05}\times r^5$$

(11)

where $d$ is normalized by a mean of 300 nm and standard deviation (std) of 143.8 nm and $r$ is normalized by a mean of 258.3 nm and std of 161.9 nm. The goodness of fit metrics is given in

Table 3. λ_max fitting model goodness of fit.

Goodness of Fit Statistics	Measure
SSE	0.02711
R-Square	0.9955
Adjusted R-square	0.9868
RMSE	0.05207

. The recorded goodness of fit is the best result obtained when trying different interpolation techniques. The goodness of fit parameters is in the acceptable range, which indicates the high accuracy of the fitting equation.

The coefficients of the fitted polynomial using the adjusted R-square method with 95% confidence bounds are given in

Table 4. λ_max fitting polynomial coefficients.

Coefficients (95% Confidence Bounds)	Coefficients (95% Confidence Bounds)
$p_{00}=1.408 \left(1.338, 1.478\right)$	$p_{40}=0.0106 \left(-0.06008, 0.08128\right)$
$p_{10}=0.006189 \left(-0.1024, 0.1148\right)$	$p_{31}=0.01223 \left(-0.0263, 0.05076\right)$
$p_{01}=0.3939 \left(0.2278, 0.56\right)$	$p_{22}=0.05302 \left(0.0147, 0.09135\right)$
$p_{20}=-0.09504 \left(-0.2524, 0.06231\right)$	$p_{13}=0.02815 \left(-0.01941, 0.07572\right)$
$p_{11}=-0.07371 \left(-0.1678, 0.0204\right)$	$p_{04}=-0.0769 \left(-0.1421,-0.01173\right)$
$p_{02}=0.0749 \left(-0.05588, 0.2057\right)$	$p_{41}=0.0732 \left(0.001308, 0.1451\right)$
$p_{30}=0.0634 \left(0.003355, 0.1234\right)$	$p_{32}=-0.02954 \left(-0.07834, 0.01927\right)$
$p_{21}=-0.1131 \left(-0.2866, 0.06051\right)$	$p_{23}=-0.02858 \left(-0.07774, 0.02059\right)$
$p_{12}=-0.007015 \left(-0.1565, 0.1424\right)$	$p_{14}=0.02178 \left(-0.03917, 0.08274\right)$
$p_{03}=-0.01361 \left(-0.2847, 0.2575\right)$	$p_{05}=0.04427 \left(-0.06033, 0.1489\right)$

. The coefficients shown are selected in the middle of the 95% confidence interval shown.

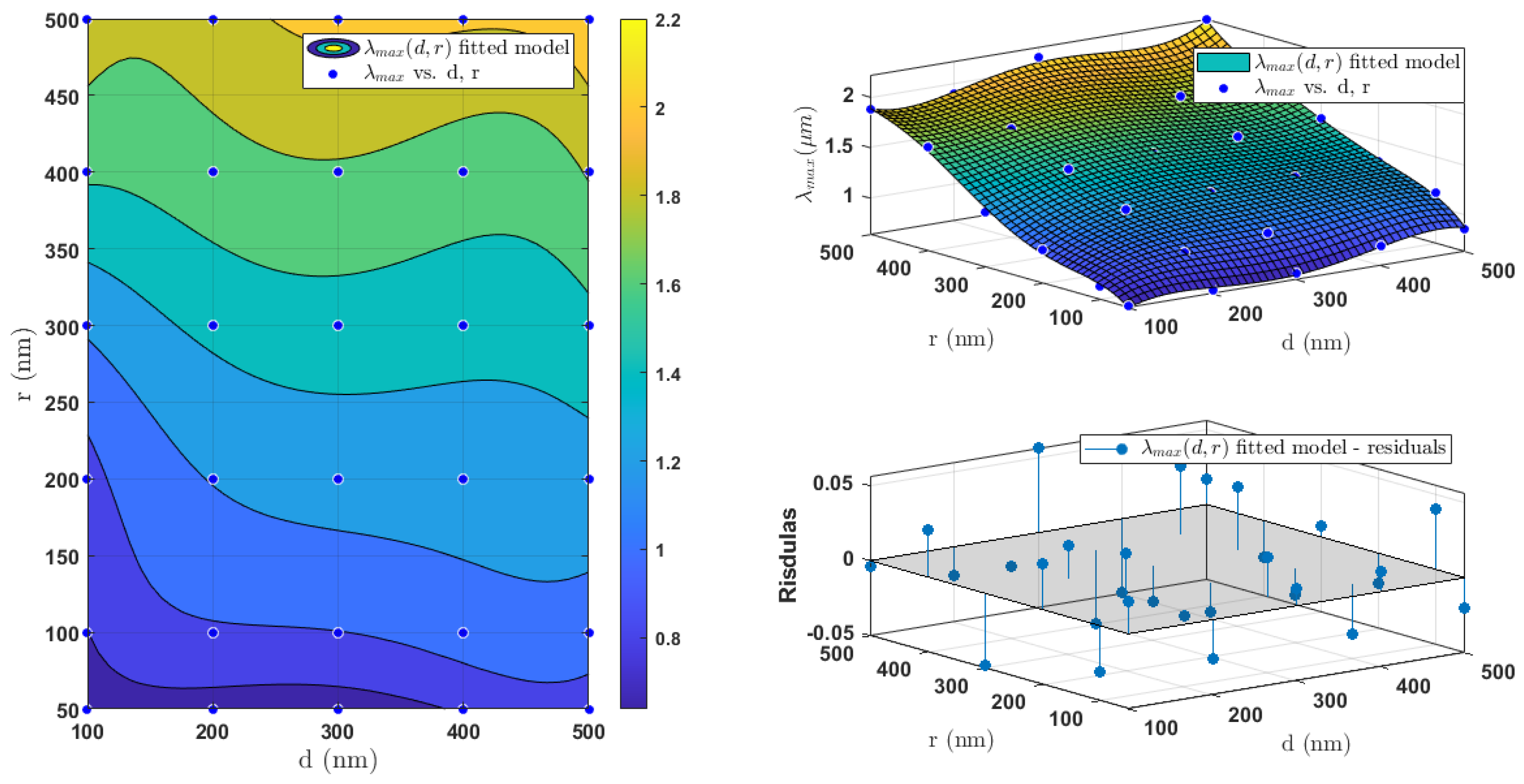
The fitted surface of ${\lambda }_{max }\left(d,r\right)$ shown in Figure 5 depicts that ${\lambda }_{max}$ is monotonically increasing as a function of both the radius and the Si layer thickness. The residuals plot in Figure 5 indicates small interpolation errors between the actual data points and the fitted surface.

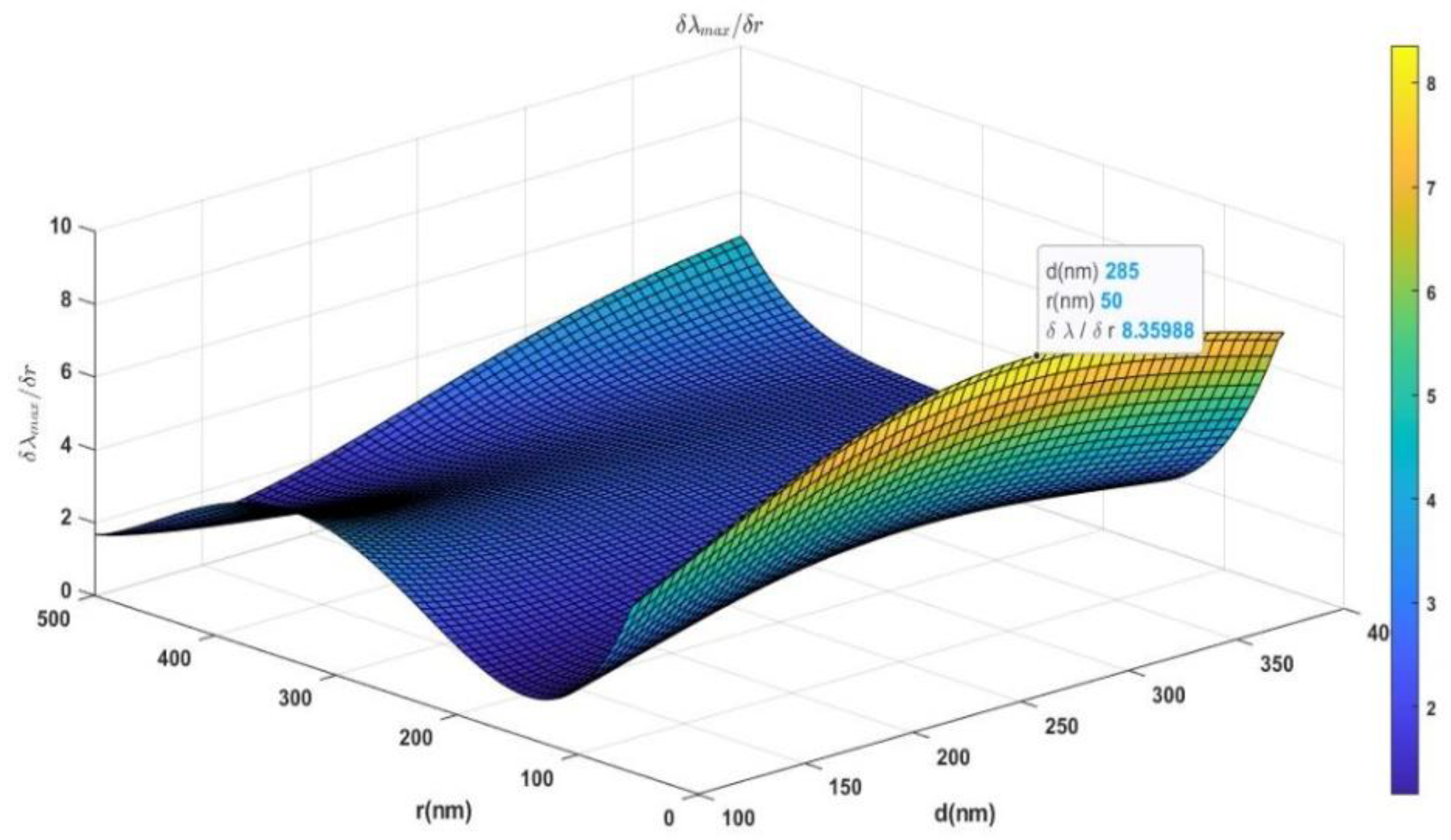
The gradient of the fitted surface, $\delta {\lambda }_{max}/\delta r$ is calculated and plotted in Figure 6. The optimized thickness of the Si layer is determined from the maximum of the gradient. This optimum point is marked in Figure 6, and it is found that the optimum thickness is 285 nm. This is the optimum thickness to detect the smallest used Au NP, r = 50 nm with size sensitivity $\delta {\lambda }_{max}/\delta r=8.36$. So, the proposed structure Si layer thickness was set to 300 nm. By maximizing the size sensitivity of the device, the absorption peak wavelength could be used to detect the particle size with high sensitivity as there is no overlap between the different peaks.

The spectral peaks shown in Figure 7 are obtained using the optimum Si layer thickness. These spectral peaks are truncated from the full absorption spectrum shown in Figure 2 to illustrate the different features of the spectral peaks for all Au NPs sizes. There is a suitable wavelength span between each spectral peak as we maximized the size sensitivity of the device.

The effect of the concentration of Au NP on the peak wavelength is investigated, and it is observed that the peak wavelength redshifts as the number of Au NP increases. Additionally, the spectrum broadens as the concentration of the Au NP increases. Figure 8 shows the dependence of the peak wavelength on the number of nanoparticles for the case where the Au NPs are of radius 200 nm and the Si layer thickness is 300 nm. The redshift of the spectrum with the increase of the number of nanoparticles is due to the coupling between different particles, which changes the electric field intensity on the surface. This causes a change in the oscillation frequency of the electrons, generating different cross-sections for the optical properties, including absorption and scattering [36,37,38]. The increased broadening in the absorption spectrum is attributed to both the surface scattering of electrons as well as increased radiation damping [33,39,40].

3.2. Sensitivity, FOM, and Q-factor

Equations (1)–(3) are utilized to calculate the sensitivity of the sensor, its FOM and Q-factor for different Au NP sizes. Maximizing the size selectivity of the device $\delta {\lambda }_{max}/\delta r=8.36$, i.e., with a 300 nm thick Si layer, maximum sensitivity, FOM, and Q-factor are 3010 nm/RIU, 300, and 32, respectively. This sensitivity is higher than the reported values for the sensitivities of Au NP sensors [12,14,41,42]. The high value of the sensitivity enables the sensor to detect very small variations in the refractive index, and the high values of the FOM and Q-factor indicated that the device has good selectivity as it has a narrow FWHM.

3.3. Detecting Water Pollutants Using the Designed Optimized Sensor

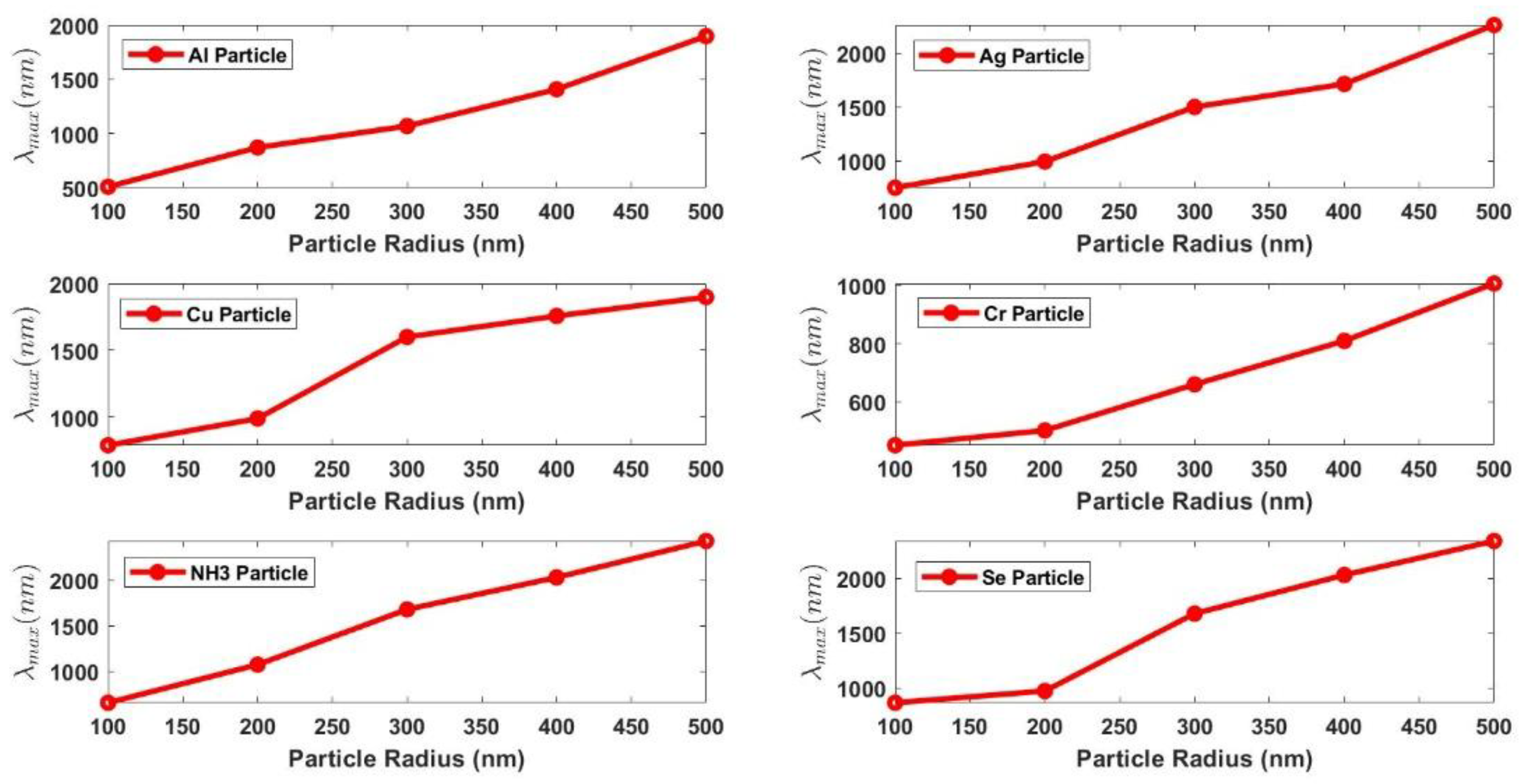
The designed Si-based sensor’s performance in detecting different sizes of water pollutants is investigated. The Au NPs on the top of the Si layer are replaced with six common water pollutants, Ag, Al, Cu, Cr, Se, and NH₃. As in the case of Au NPs, the absorption spectra are measured for different sizes ranging from 100 nm to 500 nm in a step of 100 nm. The spectrum curve’s peak wavelength, FWHM, and relative intensity are observed. Figure 9 shows that the peak wavelength redshifts with the increase of the size of the pollutants. All the six pollutants’ absorption spectrum show the same behavior but with different size selectivity $\delta {\lambda }_{max}/\delta r$, this is indicated by the different gradients of the six shown curves. The selectivity, $\delta {\lambda }_{max}/\delta r$, takes the values from 2 to 7, which indicates the good selectivity of the sensor.

The FWHM and peak amplitude of the spectral absorption curves are shown in

Table 5. (a) FWHM, and peak amplitude for different NP size, for Ag, Al, and Cu pollutants. (b) FWHM, and peak amplitude for different nanoparticle size, for Cr, Se, and NH3 pollutants.

(a)
r (nm)	Ag		Al		Cu
	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude
100	92	1	184	1	200	1
200	180	0.98	361	1	240	0.98
300	50	0.8	236	1	100	0.85
400	130	0.82	46	0.92	115	0.8
500	40	0.25	193	0.65	343	0.9
(b)
r (nm)	Cr		Se		NH3
	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude	FWHM (nm)	Peak Amplitude
100	400	0.96	49	0.78	11	0.99
200	100	1	32	0.84	19	0.96
300	310	0.97	85	0.8	7	0.93
400	189	0.98	46	0.88	3	0.9
500	210	0.96	33	0.61	5	0.83

a,b. The results for the six pollutants show that the absorption spectral shapes have a wide variation in FWHM values that are size dependent. These variations could be favorable as pollutants could be detected depending on the peak wavelength and the shape of the absorption spectrum, FWHM, and peak relative amplitude.

Figure 10 allocates all the simulated particles with different materials and different sizes. A good separation between the detected particles with different sizes is demonstrated, and the proposed structure can differentiate between these different cases. The zooming on the plotted graph shows that there is a potential that the particles can be detected efficiently. Additionally, we have normalized the features to be from 0 to 1 and plot the 3D feature space of the detected particles along with different sizes in Figure 11. Again, it still shows a good separation between the different particles.

The sensor detection parameters are then calculated from Equations (1)–(3). The calculated values for the sensitivity, FOM, and Q-factor are presented in

Table 6. Sensitivity analysis for the detection of different pollutants.

Pollutant	Sensitivity (nm/RIU)	FOM	Q-Factor
Ag	5300	105	30
Al	820	5	30
Cu	1550	14	15
Cr	760	3.5	5
Se	11,300	740	24
NH3	3000	150	670

. Our Sensitivity is comparable with the reported value for Ag, which is about 5000 nm/RIU, but our maximum sensitivity (11,300 nm/RIU) is much higher [43]. Sharp spectral curves accompany this ultimate value of sensitivity in the case of Se that is indicated from the low values for FWHM in Table 5 and large FOM values (750) in Table 6.

3.4. More Than One Pollutant at a Time

The performance of the sensor in detecting more than one pollutant when they exist simultaneously in the water sample is studied. Pollutants are added as a couple on the surface of the Si layer, and the absorption spectral parameters, peak wavelength, FWHM, and peak wavelength relative amplitude are observed. The radius of each particle is set to 200 nm. The obtained selectivity parameters are shown in

Table 7. Selectivity parameters (peak location, FWHM, and peak amplitude) in case of couple elements existing on the surface of the sensor.

Pollutants Couple	Peak Location (nm)	FWHM	Peak Amplitude
Au-Ag	996 and 1130	29 nm and 33 nm	1 and 0.96
Au-Al	986 and 1126	45 nm and 48 nm	1 and 0.97
Au-Cu	994 and 1130	35 nm and 41 nm	0.97 and 0.94
Au-Cr	580 and 1100	240 nm and 46 nm	0.95 and 0.97
Au-Se	998 and 1100	63 nm and 59 nm	1 and 0.98
Au-NH3	1330 and 1120	20 nm and 5 nm	0.8 and 0.82

.

As the table shows, two distinct peaks at different wavelengths are observed for each couple. Each peak represents the location of one of the impurities, and each impurity has its own curve characteristics (peak location, FWHM, and peak amplitude). The first row in Table 6 shows that the peak wavelength of Au blueshifts a little from 1250 nm (peak location when Au was alone) to 1130 nm, while the Ag peak remains almost at the same location. This indicates that the peak locations could be used in the detection of pollutants even if more than one pollutant exists simultaneously.

3.5. Performance Comparision of the Proposed Sensor to Other Reported Sensors

A comparison of the performance of our sensor with the reported SPR sensors’ performance is listed in

Table 8. Comparison of sensing performance indicators of refractive index change sensors.

Technique	Sensitivity (nm/RIU)	FOM	Q-Factor	Ref.
Si-based sensor	11,300	740	24	This work (Se detection)
Si-based sensor	3010	300	32	This work (Au detection)
Si-based sensor	477.54	38.16	N/A	[14]
Gold nanoring Array	544	6	N/A	[41]
Si photonic Crystal	5018	1477	2149.5	[43]
Graphene silver Coated nanocolumns	8860.9	N/A	N/A	[44]
Si resonator	636	211.3	N/A	[45]

. The listed performance indicators show that the proposed sensor has much higher sensitivity than the reported values. Beside high sensitivity, the proposed sensor structure has a low cost, and it is easily fabricated.

4. Conclusions

A low-cost optical Si-based optical sensor for water pollutant detection is introduced in this paper. The device performance is optimized by maximizing the size selectivity of the device for Au NP. The optimum Si layer thickness, 300 nm, results in maximum size selectivity $\delta {\lambda }_{max}/\delta r=8.36$. The performance parameters of the device, sensitivity, FOM, and Q-factor, are calculated. This is done for Au NP as well as other common water pollutants, Ag, Al, Cu, Cr, Se, and NH₃. The optical Si-based sensor has a high sensitivity, FOM, and Q-factor of 11,300 nm/RIU, 740, and 670, respectively. These ultimate values indicate the ability of the sensor to differentiate between different nanoparticles of different sizes.