Two-Dimensional Solitons in Bose–Einstein Condensates with Spin–Orbit Coupling and Rydberg–Rydberg Interaction

Abstract

Applying an imaginary time evolution method (AITEM) to the system of Gross–Pitaevskii equations, we find two-dimensional stable solitons in binary atomic Bose–Einstein condensates with spin–orbit coupling (SOC) and the Rydberg–Rydberg interaction (RRI). The stability of 2D solitons by utilizing their norm and energy is discussed in detail. Depending on the SOC and Rydberg–Rydberg interaction, we find stable zero-vorticity and vortical solitons. Furthermore, we show that the solitons can be effectively tuned by the local and nonlocal nonlinearities of this system.

1. Introduction

Spatial solitons, the balance between diffraction and nonlinearity in nonlinear media, have attracted wide interest in physics, such as hydrodynamics, Bose–Einstein condensates (BECs), and nonlinear optics [1]. The generation of multi-dimensional solitons is more difficult in 1D solitons due to the collapse of solitons in nonlinear media [2,3,4]. An apparent condition is the balance between an attractive and expulsive nonlinearity for the generation of solitons, which can be achieved in BECs with spin–orbit coupling and the Rydberg–Rydberg interaction. Mihalache et al. overviewed the creation of solitons in a variety of relevant physical settings, including in BECs [5]. Stable solitons in BECs with expulsive parabolic potential [6], fractionalized half-quantum vortices [7], and polarized light [8] were found. Recently, new possible themes have been proposed to generate stable solitons, such as spin–orbit coupling (SOC) in spinor BECs [9,10,11,12], the nonlinear optical system [13], and the Rydberg cold atom system [14,15,16].

In self-attractive BECs, the SOC and Rydberg interaction can promote the stability of multidimensional solitons. It is an interesting topic, how 2D stable solitons can be generated in a BEC system with both SOC and RRI. Here, we present a systematic study to address this question.

2. Materials and Methods

The system of scaled 2D Gross–Pitaevskii equations (GPEs) for the spinor wave function $\psi =({\psi }_1,{\psi }_2)$ of the binary BEC with RRI and the SOC of Rashba type is written as:

$$\begin{array}{l}i\frac{\partial {\psi }_1}{\partial t}+\frac{1}{2}{\nabla }^2{\psi }_1+[g_{11}{\left|{\psi }_1\right|}^2+g_{12}{\left|{\psi }_2\right|}^2+{\displaystyle \int d^3{r}_{\perp }^{\prime }(U_{11}(r_{\perp }^{\prime }){\left|{\psi }_1\right|}^2+U_{12}(r_{\perp }^{\prime }){\left|{\psi }_2\right|}^2})]{\psi }_1+i\lambda {\nu }_{so-}{\psi }_1=0\\ i\frac{\partial {\psi }_2}{\partial t}+\frac{1}{2}{\nabla }^2{\psi }_2+[g_{21}{\left|{\psi }_1\right|}^2+g_{22}{\left|{\psi }_2\right|}^2+{\displaystyle \int d^3{r}_{\perp }^{\prime }(U_{22}(r_{\perp }^{\prime }){\left|{\psi }_2\right|}^2+U_{21}(r_{\perp }^{\prime }){\left|{\psi }_1\right|}^2)}]{\psi }_2+i\lambda {\nu }_{so+}{\psi }_2=0\end{array}$$

(1)

where ${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ is Laplace operator and $g_{ij}$ describes the strength of local interactions due to s-wave scattering with $g_{12}=g_{21}$. $U_{ij}=c_6^{(ij)}/(R_c^6+r^6)$ is Rydberg interaction potential, where $R_c$ is Rydberg soft core radius and $c_6^{(ij)}={(\mathsf{\Omega }/2\mathsf{\Delta })}^4{C}_6$ is dispersion parameter [17,18]. Here, $\mathsf{\Omega }=\frac{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}{2{\mathsf{\Delta }}_1}$ is the effective Rabi frequency of the system and $\mathsf{\Delta }={\mathsf{\Delta }}_1+{\mathsf{\Delta }}_2$, where ${\mathsf{\Omega }}_1$ and ${\mathsf{\Omega }}_2$ are Rabi frequency of two laser fields, ${\mathsf{\Delta }}_1$ and ${\mathsf{\Delta }}_2$ are the detunings, respectively. The effective Rydberg state parameter for excitation of ${}^{87}\mathrm{Rb}$ is $C_6=9.7\times {10}^{20}\mathrm{au}$ [19]. ${\nu }_{so\mp }=\frac{\partial }{\partial x}\mp i\frac{\partial }{\partial y}$ and $\lambda$ are the strengths of the self-spin coupling in the isotropic form of SOC.

In this work, we proposed a scheme for the creation of matter-wave solitons in a Bose–Einstein condensate. The approach was based on optical dressing of a ground-state atom BEC to highly excited Rydberg states by two-photon detuning, i.e., two laser fields, ${\mathsf{\Omega }}_1$ and ${\mathsf{\Omega }}_2$, were coupled to a 3-level atomic system (see Figure 1). The BEC atoms were weakly coupled to a highly excited Rydberg state, which induced effective, soft-core interactions between the dressed ground state atoms.

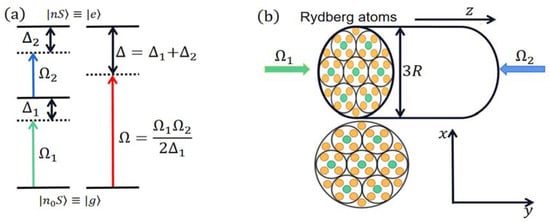
Figure 1. (a) Simplified level scheme of the considered Rydberg-dressing approach. The off-resonant coupling of condensed ground state ($|n_{0}S>\equiv |g>$) atoms to strongly interacting Rydberg states ($|nS>\equiv |e>$ ) gave rise to a stable bright soliton bound by intermediate state, ${\mathsf{\Omega }}_1$ and ${\mathsf{\Omega }}_2$ were Rabi frequency of two laser fields, ${\mathsf{\Delta }}_1$ and ${\mathsf{\Delta }}_2$ were the detunings, respectively, and $\mathsf{\Omega }=\frac{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}{2{\mathsf{\Delta }}_1}$ was the effective Rabi frequency of the system. (b) Illustration of the system.

The stationary wave function was of the form ${\psi }_{1,2}=e^{-i\mu t}{\psi }_{1,2}$, where $\mu$ was the chemical potential. Let $N={\displaystyle \iint ({\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2)dxdy}$ be the norm. The eigenvalue of Equation (1) could be obtained by using the numerical methods [18]. With perturbation, we had ${\psi }_{1(2)}=[{\psi }_{01(2)}+(u_{1(2)}+v_{1(2)})e^{bs}+(u_{1(2)}^{*}-v_{1(2)}^{*})e^{b^{*}s}]e^{ibs}$, where ${\psi }_{0(1,2)}$ is the stationary solution of Equation (1), $u_{1(2)},v_{1(2)}<<{\psi }_{01(2)}$ are the perturbation terms, and $b$ is a complex parameter indicating the perturbation growth rate. According to the criteria, the soliton solutions could be stable if $\mathrm{Re}(b)=0$ [19].

3. Results

Figure 2 shows the relationship of spin-up and spin-down atom numbers $N_1$ and $N_2$, respectively, with the local and nonlocal parameters. Figure 2a,b shows the atom number with local interaction strengths $g_{11}$ and $g_{12}$. We found that the spin-down atom numbers $N_1$ and $N_2$ were not sensitive with the change of self-local interaction strength $g_{11}$. However, $N_1$ and $N_2$ were more tunable with the cross local interaction strength $g_{12}$($g_{21}$). The spin-up and spin-down atom numbers $N_1$ and $N_2$ showed completely different behaviors with the change of $g_{12}$ in Figure 2b. $N_1$ decreased monotonously with $g_{12}$, while $N_2$ increased with $g_{12}$. $N_1$ was dominant with negative $g_{12}$, and $N_2$ was the main mode with positive $g_{12}$. In Figure 2c, we found that atoms with spin-up and spin-down modes were approximately equally populated, except for the range $-0.05<\lambda <0$, where $N_1$ was much larger than $N_2$. Figure 2d–f show the atom number $N$ with respect to the nonlocal nonlinear strength $U_{ij}(i,j=1,2)$. Similar to the $N-g_{12}$ relation, $N_1$ and $N_2$ could be tuned effectively by $U_{12}$($U_{21}$) and $U_{22}$. Combining Figure 2b,d–f, we found that the local and nonlocal nonlinear strengths were key parameters for the switch of the spin-up and spin-down modes.

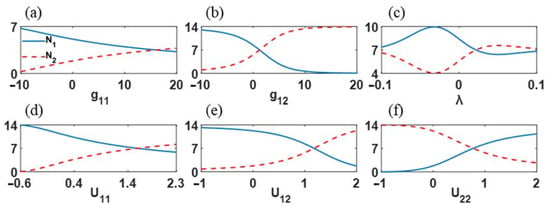
Figure 2. Relationship of spin-up and spin-down atom numbers $N_1$ and $N_2$, respectively, with the local and nonlocal parameters. The parameters chosen were the local nonlinear strength $g_{11}$ (a) and $g_{12}$ (b), spin–orbital coupling strength $\lambda$ (c), and nonlocal nonlinear strength $U_{11}$ (d), $U_{12}$ (e) and $U_{22}$ (f) for spin up (blue line, $N_1$ ) and spin down (red line, $N_2$ ). The other fixed parameters were $g_{11}=0.1$, $g_{12}=g_{21}=g_{22}=0.3$, $U_{11}=U_{12}=U_{21}=U_{22}=1$, $\lambda =0.001$, and $\mu =1.003$.

For more information on the atom numbers with spin-up and spin-down modes, the ratio $N_1/N_2$ with respect to $g_{11}$, $g_{12}$, $\lambda$, and $U_{ij}(i,j=1,2)$ was plotted in Figure 3. It indicated that the ratio $N_1/N_2$ decreased monotonously with $g_{11}$, $g_{12}$, $U_{11}$, and $U_{12}$, and increased monotonously with $U_{22}$. Comparing with Figure 2, we found that the dominant atom mode could be tuned by $g_{12}$, $U_{12}$, and $U_{22}$ effectively. In Figure 3c, we found that the number of atoms was sensitive to the change of the spin–orbital coupling strength $\lambda$. The ratio $N_1/N_2$ had a single peak with the change of $\lambda$, which indicated that the atoms with the spin-up mode were predominant only with a small range of $\lambda$, around $-0.05<\lambda <0$.

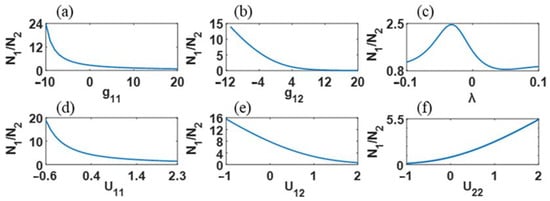
Figure 3. Ratio $N_1/N_2$ with respect to the local and nonlocal parameters. The parameters chosen were the local nonlinear strength $g_{11}$ (a) and $g_{12}$ (b), spin-orbital coupling strength $\lambda$ (c), and nonlocal nonlinear strength $U_{11}$ (d), $U_{12}$ (e) and $U_{22}$ (f). The other parameters were the same as Figure 2.

In order to obtain the stability of the solitons in the nonlinear media, the relation of the energy $E$ and the chemical potential with respect to $N$ were studied and shown in Figure 4 [19]. We found that the energy $E$ increased linearly with $N$. In Figure 4a, we observed little difference between the weak and strong local nonlinear strength $g_{12}$, which was shown in the built-in figure. The stability of the solitons was studied and shown in Figure 4b. The slope of the curve for the weak local nonlinear strength ($g_{12}=0.1$) was positive $\mathrm{d}\mu /\mathrm{d}N>0$. According to the Vakhitov–Kolokolov criterion [20], the solitons here were stable with a weak local nonlinear strength. For the strong local nonlinear conditions ($g_{12}=10$), the chemical potential $\mu$ first increased with $N$ and reached its maximum value ${\mu }_{\max }$ when $N=27$. For smaller $N$, the solitons were stable with $\mathrm{d}\mu /\mathrm{d}N>0$ (point A). When $N>27$, the solitons were unstable as we observed a negative slope of dependence $\mathrm{d}\mu /\mathrm{d}N<0$ (point B). This phase transition was not observed with a weak local nonlinear strength. In Figure 3b, we came to two conclusions: (1) The stable propagation of solitons was sensitive to the chemical potential $\mu$ with a narrow stable propagation zone $1.0032<\mu <1.0042$. (2) Solitons with weak local interactions were more stable than those with strong conditions.

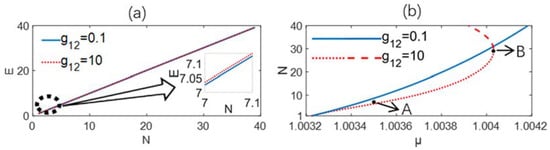
Figure 4. (a) Soliton energy versus total atom number $N$ with different $g_{12}$. (b) The relation of total atom number with the chemical potential $\mu$. The blue solid (red) line represents the weak (strong) local nonlinear strength $g_{12}=0.1, 10$, respectively. Dot A represents the stable phase, while dot B represents the phase change of the stable solitons. The other parameters were the same as Figure 2.

The density profile and spatial distributions of the zero-vorticity and vortex soliton pair are displayed in Figure 5, with both stable and unstable cases. In Figure 5a1,a2, the density of the zero-vorticity soliton was mainly distributed in the center, where the modulus of $g_{ij}$ and $U_{ij}$ was relatively small. With strong local and nonlocal nonlinear parameters, we observed an obvious diffraction beyond the center, which resulted in the collapse of the solitons, as seen in Figure 5b1,b2. For the vortex soliton, the density distributed in a circular ring instead of the center, as shown in Figure 5a3,a4. Similar to the zero-vorticity solitons, we also observed the diffraction of vortex solitons in an unstable case with strong local and nonlocal nonlinear parameters. When tuning the system parameters, the stable solitons could only be obtained when the local and local interaction were relatively small.

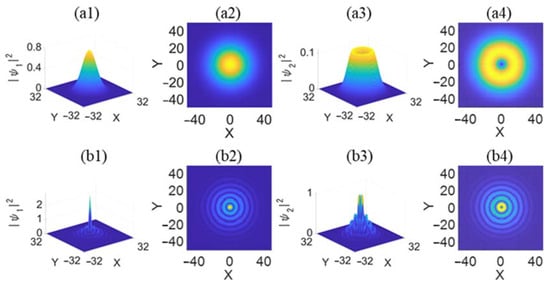
Figure 5. The density profile and spatial distributions of the soliton pairs for stable zero-vorticity (a1,a2) and vortex solitons (a3,a4), and unstable cases (b1–b4), respectively. In (a1–a4), $g_{11}=\mathrm{0.1}$, $g_{12}=g_{21}=0.3$, $g_{22}=0.3$, $U_{12}=U_{21}=1$, $\lambda =0.001$, and $\mu =1.003$. In (b1–b4), $g_{11}=-13$, $g_{12}=g_{21}=30$, $g_{22}=30$, $U_{12}=U_{21}=10$, $\lambda =0.5$, and $\mu =0.879$. The other parameters were set to be 1.

4. Conclusions and Discussion

In this paper, we constructed a three-level atomic BEC system with spin–orbit coupling and a Rydberg–Rydberg interaction. We found that the atom number of the spin-up and down soliton modes could be manipulated effectively by tuning the local and nonlocal nonlinear parameters. Two types of solitons, the zero-vorticity and vortex solitons, were found to be generated and stably propagated in the nonlinear media with spin–orbit coupling and the Rydberg–Rydberg interaction. These solitons were generated owing to the balance of attractive and repulsive forces coming from the two components of the wave function. These solitons could be tuned by the local and nonlocal nonlinearities. In strong local and nonlocal nonlinear conditions, the energy of solitons was scattered by diffraction.

The density distribution of solitons could be tuned by SOC and RRI. The solitary vortex pair in the SOC self-attractive BECs in free space had the semi-vortices and mixed modes [10], while in our work, the soliton pair was composed of zero-vorticity and vortex modes, owing to the long-range Rydberg interaction. External potential is another important way to control the generation of solitons in nonlinear media [21,22]. Liang et al. found a bright soliton in BECs in an expulsive parabolic potential with proper system parameters [6]. However, the external potential was not included in this study. In order to deeply understand the modulation of solitons in BECs, it is our future work to explore the BEC system with SOC, RRI, and external potentials.