A Single-Pixel Imaging Scheme with Obstacle Detection
Abstract
:1. Introduction
2. Methods
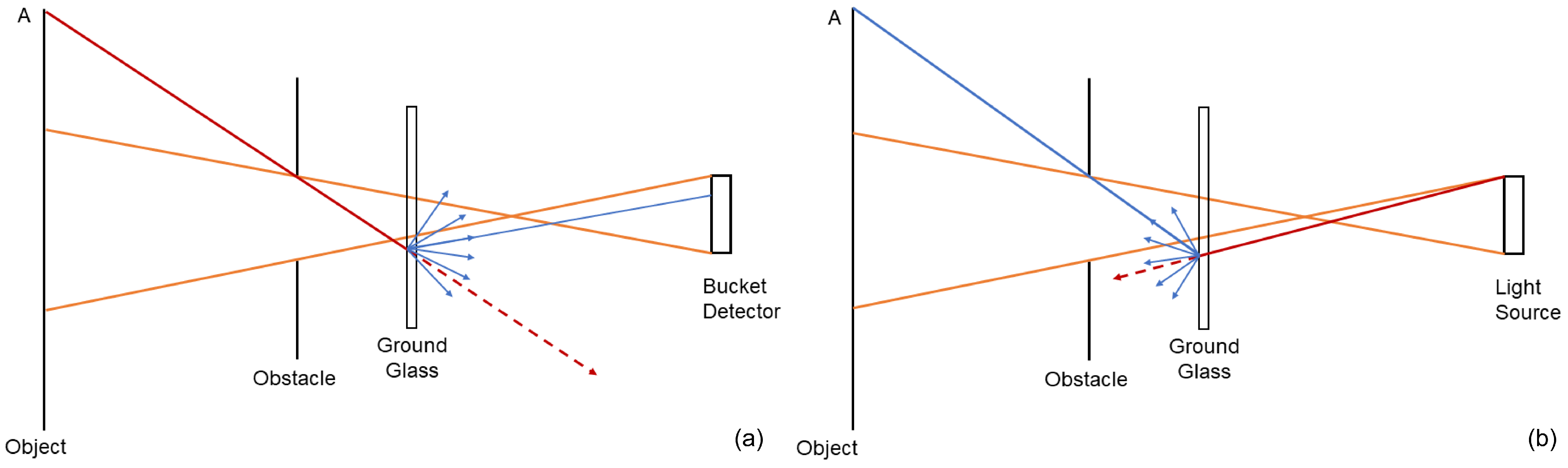
2.1. Principle of SPI
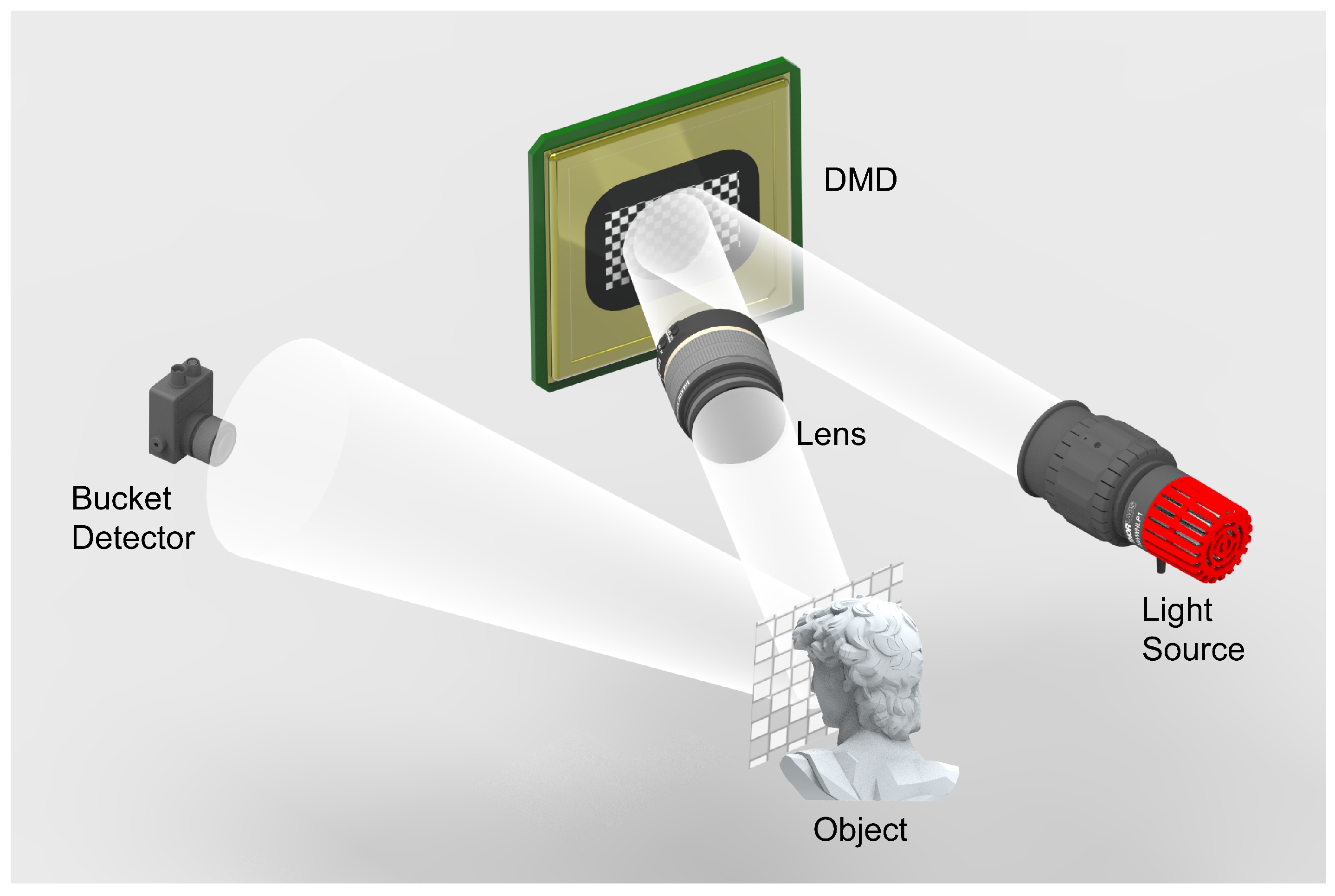
2.2. Experiment Design
3. Experiments and Discussion
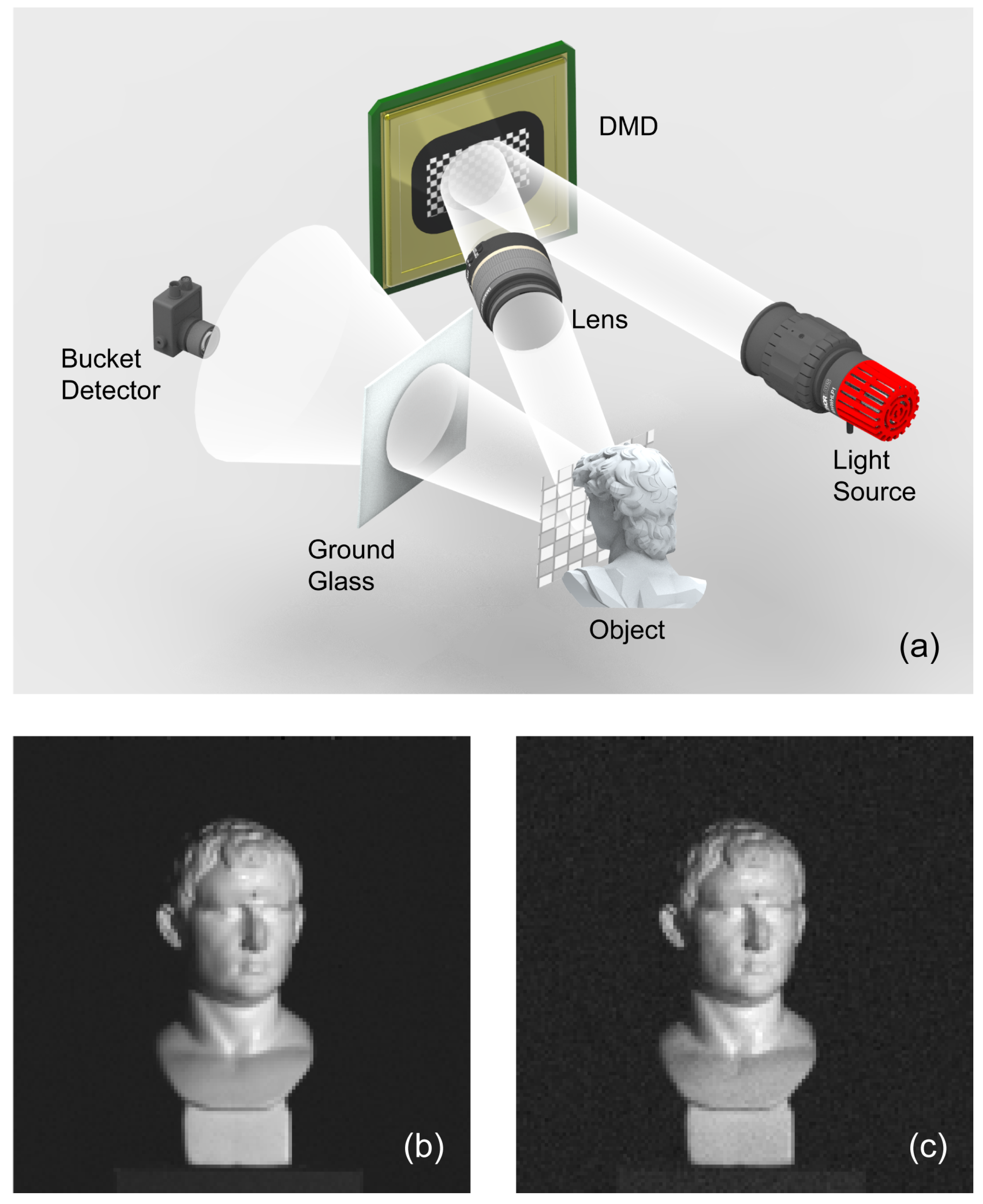
3.1. SPI with Scattering Detection
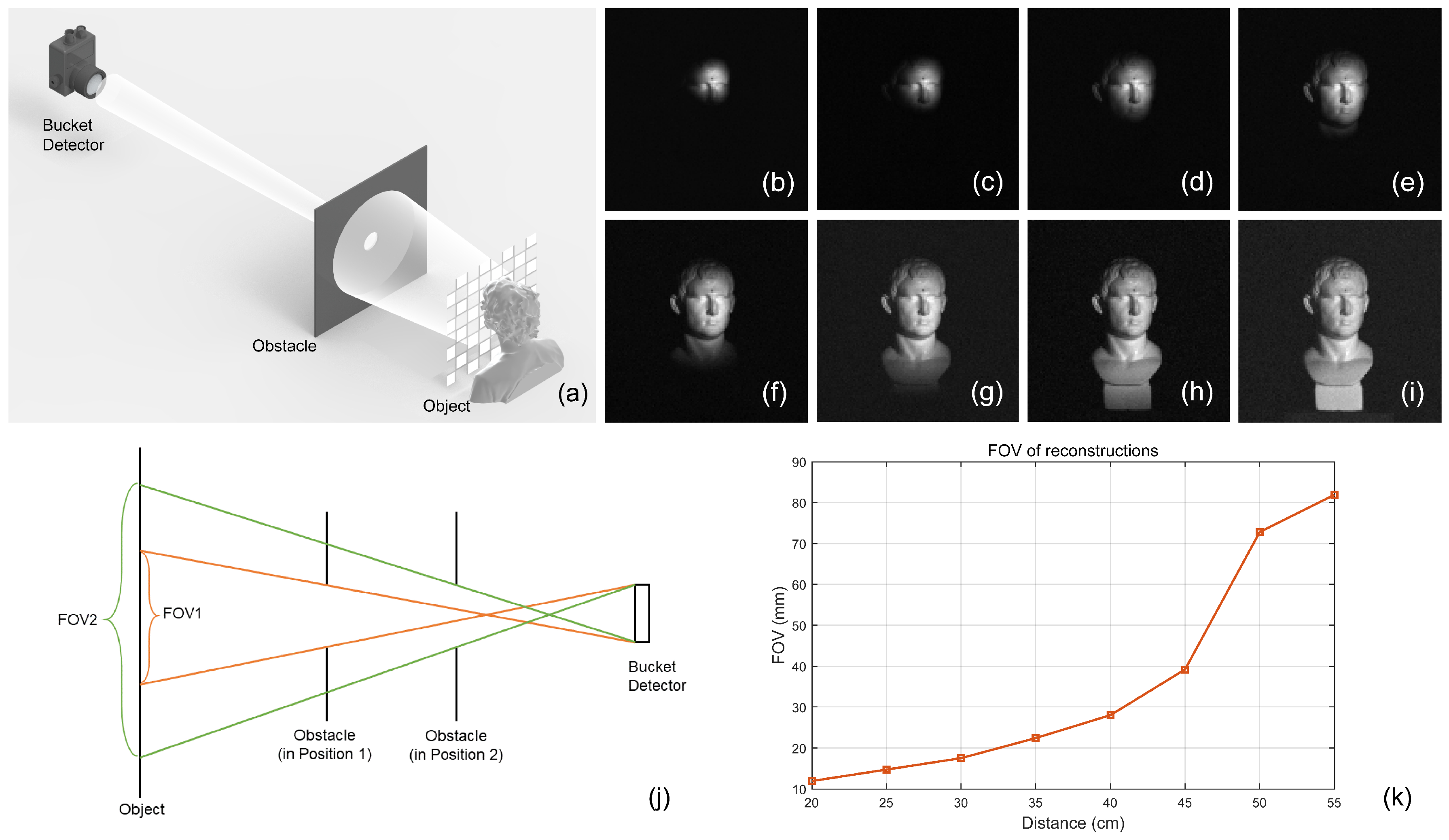
3.2. SPI with FOV Restricted Detection
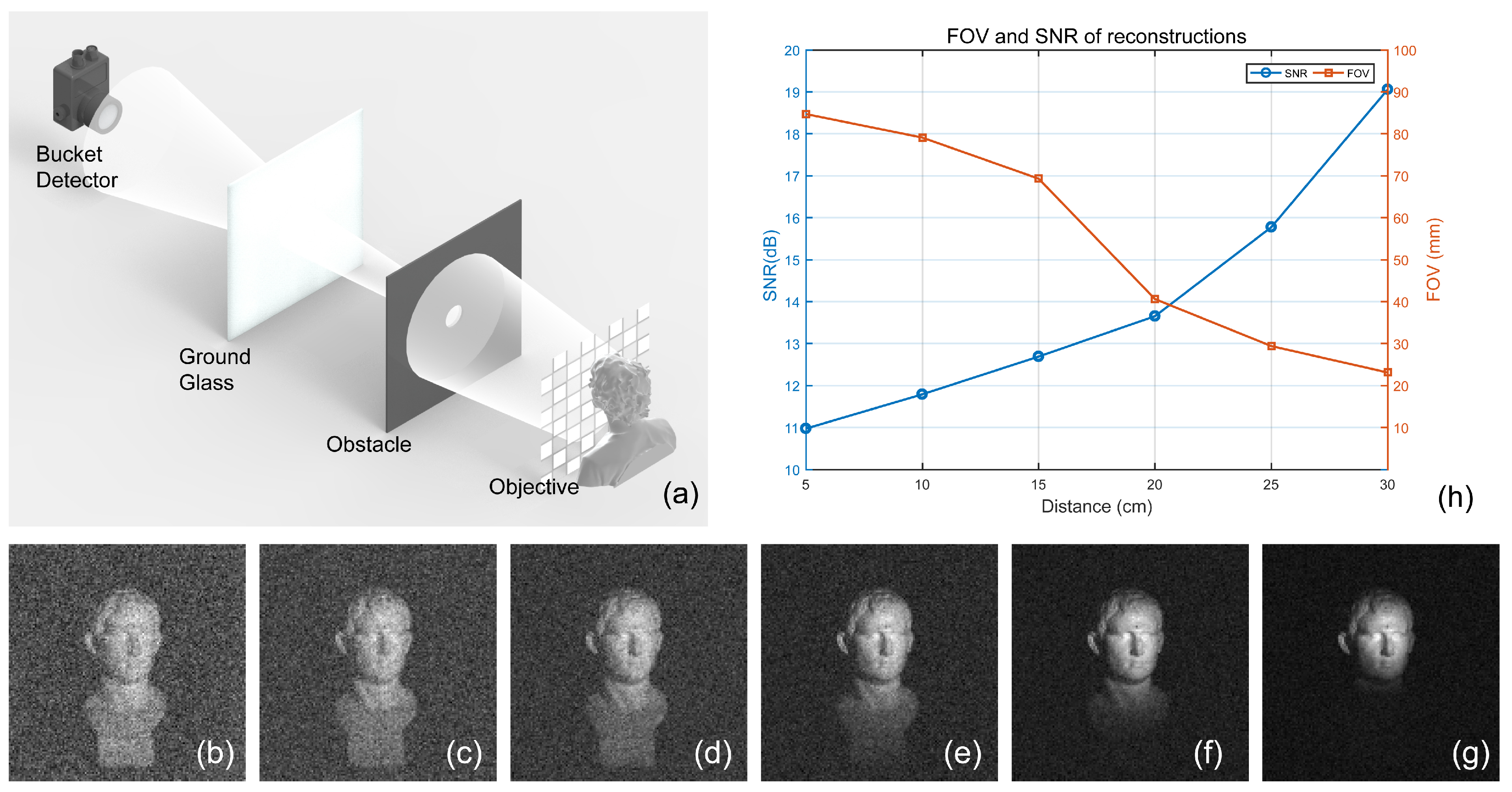
3.3. FOV Enlarged by Scattered Light
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pittman, T.B.; Shih, Y.; Strekalov, D.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429. [Google Scholar] [CrossRef] [PubMed]
- Bennink, R.S.; Bentley, S.J.; Boyd, R.W. “Two-photon” coincidence imaging with a classical source. Phys. Rev. Lett. 2002, 89, 113601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valencia, A.; Scarcelli, G.; D’Angelo, M.; Shih, Y. Two-photon imaging with thermal light. Phys. Rev. Lett. 2005, 94, 063601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Sun, B.; Edgar, M.P.; Bowman, R.; Vittert, L.E.; Welsh, S.; Bowman, A.; Padgett, M.J. 3D computational imaging with single-pixel detectors. Science 2013, 340, 844–847. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.J.; Edgar, M.P.; Gibson, G.M.; Sun, B.; Radwell, N.; Lamb, R.; Padgett, M.J. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Commun. 2016, 7, 12010. [Google Scholar] [CrossRef]
- Ma, Y.; Yin, Y.; Jiang, S.; Li, X.; Huang, F.; Sun, B. Single pixel 3D imaging with phase-shifting fringe projection. Opt. Lasers Eng. 2021, 140, 106532. [Google Scholar] [CrossRef]
- Jiang, W.; Li, X.; Peng, X.; Sun, B. Imaging high-speed moving targets with a single-pixel detector. Opt. Express 2020, 28, 7889–7897. [Google Scholar] [CrossRef]
- Xu, Z.H.; Chen, W.; Penuelas, J.; Padgett, M.; Sun, M.J. 1000 fps computational ghost imaging using LED-based structured illumination. Opt. Express 2018, 26, 2427–2434. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Gu, J.H.; Lin, H.Z.; Jiang, L.; Liu, W.T. Gradual ghost imaging of moving objects by tracking based on cross correlation. Opt. Lett. 2019, 44, 5594–5597. [Google Scholar] [CrossRef]
- Gibson, G.M.; Sun, B.; Edgar, M.P.; Phillips, D.B.; Hempler, N.; Maker, G.T.; Malcolm, G.P.; Padgett, M.J. Real-time imaging of methane gas leaks using a single-pixel camera. Opt. Express 2017, 25, 2998–3005. [Google Scholar] [CrossRef]
- Edgar, M.P.; Gibson, G.M.; Bowman, R.W.; Sun, B.; Radwell, N.; Mitchell, K.J.; Welsh, S.S.; Padgett, M.J. Simultaneous real-time visible and infrared video with single-pixel detectors. Sci. Rep. 2015, 5, 10669. [Google Scholar] [CrossRef]
- Jiang, W.; Jiao, J.; Guo, Y.; Chen, B.; Wang, Y.; Sun, B. Single-pixel camera based on a spinning mask. Opt. Lett. 2021, 46, 4859–4862. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, Q.; Dai, J.; Cai, W. Demonstration of a cost-effective single-pixel UV camera for flame chemiluminescence imaging. Appl. Opt. 2019, 58, 5248–5256. [Google Scholar] [CrossRef] [PubMed]
- Chan, W.L.; Charan, K.; Takhar, D.; Kelly, K.F.; Baraniuk, R.G.; Mittleman, D.M. A single-pixel terahertz imaging system based on compressed sensing. Appl. Phys. Lett. 2008, 93, 121105. [Google Scholar] [CrossRef] [Green Version]
- Shrekenhamer, D.; Watts, C.M.; Padilla, W.J. Terahertz single pixel imaging with an optically controlled dynamic spatial light modulator. Opt. Express 2013, 21, 12507–12518. [Google Scholar] [CrossRef]
- Stantchev, R.I.; Sun, B.; Hornett, S.M.; Hobson, P.A.; Gibson, G.M.; Padgett, M.J.; Hendry, E. Noninvasive, near-field terahertz imaging of hidden objects using a single-pixel detector. Sci. Adv. 2016, 2, e1600190. [Google Scholar] [CrossRef] [Green Version]
- Greenberg, J.; Krishnamurthy, K.; Brady, D. Compressive single-pixel snapshot x-ray diffraction imaging. Opt. Lett. 2014, 39, 111–114. [Google Scholar] [CrossRef]
- Pelliccia, D.; Rack, A.; Scheel, M.; Cantelli, V.; Paganin, D.M. Experimental x-ray ghost imaging. Phys. Rev. Lett. 2016, 117, 113902. [Google Scholar] [CrossRef] [Green Version]
- Klein, Y.; Schori, A.; Dolbnya, I.; Sawhney, K.; Shwartz, S. X-ray computational ghost imaging with single-pixel detector. Opt. Express 2019, 27, 3284–3293. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liu, S.; Peng, J.; Yao, M.; Zheng, G.; Zhong, J. Simultaneous spatial, spectral, and 3D compressive imaging via efficient Fourier single-pixel measurements. Optica 2018, 5, 315–319. [Google Scholar] [CrossRef]
- Bian, L.; Suo, J.; Situ, G.; Li, Z.; Fan, J.; Chen, F.; Dai, Q. Multispectral imaging using a single bucket detector. Sci. Rep. 2016, 6, 24752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hahn, J.; Debes, C.; Leigsnering, M.; Zoubir, A.M. Compressive sensing and adaptive direct sampling in hyperspectral imaging. Digit. Signal Process. 2014, 26, 113–126. [Google Scholar] [CrossRef]
- Yi, Q.; Heng, L.Z.; Liang, L.; Guangcan, Z.; Siong, C.F.; Guangya, Z. Hadamard transform-based hyperspectral imaging using a single-pixel detector. Opt. Express 2020, 28, 16126–16139. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Gong, W.; Shen, X.; Han, S. Correlated imaging through atmospheric turbulence. Phys. Rev. A 2010, 82, 033817. [Google Scholar] [CrossRef] [Green Version]
- Dixon, P.B.; Howland, G.A.; Chan, K.W.C.; O’Sullivan-Hale, C.; Rodenburg, B.; Hardy, N.D.; Shapiro, J.H.; Simon, D.; Sergienko, A.; Boyd, R.; et al. Quantum ghost imaging through turbulence. Phys. Rev. A 2011, 83, 051803. [Google Scholar] [CrossRef] [Green Version]
- Leihong, Z.; Zhixiang, B.; Hualong, Y.; Zhaorui, W.; Kaimin, W.; Dawei, Z. Restoration of Single pixel imaging in atmospheric turbulence by Fourier filter and CGAN. Appl. Phys. B 2021, 127, 45. [Google Scholar] [CrossRef]
- Jauregui-Sánchez, Y.; Clemente, P.; Lancis, J.; Tajahuerce, E. Single-pixel imaging with Fourier filtering: Application to vision through scattering media. Opt. Lett. 2019, 44, 679–682. [Google Scholar] [CrossRef] [Green Version]
- Soltanlou, K.; Latifi, H. Three-dimensional imaging through scattering media using a single pixel detector. Appl. Opt. 2019, 58, 7716–7726. [Google Scholar] [CrossRef]
- Seow, K.L.C.; Török, P.; Foreman, M.R. Single pixel polarimetric imaging through scattering media. Opt. Lett. 2020, 45, 5740–5743. [Google Scholar] [CrossRef]
- Deng, H.; Wang, G.; Li, Q.; Sun, Q.; Ma, M.; Zhong, X. Transmissive Single-Pixel Microscopic Imaging through Scattering Media. Sensors 2021, 21, 2721. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.H. A test of a new type if stellar interferometer on sirius. Nature 1956, 178, 1046–1048. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhao, H.; Jiang, W.; Zhang, Z.; Sun, B. A Single-Pixel Imaging Scheme with Obstacle Detection. Photonics 2022, 9, 253. https://doi.org/10.3390/photonics9040253
Li P, Zhao H, Jiang W, Zhang Z, Sun B. A Single-Pixel Imaging Scheme with Obstacle Detection. Photonics. 2022; 9(4):253. https://doi.org/10.3390/photonics9040253
Chicago/Turabian StyleLi, Peiming, Haixiao Zhao, Wenjie Jiang, Zexin Zhang, and Baoqing Sun. 2022. "A Single-Pixel Imaging Scheme with Obstacle Detection" Photonics 9, no. 4: 253. https://doi.org/10.3390/photonics9040253
APA StyleLi, P., Zhao, H., Jiang, W., Zhang, Z., & Sun, B. (2022). A Single-Pixel Imaging Scheme with Obstacle Detection. Photonics, 9(4), 253. https://doi.org/10.3390/photonics9040253




