A Full-Aperture Image Synthesis Method for the Rotating Rectangular Aperture System Using Fourier Spectrum Restoration

Abstract

The novel rotating rectangular aperture (RRA) system provides a good solution for space-based, large-aperture, high-resolution imaging tasks. Its imaging quality depends largely on the image synthesis algorithm, and the mainstream multi-frame deblurring approach is sophisticated and time-consuming. In this paper, we propose a novel full-aperture image synthesis algorithm for the RRA system, based on Fourier spectrum restoration. First, a numerical simulation model is established to analyze the RRA system’s characteristics and obtain the point spread functions (PSFs) rapidly. Then, each image is used iteratively to calculate the increment size and update the final restored Fourier spectrum. Both the simulation’s results and the practical experiment’s results show that our algorithm performs well in terms of objective evaluation and time consumption.

1. Introduction

In the field of remote sensing, a large-aperture optical system is needed to obtain high-quality and high-spatial-resolution images [1]. However, the size, weight, and power (SWaP) of traditional optical payloads cannot meet the launching requirements [2]. Recently, several novel imaging principles have been proposed to solve this problem, such as synthetic aperture (SA) imaging [3] and segmented planar interference (SPI) imaging [4]. However, due to the difficulty of phase matching between different apertures, SA technology still cannot be applied in remote sensing [5,6]. The cutting-edge SPI imaging system is still in the experimental verification stage, and the corresponding image restoration method is also not mature [7,8,9].

Compared with the imaging principles mentioned above, a better solution is the rotating rectangular aperture (RRA) imaging approach (see Figure 1a for a structure diagram). It uses a rotating primary mirror with a large aspect ratio to obtain sequence images. They contain complementary high-resolution information in different directions, as shown in Figure 1b. By utilizing the image synthesis algorithm, the RRA system can achieve almost the same imaging quality as an equivalent circular aperture system. In this way, the system’s SwaP is greatly reduced. With improvements in the synthesis algorithm, the RRA system will play an important role in future high-resolution remote sensing tasks. [10,11,12].

Due to the mechanism of rotational imaging, the whole image acquisition process of the RRA system is time-consuming. Thus, an effective image synthesis method is necessary to deal with the RRA sequence images. Since each frame contains part of the target’s spectrum information, an intuitive approach is to take the maximum part in the Fourier domain [13], but the result is not satisfactory. Existing image synthesis algorithms, such as spatial domain algorithms (based on significance detection) and transform domain algorithms (based on wavelet decomposition and principal component analysis), are not suitable for RRA image synthesis tasks, because most of them are designed to solve multi-focus or multispectral image fusion problems [14,15,16,17,18,19]. Other studies used the RRA system for star detection, and the Fourier domain matched filter algorithm was developed to maximize the signal-to-noise ratios (SNR) of the synthetic images and reach maximal contrast when finding faint companions around bright stars [20,21,22]. However, the overall clarity of the matched filter results is not satisfactory. Zhi [23] established an iterative restoration method of RRA images, but it is time-consuming because each frame’s point spread function (PSF) and gradient histogram need to be calculated. Zhou [24] synthesized RRA images using the multi-frame blinding deconvolution principle with a hyper-Laplacian prior, but the results showed few artifacts and the running time was also very long.

Multi-frame deblurring [25] methods can also be used to synthesize RRA images. They estimate the expected clear image under a Bayesian probability or maximum a posteriori probability framework. Optimization methods based on regularization priors are used, and different regularization constraints were invented to optimize the deblurring result, such as the total variation (TV) regularization, which preserves edges better [26], and sparse representation (L0 or L1 norm, etc.) which suppress the ringing effect better [27,28]. In addition, the hyper-Laplacian prior [29,30] and dark channel prior [31] have also been proven to have excellent performance. However, because multiple iterations are needed to solve for the PSFs and the latent clear image alternately, multi-frame deblurring algorithms are time-consuming. Furthermore, the tuning of hyper-parameters is also empirical.

Fourier ptychography imaging [32] is much alike RRA imaging. They both capture complementary sequence images and synthesize a high-resolution result. Inspired by this, a Fourier domain image synthesis algorithm based on Fourier spectrum restoration is proposed in this paper. First, a numerical simulation model is established to analyze the RRA system’s imaging mechanism and acquire the system’s PSF. This can save time for PSF estimation. Then, the sequence images are synthesized iteratively in the Fourier domain to maintain texture details. The use of an adaptive updating step size can make the image synthesis algorithm converge quickly. By introducing regularization constraints, even sequence images with significant noise can have high-quality synthesis results. This was the first time that the Fourier spectrum restoration method was applied to synthesize RRA sequence images. The simulation and practical experimental results verified the effectiveness of the proposed method and showed that our algorithm has excellent performance in terms of both subjective and objective evaluations.

The rest of the paper is organized as follows: Section 2 introduces the imaging mechanism and characteristics of the RRA system. In Section 3, the numerical simulation model and the proposed image synthesis algorithm based on Fourier spectrum restoration are described in detail. In Section 4, the effectiveness of the proposed algorithm is shown through both a simulation and practical experiments. Finally, we summarize the main work in this paper and put forward a prospect of RRA imaging.

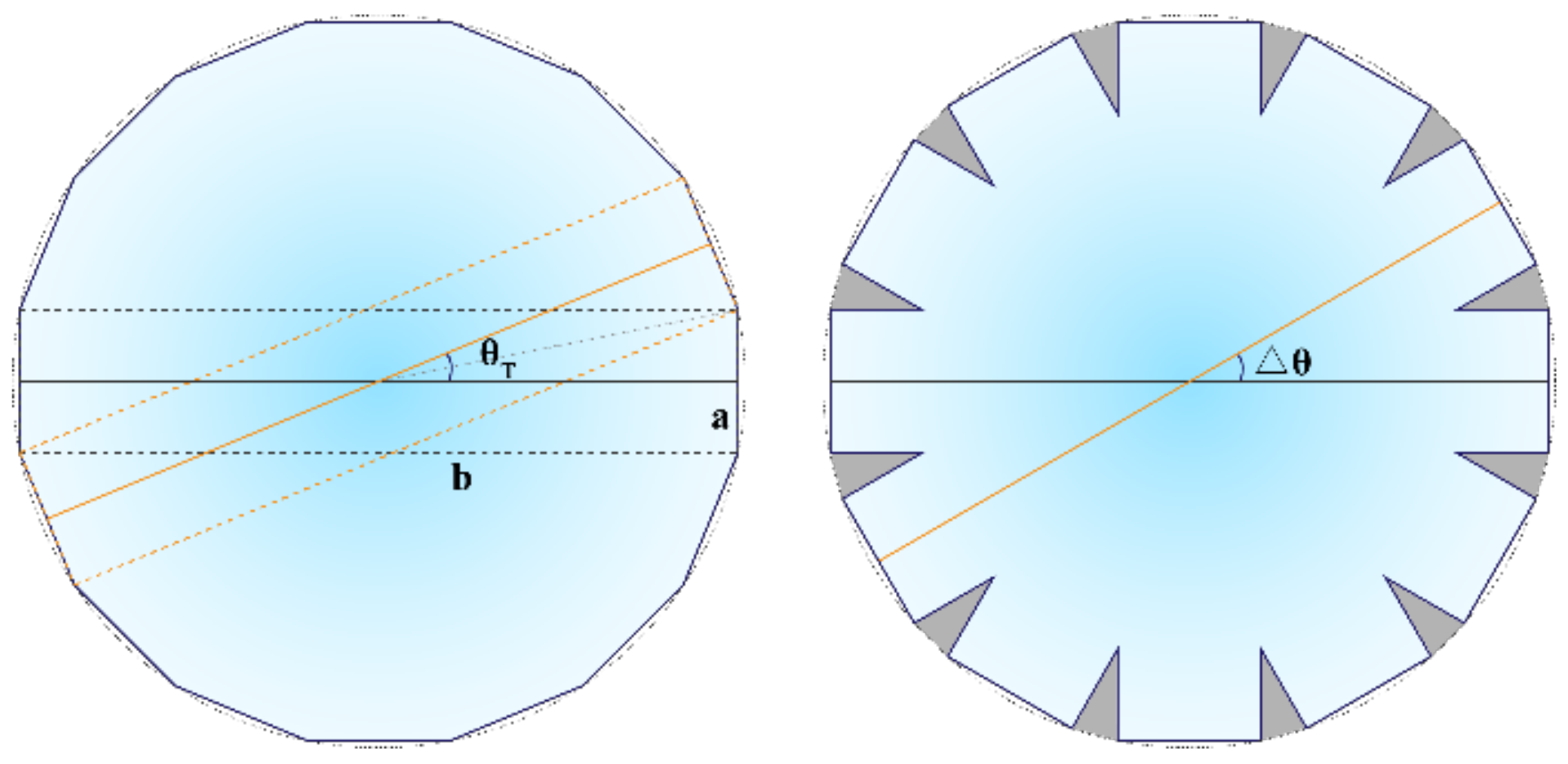
2. Imaging Mechanism of the Rotating Rectangular Aperture (RRA) System

The RRA system’s simplified imaging principle is shown in Figure 2. Its imaging process can be modeled as the convolution of the PSF and the clear target:

$$I=T\ast PSF+n$$

(1)

where $I$ stands for the captured image, $T$ is the target, n represents additive noise, and $\ast$ is the two-dimensional convolution operator.

The PSF determines the RRA system’s imaging characteristics. Differently from the conventional circular aperture, the RRA system’s aperture $P\left(\xi ,\eta \right)$ is rectangular:

$$P\left(\xi ,\eta \right)=\left\{\begin{array}{ll}1,& 0\le \xi \le w and 0\le \eta \le h\\ 0,& else\end{array}\right.$$

(2)

Here, $\left(\xi ,\eta \right)$ represents spatial coordinates; $w$ and $h$ represent the width and height of the aperture, respectively. According to Fourier optics theory, the RRA system’s PSF $h_R\left(x^{\prime },y^{\prime }\right)$ is the energy of the aperture’s Fraunhofer diffraction pattern:

$$h_R\left(x^{\prime },y^{\prime }\right)={\left|e^{i\phi }{\displaystyle \underset{D}{\iint }P\left(\xi ,\eta \right)\exp \left[-i2\pi \left(\frac{x^{\prime }}{\lambda l^{\prime }}\xi +\frac{y^{\prime }}{\lambda l^{\prime }}\eta \right)\right]d\xi d\eta }\right|}^2={\left|F\left\{P\left(\xi ,\eta \right)\right\}\right|}^2$$

(3)

Equation (1) is cited from [33]. Here, $\lambda$ is the working wavelength, $l^{\prime }$ is the imaging distance, $\left(x^{\prime },y^{\prime }\right)$ represents spatial coordinates, and $\phi =i\pi \left(x{\prime }^2+y{\prime }^2\right)/\lambda l^{\prime }$.$F\left\{\right\}$ is the Fourier transform operator.

Using the above derivation, the PSF of the RRA system can be obtained. Here, paraxial optics theory is applied, and we assume the system’s PSFs are spatially-invariant. Figure 3 compares the PSF and optical transfer function (OTF, Fourier transform of PSF) of a 0.5 m diameter circular aperture and a 5:1 aspect ratio, 0.5m long rectangular aperture:

The circular aperture’s PSF is isotropic. In contrast, the PSF and OTF of the RRA system share the same asymmetry of the aperture. Still, as long as enough images are captured with the primary mirror at different angles, the RRA system can acquire sufficient spectral information in every direction. In fact, the RRA system has a higher resolution than the equivalent traditional system. Traditional circular aperture system’s angular resolution ${\theta }_D$ depends on its diameter $D$:

$${\theta }_D=1.22\lambda /D$$

(4)

$\lambda$ refers to the working wavelength. This is exactly the central bright spot’s angular radius in the circular aperture’s Fraunhofer diffraction pattern. For the rectangular RRA system with the aperture length $X$ and width $Y$, the corresponding central bright spot’s angular radii ${\theta }_x$ and ${\theta }_y$ are calculated as follows:

$$\left\{\begin{array}{l}{\theta }_x=\lambda /X\\ {\theta }_y=\lambda /Y\end{array}\right.$$

(5)

Comparing (2) and (3), if d equals $D$, the following equation can be derived:

$${\theta }_D=1.22{\theta }_x$$

(6)

Thus, the RRA system’s PSF is 1.22 times sharper than the equivalent circular aperture system’s PSF, as shown in Figure 4. By combining the image synthesis process, the RRA system’s fundamental physical advantage is utilized, and it can achieve 1.22 times higher resolution.

In practice, the RRA system’s primary mirror can be long enough to increase the collecting area and thus maintain high imaging SNR in a single frame. For example, a 20 × 2.5 m rectangular aperture has the same single frame SNR as an 8 m circular aperture [10]. For general random additive noise, the multi-frame synthesis operation can further improve the SNR of the synthetic result by $\sqrt{N}$ times, where $N$ is the frame number.

Since each frame only contains part of the target’s information, a minimum number of images should be captured to synthesize an image of high resolution. To sample enough spatial frequency information in all directions, the angular interval of the adjacent frames $\Delta \theta$ should be less than the threshold ${\theta }_T$. Here, ${\theta }_T$ is the included angle of the diagonals of the rectangular aperture, as shown in Figure 5a. d can be calculated using Equation (7):

$${\theta }_T=2\cdot \arctan \left(\frac{a}{b}\right)$$

(7)

Here, $a$ and $b$ are the width and length of the rectangular aperture, respectively. Figure 5 shows the RRA system’s equivalent synthetic aperture when $\Delta \theta ={\theta }_T$ and $\Delta \theta >{\theta }_T$. It can be seen that in the former case (Figure 5a), the synthetic aperture forms complete regular hexadecimal. However, in the latter case (Figure 5b), the synthetic aperture cannot cover the gray triangular areas, and the spatial frequency information in these directions is missing. This will lead to a degradation in the resolution of the final synthesized image.

Thus, to reconstruct a high-resolution synthesized image, at least $N_{\min }$ images with equal angular intervals should be captured:

$$N_{\min }=ceil\left(\frac{180°}{{\theta }_T}\right)=ceil\left(\frac{90°}{\arctan \left(a/b\right)}\right)$$

(8)

Here, $ceil$ is the round-up operator. For a 5:1 aspect ratio RRA system, $N_{\min }=8$.

3. Full-Aperture Image Synthesis Algorithm Based on PSF Simulation and Fourier Spectrum Restoration

According to the analysis in Section 2, different RRA sequence images contain different parts of the target’s spectrum information. Inspired by this, we designed an image synthesis algorithm for the RRA system, based on Fourier spectrum restoration. A flow chart of the algorithm is shown in Figure 6.

In every iteration, each image is used successively to calculate the spectrum update increment, and the current frame’s influence on the final spectrum is limited (area-wise) by the corresponding OTF. To enhance high-frequency components and suppress noise, the spectrum update increment is processed by the regularized least square (RLS) filter and then added to the latent image’s spectrum. The reconstructed spectrum is obtained when a specific number of iterations are finished. The proposed algorithm is a non-blind method, and the OTF can be acquired quickly through a numerical simulation. The following sections explain the numerical simulation model of the RRA system and the Fourier spectrum restoration algorithm in detail.

3.1. PSF Acquirement Using the Numerical Simulation Model of the RRA System

The PSFs of RRA sequence images differ only in angle, so there is no need to estimate each frame’s PSF using the deblurring approach. Given the aperture length $X$, width $Y$, focal length $f$, working wavelength $\lambda$, sensor pixel size $d$, sensor pixel number $m$, and $n$, the RRA system’s imaging characteristics can be determined. According to Fourier optics theory, the system’s cutoff frequency in the length direction $C{F}_{cutX}$ and width direction d can be calculated as follows:

$$\left\{\begin{array}{l}C{F}_{cutX}=X/\lambda \sqrt{X^2+4f^2}\\ C{F}_{cutY}=Y/\lambda \sqrt{Y^2+4f^2}\end{array}\right.$$

(9)

where $\lambda$ is the system’s working wavelength. Then the coherent transfer function (CTF) is a band-pass filter:

$$CTF\left(u,v\right)=\left\{\begin{array}{ll}1,& \left|u\right|\le C{F}_{cutX}\&\left|v\right|\le C{F}_{cutY}\\ 0,& else\end{array}\right.$$

(10)

Here, $\left(u,v\right)$ represents spatial frequency coordinates. Using the inverse Fourier transform $F^{-1}\left\{\right\}$ and Equation (1), the system’s PSF can be calculated as follows:

$$PSF\left(x,y\right)={\left(F^{-1}\left\{CTF\left(u,v\right)\right\}\right)}^2$$

(11)

Using Equation (9), when the primary mirror rotates an angle $\Delta {\theta }_0$, the corresponding $PS{F}_{\Delta {\theta }_0}$ can be acquired by rotating $CTF\left(u,v\right)$ the same angle to get $CT{F}_{\Delta {\theta }_0}\left(u,v\right)$.

The numerical simulation model for the RRA system has been successfully established. Given all the parameters needed, the simulation model will return the corresponding PSF.

Table 1. Structural parameters of the built RRA prototype.

System’s Structural Parameters	Value
Rectangular aperture length X and width Y	0.1 m, 0.02 m
System’s focal length f	0.7m
Working wavelength λ	550 nm
Rotation angle interval $\Delta {\theta }_0$	10°
sensor pixel size d, row number $m$ and column number $n$	3.45 μm, 3000, 4096
Sequence images frame number $k$	18

gives the structural parameters of the built RRA prototype:

Figure 7 shows the CTF patterns and the corresponding PSF patterns with the primary mirror rotations 0°, 45°, 90°, and 135° clockwise. It can be seen that the rotation angles of the PSF and the primary mirror are the same.

Algorithm 1 summarizes the main procedure of a PSF’s numerical simulation.

Algorithm 1 A PSF numerical simulation model for the RRA system.

required: Aperture length $X$ and width $Y$, focal length $f$, rotation angle interval $\Delta {\theta }_0$

required: working wavelength $\lambda$, sensor pixel size $d$ and number $m$, $n$, frame number $k$

1: initialization $X=0.1m$, $Y=0.02m$, $f=0.7m$, $\lambda =5.5\times {10}^{-7}m$, $d=3.45\times {10}^{-6}m$, $m=3000$, $n=4096$

2: Calculate $C{F}_{cutX}$, $C{F}_{cutY}$ using Equation (7), then calculate $CT{F}_1\left(u,v\right)$ using Equation (8)

3: Calculate $PS{F}_1\left(x,y\right)$ using Equation (9)

4: for $j=2:k$ do

Given $\Delta {\theta }_0$, calculate ${\theta }_j=\left(j-1\right)\cdot \Delta {\theta }_0$

Given $CT{F}_1\left(u,v\right)$, calculate $CT{F}_j\left(u,v\right)$ using the affine transformation

Given $CT{F}_j\left(u,v\right)$, calculate $PS{F}_j\left(x,y\right)$ using Equation (9)

end for

5: return the simulated PSF sequence $PS{F}_j\left(x,y\right), j=1,2,\dots k$

3.2. Full-Aperture Image Synthesis Based on Fourier Spectrum Restoration

After the RRA sequence images $I_j^O$ and $PS{F}_j,j=1,2,\dots k$ are obtained, the image synthesis algorithm is used to get the reconstructed spectrum $F_{j,p}^H$ and the synthesized image $I_{j,p}^H$. The subscripts $j$ and $p$ refer to the $j th$ frame and $p th$ iteration. An iteration is completed when all the $k$ frames are used once. First, $I_{0,1}^H$ is initialized as the mean value of $I_j^O$, and the original spectrum $F_{0,1}^H$ to be reconstructed is calculated using the Fourier transform:

$$I_{0,1}^H={\displaystyle \sum _{j=1}^k{I}_j^O}/k, F_{0,1}^H=F\left\{I_{0,1}^H\right\}$$

(12)

Next, an estimated image $I_{j,p}^E$ is derived by extracting the corresponding spectrum from $F_{j-1,p}^H$ using the $j th$ OTF. Usually, $I_{j,p}^E$ is in the plural form. Then, following the intensity correction concepts [34], only the amplitude of $I_{j,p}^E$ is replaced by the $j th$ frame $I_j^O$, and an updated image d is acquired:

$$I_{j,p}^E{=\mathrm{F}}^{-1}\left\{F_{j-1,p}^H\cdot OT{F}_j\right\}, I_{j,p}^U=I_j^O\cdot I_{j,p}^E/\left|I_{j,p}^E\right|$$

(13)

Here, ${\mathrm{F}}^{-1}\left\{\right\}$ is the inverse Fourier transform operator. To make the reconstructed spectrum fully preserve high-resolution information in each frame, the difference between $I_{j,p}^U$ and $I_{j,p}^E$ should be as small as possible. Thus, the cost function ${\epsilon }_{j,p}$ for optimization uses the spectra of $I_{j,p}^U$ and $I_{j,p}^E$ to calculate their mean square error:

$${\epsilon }_{j,p}={\left|F\left\{I_{j,p}^U\right\}-F\left\{I_{j,p}^E\right\}\right|}^2={\left|F_{j,p}^U-F_{j-1,p}^H\cdot OT{F}_{j,p}\right|}^2$$

(14)

Then, the first derivative of ${\epsilon }_{j,p}$ for $F_{j,p}^H$ is calculated:

$$\nabla {\epsilon }_{j,p}=\frac{\partial {\epsilon }_{j,p}}{\partial F_{j,p}^H}=-2\cdot OT{F}_j^{*}\cdot \left(F_{j,p}^U-F_{j-1,p}^H\cdot OT{F}_j\right)$$

(15)

Using the gradient descent method, the spectrum increment $\Delta F_{{}^{j,p}}^H$ equals the product of the step size d, normalized OTF, and negative gradient $-\nabla {\epsilon }_{j,p}$: $\Delta F_{{}^{j,p}}^H=-\alpha \cdot OT{F}_j\cdot \nabla {\epsilon }_{j,p}$. Normally, $\alpha$ is a fixed value (for example,$\alpha =1$). The OTF term weights the spectrum increment and limits its area of influence on $F_{j,p}^H$. This weight operation is equivalent to a low-pass filtering process, which can cause a loss of high-frequency components.

To recover the missing information, we adopt the RLS filter deconvolution method. To suppress noise and ringing artifacts, our method uses the image’s second-order difference as the regularization term, which is the convolution of the image and the Laplacian operator $l$. Usually, $l=\left[0,-1,0;-1,4,-1;0,-1,0\right]$. In the frequency domain, given the degraded image $G$, the system’s PSF $H$, and the restored image $\widehat{F}$, the term ${‖G-H\ast \widehat{F}‖}^2$ is expected to be zero. Using the Lagrange multiplier method, the following optimization problem is established:

$$\underset{\widehat{F}}{\min } C, where C={‖L\widehat{F}‖}^2+\frac{1}{\mu }\cdot \left({‖G-H\cdot \widehat{F}‖}^2\right)$$

(16)

where $L$ stands for the Fourier transform of $l$. Let the first derivative of $C$ equal 0. Then, ${\widehat{F}}_{\min }$ that minimizes d is acquired:

$${\widehat{F}}_{\min }=\left[\frac{H*}{{‖H‖}^2+\mu {‖L‖}^2}\right]G$$

(17)

where $\mu$ is the weight factor. By replacing $G$ with $\Delta F_{{}^{j,p}}^H$, we can use the RLS filter to process the spectrum increment and get the final updating equation:

$$F_{j,p}^H=F_{j-1,p}^H+\alpha \cdot \frac{OT{F}_j\cdot OT{F}_j^{*}}{\left({\left|OT{F}_j\right|}^2+\mu {\left|L\right|}^2\right)}\cdot \left(F_{j,p}^U-F_{j-1,p}^H\cdot OT{F}_j\right)$$

(18)

To improve the stability of our algorithm and achieve a high convergence rate, $\alpha$ is adaptively updated using the batch cost $E_p$ of $p\hspace{0.33em}th$ iteration: $E_p={\displaystyle \sum _{j=1}^k{\epsilon }_{j,p}}$. $F_{j,p}^H$ is close to the optimal solution when the reduction rate of $E_p$ is less than the threshold $T$. Hence, $\alpha$ is reduced by half for a more precise searching:

$${\alpha }_{p+1}=\left\{\begin{array}{ll}{\alpha }_p,& \left(E_{p-1}-E_P\right)/\left(E_{p-1}+\delta \right)>T\\ {\alpha }_p/2,& else\end{array}\right.$$

(19)

Here, $\delta$ is a very small constant. The algorithm stops when $p$ reaches the preset number $s$ or ${\alpha }_p<T_{\alpha }$. By applying the inverse Fourier transform to the reconstructed spectrum $F_{k,s}^H$, the final image $I_{k,s}^H$ is obtained. The entire image synthesis algorithm is summarized in Algorithm 2.

Algorithm 2 The image synthesis algorithm based on Fourier spectrum restoration for RRA system.

required: Image sequence $I_i^O$, PSF sequence $PS{F}_i$, step size ${\alpha }_1$, iteration number $s$

required: sequence frame number $k$, regularization weight $\mu$, loss threshold $T$

1: Calculate $I_{0,1}^H$, $F_{0,1}^H$ using Equation (10)

2: for $p=1:s$ do

for $j=1:k$ do

Calculate $I_{j,p}^U$ using Equation (11)

Calculate the updated $F_{j,p}^H$ using Equation (16)

end for

Update ${\alpha }_{p+1,iter}^{}$ using Equation (17), then $F_{0,p+1}^H=F_{k,p}^H$

end for

3: return the final reconstructed synthetic image $I_{k,s}^H$

4. Discussion of Simulation Results and Experimental Results

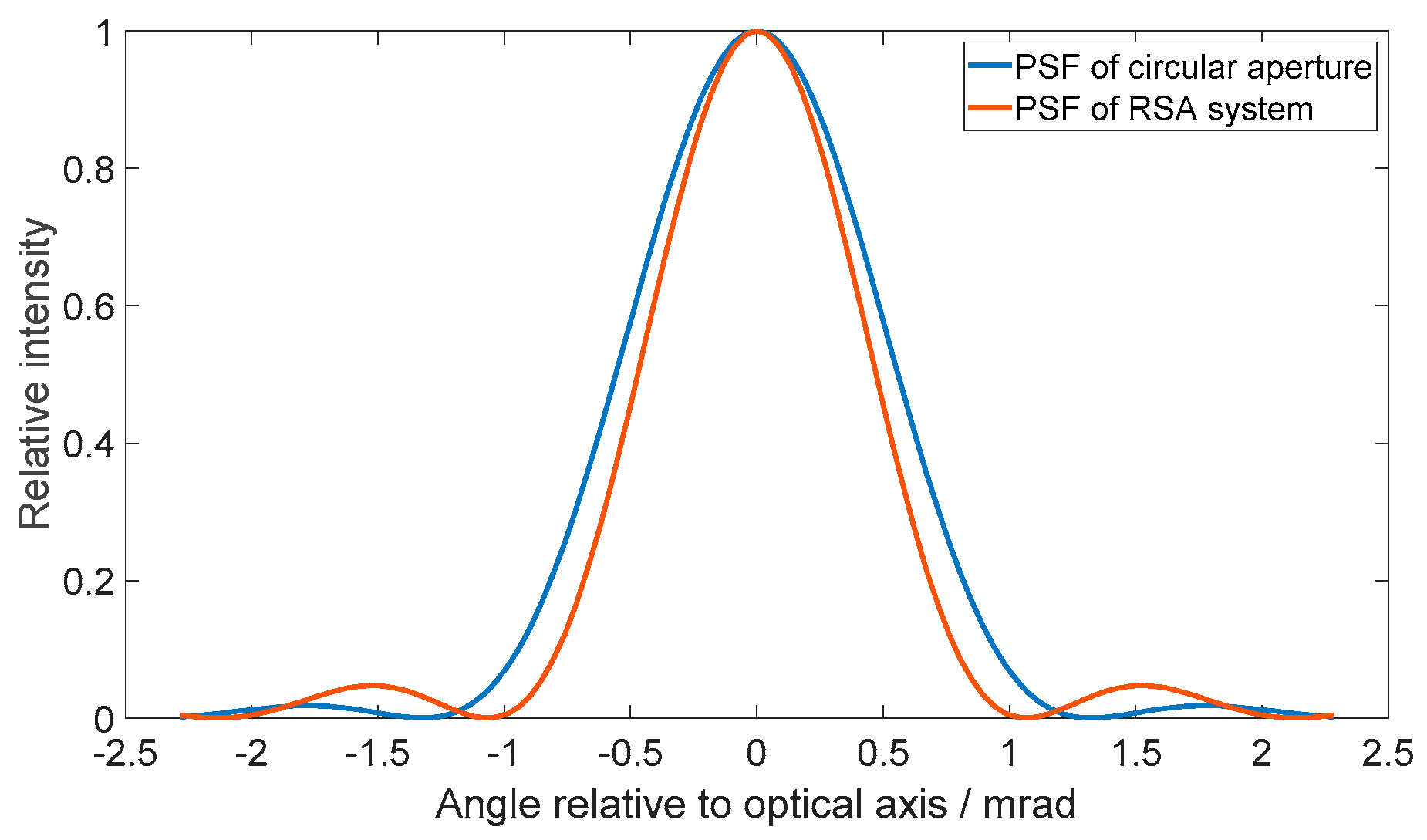
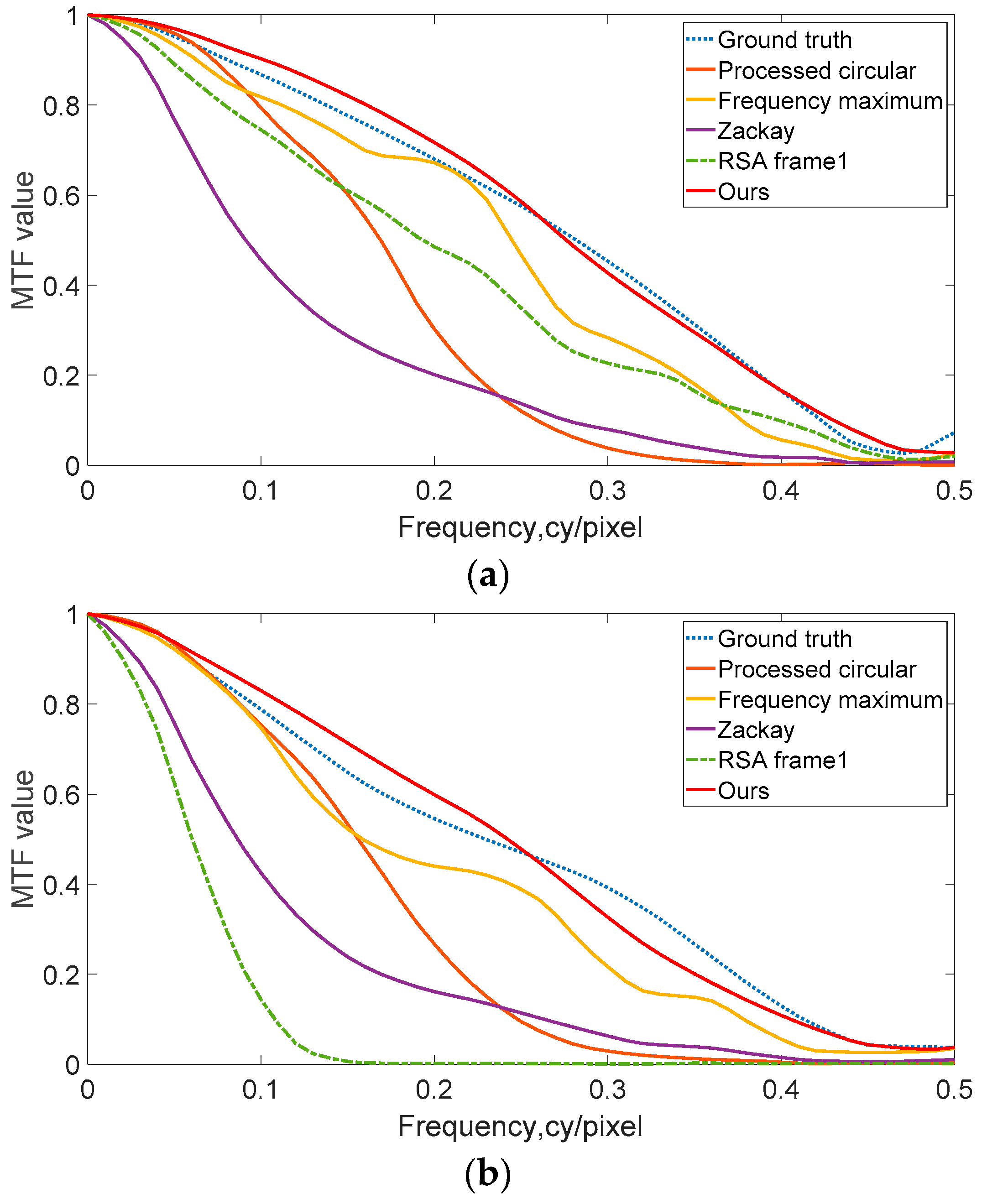
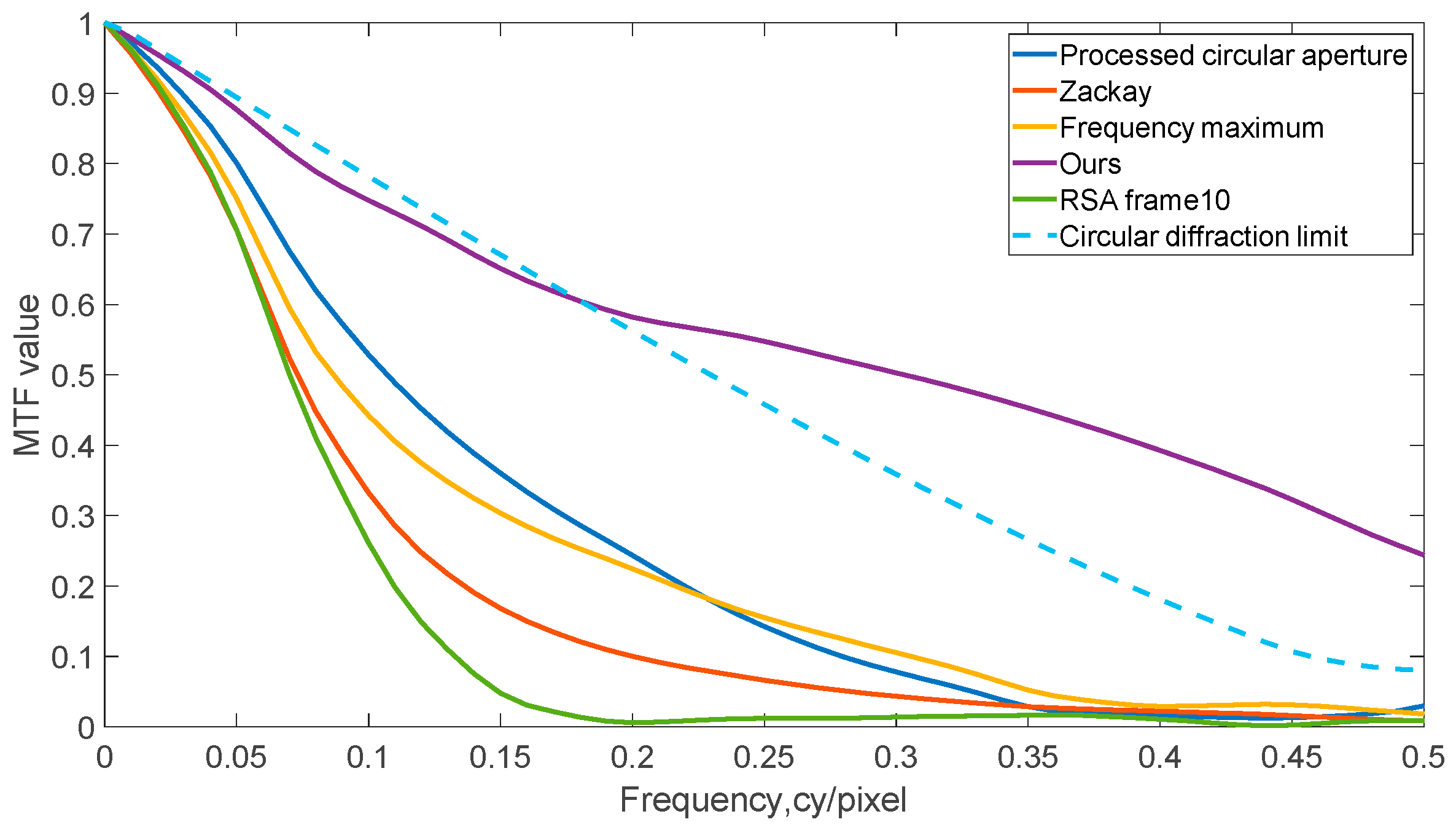
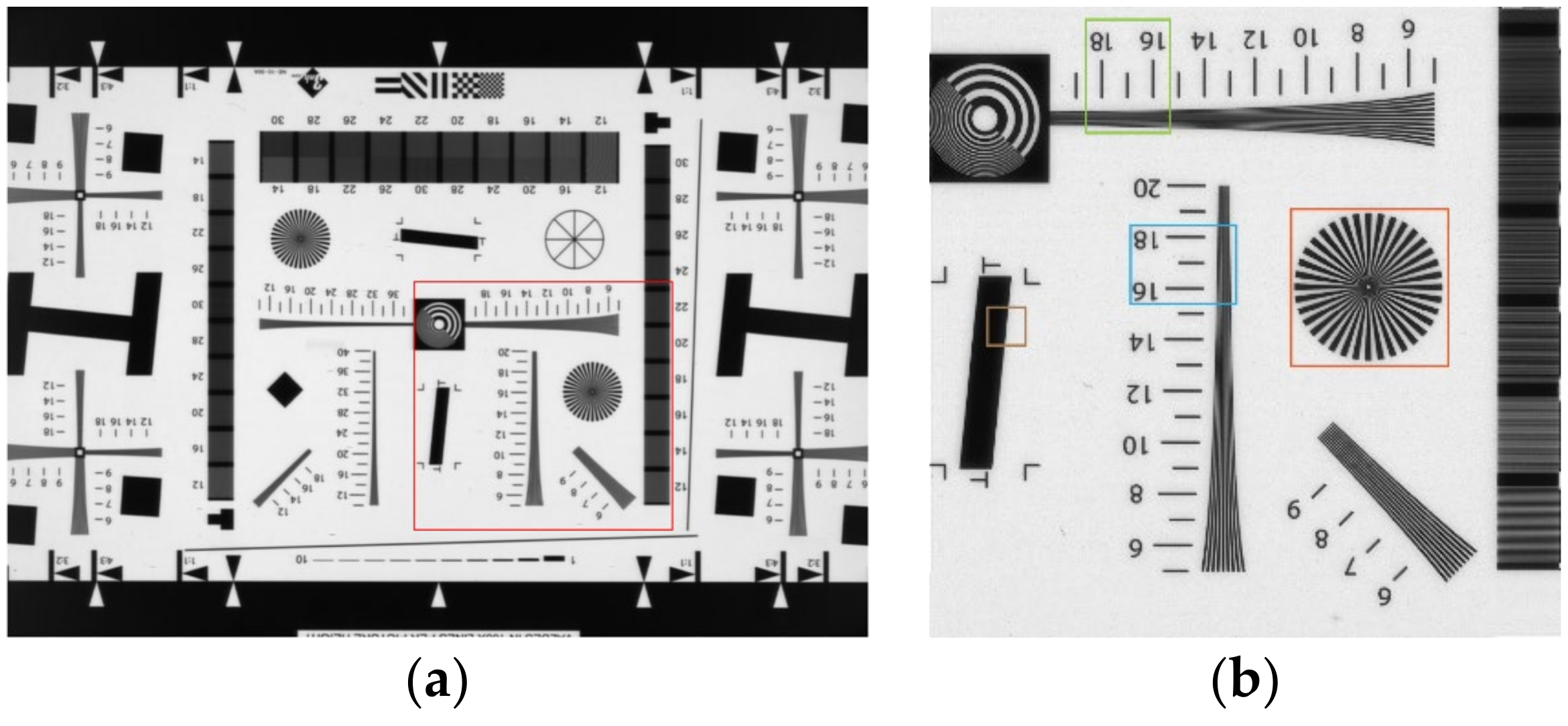
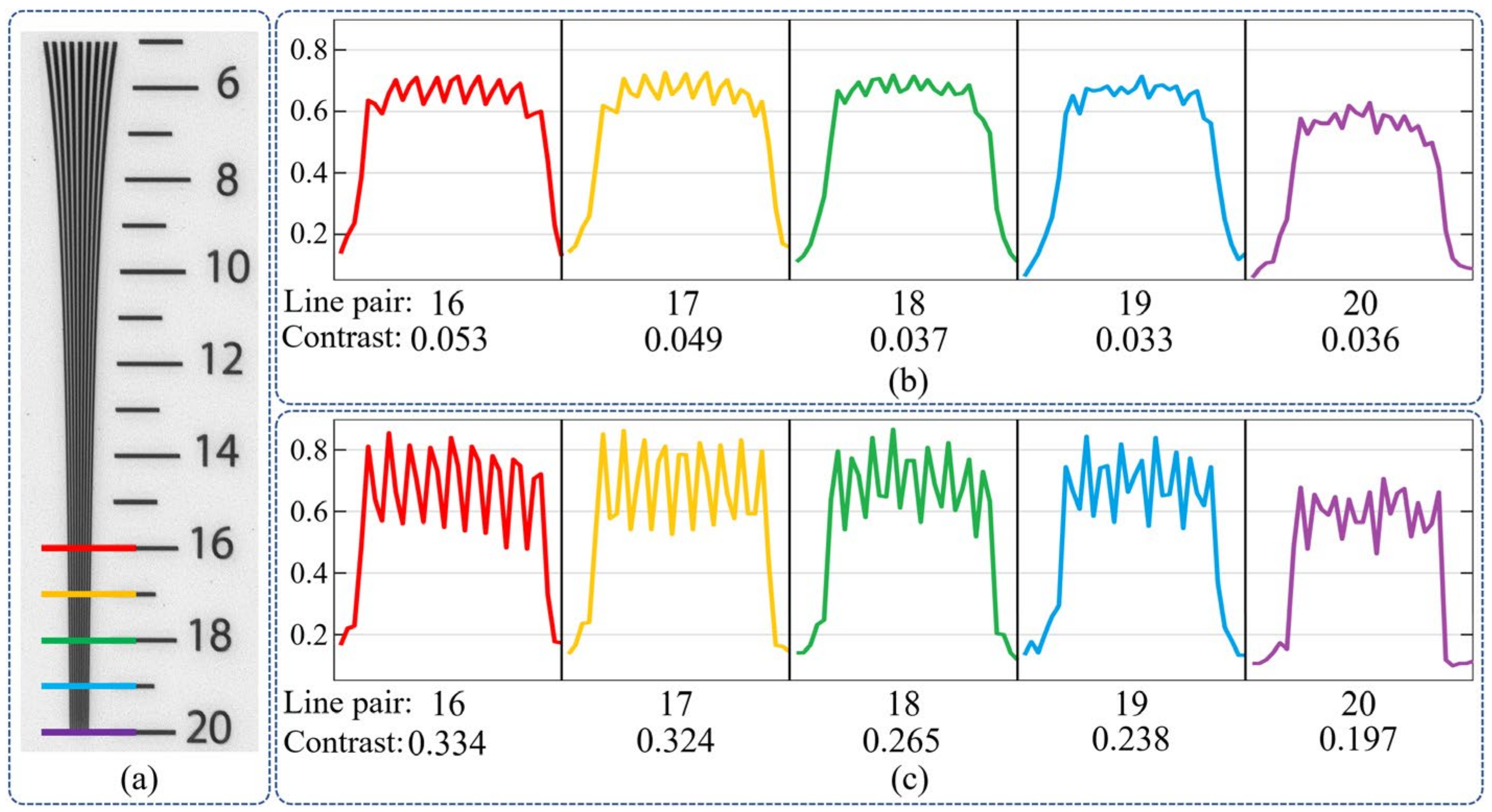
We tested the performance of our proposed algorithm through both a numerical simulation and practical experiments. We ran algorithms on a computer with a Core i5 CPU and 32GB RAM. The operating environment was MATLAB R2019a. The frequency-domain maximum method, which is intuitive and widely used [21], and Zackay’s matched filter algorithm, which can acquire the highest SNR [22], were used as comparison algorithms. All the methods were non-blind. We believe Fourier spectrum restoration can achieve better image clarity than the matched filter, and the RLS filter can solve the noise amplification problem of the maximum operation. We selected the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) as the results’ quality evaluation indicators and compared the running time of different algorithms.

4.1. Numerical Simulation Results

RRA sequence images were obtained by convolving a target image with the simulated PSFs. The structural parameters of the simulated system were the same as those of the prototype. The focal length was 0.7m, and the aperture was 0.5m long and 0.1m wide. A sequence of 18 images was obtained, and to each image was added 0 mean value, 0.01 variance Gaussian white noise. We also simulated the imaging result of an equivalent circular aperture system.

Algorithm 2 was implemented to synthesize the images. The corresponding parameters were initialized as follows: ${\alpha }_1=1$, $m=6$, $n=18$, $\lambda =1000$, $T=0.02$, $E_0=0$, $\delta =1\times {10}^{-10}$. The Fourier spectrum restoration procedure of our algorithm is shown in Figure 8.

To make the results more convincing, the RLS filter was also used to process the circular aperture system’s image. A comparison of different methods’ results is shown in Figure 9.

The maximum method preserved details well but failed to suppress noise, because the maximum operation fused not only the high-frequency information, but also the high-frequency noise. Zackay’s method was designed to achieve the highest SNR in the synthesized image by using the weighted summation in the Fourier domain, but this operation limited the restoration of high-frequency information. Thus, the result of Zackay’s method has a very low noise level, but the overall clarity is not satisfying. In contrast, our result resulted in the best visual quality. Thanks to the designed multi-frame method, both the sharpness and the noise level of our result are better than those of the circular aperture image. This verifies the physical advantage of the RRA system in resolution and multi-frame denoising. To quantitatively analyze the performance of our method, the image evaluation indicators and the time costs of different methods under different scene conditions were compared. Some experimental results are listed in

Table 2. Comparison of different methods’ evaluation indicators and time costs.

Target	Pixel Resolution	Image Restoration Method	Valuation Indicators		Running Time (s)
			PSNR (dB)	SSIM
ISO12233 (2000 lines)	1500 × 1500	Processed circular	30.23	0.760	--
		Zackay’s	26.64	0.832	2.95
		Frequency Maximum	27.33	0.692	6.29
		Ours	33.78	0.872	4.52
Wharf	2250 × 2250	Processed circular	27.99	0.747	--
		Zackay’s	25.67	0.814	6.11
		Frequency Maximum	27.49	0.673	15.47
		Ours	30.91	0.890	11.72
Boat	2736 × 2736	Processed circular	29.27	0.683	--
		Zackay’s	25.07	0.794	12.65
		Frequency Maximum	27.50	0.679	27.73
		Ours	30.58	0.817	17.28

, and the best results are indicated in bold font.

Our method achieved the highest PSNR and SSIM values for each target and converged after only two iterations. Traditional methods got unsatisfying results because of less consideration for the balance between high-frequency enhancement and noise suppression. The running time was also significantly shorter than that of the frequency maximum method. The MTF curves of different results and RRA frame 1 are displayed in Figure 10. Although the MTF curve of RRA frame 1 is severely degraded and nonuniform in different directions, our method managed to get a synthesized image that has almost the same MTF curve in each direction. The MTF of our result is also closest to that of the ground truth and is a significant improvement over RRA frame 1 and the other methods’ results. Complementary high-resolution information in different frames was successfully synthesized.

We also experimented to test the relationship between the quality of the synthesized image and the number of image frames. The same RRA system with the aspect ratio 5:1 was used, and the ISO12233 image was selected as the target. The result is shown in Figure 11. For numbers of image frames smaller than eight, the PSNR of the synthesized images are low. This verifies the theoretical derivation in Section 2 that a 5:1 aspect ratio RRA system should capture at least eight images to get a high-resolution synthesized image. When the number of image frames was bigger than 18, the synthesized image’s PSNR was maximized, and there was no need to further increase the frame number. Therefore, to ensure the quality of the synthesized image and minimize the shooting time, we suggest that a 5:1 aspect ratio RRA system should capture an image sequence of 18 frames.

4.2. Practical Experiments

To test the actual performance of our algorithm, a prototype was built to perform practical experiments with, as shown in Figure 12. This optical system has a 0.1m aperture and a 0.7 m focal length. A 1.1 inch Sony imx253 monochrome CMOS sensor with 4096 × 3000 pixel resolution was used to capture images. Figure 12d shows the design drawing of a 5:1 aspect ratio rectangular aperture slice. The rotating aperture was achieved by fixing the designed aperture slice on a Zolix RAK 200 electric rotating platform.

The ISO12233 target was placed 10 meters away from the rotating aperture. Eighteen frames with a 10° angular interval are captured, and frame 1 is shown in Figure 13a. To reduce the running time, we only cut a 1200 × 1200 pixel section, as shown in Figure 13b.

We used the same parameters as described in Section 4.1, and the threshold $T_{\alpha }$ was set to 0.05. The acquired RRA sequence images were first aligned using image registration. Then, the PSF sequence was acquired. Our simulation algorithm obtained all 18 PSFs in 2.11 s. In contrast, Zhou’s [24] deblurring method took 241 seconds to complete the estimation of 18 PSFs. Finally, different image synthesis algorithms were implemented. Figure 13b shows our synthetic image, and Figure 14 compares the zoomed areas of different methods’ results.

The visual quality of our result is significantly better than those of the other two methods. The zoomed images in the green and blue boxes in Figure 13b show that our method can improve the synthesized image’s resolution. In addition, the contents of the orange boxes indicate that our synthesized image has almost the same resolution in each direction, which means the complementary information of the image sequence is fully utilized by our method. Quantitative analysis was also performed.

Table 3. Each algorithm’s running time when processing practical images.

Real Shot Target	Pixel Resolution	Image Restoration Method	Running Time (s)
ISO 12233 (4000 lines)	1200 × 1200	Zackay’s	2.75
		Frequency maximum	4.78
		Ours	4.06

compares the running time of each algorithm, and Figure 15 shows the MTF curves of different results.

The MTF value of our result is larger than that of the equivalent circular aperture’s diffraction limit when the spatial frequency is higher than 0.2 cycle/pixel. This is because the RRA system has a sharper PSF, and the multi-frame sequence images can suppress noise. Besides, our method can also enhance the target’s high-frequency component. To make the comparison more intuitive, we cut through the wedge lines as marked in Figure 16a and obtained the profiles, as shown in Figure 16b,c. Assuming the average grayscale of bright lines is Va, and the average grayscale of dark lines is Ba, the contrast of the wedge lines is calculated as follows:

$$Contrast=\left(Va-Ba\right)/\left(Va+Ba\right)$$

(20)

The processed circular aperture image failed to distinguish all nine lines at line 18. Only eight peaks could be found in the green curve of Figure 16b. Thus, the resolution of the circular aperture was only to the level of line 17. Our method achieved a much higher contrast, and the lines in line 20 were still separable. Thus, the resolution of our system is about 1.2 times higher than an equivalent circular aperture system. We also compared the final spectrum acquired by the two systems, as shown in Figure 17. Our algorithm recovered more high-frequency information, which is consistent with the visual quality of the synthetic results. This further verified the effectiveness of our method.

5. Conclusions

In this paper, we proposed a novel full-aperture image synthesis algorithm for the RRA system, based on Fourier spectrum restoration. First, a numerical simulation model was established to analyze the RRA system’s characteristics and acquire the system’s PSFs. Then, the Fourier spectrum restoration algorithm with the RLS filter was used to get synthetic results. Both the simulation and the practical experiments verified the effectiveness of our proposed method. The results showed that our algorithm greatly improved the image clarity, and had good performance in terms of objective evaluation and time consumption. This work provides a new feasible approach for solving the RRA system’s image synthesis problem, and can provide a theoretical basis and reference for the practical use of the RRA system. Our work also found that to ensure the quality of the synthesized image, 18 frames of an equal angular interval should be captured for a 5:1 aspect ratio RRA system. Further research is needed to get an appropriate aspect ratio that can obtain the best balance between the quality of the synthesized image and the sequence acquisition time. Future research should also focus on realizing multi-frame super-resolution with the RRA system using the image synthesis algorithm based on convolutional neural networks.