Self-Supervised Deep Learning for Improved Image-Based Wave-Front Sensing
Abstract
:1. Introduction
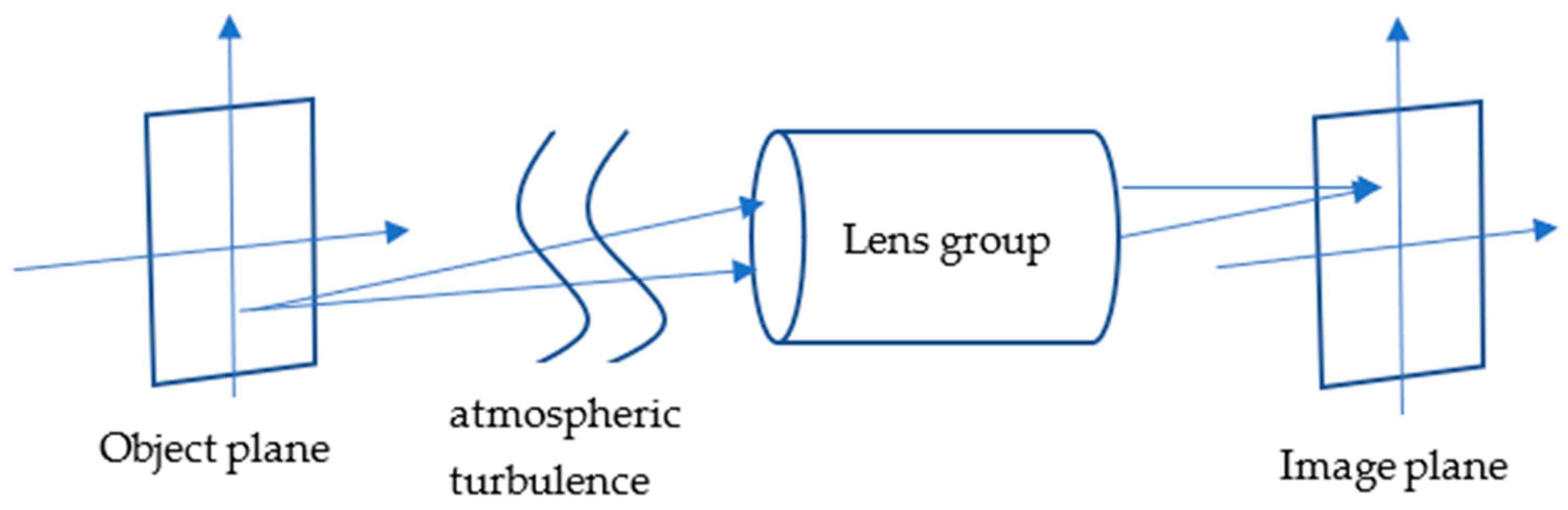
2. Method
2.1. Encoding Part
2.2. Decoding Part
2.3. Loss Function
3. Simulation Demonstration
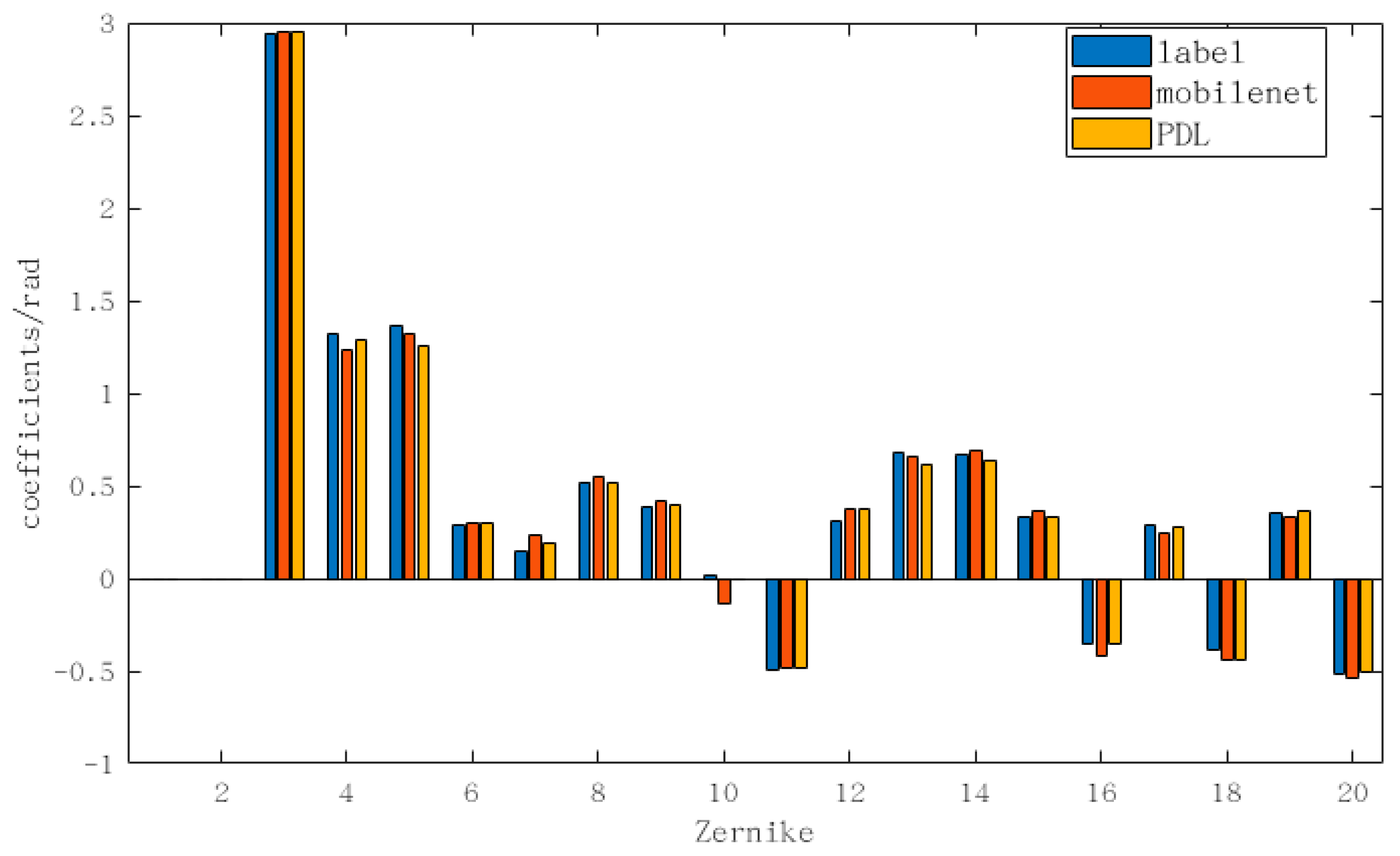
3.1. Simulation Demonstration of 3–20 Orders of Zernike Polynomials
3.2. Simulation Demonstration of 3–64 Orders of Zernike Polynomials
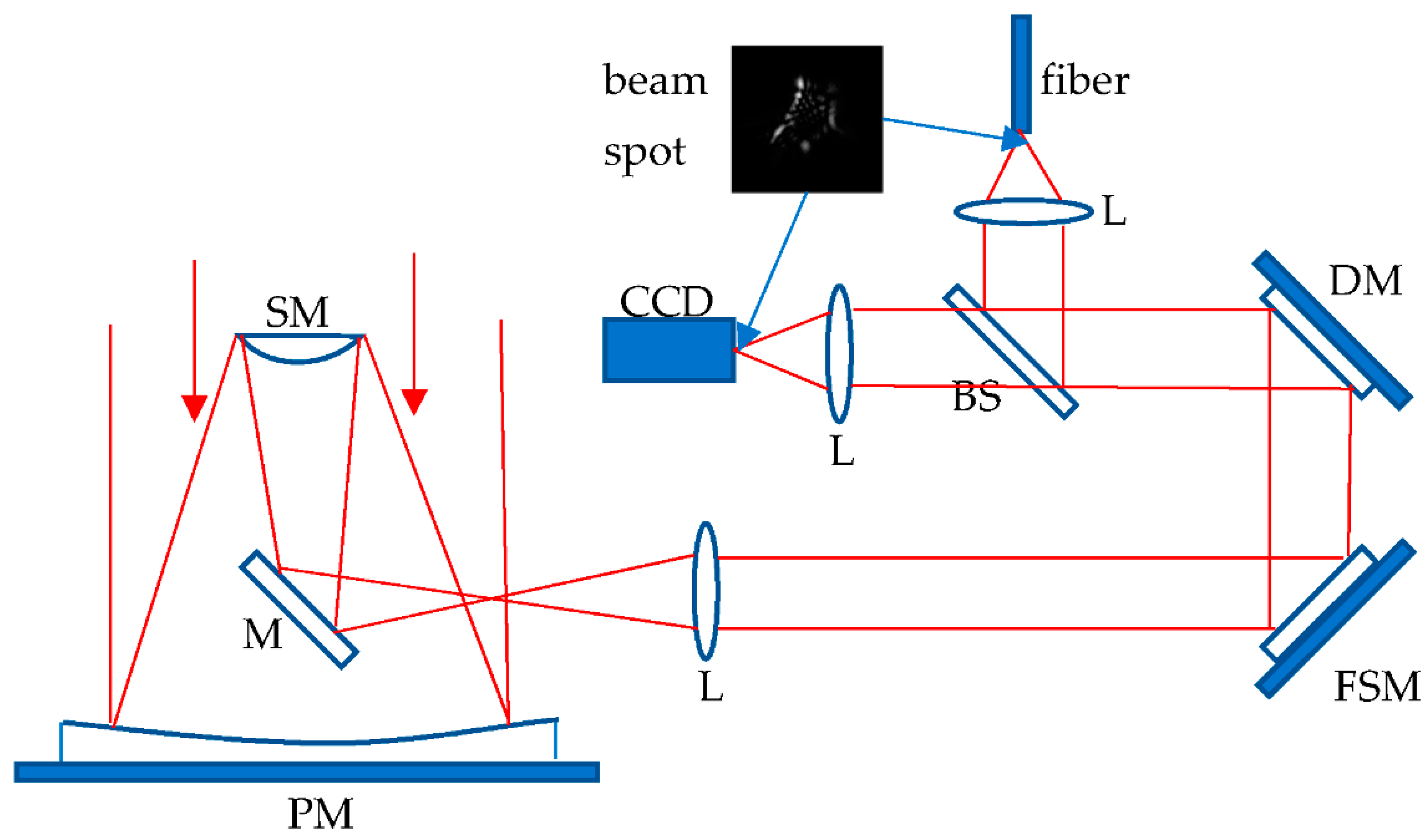
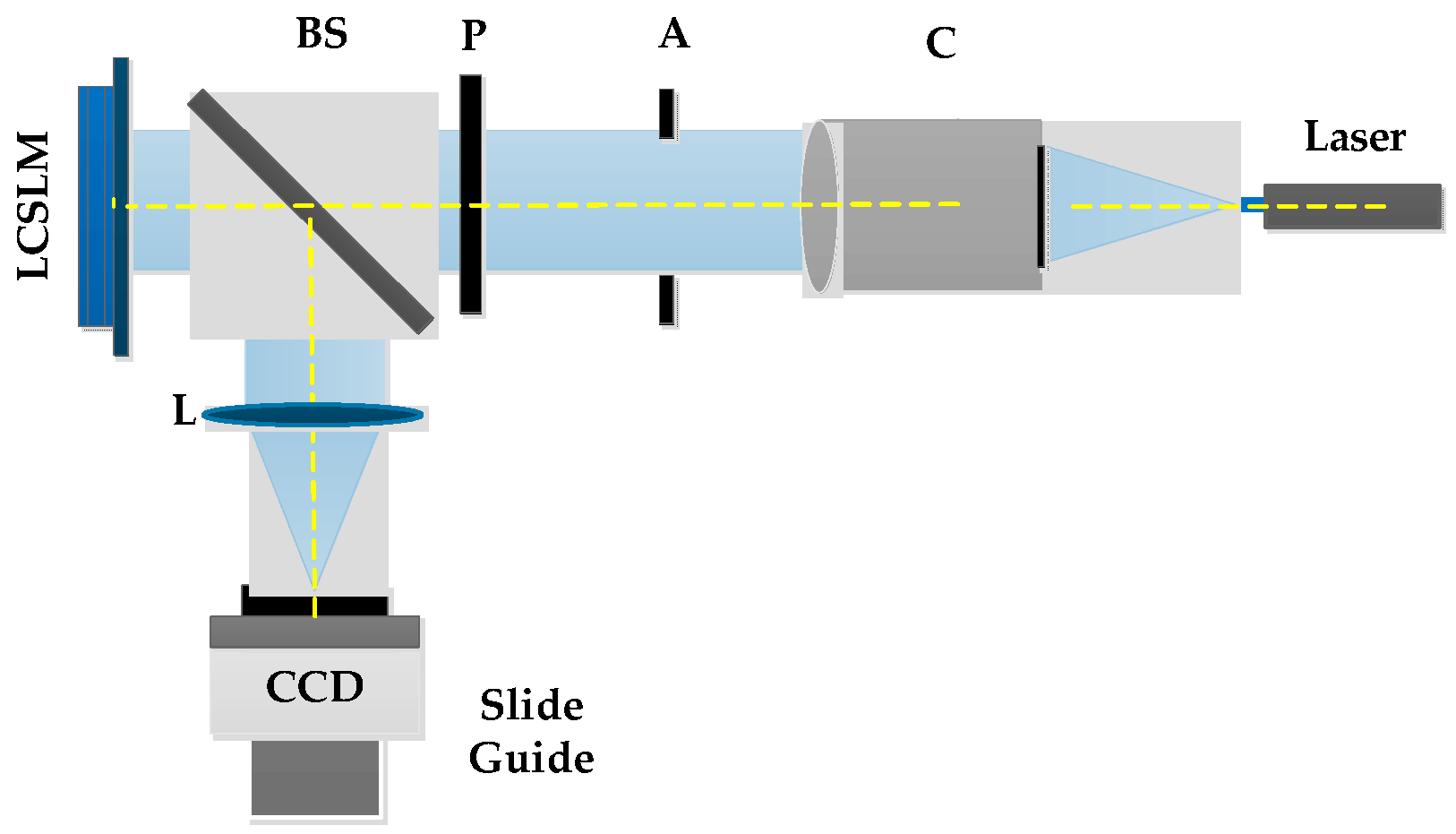
4. Experimental Demonstration
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Platt, B.C.; Shack, R. History and principles of Shack-Hartmann wavefront sensing. J. Refract. Surg. 1995, 17, 573–577. [Google Scholar] [CrossRef] [PubMed]
- Vargas, J.; González-Fernandez, L.; Quiroga, J.A.; Belenguer, T. Calibration of a Shack-Hartmann wavefront sensor as an orthographic camera. Opt. Lett. 2010, 35, 1762–1764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gonsalves, R.A. Phase retrieval and diversity in adaptive optics. Opt. Eng. 1982, 21, 829–832. [Google Scholar] [CrossRef]
- Nugent, K.A. The measurement of phase through the propagation of intensity: An introduction. Contemp. Phys. 2011, 52, 55–69. [Google Scholar] [CrossRef]
- Misell, D.L. An examination of an iterative method for the solution of the phase problem in optics and electronoptics: I. Test calculations. J. Phys. D Appl. Phys. 1973, 6, 2200–2216. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase-retrieval algorithms for a complicated optical system. Appl. Opt. 1993, 32, 1737–1746. [Google Scholar] [CrossRef]
- Allen, L.J.; Oxley, M.P. Phase retrieval from series of images obtained by defocus variation. Opt. Commun. 2001, 199, 65–75. [Google Scholar] [CrossRef]
- Carrano, C.J.; Olivier, S.S.; Brase, J.M.; Macintosh, B.A.; An, J.R. Phase retrieval techniques for adaptive optics. Adapt. Opt. Syst. Technol. 1998, 3353, 658–667. [Google Scholar]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Yang, G.Z.; Dong, B.Z.; Gu, B.Y.; Zhuang, J.Y.; Ersoy, O.K. Gerchberg–Saxton and Yang–Gu algorithms for phase retrieval in a nonunitary transform system: A comparison. Appl. Opt. 1994, 33, 209–218. [Google Scholar] [CrossRef]
- Hagan, M.T.; Beale, M. Neural Network Design; China Machine Press: Beijing, China, 2002. [Google Scholar]
- Mello, A.T.; Kanaan, A.; Guzman, D.; Guesalaga, A. Artificial neural networks for centroiding elongated spots in Shack-Hartmann wave-front sensors. Mon. Not. R. Astron. Soc. 2014, 440, 2781–2790. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.J.; Xin, Q.; Hong, C.M.; Chang, X.Y. Feature-based phase retrieval wave front sensing approach using machine learning. Opt. Express 2018, 26. [Google Scholar]
- Fienup, J.R.; Marron, J.C.; Schulz, T.J.; Seldin, J.H. Hubble Space Telescope characterized by using phase-retrieval algorithms. Appl. Opt. 1993, 32, 1747–1767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roddier, C.; Roddier, F. Wave-front reconstruction from defocused images and the testing of ground-based optical telescopes. J. Opt. Soc. Am. A 1993, 10, 2277–2287. [Google Scholar] [CrossRef]
- Redding, D.; Dumont, P.; Yu, J. Hubble Space Telescope prescription retrieval. Appl. Opt. 1993, 32, 1728–1736. [Google Scholar] [CrossRef]
- Shin, H.C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Learning D[M]; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Paine, S.W.; Fienup, J.R. Machine learning for improved image-based wavefront sensing. Opt. Lett. 2018, 43, 1235–1238. [Google Scholar] [CrossRef]
- Nishizaki, Y.; Valdivia, M.; Horisaki, R. Deep learning wave front sensing. Opt. Express 2019, 27, 240–251. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Swanson, R.; Lamb, M.; Correia, C.; Sivanandam, S.; Kutulakos, K. Wave-front reconstruction and prediction with convolutional neural networks. Adapt. Opt. Syst. VI 2018, 10703, 107031F. [Google Scholar]
- Dubose, T.B.; Gardner, D.F.; Watnik, A.T. Intensity-enhanced deep network wave-front reconstruction in Shack Hartmann sensors. Opt. Lett. 2020, 45, 1699–1702. [Google Scholar] [CrossRef]
- Hu, L.J.; Hu, S.W.; Gong, W.; Si, K. Deep learning assisted Shack-Hartmann wave-front sensor for direct wave-front detection. Opt. Lett. 2020, 45, 3741–3744. [Google Scholar] [CrossRef] [PubMed]
- Fei, W.; Bian, Y.; Wang, H.; Lyu, M.; Pedrini, G.; Osten, W.; Barbastathis, G.; Situ, G. Phase imaging with an untrained neural network. Light Sci. Appl. 2020, 9, 77. [Google Scholar]
- Bostan, E.; Heckel, R.; Chen, M.; Kellman, M.; Waller, L. Deep phase decoder: Self-calibrating phase microscopy with an untrained deep neural network. Optica 2020, 7, 559. [Google Scholar] [CrossRef] [Green Version]
- Ramos, A.A.; Olspert, N. Learning to do multiframe wave front sensing unsupervised: Applications to blind deconvolution. Astron. Astrophys. 2021, 646, A100. [Google Scholar] [CrossRef]
- Liaudat, T.; Starck, J.; Kilbinger, M.; Frugier, P. Rethinking the modeling of the instrumental response of telescopes with a differentiable optical model. arXiv 2021, arXiv:2111.12541. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Wen, Z. Photon Foundation; Zhejiang University Press: Hangzhou, China, 2000. [Google Scholar]




| Zernike Order | RMSE of Testing Set | RMSE of MobileNet | RMSE of PDL |
|---|---|---|---|
| 3–20 | 0.8284λ | 0.0447λ | 0.0648λ |
| D/r0 | RMSE of Testing Set | RMSE of MobileNet | RMSE of PDL |
|---|---|---|---|
| 30 | 1.1991λ | 0.1176λ | 0.1469λ |
| 25 | 0.9962λ | 0.0621λ | 0.0762λ |
| 20 | 0.8606λ | 0.0462λ | 0.0634λ |
| 15 | 0.6651λ | 0.0396λ | 0.0519λ |
| 10 | 0.4641λ | 0.0276λ | 0.0352λ |
| 5 | 0.2615λ | 0.0232λ | 0.0256λ |
| Zernike Order | RMSE of Testing Set | RMSE of MobileNet | RMSE of PDL |
|---|---|---|---|
| 3–64 | 0.8852λ | 0.1069λ | 0.1274λ |
| D/r0 | RMSE of Testing Set | RMSE of MobileNet | RMSE of PDL |
|---|---|---|---|
| 30 | 1.2021λ | 0.3052λ | 0.3487λ |
| 25 | 1.0438λ | 0.1887λ | 0.2136λ |
| 20 | 0.8784λ | 0.1084λ | 0.1255λ |
| 15 | 0.676λ | 0.0857λ | 0.0984λ |
| 10 | 0.4864λ | 0.0671λ | 0.0696λ |
| 5 | 0.2715λ | 0.0610λ | 0.0611λ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Guo, H.; Wang, Z.; He, D.; Tan, Y.; Huang, Y. Self-Supervised Deep Learning for Improved Image-Based Wave-Front Sensing. Photonics 2022, 9, 165. https://doi.org/10.3390/photonics9030165
Xu Y, Guo H, Wang Z, He D, Tan Y, Huang Y. Self-Supervised Deep Learning for Improved Image-Based Wave-Front Sensing. Photonics. 2022; 9(3):165. https://doi.org/10.3390/photonics9030165
Chicago/Turabian StyleXu, Yangjie, Hongyang Guo, Zihao Wang, Dong He, Yi Tan, and Yongmei Huang. 2022. "Self-Supervised Deep Learning for Improved Image-Based Wave-Front Sensing" Photonics 9, no. 3: 165. https://doi.org/10.3390/photonics9030165
APA StyleXu, Y., Guo, H., Wang, Z., He, D., Tan, Y., & Huang, Y. (2022). Self-Supervised Deep Learning for Improved Image-Based Wave-Front Sensing. Photonics, 9(3), 165. https://doi.org/10.3390/photonics9030165




