Amplification and Generation of Frequency-Modulated Soliton Pulses in Nonuniform Active Fiber Configurations

Abstract

We report on the theoretical and numerical analysis of the nonlinear Schrödinger equation describing the dynamical evolution of frequency-modulated (FM) optical signals propagating through the fiber configuration comprising active fibers with the anomalous dispersion nonuniformly distributed over the fiber length. In our consideration, a single active fiber section including segments with initially increasing and then decreasing dispersion is used for amplification and compression of an external FM pulse resulting in an increase of ~6 orders of magnitude in the pulse peak power and a 100-fold narrowing of the pulse duration down to a few picoseconds. Moreover, we demonstrate that, with a ~1 mW weakly modulated continuous wave input signal, the fiber configuration comprising two active fiber sections with different dispersion profiles is able to generate a strongly periodic pulse train, resulting in a pulse repetition rate >100 GHz, a pulse duration ~0.5 ps, and peak power up to ~1 kW. An evolution of optical signals governed by modulation instability in both fiber configurations is explored.

1. Introduction

The critical part of laser physics is the development of ultrashort pulse generators (USPs), which provide a high peak radiation power [1,2]. Extremely high concentration of energy, broadband optical spectrum, and extremely short time of light emission [3,4,5] make the ultrashort pulse (USP) of great interest for many applications such as processing and modification of materials, laser micro- and nanostructuring of materials, and nuclear and accelerator technologies [1,2,5,6,7,8,9,10,11]. Furthermore, high-frequency fiber lasers of USP with a repetition rate over 1 GHz are fabulous candidates for the development of radiophotonics technologies [12,13,14].

Despite a solid understanding [3,5,15], USP generation remains a subject of intensive studies and multiple publications [1,2,5,11]. In previous studies [16,17,18], USP generation was demonstrated in fibers with the nonlinear and dispersion parameters nonuniformly distributed over the fiber length. Fibers with slowly decreasing dispersion are promising for nonlinear fiber optics and, in particular, for ultrashort pulse generation and compression [19,20]. A number of optical fiber configurations for amplification and time compression of USP based on nonuniform fibers were proposed in [21,22,23,24]. However, pulse compression down to femtosecond durations has not yet been achieved in all-fiber format. External non-fiber devices like diffraction gratings are commonly used for this purpose [5], making the system less reliable and requiring permanent maintenance.

One of the effects accompanying USP propagation is the modulation instability (MI) that can be employed both for USP generation and control of USP repetition rate [15,25,26,27,28,29]. In this process, the light evolution exhibits periodic behavior. A harmonically modulated input continuous wave (CW) signal transforms into a train of short pulses possessing the period of initial modulation and then transforms back into the modulated CW light approaching the initial signal [15,26,27,28]. The fiber length, within which the input signal is transformed into the pulse train, depends on the initial modulation depth and commonly ranges from one to 10 dispersion lengths [15,30].

Importantly, the peak power of individual soliton-like pulses never significantly exceeds the input signal level. The light evolution dynamics becomes different when a fiber with the group velocity dispersion (GVD) nonuniformly distributed over the length is used. In this case, the generated pulse train could be much higher peak power than the input signal [19,20,31].

In this paper, we consider the mechanism for transforming continuous radiation into high-frequency pulsed radiation with a linear chirp. In addition, we consider multistage schemes that involve not only the formation of high-contrast USPs (with a peak power much higher than the average background radiation power) from CW, but also their further amplification. It is shown below that the generated pulses have a chirp close to linear. This, in turn, opens up the possibility for their further compression (for example, using a pair of “standard” diffraction gratings). In this paper, we explore the ability of active optical fibers with the dispersion parameters distributed over the fiber length to amplify soliton-like pulses and generate USP trains, getting a peak power orders of magnitude higher than that of the input optical signal. In particular, a single active fiber section including fiber segments with increasing and then decreasing anomalous dispersion is shown to enable an amplification and compression of an external FM pulse resulting in an increase of ~6 orders of magnitude in the pulse peak power and a 100-fold narrowing of the pulse duration down to a few picoseconds.

On the basis of these results, the fiber configuration comprising two fiber sections with similar dispersion profiles is demonstrated to generate a strongly periodic pulse train resulting in a pulse repetition rate >100 GHz, a pulse duration of ~0.5 ps, and a peak power of up to 1 kW that is ~5 orders of magnitude higher than the input signal level. In both cases, we explore evolution of optical signals governed by modulation instability.

2. Basic Equations

We consider propagation of a single FM wave packet (WP) in an optical fiber with the GVD nonuniformly distributed over the fiber length. The evolution of pulse envelope $A(t,z)$ is described by the nonlinear Schrödinger equation [5].

$$\frac{\partial A}{\partial z}-i\frac{d_2(z)}{2}\frac{{\partial }^{2}A}{\partial {\tau }^2}-\frac{d_3(z)}{6}\frac{{\partial }^{3}A}{\partial {\tau }^3}+iR(z)\left({\left|A\right|}^2-T_R\frac{\partial {\left|A\right|}^2}{\partial \tau }\right)A=\gamma (z)A,$$

(1)

where $d_n(z)={({\partial }^n{\beta }^{\prime }(z)/\partial {\omega }^n)}_{\omega ={\omega }_0}$ are the dispersion parameters, ${\beta }^{\prime }$ is the real part of the complex propagation constant, $\tau =t-{\displaystyle {\int }_0^{z}d\xi /u(\xi )}$ is the time in the moving reference frame, $u(z)={(\partial {\beta }^{\prime }(z)/\partial \omega )}_{\omega ={\omega }_0}^{-1}$ is the WP group velocity, $R(z)$ is the Kerr nonlinearity coefficient, $T_R$ is the Raman response time of medium, and $\gamma (z)$ is the effective gain coefficient.

The effective gain coefficient can be expressed as

$$\gamma (z)=g(z)-\frac{1}{2S_m}\frac{\partial S_m}{\partial z},$$

(2)

where $g(z)$ is the fiber material gain increment, and the second term in Equation (2) appears due to changes of effective mode area [5].

$$S_m(z)=2\pi {\displaystyle {\int }_0^{\infty }{\left|U(r,z)\right|}^{2}rdr},$$

(3)

where $U(r,z)$ is the fiber mode field distribution as a function of the coordinate $z$ along the fiber.

The optical fiber material gain increment $g(z)$ is the radially averaged function depending on the mode field profile.

$$g(z)=2\pi k_0{S}_m^{-1}(z){\displaystyle {\int }_0^{\infty }{n}^{″}(r,z){\left|U(r,z)\right|}^{2}rdr},$$

(4)

where $k_0={\omega }_0/c$, $c$ is the speed of light in vacuum, and $n^{″}$ is the imaginary part of the fiber refractive index. Bearing in mind W-shaped fibers, we can assume that nonuniform active fibers with any arbitrary distribution of the second- and even third-order dispersion parameters over the fiber length can be manufactured using an advanced control of fiber diameter during drawing [20,32].

For the WP propagating through a nonuniform active fiber, an increase in its energy is defined by the distribution of the material gain increment over the fiber length $g(z)$ as follows:

$$W(z)=W_0\exp \left(2{\displaystyle {\int }_0^{z}g(\xi )}d\xi \right),$$

(5)

where $W_0$ is the input pulse energy. The Kerr nonlinearity coefficient reads as follows [5]:

$$R(z)=2\pi k_0{S}_m^{-2}(z){\displaystyle {\int }_0^{\infty }\tilde{n}(r,z){\left|U(r,z)\right|}^{4}rdr},$$

(6)

where $\tilde{n}$ is the nonlinear refractive index of the fiber material. Note, for uniform fibers, the linear $n^{\prime }$ and nonlinear $\tilde{n}$ refractive indices, mode profile $U(r)$, and hence, $g$ and $R$ do not change with $z$.

3. Amplification of FM Soliton-Like Pulses

In this section, we describe the amplification of soliton-like FM pulses in a single active fiber segment possessing a specific distribution of the GVD over the fiber length. Let us consider first an active fiber with the gain increment varying along the fiber length according to the expression

$$g(z)=g_0/(1-2g_{0}z),$$

(7)

where $g_0$ is the gain increment at $z=0$.

The anomalous GVD and nonlinearity increment are assumed to be unchangeable over the fiber length, and the terms responsible for the third-order dispersion and Raman process are negligible.

In this case, the analytical solution of Equation (1) (at $d_{2}R<0$ and $2g_{0}z<1$) could be expressed in the form of a soliton-like pulse commonly referred to as a bright FM soliton [3,5].

$$A(\tau ,z)=\frac{A_0}{1-2g_{0}z}\mathrm{sech}\left(\frac{\tau }{{\tau }_s}\right)\exp \left(i\frac{{\alpha }_0{\tau }^2-\Gamma z}{1-2g_{0}z}\right),$$

(8)

where ${\tau }_s={\tau }_0(1-2g_{0}z)$ is the pulse width, $\Gamma =g_0/2{\alpha }_0{\tau }_0^2$, ${\alpha }_0$ is the initial pulse chirp, and the parameters are related as $2\Gamma =\left|d_2\right|/{\tau }_0^2=R{\left|A_0\right|}^2$. Let us now assume that both dispersion and nonlinearity vary with the coordinate $z$. We can introduce these changes as $d_2(z)=d_{20}\Theta (z)$ and $R(z)=R_{0}r(z)$, where $d_{20}$ and $R_0$ are the corresponding quantities at the fiber segment input. With the other introduced functions $\eta (z)={\displaystyle {\int }_0^z\Theta (\xi )d\xi }$ and $C(\tau ,z)=\sqrt{r(z)/\Theta (z)}A(\tau ,z)$, Equation (1) is reduced to

$$\frac{\partial C}{\partial \eta }-i\frac{d_{20}}{2}\frac{{\partial }^{2}C}{\partial {\tau }^2}+i{R}_0{\left|C\right|}^{2}C={\gamma }_{ef}(\eta )C.$$

(9)

In such a way, the problem of pulse propagation in the nonuniform fiber is reduced to the problem of pulse propagation in the fiber with unchangeable dispersion $d_{20}$ and nonlinearity $R_0$, but with the effective gain increment ${\gamma }_{ef}(\eta )$ distributed over the fiber length as

$${\gamma }_{ef}(\eta )=\frac{g(\eta )}{\Theta (\eta )}-\frac{1}{2}\frac{\partial }{\partial \eta }\ln \frac{\sigma (\eta )\Theta (\eta )}{r(\eta )},$$

(10)

where $\sigma =S_m(\eta )/S_m(0)$ is the normalized mode field profile.

Similarly to Equation (1), the analytical solution of Equation (9) (at $d_2(\eta )R(\eta )<0$ and $2{\gamma }_{ef}(\eta )\eta <1$) with the effective gain factor in Equation (10) ${\gamma }_{ef}(\eta )=q/(1-2q\eta )$, where $q={\gamma }_{ef}(0)$, reads as

$$C(\tau ,\eta )=\frac{A_0}{1-2q\eta }\mathrm{sech}\frac{\tau }{{\tau }_s}\exp \left(i\frac{{\alpha }_0{\tau }^2-{\Gamma }_0\eta }{1-2q\eta }\right),$$

(11)

where the parameters ${\tau }_s={\tau }_0(1-2q\eta )$, ${\Gamma }_0=q/2{\alpha }_0{\tau }_0^2$, and $q={\alpha }_0\left|d_{20}\right|$ are introduced.

As mentioned above, Equation (11) is the solution of Equation (9) under the condition of

$${\gamma }_{ef}(\eta )=-\frac{{\alpha }_0{d}_{20}}{1+2{\alpha }_0{d}_{20}\eta }=\frac{q}{1-2q\eta }.$$

(12)

Taking into account Equations (10) and (12), this can be expressed in the form

$$\left(1+2{\alpha }_0{d}_{20}{\displaystyle {\int }_0^z\Theta (\xi )d\xi }\right)\exp \left(2{\displaystyle {\int }_0^{z}g(\xi )d\xi }\right)=\Theta (z)\sigma (z)/r(z).$$

(13)

From Equation (13), the GVD profile suitable for the formation of a soliton-like pulse is

$$\Theta (z)=f(z)\exp \left(-2q{\displaystyle {\int }_0^{z}f(\xi )d\xi }\right),$$

(14)

where two functions, $f(z)=F(z)\exp \left(2{\displaystyle {\int }_0^{z}g(\xi )d\xi }\right)$ and $F(z)=r(z)\sigma (z)$, are introduced.

Correspondingly, the duration and frequency modulation (linear chirp) of FM pulses are expressed as

$${\tau }_s(z)=\frac{{\tau }_0\Theta (z)}{F(z)}\exp \left(-2{\displaystyle {\int }_0^{z}g(\xi )d\xi }\right)={\tau }_0\exp \left(-2q{\displaystyle {\int }_0^{z}f(\xi )d\xi }\right),$$

(15)

$$\alpha (z)={\alpha }_0\exp \left(2q{\displaystyle {\int }_0^{z}f(\xi )d\xi }\right).$$

(16)

Let us assume now that the gain increment does not change along the fiber length. If $F(z)=1$, and $g(z)=g_0$, the function $f(z)=\exp (2g_{0}z)$ and the expressions for the GVD distribution and pulse duration are

$$d(z)=-\left|d_{20}\right|\exp \left[-\frac{{\alpha }_0\left|d_{20}\right|}{g_0}\left(\exp (2g_{0}z)-1\right)+2g_{0}z\right],$$

(17)

$$\tau (z)={\tau }_0\exp \left[-\frac{{\alpha }_0\left|d_{20}\right|}{g_0}\left(\exp (2g_{0}z)-1\right)\right].$$

(18)

The made simplifications are reasonable. Indeed, the W-shaped fibers are considered to be suitable candidates for implementation of the discussed mechanisms [20,32]. The W-shaped fibers with almost arbitrary GVD profile can be manufactured using control of fiber diameter during drawing [20]. Moreover, it can be achieved while keeping relatively low level of the third-order dispersion $\left|d_3\right|\ll {10}^{-38}{\mathrm{s}}^2/\mathrm{m}$ and avoiding significant effects on the gain increment and Kerr nonlinear coefficient.

In the case of a low gain limit ($2g_{0}z\ll 1$), when $\exp (2g_{0}z)\approx 1+2g_{0}z$, Equations (17) and (18) are reduced to

$$d(z)\approx -\left|d_{20}\right|\exp (-2{\alpha }_0\left|d_{20}\right|z),$$

(19)

$$\tau (z)\approx {\tau }_0\exp (-2{\alpha }_0\left|d_{20}\right|z).$$

(20)

It is worth noting that the condition $F=1$ is not always true. The equation $F=1$ is right if the Kerr nonlinearity parameter is constant along the fiber length. This is possible if only the effective mode area varies weakly along the fiber length [5]. The condition of a constant nonlinearity parameter of the fiber is incorrect in the case of a tapered fiber with a varying mode area or in the case of an active fiber with nonuniform doping along the fiber length. Thus, $F$ is an additional parameter allowing control over the dynamics of the modulated and amplified wave packet.

However, in contrast to Equation (19), the dispersion profile in Equation (17) combines the ranges with increasing and decreasing GVD. Potentially, it is useful for an enhanced peak power scaling of the propagating FM pulses. In this combination, the fiber length with the increasing GVD enables a stable amplification of the pulse, while the length with decreasing GVD enables both the pulse amplification and the temporal compression of the pulse shape [19,33].

Figure 1a shows the propagation of an FM soliton-like pulse through a single fiber segment with the GVD profile described by Equation (17). The input pulse shape is expressed as

$$A(0,\tau )=A_0\mathrm{sech}(\tau /{\tau }_0)\exp (i{\alpha }_0{\tau }^2).$$

(21)

The $z_0$ position is obtained through the differential from Equation (17) and given by $z_0=\ln \left[g_0/\left({\alpha }_0\left|d_{20}\right|\right)\right]/2g_0$. GVD has a maximum at the point $z=z_0$ (Figure 1a).

The numerical simulation of the pulse propagation in an active fiber segment with the GVD profile described by Equation (17) was simulated with the split-step Fourier method (SSFM method) [5]. The calculation parameters are listed in the

Table 1. Parameters used for calculations.

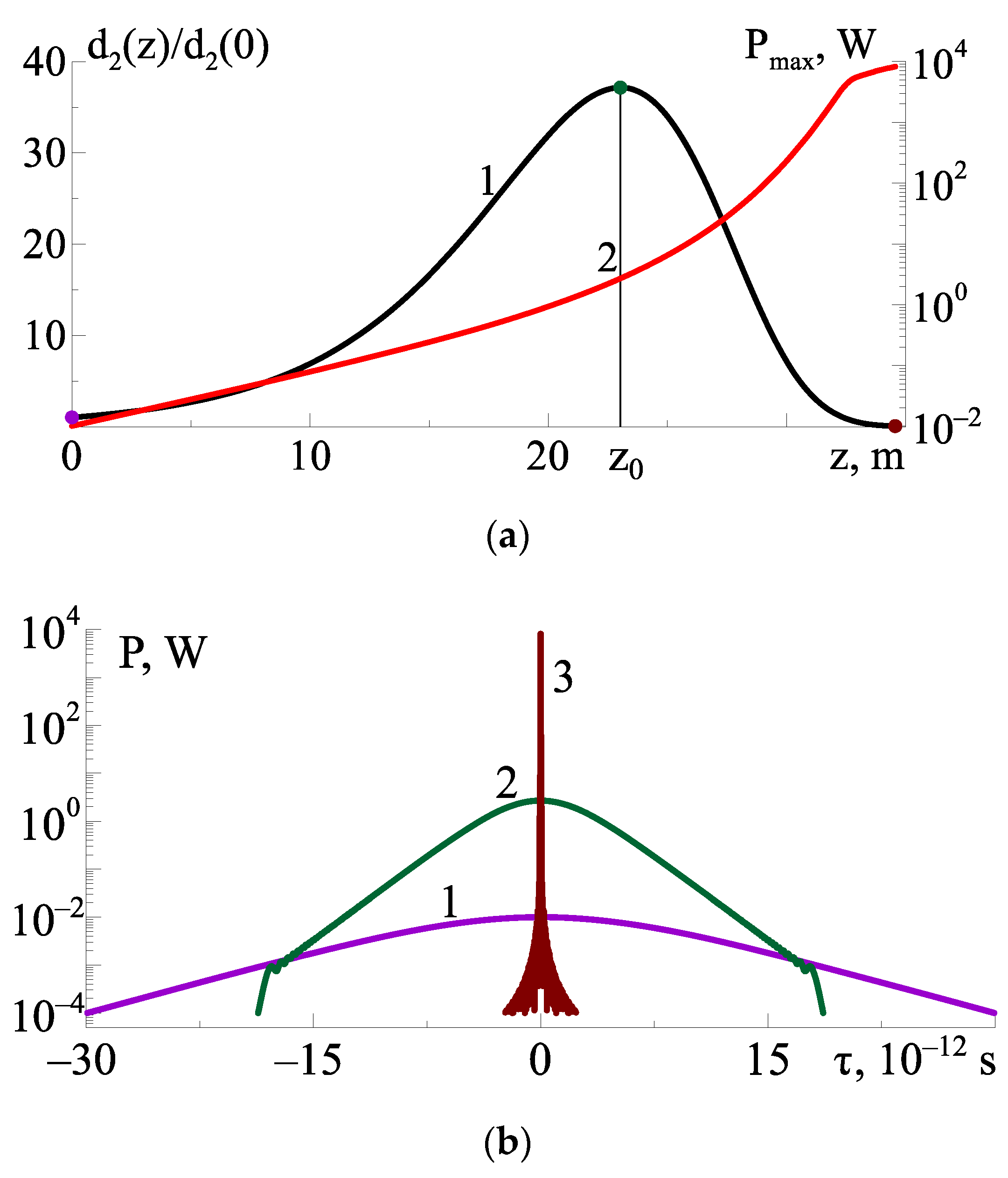
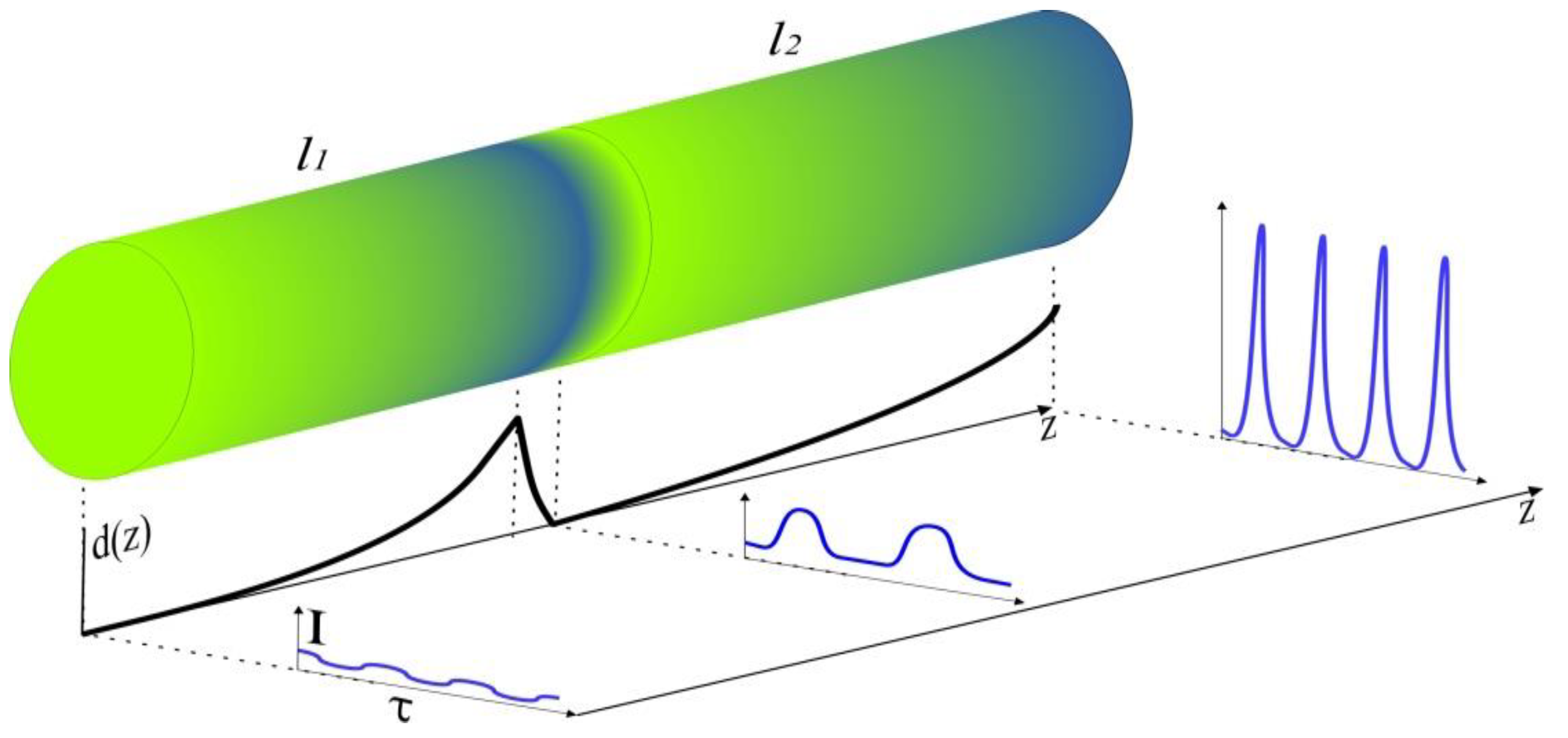
Sign	Description	Value	Figures
$P_0$	Peak power of input signal	0.01 W	1,3,4
${\tau }_0$	Input pulse duration	10 ps	1
${\alpha }_0$	Initial frequency modulation (chirp) of pulse	1024 s−2	1
$m$	Modulation depth	0.01	3,4
${\Omega }_{\mathrm{mod}}$	Modulation frequency	2 × 1012 s−1	3,4
$d_{20}$	$\mathrm{Sec}\mathrm{ond}-\mathrm{order}\mathrm{dispersion}\mathrm{at}z=0$	–10−27 s2/m	1,3,4
$d_3$	Third-order dispersion	−10−40 s3/m	3,4
$R_0$	Kerr nonlinearity coefficient	10−3 (W·m)−1	1,3,4
$T_R$	Raman response time of medium	5 × 10−15 s	1,3,4
$g_0$	Optical fiber material gain increment	0.1 m−1	1
$g_1$	Optical fiber first section material gain increment	0.1 m−1	3,4
$g_2$	Optical fiber second section material gain increment	0.015 m−1	3,4

. They satisfy the condition $P_0=\left|d_{20}\right|/{\tau }_0^2{R}_0$ at $P_0=0.01\mathrm{W}$.

The distribution of the anomalous GVD along the fiber segment length comprising the ranges with increasing and decreasing GVD values is shown in Figure 1a (curve 1), and in Figure 2 (the first segment l₁). It gets its maximum at z = z₀ corresponding to d_max ≈ 40d₂₀. The pulse shapes at the fiber segment input and at the point z = z₀, and the fiber segment output are shown in Figure 1b (curves 1, 2, and 3, respectively). While propagating in the fiber length with the increasing dispersion $z<z_0$), the FM pulse exhibits a 300-fold increase in its peak power (Figure 1a,b; curves 2). In the fiber length (z > z₀), the GVD decreases to almost its initial value (Figure 1a, curve 1), and the amplified soliton-like FM pulse is compressed. Its peak power explosively increases, reaching ~10 kW at the fiber segment output (Figure 1b, curve 3), which is ~6 orders of magnitude higher than its input signal peak power. The optimal length of this fiber range ($z>z_0$) is determined by the fiber point, where the pulse is still able to keep its shape, as $l_2=17.269\mathrm{m}$ used in our calculations (Table 1).

4. Induced MI and Generation of FM Soliton-Like Pulse Train

In the previous section, we demonstrated drastic amplification and temporal compression of a soliton FM pulse achieved in an active fiber with nonuniform GVD profile. In this section, we consider the process of soliton-like pulse generation through the modulation instability implemented in a cascade of such fibers.

We assume that a weakly modulated CW optical signal with the power $P_0$ is used as an input signal.

$$A(0,\tau )=\sqrt{P_0}\left[1+m\cos ({\Omega }_{\mathrm{mod}}\tau )\right],$$

(22)

where $m\ll 1$ is the modulation depth, and ${\Omega }_{\mathrm{mod}}$ is the modulation frequency.

We analyzed numerically that propagation of the input signal through a single fiber segment only does not allow getting pulse trains of a sufficiently high contrast. In order to generate pulse trains from the weakly modulated CW signal, a fiber configuration comprising two active fiber segments with different GVD profiles has to be considered. Such a cascaded fiber configuration is shown in Figure 2. In this configuration, the first fiber segment has the dispersion profile in Equation (17) similar to that shown in Figure 2. Propagating through this fiber, the weakly modulated CW signal increases the modulation depth and acquires a frequency chirp in each signal period. The second fiber segment is much longer than the first one. However, both fiber segments possess the GVD profiles described by Equation (17), but with different parameters. Under the condition that the parameters of the second fiber segment satisfactorily match the signal delivered by the first fiber, it enables effective and smooth conversion of the input signal into a high-power ultrashort pulse train.

Figure 3 shows the evolution of the initial weakly modulated CW signal to the picosecond pulse train in the configuration comprising two fibers with the lengths of l₁ = 28 m and l₂ = 142 m, as well as the GVD profiles described by Equation (17) with different parameters listed in Table 1.

The distributions of GVD and pulse train peak power along the fiber length are shown in Figure 3a (curves 1 and 2, respectively). Propagating through the first fiber segment, the weakly modulated CW signal is amplified adiabatically. Its shape is changed, the modulation depth increases, and the signal acquires a linear chirp in each signal period. The signal power possesses a linearly increase with the fiber length reaching ~1 W at the first fiber segment output.

The modulated light delivered by the first fiber is introduced into the second fiber. The second fiber provides its conversion into the periodic pulse train. In this process, formation of the contrast pulses occurs due to both adiabatic amplification in the active fiber and nonlinear interaction between the growing pulses and CW background. A stable highly contrast pulse train possessing the peak power of 700 W and a sub THz pulse repetition rate (Figure 3b (curve 3)) is delivered by the cascaded fiber configuration.

It is worth noting that the pulse train repetition rate is strongly defined by the frequency of initial modulation ${\Omega }_{\mathrm{mod}}$, reaching a value as high as ${\nu }_r\approx 0.5\mathrm{THz}$ for ${\Omega }_{\mathrm{mod}}=3\times {10}^{12}{\mathrm{s}}^{-1}$. However, it could be slightly tuned by a change of the gain increment in the second fiber (Figure 4). This feature makes the proposed technique useful for many practical applications.

5. Discussion and Conclusions

We proposed an advanced use of nonuniform optical active fibers with a specific dispersion profile both for amplification and generation of ultra-short FM pulse trains. With a single fiber segment, the amplification of a single FM pulse peak power by six orders of magnitude is demonstrated, whereas the cascaded fiber configuration comprising two nonuniform active fibers with different dispersion profiles is shown to enable the generation of the pulse train with a peak power of 700 W and a sub-THz repetition rate from 10 mW weakly modulated CW optical input signal. The repetition rate of the generated pulse trains can be controlled by changing the input signal modulation frequency and, more precisely, through the pump power adjustment in the second fiber segment. Further scaling of the pulse train peak power up to 10 kW, as well as a repetition rates as high as 0.5 THz could be achieved with the fiber configurations comprising three and more similar fiber segments. However, these demonstrations are beyond the scope of this paper.

There is a known scenario for the development of MI in fibers with nonlinear and dispersive parameters that are nonuniform along the length, which was considered in detail in [30,34,35,36,37,38,39,40]. In our case, which differs from the standard scenario for the development of MI [30,34,35,36,37,38,39,40], the generated pulse train is nonperiodic. CW radiation evolves into a train of USPs, which is accompanied by a steady decrease in the USP durations and an increase in their peak power. As a result, FM soliton-like pulses are formed, and their amplitude can exceed by orders of magnitude the peak powers of the so-called Akhmediev breathers, which are formed as a result of the development of MI in homogeneous fibers [40]. The closest scheme to the discussed work was presented in [41,42] for the first time.

A precise control of the pulse repetition rate by adjustment of the input power opens prospects for implementation of the proposed USP generation techniques in radiophotonics [43] and optical metrology, as well as in terahertz clocks demanded for optical computing [14]. Furthermore, the considered systems delivering peak powers over 10 kW are demanded for applications in material processing [1].