1. Introduction
Since the invention of the first laser in the 1960s, laser technology has developed rapidly, both in terms of shortening the pulse duration and increasing its energy [
1]. This was facilitated by the search for new promising and broadband laser media capable of generating and amplifying femtosecond pulses in various spectral ranges from ultraviolet (UV) to infrared (IR). A real breakthrough in femtosecond technology was the invention of the chirped pulse amplification (CPA) method. Its inventors G. Mourou and D. Strickland were awarded the Nobel Prize in 2018. After that, femtosecond lasers were able to “step” into the sub-Joule energy range of laser pulses, thereby reaching record peak powers of 1 PW. The development of special adaptive technologies in optics made it possible to focus a laser beam of such power into the diffraction limit (~λ
3), which for the sources available at that time was about several microns in space, thereby reaching intensities above 10
16 W/cm
2 and creating an ultra-strong light field inaccessible to other methods under laboratory conditions.
Thus, over the past twenty years, significant progress has been made in the field of ultrashort laser pulses generation with extremely high peak power [
2,
3,
4]. These developments offered the possibility of conducting new types of experiments [
5], such as the acceleration of charged particles by strong laser fields [
6] and the laser initiation of nuclear reactions [
7]. They also demonstrated new methods of generating X-ray radiation [
8], particularly the generation of extremely short X-ray pulses [
9]. By 1990, unique pico- and femtosecond laser systems were designed and developed, allowing us to receive high-intensity laser radiation (10
12–10
16 W/cm
2) in the UV, visible and IR ranges [
10,
11,
12]. With their help, a whole range of pioneering studies of the properties of femtosecond high-temperature laser-plasma have been carried out, and sources of ultra-bright X-rays, electrons and ions were created [
7,
11]
The development of femtosecond lasers helped us reach a new level of research in the fields of nonequilibrium states of matter and the physics of high energy densities and intensities. In the regime of a super-strong light field, it is possible to study the fundamental properties of matter in extreme states characterized by high values of temperature (10
5 K) and pressure (1 TPa). The creation of such states is essential, for example, for problems related to high-temperature laser-plasma and thermonuclear processes, which, in turn, are relevant to the modeling of many astrophysical processes [
13,
14]. In addition, the question of the effectiveness of nonlinear optical processes in strong light fields, first formulated by S.A. Akhmanov in the 1970s, is fundamental from the point of view of clarifying the limiting possibilities of nonlinear optics and the influence of higher optical nonlinearities [
15].
In the early 2000s, for the first time in Russia, a Cr:Forsterite femtosecond pulse oscillator was developed at Moscow State University (MSU) [
16,
17], and some years later, a femtosecond laser complex was created on its basis, generating high-intensity (up to 10
16 W/cm
2) radiation in the near-IR range (1.24 µm) [
18]. The optimization of its operation and expansion of its capabilities determined the vector of laboratory evolution. It is focused on studying nonlinear optical processes occurring during the interaction of high-intensity laser radiation with condensed and gaseous media [
19,
20,
21,
22,
23,
24,
25].
Increasing the wavelength of high-intensity femtosecond laser radiation from the near-IR (0.8 µm, 1.24 µm) to the mid- (2–8 µm) and far-IR (above 8 µm) ranges has clear advantages. Thus, an increase in the mean quiver energy of an electron as (I × λ
2) leads to the emergence of new regimes of particle acceleration [
26], the generation of bright X-ray, and terahertz radiation [
27]. The relativistic interaction of an electron with a laser wave field for radiation with a wavelength of 4 µm is achieved at about I = 10
17 W/cm
2. The increase in the critical power of self-focusing makes it possible to deliver higher energy levels in the controlled regime of single filamentation, which is essential for remote sensing and other practical applications [
28]. On the other hand, the filamentation of high-power mid-IR laser pulses allows for obtaining a multi-octave supercontinuum extending from the UV to the mid- and far-IR ranges, providing few-cycle pulses after post-compression [
29]. The product of laser field intensity as a result of the square of the wavelength also determines the cutoff frequency of high-order harmonics generated on the plateau. In the mid-IR range, this indicates the possibility of obtaining harmonics in the keV energy range, which is important for developing free-electron lasers [
27]. Creating an extreme state of matter in the bulk of semiconductor materials also requires the expansion of the spectrum of laser sources in the larger wavelength range. Historically, work aimed at expanding the spectral range of created laser sources (using parametric amplification processes) was developed first. Particular interest was associated with the 10 µm region [
30,
31], which gives opportunities for generating super-powerful picosecond laser pulses in the far-infrared range [
32], and is under development at present [
33].
Pioneering research carried out at Lomonosov Moscow State University made it possible to propose highly efficient amplification schemes in this promising spectral range of medium and high-pressure CO
2 amplifiers optically pumped with 3 µm laser sources [
34]. The logical development of the work on expanding the spectrum of femtosecond radiation to the longer wavelength range (λ > 1 µm) was the creation of broadband supercontinuum sources and parametric amplifiers pumped with Cr:Forsterite laser pulses [
35,
36,
37,
38,
39,
40]. The search for new regimes of effective parametric amplification in nonlinear optical crystals (BBO, KTA, AGS), pumped with a Cr:Forsterite laser, made it possible to create highly efficient (up to 10%) radiation sources tunable from 1 to 6 µm femtosecond at MSU. Further work aimed at finding methods to increase the peak power of mid-IR radiation to a multi-gigawatt level.
Currently, there are a limited number of the mid-IR laser systems providing multi-gigawatt peak power [
41,
42,
43]. Record results in the area of 3.9 µm were obtained by the Austrian group, which managed to reach a peak power of 90 GW with a pulse duration of 83 fs [
44]. Another group managed to move further along the spectrum and create a source operating at a central wavelength of 5.0 µm, which is currently providing the highest repetition rate of up to 1 kHz with an energy of up to 1 mJ at a duration of ~75 fs [
45]. As follows from these examples, the schemes for obtaining femtosecond radiation in the mid-IR range are based on the method of chirped pulses parametric amplification (OPCPA). It should be emphasized that these examples of scheme design are complex, requiring the use of picosecond pumping sources with near-ideal spatial radiation quality. They are practically limited in terms of output energy increase and wavelength tuning due to the aperture effects when using “long” nonlinear optical crystals. The development of a powerful mid-IR femtosecond laser system based on the amplification of parametric seed in a new chalcogenide active medium of Fe
2+:ZnSe is a simpler, more flexible, and scalable concept of a powerful mid-IR laser source. As an alternative method for obtaining mid-IR broadband seed radiation in the gain band of the chalcogenide medium Fe:ZnSe, we proposed and implemented the world’s first femtosecond graphene mode-locked Fe:ZnSe oscillator pumped with a continuous-wave (CW) 3 µm Er:ZBLAN fiber laser [
46]. Such a source in the future is expected to render redundant complex methods of obtaining seed radiation in parametric amplification processes in nonlinear optical crystals pumped with a Cr:Forsterite laser, and create a fully solid-state femtosecond laser system of the mid-IR (4–5 µm) range based on an Fe:ZnSe active medium. The output energy of the Fe:ZnSe CPA system can be enhanced by increasing the number of passes in the multipass amplifier (MPA) to the optimal (reaching gain saturation), by optimizing the technology and the level of the amplifier’s active element doping [
47,
48], as well by the further increasing the size of the injection mode and creating an additional amplification stage. The expansion of the generation range of such a laser system is achieved by changing the matrix (ZnS, ZnSe, CdSe, CdS) doped with iron ions while maintaining the absorption spectrum in the three-micron wavelength range, which makes it possible to use an optical pumping source developed in the laboratory [
49,
50,
51].
2. Cr:Forsterite Laser System as a “Working Horse”
As a front-end for near- and mid-IR ultrafast sources, a Cr:Forsterite laser system is used. The utilization of radiation at a wavelength of 1.24 µm is more advantageous for this kind of process than Ti:Sapphire (~800 nm). The possibility of using non-oxide crystals provides access to longer wavelengths. Additionally, such sources are preferred for other applications, such as studying energy transfer processes [
52] or free carrier absorption in dielectrics [
53]. At present, Cr:Forsterite laser sources with ~1 mJ pulse energy are commercially available. However, such applications as optical parametric conversion require high-peak power systems. For this purpose, a powerful Cr:Forsterite laser system was developed according to the standard CPA architecture with an output energy of 16 mJ in the pulse, and with a pulse duration of ~100 fs.
The system consists of a master oscillator, regenerative (RA) and multi-pass (MPA) amplifiers, a stretcher, and a compressor. A Kerr lens mode-locked master oscillator based on a Cr:Forsterite crystal is pumped by a continuous-wave (CW) ytterbium-fiber laser (1.064 µm, 10 W). The oscillator operates at a pulse repetition frequency of 95 MHz and provides light pulses of 60 fs duration with an average power of ~150–180 mW. A two-channel electro-optically Q-switched Nd:YAG laser pumps the RA and MPA (1.064 µm, 10 ns, 10 Hz, 100 mJ, and 20–30 mJ for pumping the MPA and RA, respectively). The Martinez-type stretcher and two-grating-based compressor are used for stretching and compressing the near-IR broadband pulses.
The regenerative amplifier cavity has a ring configuration. In this scheme, under the optimal matching of the seed signal, unidirectional pulse traveling is implemented. Therefore, there is no need for optical isolation of the amplifier and oscillator. It also provides higher output pulse energy compared to the linear scheme.
After the RA, the pulse is directed to a 10-pass amplifier. This consists of a pair of two curved mirrors with a radius of curvature of 700 mm. As a result, at the output of the MPA, the energy of the uncompressed pulse is up to 7 mJ. After the MPA, an amplified subnanosecond pulse is sent to the compressor. The measured transmission of the compressor for linearly polarized femtosecond laser pulses is about 80%, which makes it possible to receive pulses with energy of up to 4 mJ at the output of the laser system.
This working regime is used by us to pump mid-IR parametric amplifiers, which will be addressed below. For highly energy-demanding applications, an additional MPA is designed with an output energy of 20 mJ of uncompressed pulse. With the standard Bow-tie scheme, four passes through the active element are implemented. The beam caustics through the resonator are controlled with a telescope on the MPA input. The 80% compressor transmission provides energy at the system output of 12–16 mJ. The output spectrum of 22 nm FWHM indicates the absence of gain narrowing effects during amplification. The compression of the amplified high-power pulses is performed using our developed vacuum compressor based on a diffraction grating pair (Richardson Gratings Inc.). After adjusting the compressor and reducing the influence of chirps of various natures (temporal, spatial), it was possible to obtain a femtosecond pulse at the output with a duration of 100 fs. Thus, the approaches developed to increase the peak and average power of the near-IR femtosecond pulses of the Cr:Forsterite laser made it possible to reach a peak power level of more than 100 GW at an average power of 2 W, which indicates the prospects of using this source in solving problems of nonlinear optics and physics of super-strong light fields.
3. Mid-IR Broadband Parametric Seed Sources
Optical parametric amplification is a promising approach for mid-IR seed generation for further CPA in a solid-state active medium. First of all, optical parametric amplifiers provide broadly tunable radiation with high peak power, by selecting an optimal nonlinear crystal and scaling the energy by increasing the number of stages. This classical approach is based on the generation of a supercontinuum in bulk material, and its subsequent amplification in nonlinear crystals via difference frequency generation (DFG). To obtain femtosecond mid-IR pulses, we developed an optical parametric amplifier (OPA) pumped with Cr:Forsterite laser. Parametric sources directly pumped by a Ti:Sapphire laser are hardly tunable beyond 3–3.5 μm with reasonable efficiency due to the limited transparency of oxide crystals in the 4–5 μm range [
23,
24]. To increase the OPA efficiency at wavelengths exceeding 3–3.5 μm, long-wavelength pumping sources should be used (>0.8 μm). In this case, the higher conversion efficiency inherent to the direct parametric amplification can be combined with the broad tunability and high nonlinearity of semiconductor nonlinear crystals. The Cr:Forsterite laser combines a longer wavelength, 100–200 fs pulse duration, and up to peak TW power, which makes it a very appropriate source for OPA pumping.
The implementation of a parametric amplifier requires seed radiation in the range of 1.6–2 μm. For this purpose, parametric fluorescence or a supercontinuum generated under filamentation are conventionally used. We chose the second approach due to its high stability, broad bandwidth, and temporal and spatial coherence. In addition, CEP stable idler pulses can be directly obtained from OPA in this case [
54]. The supercontinuum was generated in a 20 mm-long Nd:YAG crystal with filamentation via a tiny part of Cr:Forsterite fundamental radiation, providing a high spectral brightness in the desired wavelength range.
When choosing an optimal nonlinear crystal, the transparency range, phase matching bandwidth, and group velocity mismatch should be considered. To prevent two-photon absorption, the short-wavelength absorption edge of the crystal should be no longer than 600 nm. This requirement does not allow the use of such highly efficient crystals as ZGP and GaSe with transparency ranges of 0.75–10 μm and 0.65–16 μm, respectively. At the same time, the long-wavelength edge should reach up to 4–5 μm, which does not allow the use of the most popular oxide crystals (BBO, LBO, KTP). We have calculated the phase-matching bandwidth and figure of merit (FOM) for all commercially available crystals. Our analysis revealed that the most broadband pulses can be obtained from KTA crystal, while the highest gain can be achieved in AGS crystals. In the following, the results obtained with each crystal are presented.
Phase matching in KTA crystals can be achieved in XZ and YZ planes. In general, phase matching in the YZ plane demonstrates a smaller nonlinearity (d
24 > d
15) [
55]; therefore, the crystal was cut in the XZ plane for type II phase-matching. We used a 5 mm-long KTA crystal. It was pumped by the fundamental radiation of the Cr:Forsterite laser (wavelength 1240 nm, pulse energy ~400 μJ). The pump intensity reached 100 GW/cm
2 at the crystal. The details of the experimental set-up can be found in [
36].
The KTA crystal pumped by 1.24 μm radiation demonstrated a specific vertical region of tuning curves located in the vicinity of the long-wavelength absorption edge of the crystal. This region can be exploited for the broadband generation of mid-IR pulses since group-velocity matching occurs at these wavelengths. In this regime, the spectral bandwidth of generated pulses reached 350 nm (FWHM) at a central wavelength of 3.8 μm, which corresponds to a 65 fs transform limited pulse duration. However, the tunability of such OPA is limited to 4.0 μm, which makes it inappropriate for seeding the Fe:ZnSe active medium with an amplification band centered at 4.4 μm under normal conditions. Note that group-velocity matching around the long-wavelength absorption edge of the crystal was also observed in type I BBO by our group [
38].
As a next step, we investigated parametric amplification in the AGS crystal [
40]. Since the calculated phase-matching bandwidth for the I type interaction is about 2 times higher than the one for type II interaction, type I oo-e phase matching was selected for amplification. In the experiment, a 2 mm-long AGS crystal cut at an angle of 42 degrees was used. The setup and laser pulses parameters were completely identical to those used with KTA crystal. At an energy value of 1.74 μm of the generated signal, the pulses reached ~1 μJ, while the corresponding idler pulse attained ~700 nJ. The maximum gain was about ~60, which significantly exceeded the value for the KTA crystal. Comparing the output characteristics of KTA and AGS OPAs, it is worth noting that the pulses generated in the AGS crystal were of a smaller bandwidth (175 cm
−1) compared to the KTA crystal (190 cm
−1), but had a much larger tuning range (up to 5 μm) limited only by the transparency of our dichroic mirrors. In addition, as expected, due to the greater nonlinearity, a higher gain was observed in the AGS crystal.
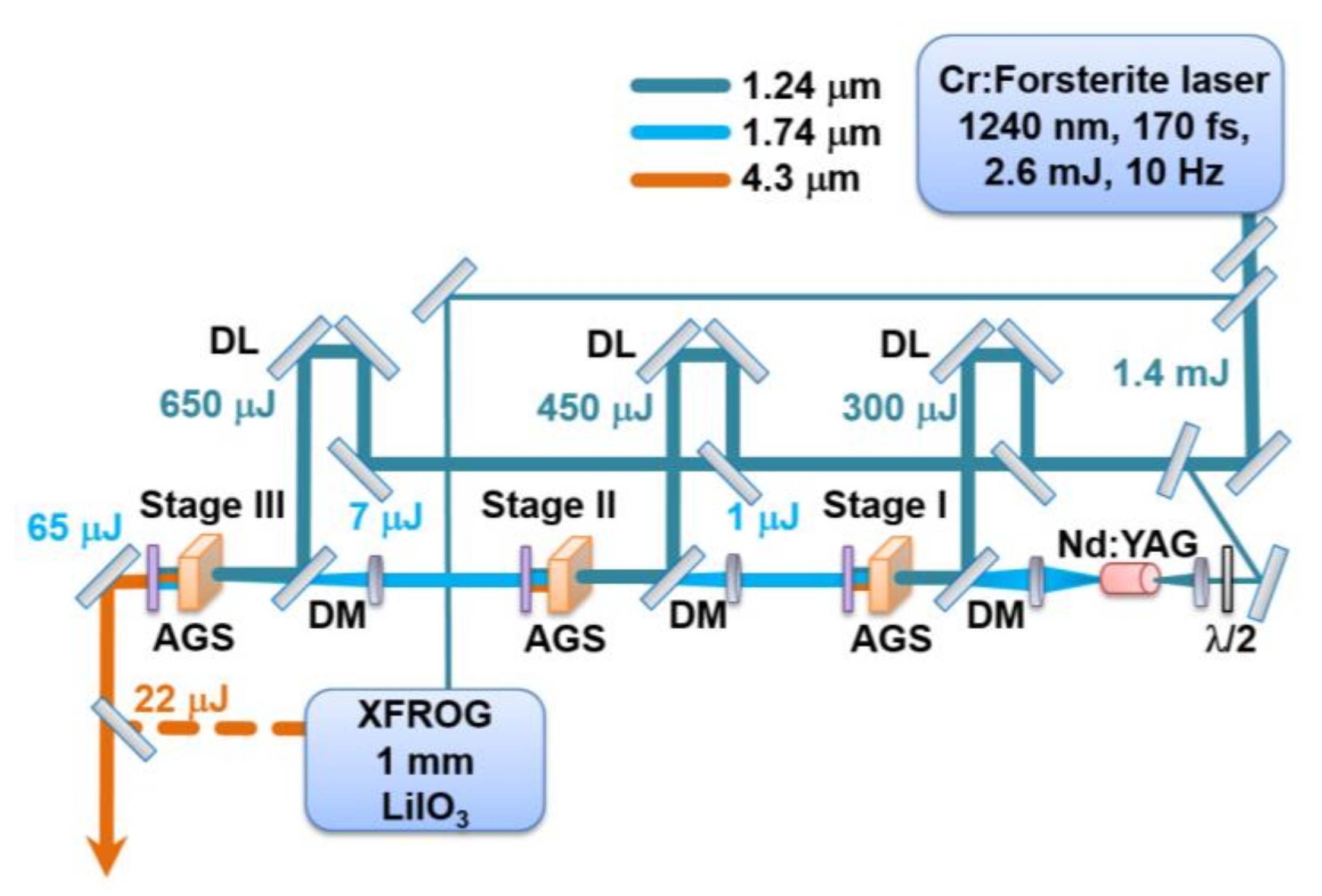
Figure 1 shows the experimental setup of the three-stage parametric amplifier based on three 2 mm-long AGS crystals. The pump intensity at the first crystal was around 100–120 GW/cm
2, while about 50 GW/cm
2 was used at the second and third stages. After the first stage, the signal energy was about ~1 μJ. We used a signal wave for amplification at the subsequent stages. After the second and third stages, the energy reached 8–10 μJ and 60–65 μJ, respectively, at the central wavelength of 1.74 μm. The corresponding idler energy was 18–22 μJ.
The signal and idler waves were tunable in the range of 1.6–2.1 μm and 3.4–5.5 μm, respectively. The maximum output energy of 22 μJ was reached at 4.0 μm (for the idler wave). Wavelength tuning further to the mid-IR range led to a decrease in output energy to 13 μJ at 4.3 μm. Up to 5 μm, the output energy remained almost unchanged, and then smoothly fell to 6 μm. In the short wavelength region, there was a sharp decline in output energy from 3.9 μm to 3.4 μm, as shown in
Figure 2. Such behavior of the output energy is associated with the spectral brightness of the supercontinuum used as a seed for the first stage and transmission of the dichroic mirrors. The spectrum width of the output pulses was 180–210 nm, depending on wavelength, which corresponds to the transform-limited duration of about 130–180 fs. Thus, the use of the AGS crystals provides both sufficient conversion efficiency (about 1.5%) and sufficient output pulse duration.
We have also revealed that the output energy of the OPA significantly depends on the pump pulse duration. The conversion efficiency can be increased by a factor of two under optimal pump chirping up to 260 fs. The maximum idler and signal energy reached 43 μJ and 110 μJ, respectively. The observed two-fold increase in the conversion efficiency originated from a longer interaction length and the improved spectral brightness of the supercontinuum. The final total conversion efficiency reached 10% for both waves, and about 3% for the idler wave, which significantly exceeds the previously values obtained with a Cr:Forsterite pumping laser (1.3% [
56], <1% [
57]), as well as some other pump sources (1.5% Yb:KGW [
58], 1.3% Ho:YAG [
59], 1.5% Ti:Sapphire [
60]).
4. Mid-IR Broadband Amplification and Generation in Fe-Doped Chalcogenide Crystals
Optical parametric laser mid-IR laser sources are effective for producing ultrashort pulses. However, as a rule, they are more expensive and complex, and provide low efficiency compared with solid-state lasers, which, in turn, offer high power levels for maintaining good beam quality. The development of novel active media based on transition metal ion-doped chalcogenides has opened up access to the ultrafast sources in the mid-IR range, covering wavelengths from 2.4 μm to 6.5 μm [
61]. Such solid-state active elements combine unique spectroscopic (ultrabroad gain band, high absorption and emission cross-sections, high quantum efficiency) and material (low-energy phonon cutoff, wide transparency bandwidth in IR, high thermal conductivity) properties. The main II-VI semiconductor materials (ZnSe, ZnS, CdSe and ZnTe) have high transparency in the visible to the far-IR range due to their wide band gap and low phonon frequency. The slight change in the refractive indices of ZnS and ZnSe in a wide spectral range minimizes optical dispersion, which is essential for femtosecond applications.
The Cr:ZnSe and Cr:ZnS lasers have undergone the most remarkable development due to the availability of CW and pulsed pumping lasers. To date, impressive success has been achieved in the creation of femtosecond oscillators [
62,
63] and amplifiers [
64,
65] based on Cr:ZnSe/S crystals. At the same time, crystals doped with iron ions with a gain band at wavelengths of 4–6 µm have attracted particular interest. The successful development of the Cr:ZnSe laser [
9] has manifested active progress in the development of Fe:ZnSe lasers, since their spectroscopic and physical characteristics are similar. The large values of absorption and emission cross-section (~1 × 10
−18 cm
2) of the crystal, as well as the possibility of doping with a high concentration of ions (~10
19 cm
−3), make this medium promising for the efficient generation and amplification of radiation in the mid-IR region.
4.1. Mid-IR CPA System with Multipass Amplification in Fe:ZnSe
In our concept of a mid-IR CPA system, we turned to a hybrid scheme with parametric seed from a Cr:Forsterite laser, and the amplification of chirped pulses in an Fe:ZnSe crystal pumped with a nanosecond 3 µm laser [
47]. While the lasing properties of Fe:ZnSe were studied intensively, we focused on the properties of this laser medium concerning the amplification of broadband laser pulses. In our previous papers, we have developed an approach for creating a high-power femtosecond laser system based on the CPA of a mid-IR seed in an optically pumped Fe:ZnSe gain medium [
66]. The amplification of nanosecond and femtosecond pulses in Fe:ZnSe was investigated in [
67,
68], correspondingly with further enhancements in energy extraction from the amplifier, up to 1.2 mJ [
69].
Fe:ZnSe has some important features distinguishing it from other vibronic mid-IR media. Firstly, it has a short lifetime at room temperature, which requires pumping with actively Q-switched 3 µm lasers, introducing the possibility of the precise synchronization of pumping and seed pulses. Secondly, the presence of a fundamental absorption line of atmospheric CO2 limits the possibility of the propagation of broadband laser pulses in the air without significant losses in or distortions of the pulse.
The first task was solved by developing a powerful 3 μm pumping laser Cr:Yb:Ho:YSGG with electro-optical Q-switching based on KTP crystal [
50]. The high gain and fast modulator switching allowed us to create an MOPA-system with output energy up to 90 mJ and a duration of 45 ns, and with a small time jitter. The second task was solved by placing the last OPA stage, the stretcher, MPA, and the compressor into the vacuum chamber.
The stretcher and the compressor were designed according to the standard Martinez and Offner schemes using gold diffraction gratings. The MPA- with AR-coated Fe:ZnSe crystal was designed with four curved mirrors with a focal length of 0.5 m, in order to maintain the caustics through the amplifier cavity. The scheme of the setup is illustrated in
Figure 3, and more detailed consideration can be found in [
47]. As a result, after using the amplifier, the pulse energy of 4.5 mJ was obtained, with a compressor of 3.5 mJ. The duration measured with the help of SHG-FROG was 150 fs, which corresponds to a peak power of ~20 GW.
However, due to the ultrabroad gain bandwidth, the Fe:ZnSe medium was able to amplify broadband pulses at a central wavelength of 4.55 µm with a spectral width of 220 nm. In such a way, the CO2 absorption line remained outside the laser pulse spectrum, which allowed this radiation to be sent to various remote experimental setups with no need to deliver it in vacuum.
A further increase in peak power was obtained by spectrum broadening in gaseous media [
70]. In this case, we used a mixture of krypton gases and oxygen. Krypton and oxygen were chosen for the experiments due to their high nonlinear refractive index, high critical pressure, the absence of their absorption lines in the vicinity of the pump spectrum, and their broad availability. In the case of pure krypton, spectral broadening develops symmetrically. However, at higher pressures, blue shifting dominates. In contrast to krypton, oxygen progressively shifts the spectrum into the mid-IR, leaving the blue side moderately broadened, despite the lower ionization potential. The generation of the pronounced red wing close to the pump spectrum is associated with the two main mechanisms discussed in the literature. The nonlinear downshift can be attributed to stimulated Raman scattering (SRS) originating from the interaction of the laser pulse with molecular rotational modes. Since the bandwidth of the laser system is around 5.4 THz at 1/e
2 of the intensity, while the oxygen rotational constant is B = 0.043 THz, SRS occurs in a cascaded manner. Another physical explanation for the strong red shifting is the combined action of the self-phase modulation (SPM) and free-electron plasma. The blue components of the spectrum, produced by the SPM at the trailing edge of the pulse, could be efficiently refracted by the generated free electrons. In this case, the formation of the red-shifted hump can be observed even in the noble gases. In our experiments, krypton and other noble gases (xenon and argon have also been tested) did not demonstrate significant spectral broadening into the mid-IR. Therefore, the formation of the pronounced red wing in oxygen is attributed to SRS in our case.
To obtain uniform spectral broadening in both the red and blue wings, a mixture of krypton and oxygen gases was used. The gases were mixed in a 2:1 ratio based on the approximate difference in their nonlinear refractive index. Controlling the laser beam caustics and changing the length of the gas cell made it possible to control the spectral broadening without reaching the filamentation regime, but while maintaining the pulse self-guiding regime. The post-compression of the accumulated chirp with a 2 mm-thick CaF2 plate placed right behind the cell provided a pulse duration of 62 fs, measured with the XFROG technique.
In the same way, the peak power of Cr:Forsterite radiation can be increased by broadening the spectrum in the gas. We have demonstrated the 3.5-fold compression of the laser pulse in supercritical xenon [
71]. Thus, this nonlinear compression concept is fairly universal, due to its low dispersion in gases and the possibility for fine tuning its nonlinearity and dispersion properties.
4.2. Ultrafast Direct Laser Amplification in Fe:CdSe Crystal at 5–5.5 μm
The Fe
2+-based laser crystal, Fe:CdSe, is interesting from the point of view of producing and amplifying ultrashort laser pulses in the longer wavelength region, up to 6 μm. Previously, the laser properties of this active medium were investigated in [
49], where nanosecond generation with an energy of 2 mJ was obtained when pumped with a nanosecond Er:YAG laser (30 mJ). Its main features are a short lifetime, high dependence on temperature, as well as the block structure of the crystal. The lifetime at room temperature was measured to be 20 ns, tripling when cooled with liquid nitrogen. Nevertheless, it’s broad gain and high cross-sections allow us to consider it as an effective mid-IR broadband amplifier.
Longer wavelength generation can be obtained in Fe:CdTe crystals [
72]. The amplification spectrum of this laser medium lies in the region of 4.5–6.8 μm; however, with direct pumping at a wavelength near 3 μm, the efficiency is quite low. In the work [
73], a cascade scheme via Fe:ZnSe was used (4.12 μm, 30 mJ) with a pumping system generator–amplifier operating on Er:YAG (2.94 μm, 90 mJ, 40 ns). This approach is relatively effective, but significantly complicates the experimental setup.
Our preliminary experiments show the significant amplification of ultrashort mid-IR pulses in Fe:CdSe crystals pumped with a Q-switched 3 μm laser. In the first experiment, laser pulses at the wavelength of 4.95 μm from OPA were used as a seed. This wavelength approximately corresponds to the center of the amplification bandwidth of the Fe:CdSe medium at room temperature. A Cr:Yb:Ho:YSGG laser (2.85 μm, 40 ns, up to 90 mJ) was used for pumping, the beam of which was focused on a crystal with an energy density of 1 J/cm2. An Fe:CdSe crystal with a thickness of 6 mm and an Fe2+ ion doping level of about 3.3 × 1018 cm−3 without anti-reflective coatings was studied. To increase the gain, the crystal was cooled by a thermoelectric cooler to −40 °C. The maximum gain observed in the experiment was 1.6 cm−1, which corresponds to a single pass gain of G = 2.4.
In the second experiment, the amplifying properties at a longer wavelength were investigated. The parametric amplifier was tuned to a wavelength of 5.5 μm with a spectrum width of 550 nm, which corresponds to the duration of a transform-limited pulse of 80 fs. An actively Q-switched Er:YAG laser (2.94 μm, 100 ns, 35 mJ) was used for pumping, since the absorption cross-section of the Fe:CdSe crystal at this wavelength is greater than 2.85 μm. The Fe:CdSe crystal was AR-coated with broadband coating to reduce the spontaneous emission. The crystal was installed in a liquid nitrogen cryostat equipped with a temperature sensor to control and vary the lifetime during the cooling. In the five-pass amplifier, pulses were amplified from 3.0 μJ to 56 μJ. At each pass, the spectrum shifted to the shorter wavelength region and was slightly narrowed. At the last pass, the central wavelength was 5067 nm with an FWHM of about 220 nm. In this regime, no beam distortion caused by small-scale filamentation was observed. The broadest spectra were realized with moderate cooling, but not at the temperature of liquid nitrogen. When cooled to cryogenic temperatures, the emission spectrum was strongly reduced from the long-wavelength side, which is characteristic of chalcogenide media and is associated with the shutdown of temperature-activated phonon transitions. Additionally, with strong cooling, an ASE background appeared in the form of a train of additional nanosecond pulses at wavelengths near the maximum of the gain spectrum at 4.5–4.7 μm.
As can be seen, the seed wavelength of 5.5 μm is not optimal for obtaining maximum energy characteristics; however, it provides access to longer wavelengths. Preliminary experiments show the possibility of obtaining more than 100 µJ as early as the third pass with the seed centered at a wavelength of 5.2 μm. Thus, this laser medium can be used as an effective amplifier of broadband laser pulses at wavelengths of more than 5 μm, with direct pumping by a Q-switched 3 μm laser.
4.3. Fe:ZnSe Mode-Locked Oscillator and Nonlinear Optical Materials
Another, perhaps more obvious, but rather more complicated, method of generating ultrashort laser pulses in the mid-IR range is the development of a mode-locked laser oscillator based on an iron-doped crystal. Such sources operate at a high repetition rate (~100 MHz), with high average power (~Watts) and high beam quality.
The development of continuous-wave and quasi-continuous-wave Fe-based lasers has been limited for a long time by the lack of powerful and reliable three-micron pumping sources. Currently, studies devoted to the transfer of excitation from chromium ions to iron ions in co-doped crystals are also being conducted, since chromium pumping sources are more accessible [
74]. However, due to the active development of Er:ZBLAN fiber lasers [
75], operating at a wavelength of 2.8 μm, the effective pumping of the Fe:ZnSe crystal has become possible. We demonstrated the first CW Fe:ZnSe laser with direct fiber pumping [
76].
The next step was the demonstration of the first femtosecond Fe:ZnSe mode-locked oscillator [
46]. As a rule, passive mode-locking is implemented based on Kerr lens nonlinear losses or using semiconductor saturable absorber mirrors (SESAM). SESAMs operating at wavelengths higher than 3 µm are just beginning to appear [
77]. The use of graphene for this purpose in the mid-IR range has been demonstrated [
62,
78]. This material is not spectral-selective, unlike SESAM, and thus does not limit generation bandwidth.
Since the Fe:ZnSe has a low lifetime at room temperature, for quasi-CW operation, cryogenic cooling is required, which was implemented using liquid nitrogen. In order not to use a crystal cryostat with input windows and not to introduce additional dispersion into the ultrashort pulse, the entire cavity was placed in a vacuum chamber with liquid nitrogen supply to a crystal. The cavity was formed by the classic scheme of the X-resonator at a pulse frequency of 100 MHz, focusing on a monolayer graphene. As a result, the train of pulses, with an average power of 415 mW and 7 W pump power offered by an Er:ZBLAN laser, was obtained. The spectrum width of 42 nm measured by the scanning monochromator supports the duration of 732 fs of transform-limited pulse.
The more desired regime is Kerr lens mode-locking in an Fe:ZnSe cavity, which as a rule allows for shorter pulse duration. However, so far, there have been no new statements about the development of mode-locked Fe:ZnSe oscillators. Probably, the Fe:ZnSe media has some properties that do not allow this regime to be implemented. In our research group, work was carried out to increase the output power of the laser (up to 1.2 W), and other cavity geometries were tested. The output radiation represents a CW signal strongly modulated by the cavity roundtrip period. We believe that this is the effect of saturation gain, which prevents traditional methods from getting rid of amplified spontaneous emissions.
A promising direction is the development of new nonlinear optical materials in the mid-IR range. They can be used as saturating absorbers in laser cavities, as well as frequency converters. Materials with high nonlinearity, whose optical properties can be changed using a low-intensity field, are required for many applications. Such applications primarily include integrated optics, the production of CMOS devices, telecommunications, data processing and storage, spectroscopy, and quantum information technologies [
79]. It has recently been found that materials with vanishingly low permittivity (Epsilon-near-zero (ENZ)) exhibit extremely high nonlinearity at certain wavelengths, which affects the efficiency of harmonic generation, frequency mixing, and the electro-optical effect [
80]. Such materials include, for example, doped semiconductors such as tin-doped indium oxide (ITO) and aluminum-doped zinc oxide (AZO), whose wavelengths of zero permittivity are in the near-IR range. In the mid-IR range, such materials include cadmium oxide doped with indium and dysprosium, which behave like ENZ materials with high electron mobility. Compared to bulk nonlinear crystals, such materials can be scaled and integrated into nanophotonics systems.
5. Strong-Field Physics Applications with the Use of Near- and Mid-IR Ultrafast Sources
5.1. THz Generation in Organic Crystals
Interest in the generation of powerful terahertz (THz) radiation (0.1–10 THz) is growing due to the maturation of nonlinear optics in the THz range and various kinds of applications, such as time-resolved spectroscopy, the study of ultrafast magnetization, imaging, etc. THz generation approaches include optical rectification in nonlinear organic [
81] and inorganic crystals [
82], as well as two-color filamentation in gases [
83]. DAST, DSTMS and OH1 organic nonlinear crystals provide high nonlinearity and high transparency for both optical pumping and THz fields, making the optical rectification process efficient (1–3%). The two-color filamentation method has significantly smaller efficiency and strong angular divergence form the conical structure of THz radiation. However, this method offers a broader bandwidth of THz pulses and is free from the risk of active medium optical breakdown caused by the high pump intensity. However, the efficiency of generation in organic crystals is limited by the process of multiphoton absorption and, as a result, the breakdown threshold of crystal. The transition to longer waves in the transparency band of the crystal allows for reducing multiphoton absorption and increasing the damage threshold, as well as increasing the efficiency of the transformation by reducing the quantum defect. However, the dispersion properties of these materials call for a near-IR (1.2–1.5 mm) pump source.
We have investigated this process in various crystals using a multi-gigawatt Cr:Forsterite laser system (1240 nm, 110 fs, 5 mJ). Preliminary experiments were performed with DAST and BNA crystals with a thickness of 0.4 mm and 0.5 mm, correspondingly. Only a fraction of the laser energy (up to 2.5 mJ) was used to avoid crystal damage. The registration of THz radiation was performed with a Golay cell and a pyroelectric detector. We used a Teflon plate, paper, and/or a Tydex LPF10.9-24 filter to cut off the laser pulses from THz radiation. The THz radiation spectrum was characterized with a Michelson interferometer, with a silicon wafer as a beam splitter.
Figure 4 shows the dependence of the output energy and conversion efficiency on the pumping energy density for the DAST crystal. The maximum conversion efficiency is about 1.7%, which is slightly lower than the results obtained earlier (2.1%) [
84]. The lower conversion efficiency may be due to the non-optimal crystal thickness (the appearance of the reverse transformation effect), or the insufficient transparency area of the filters we used for the selection of THz radiation. A significantly lower conversion efficiency was obtained in the BNA crystal, which may also be related to the spectral selection of the registered radiation.
Figure 5 shows the first-order correlation function and the spectrum of THz radiation obtained based on the Fourier transform. It can be seen that the BNA crystal allows for obtaining a significantly broader spectrum (up to 5–6 THz), while the radiation spectrum of the DAST crystal is mainly localized in the vicinity of 2 THz. In [
84], a broader spectrum of THz radiation was obtained from the DAST crystal, indicating non-optimal crystal thickness in our case. The broad spectrum of the BNA crystal is in good agreement with the results of [
85], where the signal wave of a parametric amplifier was used for pumping. It is worth noting that the Cr:Forsterite laser was used to pump the BNA crystal for the first time.
Then, we developed a two-stage mid-IR OPA pumped by a Ti:Sapphire laser (810 nm, 50 fs, 14 mJ). The OPA is based on BBO crystals with a thickness of 2 mm and type II phase-matching. The generation of supercontinuum used as a seed during the parametric gain occurred in the sapphire crystal. As a result of parametric transformation, radiation was obtained, tuning in the ranges of 1.1–1.6 μm (signal wave) and 1.6–2.6 μm (idle wave). The output energy of the generated IR pulses was 840 and 280 μJ at the wavelengths of 1.3 μm and 2 μm, respectively.
The resulting radiation was used as a pump for generating THz radiation in the DAST crystal. The OPA was tuned to the wavelengths of 1.3 μm (signal wave) and 2 μm (single wave), with a spectrum width of ~65 nm and 130 nm, respectively, which corresponds to the duration of transformed-limited pulses (40 and 45 fs). A pumping beam with a total energy of about 200 μJ in both waves was delivered to the crystal with a fluency of 5 mJ/cm2. The efficiency of optical transformation in a DAST crystal with a thickness of 500 μm was about 0.015%, and the energy of the generated THz radiation, in this case, was ~30 nJ. The fairly low value of the efficiency can be explained by the non-optimal length of the crystal used, and the insufficient transparency area of the filter used for the selection of THz radiation.
The possibility of increasing the efficiency of nonlinear conversion was studied with numerical simulation based on solving a system of shortened equations describing three-wave interaction [
86]. The generation processes of sum and difference frequencies were considered in the approximations of slowly varying amplitudes and plane waves, considering the material dispersion and absorption in the organic DAST crystal. The numerical solution of the equations was carried out using the fourth-order Runge–Kutta method with a spatial resolution of 1 μm. As a result of simulation, it was found that when using a signal wave (at a wavelength of 1.3 μm) for pumping the DAST crystal, the main factor limiting the efficiency of the optical terahertz conversion was the presence of two-photon absorption in this crystal at pump wavelengths ranging up to 1.4 μm. The chirping of signal wave pulses up to 140 fs allowed for loosening this effect by reducing the pump pulse intensity in the crystal and, therefore, increasing the efficiency of the conversion to 2.3%. The chirping of the idle pulse up to 200 fs made it possible to increase the efficiency to 3.6%, and the optimal pump saturation fluency increased to 16 mJ/cm
2.
5.2. Optical Harmonics Generation in Gases by Near- and Mid-IR Laser Pulses
The process of harmonics generation in gases and gas jets is promising for obtaining UV and X-ray radiation. Compared to solid-state targets, gas and gas jets have the advantages of the absence of the possibility of an optical breakdown of the medium, and therefore do not limit the intensity of the excitation radiation. At the same time, the properties of gases (nonlinearity, ionization cross section, dispersion) can be properly adjusted for a specific interaction regime by changing both the intensity of the driving field and the temperature and pressure of the medium. Low-order harmonic generation allows us to create the compact laser sources in the UV/VUV range required for many applications. A present, high-order harmonics are of the greatest interest in relation to attosecond physics. The use of longer-wavelength ultrafast laser sources will increase the yield of optical harmonics due to the scaling of the mean quiver energy of the electron in the laser field as a product of laser intensity and squared wavelength ∼I ×
λ2. Therefore, we investigated the efficiency of harmonic generation from ultrashort laser pulses in the near (1.24 μm) and mid-IR ranges (4.4 μm) in gases [
87].
Unlike atomic gases, molecular gases have a significant number of resonance lines and overtones in the near- and mid-IR ranges, which can be used to effectively increase the linear and nonlinear parts of the refractive index. From this point of view, most promising is the use of carbon dioxide (CO2), since this gas has the second-largest n2 in the near-IR range and absorption bands in the vicinity of 2 and 4.3 μm.
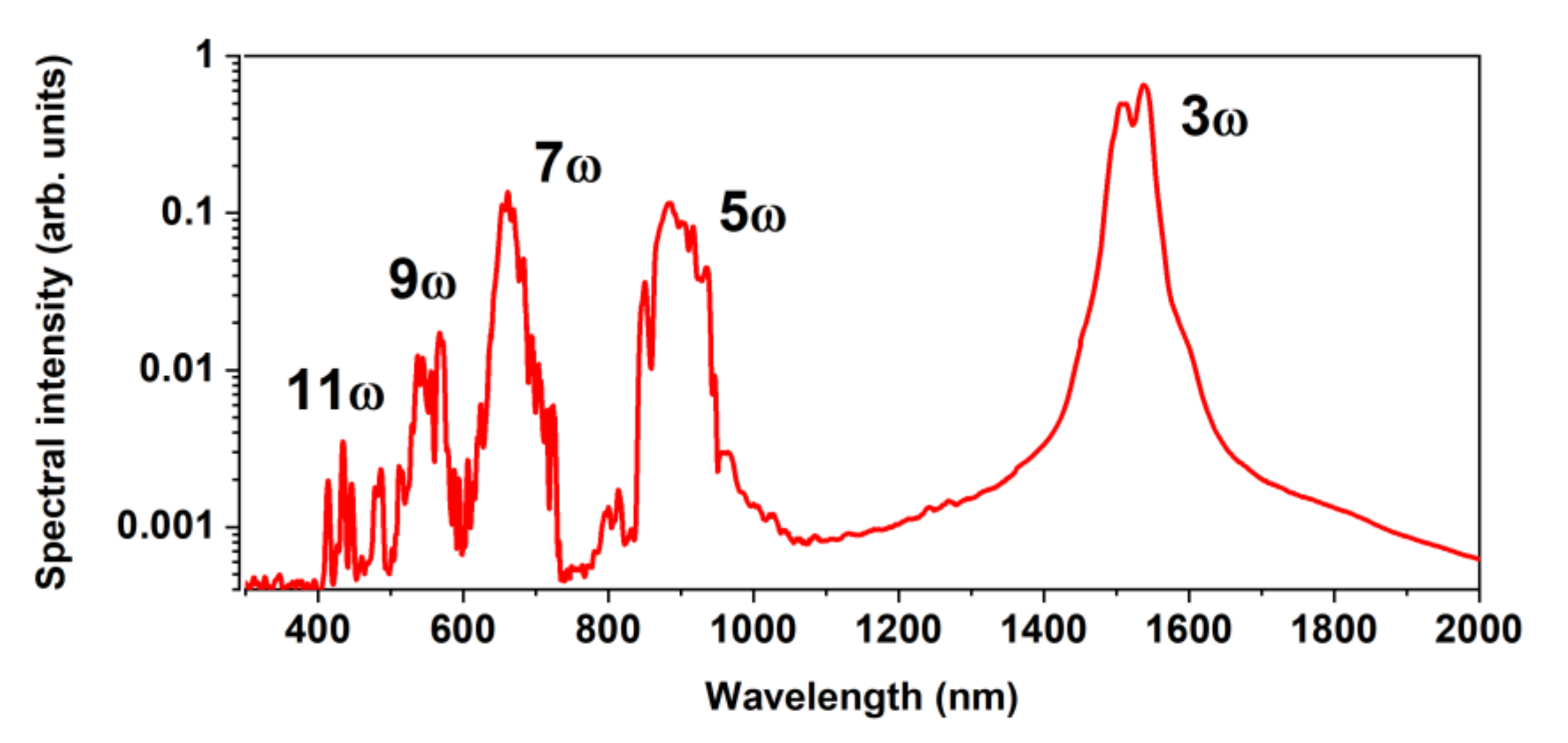
The study of the efficiency of harmonic generation under tight focusing was carried out with the near-IR radiation (1.24 μm) of a Cr:Forsterite laser system in xenon. Harmonics were generated in an 18 mm-long gas cell with sapphire windows 4 mm thick. It had a pronounced maximum, depending on the intensity of the pump radiation. The maximum conversion efficiency was 11 × 10
−4, and was 4.4 × 10
−4 for the third harmonic (TH) and the fifth harmonic (FH), respectively; these values were achieved at pressures of 8 and 5 bar (
Figure 6).
The non-monotonic behavior of the harmonic output is usually associated with the presence of a non-zero phase mismatch (Δk). However, in a regime of tight focusing inside normally dispersive media, odd harmonic generation is prohibited. To explain the obtained dependencies, we propose a simple analytical model, described in detail in our work [
87]. Within this model, the appearance of a pronounced maximum depending on the output of harmonics on pressure is associated with a change in phase relations. In the regime of the tight focusing of radiation into an isotropic medium, the signal of TH and FH is zero due to destructive interference before and after the focal plane. However, the appearance of inhomogeneity (such as plasma) removes the symmetry condition, and the signal at the exit from the medium becomes non-zero. According to the model, the TH and FH signals reach their maximum at values of Δk equal to 94 cm
−1 and 300 cm
−1, respectively. In the absence of plasma generation (at low intensities), to achieve maximum conversion efficiency, a pressure of the order of 14 and 7 bar is required for TH and FH, respectively. At high intensities, the generated plasma introduces additional phase disorder, which leads to a decrease in the value of the optimal pressure.
Recently, problems of resonant light–matter interactions have been addressed anew in the view of low- and high-harmonic generation processes, since, in this case, atomic resonances may induce enhancements in the harmonics yield. We have proposed the usage of molecular resonances located near the pump spectrum for the enhancement of the harmonics yield driven by mid-IR fields. To study the process of harmonic generation under conditions of synthesized nonlinearity in a mixture of Xe–CO
2 gases, as well as to identify the role of resonances, the high-power radiation of the mid-IR range of the Fe:ZnSe laser system was used, whose generation spectrum partially overlaps with the CO
2 absorption band (4.3 μm) [
39]. In this case, the pump radiation directly resonantly affects the medium, and is partially absorbed in it. The radiation of an Fe:ZnSe laser system operating at a central wavelength of 4.45 μm was focused in an 11 cm-long gas cell with an intensity of (1.8–1.9) × 10
13 W/cm
2. For the experiments, the cell was filled with a mixture of Xe–CO
2 gases in the proportion of 1 bar CO
2 and 48–50 bar Xe. The concentration of CO
2 and Xe molecules was on the order of 2.5 × 10
19 and 1.25 × 10
21 cm
−3, respectively. In such a mixture, the generation of optical harmonics up to the 11th was observed (
Figure 7). Additionally, the frequency–angular spectra of harmonics from the 5th to the 11th were taken with a visible range spectrometer. In addition to the axial part, harmonics also propagated with significant divergence. This may indicate the generation of a part of the harmonic signal by the mechanism of four-wave mixing on the nonlinearity of a lower (third) order [
88].
To sum up, it should be noted that the use of carbon dioxide to control the dispersion of the medium is of considerable interest for the generation of higher-order harmonics under plasma generation conditions. When using a more rarefied inert gas (1–5 bar), the refractive index for harmonic radiation may be less than the refractive index for pump radiation. In this case, the phase disorder introduced by the dispersion of the medium will be negative. To compensate for it, plasma generation is necessary, providing a positive detuning of Δkplasma, which means that the condition of phase matching Δk = 0 can be achieved in the UV and VUV spectral regions, where the conversion efficiency is low, especially in the case of using long-wave pumping sources. In addition, due to the use of gases under low pressure (up to 5 bar), the phase matching width can reach tens of nanometers, which makes it possible to generate ultrashort pulses in this wavelength range.
5.3. Optimization of Deposited Energy Density in the Process of Femtosecond Micromachining
One of the main reasons for high-power laser system development in the near and mid-IR ranges is the optimization of deposited energy density (DED) during the femtosecond 3D processing of materials (dielectrics and semiconductors). DED is a universal indicator of the laser pulse’s impact on matter [
89]. DED is defined as the absorbed energy of a laser pulse in a unit volume [
23]. The higher this parameter, the more precise and energy-efficient is the formed micromodification [
25]. If the DED is less than the threshold value of micromodification formation (determined by the latent heat of fusion), then no micromodification is formed. In the case of dielectrics, it is relatively easy to create micromodifications inside a sample. Due to the large band gap (~10 eV), plasma is produced only in the waist of the laser beam, which will make it possible to create micromodifications of micrometer size under the tight (NA > 0.3) focusing of femtosecond laser radiation [
90]. Under such high values of DED, in addition to micromodification formation, multimegabar shock waves are generated, and a cascade of phase transitions occurs. As a result, a void-like micromodification is formed: the void in the center is surrounded by the amorphous material and/or its new phases [
25]. These new phases could be detected by Raman spectroscopy or X-ray diffraction, as was demonstrated for aluminum [
91,
92].
To localize the laser effects even more effectively, it is necessary to achieve a larger DED in a smaller volume. To achieve higher DED, we applied a two-color laser impact on the dielectric [
23]. Within the framework of this method, the first laser pulse with a shorter wavelength (UV or visible) induced seed electrons. The multiphoton order for shorter wavelengths is lower, and such radiation is more focused; as a result, the localization of laser energy is higher than for IR pulses [
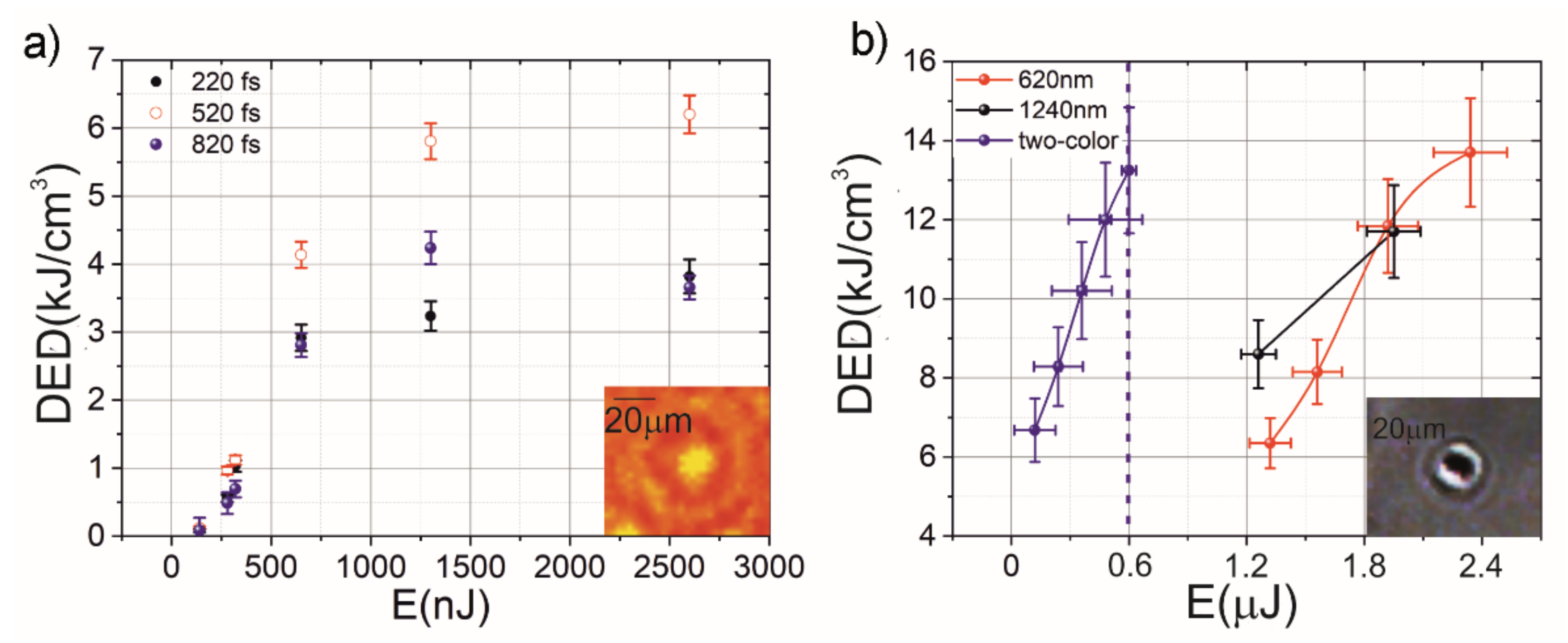
25]. Moreover, the pulse energy is set below the threshold of the formation of a micromodification. The second, more powerful IR pulse (due to the more efficient avalanche ionization (~λ
2)) efficiently transfers its energy to the electrons, induced by the first laser pulse, and leads to an increase in DED up to 15 kJ/cm
3 in SiO
2 for a 1240 + 620 nm pair (see
Figure 8b). As a result, at lower laser pulse energies, it is possible to achieve higher DED and smaller (~500 nm) micromodifications [
93]. It is possible to increase the DED further in the case of the elliptical polarization of the laser pulse, since electrons gain more energy in a circularly polarized field [
94].
In the case of semiconductors, femtosecond micromachining is a far more complicated process due to the difficulty of achieving high DED [
95]. Strong two-photon absorption, the high nonlinearity of semiconductor materials with a narrow band gap, strong spherical aberrations [
96], and the “softening” of focusing [
97] prevented the sufficient localizing of the laser’s impact in the region of the laser beam waist. The laser radiation energy was absorbed before the focal plane due to the “delocalization effect” on the formed high-density microplasma [
98]. This, in turn, prevented the optical breakdown in Si and other semiconductors. As a result, some research groups have preferred to use a multi-pulse regime (whereby micromodifications are formed by multiple pulses without focus spot moving) for semiconductors, and even nanosecond pulses [
99,
100]. Even though volumetric modification was widely discussed in the presented scientific articles, the thermal nature of the interaction does not allow one to achieve such a level of control over the spatial localization of laser energy, as in the case of femtosecond breakdown inside a dielectric, which makes such approaches unrealistic for high-precision applications.
In analogy to dielectrics, it is possible to create seed pre-plasma to localize the laser’s impact [
101]. Chirped laser pulses can also be used to increase the localization of the laser’s impact [
102]. Another way to localize laser energy inside the volume is to move to the mid-IR wavelength range. In this case (in comparison with the near-IR), the balance between tunneling, multiphoton and avalanche ionization shifts, and the heating in the laser pulse fields, begins to play an important role [
53]. In the case of semiconductors, considering the relatively high multiphoton order, plasma delivery in the pre-focal region is weaker. As a result, it becomes possible to focus laser radiation to 10 μm
2 without hyperfocusing [
103], using only lenses with a high numerical aperture (NA > 0.8). In silicon, to achieve the formation of micromodifications, it is necessary to reach a DED equal to at least 4 kJ/cm
3. Under the tight focusing (NA = 0.86) of a mid-IR femtosecond laser pulse into silicon, we achieved a DED of 7 kJ/cm
3 (
Figure 8a).
6. Conclusions
Ultrafast mid-IR laser sources, based on optical parametric amplifiers pumped with a gigawatt femtosecond near-IR laser system and chirped pulse amplification in Fe2+-ion doped chalcogenides, represent the basis for a promising multispectral (from UV up to THz) femtosecond photonic platform. Effective mid-IR optical parametric amplifiers at wavelengths greater than 4 μm can be designed with the pump of a powerful Cr:Forsterite laser system, although this practice is not widespread. Such parametric sources based on oxide (BBO) and non-oxide crystals (AGS, KTA) provide access to broadly tunable (1.6–5.6 μm), ultrashort laser pulses, which can be used as a seed in powerful chirped pulse amplification schemes based on iron ion-doped chalcogenide crystals (Fe:ZnSe, as well as Fe:CdSe). Flexible methods have been developed for controlling the spectral and temporal characteristics (center frequency shift, spectrum broadening, nonlinear compression) of powerful (>10 GW) femtosecond near- and mid-IR radiation during filamentation (self-guiding) in dense gas media, with controlled dispersion and nonlinearity, by the selection of mixtures (inert gas, molecular gas) and pressures. The developed approach allows for obtaining few-cycle optical laser pulses with the possibility of scaling the initial peak power, which will become an alternative to complex multistage laser systems based on the parametric amplification of chirped pulses, and will be useful in fundamental and applied research focused on the problems of the interaction of intense laser radiation with matter, including THz radiation, optical harmonics generation, and extreme states of matter studies.