Decoherence-Induced Sudden Death of Entanglement and Bell Nonlocality

Abstract

Decoherence due to the unwanted interaction between a quantum system and environment leads to the degradation of quantum coherence. In particular, for an entangled state, decoherence makes a loss of entanglement and Bell nonlocality known as entanglement sudden death (ESD), and Bell nonlocality sudden death (BNSD). Here, we theoretically investigate the entanglement and Bell nonlocality of a bipartite entangled state under three types of decoherence, amplitude damping, phase damping, and depolarizing. Our result provides the bound of decoherence strength that does not lose the entanglement and Bell nonlocality. In addition, we find two interesting features. One is that the entanglement can survive even though one of the entangled qubits is affected by a large strength of decoherence if the other qubit is affected by a small enough strength of decoherence except for the depolarizing. The second one is that when a specific form of entangled state is under amplitude damping, the Bell nonlocality shows an asymmetric behavior respect to the decoherence strengths on each qubit. Our work provides comprehensive information on ESD and BNSD for the bipartite entangled state which will be useful to implement quantum information processing in the presence of decoherence.

1. Introduction

Entanglement, which is a physical phenomenon that a quantum state of multi-qubit cannot be factored as a product of the individual qubit states [1], has been utilized as a basic resource of quantum information processing such as quantum communication [2,3], quantum teleportation [4,5,6], quantum computation [7], and quantum metrology [8]. One of the features of the entangled state is that a quantum nonlocal correlation can be obtained by local measurements on the distant entangled qubits, which is incompatible with a local hidden variable theory. This is the so-called Bell nonlocality [9]. Bell nonlocality also has been applied to the quantum cryptograph to analyze the security of quantum key distribution protocols [10,11,12,13].

When an entangled state is under decoherence due to the unwanted interaction between a quantum system and environment, quantum coherence is degraded which leads to the degradation of entanglement and Bell nonlocality [14]. Eventually, the effect of decoherence disturbs to implementation of various quantum information processing properly. In order to perform a proper quantum information processing under the decoherence, entanglement purification protocols such as entanglement distillation [15,16,17] and entanglement concentration [18,19] can be used to recover a maximally entangled state using a large number of copies of partially entangled states. Even a poorly entangled state can be restored to a highly entangled state with the help of the entanglement purification protocols. However, when the decoherence makes a loss of entanglement and Bell nonlocality known as entanglement sudden death (ESD) [20] and Bell nonlocality sudden death (BNSD) [21], it is not possible to apply the entanglement purification protocols which prohibits any quantum information tasks. Therefore, it is of importance to investigate the ESD and BNSD of an entangled state in the presence of decoherence and to find the bound of decoherence strength where the entanglement and Bell nonlocality are persisted.

It has been widely studied that the effect of decoherence on a bipartite entangled state results in ESD and BNSD both in theory and experiment [22,23,24,25,26,27]. However, these studies have been focused on the two types of decoherence, amplitude damping and phase damping. Moreover, it has been assumed that each qubit is affected by the same strength of decoherence which is not a realistic situation in the quantum information protocol that utilized the distributed entangled qubits.

In this paper, we theoretically investigate the entanglement and Bell nonlocality of the bipartite entangled state under three types of decoherence, amplitude damping, phase damping, and depolarizing which are the elemental noise models in quantum systems. In addition, for further study, we assume that each qubit of entangled qubits is affected by the different strengths of decoherence to investigate the ESD and BNSD. Our result shows that ESD occurs for a specific form of bipartite entangled state under amplitude damping while ESD does not occur under phase damping and occurs under depolarizing. In the case of Bell nonlocality, BNSD always occurs under amplitude damping and depolarizing, and does not occur under phase damping. Moreover, we find two interesting features for the case of that each qubit of entangled qubits is affected by the different strengths of decoherence. One is that the entanglement can survive even though one of the entangled qubits is affected by a large strength of decoherence if the other qubit is affected by a small enough strength of decoherence except for the depolarizing. The second one is that when a specific form of entangled state is under amplitude damping, the Bell nonlocality shows an asymmetric behavior respect to the decoherence strengths on each qubit. Our work provides comprehensive information on ESD and BNSD for the bipartite entangled state which will be useful to implement quantum information processing in the presence of decoherence.

2. Materials and Methods

2.1. Bipartite Entangled State under Decoherence

Decoherence caused by an unavoidable coupling between a system and environment can be expressed by operations acting on the system [22,28]. Given a single qubit state $\rho$, the system coupled to the environment can be written as

$$\rho \to \mathcal{E}\left\{\rho \right\}=\sum _{i=1}^n{E}_i\rho E_i^{†},$$

(1)

where $\mathcal{E}$ is a decoherence channel, and $E_i$ are the so-called Kraus operators satisfying ${\sum }_{i=1}^n{E}_i^{†}{E}_i=\mathbb{1}$. For the three types of decoherence, amplitude damping, phase damping, and depolarizing, the corresponding Kraus operators described with a strength of decoherence D are shown in

Table 1. Kraus operators representing three types of decoherence. Here, $0\le D\le 1$ is the magnitude of the decoherence and $\overline{D}=1-D$. ${\widehat{\sigma }}_{x,y,z}$ are the Pauli matrices.

Decoherence	Kraus Operators
Amplitude damping	$E_1=|0\rangle \langle 0|+\sqrt{\overline{D}}|1\rangle \langle 1|,$
	$E_2=\sqrt{D}|0\rangle \langle 1|.$
Phase damping	$E_1=|0\rangle \langle 0|+\sqrt{\overline{D}}|1\rangle \langle 1|,$
	$E_2=\sqrt{D}|1\rangle \langle 1|.$
Depolarizing	$E_1=\sqrt{1-3D/4}\mathbb{1},E_2=\sqrt{D/4}{\widehat{\sigma }}_x,$
	$E_3=\sqrt{D/4}{\widehat{\sigma }}_y,E_4=\sqrt{D/4}{\widehat{\sigma }}_z.$

.

Here, the strength of the decoherence D can be represented by the interaction time t between the system and environment, $D=1-\exp (-\mathrm{\Gamma }t)$ where $\mathrm{\Gamma }$ is a decay rate. If there is no interaction between the system and environment, D becomes zero, that is the system does not lose the quantum coherence. When the interaction time goes to infinity, the strength of decoherence becomes unity where the system completely loses the quantum coherence. Note that the amplitude damping exhibits an asymmetric nature in which $|1\rangle$ experiences the damping effect while $|0\rangle$ is not affected.

For a two-qubit state ${\rho }_{AB}$, the state coupled to the environment can be described as:

$${\rho }_{AB}\to {\mathcal{E}}_A\left\{{\mathcal{E}}_B\left\{{\rho }_{AB}\right\}\right\}={\mathcal{E}}_A\left\{\sum _{i=1}^n{E}_i^B{{\rho }_{AB}{E}_i^B}^{†}\right\}=\sum _{j=1}^n\sum _{i=1}^n{E}_j^A{E}_i^B{{\rho }_{AB}{E}_i^B}^{†}{E_j^A}^{†},$$

(2)

where A and B denote qubit A and qubit B, respectively. Now, we consider the pure two-qubit entangled states, $|\mathrm{\Phi }\rangle ={cos\theta |0\rangle }_A{|0\rangle }_B+{sin\theta |1\rangle }_A{|1\rangle }_B$, and $|\mathrm{\Psi }\rangle ={cos\theta |0\rangle }_A{|1\rangle }_B+{sin\theta |1\rangle }_A{|0\rangle }_B$ where $0\le \theta \le \pi /2$ to investigate the entanglement and Bell nonlocality.

2.1.1. Amplitude Damping Channel

Amplitude damping channel (ADC) describes the effect of energy dissipation from a quantum system. When qubits A and B are under ADC with the magnitude of decoherence of $D_A({\overline{D}}_A\equiv 1-D_A)$ and $D_B({\overline{D}}_B\equiv 1-D_B)$, the state $|\mathrm{\Phi }\rangle$ becomes,

$${\rho }_{\mathrm{\Phi },ADC}=\left[\begin{array}{cccc}{\rho }_{11,\mathrm{\Phi }}& 0& 0& {\rho }_{14,\mathrm{\Phi }}\\ 0& {\rho }_{22,\mathrm{\Phi }}& 0& 0\\ 0& 0& {\rho }_{33,\mathrm{\Phi }}& 0\\ {\rho }_{41,\mathrm{\Phi }}& 0& 0& {\rho }_{44,\mathrm{\Phi }}\end{array}\right],$$

(3)

where ${\rho }_{11,\mathrm{\Phi }}={cos}^2\theta +D_A{D}_B{sin}^2\theta$, ${\rho }_{14,\mathrm{\Phi }}={\rho }_{41,\mathrm{\Phi }}=\sqrt{{\overline{D}}_A{\overline{D}}_B}cos\theta sin\theta$, ${\rho }_{22,\mathrm{\Phi }}=D_A{\overline{D}}_B$${sin}^2\theta$, ${\rho }_{33,\mathrm{\Phi }}={\overline{D}}_A{D}_B{sin}^2\theta$, and ${\rho }_{44,\mathrm{\Phi }}={\overline{D}}_A{\overline{D}}_B{sin}^2\theta$, respectively. Furthermore, the state $|\mathrm{\Psi }\rangle$ becomes,

$${\rho }_{\mathrm{\Psi },ADC}=\left[\begin{array}{cccc}{\rho }_{11,\mathrm{\Psi }}& 0& 0& 0\\ 0& {\rho }_{22,\mathrm{\Psi }}& {\rho }_{23,\mathrm{\Psi }}& 0\\ 0& {\rho }_{32,\mathrm{\Psi }}& {\rho }_{33,\mathrm{\Psi }}& 0\\ 0& 0& 0& 0\end{array}\right],$$

(4)

where ${\rho }_{11,\mathrm{\Psi }}=D_A{sin}^2\theta +D_B{cos}^2\theta$, ${\rho }_{22,\mathrm{\Psi }}={\overline{D}}_B{cos}^2\theta$, ${\rho }_{23,\mathrm{\Psi }}={\rho }_{32,\mathrm{\Psi }}=\sqrt{{\overline{D}}_A{\overline{D}}_B}cos\theta sin\theta$, and ${\rho }_{33,\mathrm{\Psi }}={\overline{D}}_A{sin}^2\theta$, respectively.

2.1.2. Phase Damping Channel

Phase damping channel (PDC) describes the loss of quantum information without loss of energy. When qubits A and B are under PDC with the magnitude of decoherence of $D_A$ and $D_B$, the state $|\mathrm{\Phi }\rangle$ becomes,

$${\rho }_{\mathrm{\Phi },PDC}=\left[\begin{array}{cccc}{\rho }_{11,\mathrm{\Phi }}& 0& 0& {\rho }_{14,\mathrm{\Phi }}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ {\rho }_{41,\mathrm{\Phi }}& 0& 0& {\rho }_{44,\mathrm{\Phi }}\end{array}\right],$$

(5)

where ${\rho }_{11,\mathrm{\Phi }}={cos}^2\theta$, ${\rho }_{14,\mathrm{\Phi }}={\rho }_{41,\mathrm{\Phi }}=\sqrt{{\overline{D}}_A{\overline{D}}_B}cos\theta sin\theta$, and ${\rho }_{44,\mathrm{\Phi }}={sin}^2\theta$, respectively. Furthermore, the state $|\mathrm{\Psi }\rangle$ becomes,

$${\rho }_{\mathrm{\Psi },PDC}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& {\rho }_{22,\mathrm{\Psi }}& {\rho }_{23,\mathrm{\Psi }}& 0\\ 0& {\rho }_{32,\mathrm{\Psi }}& {\rho }_{33,\mathrm{\Psi }}& 0\\ 0& 0& 0& 0\end{array}\right],$$

(6)

where ${\rho }_{22,\mathrm{\Psi }}={cos}^2\theta$, ${\rho }_{23,\mathrm{\Psi }}={\rho }_{32,\mathrm{\Psi }}=\sqrt{{\overline{D}}_A{\overline{D}}_B}cos\theta sin\theta$, and ${\rho }_{33,\mathrm{\Psi }}={sin}^2\theta$.

2.1.3. Depolarizing Channel

Depolarizing channel (DC) describes the white noise introduced to a quantum system. When qubits A and B are under DC with the magnitude of decoherence of $D_A$ and $D_B$, the state $|\mathrm{\Phi }\rangle$ becomes,

$${\rho }_{\mathrm{\Phi },DC}=\frac{1}{4}\left[\begin{array}{cccc}{\rho }_{11,\mathrm{\Phi }}& 0& 0& {\rho }_{14,\mathrm{\Phi }}\\ 0& {\rho }_{22,\mathrm{\Phi }}& 0& 0\\ 0& 0& {\rho }_{33,\mathrm{\Phi }}& 0\\ {\rho }_{41,\mathrm{\Phi }}& 0& 0& {\rho }_{44,\mathrm{\Phi }}\end{array}\right],$$

(7)

where ${\rho }_{11,\mathrm{\Phi }}=1+{\overline{D}}_A{\overline{D}}_B+({\overline{D}}_A+{\overline{D}}_B)cos2\theta$, ${\rho }_{14,\mathrm{\Phi }}={\rho }_{41,\mathrm{\Phi }}=4{\overline{D}}_A{\overline{D}}_{B}cos\theta sin\theta$, ${\rho }_{22,\mathrm{\Phi }}=1-{\overline{D}}_A{\overline{D}}_B+(D_B-D_A)cos2\theta$, ${\rho }_{33,\mathrm{\Phi }}=1-{\overline{D}}_A{\overline{D}}_B+(D_A-D_B)cos2\theta$, and ${\rho }_{44,\mathrm{\Phi }}=1+{\overline{D}}_A{\overline{D}}_B-({\overline{D}}_A+{\overline{D}}_B)cos2\theta$, respectively. Furthermore, the state $|\mathrm{\Psi }\rangle$ becomes,

$${\rho }_{\mathrm{\Psi },DC}=\frac{1}{4}\left[\begin{array}{cccc}{\rho }_{11,\mathrm{\Psi }}& 0& 0& 0\\ 0& {\rho }_{22,\mathrm{\Psi }}& {\rho }_{23,\mathrm{\Psi }}& 0\\ 0& {\rho }_{32,\mathrm{\Psi }}& {\rho }_{33,\mathrm{\Psi }}& 0\\ 0& 0& 0& {\rho }_{44,\mathrm{\Psi }}\end{array}\right],$$

(8)

where ${\rho }_{11,\mathrm{\Psi }}=1-{\overline{D}}_A{\overline{D}}_B+(D_B-D_A)cos2\theta$, ${\rho }_{22,\mathrm{\Psi }}=1+{\overline{D}}_A{\overline{D}}_B+({\overline{D}}_A+{\overline{D}}_B)cos2\theta$, ${\rho }_{23,\mathrm{\Psi }}={\rho }_{32,\mathrm{\Psi }}=4{\overline{D}}_A{\overline{D}}_{B}cos\theta sin\theta$, ${\rho }_{33,\mathrm{\Psi }}=1+{\overline{D}}_A{\overline{D}}_B-({\overline{D}}_A+{\overline{D}}_B)cos2\theta$, and ${\rho }_{44,\mathrm{\Psi }}=1-{\overline{D}}_A{\overline{D}}_B+(D_A-D_B)cos2\theta$, respectively.

2.2. Entanglement Sudden Death

Entanglement is a physical phenomenon that a quantum state of multi-qubit cannot be factored as a product of the individual qubit states. The entanglement of a given two-qubit state $\rho$ is quantified by the concurrence defined as:

$$C=max\{0,\sqrt{{\lambda }_1}-\sqrt{{\lambda }_2}-\sqrt{{\lambda }_3}-\sqrt{{\lambda }_4}\},$$

(9)

where ${\lambda }_i$s are the Eigenvalues of

$$\rho ({\sigma }_y\otimes {\sigma }_y){\rho }^{*}({\sigma }_y\otimes {\sigma }_y),$$

(10)

in decreasing order [29]. When the concurrence becomes zero for $D_A<1$, and $D_B<1$, which means a finite interaction time between the system and environment, we call this phenomenon as the entanglement sudden death (ESD).

The Eigenvalues of Equation (10) for each quantum state are presented as follows. For the state ${\rho }_{\mathrm{\Phi },ADC}$, the Eigenvalues of matrix in Equation (10) are given as:

$$\begin{array}{cc}\hfill {\lambda }_1=& \frac{1}{4}sin\theta [{\overline{D}}_A{\overline{D}}_B(2+3D_A{D}_B)sin\theta \hfill \\ & +2\sqrt{2}{\overline{D}}_A{\overline{D}}_B\sqrt{(1+D_A{D}_B+(1-D_A{D}_B)cos2\theta ){sin}^{2}2\theta }\hfill \\ & +{\overline{D}}_A{\overline{D}}_B(2-D_A{D}_B)sin3\theta ],\hfill \\ \hfill {\lambda }_2=& {\lambda }_3=D_A{\overline{D}}_A{D}_B{\overline{D}}_B{sin}^4\theta ,\hfill \\ \hfill {\lambda }_4=& \frac{1}{4}sin\theta [{\overline{D}}_A{\overline{D}}_B(2+3D_A{D}_B)sin\theta \hfill \\ & -2\sqrt{2}{\overline{D}}_A{\overline{D}}_B\sqrt{(1+D_A{D}_B+(1-D_A{D}_B)cos2\theta ){sin}^{2}2\theta }\hfill \\ & +{\overline{D}}_A{\overline{D}}_B(2-D_A{D}_B)sin3\theta ].\hfill \end{array}$$

(11)

For the state ${\rho }_{\mathrm{\Psi },ADC}$, the Eigenvalues of matrix in Equation (10) are given as:

$${\lambda }_1={\overline{D}}_A{\overline{D}}_B{sin}^{2}2\theta ,{\lambda }_2={\lambda }_3={\lambda }_4=0.$$

(12)

For the state ${\rho }_{\mathrm{\Phi },PDC}$ and ${\rho }_{\mathrm{\Psi },PDC}$, the Eigenvalues of matrix in Equation (10) are given the same as:

$$\begin{array}{c}{\lambda }_1=\frac{1}{4}sin2\theta \left[(1+{\overline{D}}_A{\overline{D}}_B)sin2\theta +2\sqrt{{\overline{D}}_A{\overline{D}}_B{sin}^{2}2\theta }\right],\hfill \\ {\lambda }_2=\frac{1}{4}sin2\theta \left[(1+{\overline{D}}_A{\overline{D}}_B)sin2\theta -2\sqrt{{\overline{D}}_A{\overline{D}}_B{sin}^{2}2\theta }\right],\hfill \\ {\lambda }_3={\lambda }_4=0.\hfill \end{array}$$

(13)

For the state ${\rho }_{\mathrm{\Phi },DC}$ and ${\rho }_{\mathrm{\Psi },DC}$, the Eigenvalues of matrix in Equation (10) are given the same as:

$$\begin{array}{cc}\hfill {\lambda }_1=& \frac{1}{32}\left[\right(D_A^2(5-12D_B+6D_B^2)-2D_A(6-13D_B+6D_B^2)\hfill \\ & +D_A(12-5D_A+4D_A(2-D_B)D_B-2D_B(9-4D_B))cos4\theta \hfill \\ & +2(8+D_B(-12+5D_B)){sin}^{2}2\theta \hfill \\ & +4\sqrt{2}{\overline{D}}_A{\overline{D}}_B\left[\right({(2-D_A)}^2-2(2-D_A)(1-2D_A)D_B\hfill \\ & +(1-2(2-D_A)D_A)D_B^2-{({\overline{D}}_A+{\overline{D}}_B)}^{2}cos4\theta {\left){sin}^{2}2\theta \right]}^{\frac{1}{2}}],\hfill \\ \hfill {\lambda }_2=& {\lambda }_3=\frac{1}{16}\left[{(1-{\overline{D}}_A{\overline{D}}_B)}^2-{(D_A-D_B)}^2{cos}^{2}2\theta \right],\hfill \\ \hfill {\lambda }_4=& \frac{1}{32}[D_A^2(5-12D_B+6D_B^2)-2D_A(6-13D_B+6D_B^2)\hfill \\ & +D_A(12-5D_A+4D_A(2-D_B)D_B-2D_B(9-4D_B))cos4\theta \hfill \\ & +2(8+D_B(-12+5D_B)){sin}^{2}2\theta \hfill \\ & -4\sqrt{2}{\overline{D}}_A{\overline{D}}_B\left[\right({(2-D_A)}^2-2(2-D_A)(1-2D_A)D_B\hfill \\ & +(1-2(2-D_A)D_A)D_B^2-{({\overline{D}}_A+{\overline{D}}_B)}^{2}cos4\theta {\left){sin}^{2}2\theta \right]}^{\frac{1}{2}}].\hfill \end{array}$$

(14)

By substituting the given Eigenvalues in Equation (9), the concurrence can be obtained.

2.3. Bell Nonlocality Sudden Death

Bell nonlocality is a quantum nonlocal correlation that can be obtained by local measurements on the distant entangled qubits which is incompatible with a local hidden variable theory. Bell nonlocality can be quantified by the maximum violation of a Bell inequality.

If a two-qubit state $\rho$ is not factorable, there exist observables $\widehat{A}\otimes \widehat{B}$, whose correlations violate Bell’s inequality $S=\langle \widehat{A}\otimes \widehat{B}\rangle +\langle {\widehat{A}}^{\prime }\otimes \widehat{B}\rangle +\langle \widehat{A}\otimes {\widehat{B}}^{\prime }\rangle -\langle {\widehat{A}}^{\prime }\otimes {\widehat{B}}^{\prime }\rangle \le 2$, where $\langle \widehat{A}\otimes \widehat{B}\rangle =\mathrm{Tr}[\widehat{A}\otimes \widehat{B}\rho ]$. The maximum value of Bell parameter S can be given by:

$$S=max[2\sqrt{2{\lambda }_1},2\sqrt{{\lambda }_1+{\lambda }_2}],$$

(15)

where ${\lambda }_1$ and ${\lambda }_2$ are the non-negative real Eigenvalues of a matrix $U_S=U_{\rho }^T{U}_{\rho }$ (${\lambda }_1$ is the degenerated Eigenvalue) [30,31]. Here, the elements of the matrix $U_{\rho }$ is given by $U_{\rho ,nm}=\mathrm{Tr}[{\sigma }_n\otimes {\sigma }_m\rho ]$ where $n,m\in \{x,y,z\}$, and ${\sigma }_x,{\sigma }_y$, and ${\sigma }_z$ are the Pauli matrices. When the maximum value of Bell parameter does not exceed two for $D_A<1$, and $D_B<1$, we call this phenomenon as the Bell nonlocality sudden death (BNSD).

The Eigenvalues of matrix $U_S$ for each quantum state are presented as follows. For the state ${\rho }_{\mathrm{\Phi },ADC}$, the Eigenvalues of matrix $U_S$ are given as:

$$\begin{array}{c}{\lambda }_1={\overline{D}}_A{\overline{D}}_B{sin}^{2}2\theta ,\hfill \\ {\lambda }_2={({cos}^2\theta +(1-2D_A)(1-2D_B){sin}^2\theta )}^2.\hfill \end{array}$$

(16)

For the state ${\rho }_{\mathrm{\Psi },ADC}$, the Eigenvalues of matrix $U_S$ are given as:

$$\begin{array}{c}{\lambda }_1={\overline{D}}_A{\overline{D}}_B{sin}^{2}2\theta ,\hfill \\ {\lambda }_2={(-1+D_A+D_B+(-D_A+D_B)cos2\theta )}^2.\hfill \end{array}$$

(17)

For the state ${\rho }_{\mathrm{\Phi },PDC}$ and ${\rho }_{\mathrm{\Psi },PDC}$, the Eigenvalues of matrix $U_S$ are given the same as:

$${\lambda }_1={\overline{D}}_A{\overline{D}}_B{sin}^{2}2\theta ,{\lambda }_2=1.$$

(18)

For the state ${\rho }_{\mathrm{\Phi },DC}$ and ${\rho }_{\mathrm{\Psi },DC}$, the Eigenvalues of matrix $U_S$ are given the same as:

$${\lambda }_1={\overline{D}}_A^2{\overline{D}}_B^2{sin}^{2}2\theta ,{\lambda }_2={\overline{D}}_A^2{\overline{D}}_B^2.$$

(19)

By substituting the given Eigenvalues in Equation (15), the maximum value of Bell parameter can be obtained.

3. Results

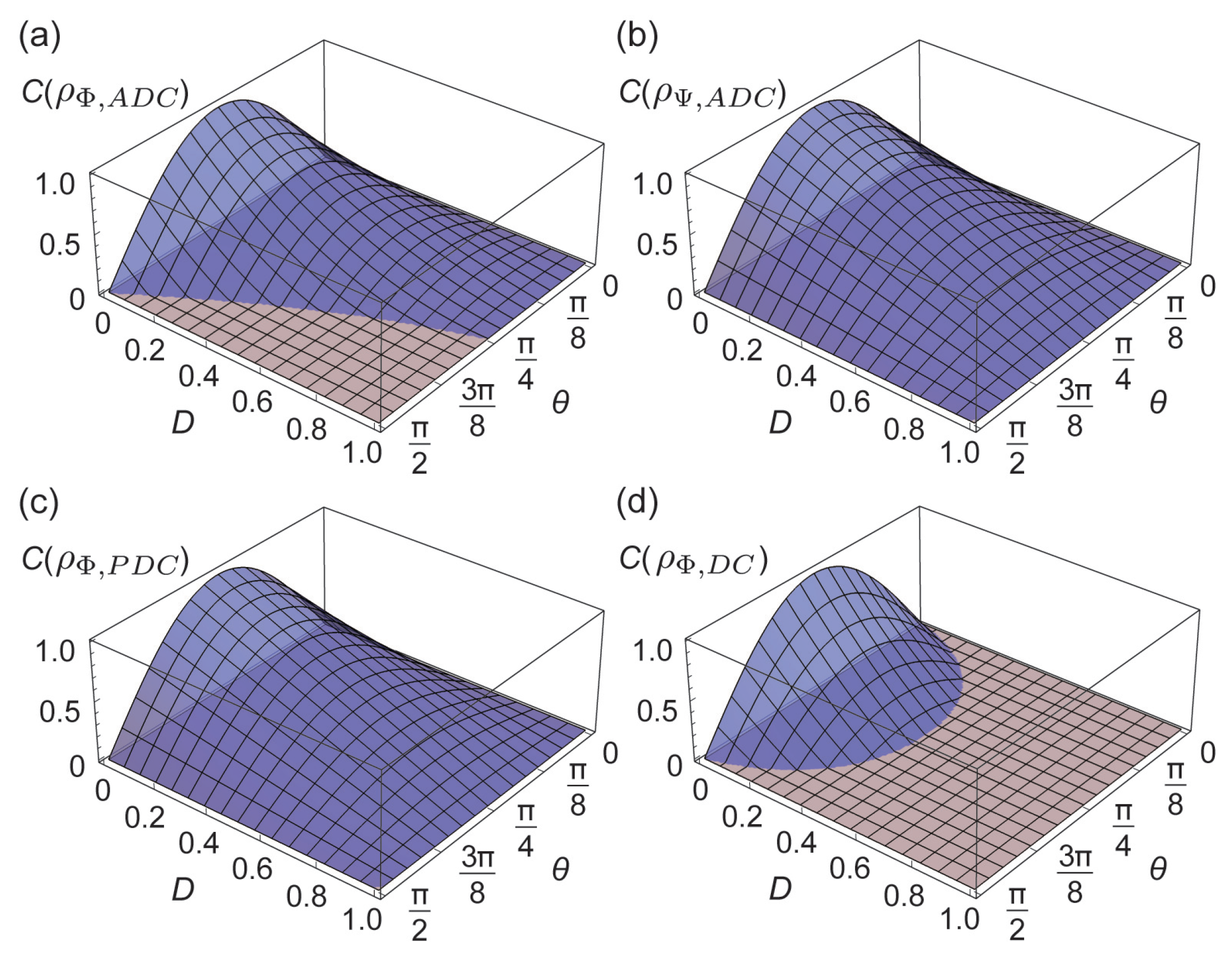
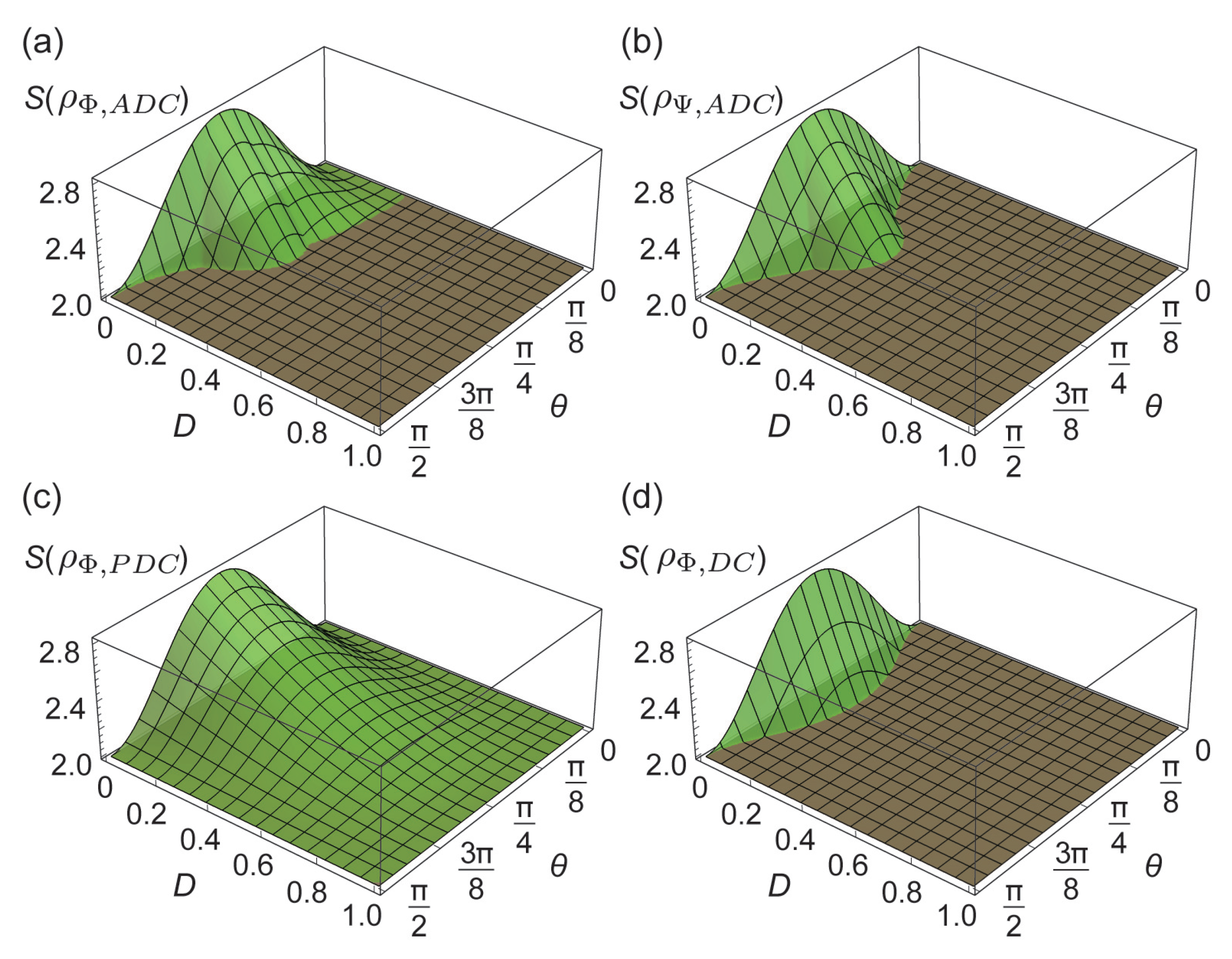
3.1. Entanglement

Firstly, we assume that both qubits are under decoherence with an equal strength $D_A=D_B=D$. In the case when the entangled state $|\mathrm{\Phi }\rangle$ is under ADC, ESD occurs when $\theta >\pi /4$ as shown in Figure 1a, while ESD does not occur when $|\mathrm{\Psi }\rangle$ is under ADC as shown in Figure 1b. Note that the asymmetric nature of ADC results in the asymmetric feature of concurrence only for ${\rho }_{\mathrm{\Phi },ADC}$ with respect to $\theta =\pi /4$. As shown in Figure 1c,d, ESD does not occur for PDC and occurs for DC. In the case of PDC and DC, as the Eigenvalues of the matrix in Equation (10) are the same for ${\rho }_{\mathrm{\Phi }}$ and ${\rho }_{\mathrm{\Psi }}$, concurrence shows the same results, i.e., $C\left({\rho }_{\mathrm{\Phi },PDC}\right)=C\left({\rho }_{\mathrm{\Psi },PDC}\right)$ and $C\left({\rho }_{\mathrm{\Phi },DC}\right)=C\left({\rho }_{\mathrm{\Psi },DC}\right)$. Note that both of the concurrence for ${\rho }_{\mathrm{\Phi },PDC}$ and ${\rho }_{\mathrm{\Phi },DC}$ shows a symmetric behavior with respect to $\theta =\pi /4$. As the entangled state becomes separable when $\theta$ goes to zero or $\pi /2$, the concurrence becomes zero regardless of the types and the strength of decoherence.

Next, we investigate the concurrence with the different strengths of decoherence on qubits A and B for three different entangled states with $\theta =\pi /8(<\pi /4)$, $\theta =\pi /4$, and $\theta =3\pi /8(>\pi /4)$. As shown in Figure 2a, ESD occurs when the entangled state $|\mathrm{\Phi }\rangle$ with $\theta >\pi /4$ is under ADC, and does not occur with $\theta \le \pi /4$. When the entangled state $|\mathrm{\Psi }\rangle$ is under ADC, ESD does not occur for all regions of $\theta$ as shown in Figure 2b. In the case of PDC, ESD does not occur (see Figure 2c) and in the case of DC, ESD occurs for all regions of $\theta$ (see Figure 2d). The result of ESD occurring shows that the entanglement can survive even though one of the entangled qubits is affected by a large strength of decoherence if the other qubit is affected by a small enough strength of decoherence except for the depolarizing.

3.2. Bell Nonlocality

Figure 3 shows the Bell parameter as functions of $\theta$ and the decoherence strength with an equal strength, $D=D_A=D_B$. When the entangled state is under ADC, BNSD occurs regardless of the form of the entangled state unlike the ESD (see Figure 3a,b). Here, the asymmetric feature of ADC is also represented in the asymmetric result of Bell parameter for ${\rho }_{\mathrm{\Phi },ADC}$ with respect to $\theta =\pi /4$. As shown in Figure 3c,d, BNSD does not occur for PDC and occurs for DC. In the case of PDC and DC, similarly to the concurrence, as the Eigenvalues of the matrix of $U_S$ are the same for ${\rho }_{\mathrm{\Phi }}$ and ${\rho }_{\mathrm{\Psi }}$, Bell parameter shows the same results, i.e., $S\left({\rho }_{\mathrm{\Phi },PDC}\right)=S\left({\rho }_{\mathrm{\Psi },PDC}\right)$ and $S\left({\rho }_{\mathrm{\Phi },DC}\right)=S\left({\rho }_{\mathrm{\Psi },DC}\right)$.

Next, we investigate the Bell parameter with the different strengths of decoherence on qubits A and B for three different entangled states with $\theta =\pi /8(<\pi /4)$, $\theta =\pi /4$, and $\theta =3\pi /8(>\pi /4)$. As shown in Figure 4a,b, BNSD occurs regardless of the form of the entangled state unlike the ESD. Interestingly, when the entangled state $|\mathrm{\Psi }\rangle$ with $\theta \ne \pi /4$ is under ADC, the Bell parameter shows an asymmetric behavior with respect to $D_A=D_B$ (see Figure 4b for $\theta =\pi /8$ and $\theta =3\pi /8$). In the case of the PDC and PC, the BNSD does not occur and occurs for all regions of $\theta$ as shown in Figure 4c,d.

4. Discussion

We theoretically investigate the entanglement and Bell nonlocality of a bipartite entangled state under three types of decoherence, amplitude damping, phase damping, and depolarizing. We show that ESD occurs for a specific form of bipartite entangled state under ADC while ESD always does not occur under PDC and occurs under DC. In the case of Bell nonlocality, BNSD always occurs under ADC and DC, and does not occur under PDC regardless of the form of bipartite entangled state. The theoretical result for ESD and BNSD are summarized in

Table 2. Entanglement sudden death (ESD), and Bell nonlocality sudden death (BNSD) for three types of decoherence channel. ◯ represents ESD and BNSD occur, and × represents ESD and BNSD do not occur.

	ESD			BNSD
	Amplitude Damping	Phase Damping	Depolarizing	Amplitude Damping	Phase Damping	Depolarizing
$\theta \le \pi /4$	×	×	◯	◯	×	◯
$\theta >\pi /4$	◯ for $|\mathrm{\Phi }\rangle$	×	◯	◯	×	◯
	× for $|\mathrm{\Psi }\rangle$

. Note that all Bell nonlocal states are entangled which satisfying a relation, Bell nonlocality ⊂ entanglement. We also find two interesting features. One is that the entanglement can survive even though one of the entangled qubits is affected by a large strength of decoherence if the other qubit is affected by a small enough strength of decoherence except for the depolarizing. The second one is that when a specific form of entangled state is under amplitude damping, the Bell nonlocality shows an asymmetric behavior respect to the decoherence strengths on each qubit.

The quantum correlations are not only significant for the fundamental aspects in quantum information but also for the applications in various quantum information processing tasks. For instance, quantum communication [2,3] and quantum teleportation [4,5,6] utilize the distributed entangled qubits as a resource, and Bell nonlocality has been applied to the quantum cryptography to analyze the security of quantum key distribution protocols [10,11,12,13]. In practice, however, these quantum information processing are not perfectly implemented due to the noisy environment, and will not give any advantage compared to the classical protocols when the entangled state completely loses its quantum coherence resulting in ESD and BNSD. In this situation, any entanglement purification protocols cannot be applied to recover the entanglement. Therefore, it is of importance to investigate the entanglement and Bell nonlocality of an entangled state in the presence of decoherence.

While the effect of decoherence on a bipartite entangled state has been widely studied, it has been lacked to study the effect of decoherence when the two qubits are under decoherence with different decoherence strengths. In particular, the quantum communication protocols which utilizes the entangled state where the two qubits are distributed to two distant parties, the different strength of decoherence on each qubit should be considered. Our result provides the bound of decoherence strength that does not lose the entanglement and Bell nonlocality by investigating the ESD and BNSD, and will help to implement the quantum information processing properly.