Abstract
Squeezing light is a critical resource in both fundamental physics and precision measurement. Squeezing light has been generated through optical-parametric amplification inside an optical resonator. However, preparing the squeezing light in an optomechanical system is still a challenge for the thermal noise inevitably coupled to the system. We consider an optically levitated nano-particle in a bichromatic cavity, in which two cavity modes could be excited by the scattering photons of the dual tweezers, respectively. Based on the coherent scattering mechanism, the ultra-strong coupling between the cavity field and the torsional motion of nano-particle could be achieved for the current experimental conditions. With the back-action of the optically levitated nano-particle, the broad single-mode squeezing light can be realized in the bad cavity regime. Even at room temperature, the single-mode light can be squeezed for more than 17 dB, which is far beyond the 3 dB limit. The two-mode squeezing light can also be generated, if the optical tweezers contain two frequencies, one is on the red sideband of the cavity mode, the other is on the blue sideband. The two-mode squeezing can be maximized near the boundary of the system stable regime and is sensitive to both the cavity decay rate and the power of the optical tweezers.
1. Introduction
Squeezing light, in which the quantum fluctuation is modulated below the shot noise level, has been regarded as a powerful resource in fundamental physics, e.g., improving the sensitivity of gravitational wave detection [1], cooling the motion of a macroscopic mechanical object below the quantum backaction limit [2], engineering matter interactions [3], and inducing the topological phase transitions [4], among many others. Squeezing light can be generated via the nonlinear optics, such as parametric down-conversion process [5,6,7,8]. The motion of the mechanical oscillator in cavity optomechanical systems could be regarded as an effective nonlinear optical medium, generating the pondermotive squeezing state by the back-action interaction [8,9,10,11]. With various optomechanical coupling mechanisms, cavity optomechanical systems produce abundant squeezing light sources [11,12,13,14,15], even in pulse driving regime [11,15]. However, due to the noise inevitably induced from the thermal bath, as well as the limitation of the nonlinear interaction, generating the substantial pondermotive squeezing light is still a challenge for the optomechanical system [9].
The levitated optomechanical system has raised widespread interest in macroscopic quantum superposition [16,17,18], quantum time crystals [19,20], and quantum information processing [21]. The squeezing has been studied in the levitated optomechanical system, in which the nano-particle is optically levitated and coupled with a cavity field [22]. Under ultra-high vacuum (gas pressure Torr), the squeezing light could be estimated over 15 dB below the vacuum noise level [22], which is much higher than the squeezing light source based on a membrane mechanical resonator embedded in an optical cavity [9]. In the levitated optomechanical system, the motional state of the optically levitated nano-particle has been squeezed dB below the thermal noise [23]. Recently, the coherent scattering mechanism has been theoretically investigated to cool both the axial and the in-plane motion of the levitated optomechanical system via a cavity mode [24,25]. The axial motion of the optically levitated nano-particle has been cooled to the ground state, either through the coherent scattering induced cavity cooling [26,27], or through the feedback cooling [28,29]. Moreover, the strong coherent scattering coupling between the cavity field and the motion of the nano-particle has also been observed in experiment [30]. With the attainable ultra-high quality factor (beyond ) of the optically nano-particle [31,32,33], it is expected that the stronger and robust squeezing light can be realized via the coherent scattering [22,24,32,34,35].
In this paper, we aim to generate both single-mode and two-mode squeezing light via a vacuum levitated optomechanical system, in which the nano-particle is optically levitated by the single and dual tweezers, respectively [22,24]. Both schemes are based on the coherent scattering mechanism [24]. We find that the ultra-strong coupling between the cavity mode and the torsion mode of the nano-particle is available by the current experimental parameters [36,37,38,39]. In order to obtain the squeezed single-mode light in steady state, the optical tweezers are detuned to the red sideband of the cavity mode. By the back-action of the optically levitated nano-particle [11], the single-mode light can be squeezed over 17 dB. The strong and broad single-mode squeezing light is observed in a bad cavity. Furthermore, in order to generate the two-mode squeezing lightly, we consider the optical tweezers with two frequencies, one is on the red sideband of the cavity mode, the other is on the blue sideband. We find that the two-mode squeezing can be maximized when the dynamics approach system instability [40]. The squeezing is sensitive to both the cavity decay rate and optical tweezers’ power. Unlike the single-mode squeezing light, the generated two-mode squeezing light is also an entangling source, which is very sensitive to thermal noise. We also find that the two-mode squeezing degree is smaller than the single-mode squeezing.
2. Model and Dynamics
We consider a uniform isotropic non-dispersive nano-ellipsoid, which is optically levitated by linearly polarized dual tweezers (A and B) in a bichromatic cavity as shown in Figure 1a. The optical tweezers A (B) with frequency are on the red (blue) sideband of cavity mode (). Under this condition, the nano-ellipsoid will be cooled and heated by the optical tweezers A and B, respectively. If the cooling rate is larger than the heating rate, the motional state can be cooled down to a low temperature and the system remains dynamically stable.
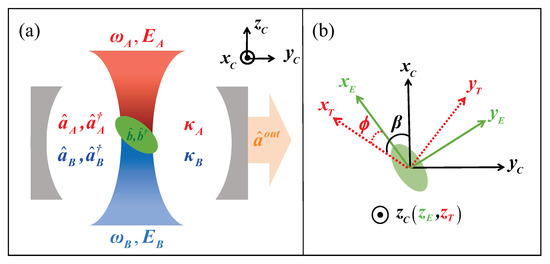
Figure 1.
(a) Schematic diagram of the levitated optomechanical system. The nano-ellipsoid is placed into a bichromatic cavity and optically levitated by the dual tweezers with two frequencies and , and amplitudes and , respectively. Two cavity modes () and () are excited by the scattering photons with the decay rates and . (b) The orientation of the nano-ellipsoid rotates under the tweezers coordinate with a small angel . is the angel between the cavity coordinate axis and tweezers coordinate axis . Tweezers propagate along the direction of axis .
The motion of the levitated nano-ellipsoid is characterized by the five degrees of freedom where for the center-of-mass motion in position and for the torsional motion in orientation , as shown in Figure 1b. By locating the nano-ellipsoid to the node (anti-node) of the cavity modes, the center-of-mass motion and torsional motion can be decoupled from each other [37]. Besides, intrinsic optomechanical coupling between the cavity mode and torsional motion of the nano-ellipsoid is typically much weaker than the coherent scattering coupling strength [24,26,37]. Therefore, we only consider the coherent scattering coupling between the cavity mode and the motion of the nano-ellipsoid. Without loss of generality, we take the torsional motion as an example in the following discussion [38,39].
With respect to the interaction picture defined by the Hamiltonian , the interaction Hamiltonian for the system can be written as [24]
where and ( and ) are the bosonic creation and annihilation operators with the commutation relations [41], is the detuning between the cavity frequency and the optical tweezers frequency . is the torsional mode frequency and is the coherent scattering coupling. They can be calculated by (see Appendix B)
and
respectively. For the current experimental parameters, the torsional frequency can be in the order of MHz as shown in Figure 2a. Interestingly, the ratio () between the coherent scattering coupling and the torsional frequency is larger than as shown in Figure 2b, in which the ultra-strong optomechanical coupling regime has been reached [36]. In this regime, both the rotating and anti-rotating wave terms have to be considered. As () depends on , one field quadrature of the cavity mode will be squeezed, while another will be anti-squeezed [5,6].
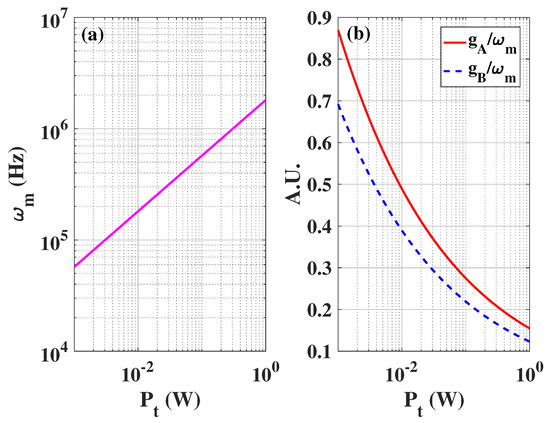
Figure 2.
The torsional frequency (a) and the ratio between the coherent scattering coupling and torsional frequency (b) as a function of the tweezers power . The parameters are given as follows: the cavity length mm, the wavelength of the optical tweezers nm ( nm), the beam waist of the tweezers in focus m, the principle axes of the nano-ellipsoid nm, the relative permittivity of the nano-ellipsoid , and the density of the nano-ellipsoid kg/m. For convenience, the power of two optical tweezers are assumed to be the same .
Derived from the system Hamiltonian (1), the dynamics of the system is characterized by the following quantum Langevin equations:
where is the damping rate of the torsional mode (see Appendix C). Note that the operators are already replaced by , where denotes the fluctuation of }. and are the zero-mean Gaussian noises, satisfying the correlation relations and respectively [41]. Here is the mean thermal excitation numbers at bath temperature T, and is Boltzmann constant. The linearized Langevin Equations (4) and (5) can be rewritten in the matrix form
where and . The drift matrix A is given by
After the Fourier transform , the steady state solutions of the Langevin Equations (4) and (5) in the frequency domain are
where the corresponding correlation noises are and , respectively. Furthermore, Equations (8) and (9) can be rewritten as where , ,
, , , , , and . Based on the standard input–output relation
the output cavity mode can be attainable.
3. Single-Mode Squeezing
We consider the case that the nano-ellipsoid is levitated by only one optical tweezer A, while the other optical tweezer B is turned off. Only one cavity mode is excited by the scattering photons of the optical tweezers A. From Equations (8) and (9), the cavity mode can be solved as
where
with . Furthermore, substituting Equation (12) in Equation (11), one can obtain the stationary squeezing spectrum of the transmitted field [6]:
where with being the measurement phase angle in homodyne detection. Or more specifically, Equation (14) can be rewritten as the form of where
and
It is noted that the maximum squeezing could reach when . Then it is easy to find out that the maximum squeezing of single output cavity mode is [13,42]
as . The output cavity mode is squeezed if decreases below the shot-noise level ().
In order to maintain the system stability, we assume that the frequency of the optical tweezer A is on the red sideband of the cavity mode, e.g. . We find that the Routh–Hurwitz criterion could be fulfilled, even under ultra-strong coupling regime [41]. Besides, the cavity mode could be highly squeezed in this regime. As shown in Figure 3, we find that the output cavity mode can be squeezed even at room temperature. Obviously, the optimal squeezing of the output cavity field occurs around resonance regime , where the dissipative part of the mechanical susceptibility has no response in dynamics [6]. In the good cavity regime , the pondermotive squeezing will be suppressed [15]. As the cavity decay rate increases from to , the minimum of decreases. The output cavity mode can be squeezed up to 17 dB when the lifetime of cavity photons approximately equals to a period of torsional motion (). As the cavity decay rate continues to increase, the broadband and strong squeezing generate a bad cavity condition . Then the broadband squeezing will split into two dips under the bad cavity regime, and the squeezing degree will reduce at for the larger dissipation [15].
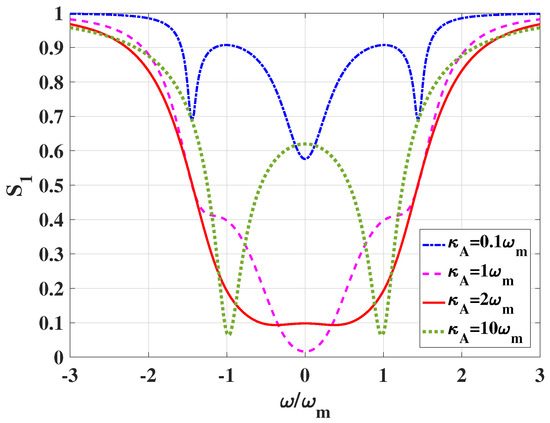
Figure 3.
as a function of the cavity decay rate . Parameters are listed as follows: optical tweezers’ power in focus W, pressure of the residual gas Pa, temperature of the residual gas K, bath temperature for the torsional mode K, and the accommodation efficient (see Appendix C). Other parameters are the same as Figure 2.
Note that the model we proposed is an open system, in which the optically levitated nano-ellipsoid irreversibly couples to the environment by the collision of the surrounding gas [33]. With the back-action interaction, the thermal disturbance could act on cavity mode, leading to decoherence. Here we investigate the effects on the squeezing light from the perspective of the surrounding gas pressure and temperature of the torsional motion. As shown in Figure 4a, , this depends on the gas pressure p. The lower pressure of the surrounding gas leads to the higher squeezing light. However, limited by the stability in ultra-high vacuum and the photons recoiling [33], the squeezing threshold exists. On the other hand, the higher temperature for the torsional mode will extremely enlarge the number of thermal phonons, which would destroy the squeezing state of the output lights. Therefore, many schemes based on optomechanics require a low-temperature environment [9,11,23]. In order to realize the stronger squeezing light, the high-quality factor and low-temperature environment are necessary for the levitated optomechanical system [11]. For our scheme, the squeezing is robust to the thermal environment as shown in Figure 4b.
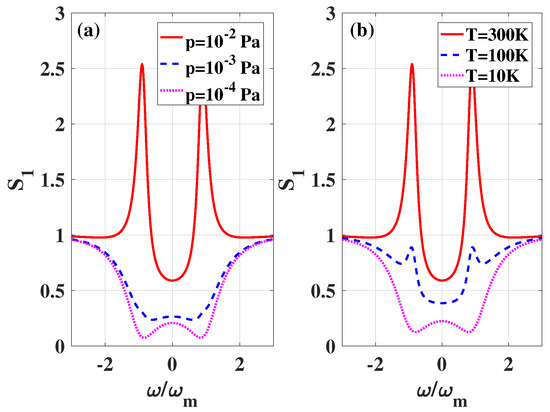
Figure 4.
as a function of the pressure of the surrounding gas p (a) and the temperature of torsional mode T (b). In pictures (a), the temperature of the torsional mode is assumed K, while the pressure of residual gas is set to Pa in picture (b). The cavity decay rate is in both picture (a) and (b). Other parameters are the same as Figure 3.
4. Two-Mode Squeezing
Our scheme can also be used for generating two-mode squeezing light, if we consider the nano-ellipsoid is optically levitated by dual tweezers, both A and B. Driven by the scattering photons, two cavity modes and are excited in the bichromatic cavity. Based on Equations (8), (9), and (11), the output cavity mode can be solved by
where
and
with . Furthermore, by introducing two phase-quadrature operators
and
the squeezing spectra and can be calculated by and [43]. The output two-mode cavity field is squeezed if .
In order to realize the two-mode squeezing light in steady state, two optical tweezers A and B are detuned to the red sideband (red-red), or the optical tweezers A is detuned to red sideband while the optical tweezers B is detuned to blue sideband (red-blue). In the red-blue case, the system will be stable in the blue sideband if the cavity photons are quickly lost to the vacuum. So, the cavity decay rates are assumed to . As the torsional mode resonance in the blue sideband, the dynamics of the torsional motion will be gradually amplified. In that case, the enhanced back-action interaction on the cavity mode will induce deeper squeezing. As shown in Figure 5, the squeezing of the red-blue case is much larger than that of the red-red case as the mechanical susceptibility of the levitated nano-ellipsoid responds in the resonant region.
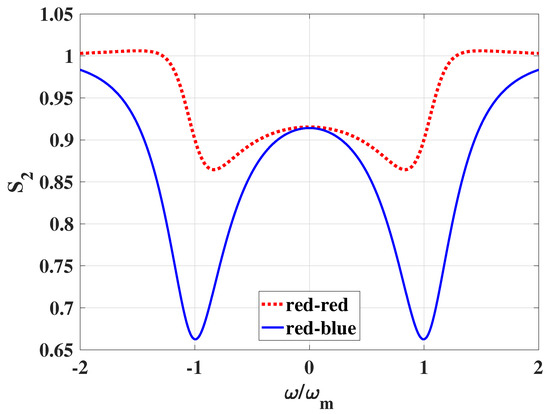
Figure 5.
Squeezing spectrum of two output modes. The legend red-red represents both two optical tweezers in red sideband of the cavity mode. The legend red-blue denotes the optical tweezers A in red sideband while another tweezers B in blue sideband. The decay rates of the cavity mode are and . Two tweezers are different in wavelength nm ( nm). Other parameters are the same as Figure 3.
Next, we will analyze the two-mode squeezing from the view of system stability. As shown in Figure 6a, none of is lower than 0.5 (3 dB). Obviously, there is a narrow and suddenly interrupted area, which splits the blue area into two parts. By comparing with Figure 6b, it corresponds to the critical boundary between the stable and unstable regions. The larger and smaller would make the system more stable. However, the squeezing will be reduced for the weak back-action. The maximum reaches its maximum as the system approaches the dynamical instability [40].
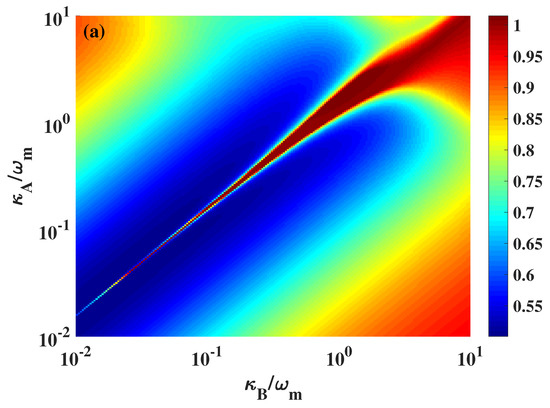
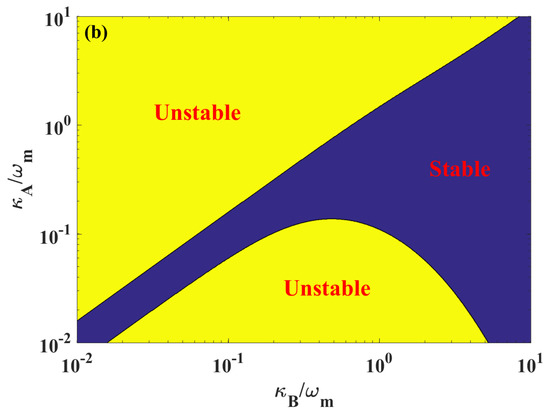
Figure 6.
(a) and the maximum eigenvalue of Equation (7) (b) as a function of the cavity decay rate . The detunings are set to the red and blue sideband , respectively. In picture (b), the yellow area means the maximum eigenvalue of Equation (7) is non-negative. According to the Routh–Hurwitz stability criterion [41], the system becomes instable in the long time limit. Conversely, the blue area denotes the system is stable. Other parameters are the same as Figure 5.
In Figure 7, we assume that the power of optical tweezer A is fixed at W. Noted that the optical tweezer A is set to the red sideband of cavity mode, while optical tweezer B is detuned to the blue sideband. With the power from 0.05 W to 0.15 W, decreases at for the enhancement of the back-action interaction. As the power up to 0.5 W, there is no squeezing on . The amplified torsional motion is overlarge on resonance. It results in the instability of the system, which shows the destruction of squeezing.
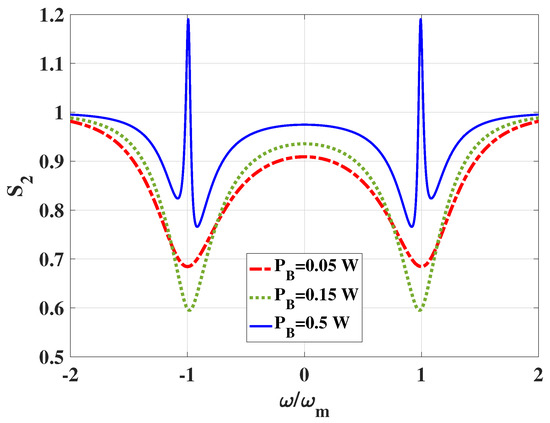
Figure 7.
as a function of . The power of optical tweezer A in focus is set to W. Tweezer A is detuned to the red sideband while tweezer B is set to be the blue sideband. Other parameters are the same as Figure 5.
5. Conclusions
We have proposed the squeezing light source based on an optically levitated nano-ellipsoid, which couples with a cavity. By the coherent scattering mechanism, the ultra-strong coupling between the cavity field and torsional mode of the nano-ellipsoid could be realized under the current experimental parameters. If the optical tweezers are on the red sideband of the cavity mode, the single-mode squeezed light source (17 dB squeezing) can be realized even at room temperature. It is noteworthy that both the strong and broadband squeezing light can be achieved under the bad cavity condition. In order to achieve the two-mode squeezing light two optical tweezers are applied to trap the nano-particle at the same time. One is on the red sideband, while another is on the blue sideband. The two-mode squeezing of the lights is sensitive to the system stability, which depends on both the cavity decay rates and the power of the optical tweezers. When the system dynamics are close to the boundary of the stable regime, the two-mode squeezing can be maximized. However, two-mode squeezing can not be over the 3 dB limit in our current scheme. In future, the 3 dB limit can be overcome either by feedback [44] or by the reservoir-engineering method [45].
Author Contributions
Writing—original draft preparation, G.L. and Z.-Q.Y.; writing—review and editing, G.L. and Z.-Q.Y.; visualization, G.L. and Z.-Q.Y.; supervision, Z.-Q.Y.; project administration, Z.-Q.Y.; funding acquisition, Z.-Q.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Natural Science Foundation of China under Grant No. 61771278 and the Beijing Institute of Technology Research Fund Program for Young Scholars.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Polarization Tensor
An uniform isotropic non-dispersive ellipsoid is assumed to be smaller than the wave length of the tweezers . By this setting, the dipole approximation is performed. The corresponding polarizability of the nano-ellipsoid in a semiaxis k is [46]
where and . With , can be analytically solved by
where denotes the eccentricity. Then the polarizability tensor for the ellipsoid is given as the matrix product:
where and
Appendix B. Hamiltonian for Coherent Scattering
As the size of the ellipsoid is assumed to be smaller than the wavelength of the optical tweezers, the dipole approximation is appropriate. The dipole moment is given as , where is the polarization tensor characterized by the rotating angles and , is the electric field of the incoming beams. The Hamiltonian interaction between the nano-ellipsoid and electric field can be written as [24,47]
where
is the electric field in cavity mode and is the tweezers field with Gaussian form . and are the bosonic annihilation and creator operators of cavity mode. (), (), and () are the frequency, wave number, and beam waist of the optical tweezers (cavity modes). denotes the cavity volume where d is the cavity length. The mode function depends on the boundary of the cavity, which can be written as in y axis. and are the amplitude and beam waist of the tweezers. and are the Rayleigh range and Gouy phase of the tweezers. , c, and are the power, speed, and wavelength of the tweezers.
Then, we assume that the nano-ellipsoid is fixed at the origin , and only the torsional motion on and is under considered. That is, when , one can expand the to the second order of . The torsional frequency of the nano-ellipsoid is
where denotes the inertia of the ellipsoid. M is the mass of the nano-ellipsoid. The corresponding intrinsic optomechanical coupling and coherent scattering coupling can be derived by expanding the and to the first order of as , given as
where is the zero-point fluctuation of torsion mode. It is noted that the torsion motion can be decoupled from the center-of-mass motion by moving the optical tweezers to the anti-node of the cavity mode ( [37]. Moreover, because is much smaller than the , the coherent scattering coupling is under considered. Then the Hamiltonian for the interaction picture can be read by [24]
where , denotes the torsional frequency , and represents the coherent scattering coupling . In this Hamiltonian, the first two terms denote the free Hamiltonian for the cavity modes and torsional mode, while the last term describes the coherent scattering interactions between the cavity modes and torsional mode.
Appendix C. Damping for Torsional Motion
As the nano-ellipsoid optically trapped in a high vacuum environment, the collision of surrounding gas on nano-ellipsoid leads to the change of angular momentum. The damping rate for the torsional motion is given by [48]
where
is the mass density, where , p, and are atom mass, pressure, and temperature of the residual gas. is the mean thermal velocity and is the density of the nano-ellipsoid. denotes the accommodation efficient which charges the diffuse and specular reflection of ellipsoidal surface.
References
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photonics 2013, 7, 613–619. [Google Scholar] [CrossRef]
- Clark, J.B.; Lecocq, F.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature 2017, 541, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Zeytinoğlu, S.; İmamoğlu, A.; Huber, S. Engineering matter interactions using squeezed vacuum. Phys. Rev. X 2017, 7, 021041. [Google Scholar] [CrossRef]
- Peano, V.; Houde, M.; Brendel, C.; Marquardt, F.; Clerk, A.A. Topological phase transitions and chiral inelastic transport induced by the squeezing of light. Nat. Commun. 2016, 7, 10779. [Google Scholar] [CrossRef] [PubMed]
- Fabre, C.; Pinard, M.; Bourzeix, S.; Heidmann, A.; Giacobino, E.; Reynaud, S. Quantum-noise reduction using a cavity with a movable mirror. Phys. Rev. A 1994, 49, 1337–1343. [Google Scholar] [CrossRef]
- Mancini, S.; Tombesi, P. Quantum noise reduction by radiation pressure. Phys. Rev. A 1994, 49, 4055–4065. [Google Scholar] [CrossRef]
- Wu, L.A.; Kimble, H.; Hall, J.; Wu, H. Generation of squeezed states by parametric down conversion. Phys. Rev. Lett. 1986, 57, 2520. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Purdy, T.P.; Yu, P.L.; Peterson, R.W.; Kampel, N.S.; Regal, C.A. Strong Optomechanical Squeezing of Light. Phys. Rev. X 2013, 3, 031012. [Google Scholar] [CrossRef]
- Ockeloen-Korppi, C.; Damskägg, E.; Pirkkalainen, J.M.; Heikkilä, T.; Massel, F.; Sillanpää, M. Noiseless quantum measurement and squeezing of microwave fields utilizing mechanical vibrations. Phys. Rev. Lett. 2017, 118, 103601. [Google Scholar] [CrossRef]
- Pontin, A.; Biancofiore, C.; Serra, E.; Borrielli, A.; Cataliotti, F.; Marino, F.; Prodi, G.; Bonaldi, M.; Marin, F.; Vitali, D. Frequency-noise cancellation in optomechanical systems for ponderomotive squeezing. Phys. Rev. A 2014, 89, 033810. [Google Scholar] [CrossRef]
- Yin, Z.Q.; Han, Y.J. Generating EPR beams in a cavity optomechanical system. Phys. Rev. A 2009, 79, 024301. [Google Scholar] [CrossRef]
- Sainadh, S.; Kumar, M.A. Effects of linear and quadratic dispersive couplings on optical squeezing in an optomechanical system. Phys. Rev. A 2015, 92, 033824. [Google Scholar] [CrossRef]
- Zippilli, S.; Di Giuseppe, G.; Vitali, D. Entanglement and squeezing of continuous-wave stationary light. New J. Phys. 2015, 17, 043025. [Google Scholar] [CrossRef][Green Version]
- Kronwald, A.; Marquardt, F.; Clerk, A.A. Dissipative optomechanical squeezing of light. New J. Phys. 2014, 16, 063058. [Google Scholar] [CrossRef]
- Yin, Z.q.; Li, T.; Zhang, X.; Duan, L. Large quantum superpositions of a levitated nanodiamond through spin-optomechanical coupling. Phys. Rev. A 2013, 88, 033614. [Google Scholar] [CrossRef]
- Romero-Isart, O.; Pflanzer, A.C.; Blaser, F.; Kaltenbaek, R.; Kiesel, N.; Aspelmeyer, M.; Cirac, J.I. Large quantum superpositions and interference of massive nanometer-sized objects. Phys. Rev. Lett. 2011, 107, 020405. [Google Scholar] [CrossRef]
- Chen, X.Y.; Yin, Z.Q. High-precision gravimeter based on a nano-mechanical resonator hybrid with an electron spin. Opt. Express 2018, 26, 31577. [Google Scholar] [CrossRef]
- Huang, Y.; Guo, Q.; Xiong, A.; Li, T.; Yin, Z.Q. Classical and quantum time crystals in a levitated nanoparticle without drive. Phys. Rev. A 2020, 102, 023113. [Google Scholar] [CrossRef]
- Huang, Y.; Li, T.; Yin, Z.Q. Symmetry-breaking dynamics of the finite-size Lipkin-Meshkov-Glick model near ground state. Phys. Rev. A 2018, 97, 012115. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Yin, Z.q. Quantum Information Processing and Precision Measurement Using a Levitated Nanodiamond. Adv. Quantum Technol. 2021, 4, 2000154. [Google Scholar] [CrossRef]
- Chang, D.E.; Regal, C.; Papp, S.; Wilson, D.; Ye, J.; Painter, O.; Kimble, H.J.; Zoller, P. Cavity opto-mechanics using an optically levitated nanosphere. Proc. Natl. Acad. Sci. USA 2010, 107, 1005–1010. [Google Scholar] [CrossRef] [PubMed]
- Rashid, M.; Tufarelli, T.; Bateman, J.; Vovrosh, J.; Hempston, D.; Kim, M.; Ulbricht, H. Experimental realization of a thermal squeezed state of levitated optomechanics. Phys. Rev. Lett. 2016, 117, 273601. [Google Scholar] [CrossRef]
- Gonzalez-Ballestero, C.; Maurer, P.; Windey, D.; Novotny, L.; Reimann, R.; Romero-Isart, O. Theory for cavity cooling of levitated nanoparticles via coherent scattering: Master equation approach. Phys. Rev. A 2019, 100, 013805. [Google Scholar] [CrossRef]
- Toroš, M.; Delić, U.; Hales, F.; Monteiro, T.S. Coherent-scattering two-dimensional cooling in levitated cavity optomechanics. Phys. Rev. Res. 2021, 3, 023071. [Google Scholar] [CrossRef]
- Delić, U.; Reisenbauer, M.; Dare, K.; Grass, D.; Vuletić, V.; Kiesel, N.; Aspelmeyer, M. Cooling of a levitated nanoparticle to the motional quantum ground state. Science 2020, 367, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, J.; Rudolph, H.; Hornberger, K.; Stickler, B.A. Cooling nanorotors by elliptic coherent scattering. Phys. Rev. Lett. 2021, 126, 163603. [Google Scholar] [CrossRef] [PubMed]
- Magrini, L.; Rosenzweig, P.; Bach, C.; Deutschmann-Olek, A.; Hofer, S.G.; Hong, S.; Kiesel, N.; Kugi, A.; Aspelmeyer, M. Real-time optimal quantum control of mechanical motion at room temperature. Nature 2021, 595, 373–377. [Google Scholar] [CrossRef]
- Tebbenjohanns, F.; Mattana, M.L.; Rossi, M.; Frimmer, M.; Novotny, L. Quantum control of a nanoparticle optically levitated in cryogenic free space. Nature 2021, 595, 378–382. [Google Scholar] [CrossRef]
- De los Ríos Sommer, A.; Meyer, N.; Quidant, R. Strong optomechanical coupling at room temperature by coherent scattering. Nat. Commun. 2021, 12, 276–281. [Google Scholar] [CrossRef]
- Asenbaum, P.; Kuhn, S.; Nimmrichter, S.; Sezer, U.; Arndt, M. Cavity cooling of free silicon nanoparticles in high vacuum. Nat. Commun. 2013, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Millen, J.; Monteiro, T.S.; Pettit, R.; Vamivakas, A.N. Optomechanics with levitated particles. Rep. Prog. Phys. 2020, 83, 026401. [Google Scholar] [CrossRef] [PubMed]
- Jain, V.; Gieseler, J.; Moritz, C.; Dellago, C.; Quidant, R.; Novotny, L. Direct measurement of photon recoil from a levitated nanoparticle. Phys. Rev. Lett. 2016, 116, 243601. [Google Scholar] [CrossRef] [PubMed]
- Černotík, O.; Filip, R. Strong mechanical squeezing for a levitated particle by coherent scattering. Phys. Rev. Res. 2020, 2, 013052. [Google Scholar] [CrossRef]
- Yin, Z.Q.; Geraci, A.A.; Li, T. Optomechanics of levitated dielectric particles. Int. J. Mod. Phys. B 2013, 27, 1330018. [Google Scholar] [CrossRef]
- Kockum, A.F.; Miranowicz, A.; De Liberato, S.; Savasta, S.; Nori, F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19–40. [Google Scholar] [CrossRef]
- Li, G.; Yin, Z.Q. Steady motional entanglement between two distant levitated nanoparticles. arXiv 2021, arXiv:2111.11620. [Google Scholar]
- Hoang, T.M.; Ma, Y.; Ahn, J.; Bang, J.; Robicheaux, F.; Yin, Z.Q.; Li, T. Torsional optomechanics of a levitated nonspherical nanoparticle. Phys. Rev. Lett. 2016, 117, 123604. [Google Scholar] [CrossRef]
- Ahn, J.; Xu, Z.; Bang, J.; Deng, Y.H.; Hoang, T.M.; Han, Q.; Ma, R.M.; Li, T. Optically levitated nanodumbbell torsion balance and GHz nanomechanical rotor. Phys. Rev. Lett. 2018, 121, 033603. [Google Scholar] [CrossRef]
- Genes, C.; Mari, A.; Tombesi, P.; Vitali, D. Robust entanglement of a micromechanical resonator with output optical fields. Phys. Rev. A 2008, 78, 032316. [Google Scholar] [CrossRef]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.C.; Wang, Y.P.; Yu, Y.F.; Zhang, Z.M. Quantum squeezing in a modulated optomechanical system. Opt. Express 2018, 26, 11915–11927. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ma, S.L.; Li, F.L. Generation of broadband two-mode squeezed light in cascaded double-cavity optomechanical systems. Phys. Rev. A 2015, 92, 023856. [Google Scholar] [CrossRef]
- Vinante, A.; Falferi, P. Feedback-enhanced parametric squeezing of mechanical motion. Phys. Rev. Lett. 2013, 111, 207203. [Google Scholar] [CrossRef]
- Dassonneville, R.; Assouly, R.; Peronnin, T.; Clerk, A.; Bienfait, A.; Huard, B. Dissipative stabilization of squeezing beyond 3 dB in a microwave mode. PRX Quantum 2021, 2, 020323. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Gonzalez-Ballestero, C.; Aspelmeyer, M.; Novotny, L.; Quidant, R.; Romero-Isart, O. Levitodynamics: Levitation and control of microscopic objects in vacuum. Science 2021, 374, eabg3027. [Google Scholar] [CrossRef]
- Halbritter, J. Torque on a rotating ellipsoid in a rarefied gas. Z. Für Naturforsch. A 1974, 29, 1717–1722. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).