Abstract
In a recent work (Antonov et al., Physical Review Letters 123, 243903 (2019)), it was shown that it is possible to amplify a train of attosecond pulses, which are produced from the radiation of high harmonics of the infrared field of the fundamental frequency, in the active medium of a plasma-based X-ray laser modulated by a replica of the infrared field of the same frequency. In this paper, we show that much higher amplification can be achieved using the second harmonic of the fundamental frequency for modulating of a hydrogen-like active medium. The physical reason for such enhanced amplification is the possibility to use all (even and odd) sidebands induced in the gain spectrum in the case of the modulating field of the doubled fundamental frequency, while only one set of sidebands (either even or odd) could participate in amplification in the case of the modulating field of the fundamental frequency due to the fact that the spectral components of the high-harmonic field are separated by twice the fundamental frequency. Using the plasma of hydrogen-like C5+ ions with an inverted transition wavelength of 3.38 nm in the water window as an example, it is shown that the use of a modulating field at a doubled fundamental frequency makes it possible to increase the intensity of amplified attosecond pulses by an order of magnitude in comparison with the previously studied case of a fundamental frequency modulating field.
1. Introduction
The beginning of the 21st century was marked by the emergence and rapid development of attosecond physics—an interdisciplinary field of research aimed at probing and controlling the ultrafast dynamics of charge carriers in atoms, molecules, and solids on their own time scales [1,2,3,4,5,6,7]. The main instrument of attosecond physics is attosecond X-ray and vacuum ultraviolet (VUV) pulses produced due to high-order harmonic generation under the action of optical laser field on a gas medium in the tunneling ionization regime [8,9,10]. Such sources make it possible to generate a spectrum of harmonics with a width of more than 1 keV and up to 12 octaves [11], as well as to generate pulses with a duration of down to 40–50 as [12,13,14]. However, the energy of such pulses in the X-ray range, from several hundred eV and above, as a rule, does not exceed hundreds of pJ or, at best, few nJ [15,16], which limits the possibilities of their practical applications, in particular, for single-pulse measurements of ultrafast processes in matter, as well as in measurements based on the “attosecond pump–attosecond probe” scheme [17,18].
In recent work [19], we proposed a method for amplifying a train of attosecond pulses formed by a set of high-order harmonics of the infrared (IR) field in a hydrogen-like active medium of a plasma-based X-ray laser, which is simultaneously irradiated with a replica of the fundamental-frequency IR field used to generate the high harmonics. Due to the linear Stark effect, the positions of the excited-state energy levels of the resonant ions of the active medium follow the local value of the electric field of the laser wave in time and space. As a result, the gain of the medium, initially localized in the vicinity of the frequency of the inverted transition, appears at the combination frequencies spaced from the resonance by even multiplies of the modulating field frequency. In this case, if one of the high-order harmonics of the modulating field is tuned into resonance with the time-averaged transition frequency of the active medium, then the harmonics of other orders are automatically in resonance with the induced gain lines. If the active medium exhibits strong plasma dispersion at the frequency of the modulating field, then harmonics of different orders are amplified independently of each other, and their relative phases are preserved. Moreover, the gain coefficients for harmonics of different orders can be made nearly equal to each other by a choice of an optimal intensity of the modulating field. In this case, if the harmonics of different orders at the entrance to the medium are comparable in amplitude, are in-phase, and form a sequence of attosecond pulses, then in the process of amplification, the spectral-temporal properties of radiation (such as the relative amplitudes and phases of harmonics and, as a consequence, the shape and duration of the pulses) are preserved. In [19], it was shown that it is possible to amplify attosecond pulses formed by a set of high harmonics in the “water window” range (2.3–4.4 nm) by one to two orders of magnitude in intensity in the active medium of hydrogen-like C5+ ions.
At the same time, if the plasma dispersion at the frequency of the modulating field is moderate, then a particular high-order harmonic tuned into resonance with any of the induced gain lines of the active medium is not only amplified, but also generates radiation at combination frequencies spaced from the seed frequency by even multiple of the modulating field frequency. Under certain conditions, the generated Raman spectral components turn out to be in phase with the radiation of the amplified harmonic, which leads to the formation of a train of subfemtosecond pulses [20,21,22]. If several harmonics are present in the incident field, and they are spaced from each other by an even multiple of the modulating field frequency, then in a plasma medium with a low free-electron concentration, the amplified harmonics are scattered into each other, which opens up the possibility to control their amplitudes and phases via interference of the amplified incident and generated scattered fields [23].
Previous work [19] referred to the case when (i) an active medium is modulated by an IR field of the fundamental frequency (the same frequency as the field used for HHG) and (ii) only a set of the induced gain lines, separated from the resonance by even multiples of the fundamental frequency, participates in amplification of the high harmonics. In this paper, it is shown that the gain spectrum of a modulated hydrogen-like medium contains sidebands not only at even, but also at odd combination frequencies; these frequencies are spaced from the resonance by odd multiples of the modulating field frequency. We show that if the second harmonic of the fundamental field is used for modulation of an active medium, then all gain components (both odd and even sidebands) induced by that field participate in amplification of a train of attosecond pulses produced by the HHG of the fundamental IR field frequency. It opens up a possibility to significantly enhance the amplification of attosecond pulses. Thus, the two representative cases are studied and compared in this work: (a) when the modulating field is of the fundamental frequency, while harmonics in the spectrum of the seed are tuned into resonance with the gain lines of either even or odd orders, (b) when the modulating field is of the doubled fundamental frequency, while harmonics are tuned into resonance with the gain lines of both even and odd orders.
The paper is organized as follows. Section 2 presents a theoretical model describing the amplification of high harmonics of the IR field in a modulated hydrogen-like active plasma medium. In Section 3, an analytical solution is derived, which makes it possible to better understand the main laws governing the amplification of harmonics. In Section 4, on the basis of the obtained analytical solution, the optimal conditions for amplification of a train of attosecond pulses formed by a combination of different numbers of high harmonics are found. In Section 5, the conclusions of the analytical theory are compared with the results of the numerical solution of the system of equations given in Section 2. Finally, Section 6 summarizes the main results of the work.
2. Theoretical Model
We will consider a plasma-based X-ray laser with population inversion at the transition from the first excited energy level to the ground state of a hydrogen-like ion C5+, n = 2 ↔ n = 1, where n is the principal quantum number; the laser wavelength is 3.38 nm. Such an active medium can be prepared by irradiating carbon atoms with a laser pulse with an intensity of the order of 1019 W/cm2 and a duration of several tens of femtoseconds [24]. In this case, the population inversion at the n = 2 ↔ n = 1 transition of hydrogen-like C5+ ions arises as a result of the recombination of electrons with the nuclei of fully ionized carbon atoms and subsequent relaxation of ions to the states with n = 2. As shown in [24], the addition of hydrogen atoms makes it possible to increase the gain due to a decrease in the effective temperature of free electrons in the plasma. In this case, the optimal values of the concentrations of carbon and hydrogen atoms are nC~1019 cm−3 and nH~1020 cm−3, respectively, and the intensity gain at the inverted transition is about 180 cm−1. Thus, the concentration of free electrons in the active medium can be estimated as ne ≈ 5nC + nH~1.5 × 1020 cm−3.
In what follows, we will assume that the active medium is a thin cylinder elongated parallel to the x axis and irradiated by two fields linearly polarized along the z axis, namely, resonant radiation of high-order harmonics and an intense IR laser field with a frequency Ω. We will assume that the transverse and longitudinal distributions of the IR field amplitude are much wider than the cross section and length of the plasma channel, respectively, which allows us to assume that the amplitude of the laser field is constant throughout the entire volume of the active medium. In addition, we will assume that the IR pulse duration is quite large compared to the time it takes to establish the induced polarization of the medium and to the lifetimes of the populations of excited states of C5+ ions with n = 2. In this case, the laser field can be represented as a plane monochromatic wave that propagates along the axis of the plasma channel (x axis) with a phase velocity :
where is the IR field amplitude, is the unit polarization vector, , c is the speed of light in vacuum, is the refractive index of plasma at the frequency of the IR field, is the plasma frequency, and e and me are the charge and mass of the electron. Note that the frequency of the laser field in the visible or infrared range, Ω, is much (at least one and a half to two orders of magnitude) lower than the frequencies of all quantum transitions from populated states of hydrogen-like C5+ ions. Thus, it does not experience resonant interaction with the medium and, as a consequence, does not change during the propagation process.
Under the action of the laser field (1), the upper energy level of the inverted transition is split into three sublevels. Two of them correspond to states and , where m is the projection of the orbital angular momentum onto the direction of polarization of the laser field, i.e., on the z axis. The energies of these states follow in time and space the local value of the electric field of the laser wave due to the linear Stark effect, and also experience a constant displacement, which is small in comparison with the photon energy of the laser field, , due to the quadratic Stark effect:
where is the dimensionless laser field amplitude, ≈ 5.14 × 109 V/cm is the atomic field, Z = 6 is the carbon nucleus charge number, and is the reduced Planck’s constant. In what follows, the laser field will also be referred to as the modulating field. The dipole moments of transitions from states and to the ground state are oriented along the z axis: , , where and is the Bohr radius. The third sublevel corresponds to states and , the energies of which experience only a small constant displacement due to the quadratic Stark effect:
The dipole moments of transitions from these states to the ground state have components along the x and y axes: , ; however, the field propagating along the axis of the plasma channel lies in the yz plane and does not interact with the x component of the dipole moments, which allows it to be neglected. It should be noted that the lower energy level corresponding to the ground state of hydrogen-like C5+ ions also turns out to be shifted relative to its unperturbed position under the action of the modulating field:
In addition, the IR field (1) causes tunneling ionization of C5+ from excited states , and , with velocities and , respectively,
where the quantities and are averaged over the period of the laser field (the rate of ionization from the ground state is negligible). To ensure that ionization does not hinder amplification at an inverted transition in the active medium, in what follows we will consider a laser field with an intensity at which the ionization rates (5) are significantly lower than the rates of radiative decay of states –. In the case of C5+ ions, this condition limits the intensity of the modulating field to 2.3 × 1016 W/cm2. In this case, both the shifts of the resonance energy levels due to the quadratic Stark effect and the ionization rate turn out to be much smaller than the frequency of the modulating field of the visible or near/mid-IR range, which allows one to take into account their effect as time-independent additions to the energy and decay rate of the corresponding states [22,25,26]. In addition, in this case, the corrections to the Stark effect of the third and higher orders turn out to be negligible.
In addition to the laser field (1), the medium is irradiated with X-ray seed radiation formed by a set of high-order harmonics of fundamental frequency linearly polarized along the z axis:
where
is the slowly changing amplitude of seed radiation, is its carrier frequency, is a natural number, is the fundamental frequency, i.e., the frequency of the laser field used to generate high harmonics, is the complex amplitude of the harmonic with the frequency , is the envelope of the field of each individual harmonic, and . We will further assume that at the entrance to the medium, all harmonics are in phase and have the same amplitudes, i.e., for any q. In the next section, an analytical solution will be obtained that is valid for an arbitrary envelope . At the same time, in numerical calculations, the envelope of the harmonic signal of the following form will be used:
where ΔtH = 50 fs and is the Heaviside function. It is assumed that the FWHM of the harmonic signal at the input to the medium is 17.5 fs.
In what follows, we will assume that the carrier frequency of the harmonic radiation is close to the frequency of the inverted transition of the active medium, . As shown in [19,20,22], in this case the propagation of X-ray radiation (6) in a hydrogen-like active medium of a plasma-based X-ray laser is described by the system of Maxwell–Bloch equations in a five-level approximation:
where is the concentration of C5+ ions, which at the time of arrival of the harmonic signal are in one of the states – (in what follows, the initial population of the ground state is assumed to be zero); is the dielectric constant of the plasma at the frequency of X-ray radiation; is the relaxation rate of the element of the density matrix of the medium,
is the rate of collisional relaxation of off-diagonal elements of the density matrix (according to [24], in the medium under consideration −1 ≈ 20 fs); is the rate of radiative relaxation of states –, −1 ≈ 1.23 ps. The Hamiltonian of the system (9) under consideration, in the presence of a resonant X-ray field and a modulating laser field, has the form:
Here , i = 1,2,3,4,5 are determined by Equations (2)–(4), and and denote the polarization components of the X-ray field, oriented along the z and y axes. While the z-component of the field is present in the seed radiation, the y-component arises in the active medium due to the amplified spontaneous emission at transitions and . These transitions lead to an increase in the population of the ground state and, as a consequence, to a decrease in the population inversion and amplification at the modulated transitions and , with which the z-polarized X-ray radiation interacts.
Next, we make a change of variables and look for a solution to system (9) in the slowly varying amplitude approximation for the X-ray field and resonant polarization of the medium, as well as in the resonance approximation (the rotating wave approximation) for the density matrix elements:
where , , , , and () satisfy the inequalities and , . Expressions (12) also imply the unidirectional propagation of X-ray radiation, which takes place in the absence of reflections from the boundaries of the medium at . The explicit form of the equations in the aforementioned approximations is given in [20] and, because of its cumbersomeness, will not be reproduced here.
To solve the formulated system of equations, it is necessary to set the initial and boundary conditions. When , the X-ray field at the front boundary of the medium coincides with the seed field (6)–(8). To set the initial conditions, we will assume that at the time instant (before the arrival of resonance radiation at a given point of the medium), the C5+ ions in the amount per unit volume of the medium are with equal probability in one of the excited states , , , and , the ground state is not populated, while the carbon ions in other states do not interact with the X-ray field. Thus,
where is the initial population difference at the transitions , i = {2,3,4,5}. At the same time, the initial values of the coherences on inverted transitions , i = {2,3,4,5} are random functions of the longitudinal coordinate x, which makes it possible to take into account the amplified spontaneous emission of the active medium [22,27,28,29,30], while the initial values of the coherences on the other transitions are equal to zero:
where R is the radius of the plasma channel, which further, in accordance with [24], we assume equal to 5 μm; xk = klelem, where k = 1,2,…,kmax is a natural number, and lelem is the thickness of the elementary layer, in which the initial value of coherence is assumed to be a random variable independent of x. In this case, the thickness lelem should be much greater than the wavelength of the X-ray field and, at the same time, much smaller than the thickness of the active medium L: . In addition, in (14) , , and , while the amplitudes and phases are random and statistically independent quantities that obey the following probability distributions:
where is the number of particles that are initially in the excited state in the volume of the k-th elementary layer.
In the next section, we derive an analytical solution for the amplified radiation of harmonics in the X-ray range, which will be further compared with the numerical solution of the system of Equations (9), (11) and (12) with the initial and boundary conditions (13), (14) and (7), respectively.
3. Analytical Solution
To derive an analytical solution, we will make a number of additional approximations. First, we will assume that the interaction of X-ray radiation with the medium occurs in a linear regime, and the change in the population differences at inverted transitions can be neglected. In this case, the z- and y-polarization components of the X-ray field are amplified independently of each other, and the amplified spontaneous emission does not affect the character of the amplification of the seed radiation [21]. Accordingly, when deriving an analytical solution for the emission of z-polarization harmonics, we exclude the transitions and from consideration. As a result, the system of equations for slowly varying X-ray field amplitudes and coherences at transitions and takes the form
where is the time-average frequency of transitions and , is the amplitude of the linear Stark effect in the modulating field, and is the difference between the wave numbers of the X-ray and IR fields, due to the plasma dispersion. Similar to [21,22], within the analytical solution, we will neglect the amplified spontaneous emission of z-polarization, which is justified at a sufficiently high intensity of the X-ray field at the entrance to the medium, and assume . At the same time, in contrast to the previous works [21,22], in the analytical solution we will not specify the form of the temporal envelope of the seed radiation. We will further represent the slowly varying amplitude of the X-ray field, , as the Fourier integral:
where denotes the complex amplitude of the spectral component of the X-ray field at the frequency at the depth x inside the medium. In particular, the Fourier transform of the slowly varying amplitude of the seed radiation (7), (8), formed by a set of NH high-order harmonics, has the form
where is the amplitude spectrum of the electric-field-envelope of an individual harmonic at the entrance to the medium.
We will further consider the second equation of system (16). We will look for its solution in the following form:
where is the modulation index (the dimensionless ratio of the amplitude of the modulating field to its frequency), and the function satisfies the equation
which is obtained from (17) taking into account the equality , where is the Bessel function of the first kind of order k. We will represent in the form of a Fourier integral . Then from (20) it is easy to obtain an algebraic equation for the spectral amplitude and, then, a solution for coherence :
In a similar way, one can obtain a solution to the third equation of system (16):
Substituting (21) and (22) into the first equation of system (16) and performing some transformations, we obtain an equation for the spectral amplitude of the X-ray field:
where is the amplitude amplification factor of resonant radiation in the absence of modulation. In accordance with (23), in a modulated active medium, the X-ray field at a frequency is amplified as a result of self-action (the first term in (23)), and also changes as a result of coherent scattering of spectral components spaced from the considered frequency by an even multiple, , of the modulating field frequency. As shown in [23], taking into account the second term in Equation (23) leads to various interference effects, in particular, to mutual amplification of high-order harmonics or to interference suppression of their amplification. However, the degree of influence of the second term in (23) is determined by the ratio ; specifically, if it is small, i.e., if the length of the coherent interaction of the X-ray and IR fields, which is limited by the dispersion of the plasma, is much shorter than the amplification length of the X-ray field, then the second term can be neglected. In the considered case of a plasma of hydrogen-like C5+ ions with an unperturbed gain g0 ≈ 90 cm−1 and concentration of free electrons ne ≈ 1.5 × 1020 cm−3, for a modulating IR field with a wavelength Ʌ = 2πc/Ω ≥ 800 nm, we have . Accordingly, the influence of mutual coherent scattering of spectral components of X-ray radiation can be neglected. The applicability of this approximation is confirmed in Section 5 by comparing the analytical solution given below with the results of numerical calculations, which take into account, in particular, the mutual harmonic scattering. In this case, the X-ray field at the exit from the modulated active medium can be written as:
where
Here is the detuning of the carrier frequency of the seed radiation (6), (7) from the time-average frequency of the transitions and with which it interacts. According to (24) and (25), the gain spectrum of the modulated active medium is centered at the frequency . In this case, the induced gain lines are spaced apart from each other by the frequency of the modulating field (and not by , as was assumed in [19,23]), and the corresponding gains differ from the gain of the unmodulated medium by a factor of . Thus, the resulting gain spectrum of the modulated medium turns out to be symmetric with respect to the time-average frequency of transitions and . Note also that since , the sum of the gains of the modulated active medium over the induced gain lines of all orders is equal to the gain in the absence of the modulating field.
4. Discussion
Consider the amplification of a set of high-order in-phase harmonics with equal amplitudes (7), (8), and (18), which form a train of attosecond pulses. Substituting (18) into (24), after some transformations, we obtain:
In what follows, we will consider two typical cases: (a) , i.e., the modulating field is a replica of the laser field used to generate high harmonics, and (b) , i.e., the modulating field is the second harmonic of the laser field of the fundamental frequency. In either case, if , where s is an integer, each of the harmonics will be in resonance with the corresponding gain line, which makes it possible to amplify the entire set of harmonics. In addition, we will assume that the frequencies and , which determine the distance between both the induced gain lines and harmonics in the emission spectrum of the seed, are much greater than the width of the gain lines, , and the width of the spectrum of each individual harmonic, which is inversely proportional to the duration of its envelope, , i.e., , and , . In the case of a plasma of C5+ ions with the considered parameters, γz−1~γcoll−1 ≈ 20 fs, and the conditions specified above are satisfied for any fields in the near and mid-IR ranges. In this case, the largest contribution to the sum in the exponent of (26) will be due to the term for which the resonance condition is fulfilled:
It follows from condition (27) and the above assumptions (in particular, ) that the harmonic with number q interacts with only one gain line with number k + s.
In the following, we will assume that the emission spectrum of harmonics at the entrance to the medium is symmetric with respect to the frequency . In this case, to the left and to the right of the frequency , there is an equal number of high harmonics (in this case, if the frequencies and do not coincide and , then ). Due to the symmetry of the induced gain spectrum of the modulated medium, this makes it possible to amplify in the same way both the left and right (with respect to frequency ) parts of the high harmonic spectrum, which ensures the homogeneity of their amplification. In the case of a modulating field of a fundamental frequency, , at , the condition (27) is satisfied for . Accordingly, the harmonics in the emission spectrum of the seed are in resonance with the gain lines of even order (even k), while the number of harmonics NH is odd. It is this case that was considered in [19]. At the same time, at and , the harmonics are in resonance with the amplification lines of odd orders, corresponding to , while the number of amplified harmonics is even. In practice, this or that case can be realized by fine tuning the harmonic frequencies. Note that in both cases, half of the amplification lines are not used, which reduces the efficiency of signal amplification. Other integer values are equivalent to or , since the carrier frequency of the harmonics is determined with an accuracy of (and the spectrum of harmonics may be asymmetric with respect to the carrier frequency, while remaining symmetric with respect to the frequencies of transitions and ).
In the case of a modulating field of doubled fundamental frequency, , at the condition (27) is satisfied for . In this case, the spectral components of the seed radiation are in resonance with the gain lines of both even and odd orders, and the gain of the active medium is used most efficiently.
Next, we investigate the optimal conditions for amplification of attosecond pulse trains formed by a set of high-order harmonics resonant with the induced gain lines of (a) even, (b) odd, and (c) all orders. In contrast to [19], we will formalize the search for optimal values of the modulation index corresponding to both the most efficient and the most uniform amplification of harmonics of different orders.
The efficiency of harmonic amplification will be characterized by the value
which determines the average harmonic gain normalized to the gain in the absence of a modulating field, . The summation in (28), as well as in (29), is carried out over those k for which condition (27) is satisfied, where , i.e., over harmonics of those orders that are present in the spectrum of incident radiation (6), (7). In this case, denotes the number of terms, not the upper limit of summation.
The homogeneity of the gain distribution of different harmonics will be characterized by the value
which corresponds to the root-mean-square (rms) deviation of the normalized gain factors of harmonics from their mean value, .
The most efficient harmonic amplification requires maximizing the value . At the same time, for the most uniform amplification of harmonics of different orders, it is required to minimize the value . Typical dependences of and on the modulation index are shown in Figure 1. Figure 1a illustrates the case of amplification of a set of 7 harmonics resonant with even-order gain lines (k = {0, ±2, ±4, ±6}, with in sums (28) and (29), whereas Figure 1b shows amplification of a set of 6 harmonics resonant with the gain lines of odd orders (k = {±1, ±3, ±5}, with ). In both cases, the modulating field of the fundamental frequency, , is used. At the same time, Figure 1c corresponds to the modulating field of the doubled fundamental frequency, , and the amplification of 7 harmonics resonant with the gain lines of all orders (k = {0, ±1, ±2, ±3} and ). The dotted lines in Figure 1a,b show the sums of the squares of the Bessel functions of all even and odd orders, divided by the number of amplified harmonics: and , respectively. In Figure 1c, the dotted line shows the sum . As follows from these figures, at low values of the modulation index, , the value in Figure 1a,b is and , respectively. Similarly, when , for in Figure 1c we have . In this case, the average harmonic gains reach their maximum values, while their standard deviation is also close to the maximum. At in Figure 1a,b and in Figure 1c, the average harmonic gain remains rather large, while the rms deviation decreases significantly. With a further increase in the modulation index, in Figure 1a,b and in Figure 1c, the average gain falls off rapidly, while the rms deviation becomes an oscillating function of .
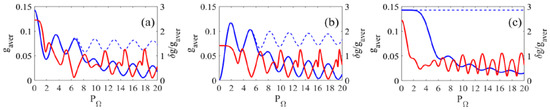
Figure 1.
Dependences of gaver (28) (left axis, blue solid curve) and δg/gaver (29) (right axis, red solid curve) on the modulation index PΩ for the cases of (a) amplification of NH = 7 high harmonics resonant with even gain lines (k = {0; ±2; ±4; ±6}), (b) amplification of NH = 6 high harmonics resonant with odd gain lines (k = {±1; ±3; ±5}), and (c) amplification of NH = 7 high harmonics resonant with gain lines of all orders (k = {0; ±1; ±2; ±3}). Blue dashed curves (left axis) show the sums of the squares of the Bessel functions of (a) all even orders, (b) all odd orders, and (c) all orders, divided by the number of amplified harmonics, NH.
This behavior of the dependences and is typical for any number of amplified harmonics and is explained as follows. In the absence of modulation, at , the gain is concentrated at the unperturbed frequency of the inverted transition. In this case, only the central component, which is resonant with the gain line with k = 0, is amplified in the harmonic emission spectrum. With an increase of the modulation index, the gain is redistributed over the combination frequencies in the amplification bandwidth . However, as long as in the case of a modulating field of the fundamental frequency, , or in the case of a modulating field of a doubled fundamental frequency, , the gain spectrum of the active medium remains narrower than the emission spectrum of the seed, . As a result, the harmonics furthest from the time-average transition frequency are not amplified, which leads to a narrowing of the X-ray spectrum and an increase in the duration of attosecond pulses in the process of their amplification, and also causes a large rms deviation of the gains of harmonics of different orders. At for the modulating field of the fundamental frequency, , or for the modulating field of the doubled fundamental frequency, , the width of the gain spectrum of the active medium reaches the width of the seed emission spectrum, . In this case, the gains become noticeably nonzero for all harmonics in the emission spectrum of the seed, which makes it possible to preserve the spectral width and duration of the amplified attosecond pulses and leads to a noticeable decrease of the rms deviation of the harmonic gains from their mean value. A further increase in the modulation index to for and to for leads to the fact that the gain spectrum of the medium becomes wider than the emission spectrum of the seed, . In this case, the gain is redistributed, among other things, over combination frequencies absent in the seed radiation spectrum, which, taking into account the constancy of the sum of the gains over all frequencies, leads to a decrease in the average harmonic gain.
Thus, the optimal combination of efficiency and homogeneity of harmonic amplification is achieved under conditions of approximate equality of the width of the gain spectrum and the width of the emission spectrum of the seed,
and corresponds to the modulation index at which the minimum value of is achieved in the vicinity of for the modulating field of the fundamental frequency, , and of for the modulating field of the doubled fundamental frequency, . Next, we investigate the dependences of the efficiency and homogeneity of harmonic amplification on the modulation index in this regime.
For this, it will be convenient to define the number of harmonics consistent with the gain spectrum of the medium, , as a following continuous function (which is a real number) of the modulation index:
where is a weighting factor that differs from zero only for those values of k, which at a given modulation index correspond to gain lines with a substantially nonzero amplitude:
where in the case of harmonics resonant with the gain lines of even or odd orders (), and for harmonics resonant with the gain lines of all orders (). The average gain of the harmonic spectrum, which corresponds to definition (31), (32), normalized to the gain in the absence of modulation, has the form
while the normalized rms deviation of the (normalized) gains from their mean value is determined by:
Note that the quantity characterizes with good accuracy the number of gain lines of a modulated active medium with a substantially nonzero amplitude. Accordingly, the quantities and are intrinsic characteristics of the efficiency and homogeneity of the gain spectrum of the modulated medium (and depend only on the modulation index), which distinguishes them from the parameters (28) and (29), which characterize the amplification of an arbitrary number of harmonics (these quantities are functions of two variables, the number of harmonics and the modulation index). The dependencies (28), (29) approximately coincide with (33), (34) only if the condition (30) is fulfilled, which makes this regime special and serves as an additional confirmation of its optimality. It should be noted here that the rms deviation of the harmonic amplification factors (29) can be reduced relative to the value (34) at the cost of reducing the average harmonic amplification factor (28) relative to the value (33) by increasing the modulation index relative to its optimal value ( in the case and in the case ) and transition to the regime (see, in particular, Figure 1).
Next, we analyze the dependences (33) and (34) on the modulation index for harmonics resonant with the gain lines of even, odd, and all orders. Note again that, in contrast to (28) and (29), these dependences imply that the number of amplified harmonics changes in proportion to the modulation index (30)–(32).
First of all, we will consider the case of harmonics resonant with the amplification lines of even orders: , . The corresponding dependences of the normalized average gain (33) and the rms deviation of the gains from their mean value (34), as well as the number of harmonics matched with the gain spectrum of the medium (31), (32) on the modulation index for this case are shown in Figure 2 as solid curves. The circles in Figure 2c show the minimum values of the function (29) for an odd number of harmonics in the vicinity of the modulation index . In Figure 2b, circles mark the corresponding values of the normalized average harmonic gain (28), whereas in Figure 2a, the circles mark the optimal (minimizing the function ) values of the modulation index for the indicated values . In all cases, the circles lie on the solid curves, while in Figure 2c, the circles are located near the local minima of the function . This agreement is achieved for the values of the modulation index corresponding to the local minima of the function under condition (30), makes the choice of these local minima special and indicates the optimality of the corresponding values. In this case, the degree of agreement between the values of the functions and , as well as between and , is determined by the value in the definition of the weight coefficients (32): for larger values of , the difference between the functions increases, while for smaller values of , functions (33) and (34) become less smooth. The dotted curves in Figure 2a,b show the functions and , respectively, reflecting the main trend of the dependences of the number of harmonics and the normalized average gain on the modulation index in the considered gain regime.
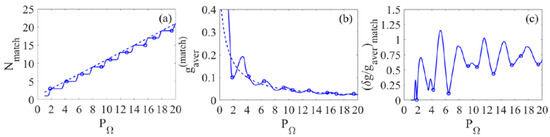
Figure 2.
(a) Number of harmonics matched with the gain spectrum of the medium, Nmatch (31), (b) the normalized average gain of the matched harmonic spectrum, (33), and (c) the normalized standard deviation of the gains, (34), as functions on the modulation index PΩ for harmonics resonant with even-order amplification lines. The circles mark the quantities NH, gaver, and δg/gaver, which correspond to the minima of function (29) for an odd number of harmonics 3 ≤ NH ≤ 19 in the vicinity of PΩ ≈ NH − 1; solid curves show dependences (31)–(34), and dashed lines in (a,b) correspond to analytical estimates Nmatch ≈ PΩ + 1 and gaver(match) ≈ 1/(2PΩ + 2).
As follows from Figure 2, the most efficient and uniform gain is achieved for a combination of 3, 5, or 7 harmonics. In these cases, the optimal values of the modulation index are equal to , , and , respectively, the average gains are , , and , and the standard deviations are equal to , , and . A further increase in the number of amplified harmonics leads to a sharp (several times) increase of the ratio with a gradual decrease of the average gain . For example, for a set of seventeen harmonics, , , and .
Next, we will consider the case of amplification of a set of high harmonics resonant with the gain lines of odd orders: , . The corresponding dependences of , , and on the modulation index in the regime of matching the widths of the amplification and harmonic emission spectra are shown in Figure 3. Designations are the same as in Figure 2. The circles show the values of the modulation index in the vicinity of , minimizing the ratio for an even number of harmonics (Figure 3a), as well as the values of the functions and for the given modulation indices (Figure 3b,c). Note that for the corresponding circle is not shown, since the value turns out to be in the vicinity of the local maximum instead of the minimum of the function for this number of harmonics; the nearest minima are reached at and . For uniform amplification of the combination of 16 harmonics, one should choose ; in this case, the gain efficiency is the same as for the set of 18 harmonics. The dotted curves in Figure 3a,b depict the functions and , respectively, reflecting the main trend of and dependences. As follows from Figure 3, one can amplify most efficiently and with minimal distortions the sets of 2, 4, 6, or 8 harmonics. The optimal values of the modulation index in these cases are equal to , , , and , respectively; the normalized mean harmonic gains are , , , and , and the normalized standard deviations of the gains are , , , and .
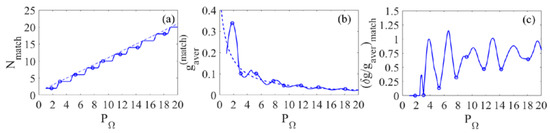
Figure 3.
Same as in Figure 2, but for a set of high harmonics resonant with odd-order gain lines. Solid curves are plotted according to (31)–(34), and dashed lines in (a,b) correspond to estimates Nmatch ≈ PΩ + 1 and gaver(match) ≈ 1/(2PΩ + 2).
In general, Figure 3 is similar to Figure 2. These figures show that, to amplify a larger number of harmonics, it is necessary to use larger values of the modulation index; with an increase of the modulation index, the efficiency of harmonic amplification decreases, and the amplification spectrum becomes more inhomogeneous. It is seen that, if the value of the modulation index is optimal (minimizes the value ) for gain lines of even orders, Figure 2c, it will be the least suitable for the gain lines of odd orders, Figure 3c; see also Figure 1a,b. In addition, the values of the modulation index corresponding to the most uniform amplification of a certain number of harmonics resonant with gain lines of odd orders, are in the interval between the values of the modulation index, which are optimal for amplification of the nearest number of harmonics resonant with amplification lines of even orders. From the above, one can conclude that the gain lines of even and odd orders can be used with equal success to amplify a set of high harmonics, and the choice between them is determined by the carrier frequency of the seed radiation (i.e., by the value ).
Finally, we will consider the case of a modulating field of doubled fundamental frequency and harmonics resonant with gain lines of all orders: , . The dependences of the quantities , , and (as well as and under condition (30)) on the modulation index for this case are shown in Figure 4. The designations are the same as in Figure 2 and Figure 3. The dotted curves in Figure 4a,b show estimates for the number of amplified harmonics matched with the gain spectrum of the medium (30) and the average harmonic gain, and , respectively. As follows from the comparison of Figure 4 with Figure 2 and Figure 3, the case under consideration differs significantly from the case of the modulating field of the fundamental frequency and harmonics resonant with the gain lines of even or odd orders (see also Figure 1). To amplify a fixed number of harmonics, the optimal value of the modulation index in Figure 4 is approximately two times smaller, and the average value of the harmonic gain is approximately two times larger than in Figure 2 and Figure 3. For example, for amplification of seven harmonics resonant with the gain lines of even orders, the optimal modulation index is , and the average value of the normalized gain is , while for amplification of seven harmonics resonant with the gain lines of all orders, and , respectively. However, for not too many amplified harmonics (and small values of the modulation index), the gain spectrum turns out to be much more inhomogeneous than for harmonics resonant with the gain lines of even or odd orders (see Figure 2c, Figure 3c and Figure 4c). In particular, for seven harmonics resonant with gain lines of even orders, , while for seven harmonics resonant with gain lines of all orders, . On the other hand, as can be seen from the comparison of Figure 4 and Figure 2 and Figure 3, with an increase in the number of amplified harmonics, the difference in the degree of gain inhomogeneity decreases, and in certain cases, the use of gain lines of all orders makes it possible to achieve a lower value of . Together with the large average harmonic gain, this makes the use of gain lines of all orders preferable for the number of harmonics . For example, when amplifying 17 harmonics using gain lines of all orders, the optimal modulation index is , which corresponds to and , while when using amplification lines of even orders, we have , , and . In addition, efficient amplification of the seed radiation when using gain lines of all orders increases the ratio of the intensity of the useful signal to the intensity of the amplified spontaneous emission of y-polarization generated at the transitions and of the active medium.
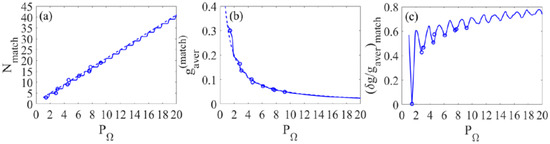
Summarizing this section, we note that the sum of the gains over all the induced gain lines does not depend on the modulation index, which is expressed by equality . With an increase of the modulation index, the number of gain lines with a substantially nonzero amplitude increases proportional to , and the average gain along such lines decreases proportional to . In this case, the gain is distributed approximately equally between the even- and odd-order gain lines, which makes them equally suitable for amplifying a set of high harmonics. The best amplification of a set of harmonics is achieved if the width of the harmonic spectrum is approximately equal to the width of the gain spectrum of the medium (30). In this case, to amplify a small number of harmonics, , it is preferable to use the gain lines of even or odd orders and, accordingly, the modulating field of the fundamental frequency, which for these values of makes it possible to achieve the most uniform amplification of harmonics of different orders. At the same time, for a larger number of harmonics, , it is preferable to use the gain lines of all orders and, accordingly, the modulating field of the doubled fundamental frequency, which in this case makes it possible to double the gain coefficients without losing the homogeneity of the gain spectrum.
In the next section, the above conclusions of the analytical theory are compared with the results of the numerical solution of the system of equations presented in Section 2, in its most general form, taking into account the nonlinearity of the medium, as well as amplified spontaneous emission on inverted transitions. We will consider the cases of (a) a relatively small number of harmonics, namely (i) 7 harmonics resonant with gain lines of even orders, (ii) 6 harmonics resonant with lines of odd orders, and (iii) 7 harmonics resonant with lines of all orders, as well as (b) a larger number of harmonics, namely, a set of 17 harmonics resonant with the amplification lines of (i) even and (ii) all orders.
5. Numerical Results
In numerical calculations, we assumed that high-order in-phase harmonics (7), (8) generated by a laser field with a wavelength ɅF = 2πc/ΩF = 2.1 μm are present at the entrance to the medium. These harmonics form a train of attosecond pulses, the temporal envelope of which is determined by Equation (8) and the peak intensity is I0 = 1012 W/cm2, regardless of the number of amplified harmonics.
First of all, we will compare the cases of amplification of (i) 7 harmonics resonant with even order gain lines, (ii) 6 harmonics resonant with odd order lines, and (iii) 7 harmonics resonant with gain lines of all orders. In these cases, the pulse duration will be 430 as and 530 as for a combination of 7 and 6 harmonics, respectively. In the case of 7 harmonics resonant with even order gain lines, the optimal modulation index is equal to and corresponds to the intensity of the modulating field of the fundamental frequency (with a wavelength of 2.1 μm). For 6 harmonics resonant with odd order gain lines, it is necessary to use a modulating field of the same wavelength (2.1 μm) and a slightly lower intensity , which corresponds to the modulation index . To amplify 7 harmonics resonant with the gain lines of all orders, the modulating field must have a doubled fundamental frequency and a wavelength of 1.05 μm. In this case, the optimal intensity of the modulating field is equal to and corresponds to the modulation index .
The results of numerical calculations for the above three cases and an active medium 5 mm thick with an unperturbed amplitude gain g0 = 90 cm−1 are shown in Figure 5. In the cases of modulation of the active medium by a laser field of fundamental frequency and amplification of a set of six, Figure 5a,b, or seven, Figure 5c,d, harmonics, resonant with the gain lines of odd or even orders, respectively, the shape of attosecond pulses is preserved with good accuracy, which is due to insignificant distortion of the spectra of harmonics, see Figure 5b,d. In these cases, in accordance with the conclusions of the analytical theory, with a decrease in the number of amplified harmonics and, as a consequence, in the used modulation index, the amplification efficiency increases. For example, the peak intensity of pulses formed by a set of 7 and 6 harmonics resonant with the gain lines of even and odd orders, respectively, increases by a factor of 26 and 49 during the amplification process. At the same time, in both cases, the amplified signal turns out to be several times weaker than the amplified spontaneous emission of y-polarization. The intensity of harmonic radiation can be raised to the level of amplified spontaneous emission by modulating the active medium of an X-ray laser by the second harmonic of the IR field of the fundamental frequency, Figure 5e,f. In this case, the train of pulses formed by a set of seven harmonics resonant with the gain lines of all orders, at the same thickness of the medium, is amplified in intensity by a factor of 220. However, the shape of the pulses in this case is significantly distorted, see the inset in Figure 5e, due to the less uniform amplification of harmonics of different orders, Figure 5f. Particularly, harmonics detuned from the time-average transition frequency by are amplified faster than the others, which leads to a transformation of the pulse sequence into the beats of these two spectral components with an increase in the thickness of the medium. It should be noted that the spectral-temporal distortions of radiation decrease with decreasing optical thickness of the medium, which, together with a high amplification efficiency, makes the use of a modulating field with a doubled fundamental frequency and gain lines of all orders preferable in the case of an active medium with a limited optical thickness. Thus, the use of a modulating field with a doubled fundamental frequency softens the requirements for the active medium of a plasma-based X-ray laser, since it makes it possible to achieve a prescribed amplification of the harmonic signal with a smaller optical thickness of the medium.
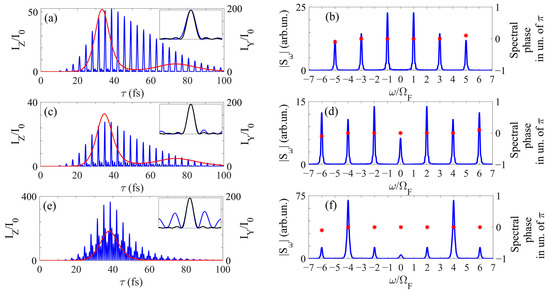
Figure 5.
(a,c,e) Time dependence of the intensity of z-polarized harmonic radiation (left axis, blue curve), as well as y-polarized amplified spontaneous radiation (right axis, red curve) at the exit from a modulated active plasma of C5+ ions with a thickness of 5 mm, free-electron density of ne = 1.5 × 1020 cm−3 and an unperturbed amplitude gain of g0 = 90 cm−1. The intensity is normalized to the peak intensity of the seed, I0 = 1012 W/cm2. (a) corresponds to the case of 6 harmonics resonant with the gain lines of odd orders with ; (c)—to the case of 7 harmonics resonant with even order gain lines with ; (e)—7 harmonics resonant with the gain lines of all orders with . The insets show the pulse shapes at the entrance (black curve) and exit (blue curve) from the medium in the envelope maxima of the corresponding pulse sequences. (b,d,f) Amplitude spectra of the amplified harmonic emission (left axis, blue curve), as well as the harmonic phases at their carrier frequencies (right axis, red stars). The spectral amplitude is normalized to the amplitude of harmonics in the emission spectrum of the seed.
Next, we will consider the amplification of a set of 17 harmonics that form a train of pulses with a duration of 160 as. If the active medium is modulated by a laser field of fundamental frequency (with a wavelength of 2.1 μm) and the harmonics are in resonance with the gain lines of even orders, then the optimal value of the modulation index is and corresponds to the intensity of the modulating field . At the same time, for a modulating field of doubled fundamental frequency with a wavelength of 1.05 μm and harmonics in resonance with the gain lines of all orders, the optimal values of the modulation index and intensity of the modulating field are and , respectively. The results of numerical calculations for these cases and an active medium 5 mm thick with an unperturbed amplitude gain g0 = 90 cm−1 are shown in Figure 6. As follows from Figure 6a, when using gain lines of even orders, the peak intensity of the pulse train increases by a factor of only 3.1, while when using the gain lines of all orders, the pulses are amplified by a factor of about 13 (Figure 6c). In this case, despite the less homogeneous spectrum of harmonics when they are in resonance with gain lines of all orders (compare Figure 6d with Figure 6b), the shape of the generated pulses is well preserved, and only the distortions of the pedestal are quite significant. Note also that due to the narrowing of the spectrum of each individual harmonic during amplification, the duration of the amplified signal envelope in Figure 5 and Figure 6 turns out to be longer than the duration of the seed radiation (8).
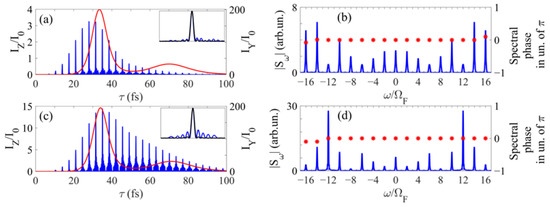
Figure 6.
Same as in Figure 5, but for (a,b) a set of 17 harmonics resonant with the gain lines of even orders, the modulation index , and (c,d) a set of 17 harmonics resonant with the gain lines of all orders, the modulation index .
Finally, we will compare the analytical solution obtained in Section 3 with the results of numerical calculations. Figure 7 shows the corresponding spatial dependences of the peak intensity of harmonic radiation for the cases considered above (see Figure 5 and Figure 6). It can be seen that the analytical solution is in good agreement with numerical calculations in the region of small thicknesses of the medium, where the interaction of X-ray radiation with the medium occurs in a linear regime, and the change in the population differences at inverted transitions is negligible. Such an agreement justifies the approximations made in deriving the analytical solution, in particular, the neglect of mutual coherent scattering of the harmonics. At the same time, with an increase in the thickness of the medium, the analytical solution overestimates the value of the peak radiation intensity, since it does not take into account the decrease in population inversion at resonance transitions. With a further increase in the thickness of the medium, the slope of the analytical dependences increases, which is due to the degeneration of the harmonic spectrum into a set of two (symmetric relative to the average transition frequency) spectral components that are in resonance with the most intense gain lines. The amplification factors for these harmonics exceed the average value, which leads to their dominance at a sufficiently large medium thickness. For example, in the case of amplification of 7 harmonics using gain lines of all orders, harmonics detuned from the average transition frequency by dominate. In numerical calculations, this effect is not observed, since the exponential growth of harmonic amplitudes is limited by the influence of nonlinearity caused by changes in the populations of the resonant states. As a result, starting with a certain thickness of the medium, the growth of the peak radiation intensity slows down and, ultimately, stops. This is due to the depletion of the population inversion by the amplified radiation (including the amplified spontaneous emission of y-polarization) and the consequent shift of the time interval, during which the amplification is achieved, to the leading edge of the harmonic pulse. Specifically, at a sufficiently large thickness of the medium, the duration of amplification becomes shorter than the duration of the amplified signal. In this case, the maximum of the envelope of the pulse train shifts towards earlier times, and the peak intensity of the pulses remains constant.
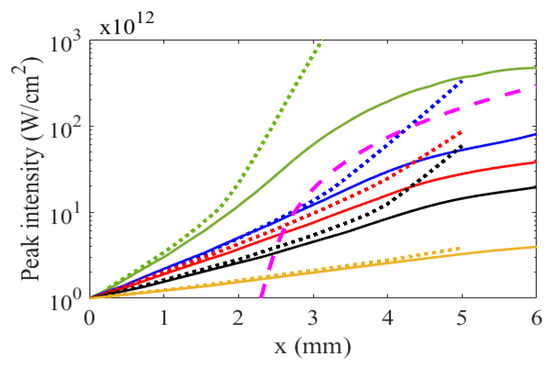
Figure 7.
Dependence of the peak intensity of the amplified harmonic radiation on the thickness of the active medium, x, with an unperturbed gain in amplitude of g0 = 90 cm−1 and the free-electron density of ne = 1.5 × 1020 cm−3. Green curves correspond to a set of 7 harmonics resonant with the gain lines of all orders and the modulation index , blue curves—to a set of 6 harmonics resonant with the gain lines of odd orders and , red curves—to a set of 7 harmonics resonant with the gain lines of even orders and , black curves—to a set of 17 harmonics resonant with the gain lines of all orders and , and orange curves—to a set of 17 harmonics resonant with the gain lines of even orders and . Solid curves show the results of the numerical solution of the system (9), and the dashed lines show the results of the analytical solution (24). The purple dashed curve shows the spatial dependence of the peak intensity of the amplified spontaneous emission of y-polarization.
Figure 7 also shows a typical spatial dependence of the peak intensity of the amplified spontaneous emission of y-polarization (purple dashed curve). It can be seen that amplified spontaneous emission can be neglected for the medium lengths up to 2.3 mm, since its intensity is much lower than the intensity of the amplified signal. Note that Figure 7 shows only one curve for the y-polarization radiation, since the modulating field and harmonic emission have no significant effect on its envelope, see Figure 5 and Figure 6.
6. Conclusions
In this work, we investigated the efficiency of amplification of attosecond pulses formed by a set of high-order in-phase harmonics of the IR field (separated by a doubled fundamental frequency of the IR field) in the hydrogen-like active medium of a plasma-based X-ray laser modulated either by a laser field of fundamental frequency or its second harmonic. The optimal conditions for the amplification of a set of a given number of harmonics in both cases are found. An analytical solution is obtained that describes the amplification of a set of high-order harmonics with an arbitrary envelope (and an arbitrary shape of the spectral line of an individual harmonic). It is shown that modulating the hydrogen-like active medium with the second harmonic of the fundamental frequency allows to significantly enhance an amplification.
When the modulating field of fundamental frequency is used, the harmonics can be in resonance with the gain lines of either even or odd orders. The choice between the gain lines to be used is determined only by the carrier frequency of the harmonic radiation, since they are equally suitable for amplifying attosecond pulses (providing comparable efficiency and homogeneity of harmonic amplification). Using the modulating field of the doubled fundamental frequency allows all sidebands (even and odd) produced by this field in the gain spectrum to contribute to amplification of high-harmonics. However, for a set of a small number of harmonics, the gain spectrum becomes much less uniform. Nevertheless, with an increase in the number of amplified harmonics, the difference in the homogeneity of the gain spectrum in all three cases (gain lines of even, odd, or all orders) practically disappears, which makes preferable the use of a modulating field with a doubled fundamental frequency.
The conclusions of the analytical theory were compared with the results of the numerical solution of the Maxwell–Bloch system of equations for an active plasma medium based on hydrogen-like ions C5+ and resonant radiation of harmonics with a wavelength in the vicinity of 3.4 nm (in the “water window” range). In particular, for realistic parameters of the active medium, it was shown that it is possible to amplify a train of pulses with a duration of 430 as, formed by a combination of seven high-order harmonics of a laser field with a wavelength of 2.1 μm, by a factor of 220 in intensity when using a modulating field of doubled fundamental frequency. When using the modulating field of the fundamental frequency with the same parameters of the active medium, the pulses are amplified by a factor of 26. In addition, it is shown that it is possible to amplify a sequence of 160 as pulses, formed by 17 high-order harmonics of a laser field with a wavelength of 2.1 μm, by a factor of 13 in intensity when using a modulating field with a doubled fundamental frequency, which is by a factor of 4.2 greater than for an active medium modulated by a laser field of fundamental frequency.
The obtained results open up the possibility of efficient amplification of high-harmonic radiation, soften the requirements for the parameters of an active medium of a plasma X-ray laser, and allow for more variable selection of the parameters of IR sources. Enhanced spectral combs and sequences of attosecond VUV/X-ray radiation pulses can be used in X-ray spectroscopy, as well as attosecond metrology and chronoscopy.
Author Contributions
Conceptualization, V.A.A., M.Y.R. and O.K.; Investigation, I.R.K. and V.A.A.; Software, I.R.K.; Supervision, V.A.A.; Visualization, I.R.K.; Writing—Original Draft, I.R.K., V.A.A. and M.Y.R.; Writing—Review and Editing, I.R.K., V.A.A., M.Y.R. and O.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Center of Excellence “Center of Photonics” funded by the Ministry of Science and Higher Education of the Russian Federation, contract 075-15-2020-906. OK appreciates the support by the National Science Foundation (grant number PHY-2012194).
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef] [Green Version]
- Gallmann, L.; Cirelli, C.; Keller, U. Attosecond science: Recent highlights and future trends. Annu. Rev. Phys. Chem. 2012, 63, 447–469. [Google Scholar] [CrossRef] [Green Version]
- Calegari, F.; Sansone, G.; Stagira, S.; Vozzi, C.; Nisoli, M. Advances in attosecond science. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 062001. [Google Scholar] [CrossRef]
- Young, L.; Ueda, K.; Gühr, M.; Bucksbaum, P.H.; Simon, M.; Mukamel, S.; Rohringer, N.; Prince, K.C.; Masciovecchio, C.; Meyer, M.; et al. Roadmap of ultrafast x-ray atomic and molecular physics. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 032003. [Google Scholar] [CrossRef]
- Schoenlein, R.; Elsaesser, T.; Holldack, K.; Huang, Z.; Kapteyn, H.; Murnane, M.; Woerner, M. Recent advances in ultrafast x-ray sources. Phil. Trans. R. Soc. A 2019, 377, 20180384. [Google Scholar] [CrossRef] [Green Version]
- Geneaux, R.; Marroux, H.J.B.; Guggenmos, A.; Neumark, D.M.; Leone, S.R. Transient absorption spectroscopy using high harmonic generation: A review of ultrafast x-ray dynamics in molecules and solids. Philos. Trans. R. Soc. A 2019, 377, 20170463. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Winterfeldt, C.; Spielmann, C.; Gerber, G. Colloquium: Optimal control of high-harmonic generation. Rev. Mod. Phys. 2008, 80, 117–140. [Google Scholar] [CrossRef]
- Kohler, M.C.; Pfeifer, T.; Hatsagortsyan, K.Z.; Keitel, C.H. Frontiers of atomic high-harmonic generation. Adv. At. Mol. Opt. Phys. 2012, 61, 159–208. [Google Scholar]
- Strelkov, V.V.; Platonenko, V.T.; Sterzhantov, A.F.; Ryabikin, M.Y. Attosecond electromagnetic pulses: Generation, measurement, and application. Generation of high-order harmonics of an intense laser field for attosecond pulse production. Phys. Usp. 2016, 59, 425–445. [Google Scholar] [CrossRef] [Green Version]
- Popmintchev, T.; Chen, M.-C.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright coherent ultrahigh harmonics in the keV x-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891–3893. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Ren, X.; Yin, Y.; Zhao, K.; Chew, A.; Cheng, Y.; Cunningham, E.; Wang, Y.; Hu, S.; Wu, Y.; et al. 53-attosecond X-ray pulses reach the carbon K-edge. Nat. Commun. 2017, 8, 186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaumnitz, T.; Jain, A.; Pertot, Y.; Huppert, M.; Jordan, I.; Ardana-Lamas, F.; Wörner, H.J. Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver. Opt. Express 2017, 25, 27506–27518. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.S.; Austin, D.R.; Wood, D.A.; Brahms, C.; Gregory, A.; Holzner, K.B.; Jarosch, S.; Larsen, E.W.; Parker, S.; Strüber, C.S.; et al. High-flux soft x-ray harmonic generation from ionizationshaped few-cycle laser pulses. Sci. Adv. 2018, 4, eaar3761. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Nishimura, K.; Shao, R.; Suda, A.; Midorikawa, K.; Lan, P.; Takahashi, E.J. High efficiency ultrafast water-window harmonic generation for single-shot soft X-ray spectroscopy. Commun. Phys. 2020, 3, 92. [Google Scholar] [CrossRef]
- Takahashi, E.J.; Lan, P.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Attosecond nonlinear optics using gigawatt-scale isolated attosecond pulses. Nat. Commun. 2013, 4, 2691. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tzallas, P.; Skantzakis, E.; Nikolopoulos, L.A.A.; Tsakiris, G.D.; Charalambidis, D. Extreme-ultraviolet pump–probe studies of one-femtosecond-scale electron dynamics. Nat. Phys. 2011, 7, 781–784. [Google Scholar] [CrossRef]
- Antonov, V.A.; Han, K.C.; Akhmedzhanov, T.R.; Scally, M.; Kocharovskaya, O. Attosecond pulse amplification in a plasma-based x-ray laser dressed by an infrared laser field. Phys. Rev. Lett. 2019, 123, 243903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akhmedzhanov, T.R.; Antonov, V.A.; Morozov, A.; Goltsov, A.; Scully, M.; Suckewer, S.; Kocharovskaya, O. Formation and amplification of sub-femtosecond x-ray pulses in a plasma medium of hydrogen-like ions with a modulated resonant transition. Phys. Rev. A 2017, 96, 033825. [Google Scholar] [CrossRef] [Green Version]
- Khairulin, I.R.; Antonov, V.A.; Ryabikin, M.Y.; Kocharovskaya, O. Sub-fs pulse formation in a seeded hydrogen-like plasma-based x-ray laser dressed by an infrared field: Analytical theory and numerical optimization. Phys. Rev. Res. 2020, 2, 023255. [Google Scholar] [CrossRef]
- Antonov, V.A.; Khairulin, I.R.; Kocharovskaya, O. Attosecond-pulse formation in the water-window range by an optically dressed hydrogen-like plasma-based C5+ x-ray laser. Phys. Rev. A 2020, 102, 063528. [Google Scholar] [CrossRef]
- Khairulin, I.R.; Antonov, V.A.; Kocharovskaya, O.A. Interference effects in the high-order harmonic amplification process in the active medium of a plasma-based X-ray laser modulated by an optical field. Quantum Electron. 2020, 50, 375–385. [Google Scholar] [CrossRef]
- Avitzour, Y.; Suckewer, S. Feasibility of achieving gain in transition to the ground state of C VI at 3.4 nm. J. Opt. Soc. Am. B 2007, 24, 819–828. [Google Scholar] [CrossRef]
- Radeonychev, Y.V.; Polovinkin, V.A.; Kocharovskaya, O. Extremely short pulses via Stark modulation of the atomic transition frequencies. Phys. Rev. Lett. 2010, 105, 183902. [Google Scholar] [CrossRef] [PubMed]
- Antonov, V.A.; Radeonychev, Y.V.; Kocharovskaya, O. Formation of ultrashort pulses via quantum interference between Stark-split atomic transitions in a hydrogenlike medium. Phys. Rev. A 2013, 88, 053849. [Google Scholar] [CrossRef]
- Glauber, R.; Haake, F. The initiation of superfluorescence. Phys. Lett. A 1978, 68, 29–32. [Google Scholar] [CrossRef]
- Haake, F.; King, H.; Schröder, G.; Haus, J.; Glauber, R.; Hopf, F. Macroscopic quantum fluctuations in super fluorescence. Phys. Rev. Lett. 1979, 42, 1740–1743. [Google Scholar] [CrossRef]
- Haake, F.; Haus, J.; King, H.; Schröder, G.; Glauber, R. Delay-time statistics and inhomogeneous line broadening in superfluorescence. Phys. Rev. Lett. 1980, 45, 558–561. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).