Deep Neural Network Based Reconciliation for CV-QKD
Abstract
1. Introduction
2. Preliminaries
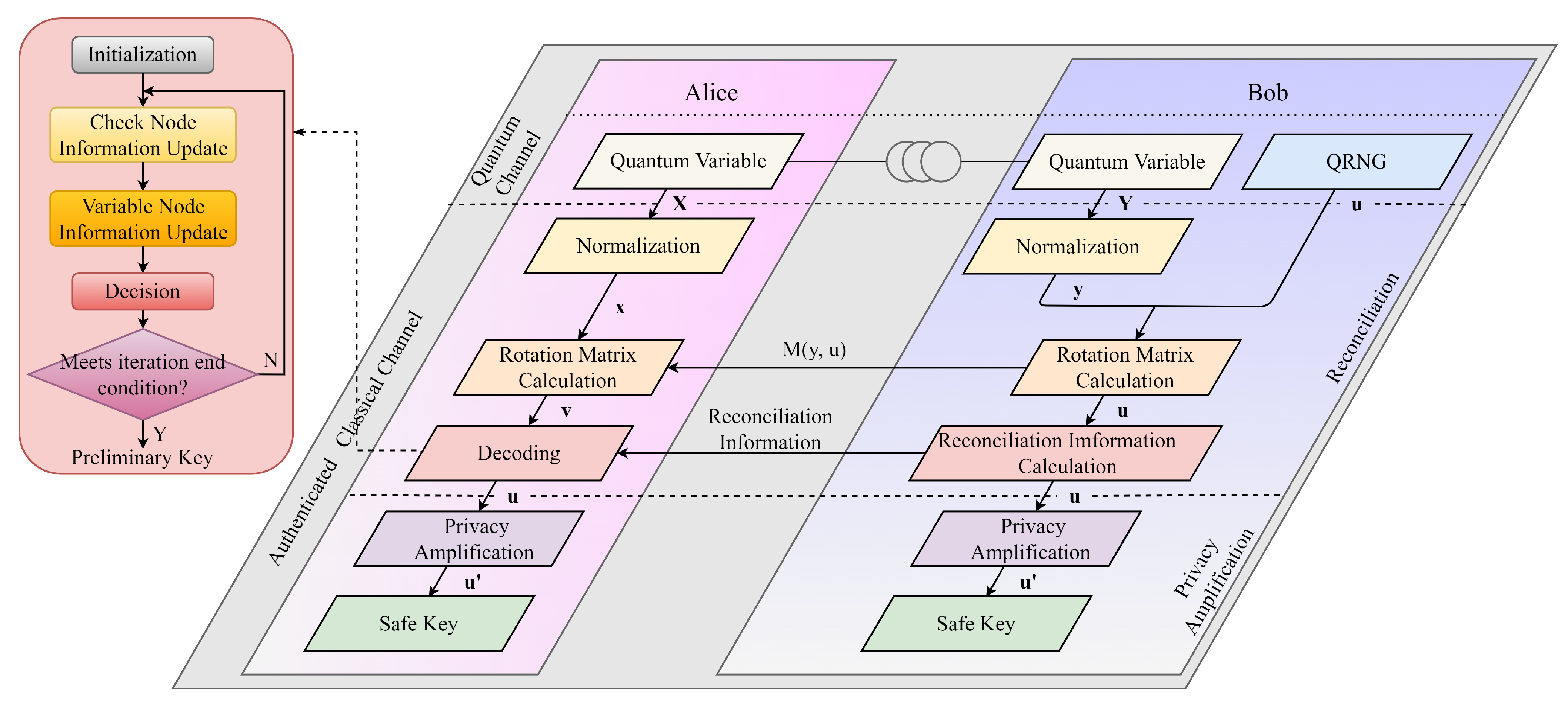
2.1. Brief Description of CV-QKD Post-Processing
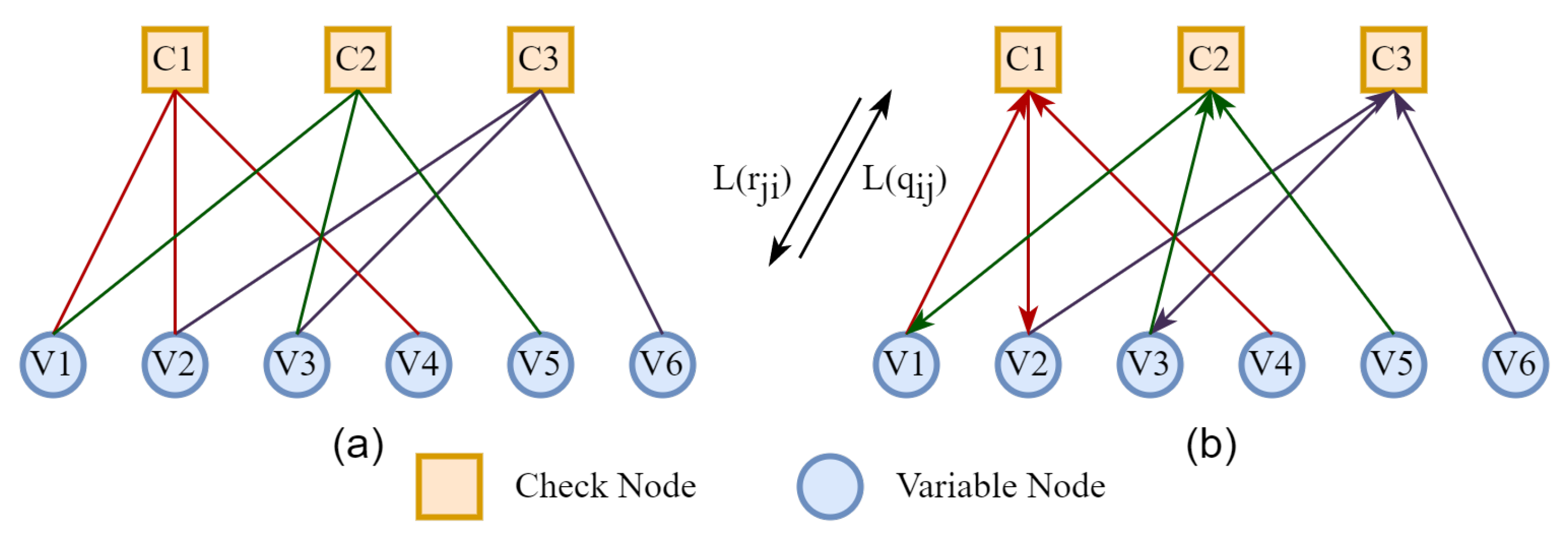
2.2. Reconciliation with LDPC Code
- Step 1, initialization.where is the ith bit of the received message and is the noise variance of the transmission channel.
- Step 2, check nodes information update.where is the information transmitted by the check node to the variable node . It is calculated based on the information from the set of all variable nodes connected to , excluding the variable node , and can be expressed as .
- Step 3, variable nodes information update.where is the information transmitted by the variable node to the check node . It is calculated based on the information from the set of all check nodes connected to , excluding the check node , and can be expressed as .
- Step 4, log-likelihood ratio of variable nodes update and decision.where is the ith bit of the decoded message. The iteration ends when k reaches the maximum number of iterations or ; otherwise, go back to Step 2.
3. High-Speed Multi-Dimensional Reconciliation
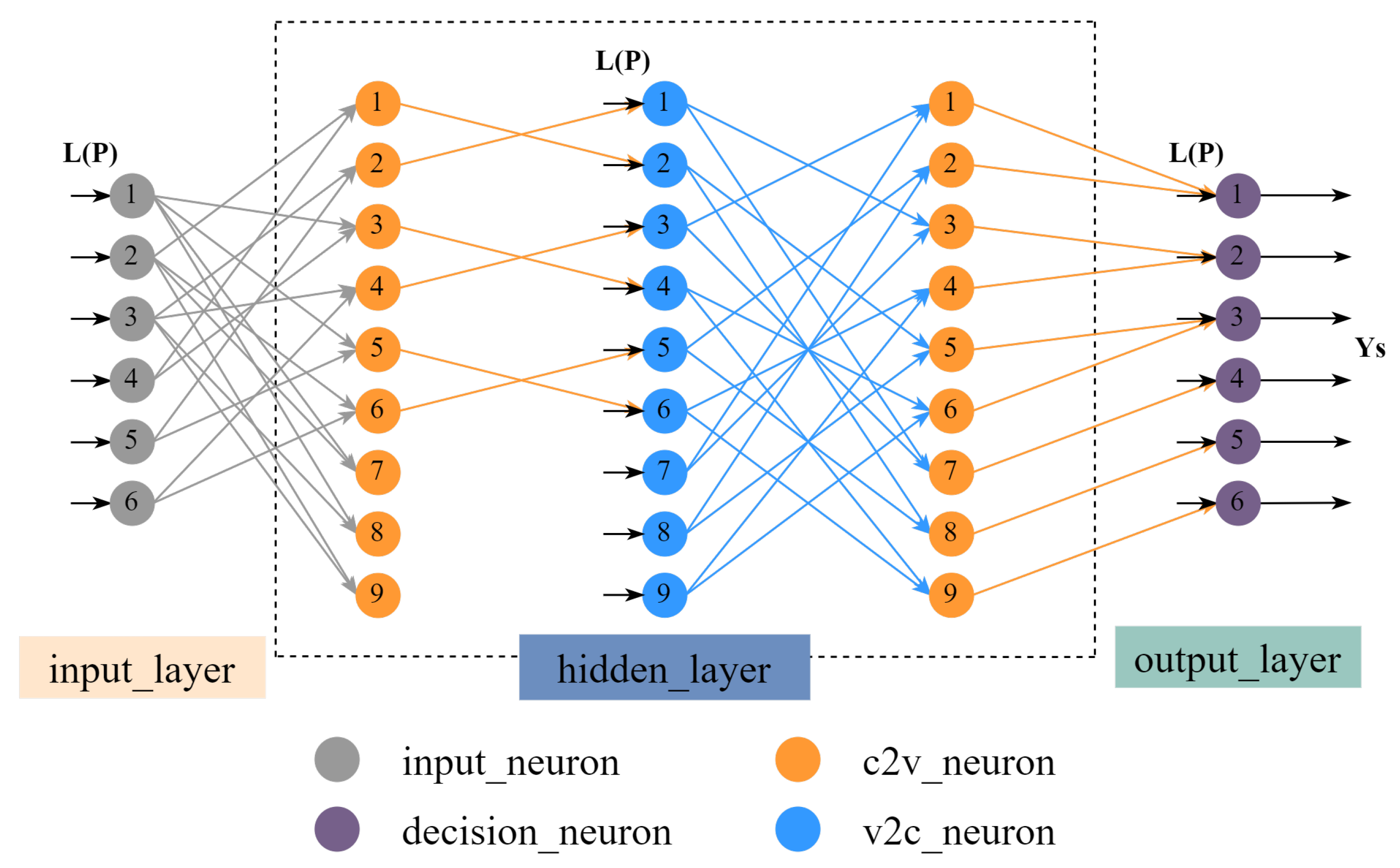
3.1. Proposed Network Structure of Decoding Implementation
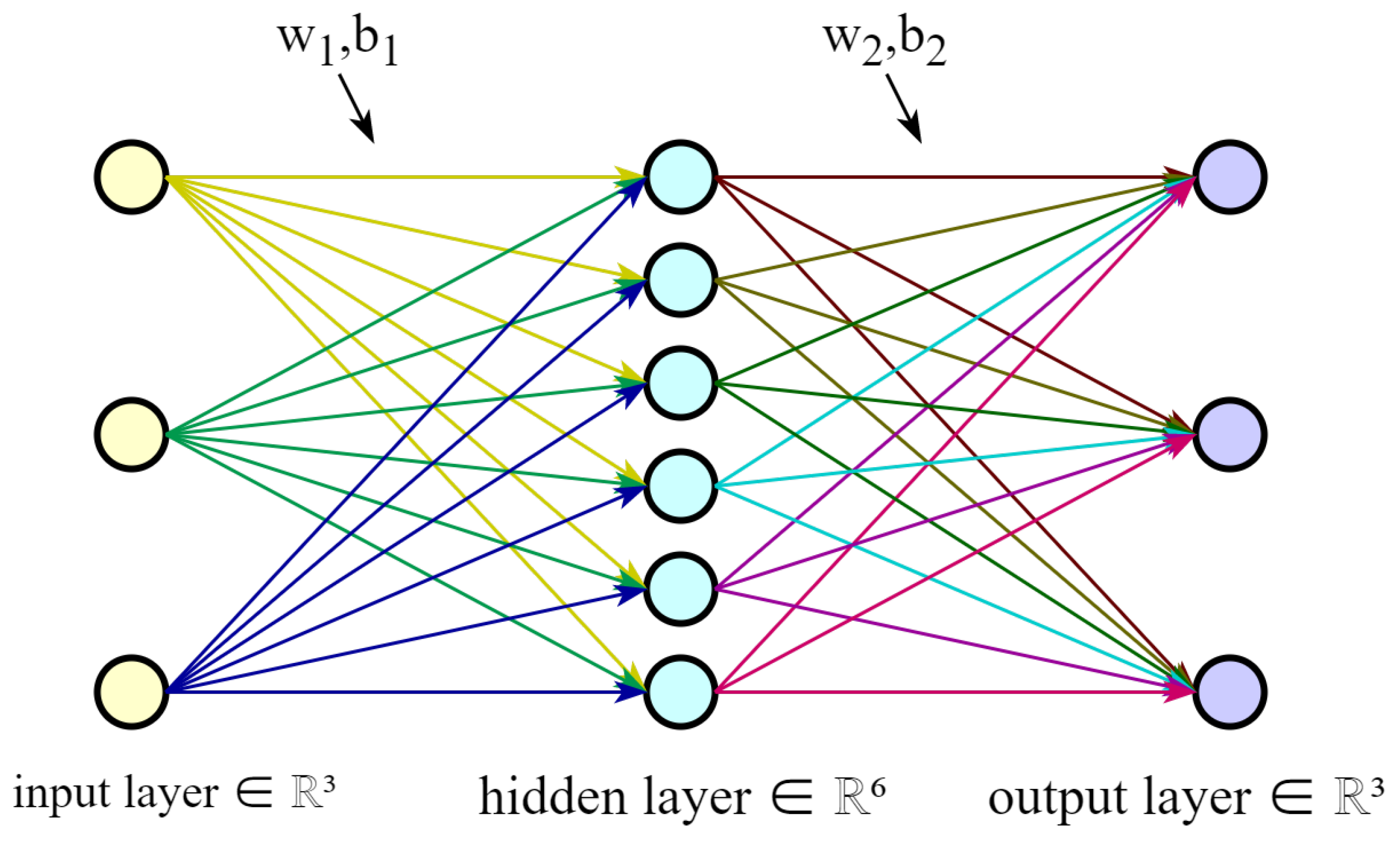
3.1.1. Multi-Layer Perceptron (MLP)
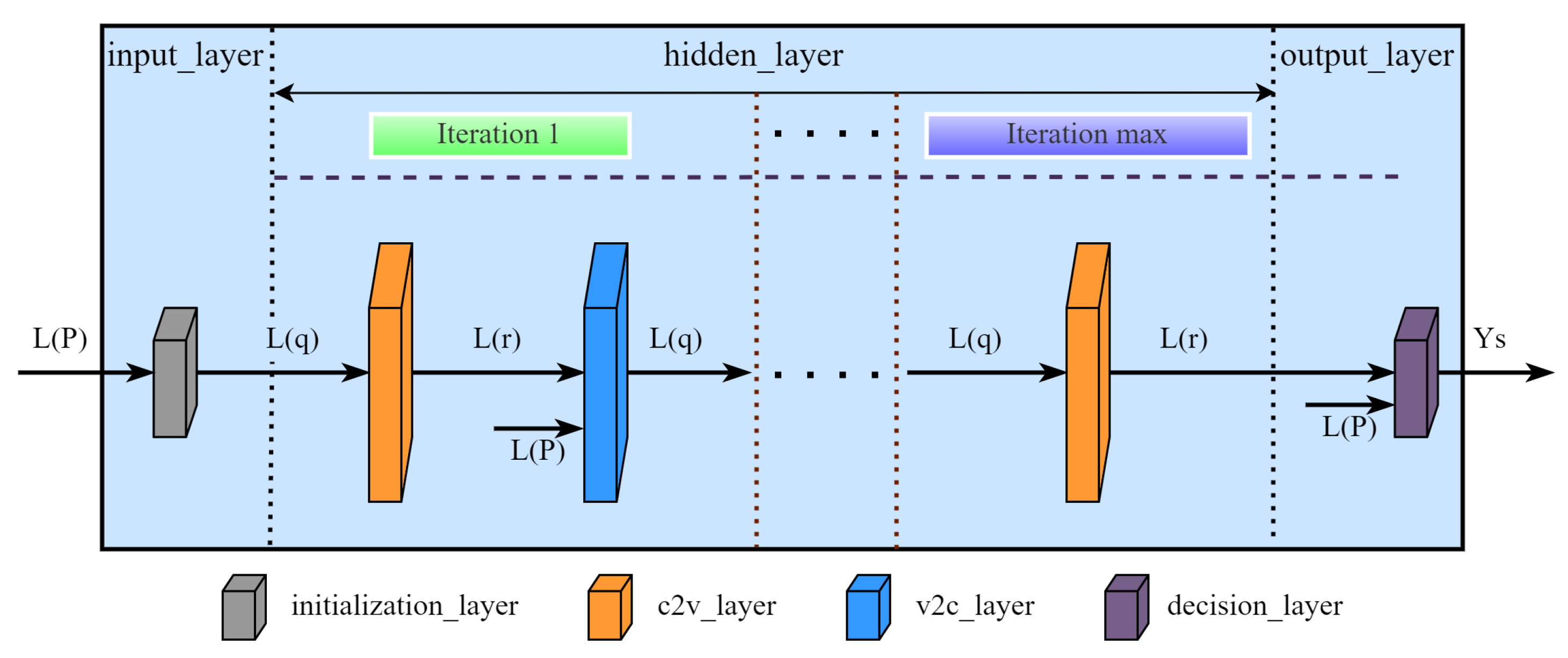
3.1.2. Proposed Decoding Network Structure
- The information update algorithm affects the error correction performance and determines the neurons’ specific connection mode between the network layers. Different from the fully connected network structure of MLP, our network connection depends on the information needed for the calculation of the neuron information. In other words, we only need to send the information needed in the calculation formula of the node to the node.
- The structure of the check matrix determines its maximum error correction capability. Furthermore, the number of columns determines the dimensions of the input and output layers, and the number of non-zero elements determines the dimensions of the hidden layer.
- The maximum number of iterations has a considerable influence on the error correction performance and determines the depth of the network. We can adjust the maximum number of iterations within a certain range to improve error correction performance. If the maximum number of iterations is set too small, the network depth is low, and the decoding success rate is low. On the contrary, if the maximum number of iterations is too large, it will cause excessive network depth and high time consumption.
3.1.3. Advantages of Proposed Network Structure
- The node information of the traditional algorithm is transmitted in the form of a matrix with the same shape as the check matrix. The network structure we proposed expands the two-dimensional matrix into a one-dimensional vector, optimizes the storage structure of the check matrix, and saves a lot of storage space.
- We arrange the transmitted information in order, which makes the memory read and write orderly, so the time delay of data read and write is significantly reduced, improving the decoding speed.
- We have neglected the update of variable nodes with degree 1 in the network construction, reducing unnecessary operations of traditional decoding algorithms.
- The forward propagation network eliminates the need for multiple iterations of decoding. Without iteration, we input the channel message into the network and obtain the decoded codewords [45].
- Since the network is fully parallel, we can use powerful hardware, such as graphics processing unit (GPU) or field-programmable logic gate array (FPGA), to process multiple data at once.
- This network structure is suitable for decoding algorithms with parallel strategy, and training network parameters can also improve the decoding algorithm. All we need to do is adjust the neuron’s calculation formula.
3.2. Linear Fitting Decoding Algorithm
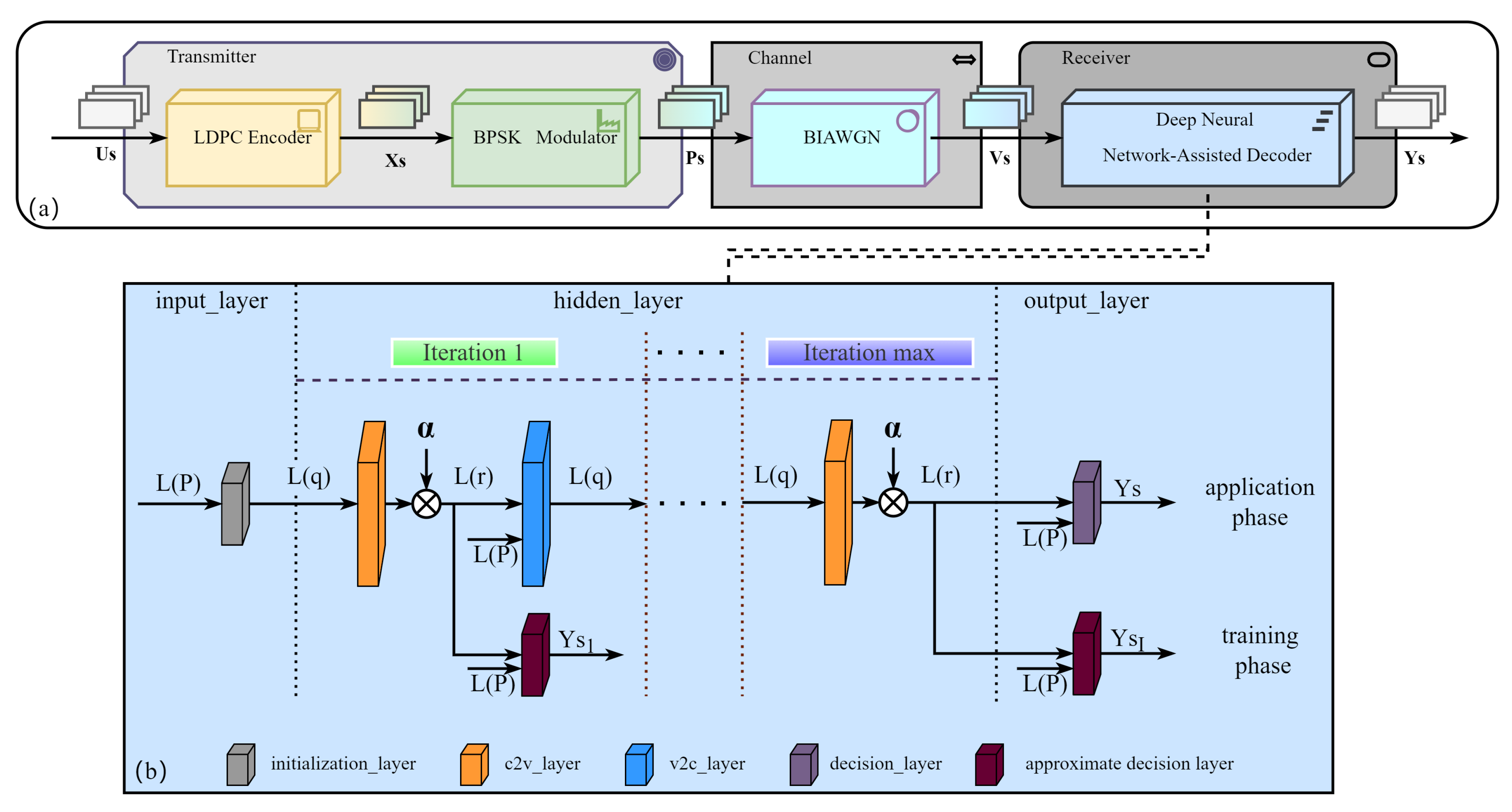
3.3. Deep Neural Network-Assisted Decoder
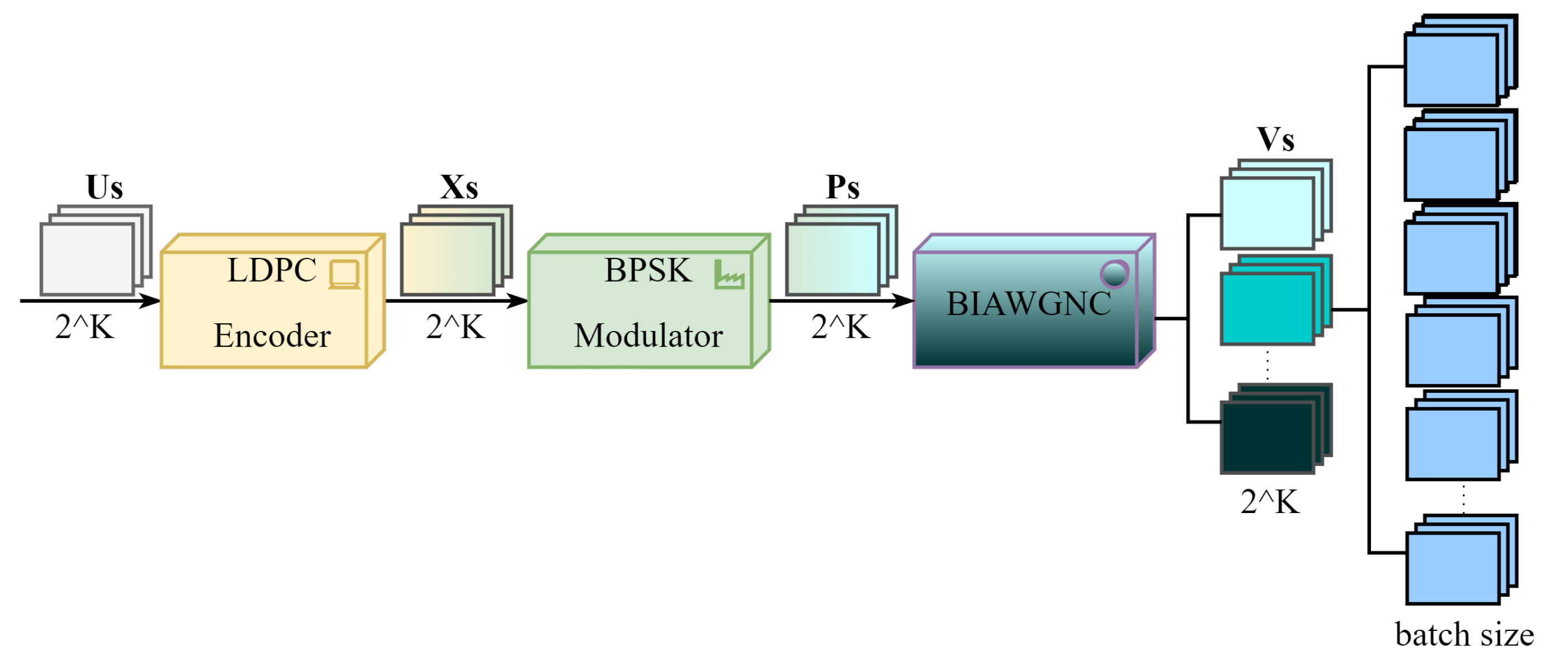
3.3.1. General Model of Simulation System
3.3.2. The Specific Structure of the Deep Neural Network-Assisted Decoder
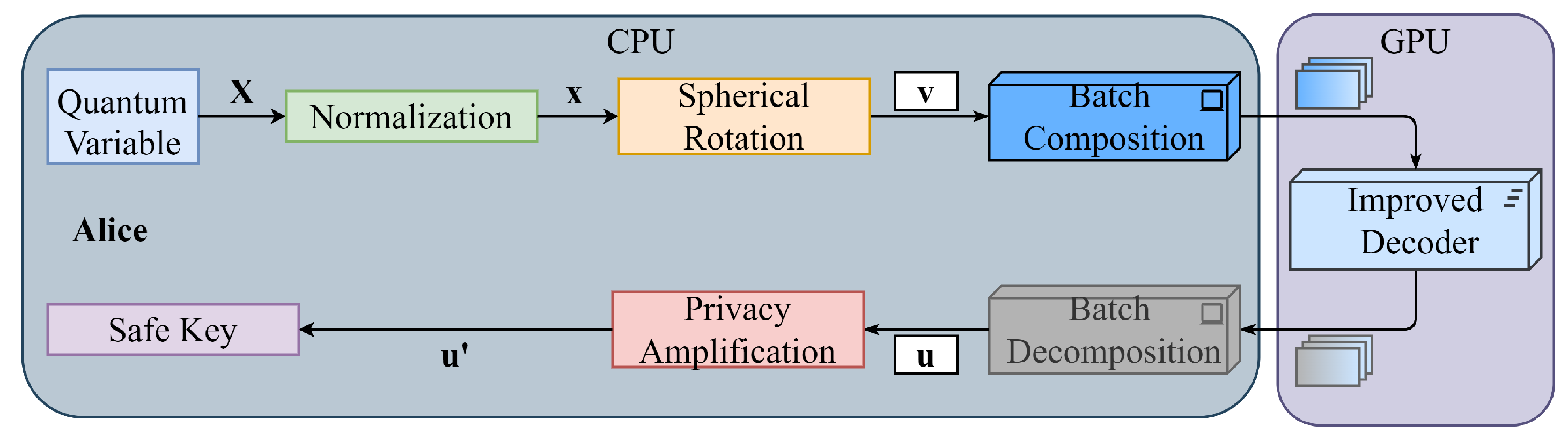
3.4. Proposed High-Speed Reconciliation Scheme
4. Simulation Results and Performance Analysis
4.1. Network Training Strategy
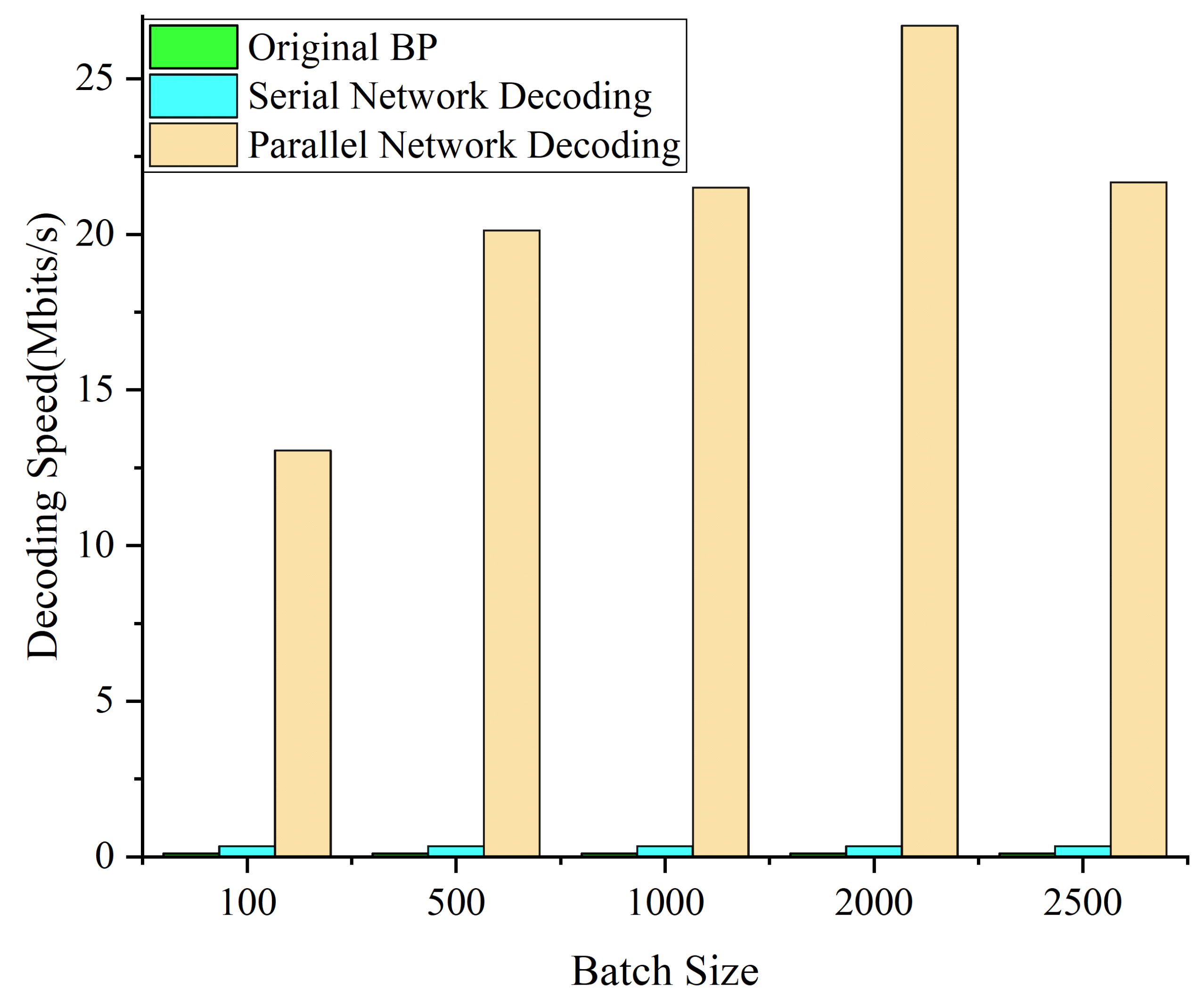
4.2. Complexity Analysis of Reconciliation Scheme
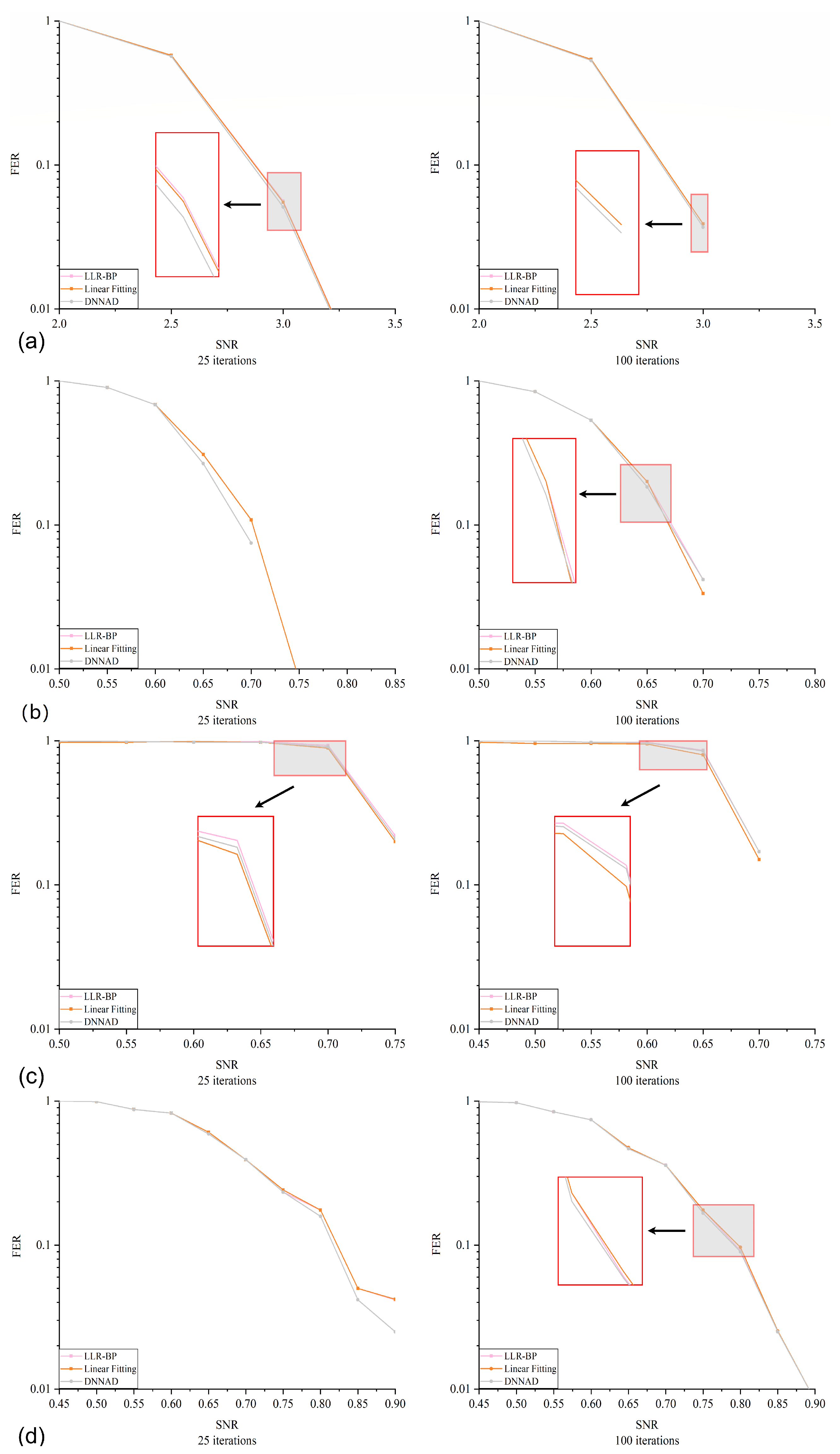
4.3. Error Correction Performance Comparison
4.4. Secret Key Rate
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mafu, M. A Simple Security Proof for Entanglement-Based Quantum Key Distribution. JQIS 2016, 6, 296–303. [Google Scholar] [CrossRef][Green Version]
- Milicevic, M.; Feng, C.; Zhang, L.M.; Gulak, P.G. Quasi-Cyclic Multi-Edge LDPC Codes for Long-Distance Quantum Cryptography. Npj Quantum Inf. 2018, 4, 21. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Bennett, C.H. Quantum Cryptography Using Any Two Nonorthogonal States. Phys. Rev. Lett. 1992, 68, 3121–3124. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous Variable Quantum Cryptography Using Coherent States. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef]
- Lodewyck, J.; Bloch, M.; García-Patrón, R.; Fossier, S.; Karpov, E.; Diamanti, E.; Debuisschert, T.; Cerf, N.J.; Tualle-Brouri, R.; McLaughlin, S.W.; et al. Quantum Key Distribution over 25 km with an All-Fiber Continuous-Variable System. Phys. Rev. A 2007, 76, 042305. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Wang, Q.; Zhang, J.; Ng, S.X.; Hanzo, L. The Evolution of Quantum Key Distribution Networks: On the Road to the Qinternet. IEEE Commun. Surv. Tutor. 2022. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in Quantum Cryptography. Adv. Opt. Photon. 2020, 12, 1012. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A. Long-Distance Continuous-Variable Quantum Key Distribution with a Gaussian Modulation. Phys. Rev. A 2011, 84, 062317. [Google Scholar] [CrossRef]
- VanAssche, G.; Cardinal, J.; Cerf, N.J. Reconciliation of a Quantum-Distributed Gaussian Key. IEEE Trans. Inform. Theory 2004, 50, 394–400. [Google Scholar] [CrossRef]
- Grosshans, F.; Cerf, N.J.; Wenger, J.; Tualle-Brouri, R.; Grangier, P. Virtual Entanglement and Reconciliation Protocols for Quantum Cryptography with Continuous Variables. arXiv 2003, arXiv:quant-ph/0306141. [Google Scholar] [CrossRef]
- Fang, J.; Huang, P.; Zeng, G. Multichannel Parallel Continuous-Variable Quantum Key Distribution with Gaussian Modulation. Phys. Rev. A 2014, 89, 022315. [Google Scholar] [CrossRef]
- Gallager, R. Low-Density Parity-Check Codes. IEEE Trans. Inform. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Xie, J.; Wu, H.; Xia, C.; Ding, P.; Song, H.; Xu, L.; Chen, X. High Throughput Error Correction in Information Reconciliation for Semiconductor Superlattice Secure Key Distribution. Sci. Rep. 2021, 11, 3909. [Google Scholar] [CrossRef]
- Wang, C.; Huang, D.; Huang, P.; Lin, D.; Peng, J.; Zeng, G. 25 MHz Clock Continuous-Variable Quantum Key Distribution System over 50 Km Fiber Channel. Sci. Rep. 2015, 5, 14607. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Yu, S.; Guo, H. High Speed Error Correction for Continuous-Variable Quantum Key Distribution with Multi-Edge Type LDPC Code. Sci. Rep. 2018, 8, 10543. [Google Scholar] [CrossRef]
- Mao, H.; Li, Q.; Han, Q.; Guo, H. High-Throughput and Low-Cost LDPC Reconciliation for Quantum Key Distribution. Quantum Inf. Process 2019, 18, 232. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Li, Y.; Xu, B.; Ma, L.; Yang, J.; Huang, W. High-Throughput GPU Layered Decoder of Quasi-Cyclic Multi-Edge Type Low Density Parity Check Codes in Continuous-Variable Quantum Key Distribution Systems. Sci. Rep. 2020, 10, 14561. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, X.; Wang, Z. High-Throughput Layered Decoder Implementation for Quasi-Cyclic LDPC Codes. IEEE J. Select. Areas Commun. 2009, 27, 985–994. [Google Scholar] [CrossRef]
- Lin, D.; Huang, D.; Huang, P.; Peng, J.; Zeng, G. High Performance Reconciliation for Continuous-Variable Quantum Key Distribution with LDPC Code. Int. J. Quantum Inform. 2015, 13, 1550010. [Google Scholar] [CrossRef]
- Daesun, O.; Parhi, K.K. Min-Sum Decoder Architectures With Reduced Word Length for LDPC Codes. IEEE Trans. Circuits Syst. I 2010, 57, 105–115. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Nachmani, E.; Be’ery, Y.; Burshtein, D. Learning to Decode Linear Codes Using Deep Learning. In Proceedings of the 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 341–346. [Google Scholar]
- Liang, F.; Shen, C.; Wu, F. An Iterative BP-CNN Architecture for Channel Decoding. IEEE J. Sel. Top. Signal Process. 2018, 12, 144–159. [Google Scholar] [CrossRef]
- Lugosch, L.; Gross, W.J. Neural Offset Min-Sum Decoding. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1361–1365. [Google Scholar]
- Zeng, G. Quantum Private Communication; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-03295-0. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Maurer, U.M. Generalized Privacy Amplification. IEEE Trans. Inform. Theory 1995, 41, 1915–1923. [Google Scholar] [CrossRef]
- Deutsch, D.; Ekert, A.; Jozsa, R.; Macchiavello, C.; Popescu, S.; Sanpera, A. Quantum Privacy Amplification and the Security of Quantum Cryptography over Noisy Channels. Phys. Rev. Lett. 1996, 77, 2818–2821. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Robert, J.-M. Privacy Amplification by Public Discussion. SIAM J. Comput. 1988, 17, 210–229. [Google Scholar] [CrossRef]
- Silberhorn, C.; Ralph, T.C.; Lütkenhaus, N.; Leuchs, G. Continuous Variable Quantum Cryptography: Beating the 3 DB Loss Limit. Phys. Rev. Lett. 2002, 89, 167901. [Google Scholar] [CrossRef]
- Leverrier, A.; Alléaume, R.; Boutros, J.; Zémor, G.; Grangier, P. Multidimensional Reconciliation for a Continuous-Variable Quantum Key Distribution. Phys. Rev. A 2008, 77, 042325. [Google Scholar] [CrossRef]
- Leverrier, A.; Grangier, P. Continuous-Variable Quantum Key Distribution Protocols with a Discrete Modulation. arXiv 2011, arXiv:1002.4083. [Google Scholar]
- Chen, J.; Fossorier, P.M.C. Density Evolution for BP-Based Decoding Algorithms of LDPC Codes and Their Quantized Versions. In Proceedings of the Global Telecommunications Conference, 2002. GLOBECOM ’02, Taipei, Taiwan, 17–21 November 2002; Volume 2, pp. 1378–1382. [Google Scholar]
- Richardson, T.J.; Urbanke, R.L. The Capacity of Low-Density Parity-Check Codes under Message-Passing Decoding. IEEE Trans. Inform. Theory 2001, 47, 599–618. [Google Scholar] [CrossRef]
- Wei, X.; Akansu, A.N. Density Evolution for Low-Density Parity-Check Codes under Max-Log-MAP Decoding. Electron. Lett. 2001, 37, 1125. [Google Scholar] [CrossRef]
- Anastasopoulos, A. A Comparison between the Sum-Product and the Min-Sum Iterative Detection Algorithms Based on Density Evolution. In Proceedings of the GLOBECOM’01. IEEE Global Telecommunications Conference (Cat. No.01CH37270), San Antonio, TX, USA, 25–29 November 2001; Volume 2, pp. 1021–1025. [Google Scholar]
- Tanner, R. A Recursive Approach to Low Complexity Codes. IEEE Trans. Inform. Theory 1981, 27, 533–547. [Google Scholar] [CrossRef]
- Luby, M.G.; Mitzenmacher, M.; Shokrollahi, M.A.; Spielman, D.A. Improved Low-Density Parity-Check Codes Using Irregular Graphs. IEEE Trans. Inform. Theory 2001, 47, 585–598. [Google Scholar] [CrossRef]
- Chen, J.; Fossorier, M.P.C. Near Optimum Universal Belief Propagation Based Decoding of Low-Density Parity Check Codes. IEEE Trans. Commun. 2002, 50, 406–414. [Google Scholar] [CrossRef]
- Forney, G.D. Codes on Graphs: Normal Realizations. IEEE Trans. Inform. Theory 2001, 47, 520–548. [Google Scholar] [CrossRef]
- Etzion, T.; Trachtenberg, A.; Vardy, A. Which Codes Have Cycle-Free Tanner Graphs? IEEE Trans. Inform. Theory 1999, 45, 2173–2181. [Google Scholar] [CrossRef]
- Yang, N.; Jing, S.; Yu, A.; Liang, X.; Zhang, Z.; You, X.; Zhang, C. Reconfigurable Decoder for LDPC and Polar Codes. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Huang, D.; Huang, P.; Wang, T.; Li, H.; Zhou, Y.; Zeng, G. Continuous-Variable Quantum Key Distribution Based on a Plug-and-Play Dual-Phase-Modulated Coherent-States Protocol. Phys. Rev. A 2016, 94, 032305. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial Neural Networks (the Multilayer Perceptron)—A Review of Applications in the Atmospheric Sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Gruber, T.; Cammerer, S.; Hoydis, J.; Brink, S. On Deep Learning-Based Channel Decoding. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Caruana, R. Multitask Learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a Convolutional Neural Network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Kim, J.-K.; Lee, M.-Y.; Kim, J.-Y.; Kim, B.-J.; Lee, J.-H. An Efficient Pruning and Weight Sharing Method for Neural Network. In Proceedings of the 2016 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), Seoul, Korea, 26–28 October 2016; pp. 1–2. [Google Scholar]
- Huang, D.; Huang, P.; Lin, D.; Zeng, G. Long-Distance Continuous-Variable Quantum Key Distribution by Controlling Excess Noise. Sci. Rep. 2016, 6, 19201. [Google Scholar] [CrossRef]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Villing, A.; Tualle-Brouri, R.; Grangier, P. Field Test of a Continuous-Variable Quantum Key Distribution Prototype. New J. Phys. 2009, 11, 045023. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, Q.; Wang, Y.; Huang, D.; Huang, P.; Zeng, G. Performance Improvement of Continuous-Variable Quantum Key Distribution with an Entangled Source in the Middle via Photon Subtraction. Phys. Rev. A 2017, 95, 032304. [Google Scholar] [CrossRef]
| n | MSE |
|---|---|
| 3 | 6.133325138919856 × 10 |
| 4 | 1.2272255835313485 × 10 |
| 5 | 8.221156127182263 × 10 |
| Items | Settings |
|---|---|
| Batch Size | 200 |
| Network Learning Rate | 0.001 |
| Network Parameter Initialization Method | Gaussian distribution method |
| Optimizer | Adam optimizer |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Zhang, L.; Wang, Y.; Huang, D. Deep Neural Network Based Reconciliation for CV-QKD. Photonics 2022, 9, 110. https://doi.org/10.3390/photonics9020110
Xie J, Zhang L, Wang Y, Huang D. Deep Neural Network Based Reconciliation for CV-QKD. Photonics. 2022; 9(2):110. https://doi.org/10.3390/photonics9020110
Chicago/Turabian StyleXie, Jun, Ling Zhang, Yijun Wang, and Duan Huang. 2022. "Deep Neural Network Based Reconciliation for CV-QKD" Photonics 9, no. 2: 110. https://doi.org/10.3390/photonics9020110
APA StyleXie, J., Zhang, L., Wang, Y., & Huang, D. (2022). Deep Neural Network Based Reconciliation for CV-QKD. Photonics, 9(2), 110. https://doi.org/10.3390/photonics9020110








