In Vivo and In Silico Study of Photodynamic Necrosis Volume in Rat Liver
Abstract
1. Introduction
2. Methods and Materials
2.1. Animal Model
2.2. In Silico Model
2.2.1. Monte Carlo Simulation
2.2.2. Reactive Oxygen Species Estimation
3. Results and Discussion
3.1. In Vivo
3.2. Light Propagation
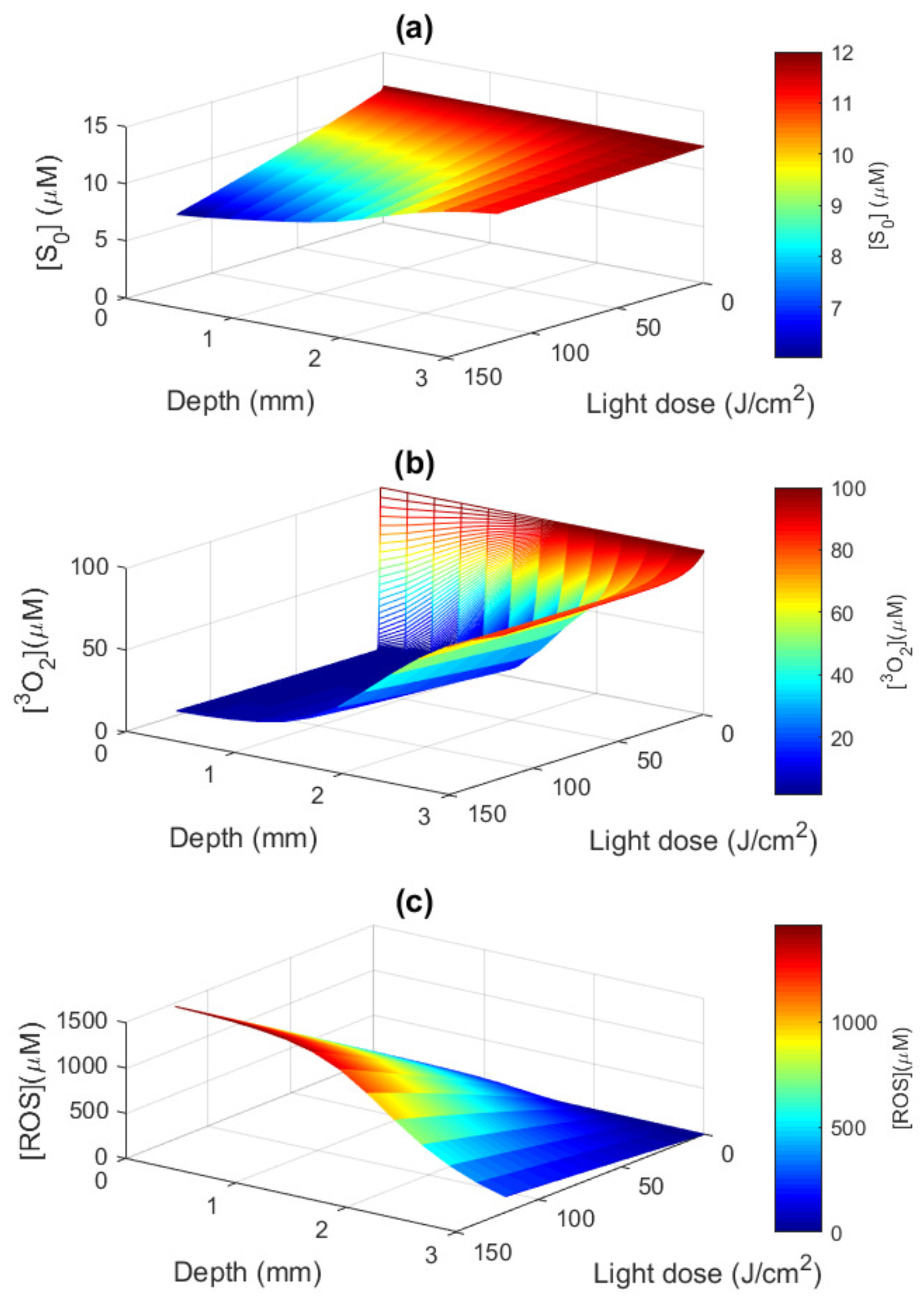
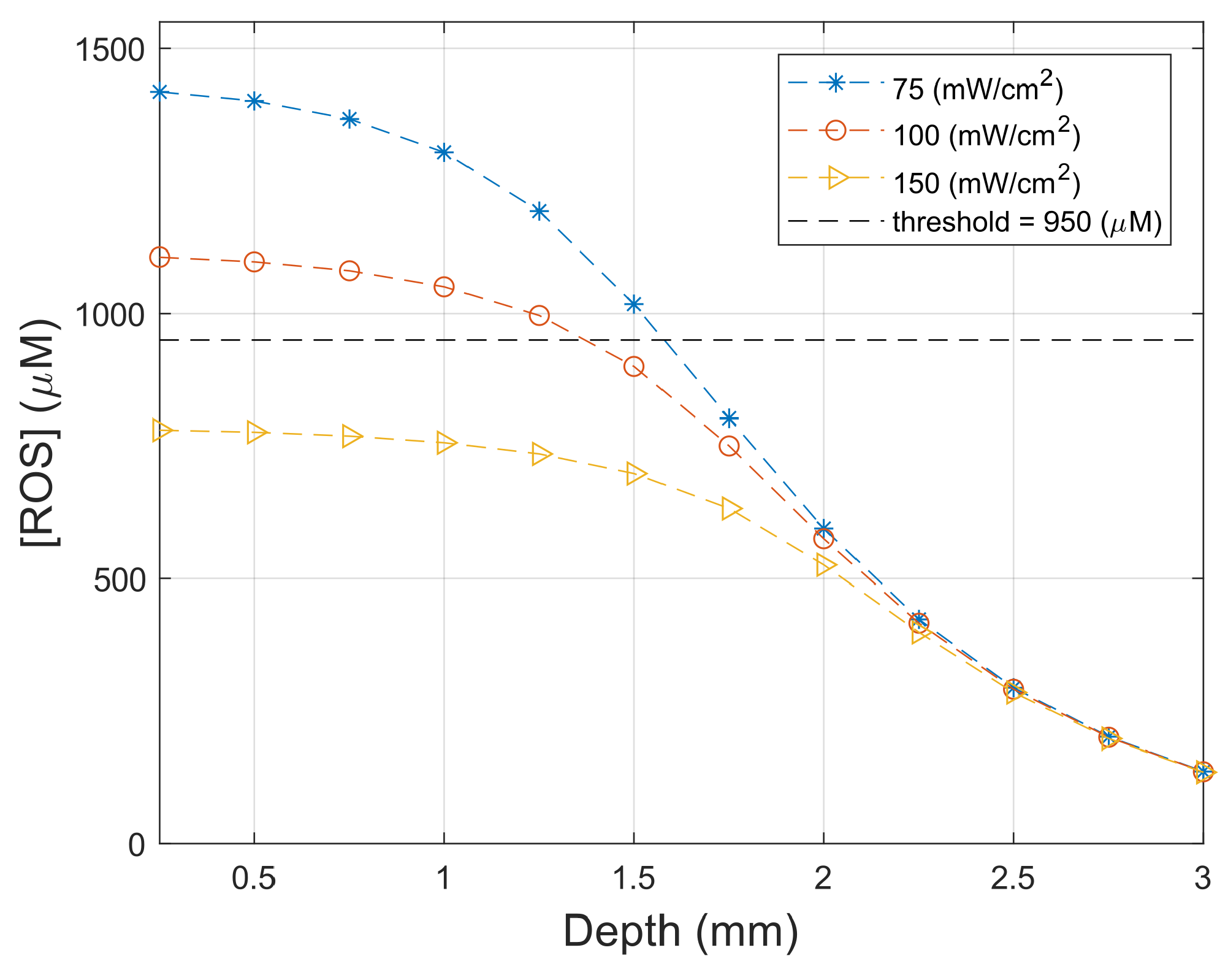
3.3. Macroscopic ROS Model
3.4. Necrosis Profile
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krutmann, J.; Honigsmann, H.; Craig, A. Dermatological Phototherapy and Photodiagnostic Methods; Springer: Berlin/Heidelberg, Germany, 2001; p. 412. [Google Scholar] [CrossRef]
- Pratavieira, S.; Requena, M.B.; Stringasci, M.D.; Ayala, E.T.P.; Bagnato, V.S. The Physics of Light and Sound in the Fight Against Skin Cancer. Braz. J. Phys. 2022, 52, 106. [Google Scholar] [CrossRef]
- Alves, F.; Ayala, E.T.P.; Pratavieira, S. Sonophotodynamic Inactivation: The power of light and ultrasound in the battle against microorganisms. J. Photochem. Photobiol. 2021, 7, 100039. [Google Scholar] [CrossRef]
- Dąbrowski, J.M. Chapter Nine—Reactive Oxygen Species in Photodynamic Therapy: Mechanisms of Their Generation and Potentiation. In Inorganic Reaction Mechanisms; van Eldik, R., Hubbard, C.D., Eds.; Academic Press: Cambridge, MA, USA, 2017; Volume 70, pp. 343–394. [Google Scholar] [CrossRef]
- Wilson, B.; Patterson, M. The physics, biophysics and technology of photodynamic therapy. Phys. Med. Biol. 2008, 53, 61–109. [Google Scholar] [CrossRef] [PubMed]
- Allison, R.R.; Downie, G.H.; Cuenca, R.; Hu, X.H.; Childs, C.J.; Sibata, C.H. Photosensitizers in clinical PDT. Photodiagn. Photodyn. Ther. 2004, 1, 27–42. [Google Scholar] [CrossRef]
- Zhu, T.; Kim, M.; Liang, X.; Finlay, J.; Busch, T. In-vivo singlet oxygen threshold doses for PDT. Photonics Lasers Med. 2015, 4, 59–71. [Google Scholar] [CrossRef] [PubMed]
- Wilson, B.C.; Patterson, M.S.; Lilge, L. Implicit and explicit dosimetry in photodynamic therapy: A new paradigm. Lasers Med. Sci. 1997, 12, 182–199. [Google Scholar] [CrossRef] [PubMed]
- Pogue, B.; Elliott, J.; Kanick, S.; Davis, S.; Samkoe, K.; Maytin, E.; Pereira, S.; Hasan, T. Revisiting photodynamic therapy dosimetry: Reductionist & surrogate approaches to facilitate clinical success. Phys. Med. Biol. 2016, 61, 57–89. [Google Scholar] [CrossRef]
- Patterson, M.; Wilson, C.; Ronald, G. In vivo test of the concept of photodynamic threshold dose in normal rat liver photosensitized by aluminum chlorosulphonated phthalocyanine. Photochem. Photobiol. 1990, 51, 343–349. [Google Scholar] [CrossRef]
- Dysart, J.S.; Singh, G.; Patterson, M.S. Calculation of Singlet Oxygen Dose from Photosensitizer Fluorescence and Photobleaching During mTHPC Photodynamic Therapy of MLL Cells. Photochem. Photobiol. 2005, 81, 196–205. [Google Scholar] [CrossRef]
- Wang, K.; Finlay, J.; Busch, T.; Hahn, S.; Zhu, T. Explicit dosimetry for photodynamic therapy: Macroscopic singlet oxygen modeling. J. Biophotonics 2010, 3, 304–318. [Google Scholar] [CrossRef]
- Ong, Y.H.; Kim, M.M.; Huang, Z.; Zhu, T.C. Reactive oxygen species explicit dosimetry (ROSED) of a type 1 photosensitizer. In Optical Methods for Tumor Treatment and Detection: Mechanisms and Techniques in Photodynamic Therapy XXVII; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 2018; Volume 10476, pp. 57–66. [Google Scholar]
- Rocha, L.B.; Soares, H.T.; Mendes, M.I.P.; Cabrita, A.; Schaberle, F.A.; Arnaut, L.G. Necrosis depth and photodynamic threshold dose with redaporfin-PDT. Photochem. Photobiol. 2020, 96, 692–698. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, V.; Garcia, M.R.; Requena, M.B.; Romano, R.A.; de Boni, L.; Guimarães, F.E.; Pratavieira, S. Theoretical and Experimental Analysis of Protoporphyrin IX Photodegradation Using Multi-Wavelength Light Sources. Photochem. Photobiol. 2020, 96, 1208–1214. [Google Scholar] [CrossRef] [PubMed]
- Salomatina, E.V.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, 37–61. [Google Scholar] [CrossRef]
- Fang, Q.; Boas, D. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt. Express 2009, 17, 20178–20190. [Google Scholar] [CrossRef] [PubMed]
- LaRochelle, E.P.; Marra, K.; LeBlanc, R.E.; Chapman, M.S.; Maytin, E.V.; Pogue, B.W. Modeling PpIX effective light fluence at depths into the skin for PDT dose comparison. Photodiagn. Photodyn. Ther. 2019, 25, 425–435. [Google Scholar] [CrossRef]
- Kareliotis, G.; Papachristou, M.; Priftakis, D.; Datseris, I.; Makropoulou, M. Computational study of necrotic areas in rat liver tissue treated with photodynamic therapy. J. Photochem. Photobiol. Biol. 2019, 192, 40–48. [Google Scholar] [CrossRef]
- Ferreira, J.; Moriyama, L.; Kurachi, C.; Sibata, C.; Castro e Silva, O., Jr.; Zucoloto, S.; Bagnato, V. Experimental determination of threshold dose in photodynamic therapy in normal rat liver. Laser Phys. Lett. 2007, 4, 469. [Google Scholar] [CrossRef]
- Farrell, T.J.; Wilson, B.C.; Patterson, M.S.; Chow, R. Dependence of photodynamic threshold dose on treatment parameters in normal rat liver in vivo. In Optical Methods for Tumor Treatment and Early Diagnosis: Mechanisms and Techniques; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 1991; Volume 1426, pp. 146–155. [Google Scholar]
- Liu, B.; Farrell, T.; Patterson, M. A dynamic model for ALA-PDT of skin: Simulation of temporal and spatial distributions of ground-state oxygen, photosensitizer and singlet oxygen. Phys. Med. Biol. 2010, 55, 5913–5932. [Google Scholar] [CrossRef]
- Sánchez, V.; Romero, M.P.; Pratavieira, S.; Costa, C. Physiological considerations acting on triplet oxygen for explicit dosimetry in photodynamic therapy. Photodiagn. Photodyn. Ther. 2017, 19, 298–303. [Google Scholar] [CrossRef]
- Zou, H.; Wang, F.; Zhou, J.J.; Liu, X.; He, Q.; Wang, C.; Zheng, Y.W.; Wen, Y.; Xiong, L. Application of photodynamic therapy for liver malignancies. J. Gastrointest. Oncol. 2020, 11, 431. [Google Scholar] [CrossRef] [PubMed]
- Stranadko, E.P.; Skobelkin, O.K.; Mironov, A.E. Photodynamic therapy of cancer by photogem. In Photodynamic Therapy of Cancer; Jori, G., Moan, J., Star, W.M., Eds.; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 1994; Volume 2078, pp. 499–501. [Google Scholar] [CrossRef]
- Vollet-Filho, J.D.; Menezes, P.F.C.; Moriyama, L.T.; Grecco, C.; Sibata, C.; Allison, R.R.; Castro e Silva, O.; Bagnato, V.S. Possibility for a full optical determination of photodynamic therapy outcome. J. Appl. Phys. 2009, 105, 102038. [Google Scholar] [CrossRef]
- Melo, C.; Kurachi, C.; Grecco, C.; Sibata, C.; Castro-e Silva, O.; Bagnato, V. Pharmacokinetics of Photogem using fluorescence monitoring in Wistar rats. J. Photochem. Photobiol. Biol. 2004, 73, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Parsa, P.; Jacques, S.L.; Nishioka, N.S. Optical properties of rat liver between 350 and 2200 nm. Appl. Opt. 1989, 28, 2325–2330. [Google Scholar] [CrossRef]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Measurement of Optical Properties of Normal and Pathological Human Liver Tissue from Deep-UV to NIR In Tissue Optics and Photonics; Tuchin, V.V., Blondel, W.C.P.M., Zalevsky, Z., Eds.; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 2020; Volume 11363, p. 113630G. [Google Scholar] [CrossRef]
- Akter, S.; Maejima, S.; Kawauchi, S.; Sato, S.; Hinoki, A.; Aosasa, S.; Yamamoto, J.; Nishidate, I. Evaluation of light scattering and absorption properties of in vivo rat liver using a single-reflectance fiber probe during preischemia, ischemia–reperfusion, and postmortem. J. Biomed. Opt. 2015, 20, 076010. [Google Scholar] [CrossRef]
- Finlay, J.C.; Mitra, S.; Patterson, M.S.; Foster, T.H. Photobleaching kinetics of Photofrin in vivo and in multicell tumour spheroids indicate two simultaneous bleaching mechanisms. Phys. Med. Biol. 2004, 49, 4837. [Google Scholar] [CrossRef]
- Zhu, T.C.; Finlay, J.C.; Zhou, X.; Li, J. Macroscopic modeling of the singlet oxygen production during PDT. In Optical Methods for Tumor Treatment and Detection: Mechanisms and Techniques in Photodynamic Therapy XVI; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 2007; Volume 6427, p. 642708. [Google Scholar]
- Pratavieira, S.; Santos, P.; Menezes, P.; Kurachi, C.; Sibata, C.; Jarvi, M.; Wilson, B.; Bagnato, V. Phototransformation of hematoporphyrin in aqueous solution: Anomalous behavior at low oxygen concentration. Laser Phys. 2009, 19, 1263–1271. [Google Scholar] [CrossRef]
- Georgakoudi, I.; Nichols, M.G.; Foster, T.H. The mechanism of Photofrin photobleaching and its consequences for photodynamic dosimetry. Photochem. Photobiol. 1997, 65, 135–144. [Google Scholar] [CrossRef]
- Nichols, M.G.; Foster, T. Oxygen diffusion and reaction kinetics in the photodynamic therapy of multicell tumour spheroids. Phys. Med. Biol. 1994, 39, 2161. [Google Scholar] [CrossRef]
- Martelli, F.; Del Bianco, S.; Ismaelli, A.; Zaccanti, G. Light Propagation through Biological Tissue and Other Diusive Media; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 2010; p. 298. [Google Scholar]
- Brancaleon, L.; Moseley, H. Laser and non-laser light sources for Photodynamic Therapy. Lasers Med. Sci. 2002, 13, 173–186. [Google Scholar] [CrossRef]
- Mang, T.S. Lasers and light sources for PDT: Past, present and future. Photodiagn. Photodyn. Ther. 2008, 1, 43–48. [Google Scholar] [CrossRef] [PubMed]
- Salas-García, I.; Fanjul-Vélez, F.; Arce-Diego, J.L. Superficial radially resolved fluorescence and 3D photochemical time-dependent model for photodynamic therapy. Opt. Lett. 2014, 39, 1845–1848. [Google Scholar] [CrossRef] [PubMed]
- Coutier, S.; Mitra, S.; Bezdetnaya, L.N.; Parache, R.M.; Georgakoudi, I.; Foster, T.H.; Guillemin, F. Effects of Fluence Rate on Cell Survival and Photobleaching in Meta-Tetra-(hydroxyphenyl) chlorin–photosensitized Colo 26 Multicell Tumor Spheroids. Photochem. Photobiol. 2001, 73, 297–303. [Google Scholar] [CrossRef]
- Qiu, H.; Kim, M.M.; Penjweini, R.; Zhu, T.C. Dosimetry study of PHOTOFRIN-mediated photodynamic therapy in a mouse tumor model. In Optical Methods for Tumor Treatment and Detection: Mechanisms and Techniques in Photodynamic Therapy XXV; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 2016; Volume 9694, pp. 123–129. [Google Scholar]
- Penjweini, R.; Kim, M.M.; Liu, B.; Zhu, T.C. Evaluation of the 2-(1-Hexyloxyethyl)-2-devinyl pyropheophorbide (HPPH) mediated photodynamic therapy by macroscopic singlet oxygen modeling. J. Biophotonics 2016, 9, 1344–1354. [Google Scholar] [CrossRef] [PubMed]
- Kareliotis, G.; Chronopoulou, E.; Makropoulou, M. In Silico, Combined Plasmonic Photothermal and Photodynamic Therapy in Mice. J. Nanotheranostics 2022, 3, 39–54. [Google Scholar] [CrossRef]
- Garcia, M.R.; Requena, M.B.; Pratavieira, S.; Moriyama, L.T.; Becker, M.; Bagnato, V.S.; Kurachi, C.; Magalhães, D.V. Development of a system to treat and online monitor photodynamic therapy of skin cancer using PpIX near-infrared fluorescence. Photodiagn. Photodyn. Ther. 2020, 30, 101680. [Google Scholar] [CrossRef]




| Wavelength | Parameter | Value [29] |
|---|---|---|
| 630 nm | 0.71 mm | |
| 14.60 mm | ||
| g | 0.95 | |
| n | 1.37 |
| Symbol | Definition | Units | |
|---|---|---|---|
| PS concentration in ground state | M | ||
| Oxygen concentration in ground state | M | ||
| Oxygen concentration in ground state at time zero | M | ||
| Concentration of ROS | M | ||
| Low PS concentration correction term | M | ||
| Maximum oxygen supply rate | – | ||
| PS absorption cross section as a function of | cm | ||
| PS activation energy as a function of | J | ||
| Light fluence rate | mW/cm | ||
| Parameter (Units) | Definition | Value | Reference |
| 0.831 | [23] | ||
| [35] | |||
| [35,36] | |||
| 11.9 | [35] | ||
| [15] | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia, M.R.; Sánchez, V.; Fortunato, T.C.; Requena, M.B.; Grecco, C.; Vollet-Filho, J.D.; Pires, L.; Moriyama, L.T.; Pratavieira, S. In Vivo and In Silico Study of Photodynamic Necrosis Volume in Rat Liver. Photonics 2022, 9, 993. https://doi.org/10.3390/photonics9120993
Garcia MR, Sánchez V, Fortunato TC, Requena MB, Grecco C, Vollet-Filho JD, Pires L, Moriyama LT, Pratavieira S. In Vivo and In Silico Study of Photodynamic Necrosis Volume in Rat Liver. Photonics. 2022; 9(12):993. https://doi.org/10.3390/photonics9120993
Chicago/Turabian StyleGarcia, Marlon Rodrigues, Víctor Sánchez, Thereza Cury Fortunato, Michelle Barreto Requena, Clóvis Grecco, José Dirceu Vollet-Filho, Layla Pires, Lilian Tan Moriyama, and Sebastião Pratavieira. 2022. "In Vivo and In Silico Study of Photodynamic Necrosis Volume in Rat Liver" Photonics 9, no. 12: 993. https://doi.org/10.3390/photonics9120993
APA StyleGarcia, M. R., Sánchez, V., Fortunato, T. C., Requena, M. B., Grecco, C., Vollet-Filho, J. D., Pires, L., Moriyama, L. T., & Pratavieira, S. (2022). In Vivo and In Silico Study of Photodynamic Necrosis Volume in Rat Liver. Photonics, 9(12), 993. https://doi.org/10.3390/photonics9120993






