Ultrahigh Q-Guided Resonance Sensor Empowered by Near Merging Bound States in the Continuum
Abstract
1. Introduction
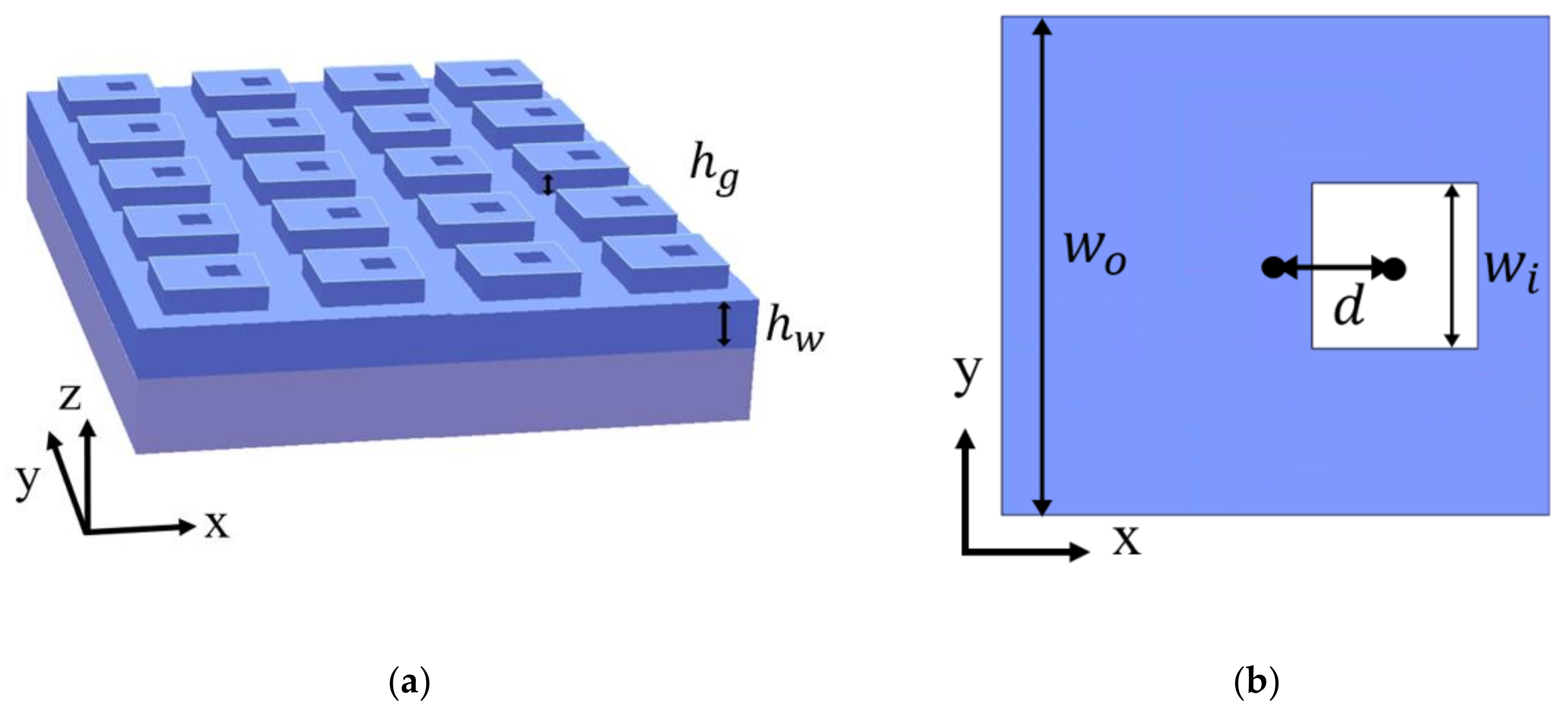
2. Design and Simulation
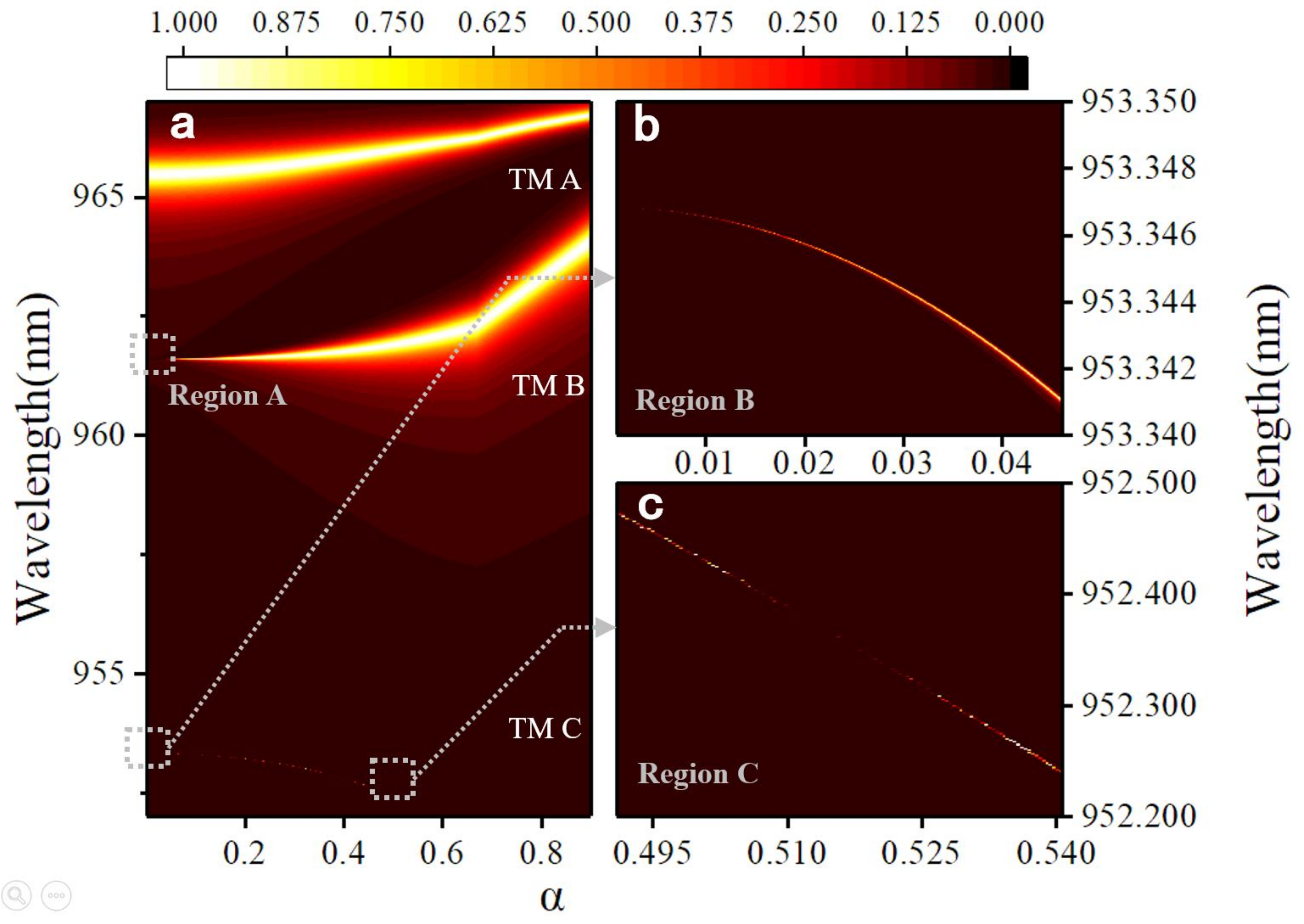
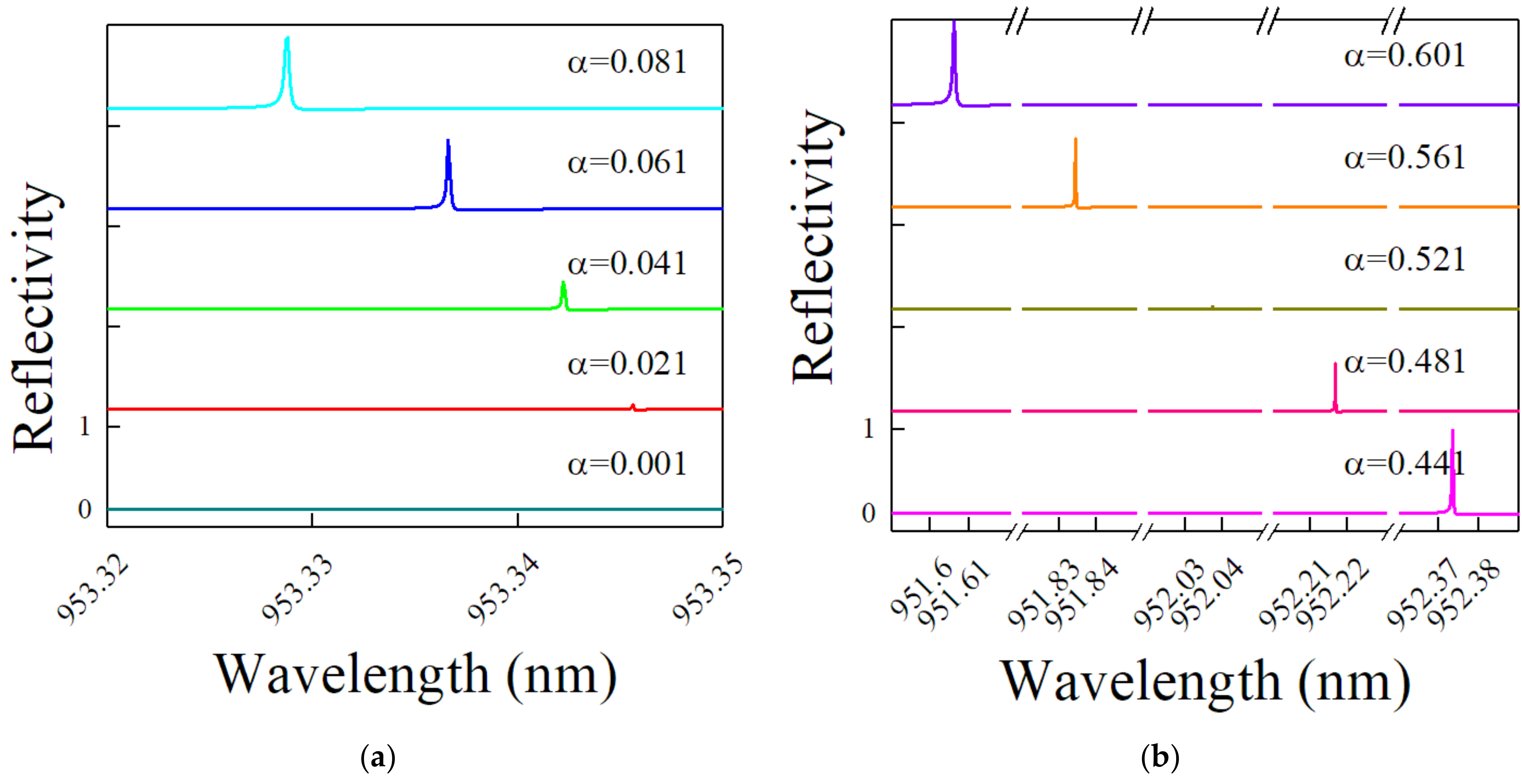
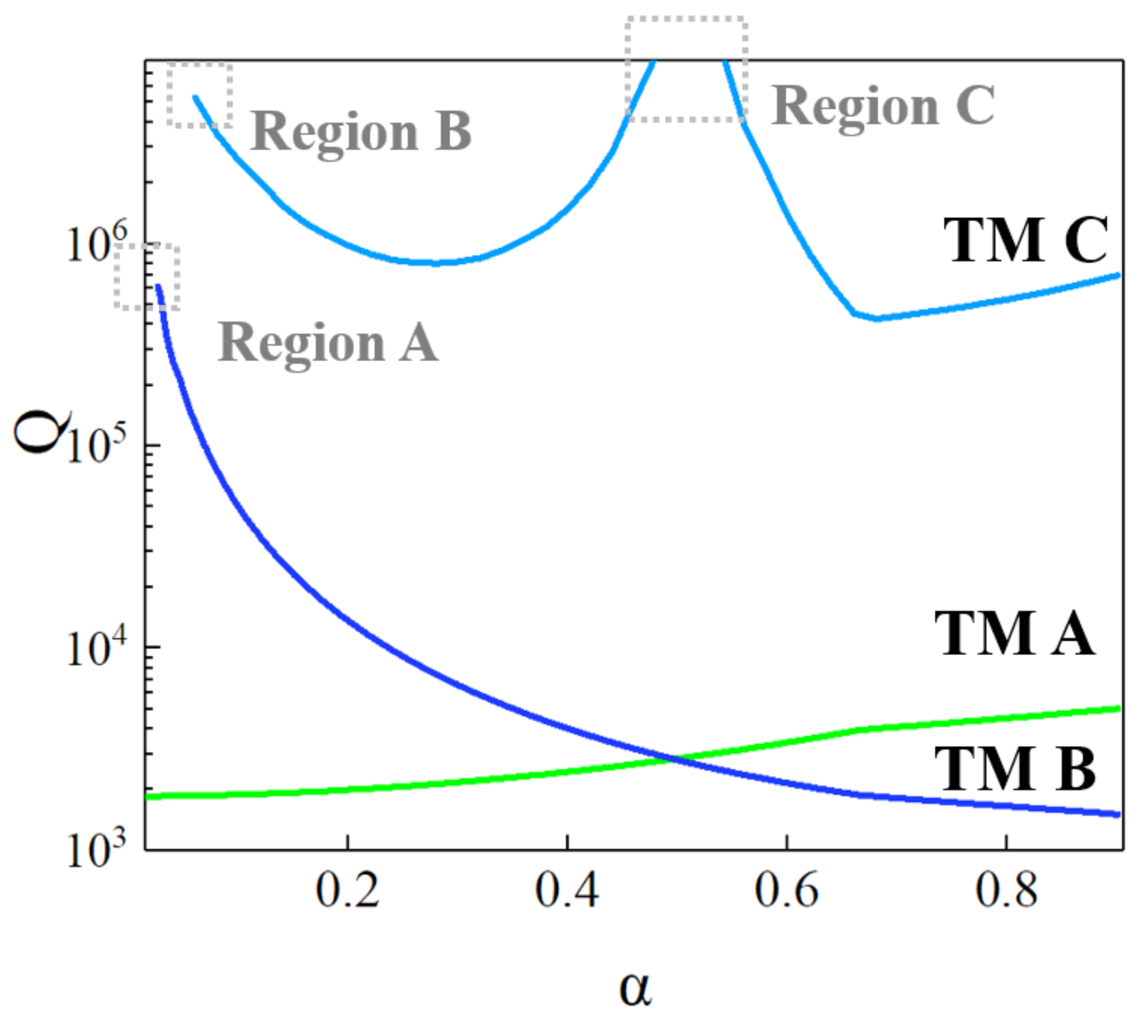
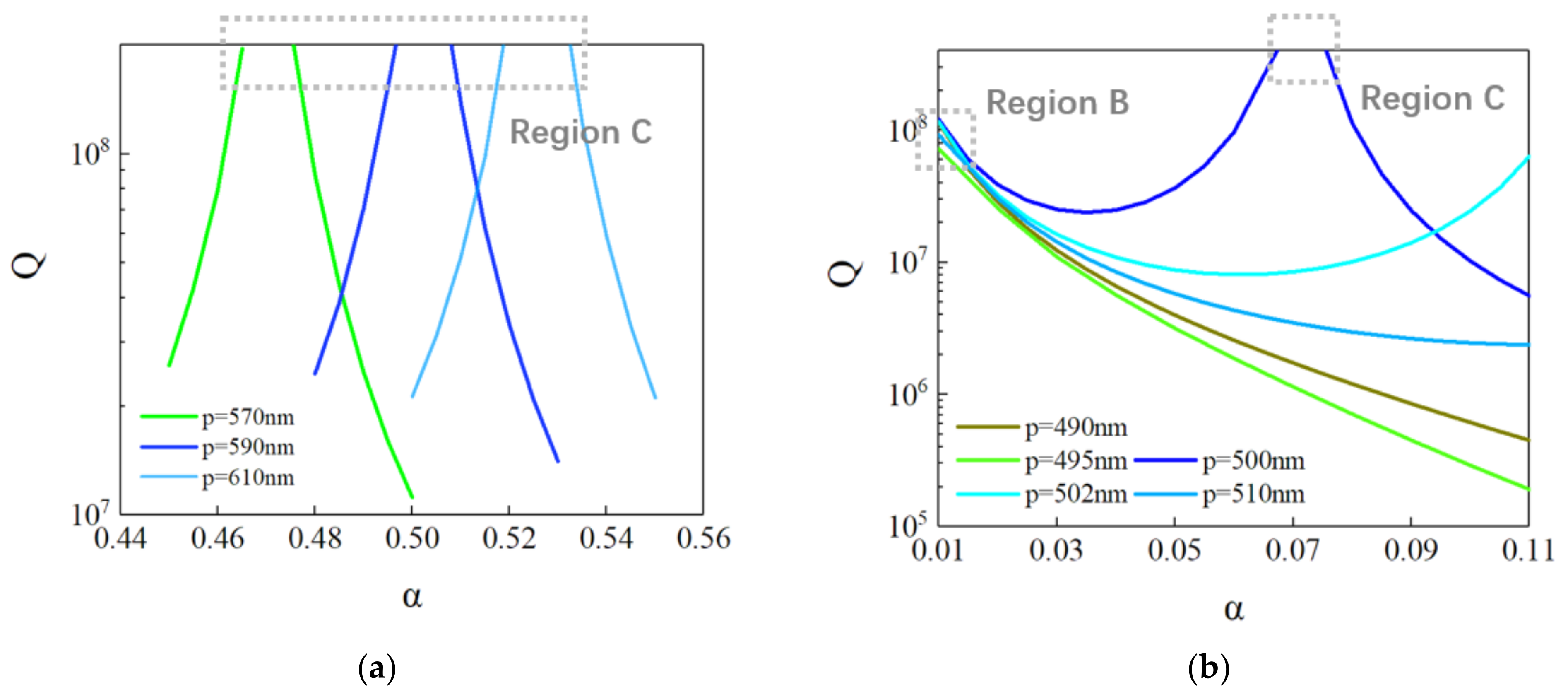
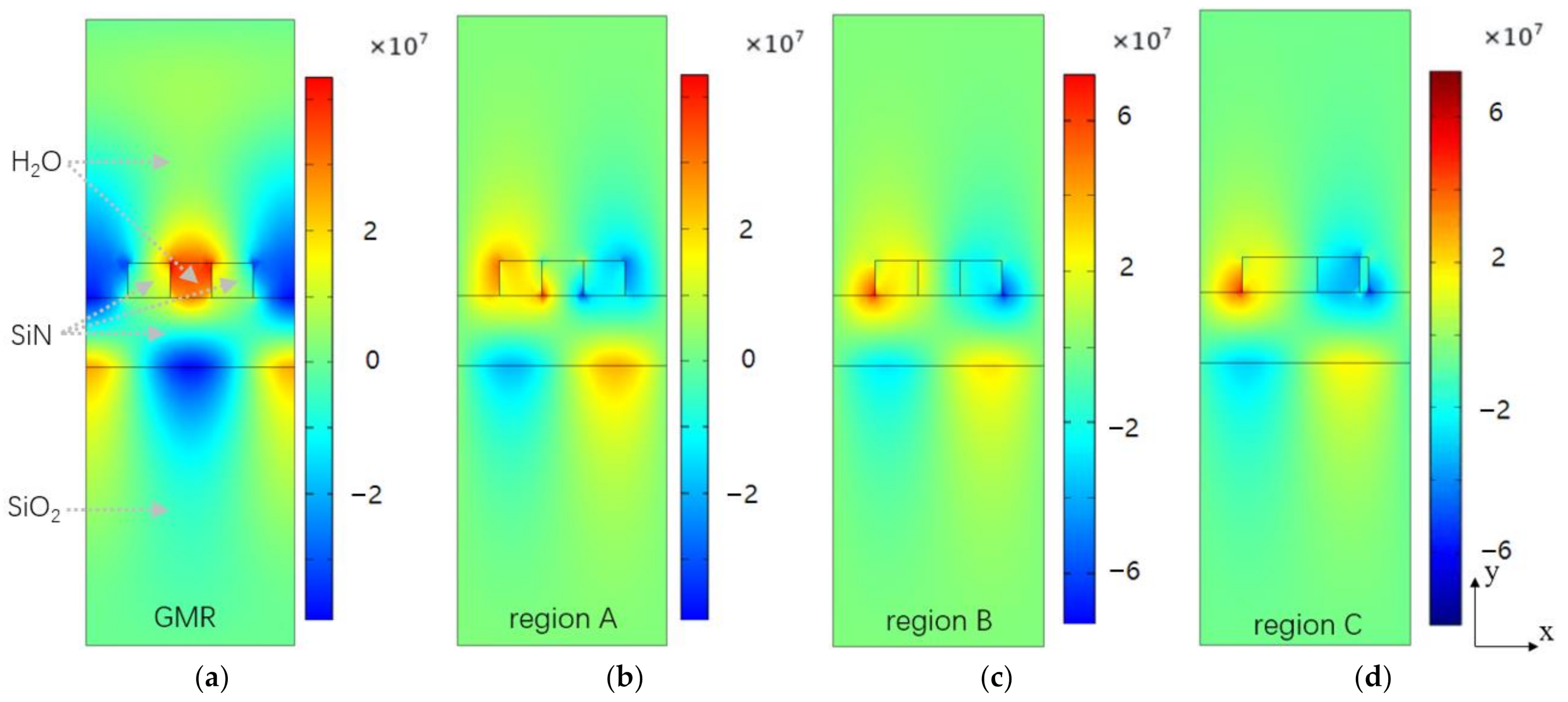
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, W.; Boulesbaa, A.; Kravchenko, I.I.; Briggs, D.P.; Puretzky, A.; Geohegan, D.; Valentine, J. Nonlinear Fano-Resonant Dielectric Metasurfaces. Nano Lett. 2015, 15, 7388–7393. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345–348. [Google Scholar] [CrossRef] [PubMed]
- Vabishchevich, P.P.; Liu, S.; Sinclair, M.B.; Keeler, G.A.; Peake, G.M.; Brener, I. Enhanced Second-Harmonic Generation Using Broken Symmetry III–V Semiconductor Fano Metasurfaces. ACS Photon. 2018, 5, 1685–1690. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Bozhevolnyi, S.I.; Pors, A.; Nielsen, M.G.; Radko, I.P.; Willatzen, M.; Albrektsen, O. Detuned Electrical Dipoles for Plasmonic Sensing. Nano Lett. 2010, 10, 4571–4577. [Google Scholar] [CrossRef]
- Luchansky, M.S.; Bailey, R.C. High-Q Optical Sensors for Chemical and Biological Analysis. Anal. Chem. 2011, 84, 793–821. [Google Scholar] [CrossRef]
- Yahiaoui, R.; Tan, S.; Cong, L.; Singh, R.; Yan, F.; Zhang, W. Multispectral terahertz sensing with highly flexible ultrathin metamaterial absorber. J. Appl. Phys. 2015, 118, 083103. [Google Scholar] [CrossRef]
- Sang, T.; Dereshgi, S.; Hadibrata, W.; Tanriover, I.; Aydin, K. Highly Efficient Light Absorption of Monolayer Graphene by Quasi-Bound State in the Continuum. Nanomaterials 2021, 11, 484. [Google Scholar] [CrossRef]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef]
- Rybin, M.; Kivshar, Y. Supercavity lasing. Nature 2017, 541, 164–165. [Google Scholar] [CrossRef]
- Ha, S.T.; Fu, Y.H.; Emani, N.K.; Pan, Z.; Bakker, R.M.; Paniagua-Domínguez, R.; Kuznetsov, A.I. Directional lasing in resonant semiconductor nanoantenna arrays. Nat. Nanotechnol. 2018, 13, 1042–1047. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of trapped light within the radiation continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef]
- Yesilkoy, F.; Arvelo, E.R.; Jahani, Y.; Liu, M.; Tittl, A.; Cevher, V.; Kivshar, Y.; Altug, H. Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces. Nat. Photon. 2019, 13, 390–396. [Google Scholar] [CrossRef]
- Tittl, A.; Leitis, A.; Liu, M.; Yesilkoy, F.; Choi, D.-Y.; Neshev, D.N.; Kivshar, Y.S.; Altug, H. Imaging-based molecular barcoding with pixelated dielectric metasurfaces. Science 2018, 360, 1105–1109. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, C.; Kaj, K.; Hammock, I.; Huang, Y.; Averitt, R.D.; Zhang, X. Terahertz investigation of bound states in the continuum of metallic metasurfaces. Optica 2020, 7, 1548–1554. [Google Scholar] [CrossRef]
- Dreisow, F.; Szameit, A.; Heinrich, M.; Keil, R.; Nolte, S.; Tünnermann, A.; Longhi, S. Adiabatic transfer of light via a continuum in optical waveguides. Opt. Lett. 2009, 34, 2405–2407. [Google Scholar] [CrossRef]
- Cong, L.; Singh, R. Symmetry-Protected Dual Bound States in the Continuum in Metamaterials. Adv. Opt. Mater. 2019, 13, 1900383. [Google Scholar] [CrossRef]
- Ndao, A.; Hsu, L.; Cai, W.; Ha, J.; Park, J.; Contractor, R.; Lo, Y.; Kanté, B. Differentiating and quantifying exosome secretion from a single cell using quasi-bound states in the continuum. Nanophotonics 2020, 9, 1081–1086. [Google Scholar] [CrossRef]
- Falcone, F.; Lopetegi, T.; Laso, M.; Baena, J.D.; Bonache, J.; Beruete, M.; Marqués, R.; Martin, F.; Sorolla, M. Babinet Principle Applied to the Design of Metasurfaces and Metamaterials. Phys. Rev. Lett. 2004, 93, 197401. [Google Scholar] [CrossRef]
- Kyaw, C.; Yahiaoui, R.; Burrow, J.A.; Tran, V.; Keelen, K.; Sims, W.; Red, E.C.; Rockward, W.S.; Thomas, M.A.; Sarangan, A.; et al. Polarization-selective modulation of supercavity resonances originating from bound states in the continuum. Commun. Phys. 2020, 3, 1–8. [Google Scholar] [CrossRef]
- Yoon, J.W.; Song, S.H.; Magnusson, R. Critical field enhancement of asymptotic optical bound states in the continuum. Sci. Rep. 2015, 5, 18301. [Google Scholar] [CrossRef] [PubMed]
- Bykov, D.A.; Bezus, E.A.; Doskolovich, L.L. Coupled-wave formalism for bound states in the continuum in guided-mode resonant gratings. Phys. Rev. A 2019, 99, 063805. [Google Scholar] [CrossRef]
- Han, S.; Cong, L.; Srivastava, Y.K.; Qiang, B.; Rybin, M.V.; Kumar, A.; Jain, R.; Lim, W.X.; Achanta, V.G.; Prabhu, S.S.; et al. All-Dielectric Active Terahertz Photonics Driven by Bound States in the Continuum. Adv. Mater. 2019, 31, e1901921. [Google Scholar] [CrossRef] [PubMed]
- Overvig, A.C.; Shrestha, S.; Yu, N. Dimerized high contrast gratings. Nanophotonics 2018, 7, 1157–1168. [Google Scholar] [CrossRef]
- Tuz, V.R.; Khardikov, V.; Kupriianov, A.S.; Domina, K.; Xu, S.; Wang, H.; Sun, H.-B. High-quality trapped modes in all-dielectric metamaterials. Opt. Express 2018, 26, 2905–2916. [Google Scholar] [CrossRef]
- Forouzmand, A.; Mosallaei, H. All-Dielectric C-Shaped Nanoantennas for Light Manipulation: Tailoring Both Magnetic and Electric Resonances to the Desire. Adv. Opt. Mater. 2017, 5, 1700147. [Google Scholar] [CrossRef]
- Campione, S.; Liu, S.; Basilio, L.I.; Warne, L.K.; Langston, W.L.; Luk, T.S.; Wendt, J.R.; Reno, J.L.; Keeler, G.A.; Brener, I.; et al. Broken Symmetry Dielectric Resonators for High Quality Factor Fano Metasurfaces. ACS Photon. 2016, 3, 2362–2367. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, X.; Zhao, Q.; Chen, L.; Wang, Y.; Li, Q.; He, X.; Li, C.; Chen, K. Fano resonance of an asymmetric dielectric wire pair. Appl. Phys. Lett. 2014, 105, 172901. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Asano, T.; Song, B.-S.; Noda, S. Analysis of the experimental Q factors (~1 million) of photonic crystal nanocavities. Opt. Express 2006, 14, 1996–2002. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Lu, L.; Stone, A.D.; Soljačić, M. Topological Nature of Optical Bound States in the Continuum. Phys. Rev. Lett. 2014, 113, 257401. [Google Scholar] [CrossRef]
- Cen, W.; Lang, T.; Wang, J.; Xiao, M. High-Q Fano Terahertz resonance based on bound states in the continuum in All-dielectric metasurface. Appl. Surf. Sci. 2021, 575, 151723. [Google Scholar] [CrossRef]
- Wang, S.S.; Moharam, M.G.; Magnusson, R.; Bagby, J.S. Guided-mode resonances in planar dielectric-layer diffraction gratings. J. Opt. Soc. Am. A 1990, 7, 1470–1474. [Google Scholar] [CrossRef]
- Han, S.; Pitchappa, P.; Wang, W.; Srivastava, Y.K.; Rybin, M.V.; Singh, R. Extended Bound States in the Continuum with Symmetry-Broken Terahertz Dielectric Metasurfaces. Adv. Opt. Mater. 2021, 9, 2002001. [Google Scholar] [CrossRef]
- Jin, J.; Yin, X.; Ni, L.; Soljačić, M.; Zhen, B.; Peng, C. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering. Nature 2019, 574, 501–504. [Google Scholar] [CrossRef]
- Conteduca, D.; Barth, I.; Pitruzzello, G.; Reardon, C.P.; Martins, E.R.; Krauss, T.F. Dielectric nanohole array metasurface for high-resolution near-field sensing and imaging. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Sancho-Fornes, G.; Avella-Oliver, M.; Carrascosa, J.; Fernandez, E.; Brun, E.M.; Maquieira, Á. Disk-based one-dimensional photonic crystal slabs for label-free immunosensing. Biosens. Bioelectron. 2018, 126, 315–323. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhou, Y.; Guo, Z.; Zhao, X.; Luo, M.; Li, Y.; Wu, X. Ultrahigh Q-Guided Resonance Sensor Empowered by Near Merging Bound States in the Continuum. Photonics 2022, 9, 852. https://doi.org/10.3390/photonics9110852
Liu Z, Zhou Y, Guo Z, Zhao X, Luo M, Li Y, Wu X. Ultrahigh Q-Guided Resonance Sensor Empowered by Near Merging Bound States in the Continuum. Photonics. 2022; 9(11):852. https://doi.org/10.3390/photonics9110852
Chicago/Turabian StyleLiu, Zhiran, Yi Zhou, Zhihe Guo, Xuyang Zhao, Man Luo, Yuxiang Li, and Xiang Wu. 2022. "Ultrahigh Q-Guided Resonance Sensor Empowered by Near Merging Bound States in the Continuum" Photonics 9, no. 11: 852. https://doi.org/10.3390/photonics9110852
APA StyleLiu, Z., Zhou, Y., Guo, Z., Zhao, X., Luo, M., Li, Y., & Wu, X. (2022). Ultrahigh Q-Guided Resonance Sensor Empowered by Near Merging Bound States in the Continuum. Photonics, 9(11), 852. https://doi.org/10.3390/photonics9110852





