Process Optimization Based on Analysis of Dynamic and Static Performance Requirements of Ion Beam Figuring Machine Tools for Sub-Nanometer Figuring
Abstract
1. Introduction
2. Materials and Methods
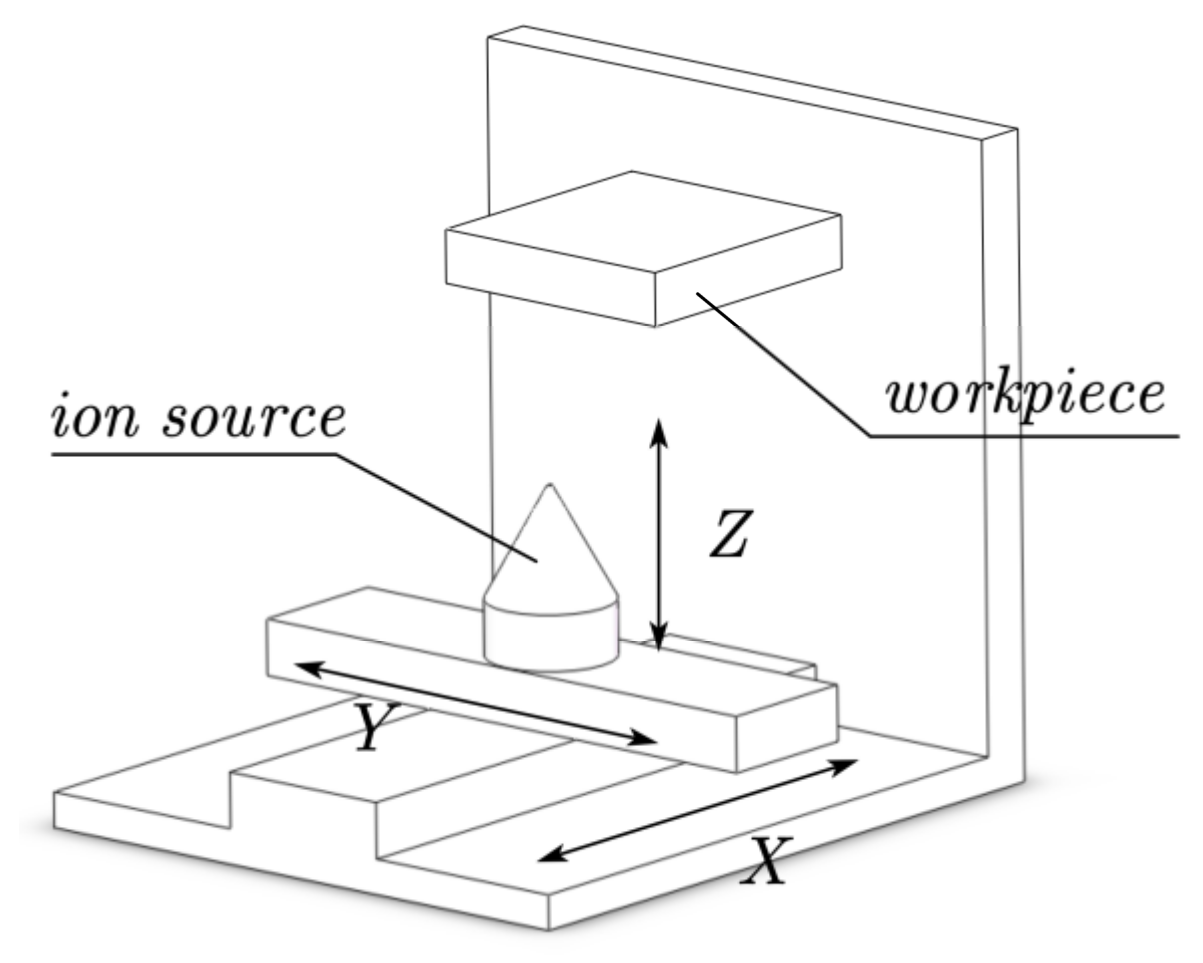
2.1. Dynamic Performance Requirements Analysis
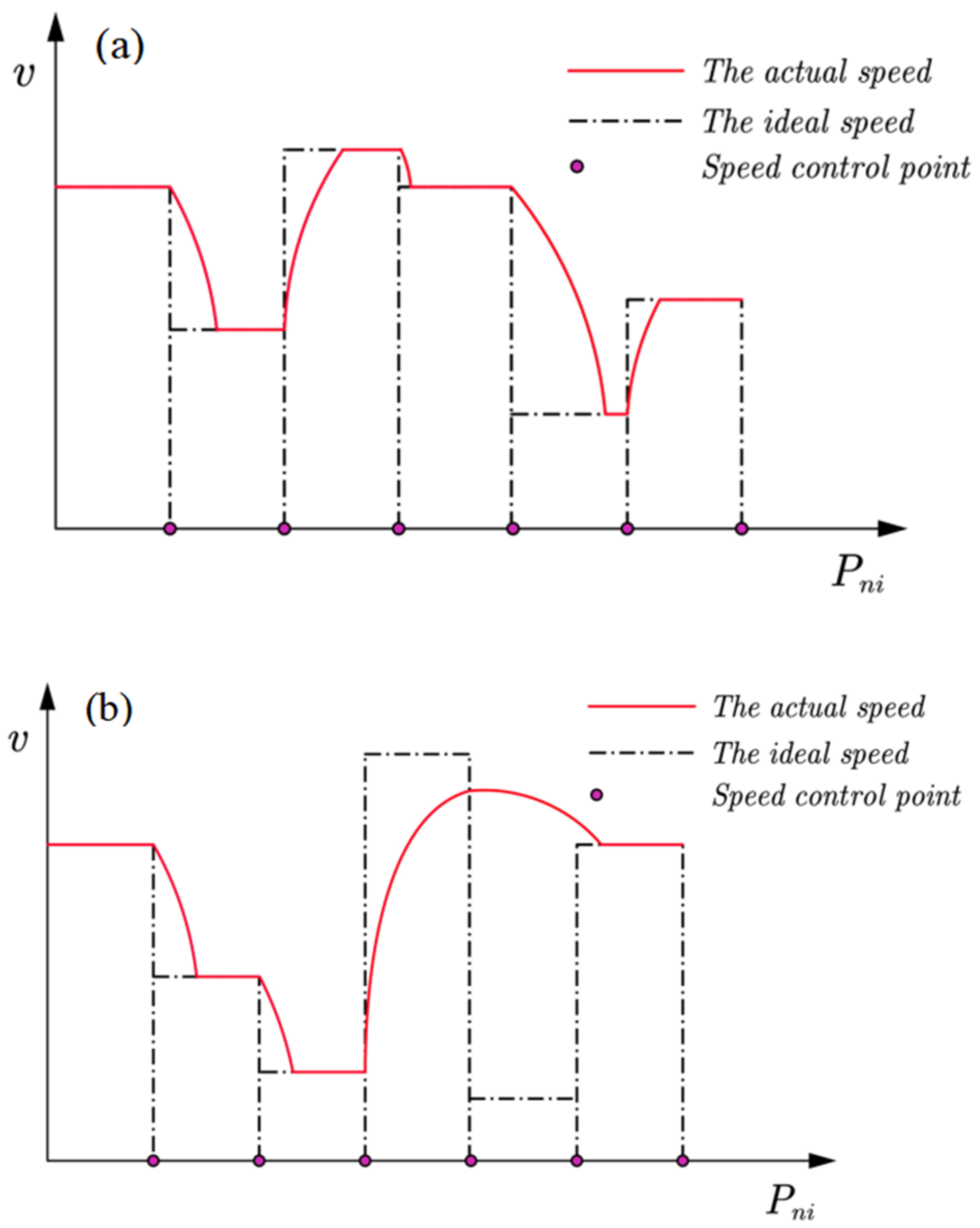
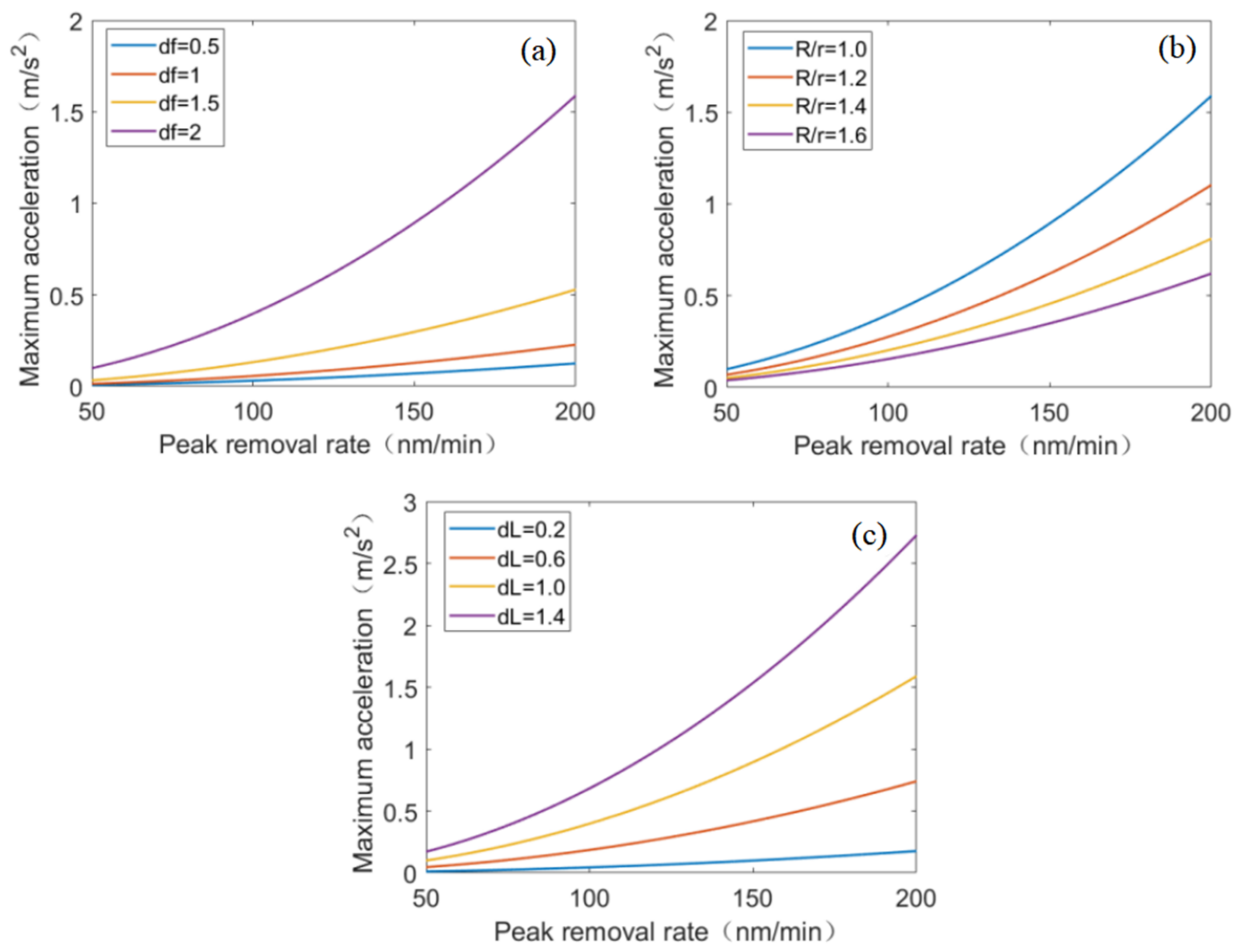
2.1.1. The Scanning Axis
2.1.2. The Target Distance Control Axis
2.2. Static Performance Requirements Analysis
2.2.1. Tangential Positioning Accuracy
2.2.2. Requirement Analysis of Angle Positioning Accuracy
2.3. Summary
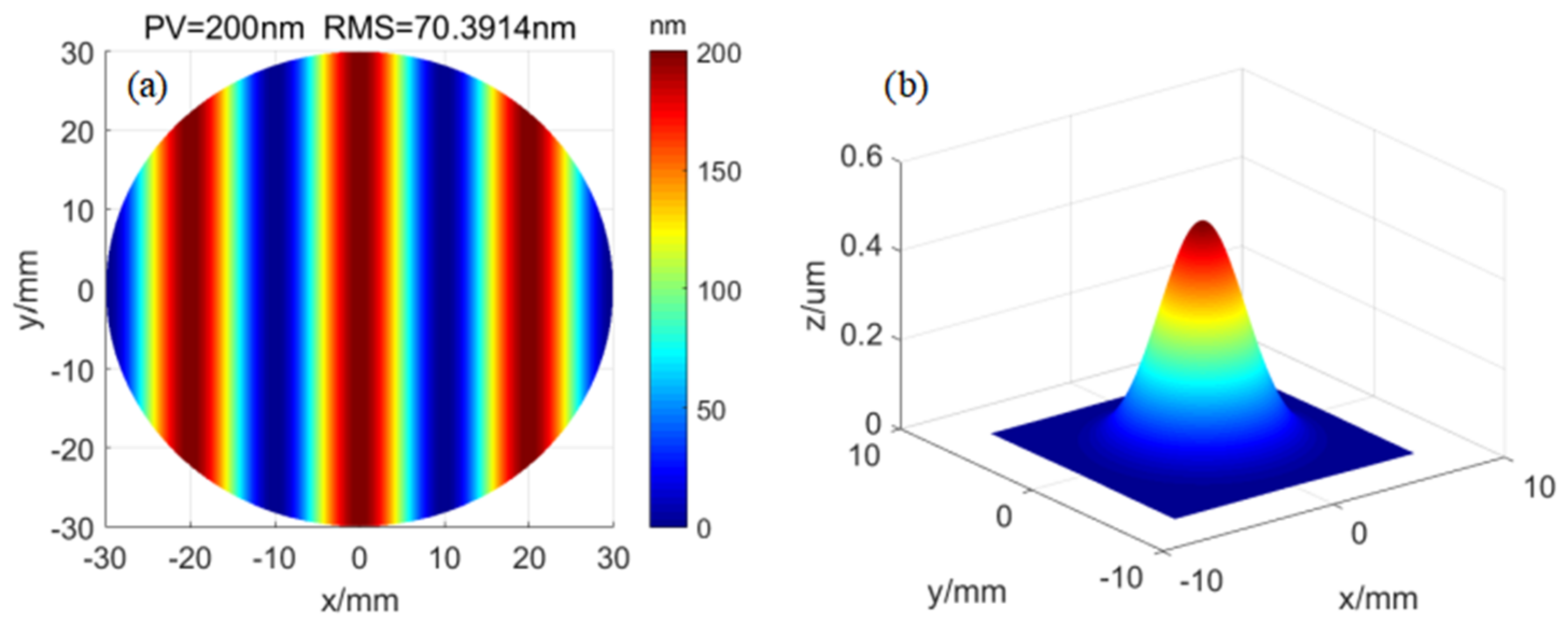
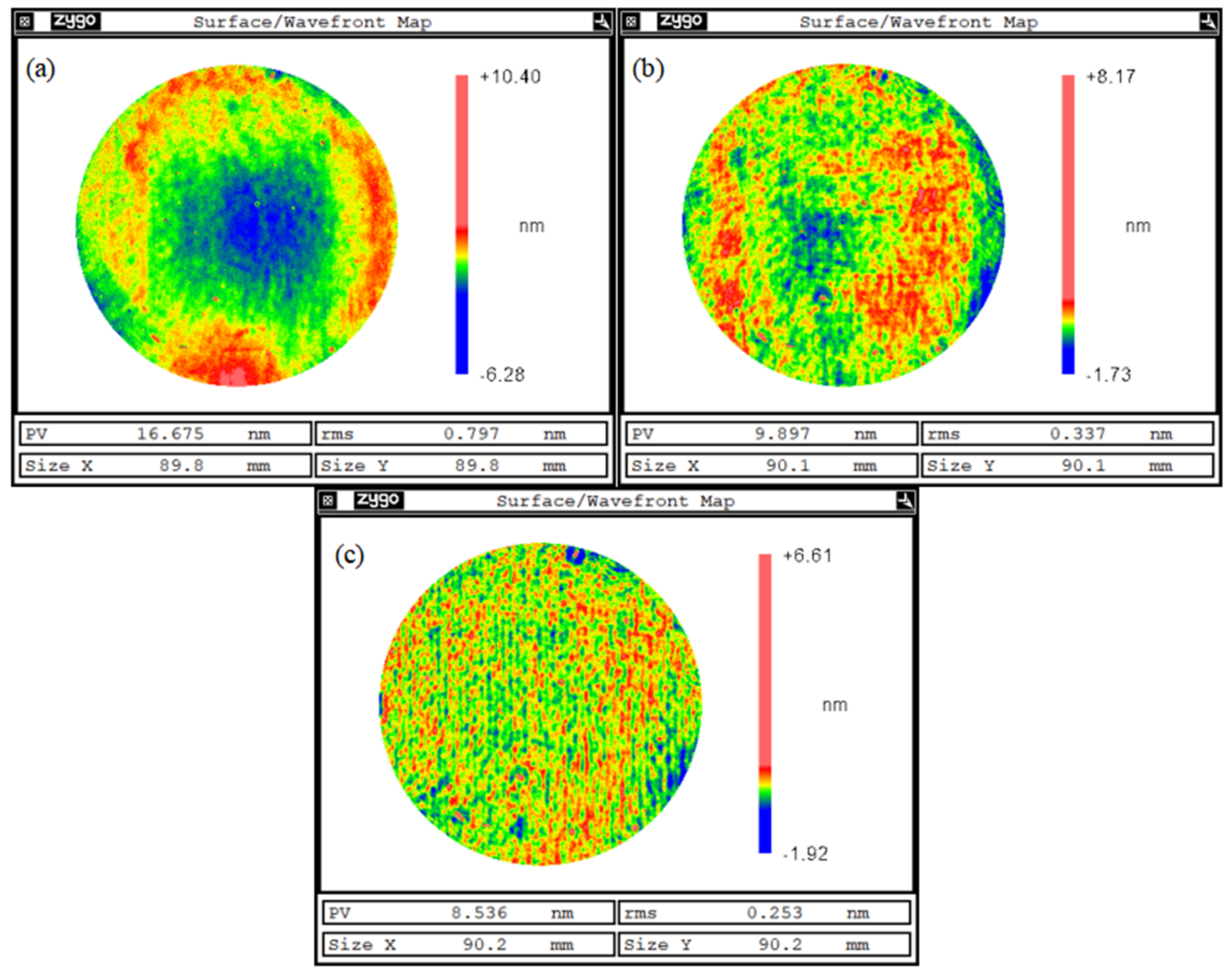
3. Results
- Measure and set the expected material removal distribution E(x,y) and removal function R(x,y);
- Discretize E(x,y) and R(x,y);
- Use the TSVD method to calculate the dwell time matrix. The dwell time is solved using the generalized minimum residual (GMRES) method;
- Obtain simulated material removal distribution through discrete two-dimensional convolution;
4. Discussion
- (1)
- A comparison of our obtained findings with previous studies is discussed below.
- ①
- The previous studies which focused on process of IBF were based on optimizing process parameters according to the figuring results and figuring phenomena, i.e., process optimization was realized by studying the figuring effects of every process parameter.
- ②
- The process optimization was conducted without detecting the performance of the IBF machine tools and without clarifying the performance requirements on IBF machine tools. Compared with the previous studies, we aimed to propose a new process optimization method based on analysis of dynamic and static performance requirements of IBF machine tools for sub-nanometer figuring. The requirements on IBF machine tools are different for different process parameters and surface figure characteristics.
- ③
- Therefore, process parameters for a given surface can be optimized according to the analysis results to reduce the performance requirements on a given IBF machine tool with measurable performance. This new process parameter optimization method may be more deterministic, efficient, and explicit. Furthermore, the performance requirements analysis results can help design three-axis IBF machine tools that have qualified dynamic and static performance to achieve sub-nanometer accuracy.
- (2)
- Some issues of the proposed method are discussed below.
- ①
- This paper mainly studied the influence of performance of IBF machine tools on low-frequency error. The IBF machine tool performance requirements for different process parameters were obtained. Then, a process optimization method based on analysis of dynamic and static performance requirements of IBF machine tools for sub-nanometer figuring was proposed. However, the performance of IBF machine tools also influences mid- and high-frequency errors (i.e., roundness and waviness). Usually, ultra-precision optics requires high accuracy within full-band frequency. Therefore, the influence of performance of IBF machine tools on mid- and high- frequency errors should be further studied. We are working on a process optimization method for sub-nanometer accuracy within full-band frequency based on an analysis of the performance requirements of IBF machine tools, and we hope to report it soon.
- ②
- X-ray mirrors in the fourth-generation synchrotron radiation source for nanometer focusing can require surface figure up to a 0.1 mm spatial period. The cutoff frequency of IBF needs to be as high as 10 mm−1. Reducing the diameter of the ion beam is the common method. The theoretical cutoff frequency can be calculated using the diameter of the ion beam. However, we found in experiments that effective figuring on the corresponding frequency error component cannot be realized by reducing the diameter of the ion beam when the diameter of the ion beam has been reduced to a certain small value. Therefore, we can infer that the practical cutoff frequency can be reduced relative to the theoretical cutoff frequency due to the influence on the performance of the IBF machine tools. The influence of performance of IBF machine tools on the cutoff frequency should be studied. Thus, the designed performance of IBF machine tools can be determined by the cutoff frequency required certain surfaces.
- ③
- Only dynamic and static performances of the IBF machine tools that seriously influence the low-frequency error were analyzed. However, the influence of the electric current loop of the IBF machine tools should be considered when we manufacture EUV lithography objective lenses that require sub-nanometer accuracy within full-band frequency. We found in preliminary experiments that the electric current loop can vibrate the tool, resulting in mid- and high- frequency error. The electric current loop together with the dynamic and static performance will influence the accuracy in full-band frequency. Therefore, the influence of the electric current loop of the IBF machine tools should be studied in the future.
- ④
- The verification was only conducted on flat surfaces. Whether the proposed method can be applied to curved surfaces remains to be verified in future work. Furthermore, a surface with a small circular aperture was used in the experiment. Whether the proposed method applies to surfaces with a large rectangle aperture (usually used in synchrotron radiation source facilities) remains to be verified.
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Poyneer, L.A.; McCarville, T.; Pardini, T.; Palmer, D.; Brooks, A.; Pivovaroff, M.J.; Macintosh, B. Sub-nanometer flattening of 45 cm long, 45 actuator x-ray deformable mirror. Appl. Opt. 2014, 53, 3404–3414. [Google Scholar] [CrossRef] [PubMed]
- Liao, W.; Dai, Y.; Xie, X. Influence of material removal programming on ion beam figuring of high-precision optical surfaces. Opt. Eng. 2014, 53, 095101. [Google Scholar] [CrossRef]
- Kurz, P.; Mann, H.-J.; Antoni, M.; Singer, W.; Muhlbeyer, M.; Melzer, F.; Dinger, U.; Weiser, M.; Stacklies, S.; Seitz, G.; et al. Optics for EUV lithography. In International Microprocesses & Nanotechnology; IEEE: Piscataway, NJ, USA, 2002. [Google Scholar]
- Glatzel, H.; Ashworth, D.; Bajuk, D.; Bjork, M.; Bremer, M.; Cordier, M.; Cummings, K.; Girard, L.; Goldstein, M.; Gullikson, E.; et al. Projection optics for EUVL micro-field exposure tools with 0.5 NA. Proc. SPIE 2014, 9048, 90481K. [Google Scholar] [CrossRef]
- Glatzel, H.; Ashworth, D.; Bremer, M.; Chin, R.; Cummings, K.; Girard, L.; Goldstein, M.; Gullikson, E.; Hudyma, R.; Kennon, J.; et al. Projection optics for extreme ultraviolet lithography (EUVL) micro-field exposure tools (METs) with a numerical aperture of 0.5. Proc. SPIE 2013, 8679, 867917. [Google Scholar] [CrossRef]
- Li, M.; Wu, J.; Wu, Y.; Xu, Y.; Zhang, D. A review on the fabrication technology of X-ray reflector. Opto-Electron. Eng. 2020, 47, 1–12. (In Chinese) [Google Scholar]
- Deng, W.H.; Jin, H.M.; Chen, X.H.; Zhong, B.; Hou, J.; Li, A.Q. Optimization of IBF parameters based on adaptive tool-path algorithm. Proc. SPIE 2018, 10710, 107102W. [Google Scholar] [CrossRef]
- Hänsel, T.; Nickel, A.; Schindler, A. Ion beam figuring of strongly curved surfaces with a (x, y, z) linear three-axes system. In Frontiers in Optics 2008/Laser Science XXIV/Plasmonics and Metamaterials/Optical Fabrication and Testing; OSA Technical Digest (CD); Optical Society of America: Washington, DC, USA, 2008; p. JWD6. [Google Scholar]
- Mühlig, C.; Bublitz, S.; Feldkamp, R.; Bernitzki, H. Effect of ion beam figuring and subsequent antireflective coating deposition on the surface absorption of CaF_2 at 193 nm. Appl. Opt. 2016, 56, C91. [Google Scholar] [CrossRef]
- Tang, W.; Deng, W.; Li, R.; Zheng, L.; Zhang, X. Correction of removal function of ion beam figuring highly steep off-axis asphere. Opt. Precision Eng. 2015, 23, 1572–1579. (In Chinese) [Google Scholar] [CrossRef]
- Hu, H.; Qi, E.; Luo, X.; Zhang, X.; Xue, D. Rapid fabrication strategy for Ø1.5m off-axis parabolic parts using com-puter-controlled optical surfacing. Appl. Opt. 2015, 57, F37–F43. [Google Scholar] [CrossRef]
- Wu, J.F.; Lu, Z.W.; Zhang, H.X.; Wang, T.S. Dwell time algorithm in ion beam figuring. Appl. Opt. 2009, 48, 3930–3937. [Google Scholar] [CrossRef]
- Yin, X.; Deng, W.; Tang, W.; Zhang, B.; Xue, D.; Zhang, F.; Zhang, X. Ion beam figuring approach for thermally sensitive space optics. Appl. Opt. 2016, 55, 8049–8055. [Google Scholar] [CrossRef]
- Wang, T.; Huang, L.; Vescovi, M.; Kuhne, D.; Tayabaly, K.; Bouet, N.; Idir, M. Study on an effective one-dimensional ion-beam figuring method. Opt. Express 2019, 27, 15368–15381. [Google Scholar] [CrossRef]
- Wang, T.; Huang, L.; Choi, H.; Vescovi, M.; Kuhne, D.; Zhu, Y.; Pullen, W.C.; Ke, X.; Kim, D.W.; Kemao, Q.; et al. RISE: Robust iterative surface extension for sub-nanometer X-ray mirror fabrication. Opt. Express 2021, 29, 15114–15132. [Google Scholar] [CrossRef]
- Wang, T.; Huang, L.; Vescovi, M.; Kuhne, D.; Zhu, Y.; Negi, V.S.; Zhang, Z.; Wang, C.; Ke, X.; Choi, H.; et al. Universal dwell time optimization for deterministic optics fabrication. Opt. Express 2021, 29, 38737. [Google Scholar] [CrossRef]
- Zhou, L.; Idir, M.; Bouet, N.; Kaznatcheev, K.; Huang, L.; Vescovi, M.; Dai, Y.; Li, S. One-dimensional ion-beam figuring for grazing-incidence reflective optics. J. Synchrotron Radiat. 2016, 23, 182–186. [Google Scholar] [CrossRef]
- Schindler, A.; Hänsel, T.; Frost, F.; Fechner, R.; Seidenkranz, G.; Nickel, A.; Thomas, H.; Neumann, H.; Hirsch, D.; Schwabe, R.; et al. Ion Beam Finishing Technology for High Precision Optics Production. In Optical Fabrication and Testing; Sawchuk, A., Ed.; OSA Trends in Optics and Photonics Series; Optical Society of America: Washington, DC, USA, 2002; Volume 76, p. OTuB5. [Google Scholar]
- Geyl, R.; Rolland, E.; Rinchet, A. Large optics ion figuring. Proc. SPIE 1999, 3739, 161–166. [Google Scholar] [CrossRef]
- Arnold, T.; Böhm, G.; Fechner, R.; Meister, J.; Nickel, A.; Frost, F.; Hänsel, T.; Schindler, A. Ultra-precision surface finishing by ion beam and plasma jet techniques—Status and outlook. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2010, 616, 147–156. [Google Scholar] [CrossRef]
- Arnold, T.; Böhm, G.; Paetzelt, H.; Pietag, F. Ion beam and plasma jet based methods in ultra-precision optics manufac-turing. Proc. SPIE 2015, 9442, 944204. [Google Scholar]
- Li, Y.; Takino, H.; Frost, F. Ion beam planarization of diamond turned surfaces with various roughness profiles. Opt. Express 2017, 25, 7828–7838. [Google Scholar] [CrossRef]
- Uzawa, S.; Kubo, H.; Miwa, Y.; Tsuji, T.; Morishima, H. Path to the HVM in EUVL through the development and evaluation of the SFET. Proc. SPIE 2007, 6517, 651708. [Google Scholar] [CrossRef]
- Murakami, K.; Oshino, T.; Kondo, H.; Chiba, H.; Komatsuda, H.; Nomura, K.; Iwata, H. Development of optics for EUV lithography tools. Proc. SPIE 2007, 6517, 65170J. [Google Scholar] [CrossRef]
- Miura, T.; Murakami, K.; Suzuki, K.; Kohama, Y.; Ohkubo, Y.; Asami, T. Nikon EUVL development progress summary. Proc. SPIE 2006, 6151, 615105. [Google Scholar] [CrossRef]
- Deng, W.-J.; Yin, X.; Tang, W.; Xue, D.; Zhang, X. Research on ion beam figuring system with five-axis hybrid mechanism for complex optical surface. Proc. SPIE 2019, 10838, 108380L. [Google Scholar] [CrossRef]
- Shi, B.; Dai, Y.; Zhou, L. Analysis on Positioning Accuracy for Ion Beam Figuring. Aviat. Precis. Manuf. Technol. 2011, 47, 9–13. (In Chinese) [Google Scholar]
- Yang, B.; Xie, X.; Zhou, L.; Hu, H. Design of a large five-axis ultra-precision ion beam figuring machine: Structure opti-mization and dynamic performance analysis. Int. J. Adv. Des. Manuf. Technol. 2017, 92, 3413–3424. [Google Scholar] [CrossRef]
- Xu, M.; Dai, Y.; Xie, X.; Zhou, L.; Liao, W. Structure optimization and fabricating capability analysis of an ion-beam machine for a subnanometer optical surface. Appl. Opt. 2015, 54, 8055–8061. [Google Scholar] [CrossRef]
- Liao, W.; Dai, Y.; Xie, X.; Zhou, L.; Yuan, Z. Corrective capability analysis and machining error control in ion beam figuring of high-precision optical mirrors. Opt. Eng. 2012, 51, 033402. [Google Scholar] [CrossRef]






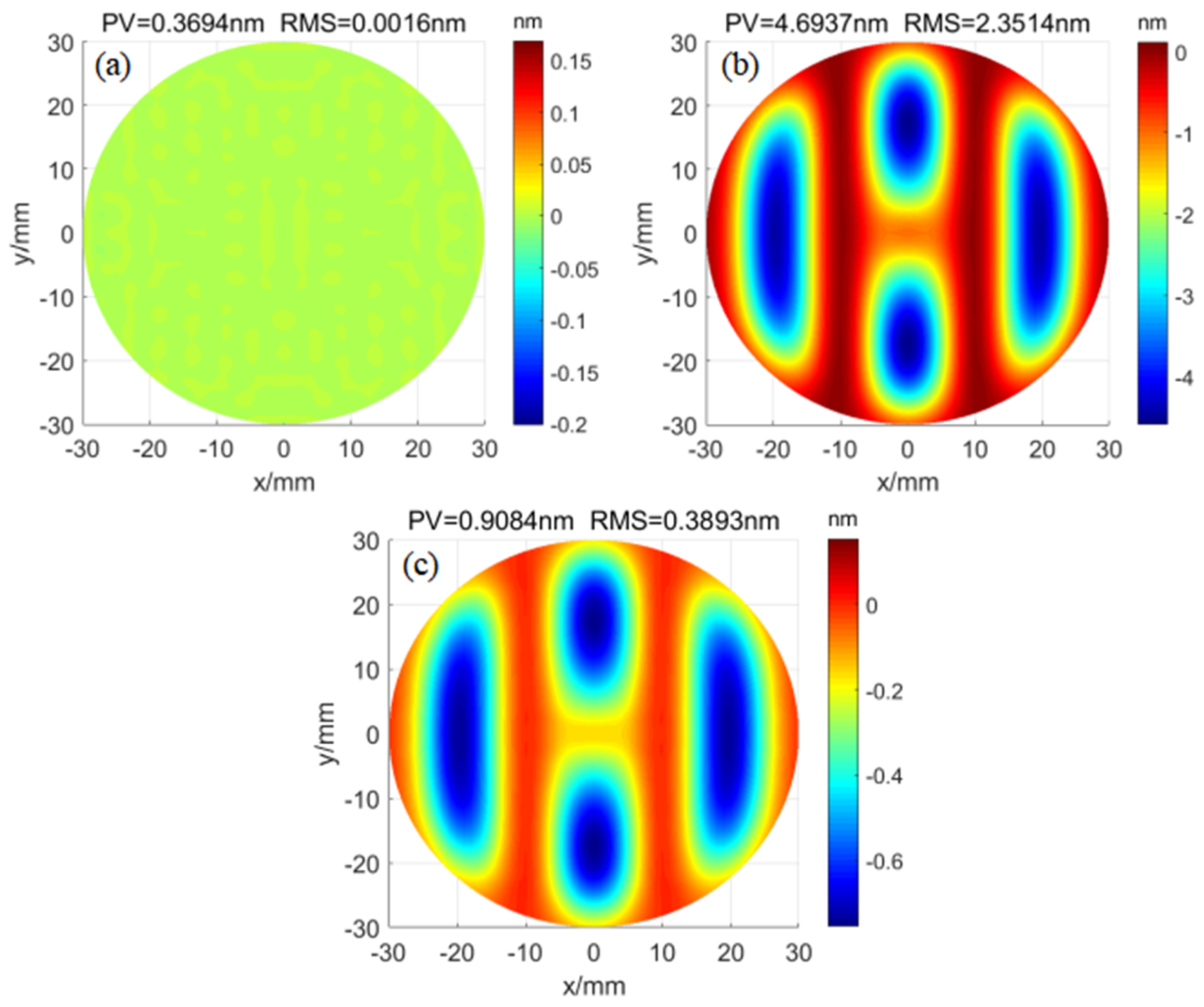

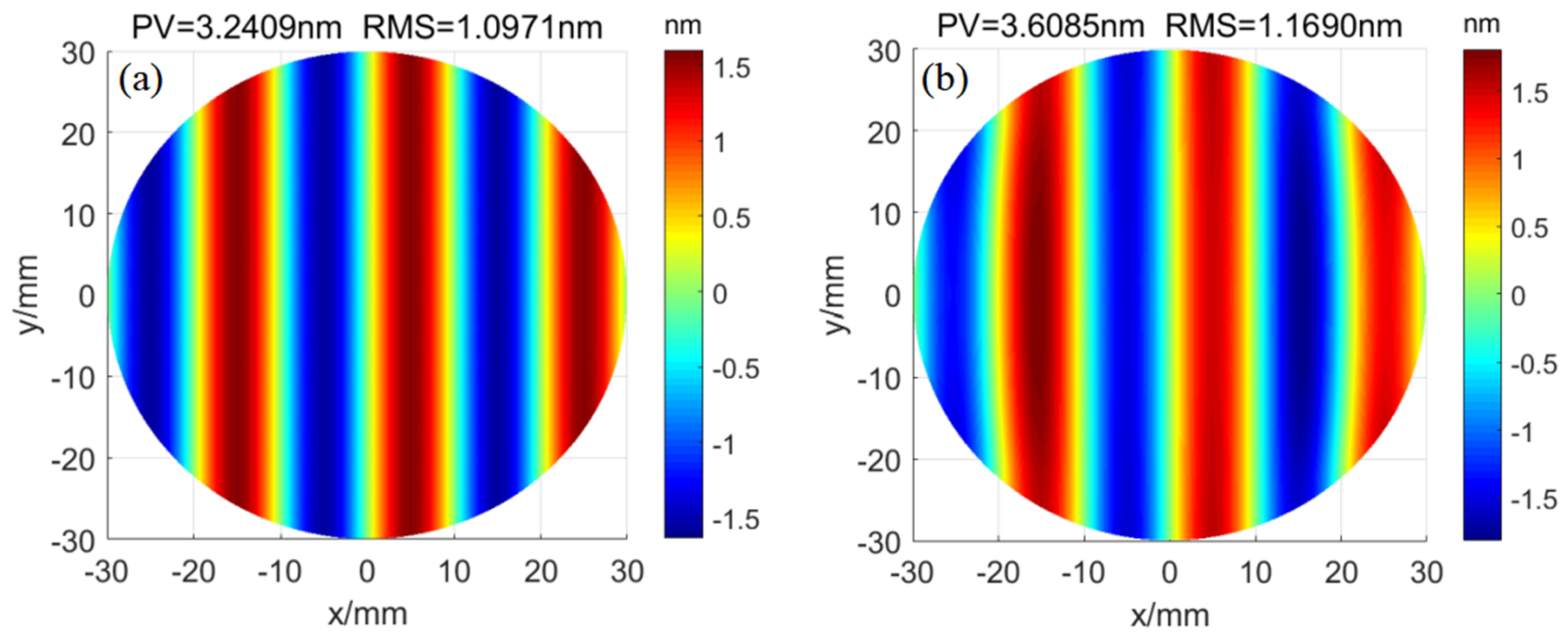

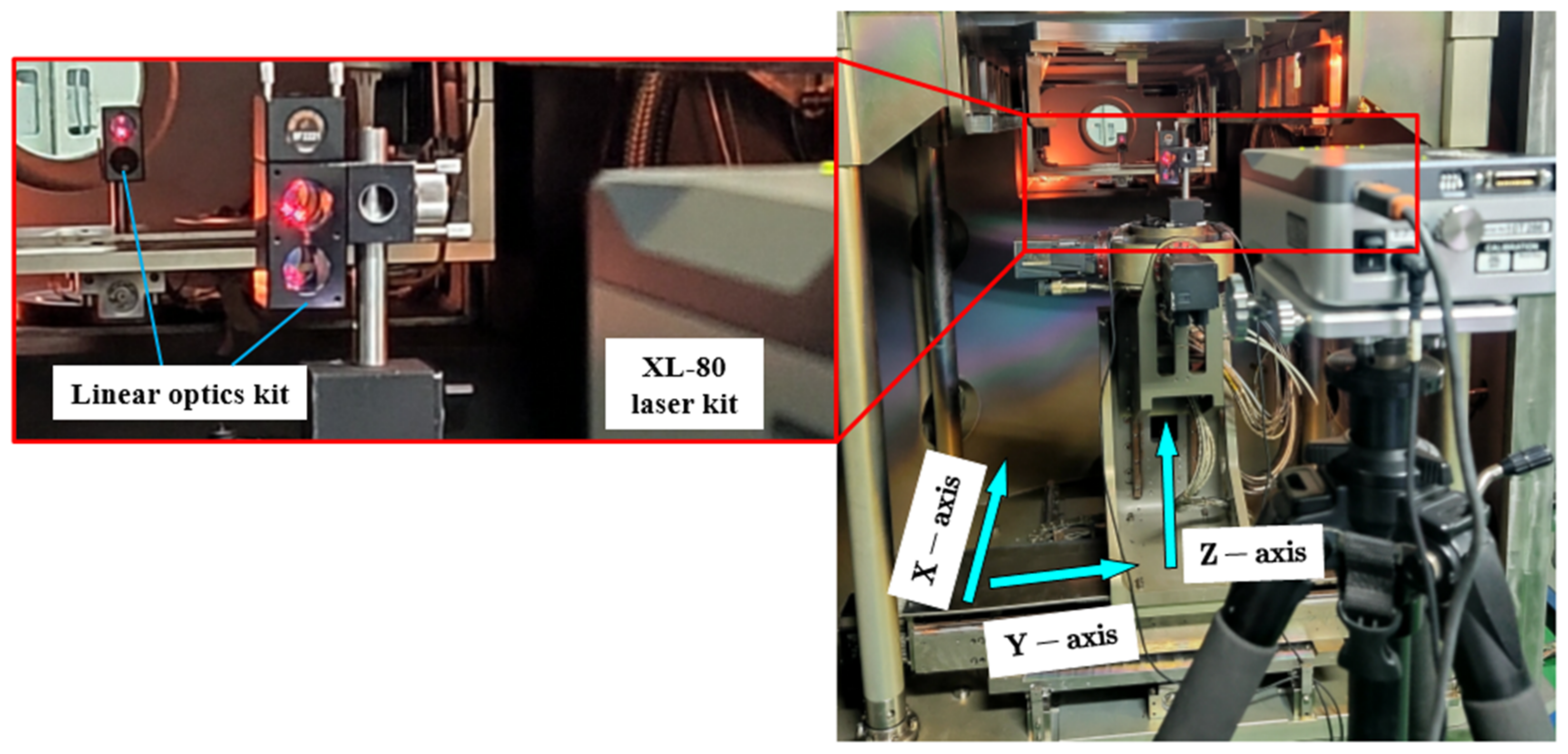
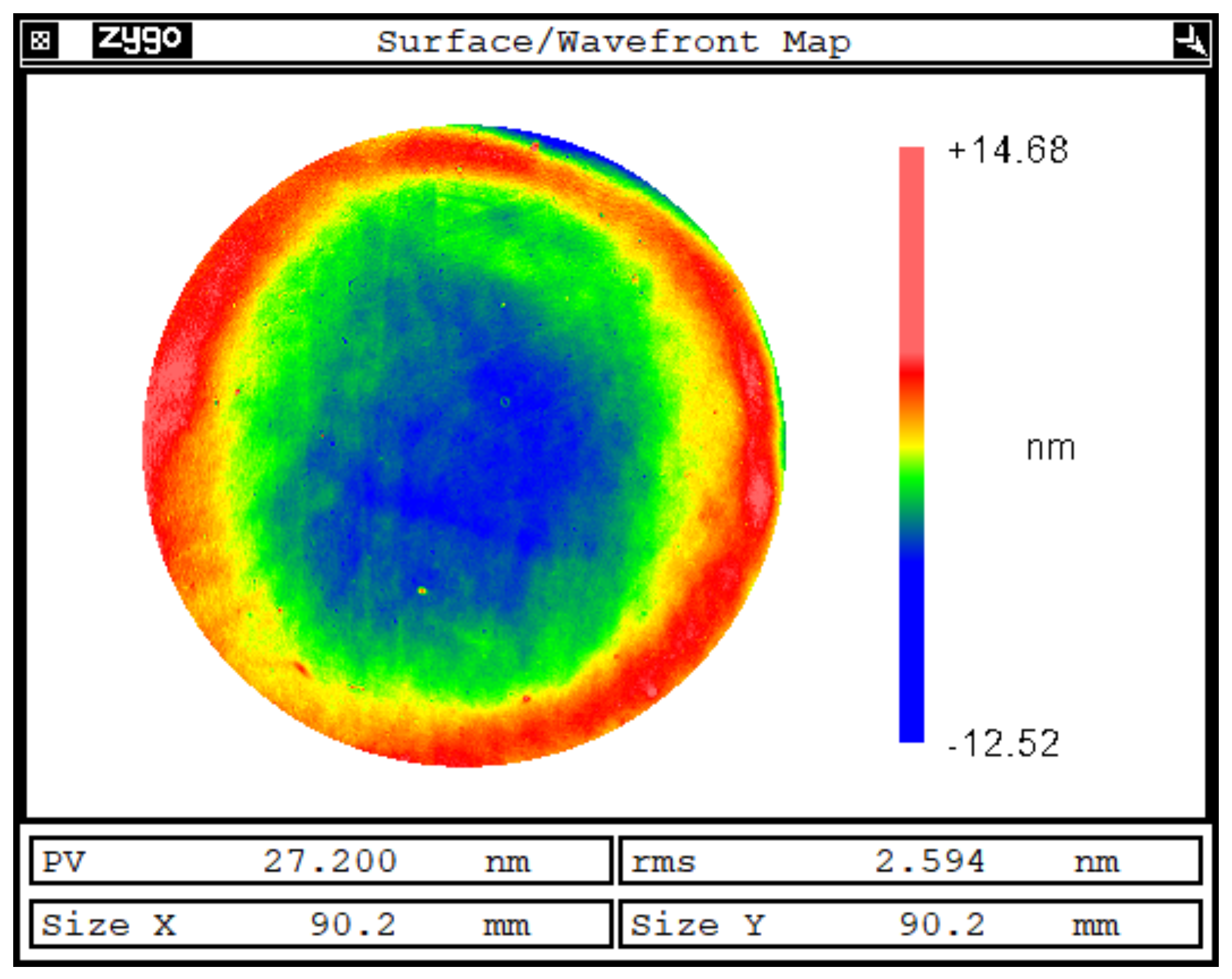

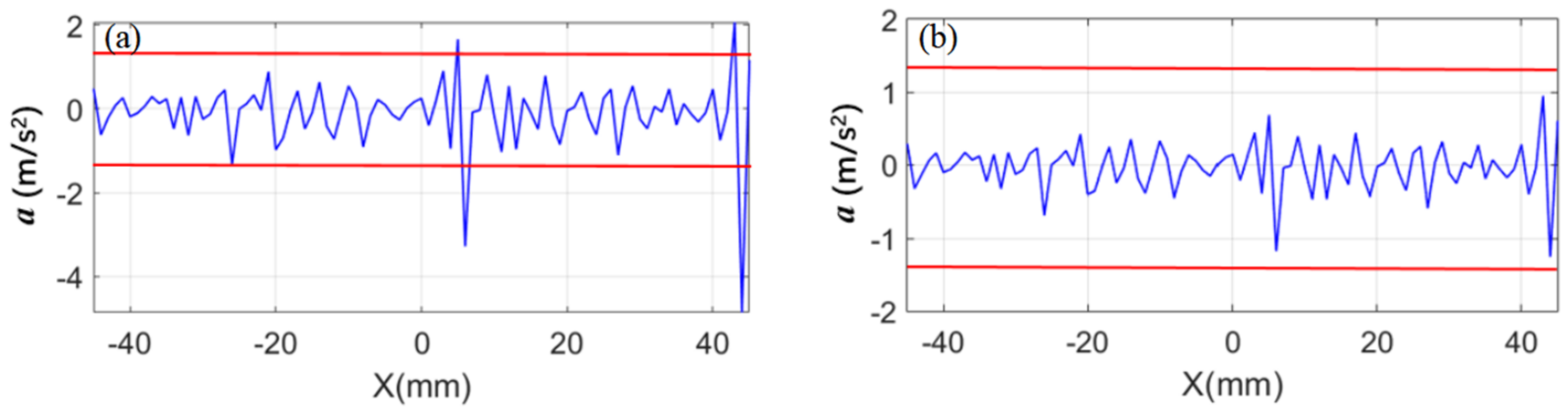


| Axis of Motion | x-Axis | y-Axis | z-Axis |
|---|---|---|---|
| Positioning error (μm) | 52.74 | 53.04 | 37.71 |
| Maximum acceleration (m·s−2) | 1.0 | 1.3 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Hu, H.; Dai, Y.; Lin, Z.; Xue, S. Process Optimization Based on Analysis of Dynamic and Static Performance Requirements of Ion Beam Figuring Machine Tools for Sub-Nanometer Figuring. Photonics 2022, 9, 839. https://doi.org/10.3390/photonics9110839
Wang Y, Hu H, Dai Y, Lin Z, Xue S. Process Optimization Based on Analysis of Dynamic and Static Performance Requirements of Ion Beam Figuring Machine Tools for Sub-Nanometer Figuring. Photonics. 2022; 9(11):839. https://doi.org/10.3390/photonics9110839
Chicago/Turabian StyleWang, Yongbin, Hao Hu, Yifan Dai, Zhifan Lin, and Shuai Xue. 2022. "Process Optimization Based on Analysis of Dynamic and Static Performance Requirements of Ion Beam Figuring Machine Tools for Sub-Nanometer Figuring" Photonics 9, no. 11: 839. https://doi.org/10.3390/photonics9110839
APA StyleWang, Y., Hu, H., Dai, Y., Lin, Z., & Xue, S. (2022). Process Optimization Based on Analysis of Dynamic and Static Performance Requirements of Ion Beam Figuring Machine Tools for Sub-Nanometer Figuring. Photonics, 9(11), 839. https://doi.org/10.3390/photonics9110839




