Abstract
In this work, we propose a mode-conversion-based chirped Bragg grating on thin-film lithium niobate (TFLN). The device is mainly composed of a 4.7-mm long chirped asymmetric Bragg grating and an adiabatic directional coupler (ADC). The mode conversion introduced by the ADC allows the chirped Bragg grating operates in reflection without using an off-chip circulator. The proposed device has experimentally achieved a total time delay of 73.4 ps over an operating bandwidth of 15 nm. This mode-conversion-based chirped Bragg grating shows excellent compatibility with other devices on TFLN, making it suitable in monolithically integrated microwave photonics, sensing, and optical communication systems.
1. Introduction
Chirped Bragg gratings have been extensively investigated for decades. In optical fibers, chirped Bragg gratings play an essential role in many applications, including dispersion control [1,2,3,4], a variety of sensing [5,6,7], mode-locked fiber lasers [8,9], microwave photonics [10,11], etc. In recent years, integrated photonic techniques, which use integrated optical components to generate, interconnect, and process signals, have become an inevitable trend. Integrated Bragg gratings can be used as on-chip optical filter devices, and numerous types of research have emerged [12,13,14,15]. Chirped Bragg gratings on integrated photonics platforms have been utilized in many applications, such as on-chip dispersion compensation [16,17], phased array antennas [18], time-frequency mapping [19,20], etc. Until now, most of the researches on integrated chirped Bragg gratings have used an optical circulator [18,20,21] or a 3-dB Y-branch [19,22,23,24] to out-couple the reflected signal. However, using an optical circulator, whose integration is not trivial, is challenging to meet the requirements of monolithic integration. A 3-dB Y-branch involves a minimum 6 dB insertion loss and excess reflections back to the input port. Therefore, realizing the drop function for integrated chirped Bragg gratings is essential for monolithic integration.
To overcome this problem, a multimode interference (MMI) coupler-based drop filter for chirped Bragg gratings on SOI was proposed [25]. Nevertheless, it has poor tolerance for fabrication errors. A minor random phase difference between the grating pairs would invalidate the drop filter [26]. Several other solutions have been applied to Bragg gratings without chirp to realize a drop function, such as grating-assisted contradirectional coupler [27], Mach-Zehnder interferometer structure [28], asymmetric Y-branch [29] and adiabatic directional coupler (ADC) [15,30]. But until now, few of them have been used in integrated chirped Bragg gratings.
Over the past few years, the thin-film lithium niobate (TFLN) platform has drawn much attention because of its excellent electro-optic and optical characteristics [31,32]. A chirped Bragg grating could be a basic building block for integrated high-performance microwave photonics systems on TFLN [31]. Recently, an electro-optic time lens was proposed, and femtosecond pulses were generated on TFLN [20]. A chirped Bragg grating with a 1.62 ps/nm dispersion was used for compressing optical pulses. However, the time lens system was not monolithically integrated, still requiring an off-chip circulator to drop the reflected beam from chirped Bragg grating.
In this work, we investigate a mode-conversion-based chirped Bragg grating on TFLN. The proposed structure is mainly composed of a 4.7 mm long chirped asymmetric Bragg grating and an ADC. The forward fundamental transverse electric (TE) mode is reflected and converted to backward TE mode in the grating. The asymmetric Bragg gratings can couple the two orthogonal modes while symmetric Bragg gratings cannot according to the coupled mode theory [29].The backward TE mode is guided into a branch waveguide by mode conversion using the ADC, which is connected to the drop port. This allows the chirped Bragg grating operates in reflection without using an off-chip circulator or introducing excess reflections back to the input port. The proposed structure has experimentally demonstrated a total time delay of 73.4 ps over an operating bandwidth of 15 nm. By this method, the chirped Bragg grating can be interconnected with other devices on TFLN, making it suitable for monolithic microwave photonics, sensing, and optical communication systems.
2. Methods
The schematic view of the proposed mode-conversion based chirped Bragg grating (CBG) is shown in Figure 1a. Three grating couplers designed for the transverse electric (TE) polarization are used for in/off-chip coupling. When the input optical signal is fed into the asymmetric CBG, the TE mode is reflected and converted into the backward TE mode. Light with different wavelengths is reflected at different positions along the CBG, with a consequent delay difference. After passing through the ADC, the backward TE mode is converted into TE mode and guided into the lower branch waveguide, which is connected to the drop port. The ADC-based mode de-multiplexer can significantly reduce the reflections back to the input port while exhibiting a high fabrication error tolerance [30]. The light with wavelengths away from the Bragg wavelength will travel through the Bragg grating to the through port.
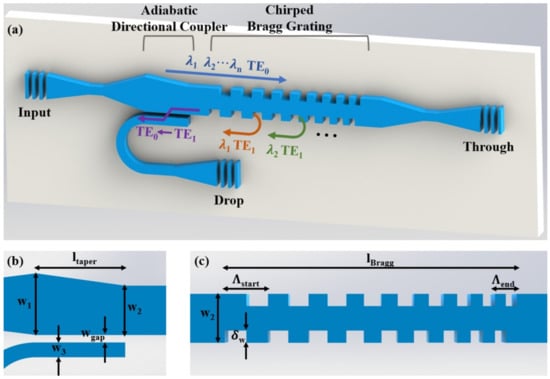
Figure 1.
(a) Schematic view of the proposed mode-conversion based chirped Bragg grating on TFLN. Schematic views of the adiabatic directional coupler (b) and the chirped Bragg grating (c) with design parameters labeled out.
Figure 1b shows the schematic view of the ADC. The ADC consists of a narrow branch with a width of and a tapered bus waveguide whose width increases from to . The gap between the branch and the bus waveguide is , and the coupling length is . When the effective index of TE mode in the bus waveguide equals the effective index of TE mode in the branch waveguide, the phase-matching condition is satisfied and efficient coupling between the modes can be achieved. Figure 2a shows the cross-section of the TFLN waveguide. The heights of the slab and the rib are both 200 nm. Due to the lithium niobate redeposition in Argon-based dry etch, the sidewall tilt angle is around 67. Figure 2b depicts the effective indexes of the TE and TE modes in the waveguide at 1550 nm. The effective indexes of the two modes are close to 1.824 when the waveguide widths are 1 m and 2.43 m, respectively. To realize a high-fabrication-tolerance design, we set the bus waveguide tapered from 2.3 m to 2.6 m, which covers the abovementioned width of 2.43 m. Using the eigenmode expansion (EME) method, we vary the gap and the coupling length to find the maximum TE – TE coupling efficiency. The light propagation of the TE – TE mode and the TE – TE mode are illustrated in Figure 2c. Figure 2d shows the calculated ADC spectrum response. From 1550 nm to 1650 nm, the input transmission (TE – TE) is above −0.017 dB, the output coupling (TE – TE) loss is decreased from −0.09 dB to −0.37 dB, and the output crosstalk (TE in the bus waveguide – TE in the branch waveguide) is reduced from −36 dB to −43 dB. The specific parameters of the designed ADC are listed as follows: = 2.6 m, = 2.3 m, = 1 m, = 300 nm and = 38 m.
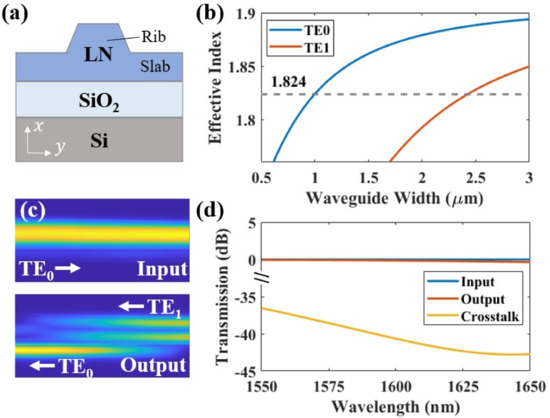
Figure 2.
(a) Cross section of the TFLN waveguide. (b) Effective indexes of the TE and TE modes versus the waveguide width. (c) Light propagation of the ADC when TE and TE modes are injected. (d) The simulated ADC spectrum response.
Figure 1c shows the schematic view of the chirped Bragg grating. The grating starts with a longer period of , and the periods linearly reduce to . This makes light with different wavelengths reflect at varying positions of the CBG. The relation between the Bragg wavelength , the effective indexes of two modes and , and the Bragg grating period is given as follows [29]
The light reflected at the end of the CBG will exhibit a time delay difference from the light reflected at the beginning. is the total time delay range of the CBG, which can be expressed as
where is the overall grating length, c is the speed of light.
From Equations (1) and (2), we determined the design parameters of the CBG, which are as follows: = 400 nm, = 440 nm, = 433 nm, and = 4.7 mm. The designed CBG is polarization sensitive. The TM modes, whose effective indexes are not satisfied the Bragg condition described in Equation (1), would travel through the grating without reflection in the desired wavelength range if injected into the CBG.
We use a commercial variational finite-difference time-domain solver (varFDTD, Ansys, Inc., Canonsburg, PA, USA) to obtain the simulated reflection spectrum and group delay of the CBG. As illustrated in Figure 3, the total group delay is 80 ps over a 21 nm operating range. It can be seen that the group delay shows ripples because of the constant corrugation widths. The ripples can be reduced by using apodization methods [22].
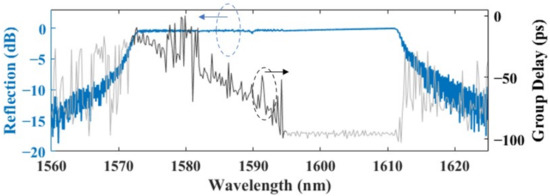
Figure 3.
Simulated reflection spectrum and group delay of the CBG.
Figure 4 shows the image of the fabricated mode-conversion-based chirped Bragg grating on TFLN and its close-up. The devices were fabricated on an x-cut lithium niobate-on-insulator wafer with a 400-nm thick TFLN. The device pattern was defined by electron beam lithography (EBL) and Argon-based inductively coupled plasma reactive ion etching. The detailed fabrication process can be found in our previous work [33].
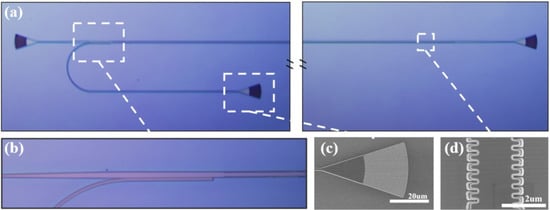
Figure 4.
(a) Microscope image of the demonstrated mode-conversion-based CBG. (b) Close-up of the ADC. SEM image of the grating coupler (c) and Bragg grating (d).
3. Results
Different kinds of measurements were used to evaluate the performance of the mode-conversion-based CBG. First, we measured the through and reflection spectrum using a tunable laser and an optical spectrum analyzer, as shown in Figure 5a. Then, we measured the group delay of the CBG using an optical vector analyzer (OVA, Luna 5100, Luna Innovations, Roanoke, VA, USA), as one can see in Figure 5b. Finally, a time-of-flight measurement was carried out to record the time delays at different wavelengths, as illustrated in Figure 5c.
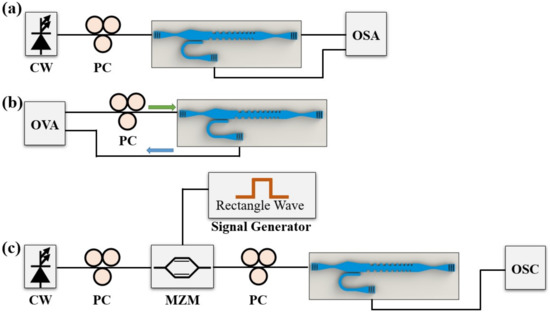
Figure 5.
Experimental setups of the reflection and transmission spectrum measurement (a), the group delay measurement (b), time-of-flight measurement (c). CW: continuous wave laser; PC: polarization controller; OSA: optical spectrum analyzer; OVA: optical vector analyzer; MZM: Mach-Zehnder modulator; OSC: oscilloscope.
The reflection spectrum from the drop port and the transmission spectrum from the through port are illustrated in Figure 6a,b, respectively. The spectrum was obtained by subtracting the transmission spectrum of the reference grating coupler from the measurement data. The fabricated CBG showed a total operating range of 15 nm (1565–1580 nm). A suppression ratio of 20 dB between the unreflected and reflected wavelengths shown in Figure 6b suggests a good reflectivity across the whole band. However, an upward-sloping curve can be seen from 1565 nm to 1580 nm in the reflection spectrum in Figure 6a. This is mainly due to the waveguide propagation loss. Light with a wavelength of 1565 nm reflected at the end of the CBG travels a total distance of 2 times the grating length. However, light with a wavelength of 1580 nm reflects at the start of the grating and the propagation distance can be considered zero. The loss is 6.87 dB at 1565 nm and 1.37 dB at 1580 nm. Therefore, the average propagation loss of the TE and TE modes is calculated to be 5.85 dB/cm. The propagation loss is mainly due to the roughness of the grating waveguide sidewalls and can be reduced by optimizing etching recipes. Figure 6a also shows the group delay measured by the optical vector analyzer. The orange dash line is the fitted group delay in the operation wavelengths. The total group delay is 73.4 ps and the negative slope of the linear dispersion is −4.89 ps/nm. The undesired ripples in the group delay response are mainly related to the strength of the index perturbation [23]. Decreasing the corrugation width () can reduce the ripples at the expense of lower reflectivity in the spectrum and higher requirements for fabrication. One can also introduce apodization methods, which adjust the corrugation width along the CBG, to suppress the ripples as mentioned previously.
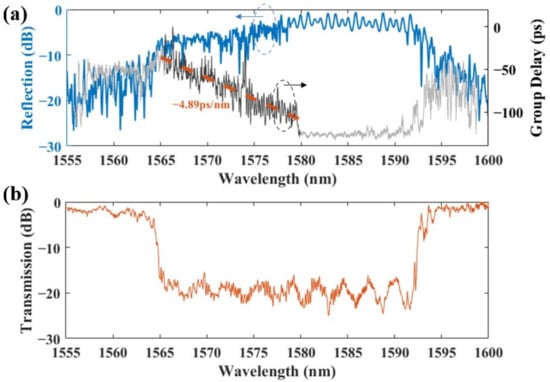
Figure 6.
(a) Measured reflection spectrum from the drop port and the corresponding group delay. (b) Measured transmission spectrum from the through port.
Figure 7 shows the time-of-flight measurement of a pulse falling edge at four different wavelengths. As one can see in Figure 5c, a Mach-Zehnder modulator together (AX-0MVS-40-PFA-PFA-LV, EOSPACE Inc., Redmond, WA, USA) with a pulse generator (81134A, Keysight, Santa Rosa, CA, USA) was used to generate an optical pulse with a falling time of 56 ps. An oscilloscope with optical ports (DSA8300, Tektronix, Inc., Beaverton, OR, USA) was used to record the delayed signals as we adjusted the wavelengths of the input continuous wave laser. The delay differences , , and were measured to be −13.7, −46.6, and −58.5 ps, respectively. The results agree well with the −4.89 ps/nm dispersion slope obtained from the above group delay measurement, as plotted in Figure 7b.
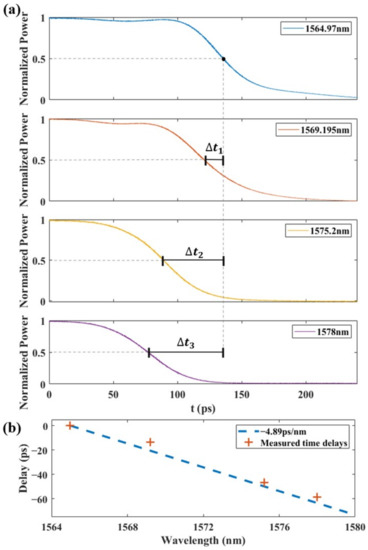
Figure 7.
(a) Measured time delays at different wavelengths of a falling edge. (b) Time delays plotted with the −4.89 ps/nm linear dispersion slope.
4. Discussion and Conclusions
The demonstrated structure uses an ADC-based mode de-multiplexer to guide reflected light to the drop port, which can conveniently interconnect CBGs with other on-chip devices. For instance, high-performance electro-optic modulators on TFLN and other integrated optical devices can be connected with the CBG via on-chip waveguides. At the same time, the excess loss and the additional reflection are relatively low. This is important for some specific applications to realize monolithic integration. A comparison of reported CBGs on integrated photonics platforms is shown in Table 1. As mentioned previously, most of the reported integrated CBGs use a 3-dB Y-branch or an off-chip circulator as the drop function method, which is challenging or unsuitable for monolithically integrated applications. As seen in Table 1, spiral CBGs exhibit a relatively large delay range because of long grating lengths. Hence, we could enlarge the delay range in our future work using spiral structures.

Table 1.
Comparison of reported integrated chirped Bragg gratings.
A tunable version of CBG can be useful in certain conditions and applications. In optical fibers, tunable spectrum and group delays can be achieved by applying strain and temperature change [3]. Similarly, the proposed CBG on TFLN can be tuned by applying refraction index change, which can shift the spectrum and the group delay response. However, compressing or stretching the spectrum, or tuning the dispersion range like the strain does to the fiber CBGs would be difficult. The change of the refraction index on TFLN can be achieved by applying an electric field along its z-axis. The Pockels effect of lithium niobate provides linear and fast-response electro-optic modulations. A tuning efficiency of 23.37 pm/V in a uniform Bragg grating was reported, and a 4 nm tuning window was achieved [34]. The operating wavelength of CBG on TFLN can also be shifted by using two electrodes across the waveguide. Additionally, thermal tuning can achieve higher efficiency, but more power consumption and slower response compared to electro-optic tuning.
In summary, we report a mode-conversion-based chirped Bragg grating on thin-film lithium niobate. The proposed device uses an ADC-based mode de-multiplexer to guide the reflected light to the drop port. This allows the CBG operates in reflection without using an off-chip circulator or introducing excess reflections back to the input. The experimental results show that the device exhibits a 73.4 ps delay range over a 15 nm operation bandwidth. The structure can be conveniently interconnected with other devices on TFLN, making it a promising solution for applications in monolithically integrated microwave photonics, sensing, and optical communication systems.
Author Contributions
Data curation, D.T. and X.H.; Funding acquisition, Z.L.; Methodology, X.H. and D.T.; Writing—original draft, D.T.; Writing—review & editing, D.T., X.H., Y.Y., H.Y., Z.Y., H.G. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key Research and Development Program of China (Grant No. 2018YFE0201900).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
Device fabrication was performed at The Engineering Research Center for Semiconductor Integrated Technology at Institute of Semiconductors, Chinese Academy of Sciences.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sumetsky, M.; Eggleton, B. Fiber Bragg gratings for dispersion compensation in optical communication systems. J. Opt. Fiber Commun. Rep. 2005, 2, 256–278. [Google Scholar] [CrossRef]
- Mustafa, F.M.; Zaky, S.A.; Khalaf, A.A.M.; Aly, M.H. A cascaded FBG scheme based OQPSK/DPSK modulation for chromatic dispersion compensation. Opt. Quantum Electron. 2022, 54, 7. [Google Scholar] [CrossRef]
- Min, R.; Korganbayev, S.; Molardi, C.; Broadway, C.; Hu, X.; Caucheteur, C.; Bang, O.; Antunes, P.; Tosi, D.; Marques, C.; et al. Largely tunable dispersion chirped polymer FBG. Opt. Lett. 2018, 43, 5106–5109. [Google Scholar] [CrossRef]
- Min, R.; Ortega, B.; Marques, C. Fabrication of tunable chirped mPOF Bragg gratings using a uniform phase mask. Opt. Express 2018, 26, 4411–4420. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.Y.; Chang, Y.C.; Sheng, H.J.; Fu, M.Y.; Liu, W.F.; Kashyap, R. An Ultra-Sensitive Liquid-Level Indicator Based on an Etched Chirped-Fiber Bragg Grating. IEEE Photonics Technol. Lett. 2016, 28, 268–271. [Google Scholar] [CrossRef]
- Tosi, D.; Macchi, E.G.; Gallati, M.; Braschi, G.; Cigada, A.; Rossi, S.; Leen, G.; Lewis, E. Fiber-optic chirped FBG for distributed thermal monitoring of ex-vivo radiofrequency ablation of liver. Biomed. Opt. Express 2014, 5, 1799–1811. [Google Scholar] [CrossRef]
- Zhou, W.; Dong, X.; Ni, K.; Chan, C.; Shum, P. Temperature-insensitive accelerometer based on a strain-chirped FBG. Sens. Actuators A Phys. 2010, 157, 15–18. [Google Scholar] [CrossRef]
- He, X.; bo Liu, Z.; Wang, D.N. Wavelength-tunable, passively mode-locked fiber laser based on graphene and chirped fiber Bragg grating. Opt. Lett. 2012, 37, 2394–2396. [Google Scholar] [CrossRef]
- Li, S.; Chan, T. Electrical wavelength-tunable actively mode-locked fiber ring laser with a linearly chirped fiber Bragg grating. IEEE Photonics Technol. Lett. 1998, 10, 799–801. [Google Scholar] [CrossRef]
- Tang, Z.; Pan, S.; Zhu, D.; Guo, R.; Zhao, Y.; Pan, M.; Ben, D.; Yao, J. Tunable Optoelectronic Oscillator Based on a Polarization Modulator and a Chirped FBG. IEEE Photonics Technol. Lett. 2012, 24, 1487–1489. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J. A Nonuniformly Spaced Microwave Photonic Filter Using a Spatially Discrete Chirped FBG. IEEE Photonics Technol. Lett. 2013, 25, 1889–1892. [Google Scholar] [CrossRef]
- Burla, M.; Cortés, L.R.; Li, M.; Wang, X.; Chrostowski, L.; Azaña, J. Integrated waveguide Bragg gratings for microwave photonics signal processing. Opt. Express 2013, 21, 25120–25147. [Google Scholar] [CrossRef] [PubMed]
- Kaushal, S.; Cheng, R.; Ma, M.; Mistry, A.; Burla, M.; Chrostowski, L.; Azaña, J. Optical signal processing based on silicon photonics waveguide Bragg gratings. Front. Optoelectron. 2018, 11, 163–188. [Google Scholar] [CrossRef]
- Cheng, R.; Chrostowski, L. Spectral design of silicon integrated Bragg gratings: A tutorial. J. Light. Technol. 2020, 39, 712–729. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Guan, H.; Yu, Z.; Wei, Q.; Fan, Z.; Han, W.; Li, Z. C-band four-channel CWDM (de-) multiplexers on a thin film lithium niobate–silicon rich nitride hybrid platform. Opt. Lett. 2021, 46, 4726–4729. [Google Scholar] [CrossRef] [PubMed]
- Strain, M.J.; Sorel, M. Design and fabrication of integrated chirped Bragg gratings for on-chip dispersion control. IEEE J. Quantum Electron. 2010, 46, 774–782. [Google Scholar] [CrossRef]
- Giuntoni, I.; Stolarek, D.; Bruns, J.; Zimmermann, L.; Tillack, B.; Petermann, K. Integrated dispersion compensator based on apodized SOI Bragg gratings. IEEE Photonics Technol. Lett. 2013, 25, 1313–1316. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Y.; Chen, L.R. Integrated discretely tunable optical delay line based on step-chirped subwavelength grating waveguide Bragg gratings. J. Light. Technol. 2020, 38, 5551–5560. [Google Scholar] [CrossRef]
- Chen, L.R. Photonic generation of chirped microwave and millimeter wave pulses based on optical spectral shaping and wavelength-to-time mapping in silicon photonics. Opt. Commun. 2016, 373, 70–81. [Google Scholar] [CrossRef]
- Yu, M.; Reimer, C.; Barton, D.; Kharel, P.; Cheng, R.; He, L.; Shao, L.; Zhu, D.; Hu, Y.; Grant, H.R.; et al. Femtosecond pulse generation via an integrated electro-optic time lens. arXiv 2021. [Google Scholar] [CrossRef]
- Du, Z.; Xiang, C.; Fu, T.; Chen, M.; Yang, S.; Bowers, J.E.; Chen, H. Silicon nitride chirped spiral Bragg grating with large group delay. APL Photonics 2020, 5, 101302. [Google Scholar] [CrossRef]
- Chen, Z.; Flueckiger, J.; Wang, X.; Zhang, F.; Yun, H.; Lu, Z.; Caverley, M.; Wang, Y.; Jaeger, N.A.; Chrostowski, L. Spiral Bragg grating waveguides for TM mode silicon photonics. Opt. Express 2015, 23, 25295–25307. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Wang, D.; Deng, C.; Lu, M.; Huang, L.; Hu, G.; Yun, B.; Zhang, R.; Li, M.; Dong, J.; et al. Large Group Delay in Silicon-on-Insulator Chirped Spiral Bragg Grating Waveguide. IEEE Photonics J. 2021, 13, 5500205. [Google Scholar] [CrossRef]
- Ma, M.; Chen, Z.; Yun, H.; Wang, Y.; Wang, X.; Jaeger, N.A.; Chrostowski, L. Apodized spiral Bragg grating waveguides in silicon-on-insulator. IEEE Photonics Technol. Lett. 2017, 30, 111–114. [Google Scholar] [CrossRef]
- Giuntoni, I.; Stolarek, D.; Kroushkov, D.I.; Bruns, J.; Zimmermann, L.; Tillack, B.; Petermann, K. Continuously tunable delay line based on SOI tapered Bragg gratings. Opt. Express 2012, 20, 11241–11246. [Google Scholar] [CrossRef]
- Giuntoni, I.; Stolarek, D.; Gajda, A.; Winzer, G.; Bruns, J.; Tillack, B.; Petermann, K.; Zimmermann, L. Integrated drop-filter for dispersion compensation based on SOI rib waveguides. In Proceedings of the Optical Fiber Communication Conference 2010, San Diego, CA, USA, 21–25 March 2010; p. OThJ5. [Google Scholar] [CrossRef]
- Shi, W.; Wang, X.; Lin, C.; Yun, H.; Liu, Y.; Baehr-Jones, T.; Hochberg, M.; Jaeger, N.A.; Chrostowski, L. Silicon photonic grating-assisted, contra-directional couplers. Opt. Express 2013, 21, 3633–3650. [Google Scholar] [CrossRef]
- Simard, A.D.; LaRochelle, S. Complex apodized Bragg grating filters without circulators in silicon-on-insulator. Opt. Express 2015, 23, 16662–16675. [Google Scholar] [CrossRef]
- Qiu, H.; Jiang, J.; Yu, P.; Dai, T.; Yang, J.; Yu, H.; Jiang, X. Silicon band-rejection and band-pass filter based on asymmetric Bragg sidewall gratings in a multimode waveguide. Opt. Lett. 2016, 41, 2450–2453. [Google Scholar] [CrossRef]
- Xiao, R.; Shi, Y.; Li, J.; Dai, P.; Ma, C.; Chen, M.; Zhao, Y.; Chen, X. Integrated Bragg grating filter with reflection light dropped via two mode conversions. J. Light. Technol. 2019, 37, 1946–1953. [Google Scholar] [CrossRef]
- Zhu, D.; Shao, L.; Yu, M.; Cheng, R.; Desiatov, B.; Xin, C.; Hu, Y.; Holzgrafe, J.; Ghosh, S.; Shams-Ansari, A.; et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photonics 2021, 13, 242–352. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Winzer, P.; Lončar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Liu, Y.; Tu, D.; Yu, Z.; Wei, Q.; Li, Z. Linearity-Enhanced Dual-Parallel Mach–Zehnder Modulators Based on a Thin-Film Lithium Niobate Platform. Photonics 2022, 9, 197. [Google Scholar] [CrossRef]
- Escalé, M.R.; Pohl, D.; Sergeyev, A.; Grange, R. Extreme electro-optic tuning of Bragg mirrors integrated in lithium niobate nanowaveguides. Opt. Lett. 2018, 43, 1515–1518. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).