A Hybrid Genetic/Powell Algorithm for Wind Measurement in Doppler Lidar
Abstract
1. Introduction
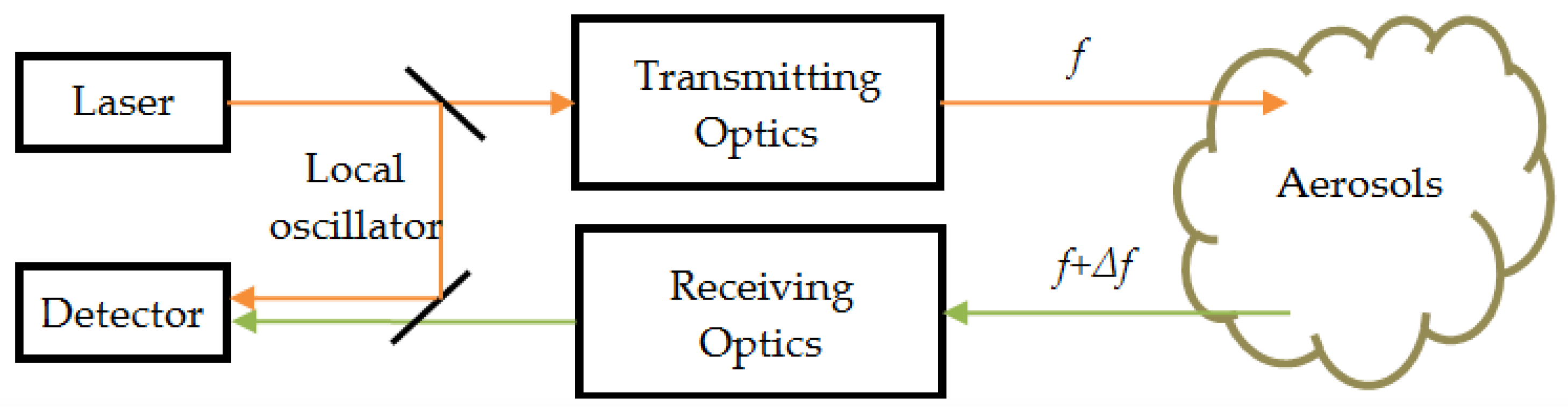
2. The CDWL System
3. HGAP
4. Test and Discussion
4.1. Test the Benchmark Functions
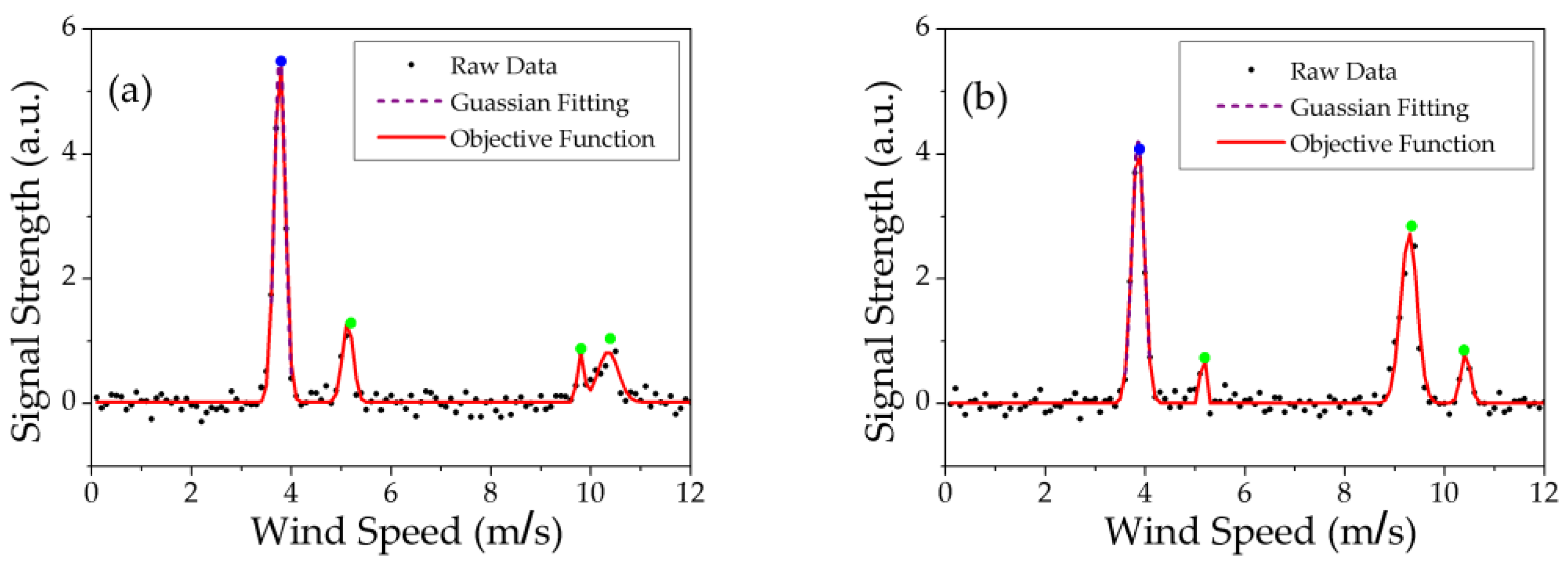
4.2. Test the Raw Data from the CDWL
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kelley, C.; Herges, T.; Martinez, L.; Mikkelsen, T. Wind turbine aerodynamic measurements using a scanning lidar. J. Phys. Conf. Ser. 2018, 1037, 052014. [Google Scholar] [CrossRef]
- Smalikho, I.; Banakh, V.; Holzäpfel, F.; Rahm, S. Method of radial velocities for the estimation of aircraft wake vortex parameters from data measured by coherent Doppler lidar. Opt. Express 2015, 23, 1194–1207. [Google Scholar] [CrossRef] [PubMed]
- Käsler, Y.; Rahm, S.; Simmet, R.; Kuhn, M. Wake Measurements of a Multi-MW Wind Turbine with Coherent Long-Range Pulsed Doppler Wind Lidar. J. Atmos. Ocean. Technol. 2010, 27, 1529. [Google Scholar] [CrossRef]
- Frehlich, R.; Hannon, S.; Henderson, S. Coherent Doppler lidar measurements of winds in the weak signal regime. Appl. Opt. 1997, 36, 3491. [Google Scholar] [CrossRef]
- Huang, J.; Kwok, M.; Chan, P. Wind Shear Prediction from Light Detection and Ranging Data Using Machine Learning Methods. Atmosphere 2021, 12, 644. [Google Scholar] [CrossRef]
- Newman, J.; Clifton, A. An error reduction algorithm to improve lidar turbulence estimates for wind energy. Wind Energy Sci. 2017, 2, 77–95. [Google Scholar] [CrossRef]
- Eberhard, W. Accuracy of maximum likelihood and least-squares estimates in the lidar slope method with noisy data. Appl. Opt. 2017, 56, 2667–2685. [Google Scholar] [CrossRef]
- Agnes, D.; Guillaume, C.; Laurent, L.; Matthieu, V.; Anne, D.; Claudine, B. Long-range wind monitoring in real time with optimized coherent lidar. Opt. Eng. 2016, 56, 031217. [Google Scholar]
- Jiang, S.; Feng, J.; Han, F.; Li, Z.; Xiong, D.; Niu, D. Generalized Rayleigh criterion for signal resolution on coherent Doppler wind measurement. Opt. Eng. 2021, 60, 044106. [Google Scholar] [CrossRef]
- Lucy, R. Progress towards an HF Radar Wind Speed Measurement Method Using Machine Learning. Remote Sens. 2022, 14, 2098. [Google Scholar]
- Williams, C.; Mazoyer, P.; Combrexelle, S. Wind field reconstruction from lidar measurements at high-frequency using machine learning. J. Phys. Conf. Ser. 2018, 1102, 012003. [Google Scholar] [CrossRef]
- Sung-Ho, H. Short-term wind speed prediction using Extended Kalman filter and machine learning. Energy Rep. 2021, 7, 1046–4054. [Google Scholar]
- Zeng, X.; Guo, W.; Yang, K.; Xia, M. Noise reduction and retrieval by modified lidar inversion method combines joint retrieval method and machine learning. Appl. Phys. B 2018, 124, 238. [Google Scholar] [CrossRef]
- Mohandes, M.; Rehman, S. Wind Speed Extrapolation Using Machine Learning Methods and LiDAR Measurements. IEEE Access 2018, 6, 77634–77642. [Google Scholar] [CrossRef]
- Newman, J.; Clifton, A. Improving Lidar-Derived Turbulence Estimates for Wind Energy. Wind Energy. Sci. 2016, 22, 072010. [Google Scholar]
- Shimada, S.; Kogaki, T.; Takeyama, Y.; Ohsawa, T.; Nakamura, S.; Kawaguchi, K. Accuray of offshore wind measurement using a scanning LiDAR. In Proceedings of the Grand Renewable Energy 2018 Proceedings, Yokohama, Japan, 17–22 June 2018; p. O-We-3-6. [Google Scholar]
- Jiang, S.; Sun, D.; Han, F.; Han, Y.; Zheng, J. Performance of continous-wave coherent Doppler Lidar for wind measurement. Curr. Opt. Photonics 2019, 3, 466–472. [Google Scholar]
- Holland, J. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992; pp. 121–140. [Google Scholar]
- Powell, M. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Lin, M.; Chen, W.; Li, B.; Zheng, Y.; Chen, Z. Fast Field Calibration of MIMU Based on the Powell Algorithm. Sensors 2014, 14, 16062–16081. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Assimi, H.; Jamali, A. A hybrid algorithm coupling genetic programming and Nelder–Mead for topology and size optimization of trusses with static and dynamic constraints. Expert Syst. Appl. 2018, 95, 127–141. [Google Scholar] [CrossRef]
- Paul, P.; Moganarangan, N.; Kumar, S.; Raju, R.; Vengattaraman, T.; Dhavachelvan, P. Performance analyses over population seeding techniques of the permutation-coded genetic algorithm: An empirical study based on traveling salesman problems. Appl. Soft Comput. 2015, 32, 383–402. [Google Scholar] [CrossRef]
- Okamoto, M.; Nonaka, T.; Ochiai, S.; Tominaga, D. Nonlinear numerical optimization with use of a hybrid genetic algorithm incorporating the modified Powell method. Appl. Math. Comput. 1998, 91, 63–72. [Google Scholar] [CrossRef]
- Virtual Library of Simulation Experiments: Test Functions and Datasets. Available online: http://www.sfu.ca/~ssurjano/optimization (accessed on 12 January 2022).



| Function ID | Function Name | Dimension | Globe Minimum |
|---|---|---|---|
| f1 | Ackley | 10 | 0 |
| f2 | Beale | 2 | 0 |
| f3 | Bent Cigar | 10 | 0 |
| f4 | Booth | 2 | 0 |
| f5 | Bukin | 2 | 0 |
| f6 | Cross-in-Tray | 2 | −2.06 |
| f7 | Discus | 10 | 0 |
| f8 | Easom | 2 | −1 |
| f9 | Goldstein-Price | 2 | −3 |
| f10 | Griewank’s | 10 | 0 |
| f11 | High Conditioned Elliptic | 10 | 0 |
| f12 | Himmelblau’s | 2 | 0 |
| f13 | Hölder table | 2 | −19.21 |
| f14 | Levy | 10 | 0 |
| f15 | Matyas | 2 | 0 |
| f16 | McCormick | 2 | −1.91 |
| f17 | Michalewicz | 5 | −4.69 |
| f18 | Rastrigin’s | 10 | 0 |
| f19 | Rosenbrock’s | 10 | 0 |
| f20 | Schaffer’s F7 | 10 | 0 |
| f21 | Schaffer N.2 | 2 | 0 |
| f22 | Schaffer N.4 | 2 | 0.29 |
| f23 | Sphere | 10 | 0 |
| f24 | Styblinski-Tang | 5 | −195.83 |
| f25 | Sum of Different Power | 10 | 0 |
| f26 | Three-hump camel | 2 | 0 |
| f27 | Zakharov | 10 | 0 |
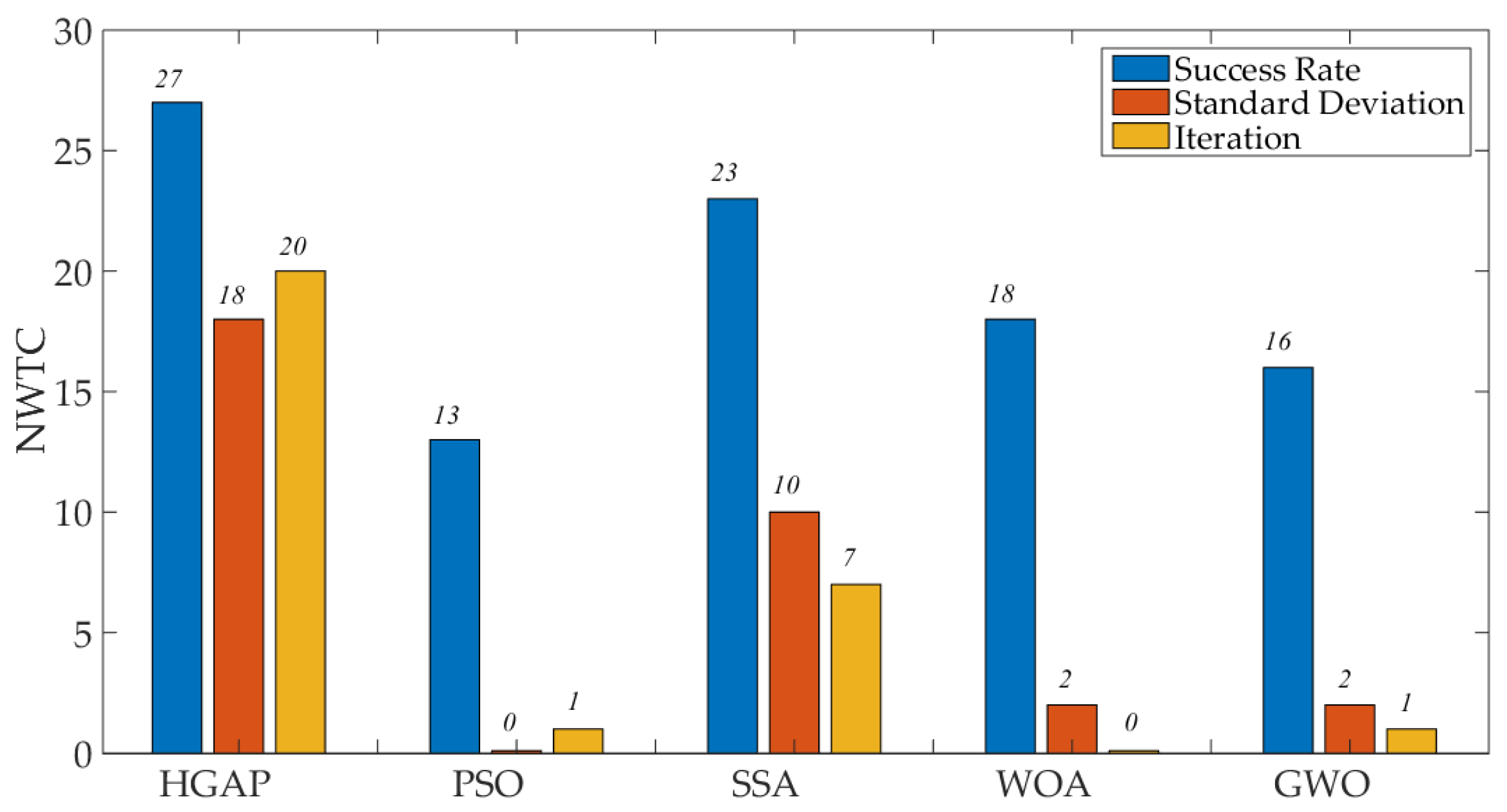
| Function Id | Criteria | HGAP | PSO | SSA | WOA | GWO |
|---|---|---|---|---|---|---|
| f1 | Success rate | 100% | 12% | 100% | 100% | 100% |
| STD | 4.97 × 10−13 | 9.49 | 0 | 6.90 × 10−5 | 2.69 × 10−9 | |
| Iteration | 1.9 | 96.83 | 5.12 | 71 | 26.72 | |
| f2 | Success rate | 100% | 100% | 100% | 100% | 98% |
| STD | 3.92 × 10−32 | 8.92 × 10−11 | 1.09 × 10−10 | 5.19 × 10−7 | 0.11 | |
| Iteration | 1.00 | 16.62 | 9.02 | 14.84 | 10.24 | |
| f3 | Success rate | 100% | 0% | 100% | 100% | 100% |
| STD | 6.21 × 10−22 | 39.04 | 5.19 × 10−40 | 5.56 × 10−6 | 6.35 × 10−13 | |
| Iteration | 1.00 | - | 7.24 | 75.6 | 30.28 | |
| f4 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 0 | 8.20 × 10−11 | 1.19 × 10−5 | 6.06 × 10−6 | 1.45 × 10−6 | |
| Iteration | 1.00 | 25.02 | 39.86 | 31.32 | 17.78 | |
| f5 | Success rate | 100% | 0% | 0% | 0% | 0% |
| STD | 2.54 × 10−6 | 0.07 | 2.96 × 10−16 | 0.13 | 0.15 | |
| Iteration | 72.86 | - | - | - | - | |
| f6 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 0 | 1.05 × 10−10 | 9.27 × 10−12 | 7.16 × 10−8 | 3.41 × 10−8 | |
| Iteration | 1.00 | 9.54 | 1.26 | 5.58 | 3.58 | |
| f7 | Success rate | 100% | 0% | 100% | 100% | 100% |
| STD | 2.95 × 10−26 | 6.12 | 1.41 × 10−56 | 1.10 × 10−9 | 4.65 × 10−18 | |
| Iteration | 1.00 | - | 7.22 | 54.74 | 17.72 | |
| f8 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 0 | 1.53 × 10−9 | 2.48 × 10−8 | 5.87 × 10−6 | 1.80 × 10−6 | |
| Iteration | 1.00 | 38.14 | 11.94 | 40.82 | 29.48 | |
| f9 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 3.14 × 10−16 | 1.86 × 10−10 | 4.98 × 10−8 | 2.33 × 10−5 | 1.02 × 10−4 | |
| Iteration | 1.00 | 27.18 | 30.32 | 35.04 | 21.34 | |
| f10 | Success rate | 100% | 0% | 100% | 38% | 4% |
| STD | 0 | 0.07 | 0 | 0.02 | 0.04 | |
| Iteration | 82.12 | - | 1.38 | 68.63 | 32.50 | |
| f11 | Success rate | 100% | 0% | 100% | 100% | 100% |
| STD | 4.96 × 10−20 | 5.17 × 10−4 | 1.69 × 10−38 | 2.36 × 10−8 | 1.72 × 10−15 | |
| Iteration | 1.00 | - | 6.02 | 65.90 | 24.82 | |
| f12 | Success rate | 100% | 100% | 100% | 100% | 98% |
| STD | 0 | 3.60 × 10−10 | 4.51 × 10−5 | 8.97 × 10−5 | 4.85 × 10−4 | |
| Iteration | 1.00 | 27.76 | 40.60 | 62.76 | 74.22 | |
| f13 | Success rate | 100% | 100% | 100% | 100% | 98% |
| STD | 3.55 × 10−15 | 3.55 × 10−10 | 5.25 × 10−6 | 2.30 × 10−4 | 5.00 × 10−3 | |
| Iteration | 1.00 | 25.22 | 36.00 | 73.78 | 86.43 | |
| f14 | Success rate | 100% | 100% | 100% | 4% | 44% |
| STD | 0 | 0.44 | 1.44 × 10−6 | 0.10 | 0.07 | |
| Iteration | 2.64 | 52.94 | 2.50 | 98.50 | 94.59 | |
| f15 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 2.31 × 10−32 | 7.79 × 10−12 | 1.03 × 10−45 | 6.70 × 10−46 | 1.47 × 10−43 | |
| Iteration | 1.00 | 11.72 | 1.00 | 8.40 | 3.16 | |
| f16 | Success rate | 100% | 78% | 90% | 100% | 100% |
| STD | 2.22 × 10−16 | 0.02 | 0.02 | 3.02 × 10−7 | 1.79 × 10−7 | |
| Iteration | 1.00 | 16.74 | 8.66 | 15.96 | 6.12 | |
| f17 | Success rate | 100% | 18% | 0% | 0% | 2% |
| STD | 3.97 × 10−16 | 0.37 | 0.46 | 0.46 | 0.26 | |
| Iteration | 81.68 | 61.11 | - | - | 100 | |
| f18 | Success rate | 100% | 0% | 100% | 74% | 22% |
| STD | 0 | 8.71 | 0 | 1.50 | 3.06 | |
| Iteration | 1.90 | - | 4.72 | 7.15 | 3.50 | |
| f19 | Success rate | 100% | 0% | 100% | 0% | 0% |
| STD | 8.23 × 10−24 | 390.47 | 2.26 × 10−7 | 97.87 | 6.15 | |
| Iteration | 1.00 | - | 6.00 | - | - | |
| f20 | Success rate | 100% | 64% | 100% | 48% | 26% |
| STD | 5.46 × 10−32 | 4.39 × 10−3 | 6.67 × 10−16 | 0.01 | 0.06 | |
| Iteration | 1.00 | 33.03 | 1.02 | 88.17 | 89.31 | |
| f21 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 0 | 0 | 0 | 0 | ||
| Iteration | 17.28 | 18.32 | 1.00 | 17.68 | 5.26 | |
| f22 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 1.76 × 10−7 | 1.17 × 10−8 | 1.20 × 10−4 | 1.33 × 10−6 | 1.39 × 10−6 | |
| Iteration | 75.50 | 20.92 | 26.02 | 19.46 | 5.94 | |
| f23 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 1.78 × 10−26 | 8.42 × 10−7 | 6.03 × 10−42 | 1.40 × 10−8 | 9.80 × 10−17 | |
| Iteration | 1.00 | 71.06 | 1.80 | 60.06 | 20.94 | |
| f24 | Success rate | 100% | 34% | 98% | 6% | 32% |
| STD | 0 | 11.94 | 8.56 × 10−4 | 6.31 | 4.24 | |
| Iteration | 50.42 | 47.11 | 25.67 | 87.65 | 95.60 | |
| f25 | Success rate | 100% | 28% | 100% | 100% | 100% |
| STD | 1.15 × 10−32 | 1.40 × 10−9 | 1.13 × 10−38 | 1.02 × 10−13 | 2.94 × 10−30 | |
| Iteration | 1.00 | 83.50 | 1.40 | 56.98 | 18.14 | |
| f26 | Success rate | 100% | 100% | 100% | 100% | 100% |
| STD | 2.25 × 10−31 | 2.76 × 10−12 | 4.44 × 10−39 | 6.08 × 10−44 | 2.91 × 10−70 | |
| Iteration | 1.00 | 15.08 | 1.54 | 9.26 | 3.20 | |
| f27 | Success rate | 100% | 0% | 100% | 100% | 100% |
| STD | 1.15 × 10−25 | 9.28 × 10−9 | 2.19 × 10−52 | 6.19 × 10−9 | 1.17 × 10−17 | |
| Iteration | 1.00 | 50.16 | 2.76 | 54.26 | 16.08 |
| Item | Parameters | Value |
|---|---|---|
| Laser | Wavelength | 1547 nm |
| Line width | 4 kHz @ 1547 nm | |
| Pulse energy | 150 uJ | |
| Pulse width | 200 ns | |
| Pulse repetition frequency | 10 kHz | |
| Telescope | Effective aperture | 150 mm |
| Balanced detector | Responsiveness | 0.95 A/W |
| 3-dB bandwidth | 250 MHz | |
| A/D converter | Sample rate | 500 MHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Wang, Z.; Ning, A.; Liu, S.; Wang, D.; Feng, J.; Yu, L. A Hybrid Genetic/Powell Algorithm for Wind Measurement in Doppler Lidar. Photonics 2022, 9, 802. https://doi.org/10.3390/photonics9110802
Jiang S, Wang Z, Ning A, Liu S, Wang D, Feng J, Yu L. A Hybrid Genetic/Powell Algorithm for Wind Measurement in Doppler Lidar. Photonics. 2022; 9(11):802. https://doi.org/10.3390/photonics9110802
Chicago/Turabian StyleJiang, Shan, Zhiping Wang, An Ning, Shaoshuai Liu, Di Wang, Junsheng Feng, and Longbao Yu. 2022. "A Hybrid Genetic/Powell Algorithm for Wind Measurement in Doppler Lidar" Photonics 9, no. 11: 802. https://doi.org/10.3390/photonics9110802
APA StyleJiang, S., Wang, Z., Ning, A., Liu, S., Wang, D., Feng, J., & Yu, L. (2022). A Hybrid Genetic/Powell Algorithm for Wind Measurement in Doppler Lidar. Photonics, 9(11), 802. https://doi.org/10.3390/photonics9110802




