Synchronization of Optomechanical Oscillators in Coupled 1D Optomechanical Crystal Nanobeam Cavities
Abstract
1. Introduction
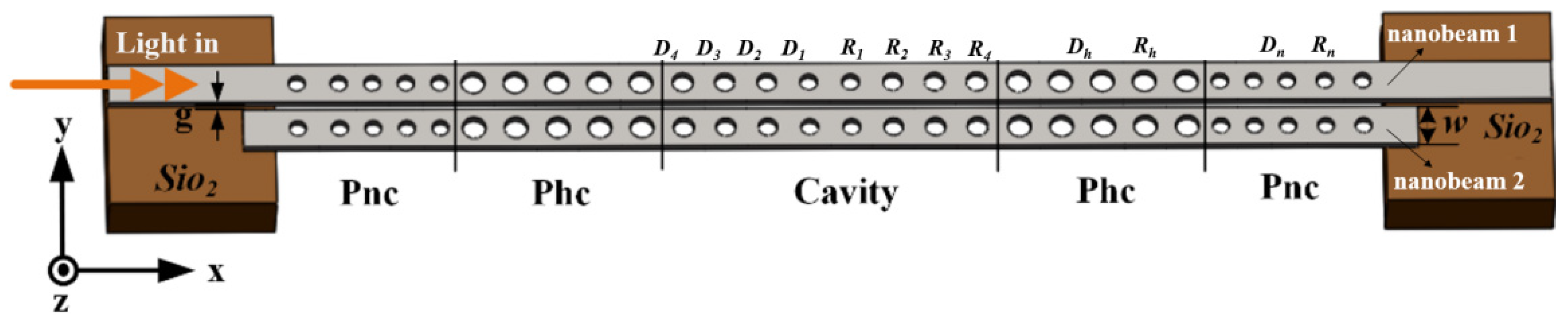
2. Theoretical Model
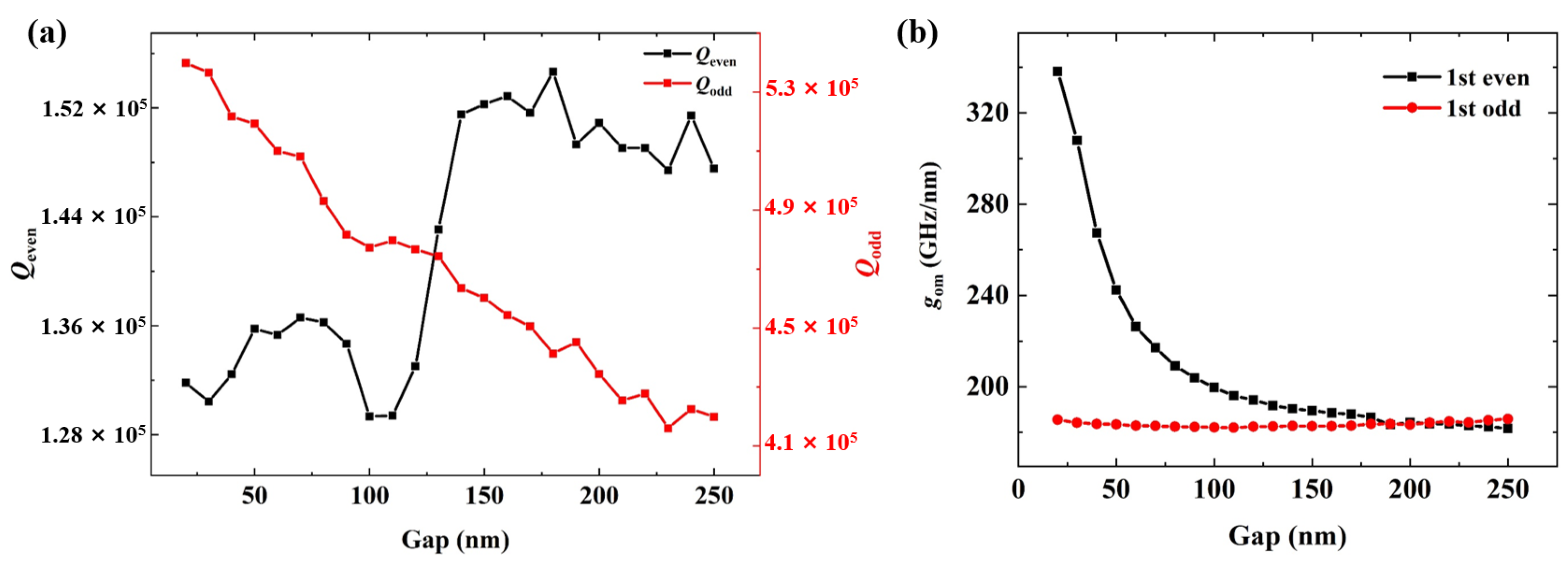
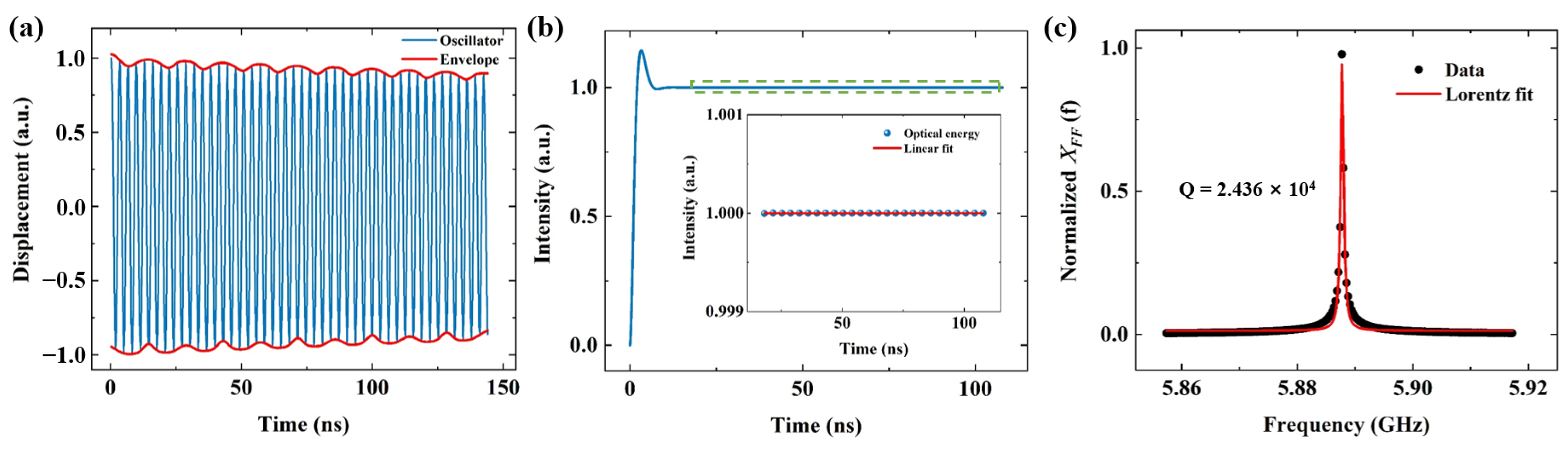
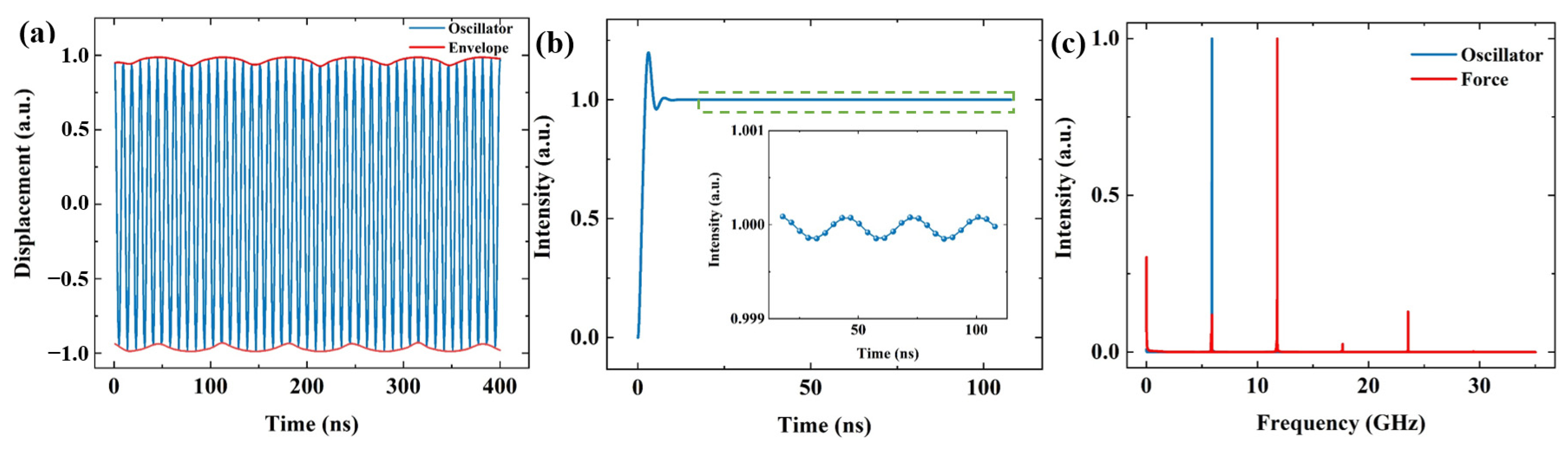
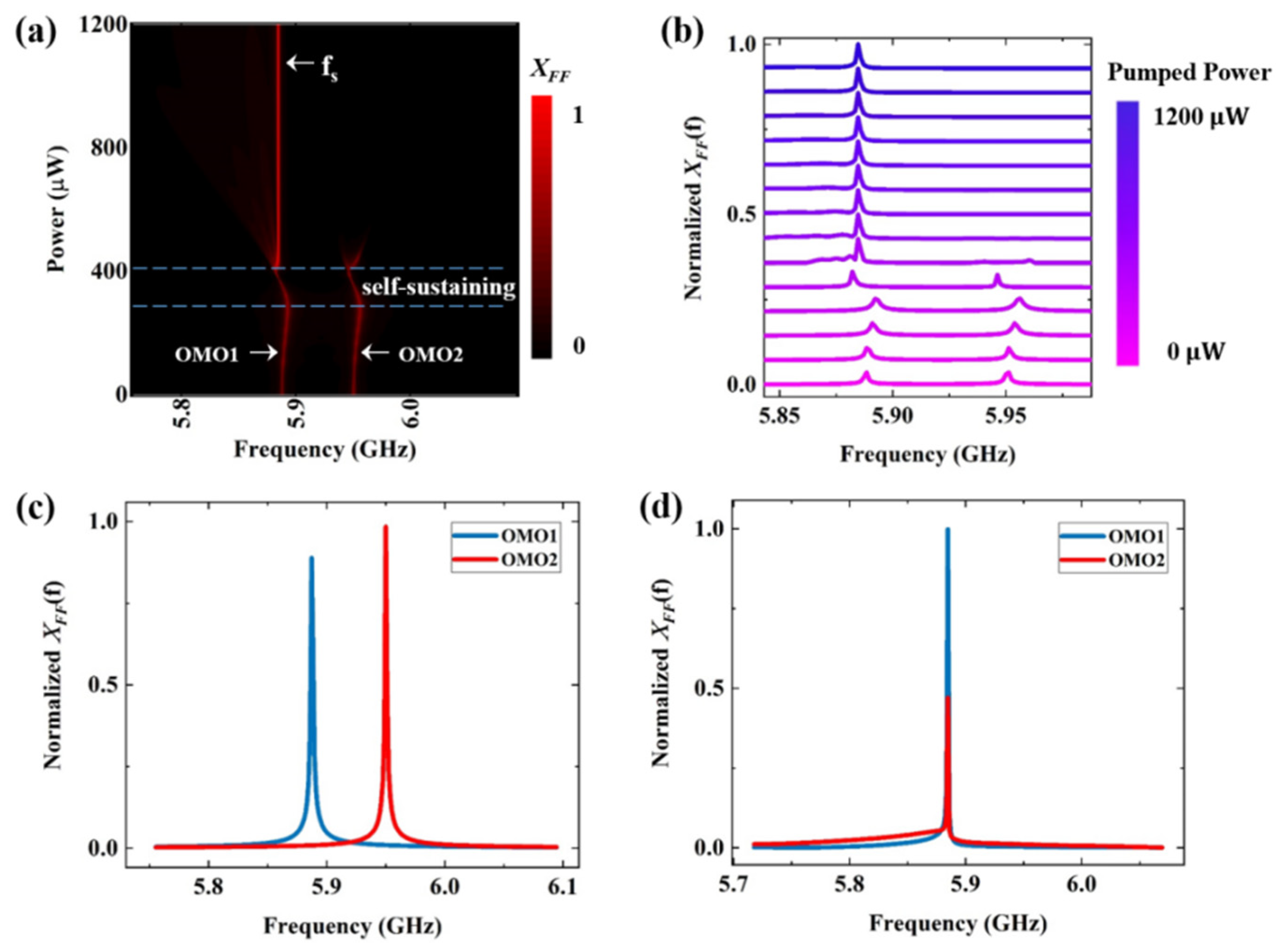
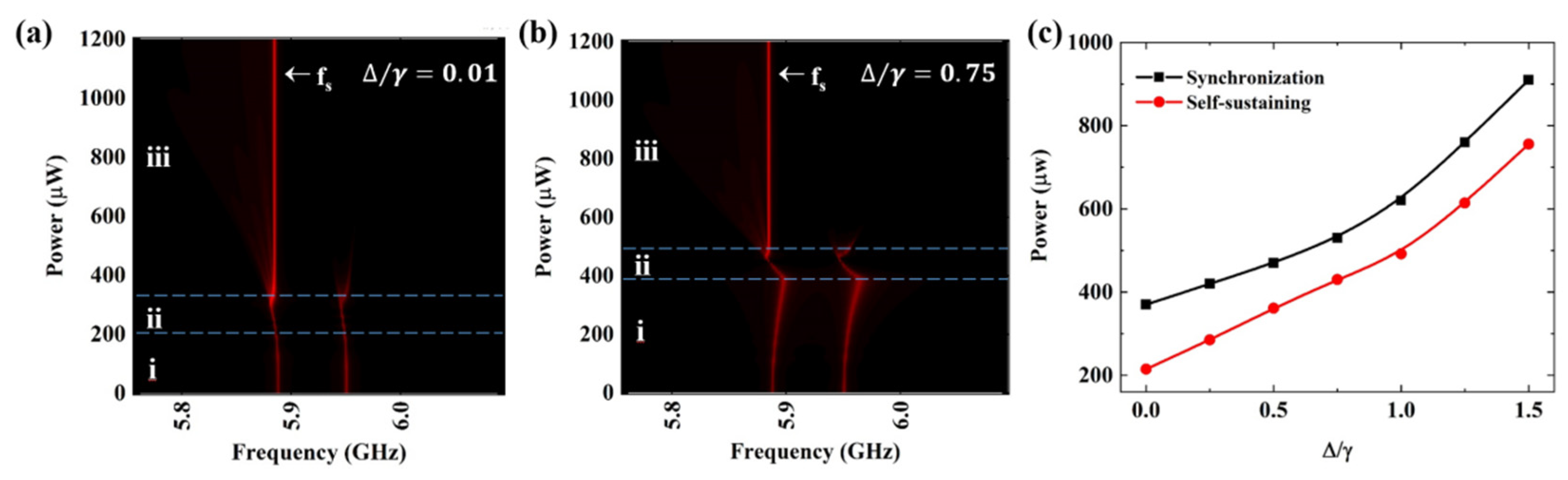
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sivrikaya, F.; Yener, B. Time synchronization in sensor networks: A survey. IEEE Network 2004, 18, 45–50. [Google Scholar] [CrossRef]
- Shanmugam, L.; Mani, P.; Rajan, R.; Joo, Y.H. Adaptive synchronization of reaction–diffusion neural networks and its application to secure communication. IEEE Trans. Cybernetics 2018, 50, 911–922. [Google Scholar] [CrossRef] [PubMed]
- Mahboob, I.; Yamaguchi, H. Bit storage and bit flip operations in an electromechanical oscillator. Nat. Nanotechnol. 2008, 3, 275–279. [Google Scholar] [CrossRef] [PubMed]
- Bagheri, M.; Poot, M.; Li, M.; Pernice, W.P.H.; Tang, H.X. Dynamic manipulation of nanomechanical resonators in the high-amplitude regime and non-volatile mechanical memory operation. Nat. Nanotechnol. 2011, 6, 726–732. [Google Scholar] [CrossRef]
- Shim, S.B.; Imboden, M.; Mohanty, P. Synchronized oscillation in coupled nanomechanical oscillators. Science 2007, 316, 95–99. [Google Scholar] [CrossRef]
- Matheny, M.H.; Grau, M.; Villanueva, L.G.; Karabalin, R.B.; Cross, M.C.; Roukes, M.L. Phase Synchronization of Two Anharmonic Nanomechanical Oscillators. Phys. Rev. Lett. 2014, 112, 014101. [Google Scholar] [CrossRef]
- Agrawal, D.K.; Woodhouse, J.; Seshia, A.A. Observation of locked phase dynamics and enhanced frequency stability in synchronized micromechanical oscillators. Phys. Rev. Lett. 2013, 111, 084101. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity opto-mechanics. Opt. Express 2007, 15, 17172–17205. [Google Scholar] [CrossRef]
- Heinrich, G.; Ludwig, M.; Qian, J.; Kubala, B.; Marquardt, F. Collective dynamics in optomechanical arrays. Phys. Rev. Lett. 2011, 107, 043603. [Google Scholar] [CrossRef]
- Shlomi, K.; Yuvaraj, D.; Baskin, I.; Suchoi, O.; Winik, R.; Buks, E. Synchronization in an optomechanical cavity. Phys. Rev. E 2015, 91, 032910. [Google Scholar] [CrossRef] [PubMed]
- Holmes, C.A.; Meaney, C.P.; Milburn, G.J. Synchronization of many nanomechanical resonators coupled via a common cavity field. Phys. Rev. E 2012, 85, 066203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wiederhecker, G.S.; Manipatruni, S.; Barnard, A.; McEuen, P.; Lipson, M. Synchronization of micromechanical oscillators using light. Phys. Rev. Lett. 2012, 109, 233906. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Shah, S.; Cardenas, J.; Lipson, M. Synchronization and phase noise reduction in micromechanical oscillator arrays coupled through light. Phys. Rev. Lett. 2015, 115, 163902. [Google Scholar] [CrossRef]
- Bagheri, M.; Poot, M.; Fan, L.; Marquardt, F.; Tang, H.X. Photonic cavity synchronization of nanomechanical oscillators. Phys. Rev. Lett. 2013, 111, 213902. [Google Scholar] [CrossRef]
- Shah, S.Y.; Zhang, M.; Rand, R.; Lipson, M. Master-slave locking of optomechanical oscillators over a long distance. Phys. Rev. Lett. 2015, 114, 113602. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Labousse, M.; Baker, C.; Goetschy, A.; Hease, W.; Gomez, C.; Lemaître, A.; Leo, G.; Ciuti, C.; Favero, I. Light-mediated cascaded locking of multiple nano-optomechanical oscillators. Phys. Rev. Lett. 2017, 118, 063605. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, J.; Flores, J.G.F.; Yu, M.; Kwong, D.L.; Wen, G.; Wong, C.W. Synchronization in air-slot photonic crystal optomechanical oscillators. Appl. Phys. Lett. 2017, 110, 111107. [Google Scholar] [CrossRef]
- Li, T.; Bao, T.Y.; Zhang, Y.L.; Zou, C.L.; Zou, X.B.; Guo, G.C. Long-distance synchronization of unidirectionally cascaded optomechanical systems. Opt. Express 2016, 24, 12336–12348. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Z.H.; Wan, S.; Zhang, Y.L.; Shen, Z.; Li, M.; Zou, C.L.; Guo, G.C.; Dong, C.H. All-optical synchronization of remote optomechanical systems. Phys. Rev. Lett. 2022, 129, 063605. [Google Scholar] [CrossRef]
- Chan, J.; Eichenfield, M.; Camacho, R.; Painter, O. Optical and mechanical design of a “zipper” photonic crystal optomechanical cavity. Opt. Express 2009, 17, 3802–3817. [Google Scholar] [CrossRef] [PubMed]
- Quan, Q.; Loncar, M. Deterministic design of wavelength scale, ultra-high Q photonic crystal nanobeam cavities. Opt. Express 2011, 19, 18529–18542. [Google Scholar] [CrossRef] [PubMed]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Cui, K.; Li, Y.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y. Strong optomechanical coupling in nanobeam cavities based on hetero optomechanical crystals. Sci. Rep. 2015, 5, 15964. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Cui, K.; Feng, X.; Huang, Y.; Huang, Z.; Liu, F.; Zhang, W. Optomechanical Crystal Nanobeam Cavity with High Optomechanical Coupling Rate. J. Opt. 2015, 17, 045001. [Google Scholar] [CrossRef]
- Wu, N.; Cui, K.Y.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y.D. Hetero-Optomechanical Crystal Zipper Cavity for Multimode Optomechanics. Photonics 2022, 9, 78. [Google Scholar] [CrossRef]
- Xu, Q.C.; Cui, K.Y.; Wu, N.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y.D. Tunable mechanical-mode coupling based on nanobeam-double optomechanical cavities. Photonics Res. 2022, 10, 1819–1827. [Google Scholar] [CrossRef]
- Colombano, M.F.; Arregui, G.; Capuj, N.E.; Pitanti, A.; Maire, J.; Griol, A.; Garrido, B.; Martinez, A.; SotomayorTorres, C.M.; Navarro-Urrios, D. Synchronization of Optomechanical Nanobeams by Mechanical Interaction. Phys. Rev. Lett. 2019, 123, 017402. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Van Thourhout, D.; Baets, R.; Van Laer, R. Controlling Phonons and Photons at the Wavelength-Scale: Silicon Photonics Meets Silicon Phononics. Optica 2019, 6, 213. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gao, F.; Yang, D.; Wang, A.; Zhou, M.; Li, S.; Gao, L.; Zhang, Z. Synchronization of Optomechanical Oscillators in Coupled 1D Optomechanical Crystal Nanobeam Cavities. Photonics 2022, 9, 743. https://doi.org/10.3390/photonics9100743
Liu Y, Gao F, Yang D, Wang A, Zhou M, Li S, Gao L, Zhang Z. Synchronization of Optomechanical Oscillators in Coupled 1D Optomechanical Crystal Nanobeam Cavities. Photonics. 2022; 9(10):743. https://doi.org/10.3390/photonics9100743
Chicago/Turabian StyleLiu, Yang, Fei Gao, Daquan Yang, Aiqiang Wang, Mengchen Zhou, Shanchuang Li, Lu Gao, and Ze Zhang. 2022. "Synchronization of Optomechanical Oscillators in Coupled 1D Optomechanical Crystal Nanobeam Cavities" Photonics 9, no. 10: 743. https://doi.org/10.3390/photonics9100743
APA StyleLiu, Y., Gao, F., Yang, D., Wang, A., Zhou, M., Li, S., Gao, L., & Zhang, Z. (2022). Synchronization of Optomechanical Oscillators in Coupled 1D Optomechanical Crystal Nanobeam Cavities. Photonics, 9(10), 743. https://doi.org/10.3390/photonics9100743






