Full Poincaré Mueller Polarimetry Using a CCD Camera
Abstract
1. Introduction
2. Full Poincaré Mueller Polarimetry
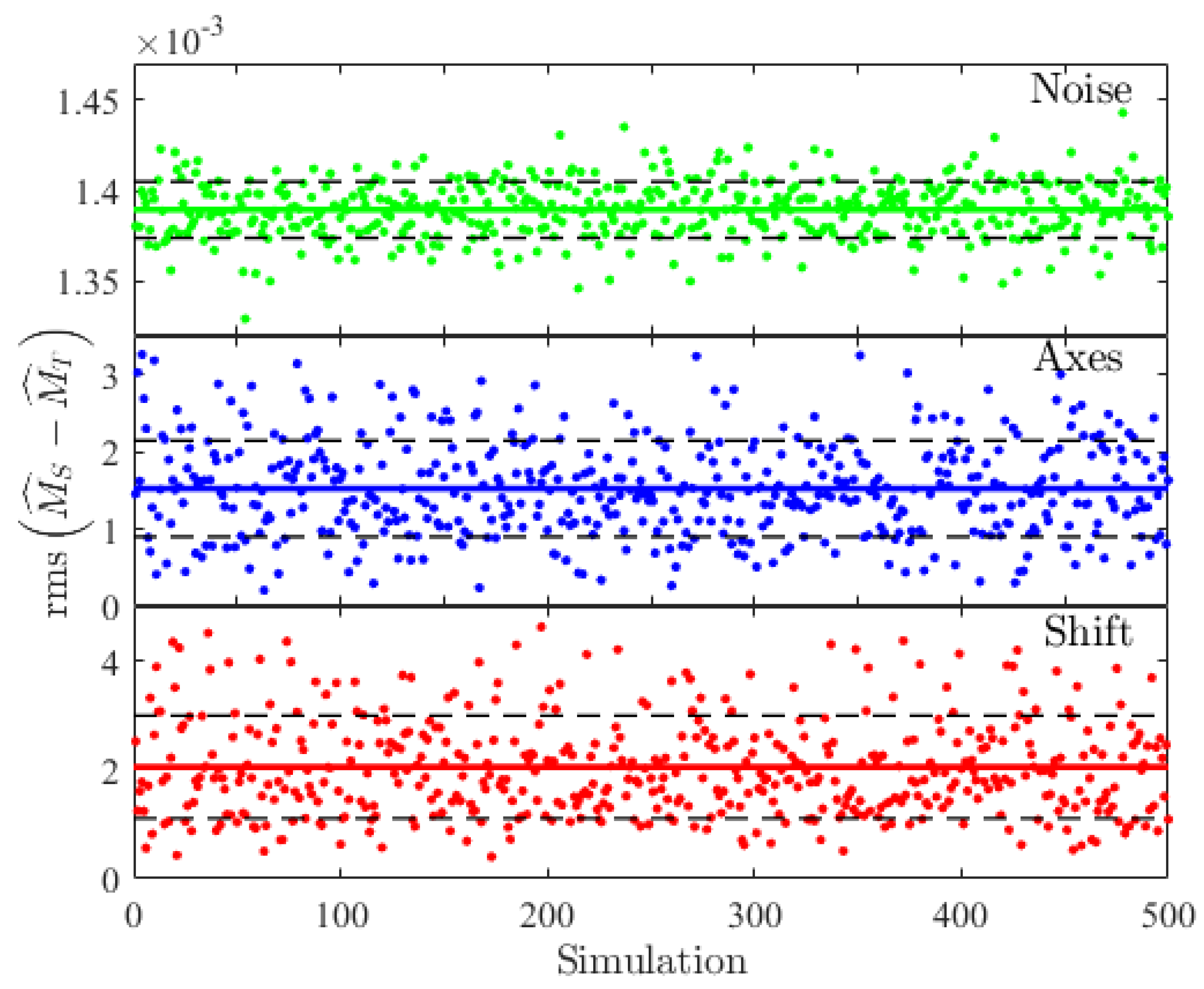
3. Errors Analysis
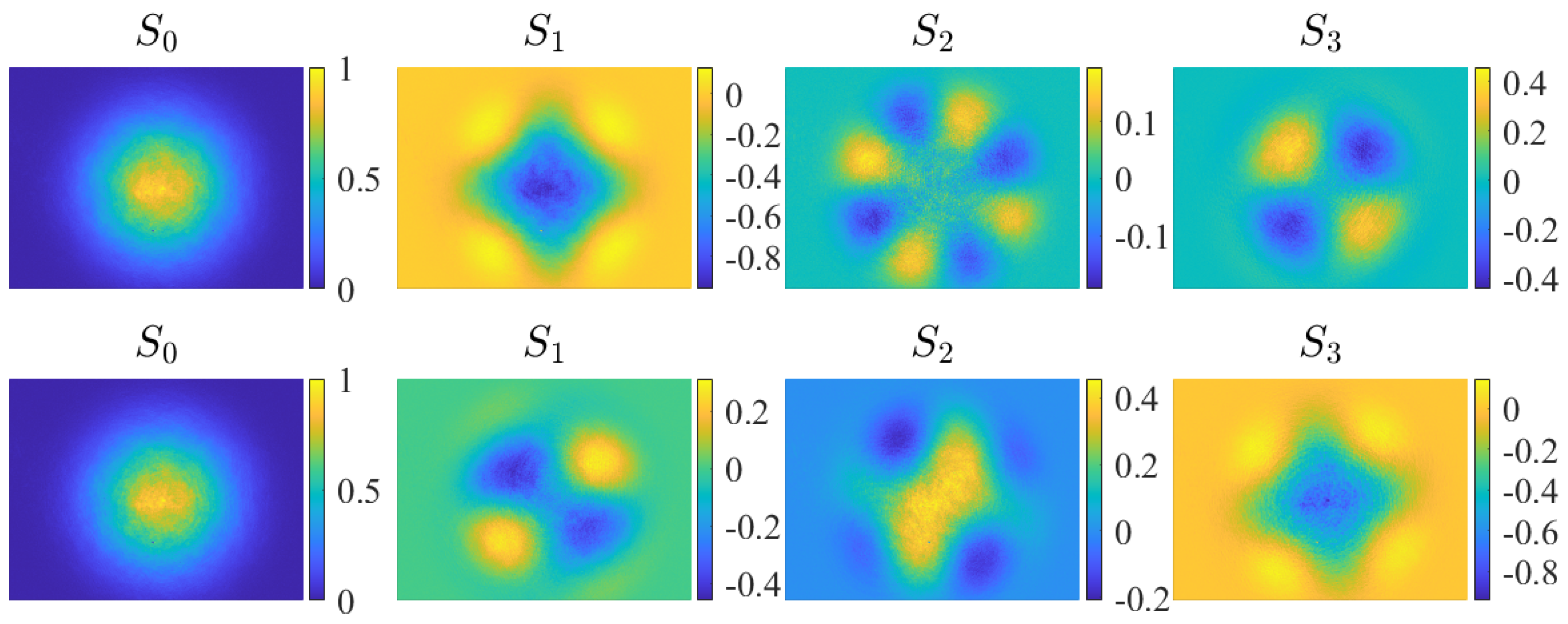
4. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGN | Additive Gaussian noise |
| CCD | Charge-coupled device |
| FPB | Full Poincaré beam |
| FPMP | Full Poincaré Mueller polarimetry |
| HWP | Half wave plate |
| LP | Linear polarizer |
| QWP | Quarter wave plate |
| PSA | Polarization state analyzer |
| PSG | Polarization state generator |
| rms | root mean square |
References
- Azzam, R.M.A. Stokes-vector and Mueller-matrix polarimetry [Invited]. J. Opt. Soc. Am. A 2016, 33, 1396–1408. [Google Scholar] [CrossRef] [PubMed]
- Chipman, R.; Lam, W.; Young, G. Polarized Light and Optical Systems; Optical Sciences and Applications of Light; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Tuchin, V.V.; Wang, L.; Zymnayakov, D.A. Optical Polarization in Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ghosh, N.; Vitkin, A.I. Tissue polarimetry: Concepts, challenges, applications, and outlook. J. Biomed. Opt. 2011, 16, 110801. [Google Scholar] [CrossRef] [PubMed]
- Alali, S.; Gribble, A.; Vitkin, I.A. Rapid wide-field Mueller matrix polarimetry imaging based on four photoelastic modulators with no moving parts. Opt. Lett. 2016, 41, 1038–1041. [Google Scholar] [CrossRef]
- Ushenko, V.; Sdobnov, A.; Syvokorovskaya, A.; Dubolazov, A.; Vanchulyak, O.; Ushenko, A.; Ushenko, Y.; Gorsky, M.; Sidor, M.; Bykov, A.; et al. 3D Mueller-Matrix Diffusive Tomography of Polycrystalline Blood Films for Cancer Diagnosis. Photonics 2018, 5, 54. [Google Scholar] [CrossRef]
- Sheng, W.; Li, W.; Qi, J.; Liu, T.; He, H.; Dong, Y.; Liu, S.; Wu, J.; Elson, D.S.; Ma, H. Quantitative Analysis of 4 × 4 Mueller Matrix Transformation Parameters for Biomedical Imaging. Photonics 2019, 6, 34. [Google Scholar] [CrossRef]
- Le, V.N.D.; Saytashev, I.; Saha, S.; Lopez, P.F.; Laughrey, M.; Ramella-Roman, J.C. Depth-resolved Mueller matrix polarimetry microscopy of the rat cornea. Biomed. Opt. Express 2020, 11, 5982–5994. [Google Scholar] [CrossRef] [PubMed]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light. Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef]
- Huynh, R.N.; Nehmetallah, G.; Raub, C.B. Mueller matrix polarimetry and polar decomposition of articular cartilage imaged in reflectance. Biomed. Opt. Express 2021, 12, 5160–5178. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Rodríguez, A.; Rodríguez, T. Spectroscopic ellipsometry determination of the refractive index of strained Si1−xGex layers in the near-infrared wavelength range (0.9–1.7 μm). Appl. Phys. Lett. 1995, 67, 3402–3404. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Serna, R.; Gonzalo, J.; Afonso, C.N.; Hole, D.E.; Naudon, A. Refractive index of Ag nanocrystals composite films in the neighborhood of the surface plasmon resonance. J. Appl. Phys. 2002, 91, 1536–1541. [Google Scholar] [CrossRef]
- Savenkov, S.N. Mueller Matrix Polarimetry in Material Science, Biomedical and Environmental Applications. In Handbook of Coherent-Domain Optical Methods: Biomedical Diagnostics, Environmental Monitoring, and Materials Science; Tuchin, V.V., Ed.; Springer: New York, NY, USA, 2013; pp. 1175–1253. [Google Scholar] [CrossRef]
- López-Morales, G.; Sánchez-López, M.d.M.; Lizana, A.; Moreno, I.; Campos, J. Mueller Matrix Polarimetric Imaging Analysis of Optical Components for the Generation of Cylindrical Vector Beams. Crystals 2020, 10, 1155. [Google Scholar] [CrossRef]
- Ray, S.K.; Ghosh, N.; Vitkin, A. Diattenuation and retardance signature of plasmonic gold nanorods in turbid media revealed by Mueller matrix polarimetry. Sci. Rep. 2021, 11, 20017. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, V.; Bisht, N.S. Combined Jones-Stokes Polarimetry and Its Decomposition into Associated Anisotropic Characteristics of Spatial Light Modulator. Photonics 2022, 9, 195. [Google Scholar] [CrossRef]
- Sierra, I.; Chialanza, M.R.; Faccio, R.; Carrizo, D.; Fornaro, L.; Pérez-Parada, A. Identification of microplastics in wastewater samples by means of polarized light optical microscopy. Environ. Sci. Pollut. Res. 2020, 27, 7409–7419. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, H.; Hayashi, M.; Shiraishi, K.; Nakura, Y.; Enomoto, T.; Miura, K.; Takahashi, H.; Igarashi, Y.; Naoe, H.; Kaneyasu, N.; et al. Development of a polarization optical particle counter capable of aerosol type classification. Atmos. Environ. 2014, 97, 486–492. [Google Scholar] [CrossRef]
- Li, D.; Chen, F.; Zeng, N.; Qiu, Z.; He, H.; He, Y.; Ma, H. Study on polarization scattering applied in aerosol recognition in the air. Opt. Express 2019, 27, A581–A595. [Google Scholar] [CrossRef]
- Qi, S.; Huang, Z.; Ma, X.; Huang, J.; Zhou, T.; Zhang, S.; Dong, Q.; Bi, J.; Shi, J. Classification of atmospheric aerosols and clouds by use of dual-polarization lidar measurements. Opt. Express 2021, 29, 23461–23476. [Google Scholar] [CrossRef] [PubMed]
- Bueno, J.M. Polarimetry using liquid-crystal variable retarders: Theory and calibration. J. Opt. A Pure Appl. Opt. 2000, 2, 216. [Google Scholar] [CrossRef]
- Martínez-Ponce, G.; Solano, C.; Pérez-Barrios, C. Hybrid complete Mueller polarimeter based on phase modulators. Opt. Lasers Eng. 2011, 49, 723–728. [Google Scholar] [CrossRef]
- Reddy, S.G.; Prabhakar, S.; Aadhi, A.; Kumar, A.; Shah, M.; Singh, R.P.; Simon, R. Measuring the Mueller matrix of an arbitrary optical element with a universal SU(2) polarization gadget. J. Opt. Soc. Am. A 2014, 31, 610–615. [Google Scholar] [CrossRef]
- Tripathi, S.; Toussaint, K.C. Rapid Mueller matrix polarimetry based on parallelized polarization state generation and detection. Opt. Express 2009, 17, 21396–21407. [Google Scholar] [CrossRef] [PubMed]
- Töppel, F.; Aiello, A.; Marquardt, C.; Giacobino, E.; Leuchs, G. Classical entanglement in polarization metrology. New J. Phys. 2014, 16, 073019. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Santarsiero, M.; Piquero, G. Spirally polarized beams for polarimetry measurements of deterministic and homogeneous samples. Opt. Lasers Eng. 2017, 91, 97–105. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Piquero, G.; Santarsiero, M. Polarimetry with azimuthally polarized light. Opt. Commun. 2018, 410, 961–965. [Google Scholar] [CrossRef]
- Suárez-Bermejo, J.C.; de Sande, J.C.G.; Santarsiero, M.; Piquero, G. Mueller matrix polarimetry using full Poincaré beams. Opt. Lasers Eng. 2019, 122, 134–141. [Google Scholar] [CrossRef]
- Beckley, A.M.; Brown, T.G.; Alonso, M.A. Full Poincaré beams. Opt. Express 2010, 18, 10777–10785. [Google Scholar] [CrossRef] [PubMed]
- Galvez, E.J.; Khadka, S.; Schubert, W.H.; Nomoto, S. Poincaré-beam patterns produced by nonseparable superpositions of Laguerre-Gauss and polarization modes of light. Appl. Opt. 2012, 51, 2925–2934. [Google Scholar] [CrossRef] [PubMed]
- Piquero, G.; Vargas-Balbuena, J. Non-uniformly polarized beams across their transverse profiles: An introductory study for undergraduate optics courses. Eur. J. Phys. 2004, 25, 793–800. [Google Scholar] [CrossRef]
- Piquero, G.; Monroy, L.; Santarsiero, M.; Alonzo, M.; de Sande, J.C.G. Synthesis of full Poincaré beams by means of uniaxial crystals. J. Opt. 2018, 20, 065602. [Google Scholar] [CrossRef]
- Suárez-Bermejo, J.C.; de Sande, J.C.G.; Santarsiero, M.; Piquero, G. Analysis of the Errors in Polarimetry with Full Poincaré Beams. In Proceedings of the 2019 PhotonIcs Electromagnetics Research Symposium-Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 2621–2627. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 6th (corrected) ed.; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Goldstein, D.H. Polarized Light, 2nd (revised and expanded) ed.; Marcel Dekker, Inc.: New York, NY, USA, 2003. [Google Scholar]
- de Sande, J.C.G.; Piquero, G.; Suárez-Bermejo, J.C.; Santarsiero, M. Beams with propagation-invariant transverse polarization pattern. arXiv 2021, arXiv:2102.00024. [Google Scholar]
- de Sande, J.C.G.; Piquero, G.; Suárez-Bermejo, J.C.; Santarsiero, M. Mueller Matrix Polarimetry with Invariant Polarization Pattern Beams. Photonics 2021, 8, 491. [Google Scholar] [CrossRef]
- Suárez-Bermejo, J.C.; De Sande, J.C.G.; Santarsiero, M.; Piquero, G. Numerical Analysis of CCD Images for Polarimetry with Full Poincaré Beams. Sens. Transducer 2020, 247, 18–24. [Google Scholar]
- Suárez-Bermejo, J.C.; de Sande, J.C.G.; Santarsiero, M.; Piquero, G. Experimental Mueller matrix polarimetry with full Poincaré beams and a CCD camera. EPJ Web Conf. 2021, 255, 12005. [Google Scholar] [CrossRef]
- Ben-Israel, A.; Greville, T.N. Generalized Inverses, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- del Hoyo, J.; Sanchez-Brea, L.M.; Gomez-Pedrero, J.A. High precision calibration method for a four-axis Mueller matrix polarimeter. Opt. Lasers Eng. 2020, 132, 106112. [Google Scholar] [CrossRef]
- Dev, K.; Asundi, A. Mueller–Stokes polarimetric characterization of transmissive liquid crystal spatial light modulator. Opt. Lasers Eng. 2012, 50, 599–607. [Google Scholar] [CrossRef]
- Zhou, G.; Li, Y.; Liu, K. Efficient calibration method of total polarimetric errors in a channeled spectropolarimeter. Appl. Opt. 2021, 60, 3623–3628. [Google Scholar] [CrossRef] [PubMed]




| Sample | Parameters | |
|---|---|---|
| QWP | ||
| HWP | ||
| LP | ||
| Sample | ||
|---|---|---|
| Air | 0.0019 | |
| QWP (0) | 0.0055 | |
| QWP | 0.0039 | |
| HWP (0) | 0.0062 | |
| HWP | 0.0044 | |
| LP | 0.0016 | |
| LP | 0.0047 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suárez-Bermejo, J.C.; González de Sande, J.C.; Piquero, G.; Failla, A.V.; Santarsiero, M. Full Poincaré Mueller Polarimetry Using a CCD Camera. Photonics 2022, 9, 702. https://doi.org/10.3390/photonics9100702
Suárez-Bermejo JC, González de Sande JC, Piquero G, Failla AV, Santarsiero M. Full Poincaré Mueller Polarimetry Using a CCD Camera. Photonics. 2022; 9(10):702. https://doi.org/10.3390/photonics9100702
Chicago/Turabian StyleSuárez-Bermejo, Juan Carlos, Juan Carlos González de Sande, Gemma Piquero, Antonio Virgilio Failla, and Massimo Santarsiero. 2022. "Full Poincaré Mueller Polarimetry Using a CCD Camera" Photonics 9, no. 10: 702. https://doi.org/10.3390/photonics9100702
APA StyleSuárez-Bermejo, J. C., González de Sande, J. C., Piquero, G., Failla, A. V., & Santarsiero, M. (2022). Full Poincaré Mueller Polarimetry Using a CCD Camera. Photonics, 9(10), 702. https://doi.org/10.3390/photonics9100702







