Fundamental Studies on Electron Dynamics in Exact Paraxial Beams with Angular Momentum

Abstract

Classical electromagnetic radiation with orbital angular momentum (OAM), described by nonvanishing vector and scalar potentials (namely, Lorentz gauge) and under Lorentz condition, is considered. They are employed to describe paraxial laser beams, thereby including non-vanishing longitudinal components of electric and magnetic fields. The relevance of the latter on electron dynamics is investigated in the reported numerical experiments. The lowest corrections to the paraxial approximation appear to have a negligeable influence in the regimes treated here. Incoherent Thomson scattering (TS) from a sample of free electrons moving subject to the paraxial fields is studied and investigated as a beam diagnosis tool. Numerical computations elucidate the nature and conditions for the so called trapped solutions (electron motions bounded in the transverse plane of the laser and drifting along the propagation direction) in long quasi-steady laser beams. The influence of laser parameters, in particular, the laser beam size and the non-vanishing longitudinal field components, essential for the paraxial approximation to hold, are studied. When the initial conditions of the electrons are sufficiently close to the origin, a simplified model Hamiltonian to the full relativistic one is introduced. It yields results comparing quite well quantitatively with the observed amplitudes, phase relationships and frequencies of oscillation of trapped solutions (at least for wide laser beam sizes). Genuine pulsed paraxial fields with OAM and their features, modeling true ultra-short pulses are also studied for two cases, one of wide laser beam spot (100 $\mathsf{\mu }$m) and other with narrow beam size of 6.4 $\mathsf{\mu }$m. To this regard, the asymptotic distribution of the kinetic energy of the electrons as a function of their initial position over the transverse section is analyzed. The relative importance of the transverse structure effects and the role of longitudinal fields is addressed. By including the full paraxial fields, the asymptotic distribution of kinetic energy of an electron population distributed across the laser beam section, has a nontrivial and unexpected rotational symmetry along the optical propagation axis.

1. Introduction

Ultra intense pulsed lasers, available nowadays in the near infrared range, have reached peak powers in the multi-petawatt domain [1]. When tightly focused they allow extraordinary intensities, or in other words extraordinary concentrations of energy. Today’s record is the ${10}^{23}$ W/cm${}^2$, that has been achieved in the Korean multi petawatt laser [2]. Neutral atoms do not survive such enormous intensities. First ionization occurs by the mechanism of above threshold ionization well before ${10}^{17}$ W/cm${}^2$ for most atoms and, arriving to ${10}^{18}$ W/cm${}^2$, the only thing we have are relativistic electrons and positive ions (singly or multiply charged). Observe that all occurs during the turn on of the pulse. Such lasers have durations of a few tens of femtoseconds for the so-called intensity lasers (as the Korean one) to picoseconds for the so-called energy lasers.

Positive ions move obviously much slower than electrons due to the different mass/charge ratio. Then, the accelerated electrons released from those atoms become highly relativistic as laser intensities increase towards ${10}^{23}$ W/cm${}^2$. The intensities considered in the present work will lie well above ${10}^{18}$ W/cm${}^2$, so that electrons will be certainly relativistic, yet without reaching ${10}^{23}$ W/cm${}^2$. Moreover, at such record peak intensities, radiation reaction [3] may start to play a role on the electron dynamics: then, we shall not be concerned with radiation reaction in the present work.

The scattering of electromagnetic radiation (Thomson Scattering, denoted hereafter by TS) by free charges provides a very interesting diagnostic. In fusion plasmas, TS yields electron distribution functions and, hence, their density distributions (see for example [4,5]). TS is also potentially useful and challenging for the diagnosis of intense or ultra-intense laser beams. In fact, as discussed above, the acceleration of the electrons is the dominant process for light scattering: electrons driven by the pulse laser move relativistically and radiate due to TS. The diagnoses in both cases are obtained from the analysis of the detected scattered radiation (spectrum, polarization, etc.).

A large part of the present work will be concerned with laser beams with orbital angular momentum (OAM). For different complementary studies about them, see for example [6,7,8,9] and also [10,11,12,13,14,15] for some experiments with light and theoretical work altogether, in states having OAM. Those beams have remarkable properties even if their structure is quite different from the ordinary plane wave ones. For example, selection rules for the photoelectric effect with OAM photons hold provided that the photon orbital angular momentum be included in the former [16]. Moreover recent experiments succeeded in getting high intensity OAM modes using off-axis spiral phase mirrors [17].

In modern petawatt laser sources it seems possible and quite appealing to include a variety of transverse structures (for instance, a general Laguerre-Gauss mode, with a step function to account for its time pulsed structure). Such structures may influence strongly the laser-atom or laser-electron interaction. Even if to achieve such OAM pulses at multi-joule level is difficult, it seems very reasonable to investigate various possible physical processes generated by them: the motion of a fully relativistic electron subject to OAM pulses is a particularly appealing case.

On the other hand, transverse pulsed plane wave beams turn out to be very useful, not only by themselves but, in particular, as possible approximations of other beams in some restricted ranges, under certain conditions. Thus, with the second purpose in mind, a comparatively small part of our study (Appendix A and Section 4) will consider transverse pulsed plane wave beams as approximations to OAM ones.

Plane wave models, or pulsed plane waves, cannot account for the total finite energy content of electromagnetic fields of current ultra-intense lasers. There is much current interest in studying ultra-intense laser fields with models beyond the simple plane wave approximation. For that purpose, paraxial fields that include the transverse structure of laser fields have been intensively studied, in particular a family of modes which have a net OAM. For interesting studies about the paraxial approximation to describe electromagnetic waves see, for instance, [18,19,20] and references therein.

It is well known that in order to fulfill the paraxial approximation the laser fields have to acquire non-vanishing longitudinal components of the electric and magnetic field, and one of the goals of this paper is to clarify their relevance on electron dynamics in well controlled numerical experiments. We remind that the longitudinal $E_z$ and $B_z$ components have an influence which scales with the inverse of the laser beam size.

In [21], we have studied the dynamics and TS of electrons subject to ultra intense laser radiations with OAM beams, mostly numerically. In [22], the analysis, combining analytical and numerical procedures, treated laser radiations represented by either plane waves with general elliptic polarization or simpler OAM beams with vanishing longitudinal components of the electric and magnetic field, and analyzed possible approximations to such OAM beams by means of plane waves, in certain regimes. The present work will extend non-trivially [22] to ultra intense laser beams with OAM and non-vanishing longitudinal components of the electric and magnetic fields. Our approach here to the paraxial approximation and eventual corrections thereof will be based on vector and scalar potentials in Lorentz gauge and under Lorentz condition.

Numerical computations will be carried out in order to compare our paraxial approach with the one by Erikson and Singh [18]. To our knowledge this model represents a very useful compromise between the complexity of a full vectorial description of the laser field and the oversimplification of using only the the transverse part of the field. Erikson and Singh’s model is a reasonable description of the focus of the laser beam or a laser pulse provided that the f# (the ratio of the focal length of a mirror or lens to its diameter) is not too short (in other words, provided that the paraxial approximation holds). As an approximate criterion we can say that this works for long focus, f#/10 or longer. In the case of very tight focus, as the f#/1.1 of [2] a more complete description of the counter propagating components is desirable. The model we present is, to our knowledge, a new way to introduce the longitudinal components to increase accuracy in the description without increasing the complexity of the model.

We discuss the TS emission from free electrons interacting with paraxial fields, and evaluate its diagnostic capabilities to ascertain averaged or statistical properties of the electron samples and of the beam under study.

Section 2 reminds the Maxwell equations in Lorentz gauge, with Lorentz condition and formulates exact equations for modulated plane-waves, which will provide the basis for the present study of the paraxial approximation and corrections thereof. Section 2 also discusses the paraxial approximation in the present framework. Section 3 analyzes trapped electron trajectories in long quasi-steady laber beams with OAM. Section 4 is devoted to ultrashort-pulse paraxial laser beams with OAM. Section 4 also deals with numerical computations for the solution for a pulsed plane wave with Gaussian envelope, given in Appendix A. Appendix A will treat analytical solutions of the electron dynamics in a pulsed plane wave with Gaussian envelope. A novel approach to corrections to the paraxial approximation is included in Appendix B.

2. General Aspects

2.1. Maxwell Equations in Lorentz Gauge

The Maxwell equations for electric ($\mathbf{E}$) and magnetic ($\mathbf{B}$) fields in vacuum and in the absence of charges read (in SI units) [23]:

$$\begin{array}{ccc}& & {\nabla }_{\mathbf{x}}·\mathbf{E}=0,\frac{\partial \mathbf{B}}{\partial t}=-{\nabla }_{\mathbf{x}}\times \mathbf{E}\hfill \\ & & {\nabla }_{\mathbf{x}}·\mathbf{B}=0,\frac{1}{c^2}\frac{\partial \mathbf{E}}{\partial t}={\nabla }_{\mathbf{x}}\times \mathbf{B}\hfill \end{array}$$

(1)

c being the velocity of light in vacuum. They all depend on the three-dimensional position $\mathbf{x}=(x,y,z)=(\overline{x},z)$ and on time t. Let $\mathbf{A}$ and $\Phi$ be the vector and scalar potentials. The Lorentz gauge will be employed and the Lorentz condition reads:

$$\begin{array}{ccc}& & \frac{1}{c^2}\frac{\partial \Phi }{\partial t}+{\nabla }_{\mathbf{x}}·\mathbf{A}=0\hfill \end{array}$$

(2)

In this gauge, the fields are:

$$\begin{array}{ccc}& & \mathbf{E}=-\frac{\partial \mathbf{A}}{\partial t}-{\nabla }_{\mathbf{x}}\Phi ,\mathbf{B}={\nabla }_{\mathbf{x}}\times \mathbf{A}.\hfill \end{array}$$

(3)

The wave equations for the potentials read:

$$\begin{array}{ccc}& & \frac{1}{c^2}\frac{{\partial }^2\mathbf{A}}{\partial t^2}={\nabla }_{\mathbf{x}}^2\mathbf{A},\frac{1}{c^2}\frac{{\partial }^2\Phi }{\partial t^2}={\nabla }_{\mathbf{x}}^2\Phi \hfill \end{array}$$

(4)

For convenience, the fields and the potentials will be supposed to be complex (the physical fields and potentials being their real parts).

2.2. Exact Modulated Plane-Wave Equations

Exact solutions of Equation (4) and hence, of the Maxwell equations, will be searched with the structure of modulated plane-waves traveling along the z-axis with wavevector $k_0$ and frequency ${\omega }_0$ (${\omega }_0=c{k}_0$). These solutions are particularly well adapted to model very long laser pulses, where their precise temporal envelope can be disregarded. They read:

$$\begin{array}{ccc}& & X=X_{ex}(\overline{x},z)expi(k_{0}z-{\omega }_{0}t+{\chi }_0)\hfill \end{array}$$

(5)

for X$=\Phi ,A,E,B$. The exact equations fulfilled by all $X_{ex}(\overline{x},z)$ will be given below. Let: ${\nabla }_{\mathbf{x}}=({\nabla }_{\overline{x}},\partial /\partial z)$, $X=(\overline{X},X_z)$ for the various X. One finds:

$$\begin{array}{ccc}& & \left({\nabla }_{\overline{x}}^2+\frac{{\partial }^2}{\partial z^2}+2i{k}_0\frac{\partial }{\partial z}\right)X_{ex}=0\hfill \end{array}$$

(6)

for $X_{ex}={\Phi }_{ex},{\overline{A}}_{ex},A_{z,ex}$ and

$$\begin{array}{ccc}& & {\nabla }_{\overline{x}}{\overline{A}}_{ex}+\frac{\partial }{\partial z}{A}_{z,ex}+i{k}_0{A}_{z,ex}=\frac{i{\omega }_0}{c^2}{\Phi }_{ex}\hfill \end{array}$$

(7)

For the electric and magnetic fields, one gets:

$$\begin{array}{ccc}& & {\overline{E}}_{ex}=-{\nabla }_{\overline{x}}{\Phi }_{ex}+i{\omega }_0{\overline{A}}_{ex}\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& & E_{z,ex}=-i{k}_0{\Phi }_{ex}-\frac{\partial }{\partial z}{\Phi }_{ex}+i{\omega }_0{A}_{z,ex}\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & B_{x,ex}=\frac{\partial }{\partial y}{A}_{z,ex}-\left(i{k}_0+\frac{\partial }{\partial z}\right)A_{y,ex}\hfill \end{array}$$

(10)

$$\begin{array}{ccc}& & B_{y,ex}=-\frac{\partial }{\partial x}{A}_{z,ex}+\left(i{k}_0+\frac{\partial }{\partial z}\right)A_{x,ex}\hfill \end{array}$$

(11)

$$\begin{array}{ccc}& & B_{z,ex}=\frac{\partial }{\partial x}{A}_{y,ex}-\frac{\partial }{\partial y}{A}_{x,ex}\hfill \end{array}$$

(12)

Without loss of generality, we shall choose:

$$\begin{array}{ccc}& & A_{z,ex}=0\hfill \end{array}$$

(13)

Then, for exact modulated plane-wave solutions, the knowledge of the two independent components $A_{x,ex}$ and $A_{y,ex}$ of ${\overline{A}}_{ex}$ just determines ${\Phi }_{ex}$, ${\mathbf{E}}_{ex}$ and ${\mathbf{B}}_{ex}$. In particular, one can develop successive approximations for $A_{x,ex}$ and $A_{y,ex}$, (independently of each other): the paraxial approximation (next section) and eventual extensions thereof (Appendix B).

2.3. General Paraxial Approximation

In general, the paraxial approximation $X_{ex}\simeq X_{par}$ for $X_{ex}={\Phi }_{ex},{\overline{A}}_{ex},A_{z,ex}$ is based, in the present framework, upon assuming that $\frac{{\partial }^2}{\partial z^2}{X}_{ex}$ can be neglected compared to $\left(2k_0\frac{\partial }{\partial z}\right)X_{ex}$. We shall disregard $A_{z,ex}$ completely, since we have chosen $A_{z,ex}=0$ exactly from the outset (prior to imposing the paraxial approximation). Equation (6) yields:

$$\begin{array}{ccc}& & \left({\nabla }_{\overline{x}}^2+2i{k}_0\frac{\partial }{\partial z}\right)X_{par}=0\hfill \end{array}$$

(14)

Consequently, the latter determine directly ${\Phi }_{par}$ and the components of ${\mathbf{E}}_{par}$ and ${\mathbf{B}}_{par}$ (all of which, on the other hand, also fulfill Equation (14)). One has:

$$\begin{array}{ccc}& & {\nabla }_{\overline{x}}{\overline{A}}_{par}=\frac{i{\omega }_0}{c^2}{\Phi }_{par}\hfill \end{array}$$

(15)

In the work by Erikson and Singh [18], their lowest paraxial approximation is given by two independent functions f and g. A comparison with [18] shows that $i{\omega }_0{A}_{x,par}=f$ and $i{\omega }_0{A}_{y,par}=g$. It is stressed that the functions f and g in [18] (carrying no subscripts) should NOT be confused with the functions $g_{m,n}$ and $f_{m,n}$ (including subscripts) to be employed throughout the present paper (since the next subsection onwards). For the electric and magnetic fields, one gets:

$$\begin{array}{ccc}& & {\overline{E}}_{par}=i{\omega }_0{\overline{A}}_{par}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}& & E_{z,par}=-i{k}_0{\Phi }_{par}\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & B_{x,par}=-i{k}_0{A}_{y,par}\hfill \end{array}$$

(18)

$$\begin{array}{ccc}& & B_{y,par}=i{k}_0{A}_{x,par}\hfill \end{array}$$

(19)

$$\begin{array}{ccc}& & B_{z,par}=\frac{\partial }{\partial x}{A}_{y,par}-\frac{\partial }{\partial y}{A}_{x,par}\hfill \end{array}$$

(20)

Equations (16)–(20) give rise to solutions of the Maxwell equations to leading paraxial approximation and coincide with the leading paraxial approximations given in [18] (upon neglecting spatial derivatives of their independent functions f and g).

2.4. OAM Waves as Particular Cases of Paraxial Approximation

Use will be made of electromagnetic waves with orbital angular momentum (OAM) with prescribed values of the integer parameters l, p (the integer l being allowed to be negative). They are generated by the functions $g_{l,p}$ given below.

Let $\rho ={(x^2+y^2)}^{1/2}$ and for given $k_0(>0)$ in Equation (5), let:

$$\begin{array}{ccc}& & g_{0,0}={(2/\pi )}^{1/2}exp[-\frac{{\rho }^2}{w{\left(z\right)}^2}]exp[i\frac{z}{z_0}\frac{{\rho }^2}{w{\left(z\right)}^2}]f_{0,0}(\frac{z}{z_0})\hfill \end{array}$$

(21)

$$\begin{array}{ccc}& & f_{0,0}(\frac{z}{z_0})=\frac{w_0}{w\left(z\right)}exp[-iarctan\frac{z}{z_0}]\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& & w\left(z\right)=w_0{(1+{(z/z_0)}^2)}^{1/2},z_0=\frac{k_0{w}_0^2}{2}\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& & {ϵ}_0=\frac{w_0}{z_0}=\frac{2}{k_0{w}_0}\hfill \end{array}$$

(24)

${ϵ}_0$ is different from (and, hence, should be not confused with) the dielectric permittivity of vacuum. $g_{0,0}$ corresponds to $l=0$, $p=0$. For general integer values of l, p, one considers the following functions (directly related to the Laguerre-Gauss (LG) functions $L{G}_{l,p}(\rho ,z)$):

$$\begin{array}{ccc}& & g_{l,p}={[\frac{p!}{(\mid l\mid +p)!}]}^{1/2}{L}_p^{\mid l\mid }(\frac{2{\rho }^2}{w{\left(z\right)}^2}){(\frac{2^{1/2}\rho }{w\left(z\right)})}^{\mid l\mid }\times expi[l\varphi -(2p+\mid l\mid )arctan\frac{z}{z_0}]g_{0,0}\hfill \end{array}$$

with $\varphi =arctan(y/x)$. $L_p^{\mid l\mid }\left(u\right)$ are the generalized Laguerre polynomials:

$$\begin{array}{ccc}& & L_p^{\mid l\mid }\left(u\right)=\sum _{m=0}^p{(-1)}^m\frac{(\mid l\mid +p)!}{(p-m)!(\mid l\mid +m)!m!}{u}^m\hfill \end{array}$$

(25)

A very important property of any $g_{l,p}$, for general integer $l,p$, is that:

$$\begin{array}{ccc}& & \left({\nabla }_{\overline{x}}^2+2i{k}_0\frac{\partial }{\partial z}\right)g_{l,p}=0\hfill \end{array}$$

(26)

The comparison of Equation (26) with Equation (14) shows that $g_{l,p}$ provides one important case of paraxial approximation. Then, in particular, one can always choose the components $A_{x,par}$ and $A_{y,par}$ of ${\overline{A}}_{par}(\simeq {\overline{A}}_{ex})$ to be equal to some suitable linear combination of $g_{l,p}$’s. Thus, the above $g_{l,p}$ yielding OAM electromagnetic waves provide one important example of paraxial approximation. However, there are other cases of paraxial approximation which do not correspond to the above OAM electromagnetic waves.

3. Trapped Trajectories in Quasi-steady Laser Beams with OAM

In this section, results are reported about trajectories which are trapped in the plane transverse to the propagation direction of the laser beam. The physical effect behind this trapping is the ponderomotive force [24]. Such force is ubiquitous in any laser experiment with free charges but is only relevant for electrons inside strong laser fields. It expels electrons from the high intensity regions. For modes with a nodal axis, a tube of intensity is created. Moore calculated for the first time the possibility of electron confinement [25] inside such light tubes. Specifically, trapped trajectories are solutions to the relativistic Lorentz equation that perform a confined motion in the transverse $xy$ plane, (not any sort of drifting motion in the latter). Compatibly with that, those trajectories may (do) acquire a net drift in the z direction and oscillate in a more or less complicated way in the transverse plane for many (typically for hundreds of) optical cycles.

We focus on the case of laser beams with net orbital angular momentum, namely $(l,p)=(1,0)$ in our case, interacting with free electrons of initial kinetic energy equal to zero, except otherwise stated. Two case-studies will be analyzed in detail, one of a relatively wide laser beam spot, $w_0=100.0$ $\mathsf{\mu }$m, the other of a narrow laser spot of $w_0=6.4$ $\mathsf{\mu }$m. The beam waist, the f-number and ${\lambda }_0$ verify $w_0=0.87\times {\lambda }_0\times f\#$, hence the case of a small waist corresponds to f#/9.2 and it is a very common case in many of today’s petawatt lasers with a long focal parabola. However, the case for the large waist corresponds to f#/143. This is an extremely long focus (probably to be achieved with a close to axis spherical mirror). In this case, keeping such intensity level over a so broad area will require probably a laser close to 40 PW at this mode, and using techniques as the indicated in [17] a power after compression close to 100 PW. This is one step beyond present day possibilities, but foreseen in the mid term at several world initiatives, as the Shanghai’s Station of Extreme Light [1,26].

The rest of the parameters characterizing the laser are: ${\lambda }_0=800.0$ nm, ${\chi }_0=-\pi$, $E_0=100\times E_{atomic}/\sqrt{2}$ ($E_{atomic}=5.14\times {10}^{11}$ V/m), electric field mainly polarized along the x-axis (that is, we choose $A_{x,par}\ne 0$, $A_{y,par}=0$), the laser pulse is assumed to be much longer than the integration time to obtain the trapped solutions. Electrons are assumed to be located in all the cases at the beam waist position, i.e., at $z_0=0$, at $t_0=0$. From these values, the dimensionless laser parameter currently used in the literature, namely, $\left|q\right|A_0/\left(mc\right)$ = $\left|q\right|E_0/\left({\omega }_{0}mc\right)$ = $\left|q\right|E_0/\left(k_{0}m{c}^2\right)$ can be defined, which turns out to be ≈9.0 in our case. This is indeed a large value, indicating the important role of nonlinearity in the simulations presented in the paper.

In both case-studies, a disk centered at the origin in the $xy$-plane of radius $w_0/20$ will be explored. Note that the region to be explored is well inside $w_0/\sqrt{2}$, the limit where the ponderomotive force tends to keep the electrons confined. Inside this zone, random initial conditions for the electrons will be generated, and subsequently integrated using the relativistic Lorentz equation with the exact paraxial fields discussed in earlier sections of the paper. Plots of the trajectory components, velocity components and eventually the relativistic $\gamma$ factor will be provided to illustrate the main features of trapped solutions. The characterization of the set of trajectories as a whole will be obtained from their TS spectra, averaged at a selected detection point. As it is well known, the scattering of electromagnetic radiation by free charges is a standard diagnostic of their distribution functions (see for example [4,5] for applications in fusion plasmas), and also for the diagnosis of intense or ultra-intense laser beams.

It will be shown that in the case of wide laser spot, a Hamiltonian function can be introduced that substantially simplifies the equations of motion capturing at the same time many of the observed phenomena. As it will become clear in the discussion that follows, the main result is that $B_z$ and $E_z$ (the longitudinal field components) play an essential role in accounting for the existence and character of these trapped solutions. Let us now begin a more detailed discussion of the two case-studies mentioned above.

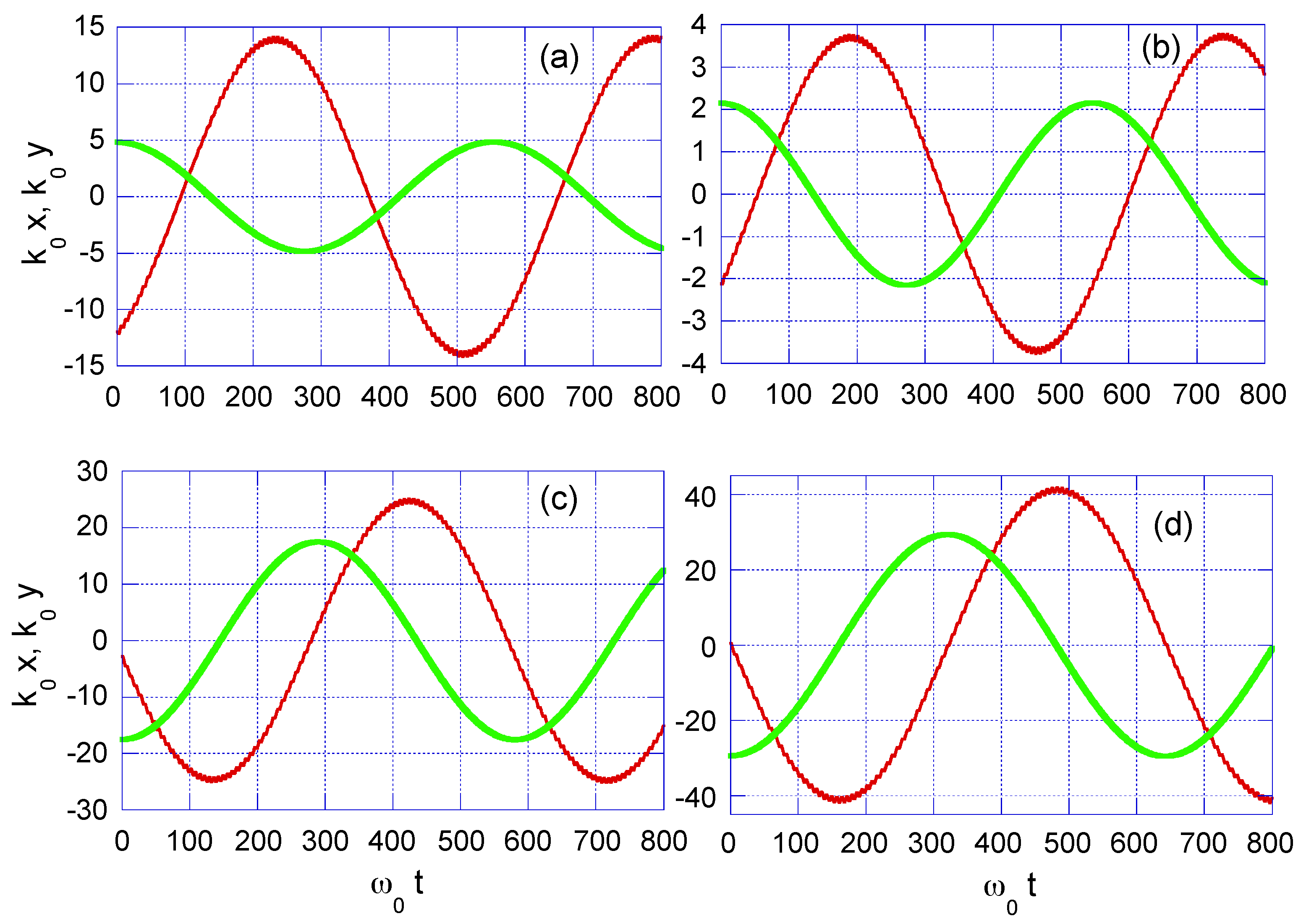
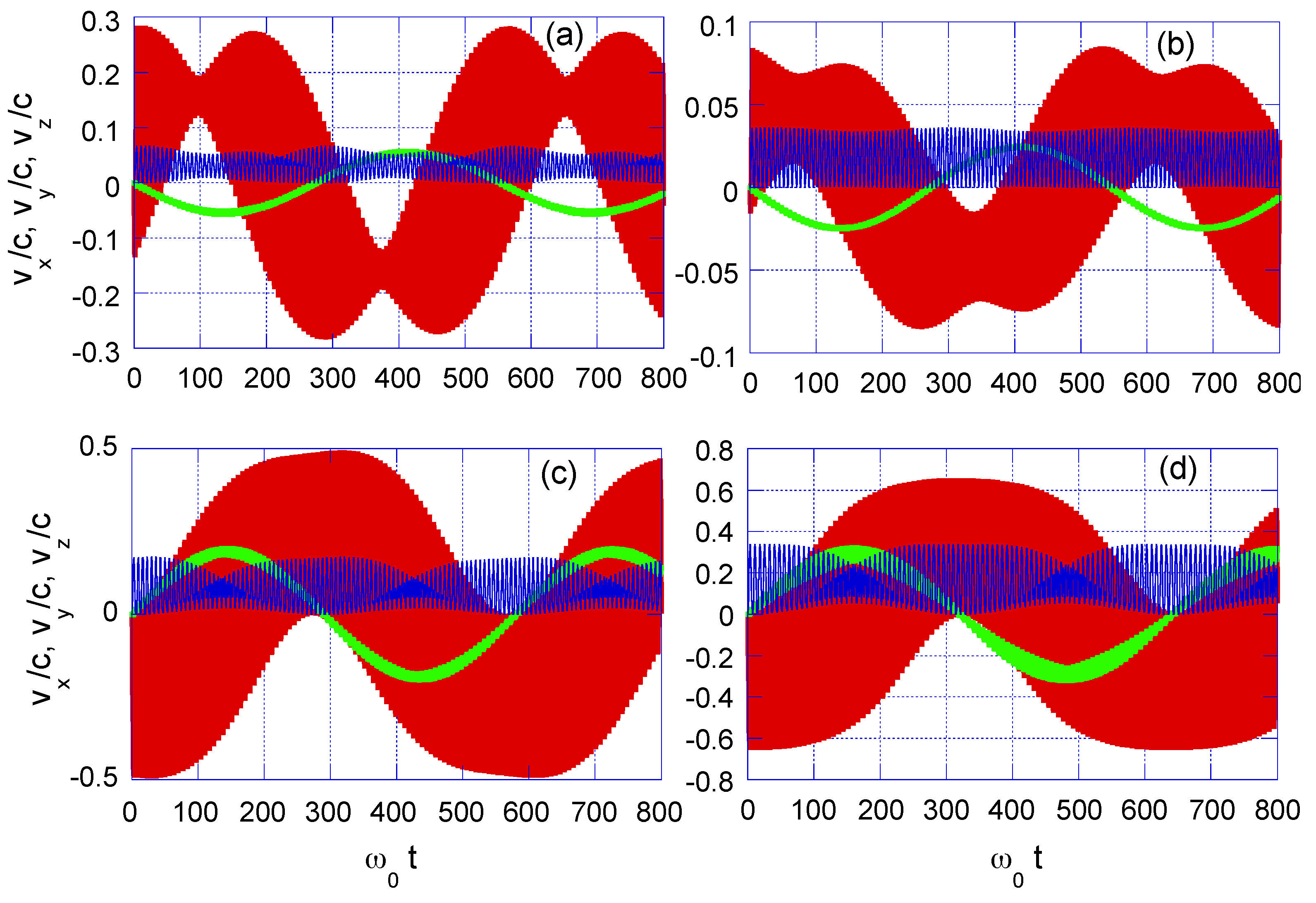
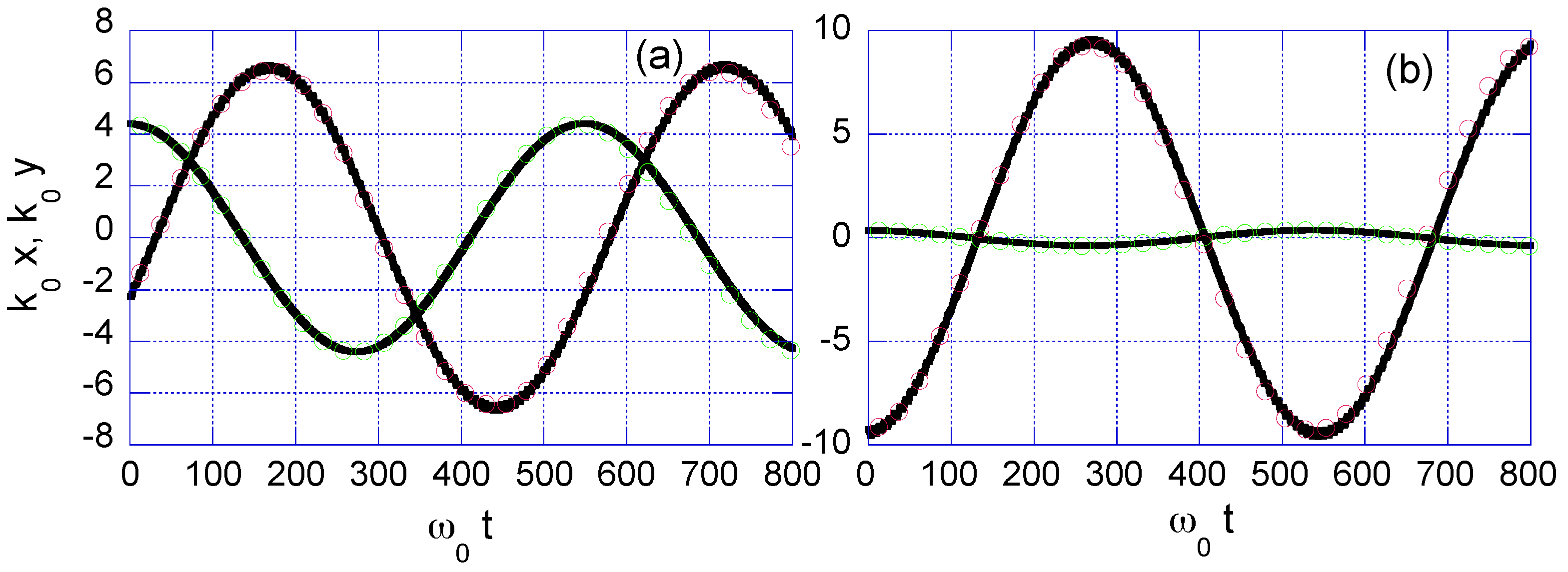
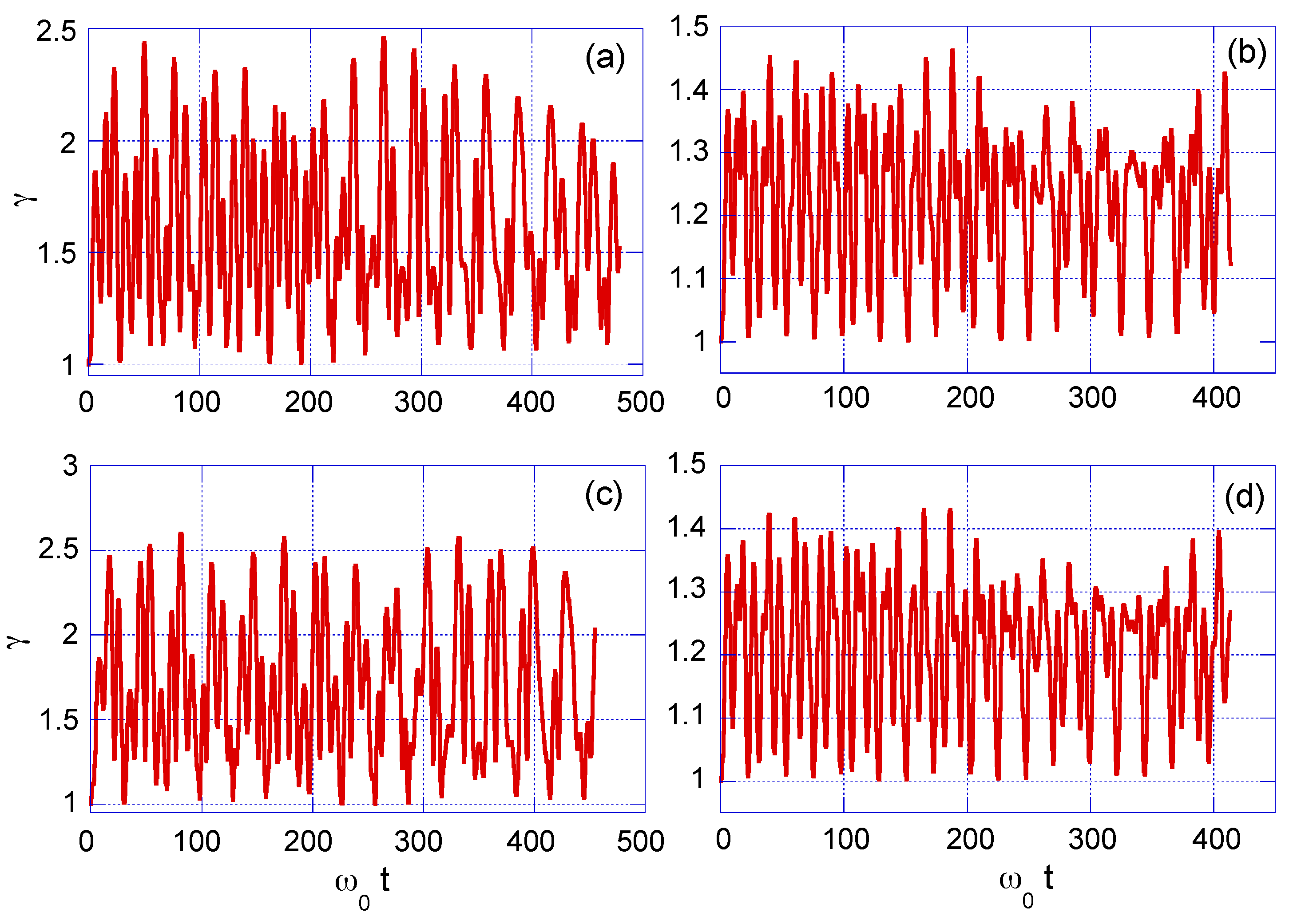
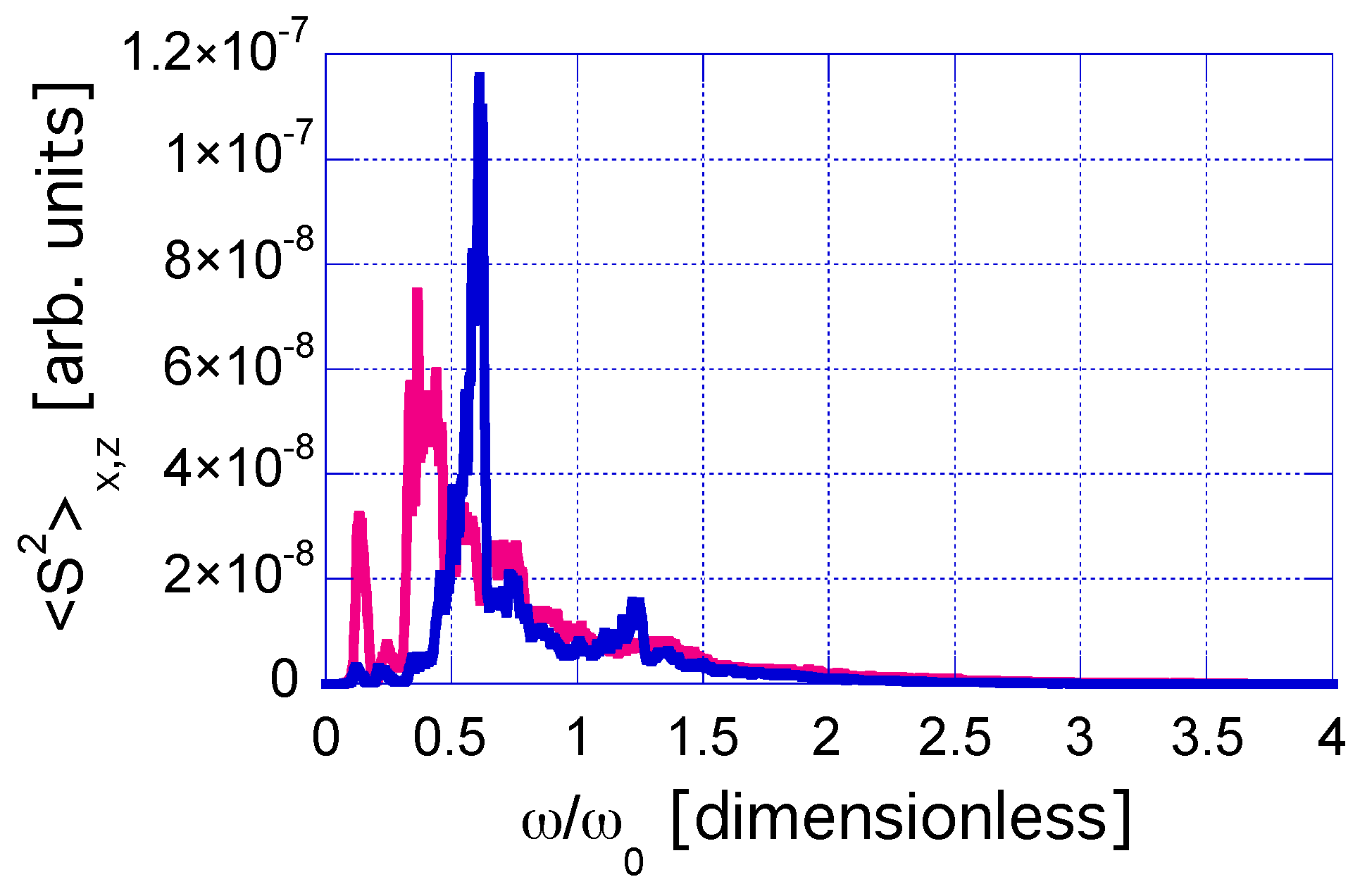
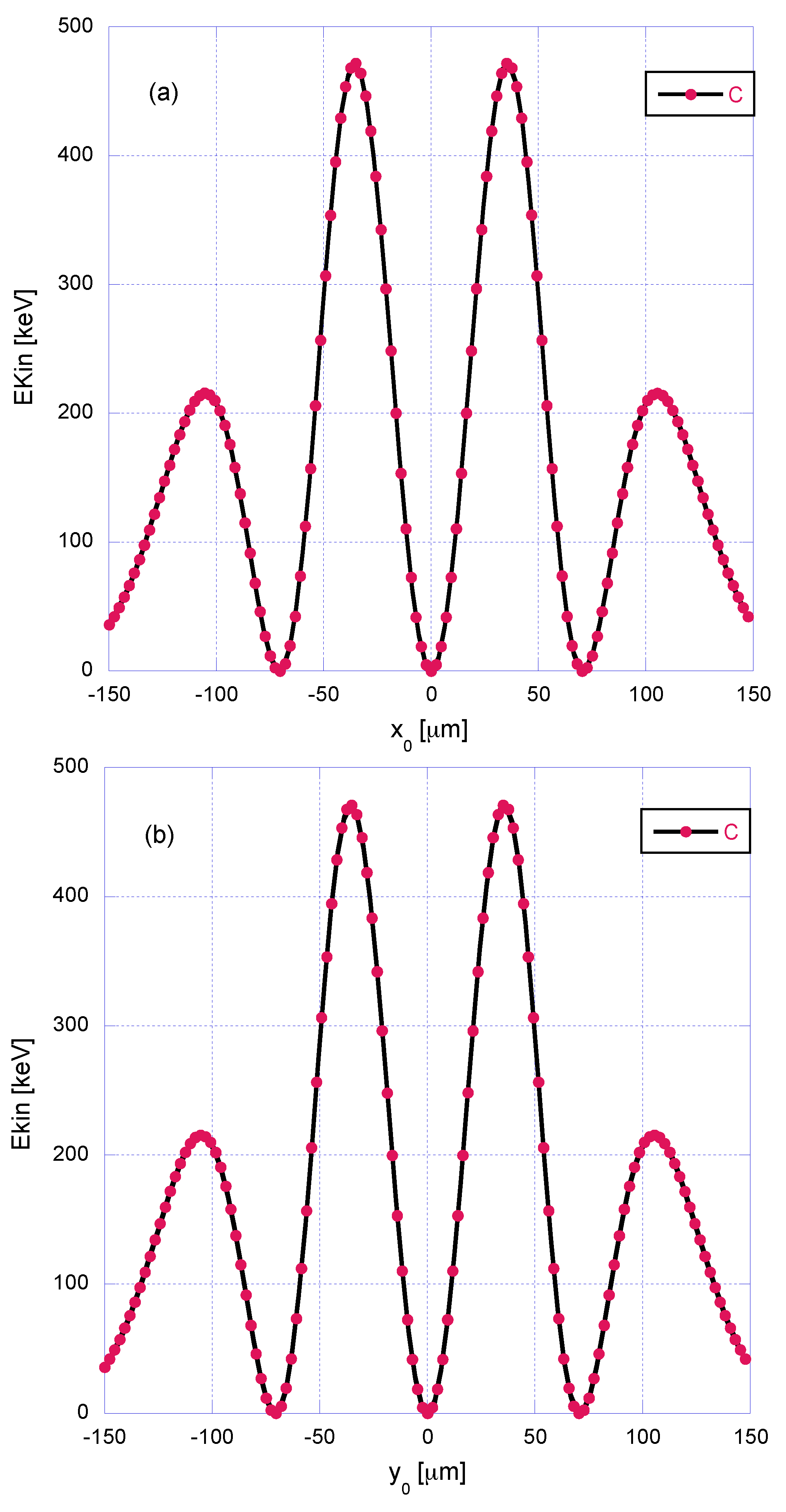
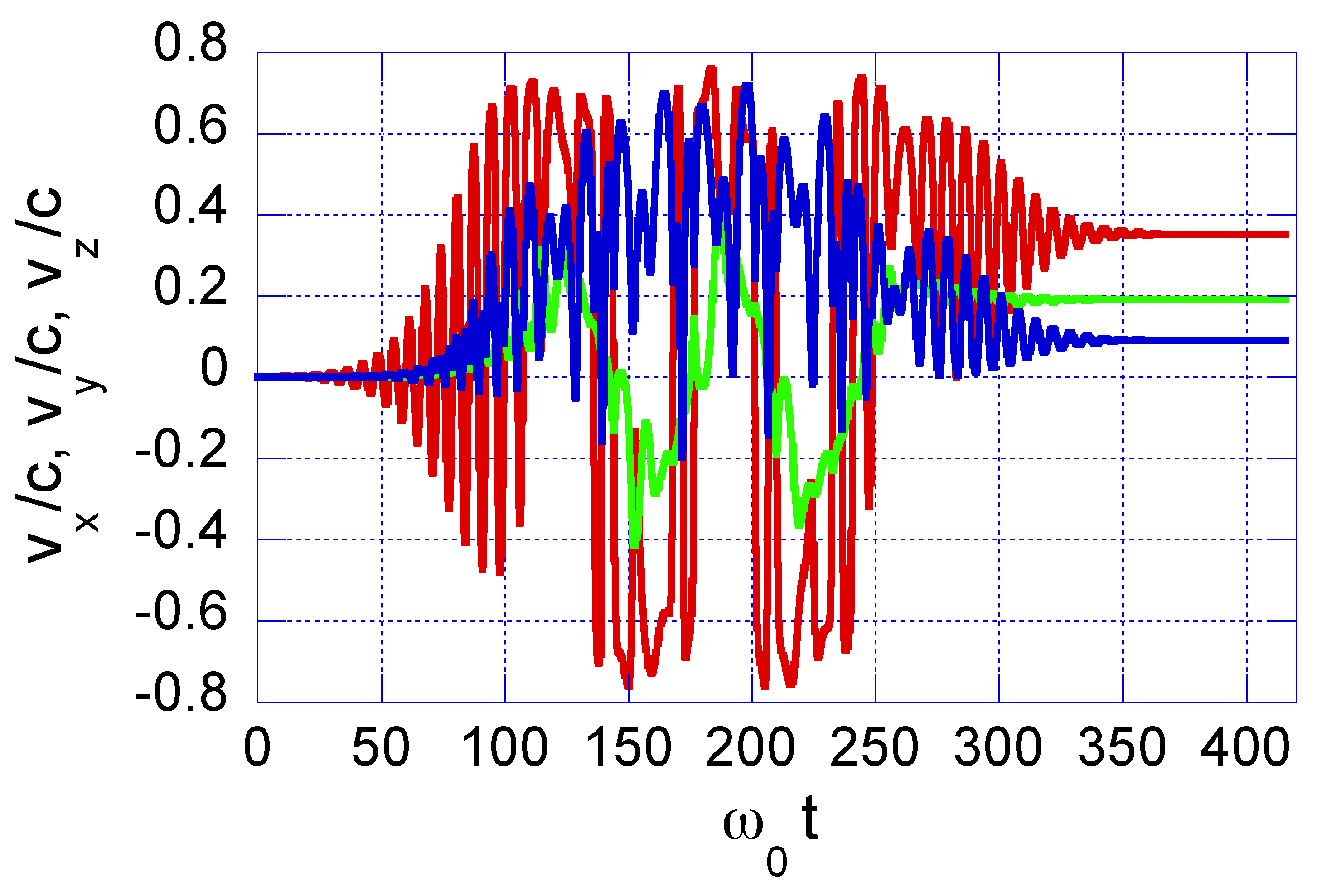
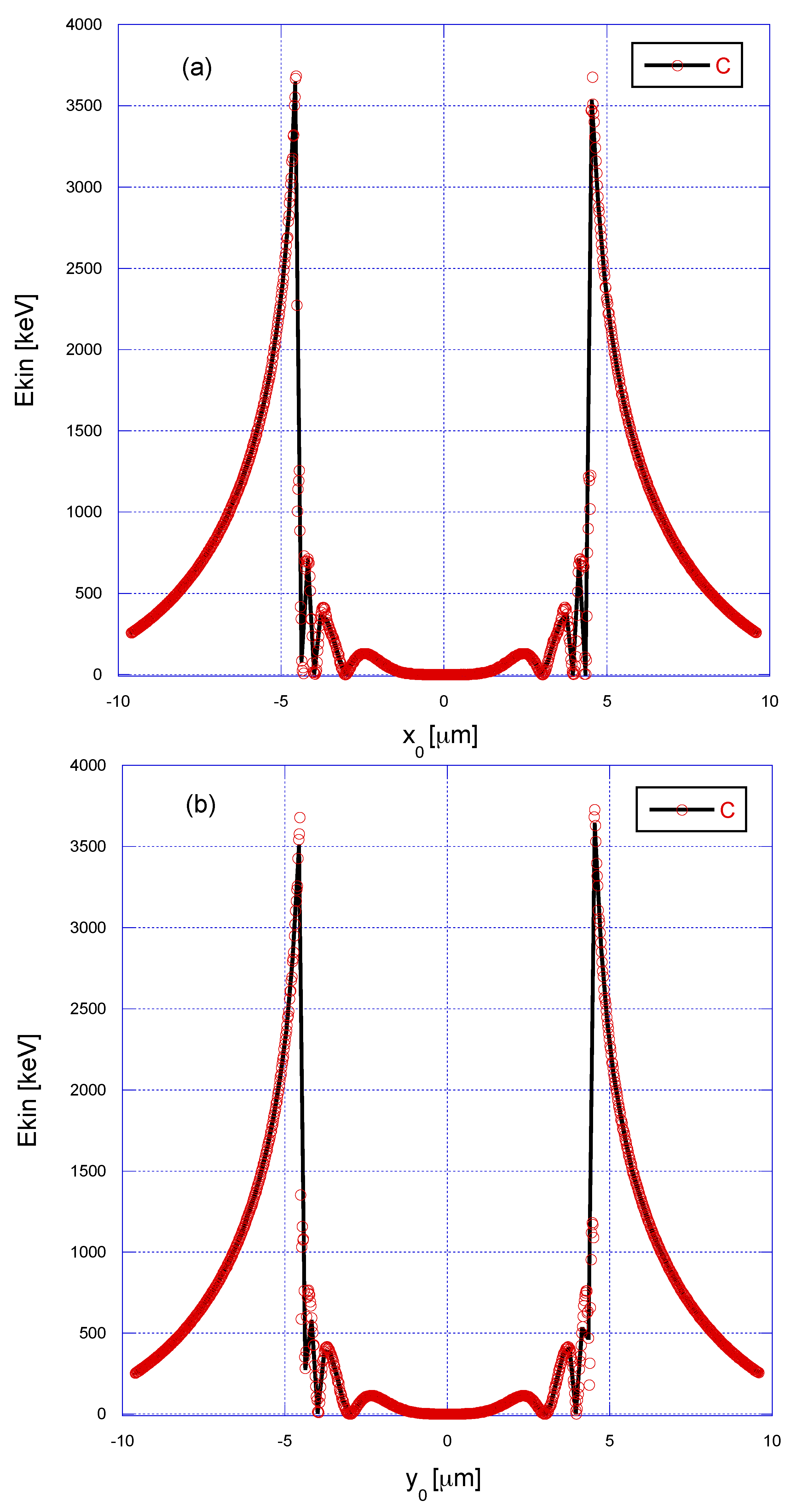
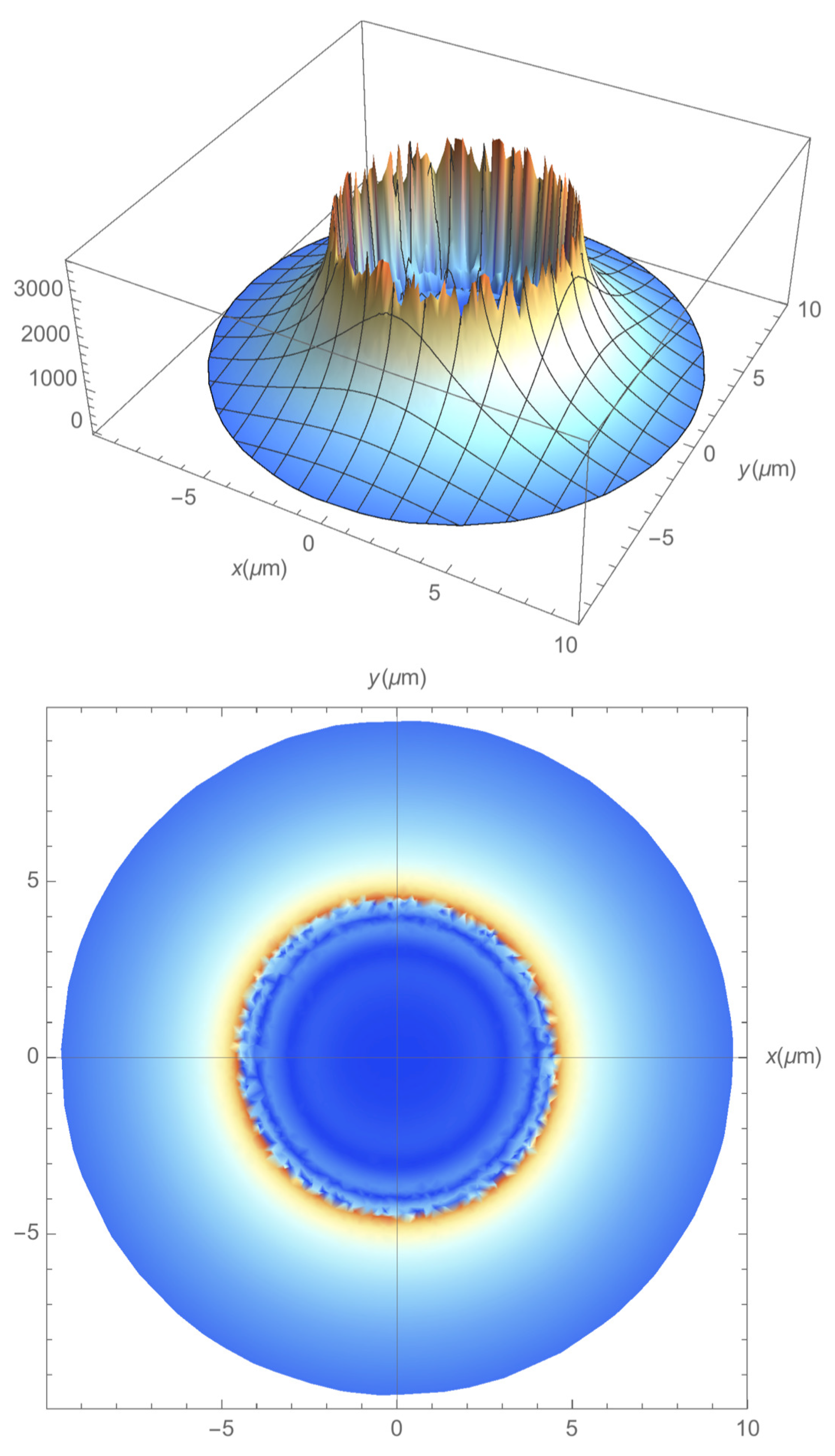
3.1. Case-Study 1: Wide Laser Beam Spot, $w_0$ = 100.0 $\mathsf{\mu }$m

Figure 1 shows four examples of trapped trajectories with initial conditions inside a circle or radius $w_0/20$ around the centre of the laser beam, see

Table 1. Sample initial conditions for trapped trajectories, case-study with $w_0=100$ $\mathsf{\mu }$m.

$x_0$ [$\mathsf{\mu }$m]	$y_0$ [$\mathsf{\mu }$m]	$z_0$ [$\mathsf{\mu }$m]
−1.5212	0.6148	0.0
−0.2693	0.2734	0.0
−0.3553	−2.2284	0.0
0.0596	−3.7369	0.0

for details. Two characteristics of these solutions seem clear: in the first place, the appearance of a relatively large, low frequency modulation of both the x and y coordinates of the electron, and on the second place the different amplitudes and phase relationship between these components for different initial conditions. Figure 2 and Figure 3 show, respectively, the projection onto the $xy$ plane and the velocity components for the trajectories in Figure 1: all of them show more or less pronounced modulations to the fast optical frequency, which should be traced back to the appearance of the above mentioned low frequency of dynamical origin.

It is easy to argue that to explain the observed modulations, it is essential to include the longitudinal field components $B_z(x,y,z,t)$ and $E_z(x,y,z,t)$. The argument is as follows: if we assume that the initial kinetic energy of the electron is zero, hence the initial values of the velocity components are exactly zero at $t=0$. But according to the relativistic Lorentz equation, written in terms of the acceleration

$$\begin{array}{c}\hfill d\mathbf{v}/dt=(q/m)\sqrt{1-{\mathbf{v}}^2/c^2}\left(\mathbf{E}+\mathbf{v}\times \mathbf{B}-\mathbf{v}(\mathbf{v}·\mathbf{E})/c^2\right),\end{array}$$

(27)

the time evolution of e.g. $v_y\left(t\right)$ is given by

$$\begin{array}{c}\hfill d{v}_y/dt=(q/m)\sqrt{1-{\mathbf{v}}^2/c^2}\left(E_y+(v_z{B}_x-v_x{B}_z)-v_y(v_x{E}_x+v_y{E}_y+v_z{E}_z)/c^2\right).\end{array}$$

(28)

Now, if we set $E_y=0,B_x=0$ (electric field is assumed to be linearly polarized along the x-axis (no $E_y$ component), and hence $\mathbf{B}$ is polarized along y-axis), and $B_z=0$, $E_z=0$ the previous equation would read

$$\begin{array}{c}\hfill d{v}_y/dt=(q/m)\sqrt{1-{\mathbf{v}}^2/c^2}\left(-v_y\left(v_x{E}_x\right)/c^2\right),\end{array}$$

(29)

and it can be checked that $v_y\left(t\right)\equiv 0$ is indeed an exact solution of the previous equation, since its right-hand side evaluates to zero upon substituting $v_y\left(t\right)\equiv 0$, and the left-hand side (being the derivative of a constant) is also zero. Hence, any deviation of the y-component from its initial value, in particular any modulation appearing on it, must be accounted for by non-zero longitudinal components of the laser electromagnetic fields, in particular by a nonzero $B_z$ in the case of y.

Trapped solutions which are born close to the laser beam axis (${\rho }_0=\sqrt{x_0^2+y_0^2}\le w_0/20$) are characterized by their TS averaged spectrum (over many independent realizations of electron trajectories). A detection point located 0.5 m along the y-axis, is chosen to compute the spectrum. With this geometry (approximate 90 degrees scattering) there are in general two possible contributions to the spectrum, namely along the x and z-axis. Taking into account that the laser electric field has been chosen to be polarized along the x-axis, it is expected that the spectrum is also highly polarized in that direction. Figure 4 shows the averaged spectrum over 2048 trajectories. It shows a main band approximately centered at $\omega /{\omega }_0=1$, but also substantial power at the second and third harmonics of this. The spectrum clearly shows the scattered radiation to be highly polarized along the x axis, the z component representing only 10% of the former one.

Let us now try an approach to the understanding of the trapped solutions based on simplified dynamical equations that capture the essential features of the problem. To do this, a first consideration is that the paraxial laser beam with net OAM we are considering has an equilibrium point at the laser beam centre, i.e., a point where electric and magnetic fields are zero. The idea is to obtain approximate equations of motion which are valid in a sufficiently small zone around the centre of the laser beam, and study them in order to obtain information for these trajectories.

Our starting point will be the general relativistic Hamiltonian of a free charged particle, acted on by completely general electric and magnetic fields, namely

$$\begin{array}{ccc}& & H(x,y,z,t)=c\sqrt{{(\mathbf{P}(x,y,z,t)-q\mathbf{A}(x,y,z,t))}^2+m_0^2{c}^2}+q\Phi (x,y,z,t)\hfill \end{array}$$

(30)

where as usual $\mathbf{A}(x,y,z,t)$ and $\Phi (x,y,z,t)$ stand for the vector and scalar potentials, q is the charge of the particle, $\mathbf{P}$ is the canonical momentum and the $\mathbf{E}(x,y,z,t)$ and $\mathbf{B}(x,y,z,t)$ fields are obtained from the general rules in Equation (3). Now, take $A_y=0,A_z=0,A_x(x,y,z,t)=Re[A_{x,par}(x,y,z)\times exp\left[i(k_{0}z-{\omega }_{0}t+{\chi }_0)\right]$ with $A_{x,par}(x,y,z)=g_{1,0}(x,y,z)$ and $\Phi (x,y,z,t)=Re[{\Phi }_{par}(x,y,z)\times exp\left[i(k_{0}z-{\omega }_{0}t+{\chi }_0)\right]$, ${\Phi }_{par}(x,y,z)=-\frac{i{c}^2}{{\omega }_0}\frac{\partial }{\partial x}{g}_{1,0}(x,y,z)$, according to the rules stated above. Then, a series expansion is made (with the help of the computer algebra system Mathematica^TM) keeping terms to quadratic order in any of the dimensionless variables ${\pi }_x=P_x/mc,{\pi }_y=P_y/mc,{\pi }_z=P_z/mc,X=k_{0}x,Y=k_{0}y,Z=k_{0}z$. The sine and cosine functions, including the propagating phase term $\psi =\psi (z,t)=k_{0}z-{\omega }_{0}t+{\chi }_0=Z-\tau +{\chi }_0$, are kept unexpanded: they will act as a kind of (non-autonomous) forcing terms in the canonical equations thus obtained.

The normalized Hamiltonian $h({\pi }_x,{\pi }_y,{\pi }_z,X,Y,Z,\tau )=H(P_x,P_y,P_z,x,y,z,t)/m{c}^2$, $\tau ={\omega }_{0}t$, keeping terms up to (maximum) second order in any product of the canonical variables, is given explicitly as:

$$\begin{array}{c}\hfill (\frac{1}{2}\left({\pi }_x^2+{\pi }_y^2+{\pi }_z^2+\frac{{\alpha }^2\left[Xcos\left(Z-\tau +{\chi }_0\right)-Ysin\left(Z-\tau +{\chi }_0\right)\right]{}^2}{k_0^2{w}_0^2}-\right.\\ \hfill \frac{2\alpha \left[Xcos\left(Z-\tau +{\chi }_0\right)-Ysin\left(Z-\tau +{\chi }_0\right)\right]{\pi }_x}{k_0{w}_0}-\\ \hfill \left.\frac{2\alpha \left[2XYcos\left(Z-\tau +{\chi }_0\right)+\left(3X^2+Y^2-k_0^2{w}_0^2\right)sin\left(Z-\tau +{\chi }_0\right)\right]}{k_0^3{w}_0^3}\right))\end{array}$$

(31)

The corresponding canonical equations for Equation (31) are written below, and turn out to depend solely on a dimensionless parameter having to do with the laser intensity, labelled $\alpha$ and on the dimensionless product $k_0{w}_0$. For a fixed wavelength and a fixed laser intensity, the behavior of the trapped solutions is determined hence by the size of the laser beam spot size, which is the parameter explored in this investigation.

$$\begin{array}{ccc}& & dX/d\tau ={\pi }_x-\frac{\alpha }{k_0{w}_0}(Xcos\psi -Ysin\psi ),\hfill \end{array}$$

(32)

$$\begin{array}{ccc}& & dY/d\tau ={\pi }_y,\hfill \end{array}$$

(33)

$$\begin{array}{ccc}& & dZ/d\tau ={\pi }_z,\hfill \\ & & d{\pi }_x/d\tau =\frac{\alpha {\pi }_{x}cos\psi }{k_0{w}_0}-\frac{{\alpha }^2(Xcos\psi -Ysin\psi )cos\psi }{k_0^2{w}_0^2}+\hfill \end{array}$$

(34)

$$\begin{array}{ccc}& & \frac{2\alpha (Ycos\psi +3Xsin\psi )}{k_0^3{w}_0^3},\hfill \\ & & d{\pi }_y/d\tau =-\frac{\alpha {\pi }_{x}sin\psi }{k_0{w}_0}+\frac{{\alpha }^2(Xcos\psi -Ysin\psi )sin\psi }{k_0^2{w}_0^2}+\hfill \end{array}$$

(35)

$$\begin{array}{ccc}& & \frac{2\alpha (Xcos\psi +Ysin\psi )}{k_0^3{w}_0^3},\hfill \\ & & d{\pi }_z/d\tau =-\frac{\alpha {\pi }_x(Xsin\psi +Ycos\psi )}{k_0{w}_0}+\hfill \\ & & \frac{{\alpha }^2(Xsin\psi +Ycos\psi )(Xcos\psi -Ysin\psi )}{k_0^2{w}_0^2}-\hfill \end{array}$$

(36)

$$\begin{array}{ccc}& & \frac{\alpha (2XYsin\psi +(k_0^2{w}_0^2-(3X^2+Y^2))cos\psi )}{k_0^3{w}_0^3}.\hfill \end{array}$$

(37)

To test whether these equations can capture the main features of trapped trajectories for the case study at hand, Figure 5 gives a representative example of two sample trajectories that are born quite close to the laser beam origin, computed from the numerical solution of the full relativistic Lorentz equation and from the canonical equations above. Quantitative agreement is very good, allowing to predict the low frequency modulation of the transverse variables, and how their amplitudes and mutual phase depend on the initial conditions.

The approximate Equation (31) has the structure of a non-relativistic Hamiltonian. Then, one would expect that it may be an unreliable approximation when the electron separation from the origin of coordinates increases and/or the electron velocities increase towards c.

3.2. Case-Study 2: Narrow Laser Beam Spot, $w_0$ = 6.4 $\mathsf{\mu }$m

Figure 6 and Figure 7 show four examples of trapped trajectories with initial conditions inside a circle or radius $w_0/20$ around the centre of the laser beam (see

Table 2. Sample initial conditions for trapped trajectories, case-study with $w_0=6.4$ $\mathsf{\mu }$m.

$x_0$ [$\mathsf{\mu }$m]	$y_0$ [$\mathsf{\mu }$m]	$z_0$ [$\mathsf{\mu }$m]
−0.2185	0.2189	0.0
0.1244	−0.069	0.0
0.2846	−0.1308	0.0
0.1123	−0.072	0.0

for details).

The first characteristic to note about trapped solutions in this case study, differing markedly from case study 1, is their rather complex temporal behavior, perhaps more easily seen in terms of the velocity components and the $\gamma \left(t\right)$ factor (Figure 8 and Figure 9). The oscillations in the transverse plane proceed at a much faster characteristic frequency than in case-study 1 treated before. It seems clear that the growing amplitudes of the $B_z$ and $E_z$ components, that scale with the dimensionless parameter $1/(k_0\times w_0)$, play a key role in this connection.

A parametric plot of the trajectories’ projection onto the $xy$ plane shows them to become quite complex with decreasing $w_0$. Of course, the character of the movements (whether they are quasi periodic or even chaotic for some combination of the parameters) cannot be ascertained simply from those plots. A more extensive numerical study of these aspects lies outside the scope of this paper, and should be addressed elsewhere.

As in case-study 1 in the previous subsection, trapped solutions are also characterized here by their TS spectrum, averaged over many independent realizations of electron trajectories. A detection point located 0.5 m from the beam centre, along the y axis, is chosen to compute the spectrum. Figure 10 shows the averaged spectrum, featuring an overall shift towards lower frequencies in this case ( as compared with case-study 1), the appearance of spectral peaks at rather low frequencies, and a more balanced contribution of its x and z quadratures.

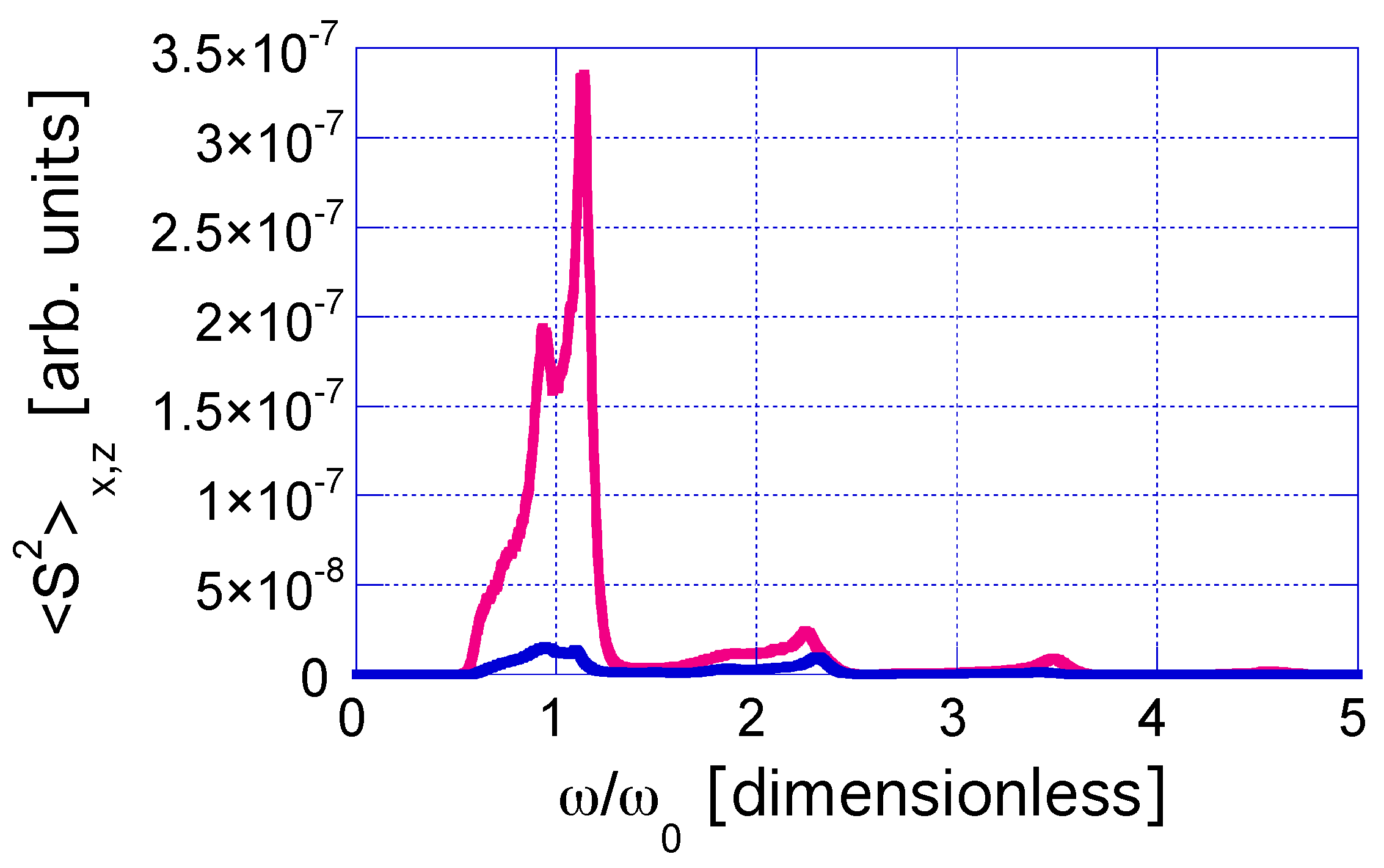
4. Electron Dynamics in Ultrashort-Pulse, Paraxial Laser Beams with OAM

In this section, we report results about electron dynamics in genuine ultrashort laser pulses with paraxial OAM fields. The fields are in this case

$$\begin{array}{ccc}& & {\overline{E}}_{par}=i{\omega }_0{\overline{A}}_{par,0}\times e^{-{\left(\frac{k_{0}z-{\omega }_{0}t-k_0{z}_{0p}}{{\omega }_0{T}_p}\right)}^2}\hfill \end{array}$$

(38)

$$\begin{array}{ccc}& & E_{z,par}=-i{k}_0{\Phi }_{par,0}\times e^{-{\left(\frac{k_{0}z-{\omega }_{0}t-k_0{z}_{0p}}{{\omega }_0{T}_p}\right)}^2}\hfill \end{array}$$

(39)

$$\begin{array}{ccc}& & B_{x,par}=-i{k}_0{A}_{y,par,0}\times e^{-{\left(\frac{k_{0}z-{\omega }_{0}t-k_0{z}_{0p}}{{\omega }_0{T}_p}\right)}^2}\hfill \end{array}$$

(40)

$$\begin{array}{ccc}& & B_{y,par}=i{k}_0{A}_{x,par,0}\times e^{-{\left(\frac{k_{0}z-{\omega }_{0}t-k_0{z}_{0p}}{{\omega }_0{T}_p}\right)}^2}\hfill \end{array}$$

(41)

$$\begin{array}{ccc}& & B_{z,par}=(\frac{\partial }{\partial x}{A}_{y,par,0}-\frac{\partial }{\partial y}{A}_{x,par,0})\times e^{-{\left(\frac{k_{0}z-{\omega }_{0}t-k_0{z}_{0p}}{{\omega }_0{T}_p}\right)}^2}\hfill \end{array}$$

(42)

where $T_p$ defines the temporal width of the laser pulse and $z_{0p}$ the center of the gaussian envelope at the initial time $t=0$. $T_p=8\times {\lambda }_0/c$ and $z_{0p}=-24\times {\lambda }_0$ are chosen in the computations. $T_p$ is connected with the temporal FWHM of the pulse by the simple relation FWHM = $2\sqrt{(ln2)}Tp$, and is equal to 35.52 [fs] in our case. We now impose $A_{y,par},0=0$. $A_{x,par,0},{\Phi }_{par,0}$ are respectively equal to $A_{x,par},{\Phi }_{par}$ in Section 3, except for the factor $e^{-{\left(\frac{k_{0}z-{\omega }_{0}t-k_0{z}_{0p}}{{\omega }_0{T}_p}\right)}^2}$, which has been displayed explicitly for convenience. The laser parameters are also the same as in Section 3. The electrons are located initially at $z_0=0$, hence very far away from the center of the Gaussian envelope, and in all cases $E_{kin0}=0$. Their transverse distribution is discussed below. The physical picture is that of an ultra-intense laser pulse that propagates towards the electron and the transient dynamics is studied. We look for specific effects related with the OAM pulsed fields, either with their transverse structure or the presence of longitudinal fields.

A convenient tool to investigate those effects that are genuinely associated to the paraxial characteristics of the laser fields, is the analytical solution found for the electron dynamics in a Gaussian pulsed plane wave (Appendix A). That analytical solution is completely general as regards the intensity of the electromagnetic field or the energy and initial position of the electron, but it considers neither any structure transverse to the propagation direction nor any longitudinal fields. But it turns out, nevertheless, that in some specific cases, the analytical solution in Appendix A provides an excellent quantitative fit to the more complex paraxial dynamics. Hence, we have the opportunity to contrast the analytical solution against the paraxial one, in order to clarify the role of the different mechanisms leading to the observed dynamics.

We study two cases, one of a wide laser beam spot, $w_0=100.0$ $\mathsf{\mu }$m and the other of a narrow laser beam spot $w_0=6.4$$\mathsf{\mu }$m.

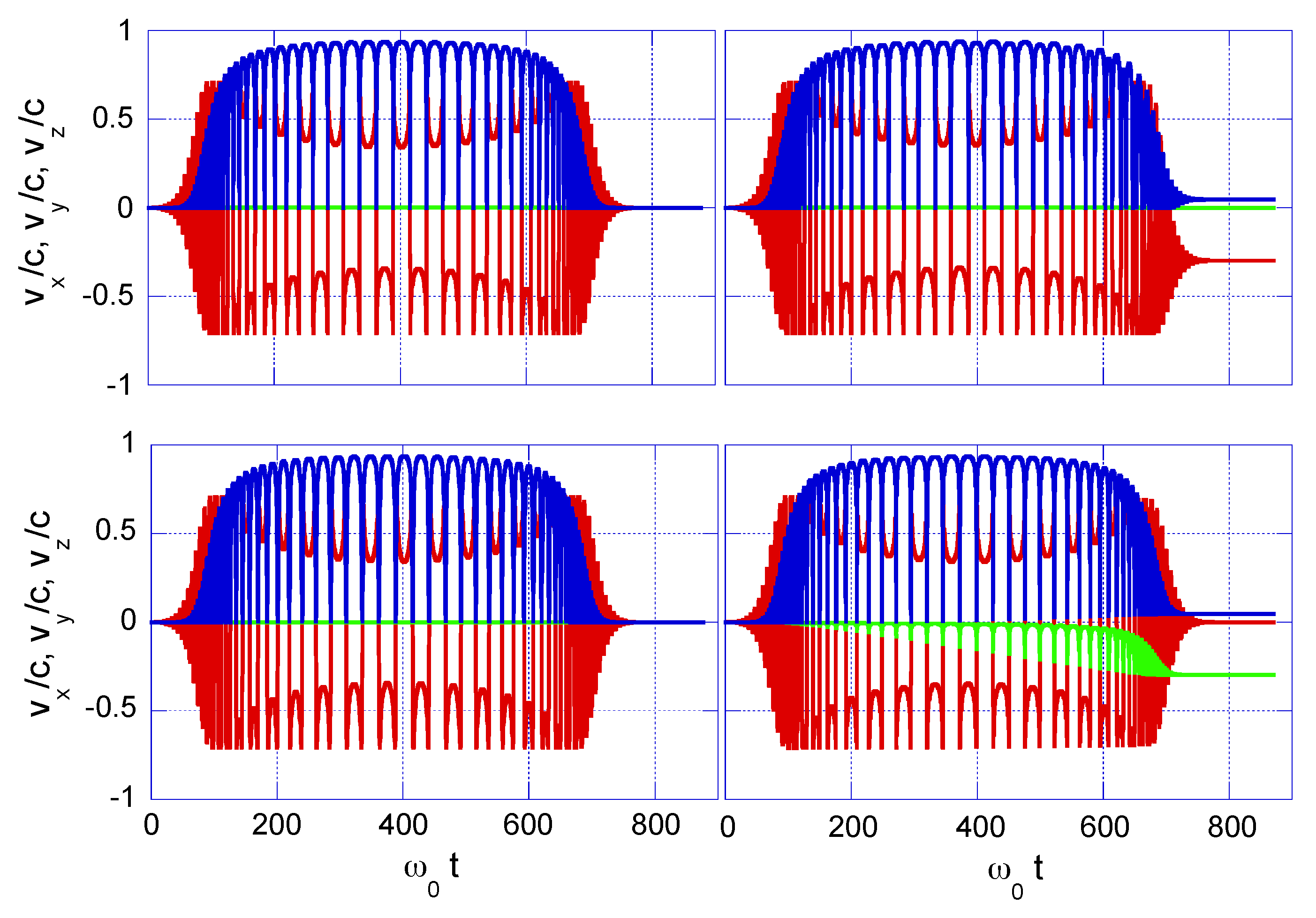
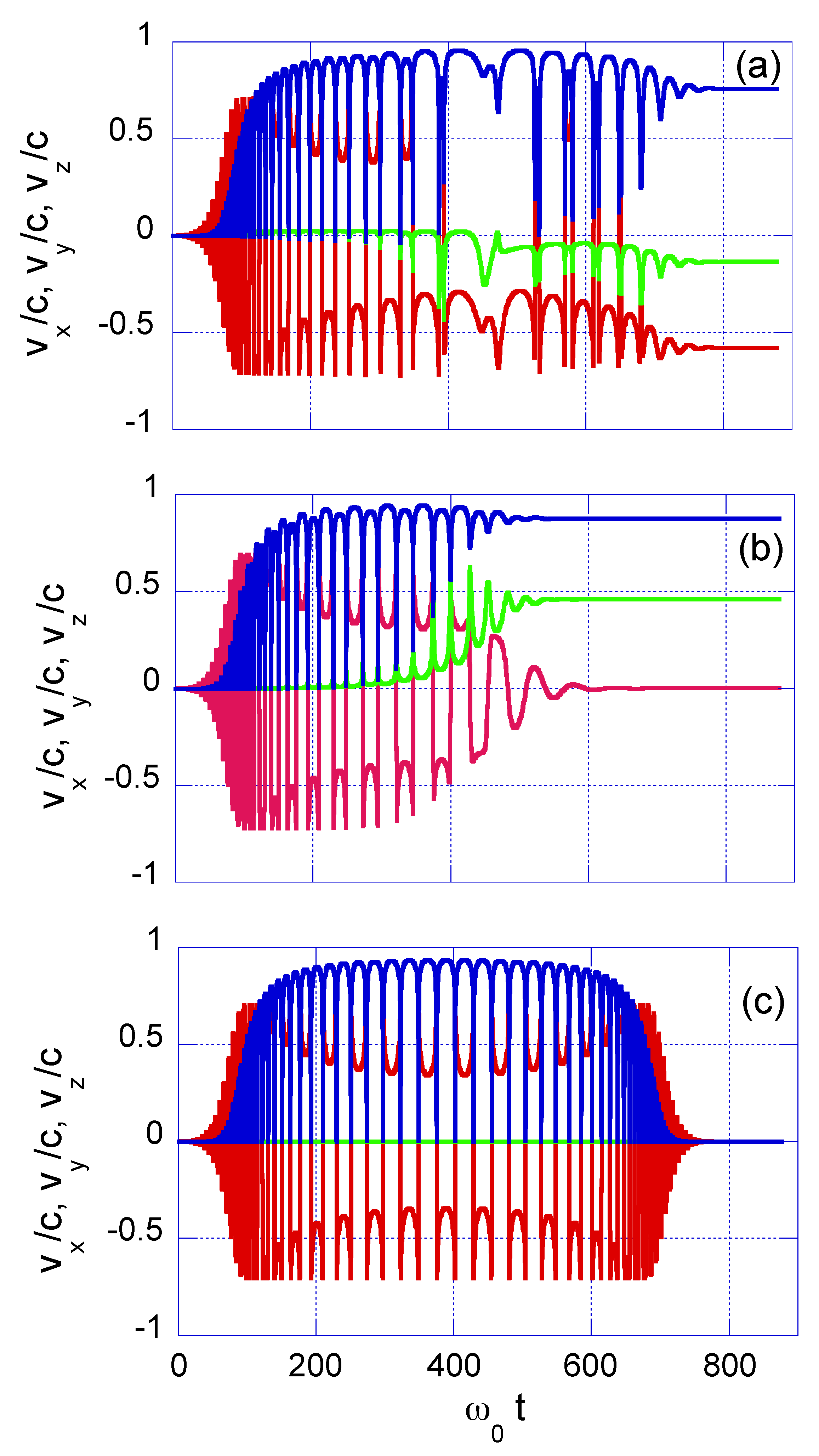
4.1. Case-Study 1: Pulsed Laser with Wide Beam Spot, $w_0$ = 100.0 $\mathsf{\mu }$m

We find that electrons initially located at ${\rho }_0=\sqrt{x_0^2+y_0^2}=w_0/\sqrt{2}$ (or very close to it) in the transverse plane and $z_0=0$ are amenable to an excellent fit with the analytical solution, see Figure 11 for the case $x_0=w_0/\sqrt{2},y_0=0$. For other values of $x_0\in [-1.5\times w_0,1.5\times w_0]$ ($y_0=0$), the observed discrepancies of the paraxial solution with the analytical one arise because the electron acquires (asymptotically) in general non-vanishing values for $v_x$ and $v_z$, hence a substantial kinetic energy from the laser field, see Figure 11. If initial conditions of the form $x_0=0$, $y_0\in [-1.5\times w_0,1.5\times w_0]$ are considered instead, the electron acquires in general asymptotic non-vanishing values for $v_y$ and $v_z$. In particular, an asymptotic $v_y\ne 0$ is directly related with the longitudinal paraxial fields being different from zero. Hence, it is impossible that this behavior be modeled by the analytical solution: see Figure 11.

That the paraxial behavior cannot, in general, be modeled by the pulsed analytical solution is easy to see. Consider for example, the asymptotic value of the kinetic energy according to the latter one, which is found to be:

$$m_0{c}^2\left(\sqrt{1+\frac{f_{10}^2+f_{20}^2+\frac{{(m_0^2{c}^2-{\gamma }_1^2)}^2+f_{10}^2+f_{20}^2}{4{\gamma }_1^2}}{m_0^2{c}^2}}-1\right)$$

(43)

where

$$\begin{array}{c}\hfill f_{10}=p_{x0}+q{A}_x(t=0,z=0)\end{array}$$

(44)

$$\begin{array}{c}\hfill f_{20}=p_{y0}+q{A}_y(t=0,z=0)\end{array}$$

(45)

$$\begin{array}{c}\hfill {\gamma }_1=\sqrt{m_0^2{c}^2+p_{x0}^2+p_{y0}^2+p_{z0}^2}-p_{z0}\end{array}$$

(46)

As we are assuming that the initial kinetic energy of the electrons is zero, and that the electric field is polarized along the x-axis one gets $p_{x0}=p_{y0}=p_{z0}=0$, $f_{10}=q{A}_x(t=0,z=0)$, $f_{20}=0$, ${\gamma }_1=m_{0}c$. Considering the very low contribution of the term $q{A}_x(t=0,z=0)$ in our case (the electron is located very far away from the center of the gaussian pulse), the asymptotic kinetic energy would be essentially zero in all cases, no matter how large the maximum value of $\gamma \left(t\right)$ is in the course of the interaction with the gaussian plane wave pulse (Lawson-Woodward theorem). This proves that a good fit between the paraxial and analytical solutions is not to be expected, since the former predicts a substantial increase of the kinetic energy of the electron (in general) after the pulse has overtaken it, and the latter not.

But note that this could be radically changed if the electron initial position with respect to the plane pulsed wave is changed, so that the contributions from $q{A}_x$ (and eventually $q{A}_y$) is significant. In that case, the analytic pulsed solution shows that the asymptotic value of $E_{kin}$ depends not only on the initial momentum of the electron, but also on the amplitude and phase of the vector potential at its initial position. For ultra-intense lasers this contribution can be very high in absolute terms, although small if compared with the peak values of the pulsed field, and one can have a net energy change of the electron.

The asymptotic values for the final kinetic energy of the electrons have been studied as a function of their initial positions across the laser beam. For that purpose, we generate random initial conditions uniformly distributed across the laser beam up to a maximum radius of $1.5\times w_0$. The resulting distribution turns out to have a non-trivial rotational symmetry around the optical axis, that is broken to a lower one if the contributions of axial fields $E_z$ and $B_z$ are set to zero in the numerical simulations. The maximum value of asymptotic kinetic energy is found to be 472.11 keV for a sample of 2048 initial conditions, see Figure 12 and Figure 13.

4.2. Case-Study 2: Pulsed Laser with Narrow Beam Spot, $w_0$ = 6.4 $\mathsf{\mu }$m

This case differs substantially from the previous one in several respects: on the one side, the (pulsed) temporal evolution is less ordered, and no clear quantitative match of the paraxial solution and the analytical solution is found, see Figure 14 and Figure 15. A fraction of the initial conditions studied (randomly distributed inside a circle of radius $1.5\times w_0$) leads the electron to leave the laser spot quite fast, consequently acquiring a very large final kinetic energy.

The asymptotic kinetic energy of the electron has also been studied in this case as a function of the initial position across the laser beam. Initial conditions uniformly distributed across the laser beam up to a maximum radius of $1.5\times w_0$ have been generated. The resulting distribution turns out also to have a non-trivial rotational symmetry around the optical axis (substantially different in shape from the one in the former case) and with a maximum value (in a sample of 16384 initial conditions) equal to 3.74 MeV, see Figure 16 and Figure 17.

5. Conclusions and Discussions

Our approach in this paper employs the Lorentz gauge (namely, non-vanishing vector and scalar potentials) for describing the electromagnetic field and, moreover, the Lorentz condition. One generic advantage of such a framework is a systematic treatment of the paraxial approximation and the corrections to it. Upon identifying clearly the vector potential and the scalar potential of the paraxial field, our method has, in particular, the following advantage: it allows, at a later stage, a systematic approximation of the full relativistic Hamiltonian for the electron by a simpler form, capturing the main phenomenology of trapped solutions, for instance.

The numerical experiments in this paper show, in particular, that the “extra” terms appearing in [18] (the lowest corrections to the paraxial approximation in their method), as compared to our approach, have a negligible influence in the studies reported here. Hence, those extra terms are of extremely small magnitude.

In Section 3, the paper presents results on electron dynamics in ultra-intense paraxial laser beams with net orbital angular momentum (OAM). The paper elucidates the nature and conditions for so called trapped solutions, that is, solutions that are bounded in the transverse plane of the laser and drifting, in general, along the propagation direction. The influence of laser parameters on them, in particular the laser beam size and the non-vanishing longitudinal field components, essential for the paraxial approximation to be fulfilled, is studied. When the initial conditions of the electrons are sufficiently close to the origin, a simplified model Hamiltonian to the full relativistic one is introduced, depending basically on the dimensionless combination $k_0{w}_0$ for fixed laser intensity. The results from this simplified Hamiltonian compare quite well quantitatively with the observed amplitudes, phase relationships and frequencies of oscillation of trapped solutions, at least for the case of wide laser beam size, $w_0=100.0$ $\mathsf{\mu }$m.

Section 4 is devoted to ultrashort-pulse paraxial laser beams with OAM, including also a comparison of the paraxial dynamics with the results of the analytical solution for a pulsed plane wave with Gaussian envelope, given in Appendix A.

In Appendix A, we obtain an exact analytical solution of the electron dynamics in a pulsed plane wave with a Gaussian envelope. The solution is valid for any field intensity or initial energy of the electron and its predictions are compared with the dynamics in more complex paraxial fields with OAM. In some cases that are quantitatively characterized, the analytical model is an excellent approximation to the paraxial dynamics. Departures from the analytical solution are traced back to the combined influence of the transverse structure of the laser field and the longitudinal $E_z$ and $B_z$ components whose influence scale with the inverse of the laser beam size. It is argued that one of the limitations of the analytical solution to fit the paraxial one (in the particular set up studied in this paper) is the very small contribution of the laser fields at the initial position of the electron. A comparison of the paraxial and analytical solutions in a set-up where the effect of $q{A}_x(t=0,z=0),q{A}_y(t=0,z=0)$ is not negligible can contribute to gain some analytical insight into paraxial dynamics, but this issue should be addressed elsewhere.

We study the asymptotic distribution of the kinetic energy of the electrons as a function of their initial position over the transverse section of pulsed beams with OAM, both for a wide beam of $w_0=$ 100.0 $\mathsf{\mu }$m and for a narrow beam of $w_0=$ 6.4 $\mathsf{\mu }$m. The relative importance of the transverse structure effects and the role of longitudinal fields are addressed. We find that including the full paraxial fields with their longitudinal components, the asymptotic distribution of kinetic energy of an electron population distributed across the laser beam section, has a nontrivial rotational symmetry along the optical propagation axis. If we set $E_z=0$, $B_z=0$ in the numerical codes, the mentioned symmetry is broken to a lower one.

Position and velocity have been used in this work (Section 3.1 and Figure 3, Figure 8, Figure 11, Figure 14 and Figure 15) as dynamical variables to characterize the electron behavior; in other more theoretical studies, position and momentum are commonly used (Section 3.1 and Section 4, Appendix A). In some of our most recent computations, and taking advantage of the identification of the scalar and vector potentials for paraxial fields, the Hamiltonian approach is used. Further results of this approach, under investigation but not included here, are fully compatible with those presented in the paper, and the computer algebra system Mathematica seems to deal with both descriptions of the dynamics in an efficient way.

A novel approach to corrections to the paraxial approximation is summarized in Appendix B. The exact solution $X_{ex}$ of Equation (6), associated to Equation (5), is shown to fulfill a linear integral equation. The latter contains the paraxial function $X_{par}$ (displaying a Gaussian structure) given in Equation (14) as the inhomogeneous term, a suitable Green function and $-\frac{{\partial }^2}{\partial z^2}$ (discarded in the framework of the paraxial approximation) as perturbation. The successive iterations of the integral equation give rise to corrections to $X_{par}$. One result of the analysis is that any iteration displays the same Gaussian structure as $X_{par}$.