Theoretical Comparison of Optothermal Absorption in Transmissive Metalenses Composed of Nanobricks and Nanoholes
Abstract
:1. Introduction
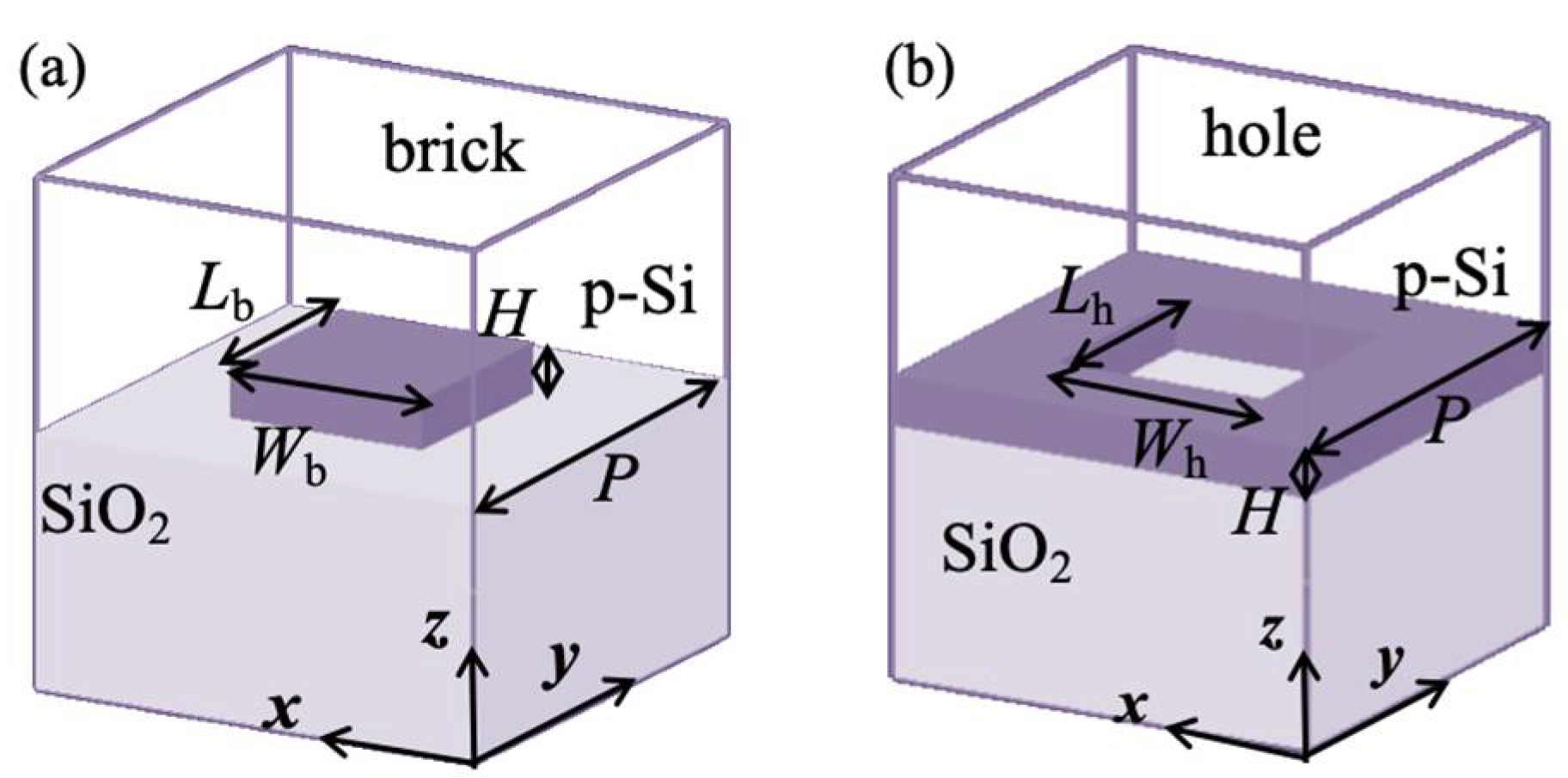
2. Materials and Methods
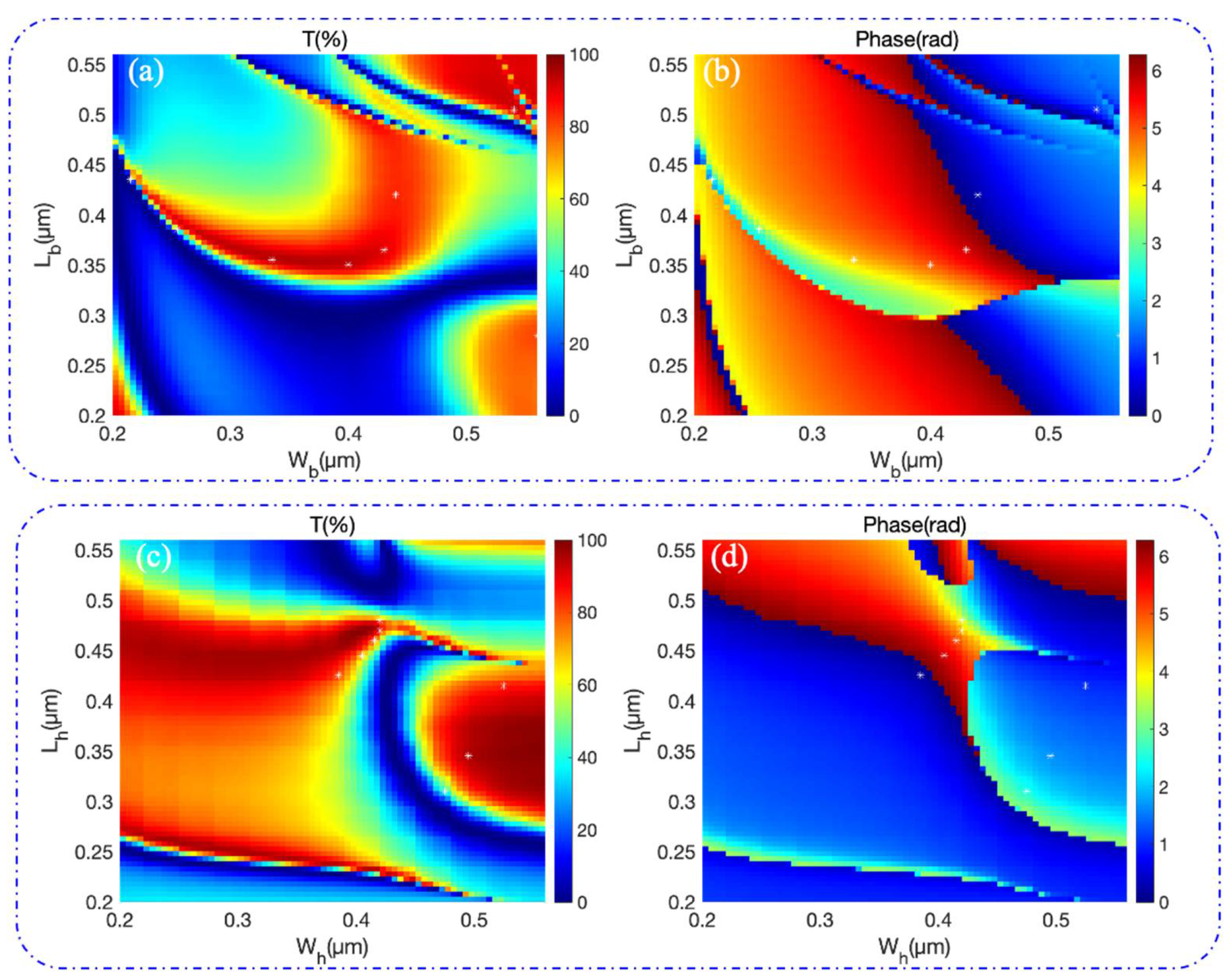
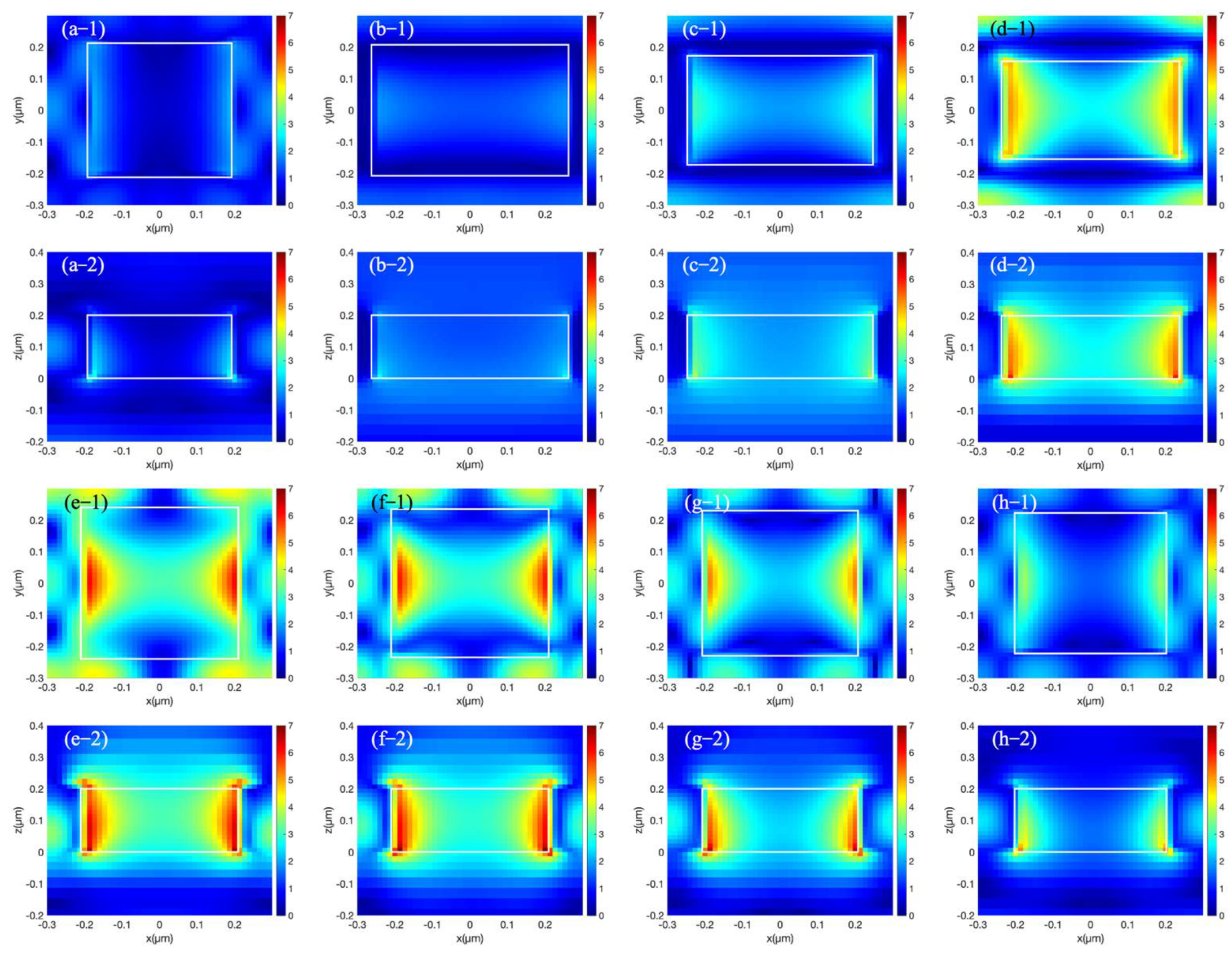
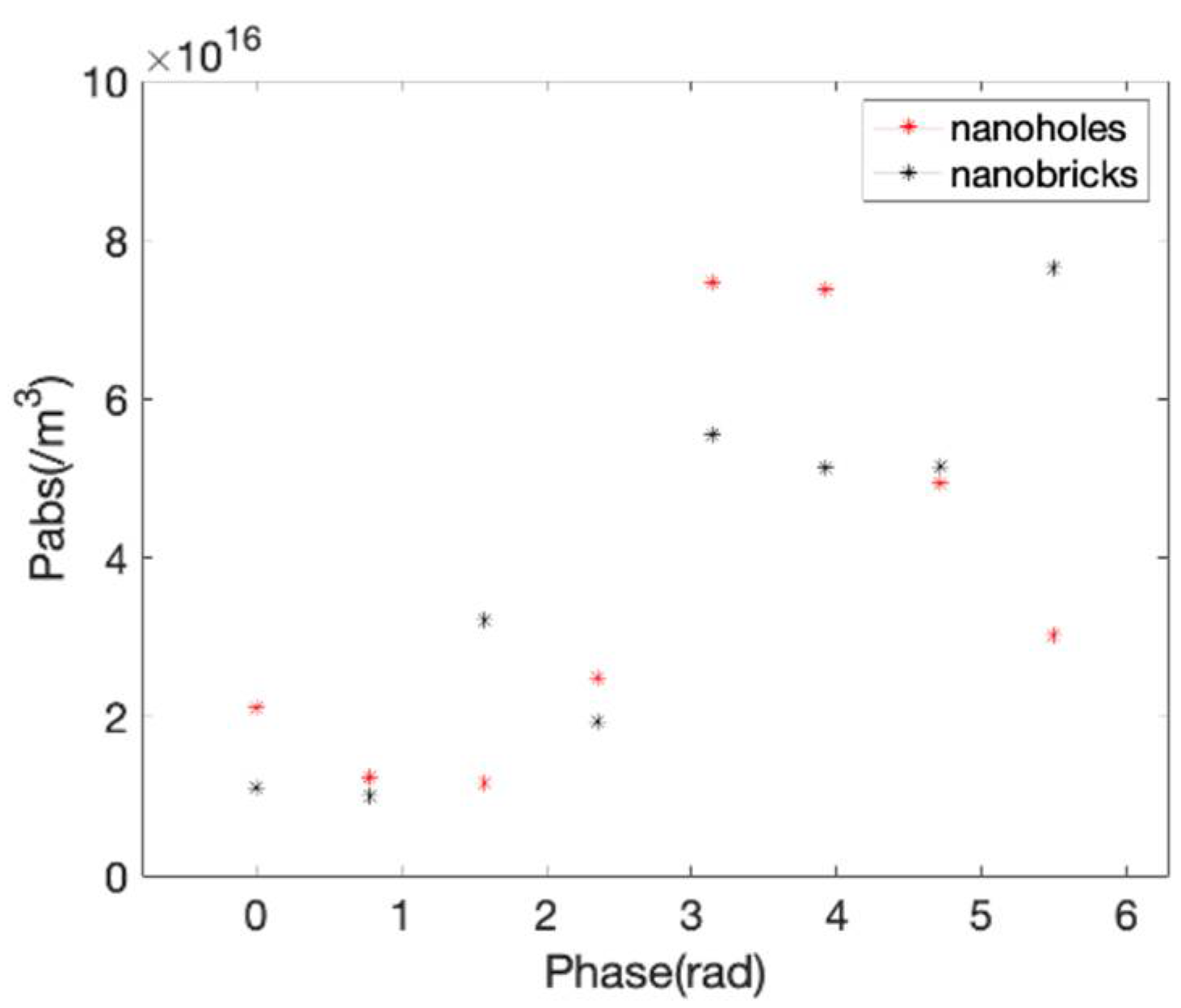
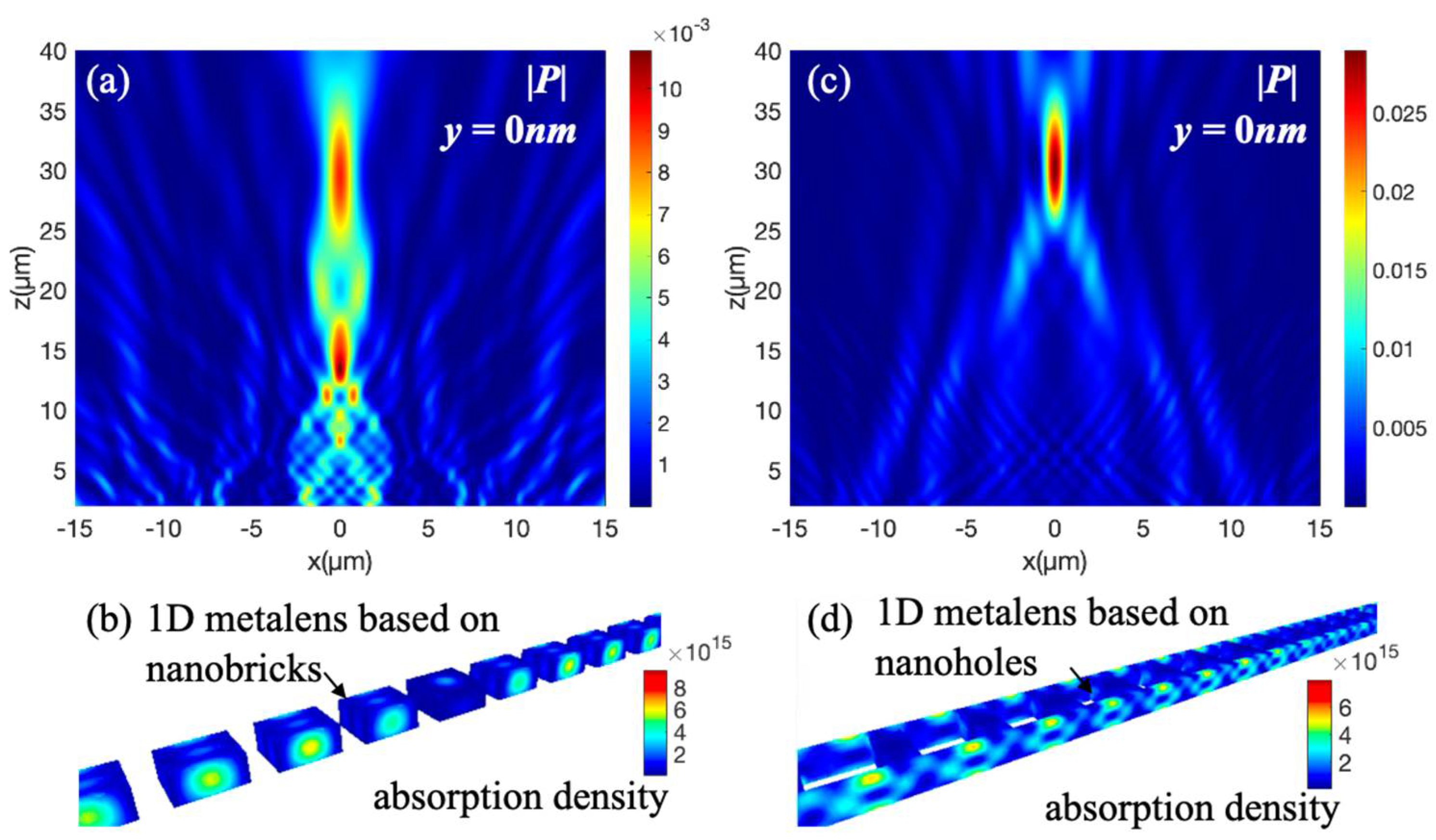
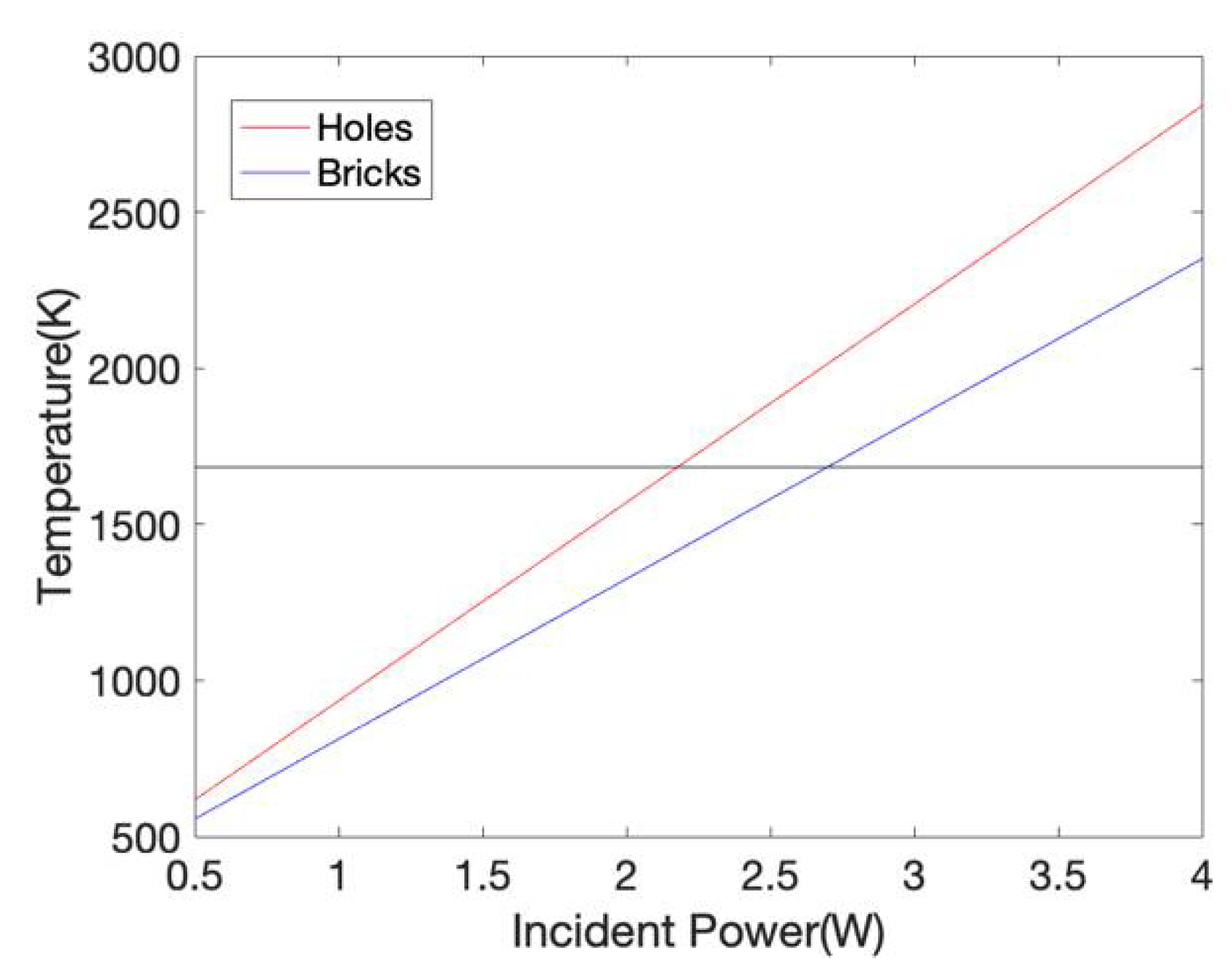
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xie, X.; Weng, Q.; Luo, Z.; Long, J.; Wei, X. Thermal performance of the flat micro-heat pipe with the wettability gradient surface by laser fabrication. Int. J. Heat Mass Transf. 2018, 125, 658–669. [Google Scholar] [CrossRef]
- Wang, Z.; Palmer, T.A.; Beese, A. Effect of processing parameters on microstructure and tensile properties of austenitic stainless steel 304L made by directed energy deposition additive manufacturing. Acta Mater. 2016, 110, 226–235. [Google Scholar] [CrossRef] [Green Version]
- Miquel, J.-L.; Lion, C.; Vivini, P. The Laser Mega-Joule: LMJ & PETAL status and Program Overview. J. Phys. Conf. Ser. 2016, 688, 012067. [Google Scholar] [CrossRef]
- Moses, E.I.; Lindl, J.D.; Spaeth, M.L.; Patterson, R.W.; Sawicki, R.H.; Atherton, L.J.; Baisden, P.A.; Lagin, L.J.; Larson, D.W.; MacGowan, B.J.; et al. Overview: Development of the National Ignition Facility and the Transition to a User Facility for the Ignition Campaign and High Energy Density Scientific Research. Fusion Sci. Technol. 2016, 69, 1–24. [Google Scholar] [CrossRef]
- Faraji-Dana, M.; Arbabi, E.; Arbabi, A.; Kamali, S.M.; Kwon, H.; Faraon, A. Compact folded metasurface spectrometer. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef]
- Li, Z.; Tang, F.; Shang, S.; Wu, J.; Shao, J.; Liao, W.; Kong, B.; Zeng, T.; Ye, X.; Jiang, X.; et al. Compact metalens-based integrated imaging devices for near-infrared microscopy. Opt. Express 2021, 29, 27041. [Google Scholar] [CrossRef] [PubMed]
- Paniagua-Domínguez, R.; Yu, Y.F.; Khaidarov, E.; Choi, S.; Leong, V.; Bakker, R.M.; Liang, X.; Fu, Y.H.; Valuckas, V.; Krivitsky, L.A.; et al. A Metalens with a Near-Unity Numerical Aperture. Nano Lett. 2018, 18, 2124–2132. [Google Scholar] [CrossRef] [Green Version]
- Pu, M.; Li, X.; Guo, Y.; Ma, X.; Luo, X. Nanoapertures with ordered rotations: Symmetry transformation and wide-angle flat lensing. Opt. Express 2017, 25, 31471–31477. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, Y.; Han, H.; Wang, X.; Zhou, L.; Yi, Z.; Fu, Z.; Wu, X.; Li, G.; Zeng, L. Optical and magnetic properties of small-size core–shell Fe3O4@C nanoparticles. Mater. Today Chem. 2021, 22, 100556. [Google Scholar] [CrossRef]
- Zhou, F.; Qin, F.; Yi, Z.; Yao, W.-T.; Liu, Z.; Wu, X.; Wu, P. Ultra-wideband and wide-angle perfect solar energy absorber based on Ti nanorings surface plasmon resonance. Phys. Chem. Chem. Phys. 2021, 23, 17041–17048. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, Y.; Luo, Y.; Zhang, J.; Yi, Z.; Wu, X.; Cheng, S.; Yang, W.; Yu, Y.; Wu, P. A four-band and polarization-independent BDS-based tunable absorber with high refractive index sensitivity. Phys. Chem. Chem. Phys. 2021, 23, 26864–26873. [Google Scholar] [CrossRef]
- Hsiao, H.-H.; Chu, C.H.; Tsai, D.P. Fundamentals and Applications of Metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Xu, Z.; Dong, Y.; Hu, T.; Zhong, Q.; Fu, Y.H.; Zhu, S.; Singh, N. Large-area metasurface on CMOS-compatible fabrication platform: Driving flat optics from lab to fab. Nanophotonics 2020, 9, 3071–3087. [Google Scholar] [CrossRef]
- Hou-Tong, C.; Antoinette, J.T.; Nanfang, Y. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar]
- Lin, R.J.; Su, V.-C.; Wang, S.; Chen, M.K.; Chung, T.L.; Chen, Y.H.; Kuo, H.Y.; Chen, J.-W.; Chen, J.; Huang, Y.-T.; et al. Achromatic metalens array for full-colour light-field imaging. Nat. Nanotechnol. 2019, 14, 227–231. [Google Scholar] [CrossRef]
- Wang, S.; Lai, J.; Wu, T.; Chen, C.; Sun, J. Wide-band achromatic flat focusing lens based on all-dielectric subwavelength metasurface. Opt. Express 2017, 25, 7121–7130. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.F.; Zhu, A.Y.; Paniagua-Dominguez, R.; Fu, Y.H.; Luk’Yanchuk, B.; Kuznetsov, A.I. High-transmission dielectric metasurface with 2π phase control at visible wavelengths. Laser Photon Rev. 2015, 9, 412–418. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Sun, J.; Tsukernik, A.; Pandey, A.; Nikolskiy, K.; Litchinitser, N.M. High-Efficiency All-Dielectric Metasurfaces for Ultracompact Beam Manipulation in Transmission Mode. Nano Lett. 2015, 15, 6261–6266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, L.; Zhang, X.; Kenney, M.; Su, X.; Xu, N.; Ouyang, C.; Shi, Y.; Han, J.; Zhang, W.; Zhang, S. Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 2014, 26, 5031–5036. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, X.; Chen, Y.; Liu, Q.; Li, X.; Wang, Y.; Liu, N.; Duan, H. 3D-Integrated metasurfaces for full-colour holography. Light. Sci. Appl. 2019, 8, 1–9. [Google Scholar] [CrossRef]
- Lingling, H.; Shuang, Z.; Thomas, Z. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar]
- Berzinš, J.; Indrišiūnas, S.; Fasold, S.; Steinert, M.; Žukovskaja, O.; Cialla-May, D.; Gečys, P.; Bäumer, S.M.B.; Pertsch, T.; Setzpfandt, F. Laser-induced spatially-selective tailoring of high-index dielectric metasurfaces. Opt. Express 2020, 28, 1539–1553. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Y.; Yan, M.; Qiu, M. Nanosecond Photothermal Effects in Plasmonic Nanostructures. ACS Nano 2012, 6, 2550–2557. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, L.; Hu, D.; Chen, S.; Xie, S.; Lu, Y.; Cao, Y.; Zhu, Z.; Jin, L.; Guan, B.-O.; et al. Full-visible multifunctional aluminium metasurfaces by in situ anisotropic thermoplasmonic laser printing. Nanoscale Horiz. 2019, 4, 601–609. [Google Scholar] [CrossRef]
- Zhu, X.; Yan, W.; Levy, U.; Mortensen, N.A.; Kristensen, A. Resonant laser printing of structural colors on high-index dielectric metasurfaces. Sci. Adv. 2017, 3, e1602487. [Google Scholar] [CrossRef] [Green Version]
- Aouassa, M.; Mitsai, E.; Syubaev, S.; Pavlov, D.; Zhizhchenko, A.; Jadli, I.; Hassayoun, L.; Zograf, G.; Makarov, S.; Kuchmizhak, A. Temperature-feedback direct laser reshaping of silicon nanostructures. Appl. Phys. Lett. 2017, 111, 243103. [Google Scholar] [CrossRef]
- Ye, X.; Hu, X.; Tang, F.; Wu, J.; Yang, L.; Huang, J.; Zheng, W. Laser field manipulation and laser damage resistance property of nanotextures on fused silica optics. Results Phys. 2020, 18, 103262. [Google Scholar] [CrossRef]
- Jing, X.; Tian, Y.; Han, J.; Ma, J.; Jin, Y.; Shao, J.; Fan, Z. Polarization effect of femtosecond pulse breakdown in subwavelength antireflective relief grating. Opt. Commun. 2011, 284, 4220–4224. [Google Scholar] [CrossRef]
- Yu, H.; Tang, F.; Chen, J.; Yi, Z.; Ye, X.; Wang, Y. Reflective Meta-Films with Anti-Damage Property via Field Distribution Manipulation. Coatings 2021, 11, 640. [Google Scholar] [CrossRef]
- Yu, H.; Tang, F.; Wu, J.; Yi, Z.; Ye, X.; Wang, Y. Meta-Deflectors Made of Dielectric Nanohole Arrays with Anti-Damage Potential. Photonics 2021, 8, 107. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, F.; Li, Q.; Yu, H.; Yi, Z.; Ye, X. Theoretical Comparison of Optothermal Absorption in Transmissive Metalenses Composed of Nanobricks and Nanoholes. Photonics 2022, 9, 39. https://doi.org/10.3390/photonics9010039
Tang F, Li Q, Yu H, Yi Z, Ye X. Theoretical Comparison of Optothermal Absorption in Transmissive Metalenses Composed of Nanobricks and Nanoholes. Photonics. 2022; 9(1):39. https://doi.org/10.3390/photonics9010039
Chicago/Turabian StyleTang, Feng, Qingzhi Li, Haichao Yu, Zao Yi, and Xin Ye. 2022. "Theoretical Comparison of Optothermal Absorption in Transmissive Metalenses Composed of Nanobricks and Nanoholes" Photonics 9, no. 1: 39. https://doi.org/10.3390/photonics9010039
APA StyleTang, F., Li, Q., Yu, H., Yi, Z., & Ye, X. (2022). Theoretical Comparison of Optothermal Absorption in Transmissive Metalenses Composed of Nanobricks and Nanoholes. Photonics, 9(1), 39. https://doi.org/10.3390/photonics9010039





