Competition between Entrainment Phenomenon and Chaos in a Quantum-Cascade Laser under Strong Optical Reinjection

Abstract

The topic of external optical feedback in quantum-cascade lasers is relevant for stability and beam-properties considerations. Albeit less sensitive to external optical feedback than other lasers, quantum-cascade lasers can exhibit several behaviors under such feedback, and those are relevant for a large panel of applications, from communication to ranging and sensing. This work focused on a packaged Fabry–Perot quantum-cascade laser under strong external optical feedback and shows the influence of the beam-splitter characteristics on the optical power properties of this commercially available laser. The packaged quantum-cascade laser showed extended conditions of operation when subject to strong optical feedback, and the maximum power that can be extracted from the external cavity was also increased. When adding a periodic electrical perturbation, various non-linear dynamics were observed, and this complements previous efforts about the entrainment phenomenon in monomode quantum-cascade lasers, with the view of optimizing private communication based on mid-infrared quantum-cascade lasers. Overall, this work is a step forward in understanding the behavior of the complex quantum-cascade-laser structure when it is subjected to external optical feedback.

1. Introduction

Quantum-cascade lasers (QCLs) are semiconductor lasers relying on intersubband transitions that are able to exhibit high optical power and superior beam-quality features in the mid-infrared domain [1]. Free-running QCLs are touted for applications such as countermeasure systems [2] and selective surgery [3], because of mid-infrared high-atmosphere transmission and strong human-tissue absorption, respectively. Due to their overdamped nature, QCLs are less sensitive to external optical feedback (also called reinjection) than interband semiconductor lasers exhibiting relaxation oscillations [4,5,6]. Recent developments brought new insights about QCLs under reinjection [7,8], but both experimental and numerical breakthroughs are still expected in order to bridge the gaps and understand some peculiar features of QCLs under reinjection, such as the limited bandwidth of QCLs’ non-linear dynamics [9]. External optical feedback can stabilize QCLs [10], which is of prime interest for sensing applications, and can modify the far-field characteristics of the beam in the case of broad-area QCLs [11] or can increase the optical power of the laser. Interestingly, high feedback ratios can also lead to various non-linear dynamics in the output of the QCL [12,13,14]. One of the dynamics of paramount importance is called chaos, corresponding to the coherence collapse regime, and is used for private communication [15]. Optical chaos is also found useful in LIDAR [16] because of the unpredictability of the generated optical signal. That allows a very precise matching between the emitted wave and the reflected wave, which, in turn, leads to an accurate distance measurement. Moreover, the use of chaotic signals instead of modulated waves leads to detection systems resistant to noise and jamming. When a QCL is under external optical feedback and periodic forcing, a pattern called the entrainment phenomenon can be found in the laser output [17]. Entrainment corresponds to dynamics where the dropouts, commonly found with chaos fluctuations, are synchronized with the external modulation [18,19,20]. Previous studies about QCLs only focused on a fixed feedback ratio when applying external modulation at various frequencies and did not observe any distortion of the entrainment pattern. In this work, we focused on a Fabry–Perot (FP)-packaged QCL, and we showed in a first part that the maximum output power of a QCL can be increased by applying a strong optical reinjection. Furthermore, this configuration was also found to increase the maximum temperature at which the laser can be operated. In a second part, we varied the optical reinjection scheme to show that the entrainment phenomenon can be observed simultaneously with coherence collapse dynamics. Low and strong feedback ratios lead to a stable sine pattern, and when changing the feedback ratio, destabilization islands were found with a combination of various dynamics. These findings impact on the understanding of non-linear dynamics of QCLs, and this is a key step in order to build reliable, real-field systems taking advantage of mid-infrared optical chaos, such as private-communication emitters/receivers and eye-safe LIDAR.

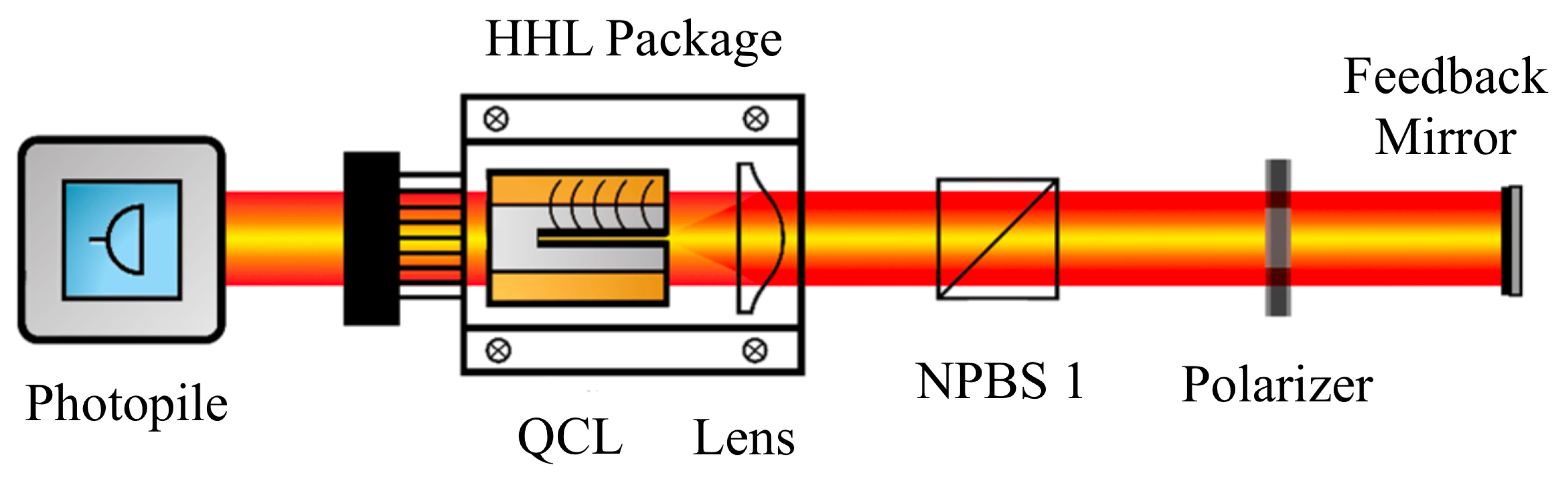
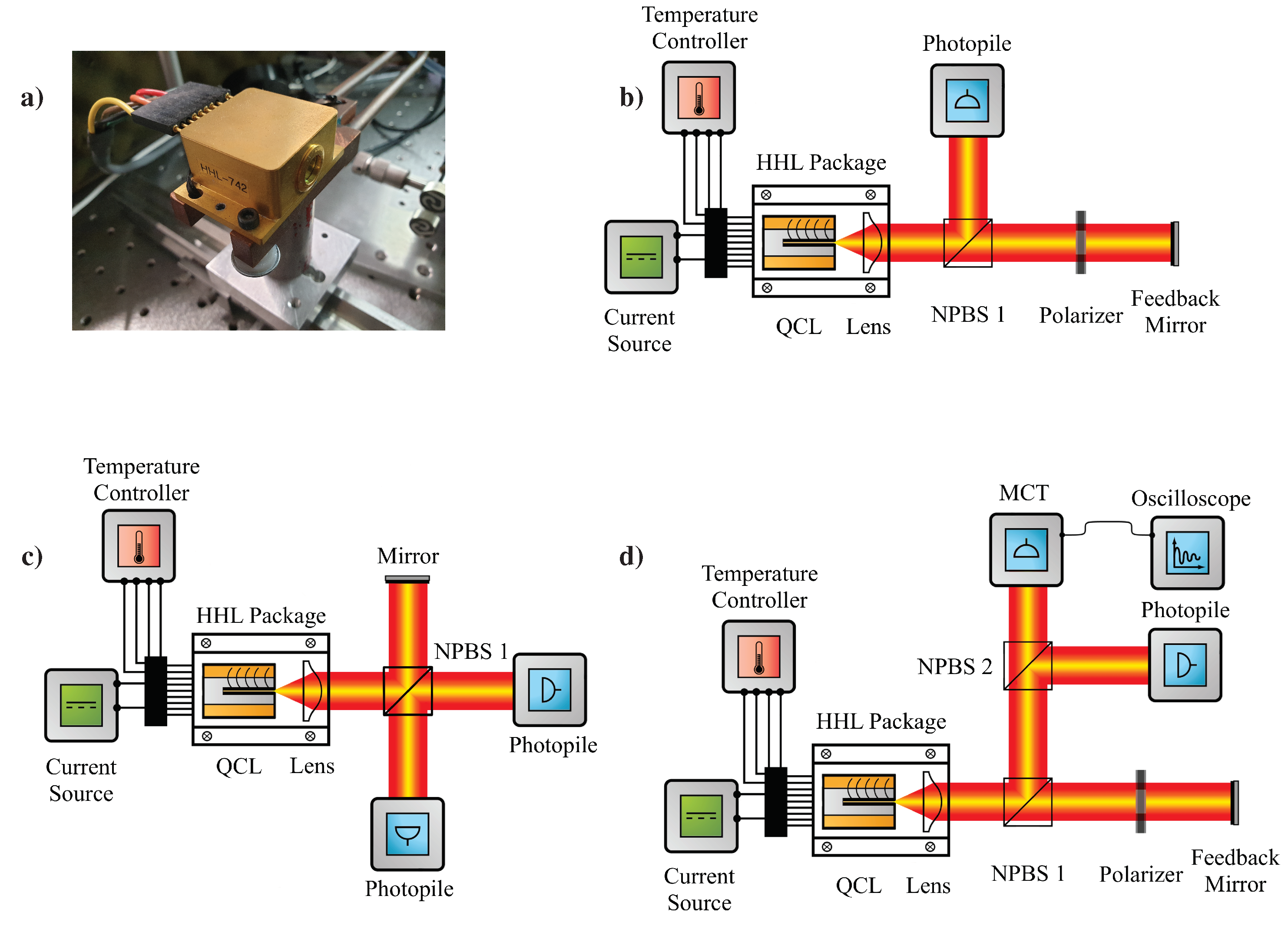
2. Materials and Methods

The QCL under study was a commercially available multimode laser emitting at a wavelength near 4 $\mathsf{\mu }$m. This device was purchased from Alpes Lasers. It is housed in a high-heat load (HHL) package that can be visualized in Figure 1a. This off-the-shelf case is sealed with a QCL Peltier system and a focusing lens inside and connectors for the current source and the temperature controller outside. The main characteristics of operation of this laser are described in Ref. [21]. Figure 1b describes the configuration under study with external optical feedback provided by a feedback mirror. The non-polarizing beam-splitter (NPBS) allows applying reinjection and studying the QCL’s beam simultaneously. Two different NPBS were considered during the experiment in order to maximize either the output power of the laser or the feedback ratio to display rich non-linear dynamics. The first one is a CaF${}_2$ NPBS, and it has a transmission ratio of 0.51, a reflection ratio of 0.45, and an absorption ratio of 0.04. In reinjection experiments, it is extremely complex to determine the exact amount of optical power that couples back into the laser’s cavity. This is due to the size of the laser waist and possible aberration from optical elements. However, in order to compare our results with the existing literature, we give a reference feedback ratio f${}_r$ in the following, but one has to keep in mind that part of this power can fall on the substrate, the p- and n-contacts, or shine outside of the global structure. Details about the measurement of this reference feedback ratio can be found in Appendix A. The maximum reference feedback ratio that can be achieved after one roundtrip into the external cavity is 0.24. This result takes into account the losses induced by the beam reflection on the mirror. The second one is a platinum NPBS, and it has a transmission ratio of 0.93, a reflection ratio of 0.06, and an absorption ratio of 0.01. The maximum reference feedback ratio that can be achieved after one roundtrip into the external cavity is now 0.80. After studying the influence of the type of NPBS, our efforts focused on the maximum optical power that is emitted by the QCL; so, two photopiles (Thorlabs S401C) connected to a power meter (Thorlabs PM320E) were placed in the detection paths, as shown in Figure 1c. In the last part, we investigated non-linear dynamics, and, consequently, the photopile facing the laser’s emitting facet was replaced by a fast HgCdTe (MCT) detector with a 700 MHz bandwidth (Figure 1d). The electrical signal from the MCT detector was then recorded by an oscilloscope (Tektronix MSO64 with a 1 GHz bandwidth and a 25 GSa/s sampling rate) when we studied the timetraces or by a signal analyzer (Rohde & Schwarz FSW 50 GHz) when we displayed the spectrogram. To adjust the feedback ratio, a polarizer was placed before the feedback mirror. This polarizer was mounted on a piezoelectric controller so that its rotation angle can be remote-controlled with high precision (Thorlab K10CR1).

3. Results

3.1. Optical Power Tuning with External Optical Feedback

External optical feedback is known for increasing the output power of QCLs while reducing the threshold current, and optimizing the alignment of the back-reflected light can be performed by maximizing the optical power or by achieving the minimum threshold current for a given feedback ratio. Previous experimental efforts have already shown these features in QCLs, but generally, the threshold reduction is in the order of a few percent of the free-running threshold current [22,23]. In other semiconductor lasers, the threshold reduction can be close to 30% of the free-running threshold bias [24,25]. For the packaged QCL under study, it can reach 36% under strong reinjection, as we show in the following. Figure 2 describes the light-intensity–voltage (LIV) curves at 25 ${}^{\circ }$C when the two aforementioned NPBS are used. On the one hand, one can see that the QCL’s voltage remains almost unchanged when varying f${}_r$. Even under a very strong reference feedback ratio, the voltage drop is in the order of 1% for the maximum bias current of our study, i.e., 800 mA. On the other hand, reinjection has a strong influence on the QCL’s optical power. For the configuration with the platinum beam splitter (Figure 2a), the maximum f${}_r$ was 0.80, and the threshold current was decreased to 350 mA under this condition, while it was 550 mA for the same free-running QCL. Decreasing f${}_r$ increases the threshold current in a non-linear trend: the threshold current was 410 mA for f${}_r$ = 0.32 then 460 mA for f${}_r$ = 0.18, and it finally reached 510 mA for f${}_r$ = 0.12. The same evolution can be observed for the CaF${}_2$ beam splitter (Figure 2b). Moreover, the maximum output power of the laser was drastically enhanced under strong reinjection. For the platinum NPBS, the maximum optical power was increased by a factor of 2.4, from 5.3 mW to 12.8 mW. Though this very strong reinjection leads to the largest power ratio with this packaged FP QCL, end-users are generally more interested in achieving the maximum output power with a given laser. The CaF${}_2$ NPBS has a lower transmission coefficient, and this means a lower f${}_r$, but its higher reflection coefficient means that more power can be extracted from our experimental configuration. Figure 2b shows that with this beam splitter and f${}_r$ = 0.24, the output power was 65.5 mW, which is an improvement compared to the zero-feedback case, but it is still lower than the free-running optical power of 86 mW at 25 ${}^{\circ }$C, as visualized in Figure 2c. Consequently, the idea was to modify the conventional reinjection scheme where the feedback mirror faces the laser and the photopile gathers the reflected light by a setup where the mirror reinjects the reflected light and two photopiles measure the total optical power escaping the cavity, as shown in Figure 1c. With this new configuration, we were able to outperform the performances of the free-running QCL when combining the power of the beams hitting the two photopiles, as illustrated in Figure 2c. The combined optical power was 173.5 mW at 25 ${}^{\circ }$C, while the free-running power was 86 mW. In addition, the evolution of power with temperature does not follow the same trend for the reinjected QCL and for the free-running QCL. For the latter, the optical power can be measured up to 35 ${}^{\circ }$C, while for the former, the linear trend indicates that one can theoretically detect power up to 50 ${}^{\circ }$C. As the manufacturer does not recommend using the packaged QCL above 35 ${}^{\circ }$C, we cannot confirm this prediction. Still, the change in the behavior of the packaged QCL is consistent for the transmitted beam and for the reflected beam. This finding is relevant in applications with compact packaged QCLs that require optimization of mid-infrared power or with long-wavelength QCLs for which it is still challenging to have continuous-wave operation at room temperature.

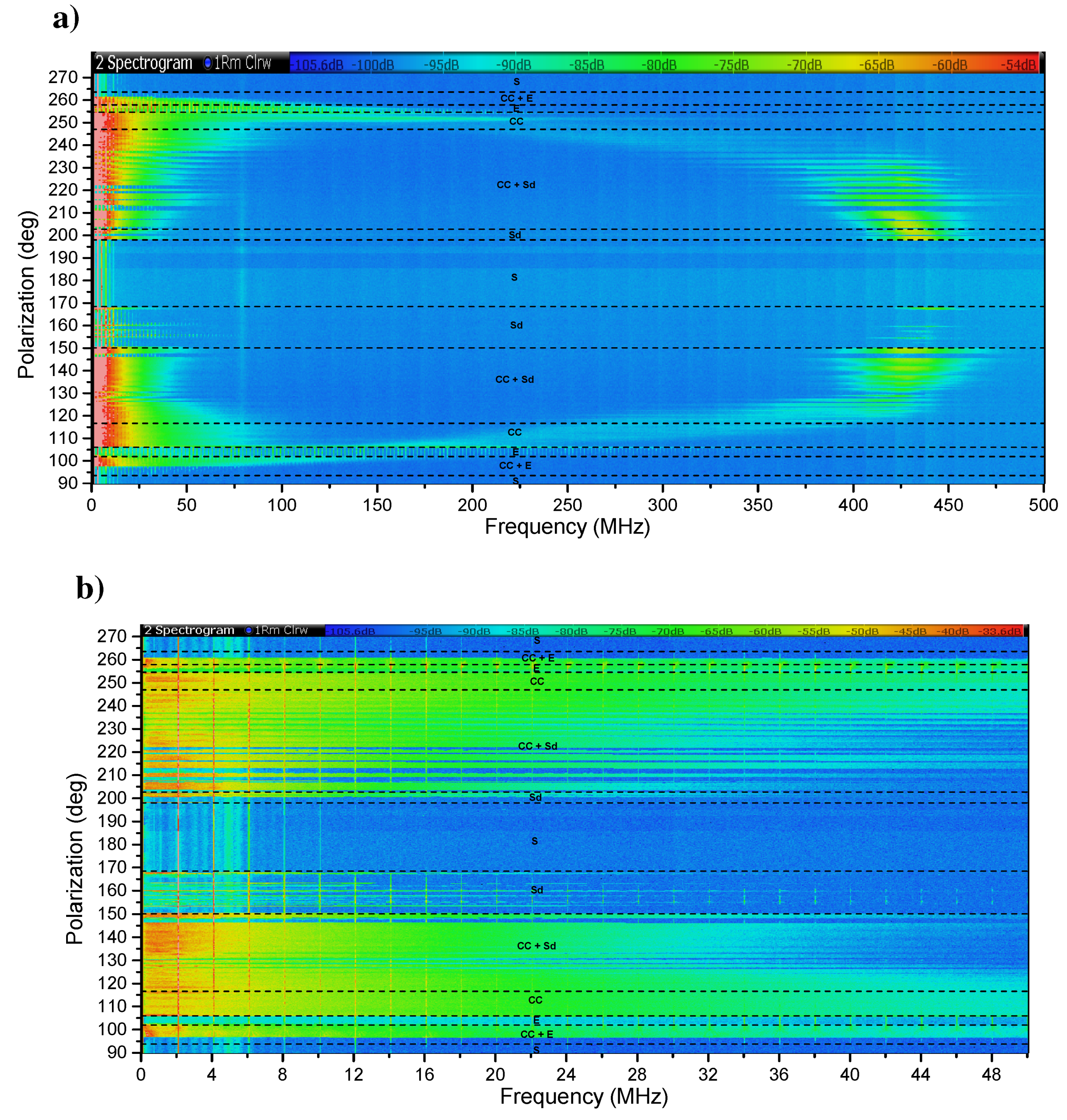
3.2. Entrainment Phenomenon and Non-Linear Dynamics under Strong Reinjection

In this section, we study the evolution of the non-linear dynamics with the feedback ratio, when the bias current of the packaged QCL is modulated with a sine wave at 2 MHz and a 500 mV peak-to-peak amplitude. Previous experimental efforts have shown that a non-linear phenomenon is triggered [17,26], but that was obtained for a small feedback ratio in comparison with the one we can achieve with the platinum NPBS. The setup is thus the one shown in Figure 1d, where a beam splitter with 93% transmission allows strong reinjection, and an MCT detector analyzes the light coming from the reflected beam. Figure 3 shows a RF spectrum analysis of the electrical signal coming from the MCT detector when the angle of the polarizer, and thus the feedback ratio, is continuously varied. This was achieved with the piezo-electric controller described in the method section. The maximum feedback ratio corresponds to a polarizer angle of 90${}^{\circ }$ and 270${}^{\circ }$, i.e., a reference feedback of 0.80, while the minimum feedback ratio corresponds to a polarizer angle of 180${}^{\circ }$, i.e., a reference feedback of 0.006 as evaluated with the Appendix method. In comparison, using the CaF${}_2$ beam splitter would lead to a maximum f${}_r$ of 0.24 and a minimum f${}_r$ of 0.004, but we wanted to study the largest range of feedback strength in this section. The output of the QCL alternates between stable sine behavior (S) for low/high feedback ratios and unstable behaviors. Stability for high feedback ratios while exhibiting non-linear patterns for moderate feedback ratios has already been observed in the case of conventional feedback without periodic forcing and is often referred as the restabilization process [27]. The unstable behaviors show diverse non-linear patterns with a combination of the entrainment phenomenon (E) and coherence-collapse dynamics (CC). In particular, entrainment states are easily assessed in the RF spectrum because they are characterized by periodic spikes corresponding to multiple integers of the forcing frequency [28]. This is, for instance, the case between 102${}^{\circ }$ and 106${}^{\circ }$ or between 255${}^{\circ }$ and 258${}^{\circ }$ where one can observe the 2 MHz-repetition pattern (this value is set by the frequency of the sine forcing) up to 250 MHz. Sometimes, the observed signal is mainly sinusoidal with characteristics that cannot be attributed to entrainment or chaos fluctuations, and this is called sine wave with distortion (Sd) in the following. When the QCL’s output is in a CC state (or, in other words, in a high-dimensional chaos state), the RF spectrum spreads in the low-frequency part of the spectrogram, with maximum values in the order of 100 MHz. Moreover, the external cavity frequency, which is around 425 MHz was not observed. When the excitation sine wave is clearly visible, simultaneously with the coherence collapse dynamics (CC + Sd), the low frequency bandwidth was reduced to values below 50 MHz, but the external cavity frequency was clearly observed in the spectrum. This spectrogram shows the complexity of the non-linear patterns that can be exhibited in the presence of external modulation, and this configuration could be relevant to shape unpredictable dynamics at a mid-infrared wavelength.

Visualization of the RF spectrum is helpful to characterize the aforementioned dynamics. This characterization can be complemented by the analysis of the temporal timetraces that we retrieved with the MCT detector and a high-speed oscilloscope. Figure 4 shows six panels illustrating the phenomena we described (S, Sd, E, CC + Sd, CC + E, and CC, respectively). Likewise, the sine wave is considered distorted (Sd) when fluctuations cannot be found in the timetrace. For the entrainment pattern, spikes are clearly visible and are synchronized with the sine forcing. As already described in Ref. [17], the spikes are generally popping up near the maxima and near the minima of the sine excitation, but, depending on the frequency of this excitation, those spikes can also be found periodically all along the sine pattern. The case (CC + Sd) corresponds to a distorted sine wave with, on top of it, complex chaos oscillations resulting from the coherence collapse process [29]. For this phenomenon, the chaos contribution has a small amplitude compared to the sine signal. When there is a competition between coherence collapse and the entrainment phenomenon (CC + E), the sine wave with the periodic dropouts is still visible, but the chaos waveform now has a comparable amplitude. Finally, some timetraces show dynamics where the sine pattern is totally concealed within the large amplitude chaos, and, for these traces, we considered that the coherence collapse (CC) has the main influence. The boundaries between those types of waveform can be thin, and specific features found in the RF spectrum help categorizing the intensity fluctuations we observed.

It is relevant to note that the configuration presented in the previous paragraph (a sine amplitude of 500 mV peak-to-peak and a modulation frequency of 2 MHz) corresponds to a case where various output states (among them, the entrainment phenomenon, coherence collapse dynamics, or stability) can be observed. For a modulation frequency above 5 MHz, the entrainment phenomenon is not observed at all, and it is difficult to trigger coherence collapse dynamics, meaning that the output of the QCL mainly displays a stable sine wave. This unfortunately hinders the comparison with many efforts carried out with laser diodes where the forcing frequency is at a few dozens of MHz [20] or even higher [28]. In particular, the case where the modulation frequency is exactly that of the external cavity and leads to the suppression of the entrainment phenomenon [30] cannot be observed with our configuration.

4. Discussion

This work addressed optimization of feedback for high-power operation with mid-infrared QCLs. In the near term, free-space communication systems will be implemented in the mid-infrared domain to accommodate the exponentially increasing data traffic in our digital society, where conventional fiber networks become saturated [31]. Taking advantage of external modulators at a mid-infrared wavelength [32] is very promising to achieve dozens of Gbits/s transfer speeds, and increasing the available output power of QCLs will enable long-distance, weather-insensitive propagation. As we saw that strong feedback was also able to increase the maximum temperature of operation of a mid-infrared QCL, experiments could be carried out with terahertz QCLs, for which low-temperature and pulsed operation still hinder large-scale deployment, even though the last years have seen key breakthroughs towards high-temperature terahertz QCLs [33,34]. More generally, very high-power QCLs are required for various civilian and military applications, and any increase in the optical power with external, easy-to-implement methods can impact on the QCL community [35]. Investigations are also required to understand why, in our case, the threshold reduction under external optical feedback is extremely strong while it is generally less important in QCLs. Even if the QCL multiple-stack structure is more complex than that of near-infrared interband semiconductor lasers, previous works with such lasers [36] can provide guidelines for theoretical explanations in QCLs.

Our configuration with strong optical feedback was also proven useful to trigger complex phenomena in a configuration that is usually known for entrainment dynamics. Those findings are relevant in order to obtain the largest chaos bandwidth with a QCL and that is poised to play a key role in increasing the data rate of private free-space communication. Further work will analyze the coherence collapse timetraces retrieved in this experimental effort in order to determine the number of positive Lyapunov exponents, because multiple positive Lyapunov exponents is a mandatory requirement to improve the encoding resistance against illegitimate receivers [37]. It is also relevant to note that the largest feedback ratio we achieved in this work was associated with a stable sine wave, without entrainment or chaos fluctuations. This means that large feedback ratios may stabilize the QCL’s output while increasing the optical power, leading to an optimal configuration for long-haul free-space transmission. However, as the frequencies injected in direct-modulation communication [21] are far above the 2 MHz frequency studied in this work, further work is required to confirm this claim. As we saw that very strong optical reinjection induced a decrease in beam intensity compared with the free-running case, a trade-off between an enhanced optical power and stabilization of the laser properties is required to implement this technique in novel wireless technologies based on QCLs.