Ultrahigh-Q Tunable Terahertz Absorber Based on Bulk Dirac Semimetal with Surface Lattice Resonance
Abstract
:1. Introduction
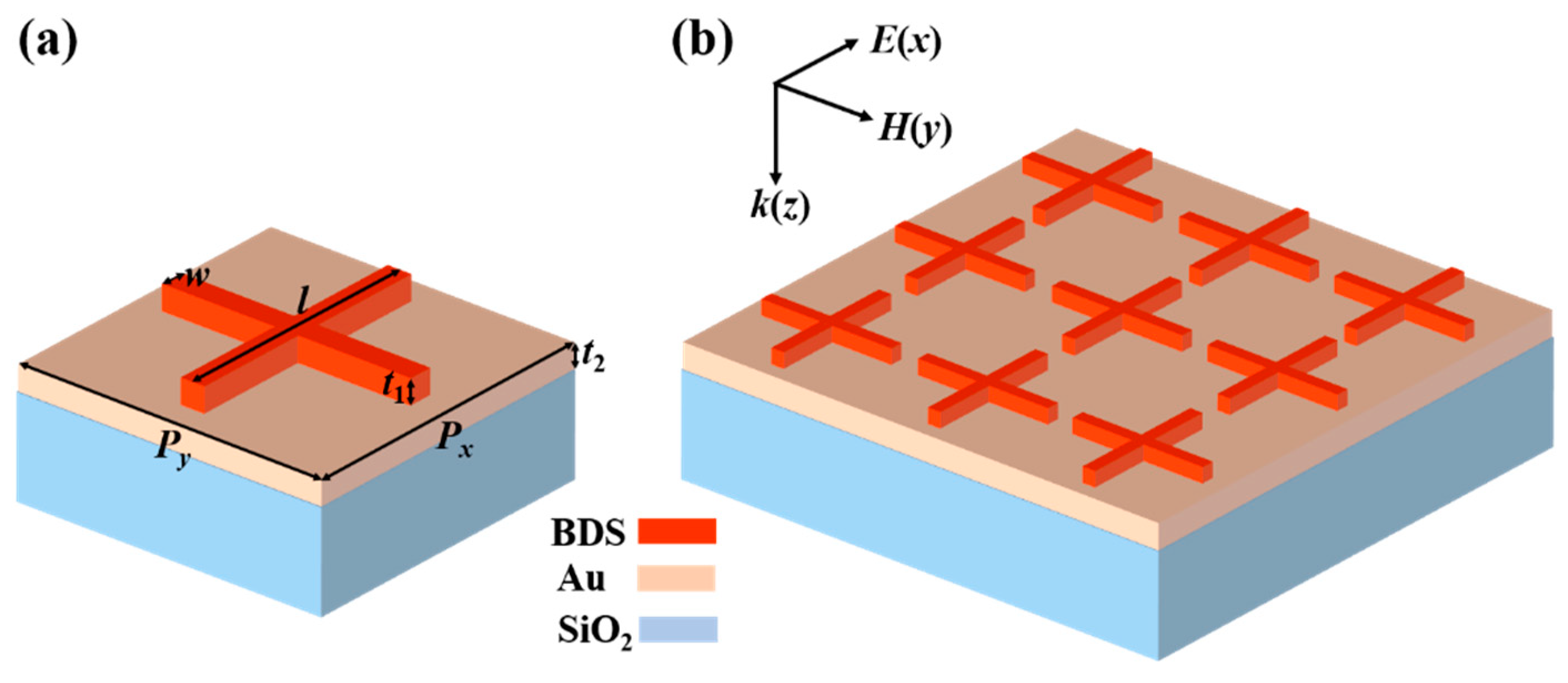
2. Structures and Methods
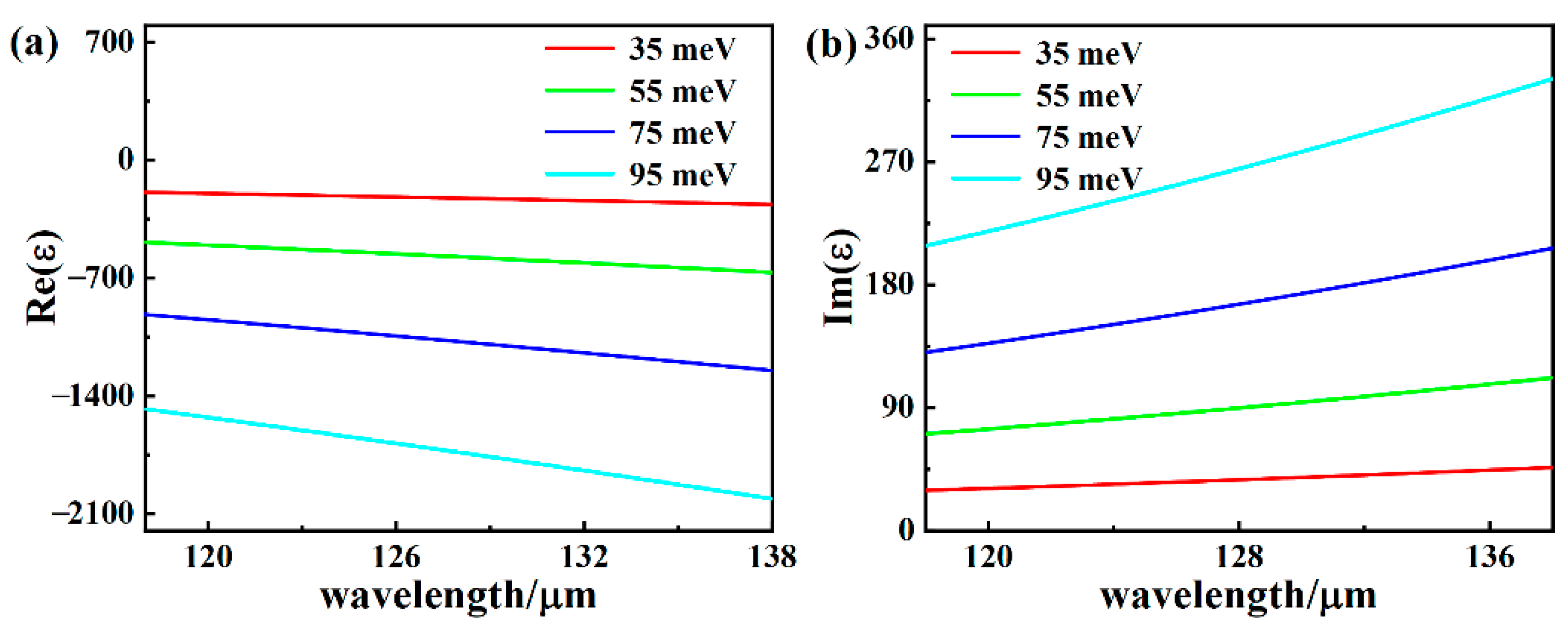
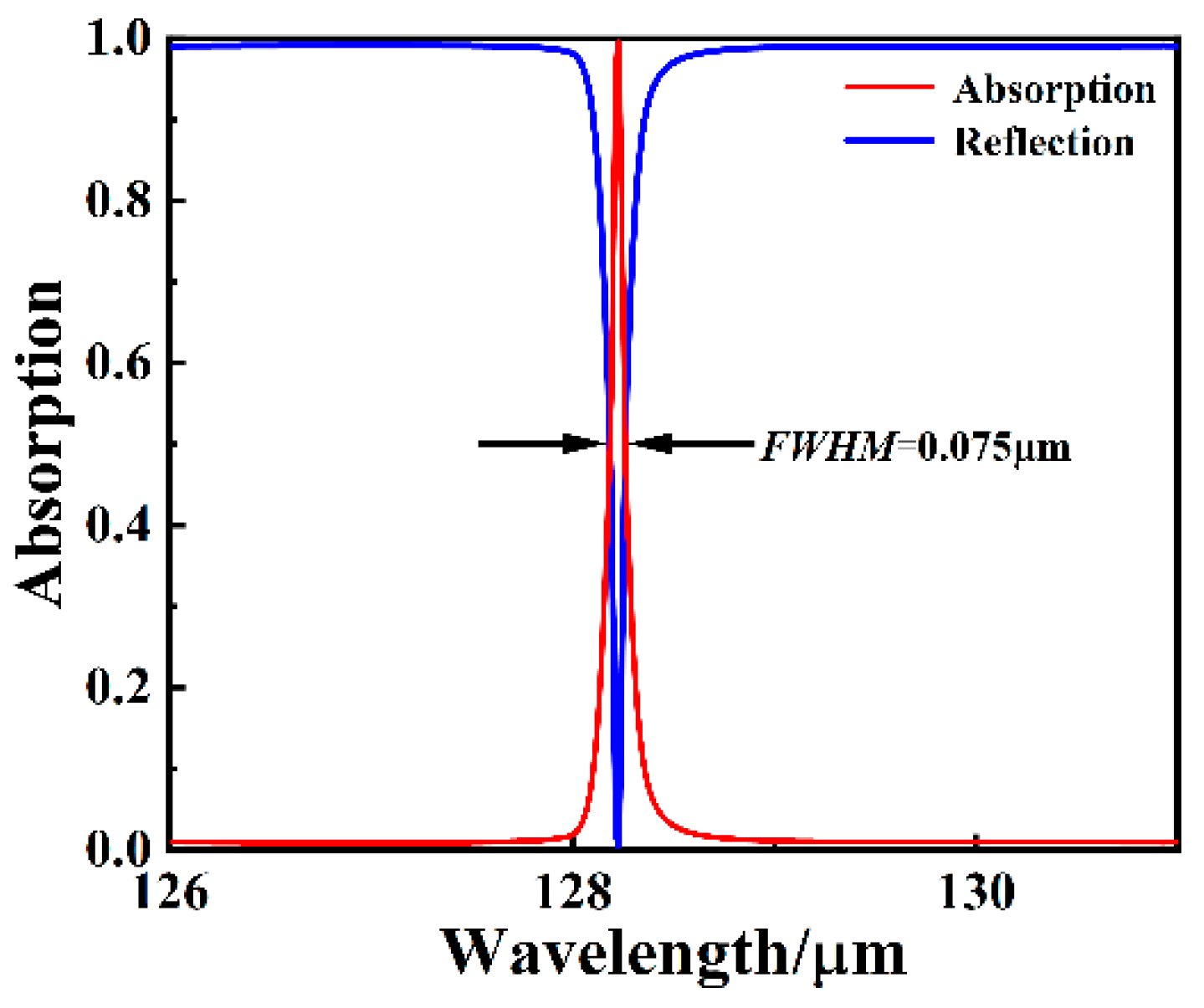
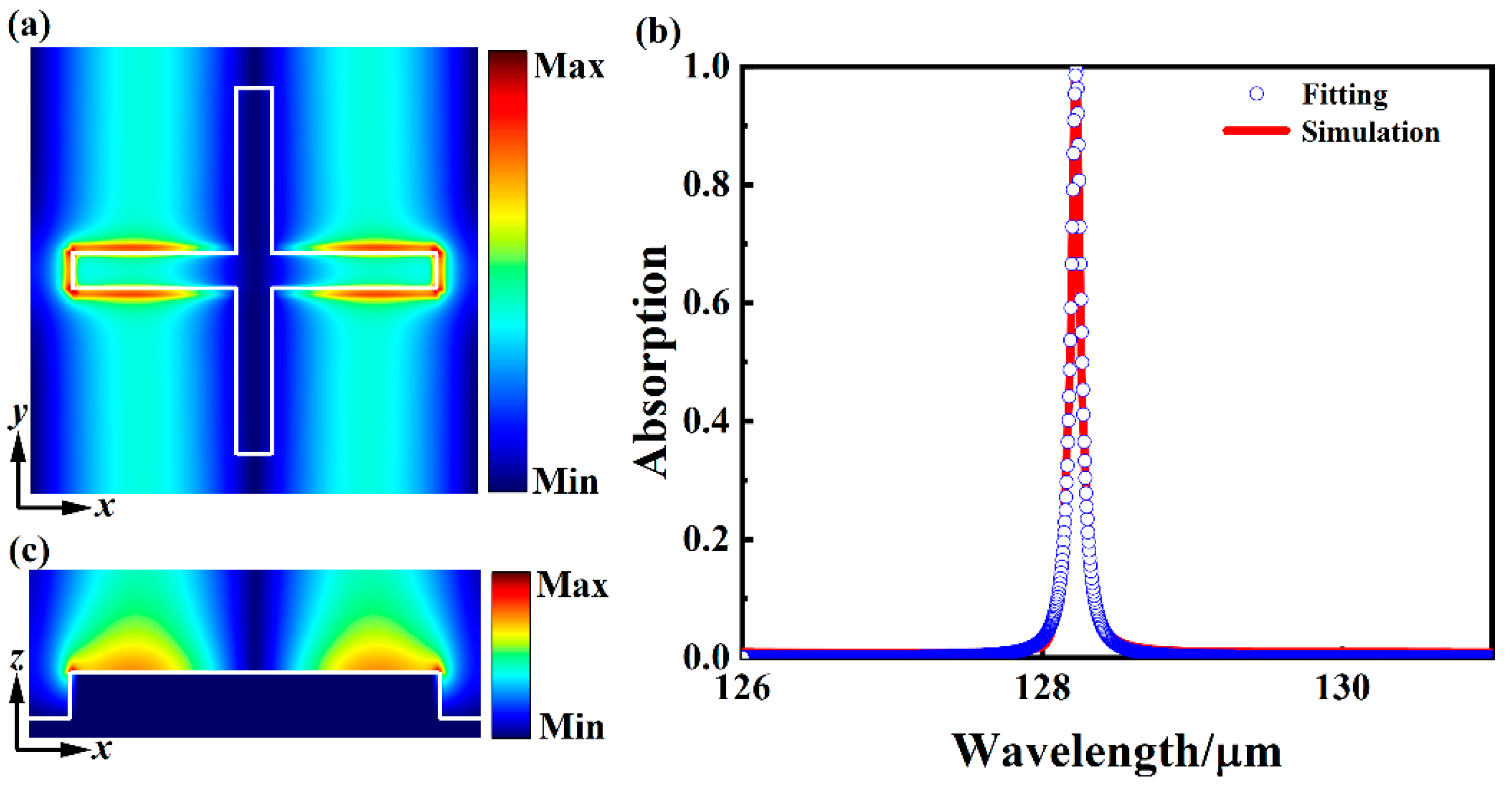
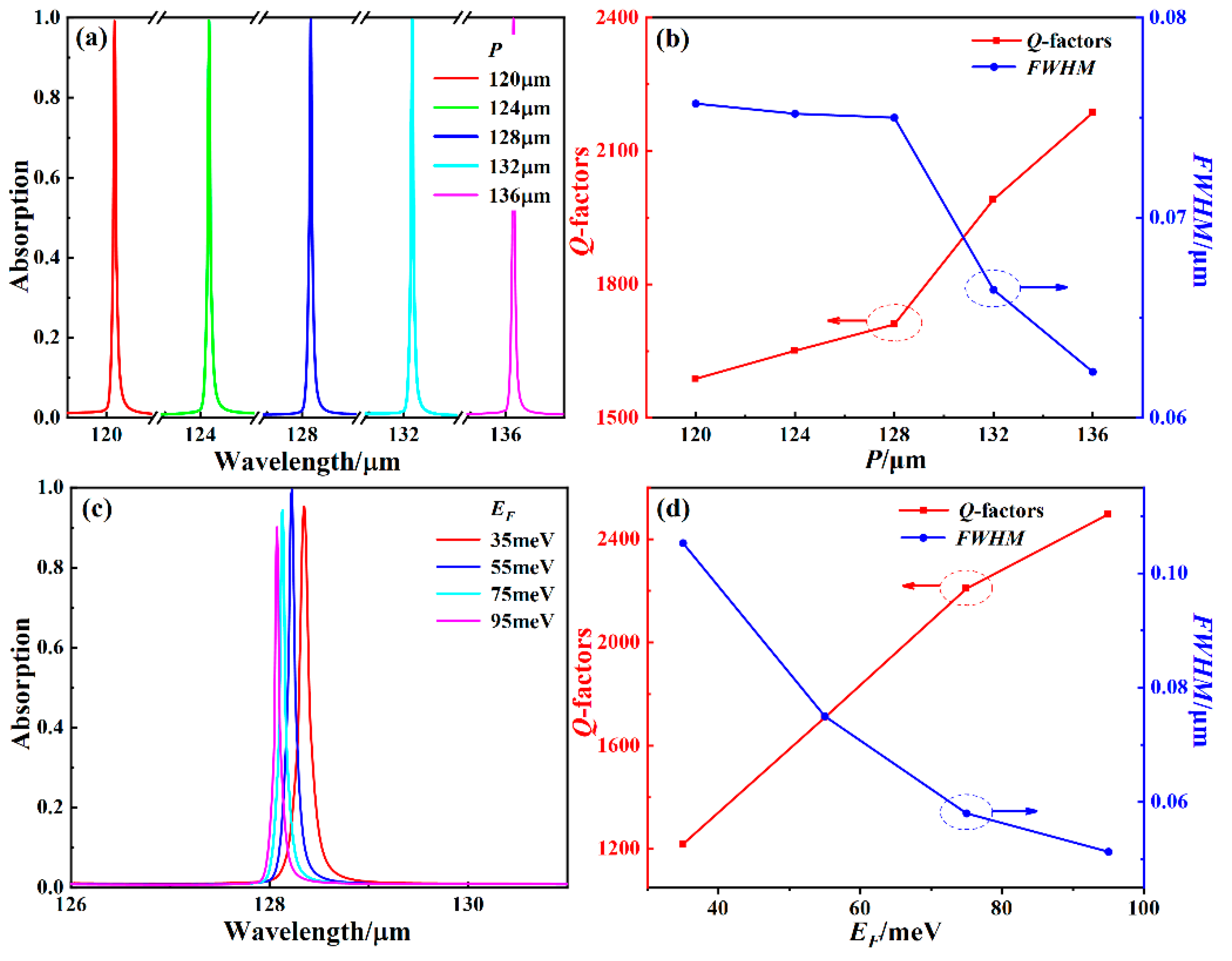
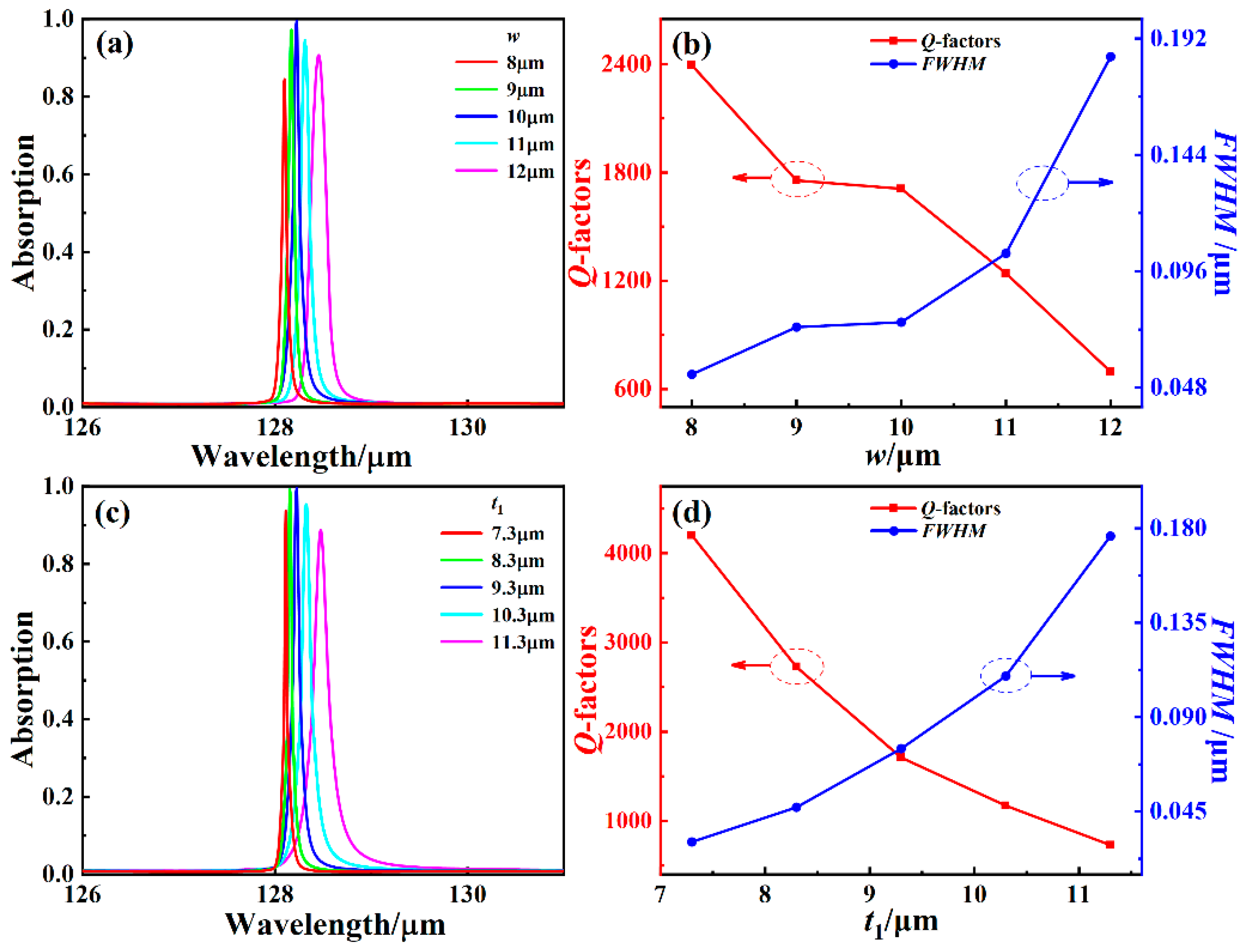
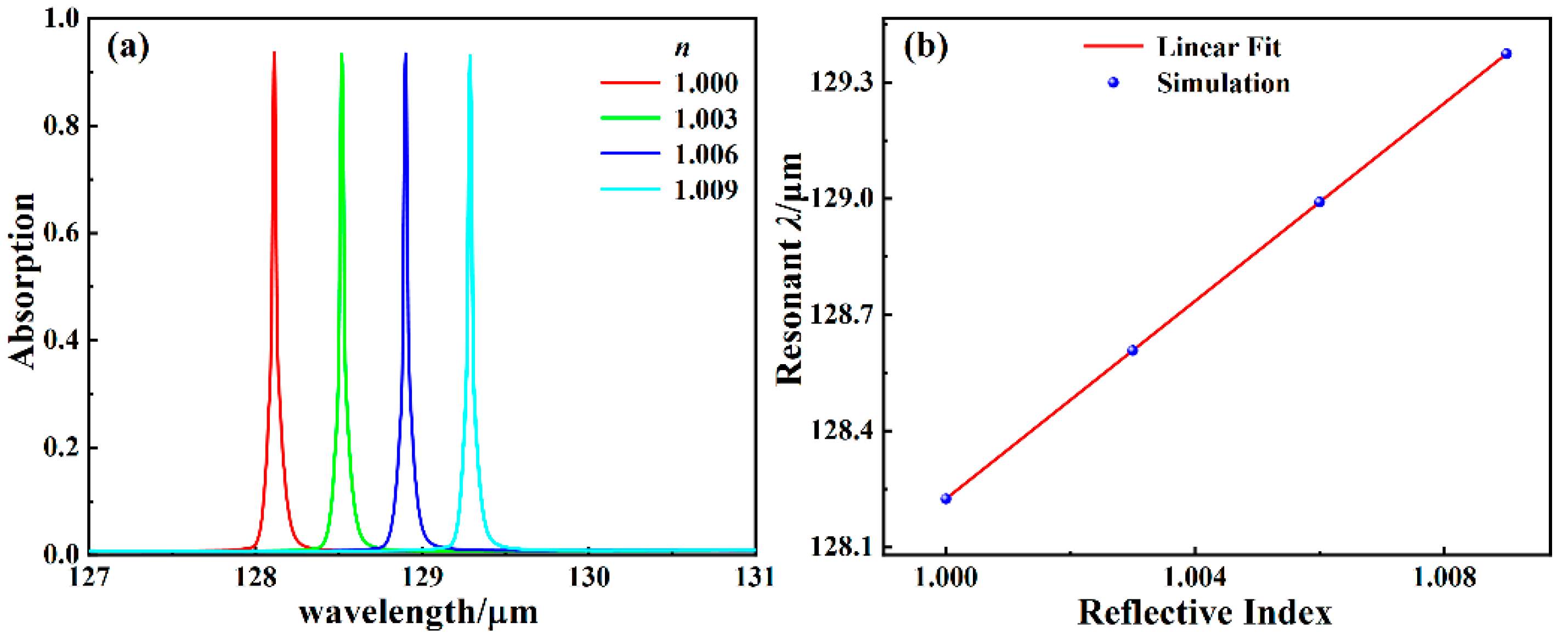
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. A Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Ding, F.; Cui, Y.; Ge, X.; Jin, Y.; He, S. Ultra-Broadband Microwave Metamaterial Absorber. Appl. Phys. Lett. 2012, 100, 103506. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Cui, T.J.; Xu, Q.; Bao, D.; Du, L.; Wan, X.; Tang, W.X.; Ouyang, C.; Zhou, X.Y.; Yuan, H.; et al. Anisotropic Coding Metamaterials and Their Powerful Manipulation of Differently Polarized Terahertz Waves. Light Sci. Appl. 2016, 5, e16076. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tyler, T.; Starr, T.; Starr, A.F.; Jokerst, N.M.; Padilla, W.J. Taming the Blackbody with Infrared Metamaterials as Selective Thermal Emitters. Phys. Rev. Lett. 2011, 107, 045901. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Xiao, F.; Rukhlenko, I.D.; Geng, J.; Liang, X.; Premaratne, M.; Jin, R. Wideband Visible-Light Absorption in an Ultrathin Silicon Nanostructure. Opt. Express 2017, 25, 5781. [Google Scholar] [CrossRef] [PubMed]
- Atwater, H.A.; Polman, A. Plasmonics for Improved Photovoltaic Devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhu, Z.; Liu, W.; Yuan, X.; Qin, S. Towards Photodetection with High Efficiency and Tunable Spectral Selectivity: Graphene Plasmonics for Light Trapping and Absorption Engineering. Nanoscale 2015, 7, 13530–13536. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Li, Q.; Gong, H.; Du, K.; Bai, S.; Zhao, D.; Ye, H.; Qiu, M. Spatially and Spectrally Resolved Narrowband Optical Absorber Based on 2D Grating Nanostructures on Metallic Films. Adv. Opt. Mater. 2016, 4, 480–486. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, L.; Zhang, T. Nanoslit-Microcavity-Based Narrow Band Absorber for Sensing Applications. Opt. Express 2015, 23, 20715. [Google Scholar] [CrossRef]
- Yu, C.; Fan, S.; Sun, Y.; Pickwell-MacPherson, E. The Potential of Terahertz Imaging for Cancer Diagnosis: A Review of Investigations to Date. Quant. Imaging Med. Surg. 2012, 2, 13. [Google Scholar]
- Xu, W.; Xie, L.; Zhu, J.; Xu, X.; Ye, Z.; Wang, C.; Ma, Y.; Ying, Y. Gold Nanoparticle-Based Terahertz Metamaterial Sensors: Mechanisms and Applications. ACS Photonics 2016, 3, 2308–2314. [Google Scholar] [CrossRef]
- Salim, A. Recent Advances in the Metamaterial-Inspired Biosensors. Biosens. Bioelectron. 2018, 117, 398–402. [Google Scholar] [CrossRef]
- Liu, G.; He, M.; Tian, Z.; Li, J.; Liu, J. Terahertz Surface Plasmon Sensor for Distinguishing Gasolines. Appl. Opt. 2013, 52, 5695. [Google Scholar] [CrossRef]
- Hu, X.; Xu, G.; Wen, L.; Wang, H.; Zhao, Y.; Zhang, Y.; Cumming, D.R.S.; Chen, Q. Metamaterial Absorber Integrated Microfluidic Terahertz Sensors: Metamaterial Absorber Integrated Microfluidic Terahertz Sensors. Laser Photonics Rev. 2016, 10, 962–969. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.-X.; Huang, W.-Q.; Wang, L.-L. Ultra-Narrow Terahertz Perfect Light Absorber Based on Surface Lattice Resonance of a Sandwich Resonator for Sensing Applications. RSC Adv. 2017, 7, 42956–42963. [Google Scholar] [CrossRef] [Green Version]
- Meng, H.; Shang, X.; Xue, X.; Tang, K.; Xia, S.; Zhai, X.; Liu, Z.; Chen, J.; Li, H.; Wang, L. Bidirectional and Dynamically Tunable THz Absorber with Dirac Semimetal. Opt. Express 2019, 27, 31062. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhai, X.; Xia, S.; Li, H.; Wang, L. Active Control of Narrowband Total Absorption Based on Terahertz Hybrid Dirac Semimetal-Graphene Metamaterials. J. Phys. D Appl. Phys. 2020, 53, 205106. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Liu, M.; Zhao, Y.; Guo, X.; Zhang, Y. Realization of Tunable Plasmon-Induced Transparency by Bright-Bright Mode Coupling in Dirac Semimetals. Opt. Mater. Express 2017, 7, 3397. [Google Scholar] [CrossRef]
- Liu, G.-D.; Zhai, X.; Meng, H.-Y.; Lin, Q.; Huang, Y.; Zhao, C.-J.; Wang, L.-L. Dirac Semimetals Based Tunable Narrowband Absorber at Terahertz Frequencies. Opt. Express 2018, 26, 11471. [Google Scholar] [CrossRef]
- Jiang, Y.; Xinguo, W.; Wang, J.; Wang, J. Tunable Terahertz Absorber Based on Bulk-Dirac-Semimetal Metasurface. IEEE Photonics J. 2018, 10, 1–7. [Google Scholar] [CrossRef]
- Ooi, K.J.A.; Ang, Y.S.; Zhai, Q.; Tan, D.T.H.; Ang, L.K.; Ong, C.K. Nonlinear Plasmonics of Three-Dimensional Dirac Semimetals. APL Photonics 2019, 4, 034402. [Google Scholar] [CrossRef]
- Ullah, K.; Meng, Y.; Sun, Y.; Yang, Y.; Wang, X.; Wang, A.; Wang, X.; Xiu, F.; Shi, Y.; Wang, F. Third Harmonic Generation in Dirac Semimetal Cd3 As2. Appl. Phys. Lett. 2020, 117, 011102. [Google Scholar] [CrossRef]
- Timusk, T.; Carbotte, J.P.; Homes, C.C.; Basov, D.N.; Sharapov, S.G. Three-Dimensional Dirac Fermions in Quasicrystals as Seen via Optical Conductivity. Phys. Rev. B 2013, 87, 235121. [Google Scholar] [CrossRef] [Green Version]
- Kharzeev, D.E.; Pisarski, R.D.; Yee, H.-U. Universality of Plasmon Excitations in Dirac Semimetals. Phys. Rev. Lett. 2015, 115, 236402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Zhang, K.; Zhang, L.; Hong, G.; Chen, C.; Jing, H.; Lu, J.; Wang, P.; Chen, X.; Wang, L.; et al. Controllable Growth of Type-II Dirac Semimetal PtTe2 Atomic Layer on Au Substrate for Sensitive Room Temperature Terahertz Photodetection. InfoMat 2021, 3, 705–715. [Google Scholar] [CrossRef]
- Luo, J.; Lin, Q.; Wang, L.; Xia, S.; Meng, H.; Zhai, X. Ultrasensitive Tunable Terahertz Sensor Based on Five-Band Perfect Absorber with Dirac Semimetal. Opt. Express 2019, 27, 20165. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chowdhury, D.R.; Ramani, S.; Reiten, M.T.; Luo, S.-N.; Azad, A.K.; Taylor, A.J.; Chen, H.-T. Impact of Resonator Geometry and Its Coupling with Ground Plane on Ultrathin Metamaterial Perfect Absorbers. Appl. Phys. Lett. 2012, 101, 101102. [Google Scholar] [CrossRef] [Green Version]
- Kotov, O.V.; Lozovik, Y.E. Dielectric Response and Novel Electromagnetic Modes in Three-Dimensional Dirac Semimetal Films. Phys. Rev. B 2016, 93, 235417. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Butun, S.; Aydin, K. Ultranarrow Band Absorbers Based on Surface Lattice Resonances in Nanostructured Metal Surfaces. ACS Nano 2014, 8, 8242–8248. [Google Scholar] [CrossRef]
- Zou, S.; Janel, N.; Schatz, G.C. Silver Nanoparticle Array Structures That Produce Remarkably Narrow Plasmon Lineshapes. J. Chem. Phys. 2004, 120, 10871–10875. [Google Scholar] [CrossRef]
- Chu, Y.; Schonbrun, E.; Yang, T.; Crozier, K.B. Experimental Observation of Narrow Surface Plasmon Resonances in Gold Nanoparticle Arrays. Appl. Phys. Lett. 2008, 93, 181108. [Google Scholar] [CrossRef]
- Lamprecht, B.; Schider, G.; Lechner, R.T.; Ditlbacher, H.; Krenn, J.R.; Leitner, A.; Aussenegg, F.R. Metal Nanoparticle Gratings: Influence of Dipolar Particle Interaction on the Plasmon Resonance. Phys. Rev. Lett. 2000, 84, 4721–4724. [Google Scholar] [CrossRef]
- Meier, M.; Liao, P.F.; Wokaun, A. Enhanced Fields on Rough Surfaces: Dipolar Interactions among Particles of Sizes Exceeding the Rayleigh Limit. J. Opt. Soc. Am. B 1985, 2, 931. [Google Scholar] [CrossRef]
- Li, Z.; Sun, X.; Ma, C.; Li, J.; Li, X.; Guan, B.; Chen, K. Ultra-Narrow-Band Metamaterial Perfect Absorber Based on Surface Lattice Resonance in a WS 2 Nanodisk Array. Opt. Express 2021, 29, 27084. [Google Scholar] [CrossRef]
- García de Abajo, F.J. Colloquium: Light Scattering by Particle and Hole Arrays. Rev. Mod. Phys. 2007, 79, 1267–1290. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Fan, W. Ultrasensitive Terahertz Metamaterial Sensor Based on Spoof Surface Plasmon. Sci. Rep. 2017, 7, 2092. [Google Scholar] [CrossRef] [Green Version]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef]
- Zhang, K.; Ma, T.; Liu, J.; Tian, X.; Zhu, J.; Tan, C. Dynamically Tunable and Polarization-Insensitive Dual-Band Terahertz Metamaterial Absorber Based on TiNi Shape Memory Alloy Films. Results Phys. 2021, 23, 104001. [Google Scholar] [CrossRef]
- Liang, L.; Hu, X.; Wen, L.; Zhu, Y.; Yang, X.; Zhou, J.; Zhang, Y.; Carranza, I.E.; Grant, J.; Jiang, C.; et al. Unity Integration of Grating Slot Waveguide and Microfluid for Terahertz Sensing. Laser Photonics Rev. 2018, 12, 1800078. [Google Scholar] [CrossRef] [Green Version]
- Mejía-Salazar, J.R.; Rodrigues Cruz, K.; Materón Vásques, E.M.; de Oliveira, O.N., Jr. Microfluidic Point-of-Care Devices: New Trends and Future Prospects for EHealth Diagnostics. Sensors 2020, 20, 1951. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Liu, M.; Wang, Z.; Li, S.; Deng, Y.; He, N. Point-of-Care Diagnostics for Infectious Diseases: From Methods to Devices. Nano Today 2021, 37, 101092. [Google Scholar] [CrossRef]
- Mauriz, E. Clinical Applications of Visual Plasmonic Colorimetric Sensing. Sensors 2020, 20, 6214. [Google Scholar] [CrossRef] [PubMed]
- Borisenko, S.; Gibson, Q.; Evtushinsky, D.; Zabolotnyy, V.; Büchner, B.; Cava, R.J. Experimental Realization of a Three-Dimensional Dirac Semimetal. Phys. Rev. Lett. 2014, 113, 027603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weng, H.; Dai, X.; Fang, Z. Transition-Metal Pentatelluride ZrTe5 and HfTe5: A Paradigm for Large-Gap Quantum Spin Hall Insulators. Phys. Rev. X 2014, 4, 011002. [Google Scholar] [CrossRef] [Green Version]
- Manzoni, G.; Gragnaniello, L.; Autès, G.; Kuhn, T.; Sterzi, A.; Cilento, F.; Zacchigna, M.; Enenkel, V.; Vobornik, I.; Barba, L.; et al. Evidence for a Strong Topological Insulator Phase in ZrTe 5. Phys. Rev. Lett. 2016, 117, 237601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, X.; Fan, W. Toroidal Metasurfaces Integrated with Microfluidic for Terahertz Refractive Index Sensing. J. Phys. D Appl. Phys. 2019, 52, 485104. [Google Scholar] [CrossRef]
- Ng, B.; Wu, J.; Hanham, S.M.; Fernández-Domínguez, A.I.; Klein, N.; Liew, Y.F.; Breese, M.B.H.; Hong, M.; Maier, S.A. Spoof Plasmon Surfaces: A Novel Platform for THz Sensing. Adv. Opt. Mater. 2013, 1, 543–548. [Google Scholar] [CrossRef]
- Astley, V.; Reichel, K.S.; Jones, J.; Mendis, R.; Mittleman, D.M. Terahertz Multichannel Microfluidic Sensor Based on Parallel-Plate Waveguide Resonant Cavities. Appl. Phys. Lett. 2012, 100, 231108. [Google Scholar] [CrossRef]
- Cong, L.; Tan, S.; Yahiaoui, R.; Yan, F.; Zhang, W.; Singh, R. Experimental Demonstration of Ultrasensitive Sensing with Terahertz Metamaterial Absorbers: A Comparison with the Metasurfaces. Appl. Phys. Lett. 2015, 106, 031107. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Ou, Y.; Wang, S.; Meng, Y.; Wang, Z.; Zhai, X.; Wang, L.; Xia, S. Ultrahigh-Q Tunable Terahertz Absorber Based on Bulk Dirac Semimetal with Surface Lattice Resonance. Photonics 2022, 9, 22. https://doi.org/10.3390/photonics9010022
Wang Z, Ou Y, Wang S, Meng Y, Wang Z, Zhai X, Wang L, Xia S. Ultrahigh-Q Tunable Terahertz Absorber Based on Bulk Dirac Semimetal with Surface Lattice Resonance. Photonics. 2022; 9(1):22. https://doi.org/10.3390/photonics9010022
Chicago/Turabian StyleWang, Zhiyong, Yanghong Ou, Shiyu Wang, Yanzi Meng, Zi Wang, Xiang Zhai, Lingling Wang, and Shengxuan Xia. 2022. "Ultrahigh-Q Tunable Terahertz Absorber Based on Bulk Dirac Semimetal with Surface Lattice Resonance" Photonics 9, no. 1: 22. https://doi.org/10.3390/photonics9010022
APA StyleWang, Z., Ou, Y., Wang, S., Meng, Y., Wang, Z., Zhai, X., Wang, L., & Xia, S. (2022). Ultrahigh-Q Tunable Terahertz Absorber Based on Bulk Dirac Semimetal with Surface Lattice Resonance. Photonics, 9(1), 22. https://doi.org/10.3390/photonics9010022





