Adaptive Wave-Front Shaping and Beam Focusing through Fiber Bundles for High-Resolution Bioimaging
Abstract
:1. Introduction
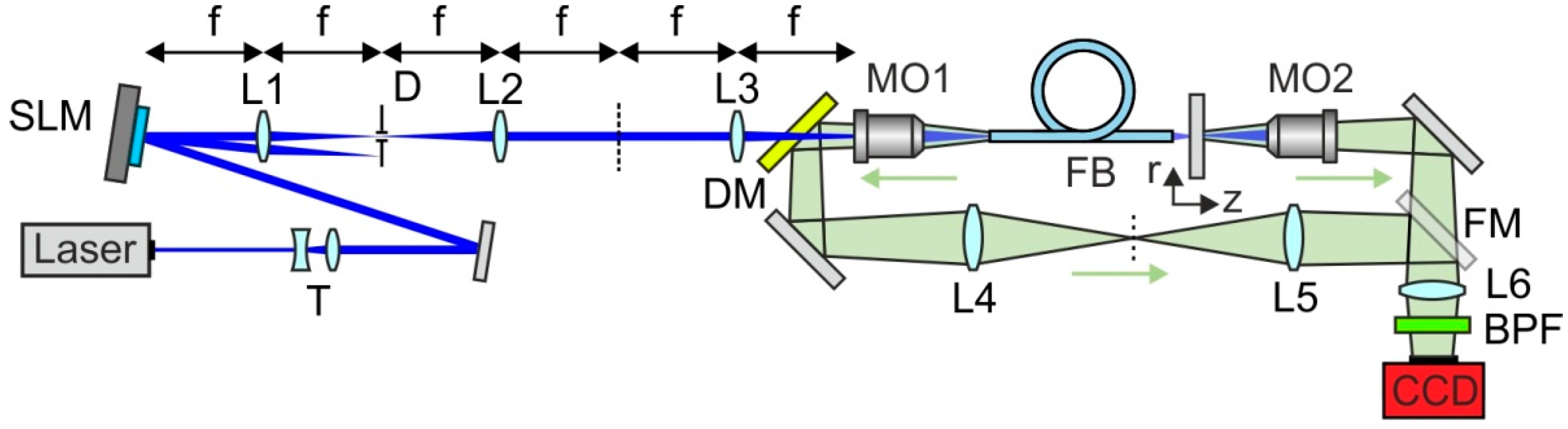
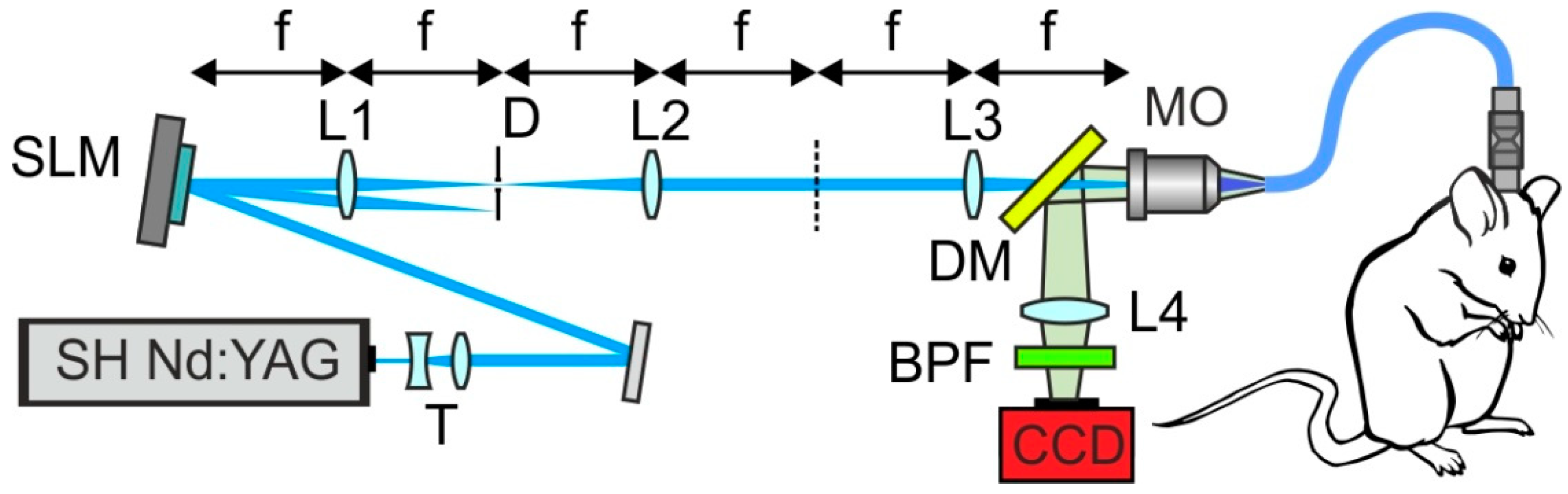
2. Imaging through Fiber Bundles
3. Adaptive Beam Shaping
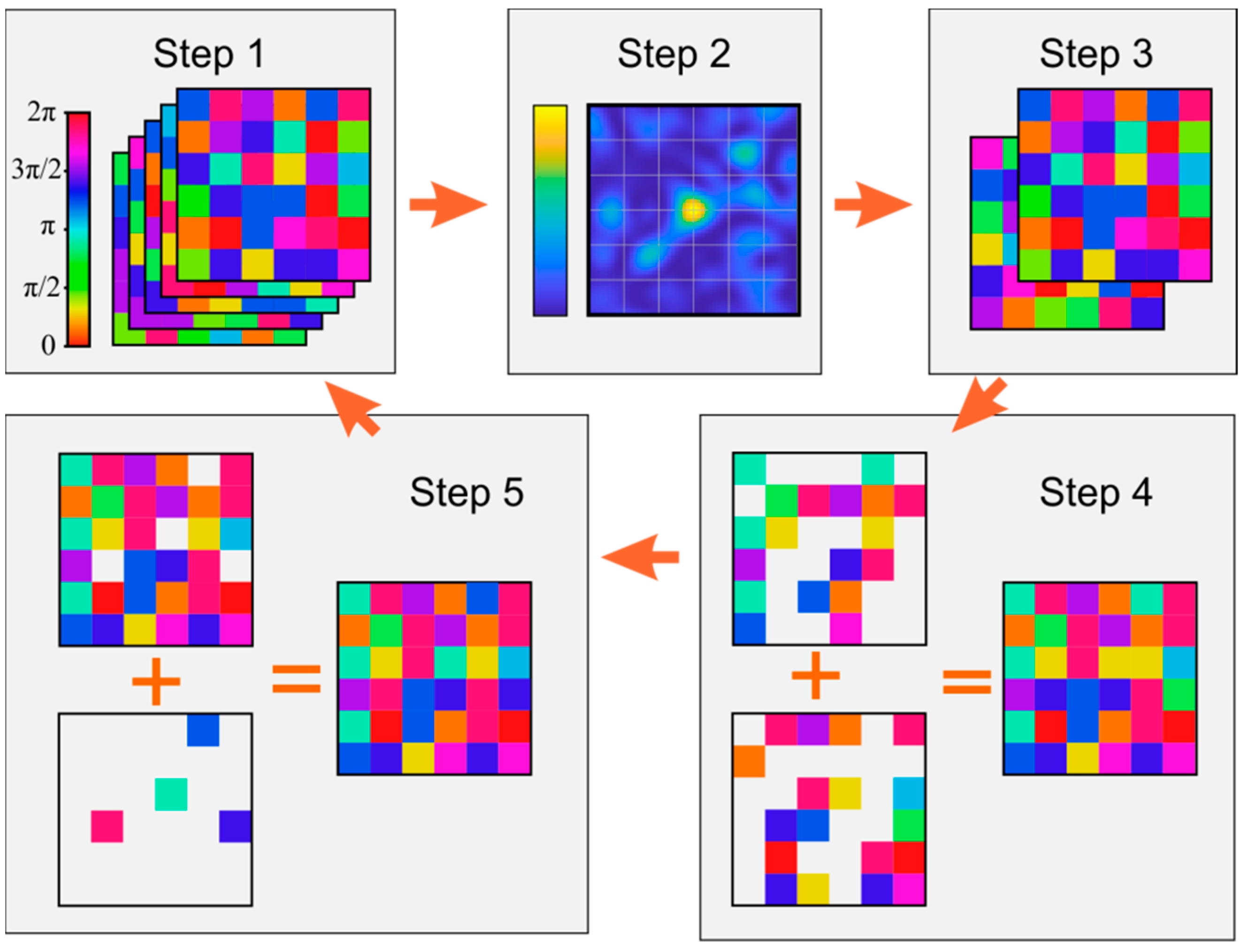
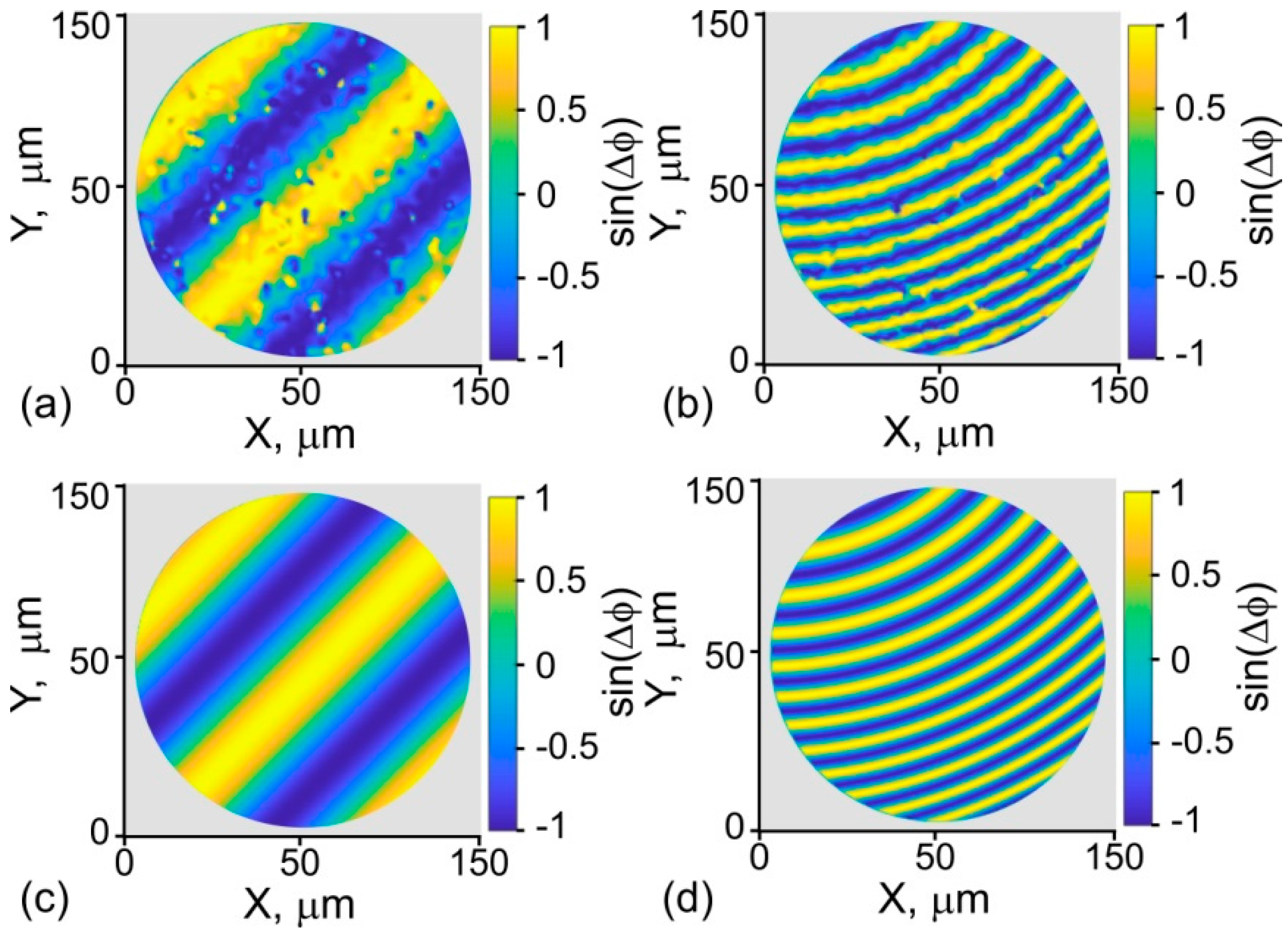
4. Phase-Mask Synthesis
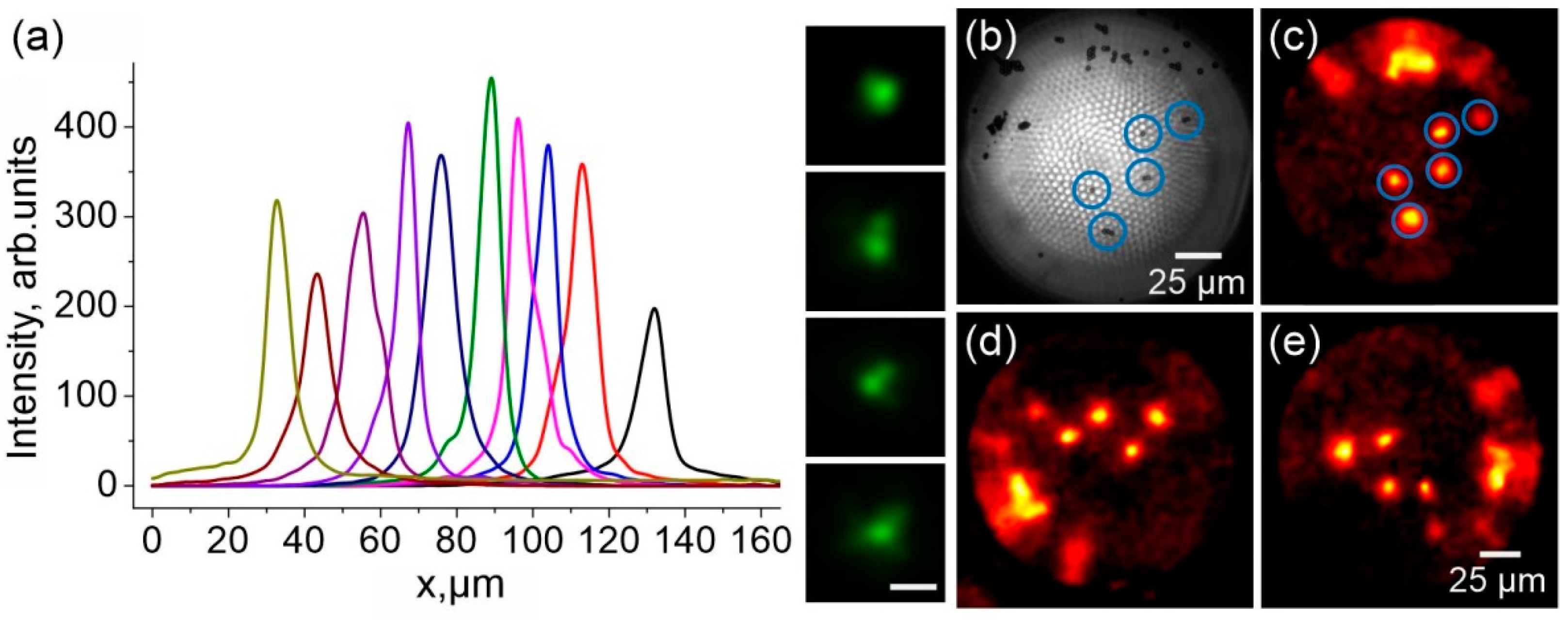
5. Multiple-Beamlet Wave-Front Shaping
6. Adaptive Beam Focusing
6.1. Field-Intensity Profiles
6.2. Coherent-Peak-to-Speckle-Background Contrast
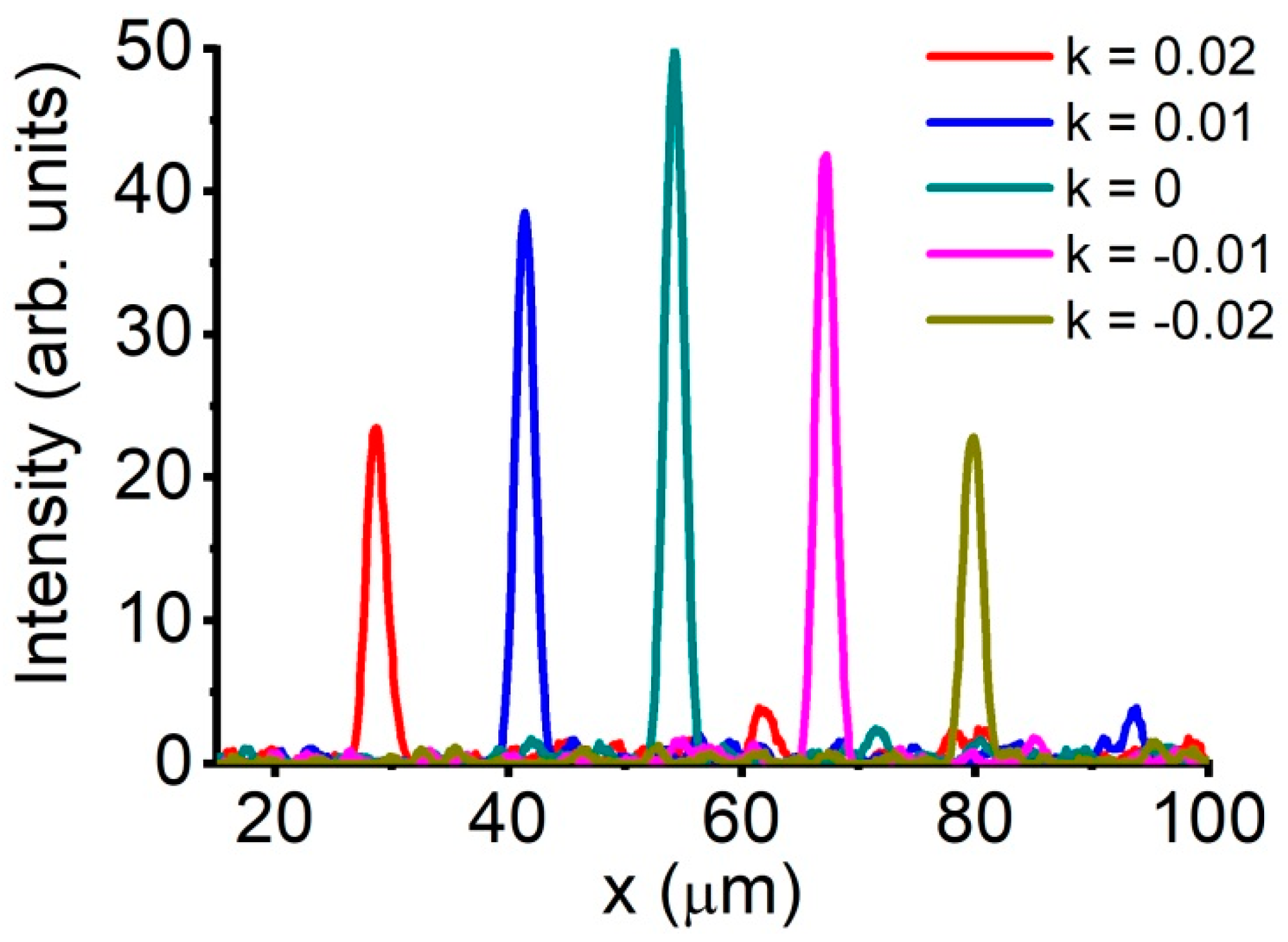
7. Fast Beam-Focus Scanning
8. Toward New Bioimaging Modalities: Combining Adaptive Beam Shaping with Reconfigurable Fiber-Bundle-to-Fiber-Bundle Connection
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hansell, C.W. Picture Transmission. US Patent 1751584, 25 March 1930. Available online: https://patents.google.com/patent/US1751584A/en (accessed on 1 December 2021).
- Lamm, H. Biegsame optische Geräte. Z. Instrum. 1930, 50, 579–581. [Google Scholar]
- Flusberg, B.A.; Cocker, E.D.; Piyawattanametha, W.; Jung, J.C.; Cheung, E.L.M.; Schnitzer, M.J. Fiber-Optic Fluorescence Imaging. Nat. Methods 2005, 2, 941–950. [Google Scholar] [CrossRef]
- Russell, P. Photonic Crystal Fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef] [PubMed]
- Cregan, R.F.; Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Roberts, P.J.; Allan, D.C. Single-Mode Photonic Band Gap Guidance of Light in Air. Science 1999, 285, 1537–1539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, C.M.; Venkataraman, N.; Gallagher, M.T.; Müller, D.; West, J.A.; Borrelli, N.F.; Allan, D.C.; Koch, K.W. Low-Loss Hollow-Core Silica/Air Photonic Bandgap Fibre. Nature 2003, 424, 657–659. [Google Scholar] [CrossRef] [PubMed]
- Zheltikov, A.M. Holey Fibers. Phys.-Uspekhi 2000, 43, 1125–1136. [Google Scholar] [CrossRef]
- Zheltikov, A.M. Optical Devices: The Friendly Gas Phase. Nat. Mater 2005, 4, 267–268. [Google Scholar] [CrossRef]
- Stuber, G.D.; Sparta, D.R.; Stamatakis, A.M.; van Leeuwen, W.A.; Hardjoprajitno, J.E.; Cho, S.; Tye, K.M.; Kempadoo, K.A.; Zhang, F.; Deisseroth, K.; et al. Excitatory Transmission from the Amygdala to Nucleus Accumbens Facilitates Reward Seeking. Nature 2011, 475, 377–380. [Google Scholar] [CrossRef]
- Warden, M.R.; Cardin, J.A.; Deisseroth, K. Optical Neural Interfaces. Annu. Rev. Biomed. Eng. 2014, 16, 103–129. [Google Scholar] [CrossRef] [Green Version]
- Doronina-Amitonova, L.V.; Fedotov, I.V.; Fedotov, A.B.; Anokhin, K.V.; Zheltikov, A.M. Neurophotonics: Optical Methods to Study and Control the Brain. Phys.-Uspekhi 2015, 58, 345. [Google Scholar] [CrossRef]
- Doronina-Amitonova, L.V.; Fedotov, I.V.; Ivashkina, O.I.; Zots, M.A.; Fedotov, A.B.; Anokhin, K.V.; Zheltikov, A.M. Implantable Fiber-Optic Interface for Parallel Multisite Long-Term Optical Dynamic Brain Interrogation in Freely Moving Mice. Sci. Rep. 2013, 3, 3265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, C.K.; Yang, S.J.; Pichamoorthy, N.; Young, N.P.; Kauvar, I.; Jennings, J.H.; Lerner, T.N.; Berndt, A.; Lee, S.Y.; Ramakrishnan, C.; et al. Simultaneous Fast Measurement of Circuit Dynamics at Multiple Sites across the Mammalian Brain. Nat. Methods 2016, 13, 325–328. [Google Scholar] [CrossRef]
- Sych, Y.; Chernysheva, M.; Sumanovski, L.T.; Helmchen, F. High-Density Multi-Fiber Photometry for Studying Large-Scale Brain Circuit Dynamics. Nat. Methods 2019, 16, 553–560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vincent, P.; Maskos, U.; Charvet, I.; Bourgeais, L.; Stoppini, L.; Leresche, N.; Changeux, J.-P.; Lambert, R.; Meda, P.; Paupardin-Tritsch, D. Live Imaging of Neural Structure and Function by Fibred Fluorescence Microscopy. EMBO Rep. 2006, 7, 1154–1161. [Google Scholar] [CrossRef] [Green Version]
- Doronina-Amitonova, L.V.; Fedotov, I.V.; Efimova, O.; Chernysheva, M.; Fedotov, A.B.; Anokhin, K.V.; Zheltikov, A.M. Multicolor In Vivo Brain Imaging with a Microscope-Coupled Fiber-Bundle Microprobe. Appl. Phys. Lett. 2012, 101, 233702. [Google Scholar] [CrossRef]
- Doronina-Amitonova, L.V.; Fedotov, I.V.; Ivashkina, O.I.; Zots, M.A.; Fedotov, A.B.; Anokhin, K.V.; Zheltikov, A.M. Fiber-Optic Raman Sensing of Cell Proliferation Probes and Molecular Vibrations: Brain-Imaging Perspective. Appl. Phys. Lett. 2012, 101, 113701. [Google Scholar] [CrossRef] [Green Version]
- Pochechuev, M.S.; Fedotov, I.V.; Ivashkina, O.I.; Roshchina, M.A.; Meshchankin, D.V.; Sidorov-Biryukov, D.A.; Fedotov, A.B.; Anokhin, K.V.; Zheltikov, A.M. Reconnectable Fiberscopes for Chronic in Vivo Deep-Brain Imaging. J. Biophotonics 2018, 11, e201700106. [Google Scholar] [CrossRef]
- Pochechuev, M.S.; Fedotov, I.V.; Zheltikov, A.M. An Ultraslim All-Fiber Microendoscope for Depth-Resolved Imaging. Appl. Phys. Lett. 2018, 113, 191102. [Google Scholar] [CrossRef]
- Pochechuev, M.S.; Solotenkov, M.A.; Fedotov, I.V.; Ivashkina, O.I.; Anokhin, K.V.; Zheltikov, A.M. Multisite Cell- and Neural-dynamics-resolving Deep Brain Imaging in Freely Moving Mice with Implanted Reconnectable Fiber Bundles. J. Biophotonics 2020, 13, e202000081. [Google Scholar] [CrossRef]
- Fedotov, I.V.; Solotenkov, M.A.; Pochechuev, M.S.; Ivashkina, O.I.; Kilin, S.Y.; Anokhin, K.V.; Zheltikov, A.M. All-Optical Brain Thermometry in Freely Moving Animals. ACS Photonics 2020, 7, 3353–3360. [Google Scholar] [CrossRef]
- Spitz, E.; Wertz, A. Transmission des images a travers une fibre optique. Comptes Rendus Hebd. Seances Acad. Sci. Ser. B 1967, 264, 1015–1018. [Google Scholar]
- Yariv, A. Three-dimensional Pictorial Transmission in Optical Fibers. Appl. Phys. Lett. 1976, 28, 88–89. [Google Scholar] [CrossRef] [Green Version]
- Yariv, A. On Transmission and Recovery of Three-Dimensional Image Information in Optical Waveguides. J. Opt. Soc. Am. 1976, 66, 301–306. [Google Scholar] [CrossRef] [Green Version]
- Čižmár, T.; Dholakia, K. Shaping the Light Transmission through a Multimode Optical Fibre: Complex Transformation Analysis and Applications in Biophotonics. Opt. Express 2011, 19, 18871–18884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Čižmár, T.; Dholakia, K. Exploiting Multimode Waveguides for Pure Fibre-Based Imaging. Nat. Commun. 2012, 3, 1027. [Google Scholar] [CrossRef] [Green Version]
- Papadopoulos, I.N.; Farahi, S.; Moser, C.; Psaltis, D. Focusing and Scanning Light through a Multimode Optical Fiber Using Digital Phase Conjugation. Opt. Express 2012, 20, 10583–10590. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Yoon, C.; Kim, M.; Yang, T.D.; Fang-Yen, C.; Dasari, R.R.; Lee, K.J.; Choi, W. Scanner-Free and Wide-Field Endoscopic Imaging by Using a Single Multimode Optical Fiber. Phys. Rev. Lett. 2012, 109, 203901. [Google Scholar] [CrossRef]
- Papadopoulos, I.N.; Farahi, S.; Moser, C.; Psaltis, D. High-Resolution, Lensless Endoscope Based on Digital Scanning through a Multimode Optical Fiber. Biomed. Opt. Express 2013, 4, 260–270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plöschner, M.; Tyc, T.; Čižmár, T. Seeing through Chaos in Multimode Fibres. Nat. Photonics 2015, 9, 529–535. [Google Scholar] [CrossRef]
- Andresen, E.R.; Bouwmans, G.; Monneret, S.; Rigneault, H. Two-Photon Lensless Endoscope. Opt. Express 2013, 21, 20713–20721. [Google Scholar] [CrossRef] [PubMed]
- Andresen, E.R.; Bouwmans, G.; Monneret, S.; Rigneault, H. Toward Endoscopes with No Distal Optics: Video-Rate Scanning Microscopy through a Fiber Bundle. Opt. Lett. 2013, 38, 609–611. [Google Scholar] [CrossRef] [PubMed]
- Tsvirkun, V.; Sivankutty, S.; Bouwmans, G.; Vanvincq, O.; Andresen, E.R.; Rigneault, H. Bending-Induced Inter-Core Group Delays in Multicore Fibers. Opt. Express 2017, 25, 31863–31875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Warren, S.C.; Kim, Y.; Stone, J.M.; Mitchell, C.; Knight, J.C.; Neil, M.A.A.; Paterson, C.; French, P.M.W.; Dunsby, C. Adaptive Multiphoton Endomicroscopy through a Dynamically Deformed Multicore Optical Fiber Using Proximal Detection. Opt. Express 2016, 24, 21474–21484. [Google Scholar] [CrossRef]
- Sivankutty, S.; Tsvirkun, V.; Bouwmans, G.; Kogan, D.; Oron, D.; Andresen, E.R.; Rigneault, H. Extended Field-of-View in a Lensless Endoscope Using an Aperiodic Multicore Fiber. Opt. Lett. 2016, 41, 3531–3534. [Google Scholar] [CrossRef] [Green Version]
- Sivankutty, S.; Tsvirkun, V.; Vanvincq, O.; Bouwmans, G.; Andresen, E.R.; Rigneault, H. Nonlinear Imaging through a Fermat’s Golden Spiral Multicore Fiber. Opt. Lett. 2018, 43, 3638–3641. [Google Scholar] [CrossRef] [Green Version]
- Tsvirkun, V.; Sivankutty, S.; Baudelle, K.; Habert, R.; Bouwmans, G.; Vanvincq, O.; Andresen, E.R.; Rigneault, H. Flexible Lensless Endoscope with a Conformationally Invariant Multi-Core Fiber. Optica 2019, 6, 1185–1189. [Google Scholar] [CrossRef] [Green Version]
- Tsvirkun, V.; Sivankutty, S.; Bouwmans, G.; Katz, O.; Andresen, E.R.; Rigneault, H. Widefield Lensless Endoscopy with a Multicore Fiber. Opt. Lett. 2016, 41, 4771–4774. [Google Scholar] [CrossRef] [Green Version]
- Scharf, E.; Dremel, J.; Kuschmierz, R.; Czarske, J. Video-Rate Lensless Endoscope with Self-Calibration Using Wavefront Shaping. Opt. Lett. 2020, 45, 3629–3632. [Google Scholar] [CrossRef]
- Weiss, U.; Katz, O. Two-Photon Lensless Micro-Endoscopy with in-Situ Wavefront Correction. Opt. Express 2018, 26, 28808–28817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pochechuev, M.S.; Lanin, A.A.; Kelmanson, I.V.; Bilan, D.S.; Kotova, D.A.; Chebotarev, A.S.; Tarabykin, V.; Fedotov, A.B.; Belousov, V.V.; Zheltikov, A.M. Stain-Free Subcellular-Resolution Astrocyte Imaging Using Third-Harmonic Generation. Opt. Lett. 2019, 44, 3166–3169. [Google Scholar] [CrossRef]
- Lanin, A.A.; Pochechuev, M.S.; Chebotarev, A.S.; Kelmanson, I.V.; Bilan, D.S.; Kotova, D.A.; Tarabykin, V.S.; Ivanov, A.A.; Fedotov, A.B.; Belousov, V.V.; et al. Cell-Specific Three-Photon-Fluorescence Brain Imaging: Neurons, Astrocytes, and Gliovascular Interfaces. Opt. Lett. 2020, 45, 836. [Google Scholar] [CrossRef]
- Pochechuev, M.S.; Lanin, A.A.; Lanin, A.A.; Kelmanson, I.V.; Chebotarev, A.S.; Fetisova, E.S.; Bilan, D.S.; Shevchenko, E.K.; Ivanov, A.A.; Fedotov, A.B.; et al. Multimodal Nonlinear-Optical Imaging of Nucleoli. Opt. Lett. 2021, 46, 3608–3611. [Google Scholar] [CrossRef] [PubMed]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Musin, R.R.; Zheltikov, A.M. Designing Dispersion-Compensating Photonic-Crystal Fibers Using a Genetic Algorithm. Opt. Commun. 2008, 281, 567–572. [Google Scholar] [CrossRef]
- Conkey, D.B.; Brown, A.N.; Caravaca-Aguirre, A.M.; Piestun, R. Genetic Algorithm Optimization for Focusing through Turbid Media in Noisy Environments. Opt. Express 2012, 20, 4840–4849. [Google Scholar] [CrossRef]
- Mosk, A.P.; Lagendijk, A.; Lerosey, G.; Fink, M. Controlling Waves in Space and Time for Imaging and Focusing in Complex Media. Nat. Photonics 2012, 6, 283–292. [Google Scholar] [CrossRef] [Green Version]
- Freund, I.; Rosenbluh, M.; Feng, S. Memory Effects in Propagation of Optical Waves through Disordered Media. Phys. Rev. Lett. 1988, 61, 2328–2331. [Google Scholar] [CrossRef] [PubMed]
- Stasio, N.; Conkey, D.B.; Moser, C.; Psaltis, D. Light Control in a Multicore Fiber Using the Memory Effect. Opt. Express 2015, 23, 30532–30544. [Google Scholar] [CrossRef]
- Boyden, E.S.; Zhang, F.; Bamberg, E.; Nagel, G.; Deisseroth, K. Millisecond-Timescale, Genetically Targeted Optical Control of Neural Activity. Nat. Neurosci. 2005, 8, 1263–1268. [Google Scholar] [CrossRef]
- Diester, I.; Kaufman, M.T.; Mogri, M.; Pashaie, R.; Goo, W.; Yizhar, O.; Ramakrishnan, C.; Deisseroth, K.; Shenoy, K.V. An Optogenetic Toolbox Designed for Primates. Nat. Neurosci. 2011, 14, 387–397. [Google Scholar] [CrossRef] [Green Version]
- Deisseroth, K. Optogenetics. Nat. Methods 2011, 8, 26–29. [Google Scholar] [CrossRef]
- Miesenböck, G. The Optogenetic Catechism. Science 2009, 326, 395–399. [Google Scholar] [CrossRef] [PubMed]
- Deisseroth, K. Optogenetics: 10 Years of Microbial Opsins in Neuroscience. Nat. Neurosci. 2015, 18, 1213–1225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, C.K.; Adhikari, A.; Deisseroth, K. Integration of Optogenetics with Complementary Methodologies in Systems Neuroscience. Nat. Rev. Neurosci. 2017, 18, 222–235. [Google Scholar] [CrossRef]
- Fedotov, I.V.; Safronov, N.A.; Ermakova, Y.G.; Matlashov, M.E.; Sidorov-Biryukov, D.A.; Fedotov, A.B.; Belousov, V.V.; Zheltikov, A.M. Fiber-Optic Control and Thermometry of Single-Cell Thermosensation Logic. Sci. Rep. 2015, 5, 15737. [Google Scholar] [CrossRef] [Green Version]
- Lanin, A.A.; Fedotov, I.V.; Ermakova, Y.G.; Sidorov-Biryukov, D.A.; Fedotov, A.B.; Hemmer, P.; Belousov, V.V.; Zheltikov, A.M. Fiber-Optic Electron-Spin-Resonance Thermometry of Single Laser-Activated Neurons. Opt. Lett. 2016, 41, 5563. [Google Scholar] [CrossRef]
- Ermakova, Y.G.; Lanin, A.A.; Fedotov, I.V.; Roshchin, M.; Kelmanson, I.V.; Kulik, D.; Bogdanova, Y.A.; Shokhina, A.G.; Bilan, D.S.; Staroverov, D.B.; et al. Thermogenetic Neurostimulation with Single-Cell Resolution. Nat. Commun. 2017, 8, 15362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ermakova, Y.G.; Roshchin, M.V.; Lanin, A.A.; Balaban, P.M.; Zheltikov, A.M.; Belousov, V.V.; Nikitin, E.S. Thermogenetics as a New Direction in Controlling the Activity of Neural Networks. Neurosci. Behav. Phys. 2020, 50, 1018–1023. [Google Scholar] [CrossRef]
- Kelmanson, I.V.; Shokhina, A.G.; Kotova, D.A.; Pochechuev, M.S.; Ivanova, A.D.; Kostyuk, A.I.; Panova, A.S.; Borodinova, A.A.; Solotenkov, M.A.; Stepanov, E.A.; et al. In Vivo Dynamics of Acidosis and Oxidative Stress in the Acute Phase of an Ischemic Stroke in a Rodent Model. Redox Biol. 2021, 48, 102178. [Google Scholar] [CrossRef]
- Fedotov, I.V.; Ivashkina, O.I.; Pochechuev, M.S.; Roshchina, M.A.; Toropova, K.A.; Fedotov, A.B.; Anokhin, K.V.; Zheltikov, A.M. Quantitative Cognitive-Test Characterization of Reconnectable Implantable Fiber-Optic Neurointerfaces for Optogenetic Neurostimulation. J. Biophotonics 2017, 10, 1485–1491. [Google Scholar] [CrossRef] [PubMed]
- Zheltikov, A. Optical beam shift as a vectorial pointer of curved-path geodesics: An evolution-operator perspective. Opt. Express 2020, 28, 12302–12310. [Google Scholar] [CrossRef] [PubMed]
- Horstmeyer, R.; Ruan, H.; Yang, C. Guidestar-assisted wavefront-shaping methods for focusing light into biological tissue. Nat. Photonics 2015, 9, 563–571. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pochechuev, M.S.; Fedotov, I.V.; Solotenkov, M.A.; Andreeva, M.S.; Lanin, A.A.; Fedotov, A.B.; Zheltikov, A.M. Adaptive Wave-Front Shaping and Beam Focusing through Fiber Bundles for High-Resolution Bioimaging. Photonics 2022, 9, 21. https://doi.org/10.3390/photonics9010021
Pochechuev MS, Fedotov IV, Solotenkov MA, Andreeva MS, Lanin AA, Fedotov AB, Zheltikov AM. Adaptive Wave-Front Shaping and Beam Focusing through Fiber Bundles for High-Resolution Bioimaging. Photonics. 2022; 9(1):21. https://doi.org/10.3390/photonics9010021
Chicago/Turabian StylePochechuev, Matvey S., Ilya V. Fedotov, Maxim A. Solotenkov, Maria S. Andreeva, Aleksandr A. Lanin, Andrei B. Fedotov, and Aleksei M. Zheltikov. 2022. "Adaptive Wave-Front Shaping and Beam Focusing through Fiber Bundles for High-Resolution Bioimaging" Photonics 9, no. 1: 21. https://doi.org/10.3390/photonics9010021
APA StylePochechuev, M. S., Fedotov, I. V., Solotenkov, M. A., Andreeva, M. S., Lanin, A. A., Fedotov, A. B., & Zheltikov, A. M. (2022). Adaptive Wave-Front Shaping and Beam Focusing through Fiber Bundles for High-Resolution Bioimaging. Photonics, 9(1), 21. https://doi.org/10.3390/photonics9010021




