Optimization of Hole and Electron Transport Layer for Highly Efficient Lead-Free Cs2TiBr6-Based Perovskite Solar Cell
Abstract
:1. Introduction
2. Simulation Methodology and Material Parameters
2.1. Simulation Methodology
2.2. Device Structure
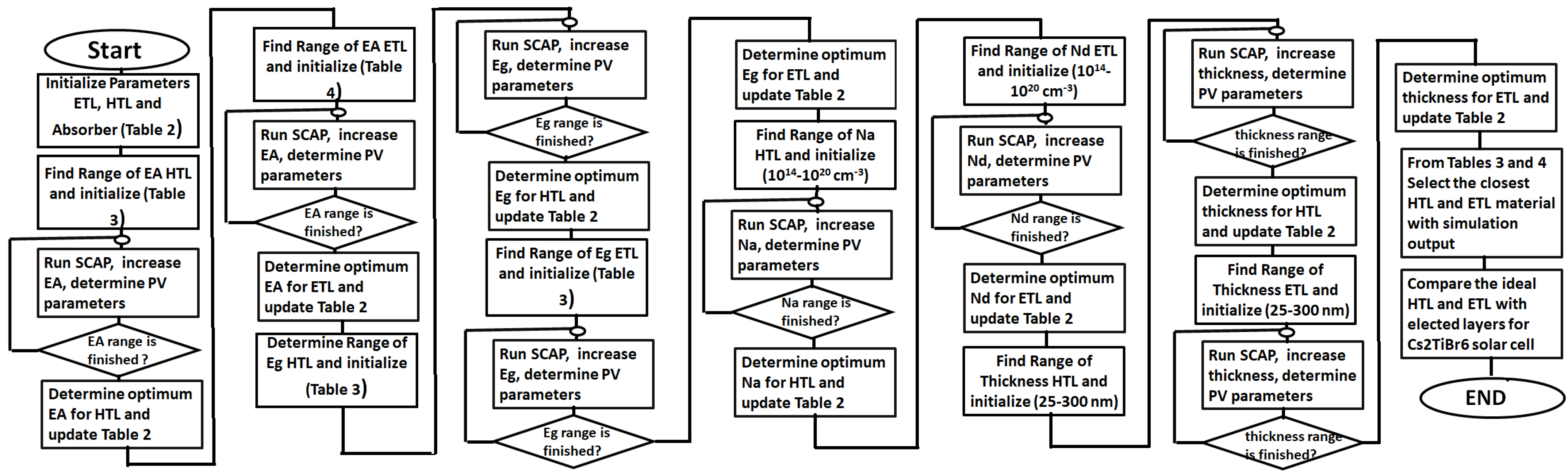
2.3. Simulation Flow Chart
2.4. Physical Parameters
3. Results
3.1. Optimization of Electron Affinity for Hole and Electron Transport Layer
3.2. Optimization of Energy Bandgap for Hole and Electron Transport Layer
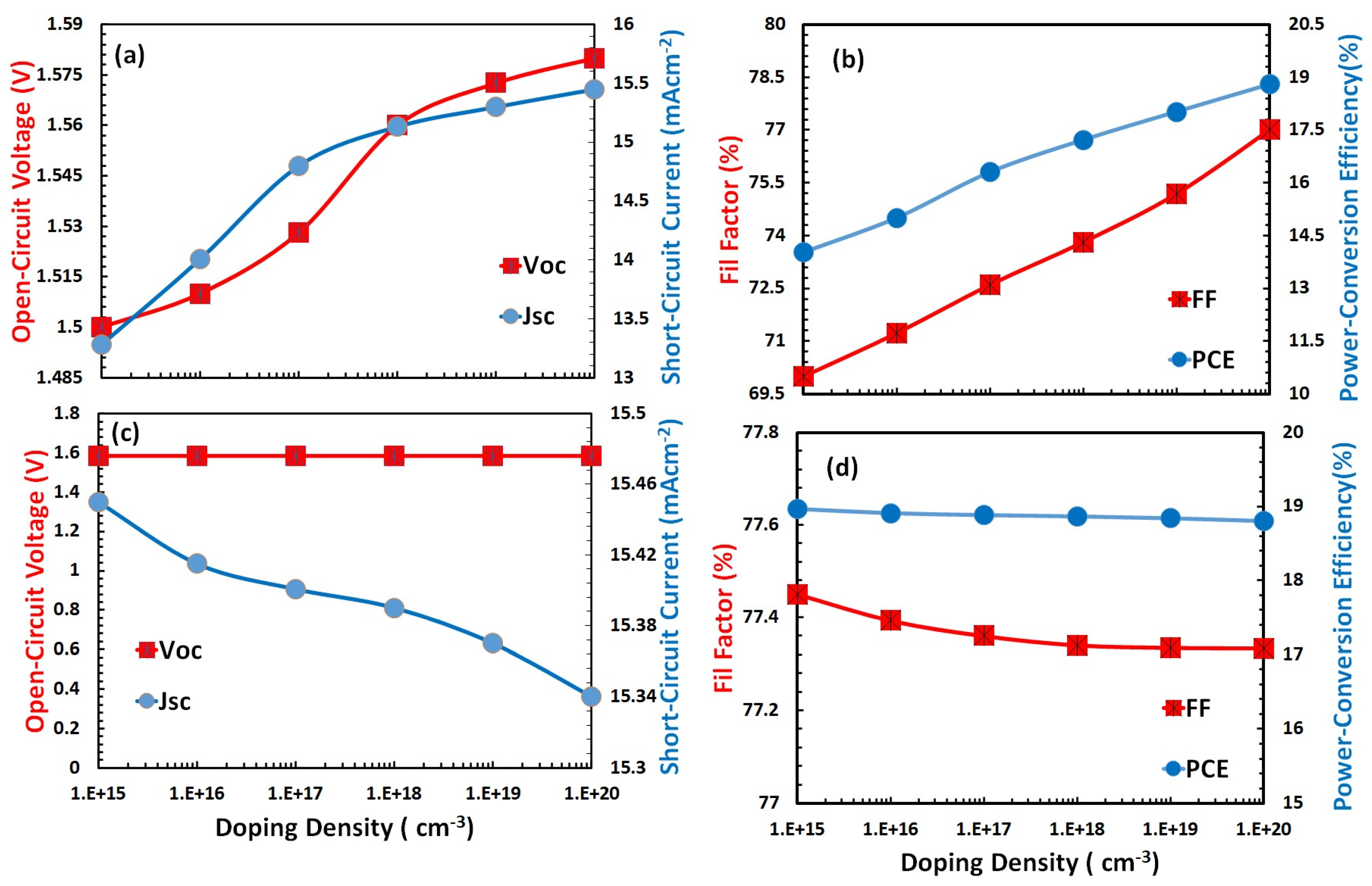
3.3. Optimization of Doping Density for Hole and Electron Transport Layer
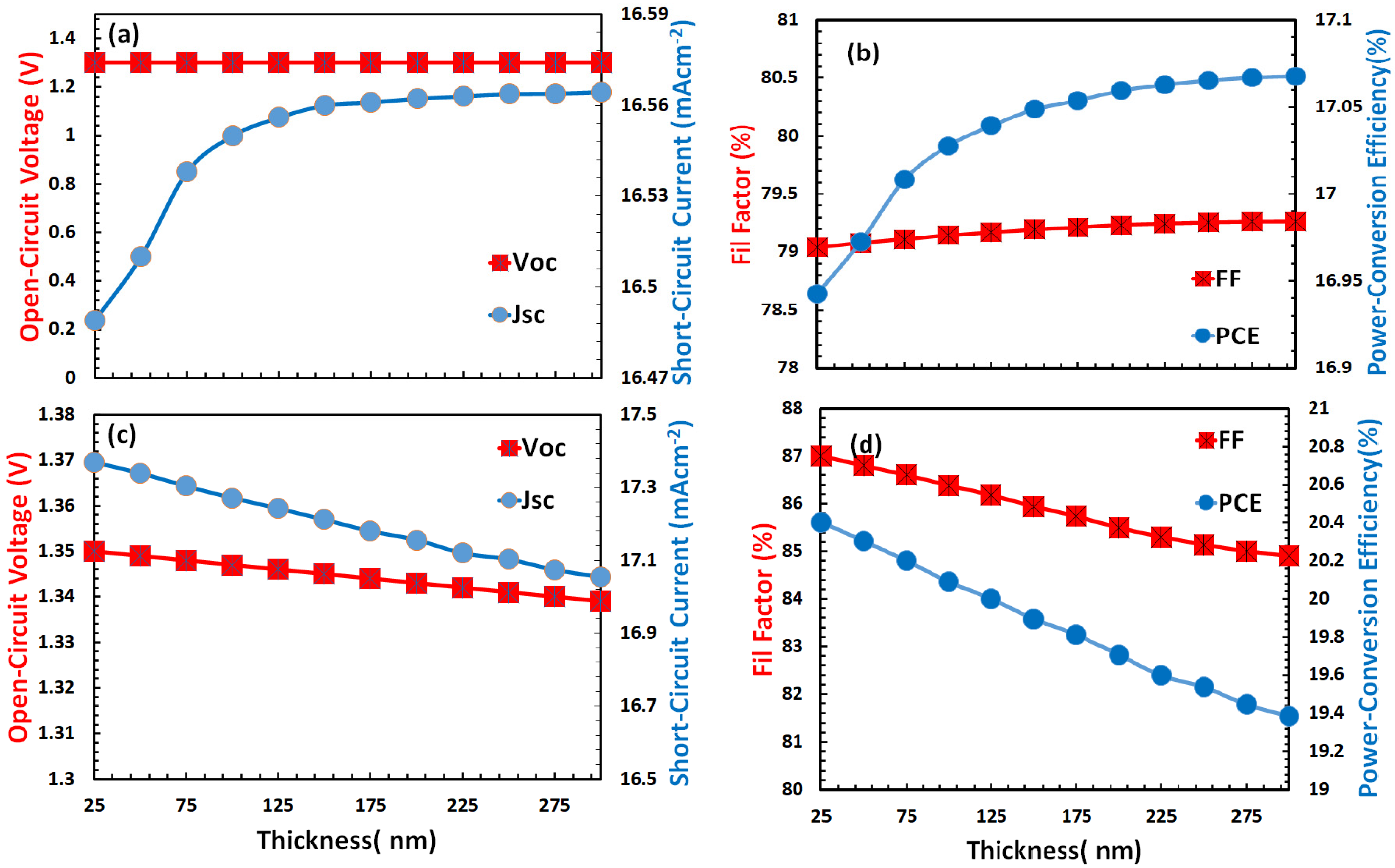
3.4. Optimization of Thickness for Hole and Electron Transport Layer
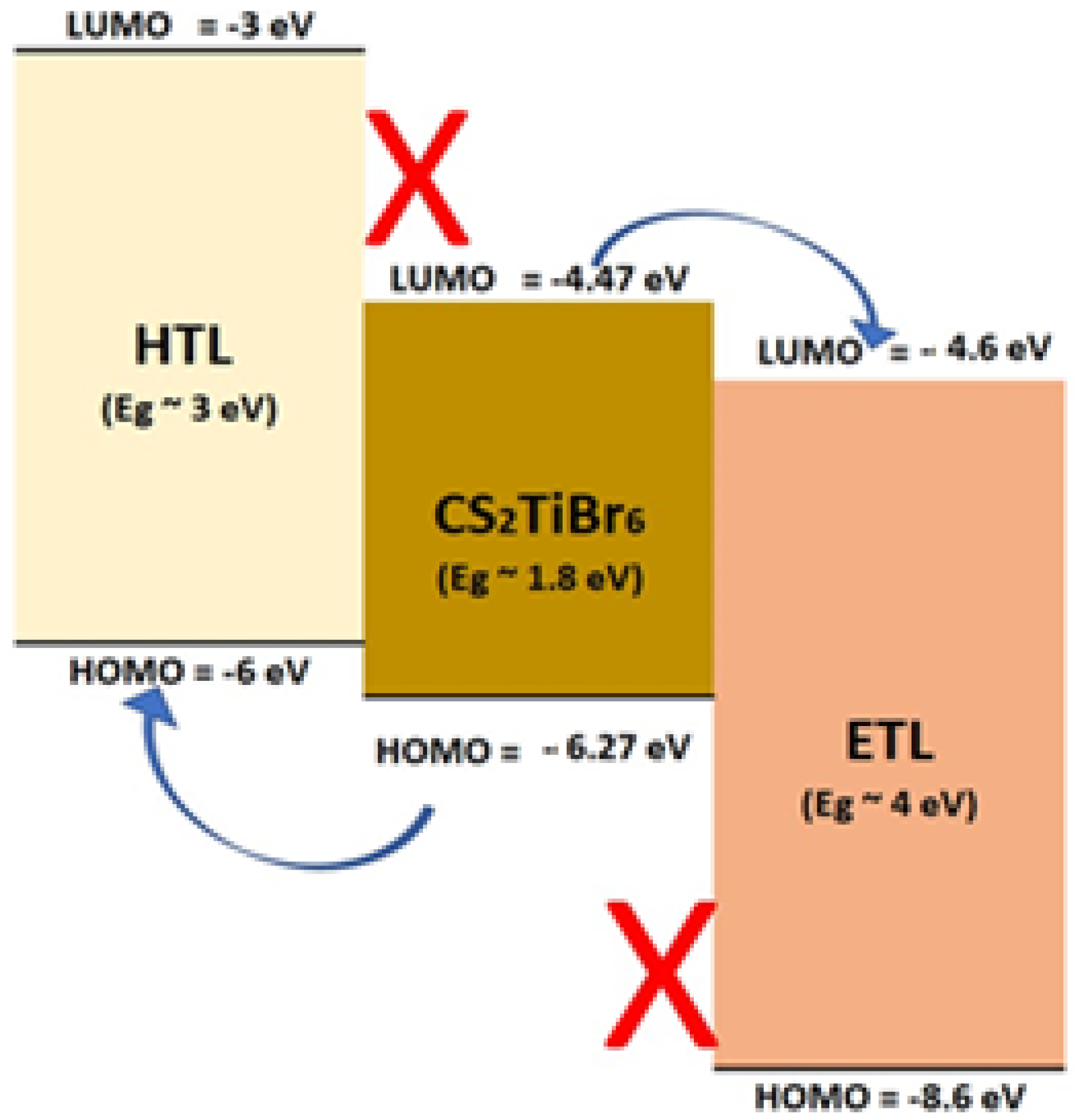
3.5. Device Energy Level and Electric Field Distribution of ETL/Cs2TiBr6/HTL
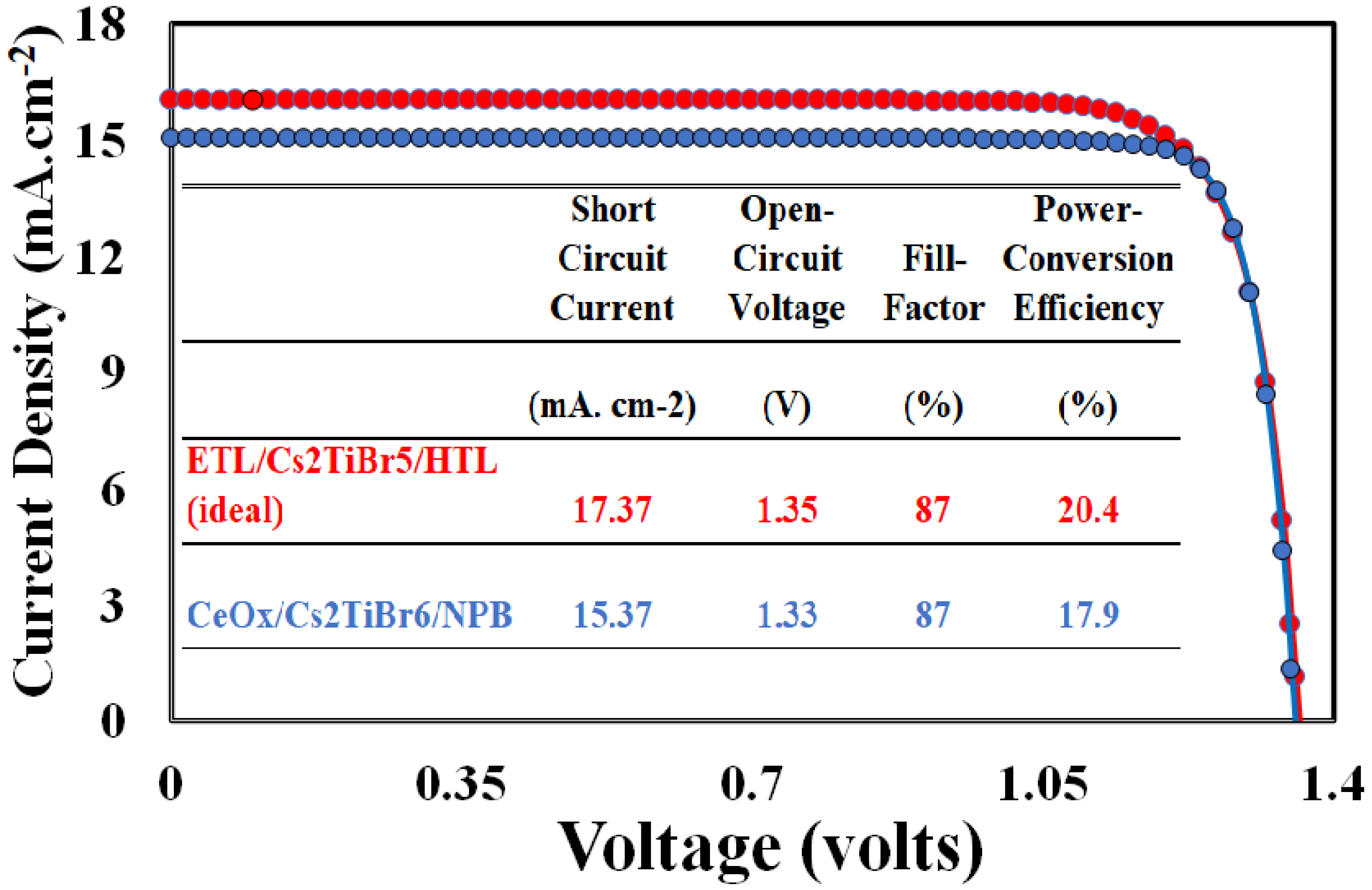
3.6. Selection of Hole and Electron Transport Layer
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kabir, E.; Kumar, P.; Kumar, S.; Adelodun, A.A.; Kim, K.-H. Solar energy: Potential and future prospects. Renew. Sustain. Energy Rev. 2018, 82, 894–900. [Google Scholar] [CrossRef]
- Nazeeruddin, M.K. Twenty-five years of low-cost solar cells. Nature 2016, 538, 463–464. [Google Scholar] [CrossRef] [PubMed]
- Karimov, K.S.; Ahmed, M.; Moiz, S.; Fedorov, M. Temperature-dependent properties of organic-on-inorganic Ag/p-CuPc/n-GaAs/Ag photoelectric cell. Sol. Energy Mater. Sol. Cells 2005, 87, 61–75. [Google Scholar] [CrossRef]
- Green, M.A. The path to 25% silicon solar cell efficiency: History of silicon cell evolution. Prog. Photovolt. Res. Appl. 2009, 17, 183–189. [Google Scholar] [CrossRef]
- Pizzini, S. Towards solar grade silicon: Challenges and benefits for low cost photovoltaics. Sol. Energy Mater. Sol. Cells 2010, 94, 1528–1533. [Google Scholar] [CrossRef]
- Kim, G.-H.; Kim, D.S. Development of perovskite solar cells with >25% conversion efficiency. Joule 2021, 5, 1033–1035. [Google Scholar] [CrossRef]
- Babayigit, A.; Ethirajan, A.; Muller, M.; Conings, B. Toxicity of organometal halide perovskite solar cells. Nat. Mater. 2016, 15, 247–251. [Google Scholar] [CrossRef]
- Giustino, F.; Snaith, H.J. Toward Lead-Free Perovskite Solar Cells. ACS Energy Lett. 2016, 1, 1233–1240. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Ju, M.-G.; Carl, A.; Zong, Y.; Grimm, R.L.; Gu, J.; Zeng, X.C.; Zhou, Y.; Padture, N.P. Cesium Titanium(IV) Bromide Thin Films Based Stable Lead-free Perovskite Solar Cells. Joule 2018, 2, 558–570. [Google Scholar] [CrossRef] [Green Version]
- Ju, M.-G.; Chen, M.; Zhou, Y.; Garces, H.F.; Dai, J.; Ma, L.; Padture, N.P.; Zeng, X.C. Earth-Abundant Nontoxic Titanium(IV)-based Vacancy-Ordered Double Perovskite Halides with Tunable 1.0 to 1.8 eV Bandgaps for Photovoltaic Applications. ACS Energy Lett. 2018, 3, 297–304. [Google Scholar] [CrossRef]
- Pecunia, V.; Occhipinti, L.G.; Chakraborty, A.; Pan, Y.; Peng, Y. Lead-free halide perovskite photovoltaics: Challenges, open questions, and opportunities. APL Mater. 2020, 8, 100901. [Google Scholar] [CrossRef]
- Grandhi, G.; Matuhina, A.; Liu, M.; Annurakshita, S.; Ali-Löytty, H.; Bautista, G.; Vivo, P. Lead-Free Cesium Titanium Bromide Double Perovskite Nanocrystals. Nanomaterials 2021, 11, 1458. [Google Scholar] [CrossRef]
- Chakraborty, K.; Choudhury, M.G.; Paul, S. Numerical study of Cs2TiX6 (X = Br−, I−, F− and Cl−) based perovskite solar cell using SCAPS-1D device simulation. Sol. Energy 2019, 194, 886–892. [Google Scholar] [CrossRef]
- Jani, R.; Islam, T.; Al Amin, S.M.; Sami, S.U.; Shorowordi, K.M.; Hossain, M.I.; Chowdhury, S.; Nishat, S.S.; Ahmed, S. Exploring solar cell performance of inorganic Cs2TiBr6 halide double perovskite: A numerical study. Superlattices Microstruct. 2020, 146, 106652. [Google Scholar] [CrossRef]
- Moiz, S.; Alahmadi, A. Design of Dopant and Lead-Free Novel Perovskite Solar Cell for 16.85% Efficiency. Polymers 2021, 13, 2110. [Google Scholar] [CrossRef] [PubMed]
- Moiz, S.A.; Alahmadi, A.N.M.; Aljohani, A.J. Design of a Novel Lead-Free Perovskite Solar Cell for 17.83% Efficiency. IEEE Access 2021, 9, 54254–54263. [Google Scholar] [CrossRef]
- Qiao, L.; Fang, W.-H.; Long, R. Dopant Control of Electron–Hole Recombination in Cesium–Titanium Halide Double Perovskite by Time Domain Ab Initio Simulation: Codoping Supersedes Monodoping. J. Phys. Chem. Lett. 2018, 9, 6907–6914. [Google Scholar] [CrossRef] [PubMed]
- Park, S.M.; Mazza, S.M.; Liang, Z.; Abtahi, A.; Boehm, A.M.; Parkin, S.R.; Anthony, J.E.; Graham, K.R. Processing Dependent Influence of the Hole Transport Layer Ionization Energy on Methylammonium Lead Iodide Perovskite Photovoltaics. ACS Appl. Mater. Interfaces 2018, 10, 15548–15557. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Varo, P.; Jiménez-Tejada, J.A.; García-Rosell, M.; Ravishankar, S.; Garcia-Belmonte, G.; Bisquert, J.; Almora, O. Device Physics of Hybrid Perovskite Solar cells: Theory and Experiment. Adv. Energy Mater. 2018, 8, 1702772. [Google Scholar] [CrossRef]
- Yin, W.-J.; Shi, T.; Yan, Y. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Appl. Phys. Lett. 2014, 104, 063903. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alahmadi, A.N.M.; Aljohani, A.J. Design of Silicon Nanowire Array for PEDOT:PSS-Silicon Nanowire-Based Hybrid Solar Cell. Energies 2020, 13, 3797. [Google Scholar] [CrossRef]
- Moiz, S.A.; Nahhas, A.; Um, H.-D.; Jee, S.-W.; Cho, H.K.; Kim, S.-W.; Lee, J.-H. A stamped PEDOT:PSS–silicon nanowire hybrid solar cell. Nanotechnology 2012, 23, 145401. [Google Scholar] [CrossRef]
- Verschraegen, J.; Burgelman, M. Numerical modeling of intra-band tunneling for heterojunction solar cells in scaps. Thin Solid Films 2007, 515, 6276–6279. [Google Scholar] [CrossRef]
- Burgelman, M.; Verschraegen, J.; Degrave, S.; Nollet, P. Modeling thin-film PV devices. Prog. Photovolt. Res. Appl. 2004, 12, 143–153. [Google Scholar] [CrossRef]
- Xiao, Z.; Yuan, Y.; Wang, Q.; Shao, Y.; Bai, Y.; Deng, Y.; Dong, Q.; Hu, M.; Bi, C.; Huang, J. Thin-film semiconductor perspective of organometal trihalide perovskite materials for high-efficiency solar cells. Mater. Sci. Eng. R Rep. 2016, 101, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Burgelman, M.; Decock, K.; Khelifi, S.; Abass, A. Advanced electrical simulation of thin film solar cells. Thin Solid Films 2013, 535, 296–301. [Google Scholar] [CrossRef]
- Liu, T.; Chen, K.; Hu, Q.; Zhu, R.; Gong, Q. Inverted Perovskite Solar Cells: Progresses and Perspectives. Adv. Energy Mater. 2016, 6, 1600457. [Google Scholar] [CrossRef]
- Wang, X.; Deng, L.-L.; Wang, L.-Y.; Dai, S.-M.; Xing, Z.; Zhan, X.-X.; Lu, X.-Z.; Xie, S.-Y.; Huang, R.-B.; Zheng, L.-S. Cerium oxide standing out as an electron transport layer for efficient and stable perovskite solar cells processed at low temperature. J. Mater. Chem. A 2016, 5, 1706–1712. [Google Scholar] [CrossRef]
- Azri, F.; Meftah, A.; Sengouga, N.; Meftah, A. Electron and hole transport layers optimization by numerical simulation of a perovskite solar cell. Sol. Energy 2019, 181, 372–378. [Google Scholar] [CrossRef]
- Lin, P.; Lin, L.; Yu, J.; Cheng, S.; Lu, P.; Zheng, Q. Numerical Simulation of Cu2ZnSnS4 Based Solar Cells with In2S3 Buffer Layers by SCAPS-1D. J. Appl. Sci. Eng. 2014, 17, 383–390. [Google Scholar] [CrossRef]
- Ahmed, S.; Jannat, F.; Khan, A.K.; Alim, M.A. Numerical development of eco-friendly Cs2TiBr6 based perovskite solar cell with all-inorganic charge transport materials via SCAPS-1D. Optik 2020, 225, 165765. [Google Scholar] [CrossRef]
- Lam, N.D.; Nguyen, D.L. Modelling and numerical analysis of ZnO/CuO/Cu2O heterojunction solar cell using SCAPS. Eng. Res. Express 2020, 2, 025033. [Google Scholar] [CrossRef]
- Hima, A.; Lakhdar, N. Enhancement of efficiency and stability of CH3NH3GeI3 solar cells with CuSbS2. Opt. Mater. 2019, 99, 109607. [Google Scholar] [CrossRef]
- Jayan, K.D. Enhancement of efficiency of (FA)2BiCuI6 based perovskite solar cells with inorganic transport layers. Opt. Mater. 2021, 122, 111671. [Google Scholar] [CrossRef]
- Karthick, S.; Bouclé, J.; Velumani, S. Effect of bismuth iodide (BiI3) interfacial layer with different HTL’s in FAPI based perovskite solar cell—SCAPS—1D study. Sol. Energy 2021, 218, 157–168. [Google Scholar] [CrossRef]
- Pham, D.P.; Lee, S.; Kim, Y.; Yi, J. Band-offset reduction for effective hole carrier collection in bifacial silicon heterojunction solar cells. J. Phys. Chem. Solids 2021, 154, 110059. [Google Scholar] [CrossRef]
- Um, H.-D.; Moiz, S.A.; Park, K.-T.; Jung, J.-Y.; Jee, S.-W.; Ahn, C.H.; Kim, D.-W.; Cho, H.K.; Lee, J.-H. Highly selective spectral response with enhanced responsivity of n-ZnO/p-Si radial heterojunction nanowire photodiodes. Appl. Phys. Lett. 2011, 98, 033102. [Google Scholar] [CrossRef]
- Subair, R.; Di Girolamo, D.; Bodik, M.; Nadazdy, V.; Li, B.; Nadazdy, P.; Markovic, Z.; Benkovicova, M.; Chlpik, J.; Kotlar, M.; et al. Effect of the doping of PC61BM electron transport layer with carbon nanodots on the performance of inverted planar MAPbI3 perovskite solar cells. Sol. Energy 2019, 189, 426–434. [Google Scholar] [CrossRef]
- Gotanda, T.; Kimata, H.; Xue, D.; Asai, H.; Shimazaki, A.; Wakamiya, A.; Marumoto, K. Direct observation of charge transfer at the interface between PEDOT:PSS and perovskite layers. Appl. Phys. Express 2019, 12, 041002. [Google Scholar] [CrossRef]
- Moiz, S.A.; Khan, I.A.; Younis, W.A.; Masud, M.I.; Ismail, Y.; Khawaja, Y.M. Solvent induced charge transport mechanism for conducting polymer at higher temperature. Mater. Res. Express 2020, 7, 095304. [Google Scholar] [CrossRef]
- Schloemer, T.H.; Christians, J.A.; Luther, J.M.; Sellinger, A. Doping strategies for small molecule organic hole-transport materials: Impacts on perovskite solar cell performance and stability. Chem. Sci. 2019, 10, 1904–1935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marinova, N.; Tress, W.; Humphry-Baker, R.; Dar, M.I.; Bojinov, V.; Zakeeruddin, S.M.; Nazeeruddin, M.K.; Grätzel, M. Light Harvesting and Charge Recombination in CH3NH3PbI3 Perovskite Solar Cells Studied by Hole Transport Layer Thickness Variation. ACS Nano 2015, 9, 4200–4209. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.-W.; Shinde, D.V.; Park, T. Thickness of the hole transport layer in perovskite solar cells: Performance versus reproducibility. RSC Adv. 2015, 5, 99356–99360. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, Y.; Wen, J.; Liu, H.; Yang, G.; Qin, P.; Fang, G. Review on the Application of SnO2 in Perovskite Solar Cells. Adv. Funct. Mater. 2018, 28, 1802757. [Google Scholar] [CrossRef]
- Karimi, E.; Ghorashi, S. Investigation of the influence of different hole-transporting materials on the performance of perovskite solar cells. Optik 2017, 130, 650–658. [Google Scholar] [CrossRef]
- Ahmmed, S.; Karim, A.; Rahman, H.; Aktar, A.; Islam, R.; Islam, A.; Ismail, A.B.M. Performance analysis of lead-free CsBi3I10-based perovskite solar cell through the numerical calculation. Sol. Energy 2021, 226, 54–63. [Google Scholar] [CrossRef]
- Wu, M.-C.; Chan, S.-H.; Jao, M.-H.; Su, W.-F. Enhanced short-circuit current density of perovskite solar cells using Zn-doped TiO2 as electron transport layer. Sol. Energy Mater. Sol. Cells 2016, 157, 447–453. [Google Scholar] [CrossRef]
- Schulz, P.; Kelly, L.L.; Winget, P.; Li, H.; Kim, H.; Ndione, P.F.; Sigdel, A.K.; Berry, J.J.; Graham, S.; Brédas, J.-L.; et al. Tailoring Electron-Transfer Barriers for Zinc Oxide/C60Fullerene Interfaces. Adv. Funct. Mater. 2014, 24, 7381–7389. [Google Scholar] [CrossRef]
- Park, Y.I.; Kuo, C.-Y.; Martinez, J.S.; Park, Y.-S.; Postupna, O.; Zhugayevych, A.; Kim, S.; Park, J.; Tretiak, S.; Wang, H.-L. Tailored Electronic Structure and Optical Properties of Conjugated Systems through Aggregates and Dipole–Dipole Interactions. ACS Appl. Mater. Interfaces 2013, 5, 4685–4695. [Google Scholar] [CrossRef]
- Moiz, S.; Alahmadi, A.; Karimov, K. Improved organic solar cell by incorporating silver nanoparticles embedded polyaniline as buffer layer. Solid-State Electron. 2019, 163, 107658. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, R.; Yao, H.; Xie, S.; Zhang, Y.; Hou, J.; Zhou, H.; Tang, Z. Polyamino acid interlayer facilitates electron extraction in narrow band gap fullerene-free organic solar cells with an outstanding short-circuit current. Nano Energy 2018, 50, 169–175. [Google Scholar] [CrossRef]




| Year | Device | Study | HTL | ETL | Jsc | Voc | FF | PCE | Ref |
|---|---|---|---|---|---|---|---|---|---|
| 2018 | FTO/TiO2/Cs2TiBr6/P3HT/Au | Experimental | P3HT | TiO2 /C60 | 3.87 | 0.89 | 59.5 | 2.15 | [9] |
| 2018 | FTO/TiO2/C60/Cs2TiBr6/P3HT/Au | Experimental | P3HT | TiO2 | 5.75 | 0.99 | 54.9 | 3.12 | [9] |
| 2019 | CuSCN/ Cs2TiBr6/CdS/Si | Simulation | CuSCN | CdS | 8.9 | – | – | 6.68 | [13] |
| 2020 | Glass/FTO/TiO2/Cs2TiBr6/Cu2O/A | Simulation | Cu2O | TiO2 | 25.82 | 1.1 | 51.7 | 14.68 | [14] |
| 2021 | Ag/BCP/PCBM/Cs2TiBr6/NPB/ITO | Simulation | NPB | BCP/PCBM | 16.66 | 1.29 | 78.1 | 16.85 | [15] |
| 2021 | Au/PEDOT:PSS/Cs2TiBr6/TiO2/AZO | Simulation | PEDOT:PSS | TiO2 | 18.2 | 1.38 | 71% | 17.83 | [16] |
| Transport Layer Material | Energy Band Gap (Eg, eV) | Electron Affinity (EA, eV) | Reference |
|---|---|---|---|
| Cu2O | 2.17 | 3.2 | [13] |
| Spiro-OMeTAD | 3.2 | 2.1 | [28] |
| PEDOT:PSS | 1.6 | 3.5 | [16] |
| NPB | 3 | 2.4 | [15] |
| P3HT | 1.85 | 3.1 | [29] |
| CuSCN | 3.4 | 1.9 | [29] |
| NiO | 3.6 | 1.46 | [28] |
| CZTS | 1.5 | 4.5 | [30] |
| CuI | 2.98 | 2.1 | [29,31] |
| CuO | 1.3 | 4 | [32] |
| MoO3 | 3 | 2.5 | [29] |
| NiO | 3.8 | 1.46 | [29] |
| CuSbS2 | 1.58 | 4.2 | [33] |
| Transport Layer Material | Energy Band Gap (Eg, eV) | Electron Affinity (EA, eV) | Reference |
|---|---|---|---|
| TiO2 | 3.26 | 4.26 | [13,16] |
| ZnO:Al | 3.3 | 4.6 | [16,30] |
| IGZO | 3.05 | 4.16 | [29] |
| ZnO | 3.2 | 4.26 | [34] |
| SnO2 | 3.5 | 4 | [35] |
| In2S3 | 2.8 | 4.7 | [30] |
| CeOx | 3.5 | 4 | [28] |
| PCBM | 1.9 | 3.9 | [15] |
| BCP | 3.5 | 3.7 | [15] |
| CdS | 2.4 | 1.8 | [31] |
| Physical Parameters | Symbol | Unit | HTL | Cs2TiB6 | ETL |
|---|---|---|---|---|---|
| Thickness | Th | nm | 250 | 200 | 250 |
| Energy Band Gap | Eg | eV | 2 | 1.8 | 2 |
| Electron Affinity | χ | eV | 4.5 | 4.47 | 4 |
| Dielectric Permittivity (Relative) | ε | - | 10 | 10 | 10 |
| Effective Density of States at Valence Band | NV | cm−3 | 1 × 1020 | 6 × 1019 | 1 × 1019 |
| Effective Density of States at Conduction Band | NC | cm−3 | 1 × 1020 | 2 × 1019 | 1 × 1019 |
| Hole Thermal Velocity | Ve | cm/s | 1 × 107 | 1 × 107 | 1 × 107 |
| electron Thermal Velocity | Vh | cm/s | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Mobility | μe | cm2/V.s | 0.01 | 4.4 | 1 |
| Hole Mobility | μh | cm2/V.s | 0.1 | 2.5 | 0.1 |
| Uniform Shallow Donor Doping | Nd | cm−3 | 0 | 1 × 1019 | 1 × 1018 |
| Uniform Shallow Acceptor Doping | Na | cm−3 | 1 × 1018 | 1 × 1019 | 0 |
| Defect Density | Nt | cm−3 | 1 × 1015 | 1 × 1015 | 1 × 1015 |
| References | Random | [9,10,13] | Random |
| Physical Parameters | Symbol | Unit | NPB (HTL) | Cs2TiB6 | CeOx (ETL) |
|---|---|---|---|---|---|
| Thickness | Th | nm | 250 | 150 | 25 |
| Energy Band Gap | Eg | eV | 2.4 | 1.8 | 3.5 |
| Electron Affinity | χ | eV | 3 | 4.47 | 4.4 |
| Dielectric Permittivity (Relative) | ε | - | 3 | 10 | 9 |
| Effective Density of States at Valence Band | NV | cm−3 | 1 × 1021 | 6 × 1019 | 1x 1020 |
| Effective Density of States at Conduction Band | NC | cm−3 | 1 × 1021 | 2 × 1019 | 2 × 1021 |
| Hole Thermal Velocity | Ve | cm/s | 1 × 107 | 1 × 107 | 1 × 107 |
| electron Thermal Velocity | Vh | cm/s | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Mobility | μe | cm2/V.s | 6 × 10−6 | 4.4 | 100 |
| Hole Mobility | μh | cm2/V.s | 6.1 × 10−4 | 2.5 | 25 |
| Uniform Shallow Donor Doping | Nd | cm−3 | 0 | 1 × 1017 | 1 × 1016 |
| Uniform Shallow Acceptor Doping | Na | cm−3 | 1 × 1020 | 1 × 1017 | 0 |
| Defect Density | Nt | cm−3 | 1 × 1014 | 1 × 1015 | 1 × 1015 |
| References | [15,45] | [9,10,13,14] | [46] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moiz, S.A. Optimization of Hole and Electron Transport Layer for Highly Efficient Lead-Free Cs2TiBr6-Based Perovskite Solar Cell. Photonics 2022, 9, 23. https://doi.org/10.3390/photonics9010023
Moiz SA. Optimization of Hole and Electron Transport Layer for Highly Efficient Lead-Free Cs2TiBr6-Based Perovskite Solar Cell. Photonics. 2022; 9(1):23. https://doi.org/10.3390/photonics9010023
Chicago/Turabian StyleMoiz, Syed Abdul. 2022. "Optimization of Hole and Electron Transport Layer for Highly Efficient Lead-Free Cs2TiBr6-Based Perovskite Solar Cell" Photonics 9, no. 1: 23. https://doi.org/10.3390/photonics9010023
APA StyleMoiz, S. A. (2022). Optimization of Hole and Electron Transport Layer for Highly Efficient Lead-Free Cs2TiBr6-Based Perovskite Solar Cell. Photonics, 9(1), 23. https://doi.org/10.3390/photonics9010023





