Efficiency of Photoconductive Terahertz Generation in Nitrogen-Doped Diamonds

Abstract

The efficiency of the generation of terahertz radiation from nitrogen-doped (∼$0.1$–100 ppm) diamonds was investigated. The synthetic polycrystalline and monocrystalline diamond substrates were pumped by a 400 nm femtosecond laser and tested for the photoconductive emitter operation. The dependency of the emitted THz power on the intensity of the optical excitation was measured. The nitrogen concentrations of the diamonds involved were measured from the optical absorbance, which was found to crucially depend on the synthesis technique. The observed correlation between the doping level and the level of the performance of diamond-based antennas demonstrates the prospects of doped diamond as a material for highly efficient large-aperture photoconductive antennas.

1. Introduction

Various techniques are used to generate THz radiation, including the acceleration of photoexcited carriers in photoconductive antennas (PCAs) [1], second-order nonlinear phenomena in electro-optical crystals (optical rectification) [2] and laser-breakdown plasmas [3]. PCAs pumped by femtosecond laser radiation are one of the most commonly used pulsed THz radiation sources [4,5]. The main features of the radiation generated by large-aperture PCAs are the low-frequency peak in the emission spectrum and the quasi-half-cycle pulse of the emitted radiation [6,7]. Currently, the study of promising substrate materials suitable for different pump lasers is of great interest for high-power large-aperture PCA devices [8,9,10,11,12,13].

One of the ways to boost the amplitude of the THz field is to increase the bias voltage applied to the PCA. Diamond has the highest dielectric strength out of all the THz-emitting substrates: its breakdown electric field was demonstrated to achieve 10 MV/cm [14]. There are additional extraordinary properties that make diamond attractive for PCA applications. Diamond is highly transparent in the THz region [15] and has already been used for THz optics [16]. Monocrystalline diamonds have a record mobility of ∼4500 cm${}^2$ V${}^{-1}$ s${}^{-1}$ at room temperature among crystalline materials [17]. Polycrystalline diamond wafers produced in a chemical vapor deposition (CVD) process are available now with diameters of over 100 mm. On the other hand, diamond is a wide-bandgap (5.46 eV) semiconductor and requires deep ultraviolet radiation for the efficient one-photon excitation of the electronic subsystem. Therefore, the first diamond PCA was pumped by an excimer laser operated at 248 nm [8]. Femtosecond UV lasers are complex systems and can hardly be used to build table-top THz sources.

Recently, nitrogen-doped diamonds were shown to be prospective candidates for THz PCAs [18]. The substitutional nitrogen evidently appeared to be an effective source of photoelectrons promoted to the conduction band by the second harmonic of a Ti:sapphire laser (400 nm). In our previous work [18], two monocrystalline CVD and HPHT (high-pressure high-temperature) diamonds were used. The nitrogen concentration of the HPHT sample was ∼10 times the nitrogen concentration of the CVD sample. In this work, the nitrogen content in the diamonds varied over three orders of magnitude (∼$0.1$–100 ppm), which allowed a detailed analysis of the effect of the nitrogen concentration on the performance of diamond PCAs to be carried out.

2. Materials and Methods

Nineteen diamond substrates of different origins with different nitrogen impurity levels were tested as PCAs. Polycrystalline and monocrystalline CVD and monocrystalline HPHT diamonds were used; they were purchased from different sellers. The typical sample size varied from 3 mm to 7 mm, and the thickness varied from 250 $\mathsf{\mu }$m to 1570 $\mathsf{\mu }$m. Face and edge surfaces were polished mechanically to an optical quality. Each of the assembled diamond antennas constituted the sample, with aluminum foil electrodes glued to their edges. The gap between the electrodes was limited by the substrate geometry and ranged from 0.5 to 2 mm.

The femtosecond Ti:sapphire laser system Coherent Elite Pro (800 nm fundamental wavelength, 3 mJ pulse energy, 150 fs pulse duration, 12 mm beam diameter at the $1/e^2$ level, 1 kHz repetition rate) was used for the excitation of the diamond PCAs. The experimental scheme is depicted in detail in Figure 1. The output laser beam was reduced two-fold in diameter by a telescope. Second harmonic radiation with a maximum pulse energy of 1 mJ was produced in a BBO crystal ($\beta$-barium borate, I-type, $10\times 10\times 0.2$ mm${}^3$). The second harmonic pump was filtered by a cold mirror reflecting the 400 nm radiation. The energy of the second harmonic pulse was adjusted by tilting the second harmonic crystal.

The antennas were irradiated by the central part of the unfocused pump beam with a maximum laser fluence of ∼7200 $\mathsf{\mu }$J/cm${}^2$. A pulsed bias voltage (up to 3 kV) with a pulse duration of ∼10 ns was synchronized with the laser radiation. It should be noted that we have not achieved any THz yield with static high voltage applied to the diamond samples. THz radiation from the antennas was collected by a telescope consisting of two polytetrafluoroethylene (PTFE) lenses (50 mm diameter, 6 cm focal length and 50 mm diameter, 10 cm focal length). The power of the THz signal was measured by a Golay cell (Tydex GC-1P, 6 mm detector aperture, ${10}^5$ V/W illumination responsivity) with a 15 Hz modulation of the laser output.

3. Results and Discussion

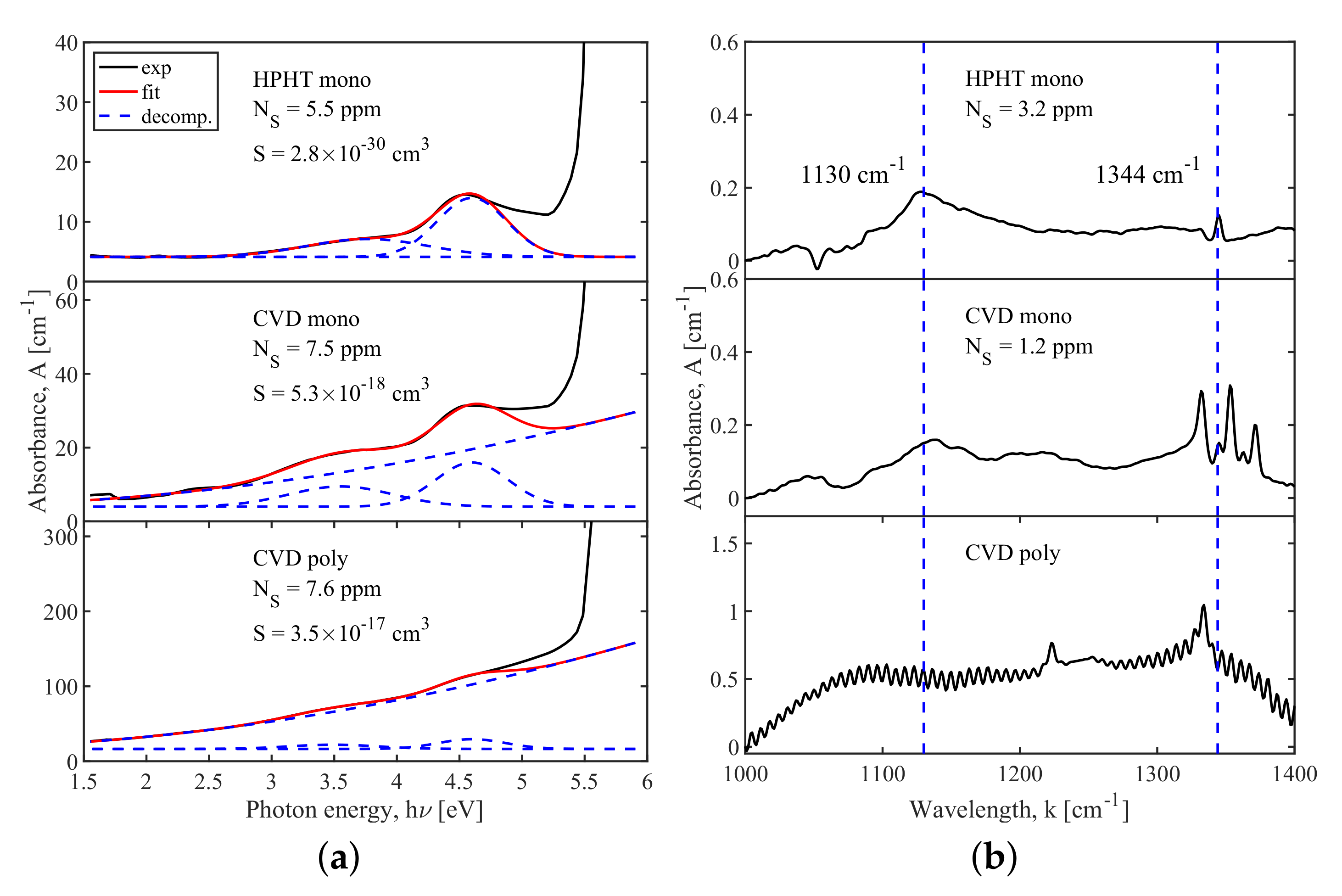
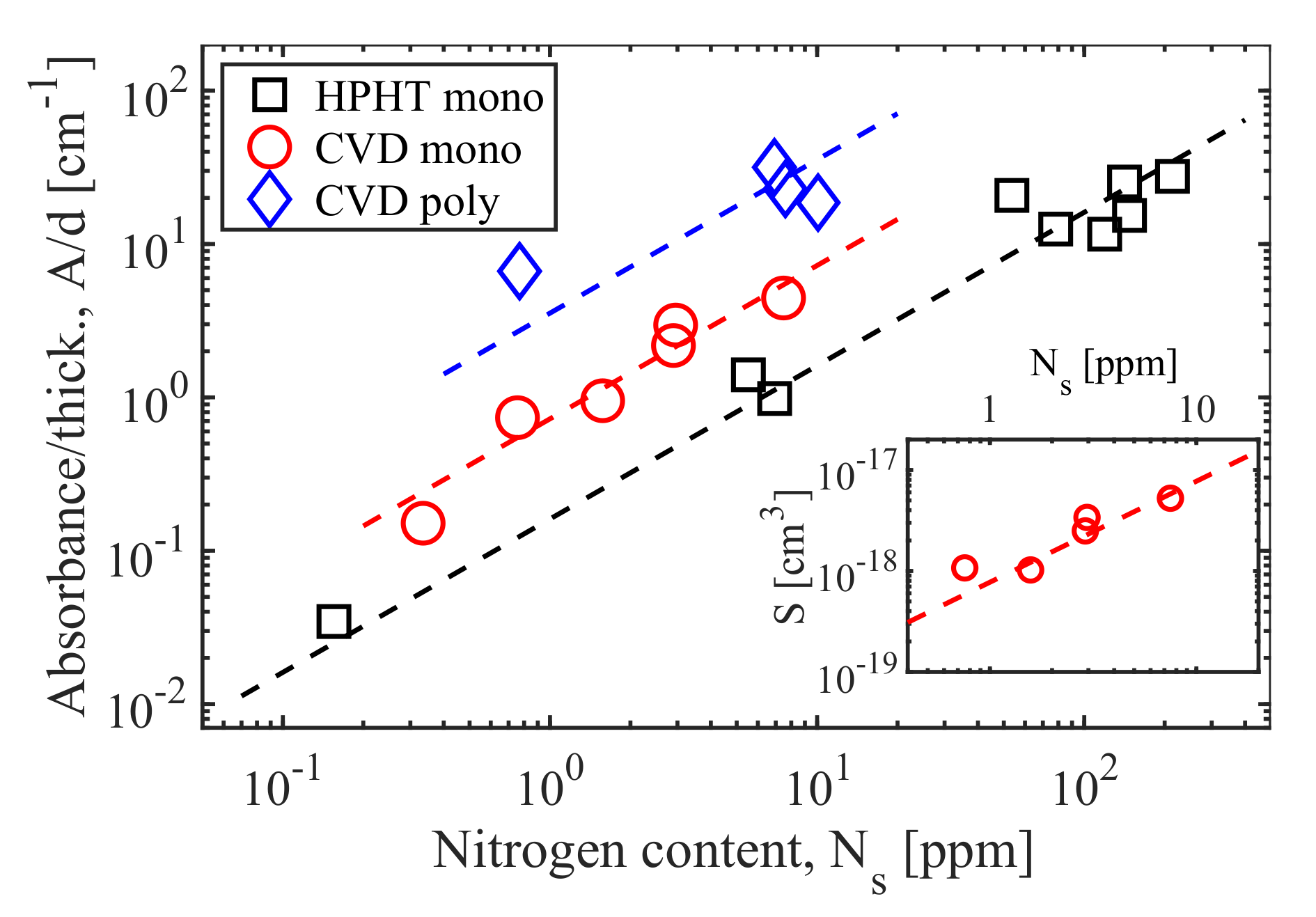
3.1. Optical Properties of Nitrogen-Doped Monocrystalline HPHT and Monocrystalline and Polycrystalline CVD Diamonds

Figure 2 depicts the typical UV-visible and IR spectra of optical losses in the three types of diamonds used. The main information was deduced from the spectral data of the UV-visible range. The blue curves in Figure 2a indicate spectral decomposition in different optical loss channels, including nitrogen absorption and Rayleigh scattering. The red curve represents a sum of these individual channels of optical losses. (Band-to-band transitions were excluded from the spectral analysis.)

The absorption was approximated by two Gaussian peaks at 4.6 eV (270 nm) and 3.6 eV (345 nm) with peak widths of ∼$0.4$ eV and ∼$0.6$ eV, respectively. The visible band is assigned to the transition from the defect level of substitutional nitrogen to the conduction band, while the UV band is assigned to the transition from the valence band to the unoccupied defect level [19]. The 4.6 eV peak is the most intensive and is considered to be the most preferable in order to determine the nitrogen content level in diamonds [20]. On the whole, the intensity of the 3.6 eV peak changed in accordance with the 4.6 eV peak. While the amplitude of each peak changed over three orders of magnitude, their ratio was $2.1\pm 1.0$ in our experiments.

The nitrogen level in the diamonds involved was calculated as $N_S=I_{abs}(4.6$eV$)·k(4.6$eV), where k(4.6 eV) ≈ 1 ppm/cm${}^{-1}$ is a calibration coefficient obtained in [20] using electron spin resonance (ESR) spectroscopy. In the presented set of diamond samples, the calculated content of substitutional nitrogen ranged from ${10}^{-1}$ ppm to ${10}^2$ ppm. The HPHT samples filled this range entirely ($N_{HPHT}$≈${10}^{-1}$–${10}^2$ ppm), while the CVD samples had rather moderate concentrations of nitrogen up to $N_{CVD}<10$ ppm because of the known difficulties of introducing nitrogen into diamond during this deposition process. IR data (Figure 2b) enabled us to estimate the $N_S$ content level for monocrystalline diamonds only (both HPHT and CVD). The bands 1130 cm${}^{-1}$ and 1344 cm${}^{-1}$, which are usually ascribed to the N${}_S$ center, were not detected for the relatively thin polycrystalline CVD samples that are typical for these diamonds [19]. The nitrogen contents estimated from UV-visible data and, where it was possible, from IR data differed widely (compare Figure 2a,b) but were of the same order of magnitude. Hereafter, we use $N_S$ values calculated from the 4.6 eV absorption peak.

The samples whose spectra are depicted in Figure 2a have approximately equal nitrogen concentrations. These data clearly indicate that the magnitude of the optical losses in the visual-UV range crucially depends on the substrate origin. The polycrystalline CVD diamond substrate showed the maximum losses. The reason for this is the Rayleigh scattering that arises from subwavelength fluctuations of medium permittivity, which are the most intensive for the polycrystalline diamond. The scattering component of the absorbance was calculated as follows:

$$A_S=Sd{\lambda }^4,$$

(1)

where d is the sample thickness, $\lambda$ is the wavelength and S is a scattering factor, which depends on the number of scattering centers in the medium $N_{scatt}$, the diameter D of such centers and the substrate refractive index n:

$$S=N_{scatt}\frac{2{\pi }^5}{3}{D}^6{\left[\frac{n^2-1}{n^2+2}\right]}^2.$$

(2)

As can be seen in Figure 2a, for the HPHT diamond, the absorption losses dominate, while the scattering is close to zero. For the monocrystalline CVD diamond, these components are rather similar. This result is not quite surprising because the CVD technique is known to favor the formation of linear defects in the lattice. Additionally, as already mentioned, scattering is the main reason for the high optical density of the polycrystalline plates.

This conclusion was corroborated by the measurement of the diamonds’ optical properties using the second harmonic of a Ti:sapphire laser. Figure 3 illustrates the dependence of the diamond absorbance per unit depth on the nitrogen concentration. The plotted data are obviously separated into three groups. Each of them exactly corresponds to the origin of the diamonds and linearly depends on the nitrogen concentration. The first group included HPHT diamonds and describes “pure” absorption losses characterized by a minimum optical density per ppm of nitrogen. The second group included CVD monocrystalline diamonds and had an absorbance per sample that was ∼4 times higher than in the case of HPHT diamonds. The absorbance of the diamonds in the third group (polycrystalline diamonds) was found to be about 20 times higher.

It is noteworthy that there is some discrepancy between the spectroscopy of monocrystalline CVD diamonds and the corresponding laser measurements. The results of the laser experiments (Figure 3) indicate that the variation of an absorbance/thickness parameter in CVD monocrystals can be completely attributed to the absorption effect. In other words, the scattering magnitude does not depend on the nitrogen level and the scattering factor S is an approximately constant value over this sample set. On the other hand, the scattering factors S calculated from spectral data with Equation (1) and depicted in the insert of Figure 3 demonstrate that optical scattering linearly increases with $N_s$. Therefore, at the moment, we cannot conclusively determine if the nitrogen impurity is the factor enhancing the scattering in diamonds. However, it is of interest to estimate the possible size of optical fluctuations in CVD diamonds. Using a factor $S\approx {10}^{-18}$ cm${}^3$ and a scattering center number of $N_{scatt}\approx {10}^{17}$ cm${}^{-3}$ (∼$N_S$), Equation (2) gives D∼ 10 nm, which is a more-or-less reasonable value in terms of the typical dislocation size.

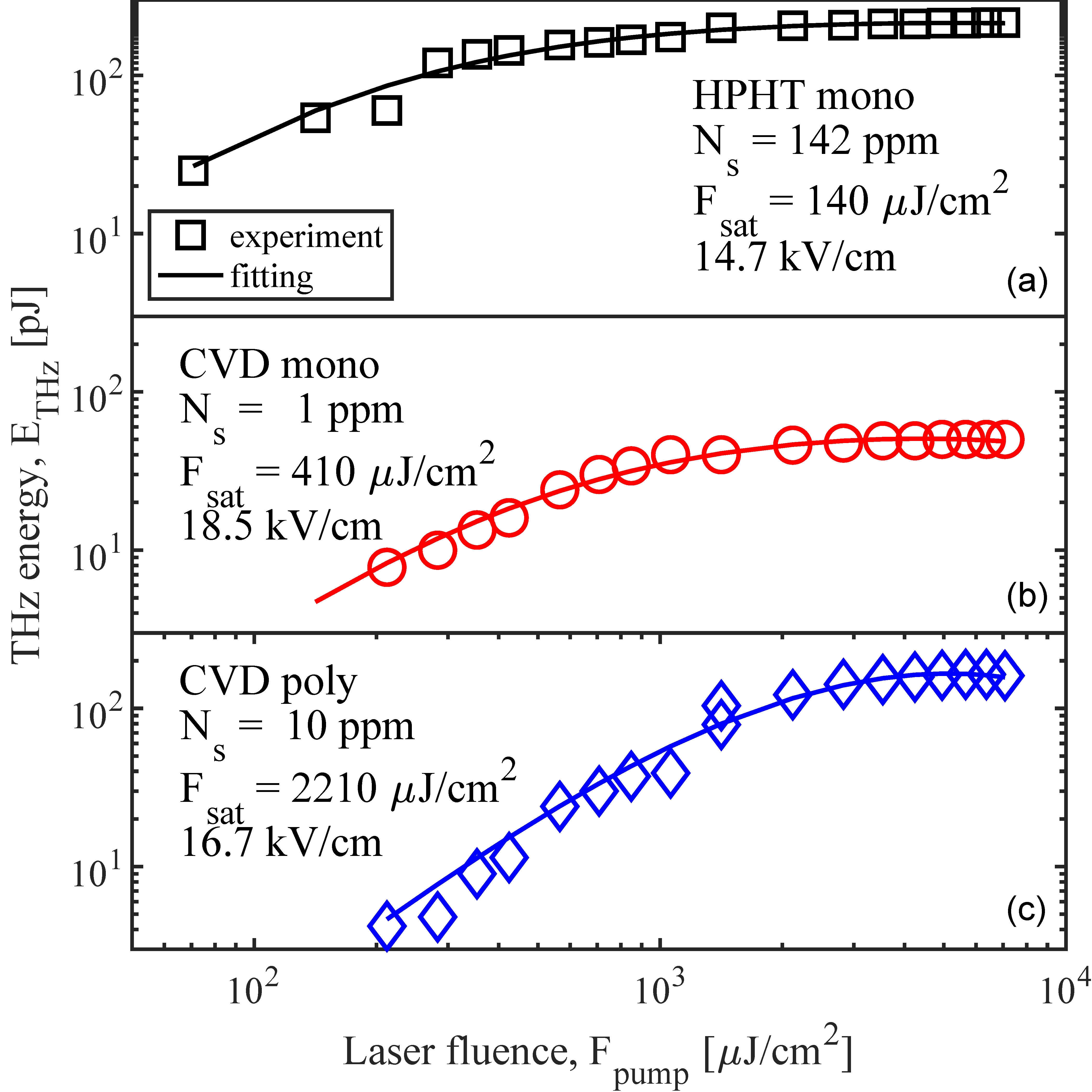
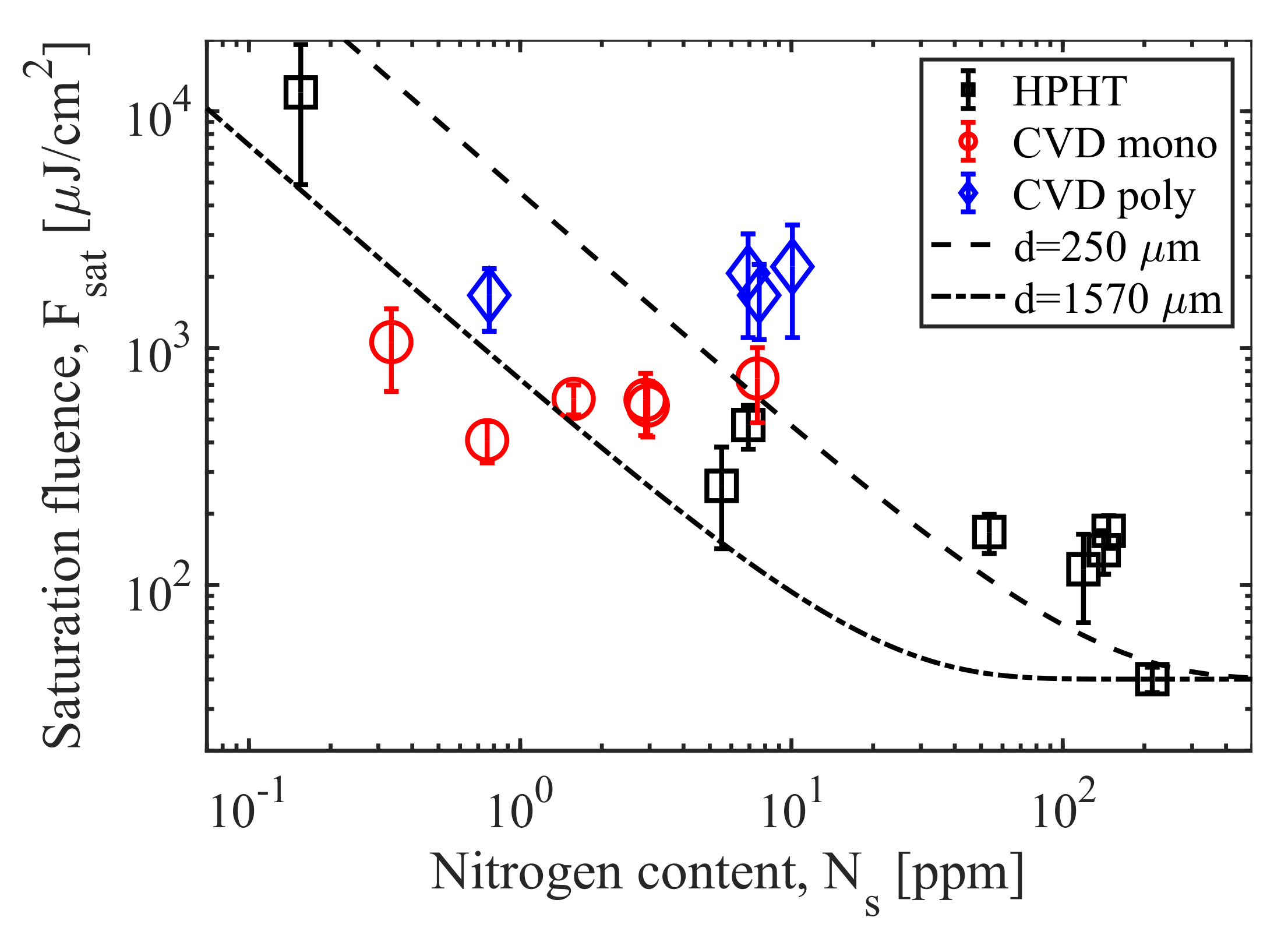
3.2. Photoconductive THz Antennas Based on Nitrogen-Doped Monocrystalline HPHT and Monocrystalline and Polycrystalline CVD Diamonds

The dependence of the THz pulse energies on the optical pump fluence is shown in Figure 4. The fitting of the experimental data was performed using a model of THz generation that predicted the saturation of the THz field due to its interaction with a bias field [21]. According to this model, the emitted THz fluence can be written as:

$$F_{THz}=\frac{\tau E_{bias}^2}{2Z_0}{\left(\frac{F_{pump}}{F_{pump}+F_{sat}^{ideal}}\right)}^2,$$

(3)

where $E_{bias}$ is the applied bias field, $\tau$ is the THz pulse duration, $Z_0$ is the free space impedance, $F_{pump}$ is the pump fluence, and $F_{sat}^{ideal}$ is the saturation fluence, which is the key parameter characterizing the antenna performance. In [21], this is given as

$$F_{sat}^{ideal}=\frac{h\nu (1+n_{THz})}{e\mu Z_0(1-R)},$$

(4)

where $n_{THz}$ is a medium refractive index in the THz range, $h\nu$ is the optical photon energy, e is the electron charge, $\mu$ is the carrier mobility, and R is the optical reflection of the substrate. We use the superscript “ideal” to emphasize that the expression for the saturation fluence is valid for non-transparent semiconductors and explicitly suggests the total surface absorption of pump radiation.

As can be seen in Figure 4, the generated THz energy is approximated satisfactorily by Equation (4): at small $F_{pump}$ values, the emitted energy increases as the square of $F_{pump}$, and then saturates. In the best case, the THz power achieved a maximum of ∼200 pJ with a bias field of 25 kV/cm. For an irradiated area of $2.7\times 1.5$ mm${}^2$, this relatively weak field provided an optical-to-THz conversion efficiency at the level of $\eta \approx 0.002$%. The THz yield in a diamond PCA grows as the square of the applied electric field [18] and, therefore, an increase of the bias voltage up to 1 MV/cm (the breakdown electric field of diamond is 10 MV/cm [14]) is expected to scale the conversion efficiency up to ∼3% and more.

The waveform of a THz pulse measured by electro-optical sampling is exemplified in Figure 5. Note that all the measured waveforms featured a clear asymmetry in the electrical field polarity and the corresponding spectra (not shown here) obtained via Fourier transform had a low-frequency maximum (0.2–0.3 THz).

The deduced saturation laser fluence is plotted in Figure 6 against the concentration of nitrogen in diamonds. The $F_{sat}$ value is evidently correlated with the $N_S$ content, gradually decreasing as the doping level increases. In order to model this saturation fluence behavior, a quite obvious approach was used. In Equation (4), we introduced a factor that allows only a part of the pump pulse to be deposited in a transparent diamond. The real saturation fluence will then depend on the nitrogen concentration in the substrate:

$$F_{sat}=\frac{F_{sat}^{ideal}}{1-exp(-\alpha d)},$$

(5)

where $\alpha$ is the nitrogen-doped diamond absorption and d is the sample thickness. As the sample thickness varied over a wide range (from 250 $\mathsf{\mu }$m to 1570 $\mathsf{\mu }$m), Figure 6 contains two marginal curves calculated with the marginal thicknesses from Equation (5). The absorption value was taken from the laser experiment (Figure 3). The minimum experimental saturation fluence of ∼40 $\mathsf{\mu }$J/cm${}^2$, demonstrated by the ∼200 ppm HPHT diamond, was taken as an “ideal” $F_{sat}$. This is, to the best of our knowledge, the lowest saturation fluence under 400 nm pumping.

Taken as a whole, the data in Figure 6 support the theoretical model. The best ($F_{sat}$≈ 40 $\mathsf{\mu }$J/cm${}^2$) and the worst ($F_{sat}$≈12,000 $\mathsf{\mu }$J/cm${}^2$) performances were demonstrated by HPHT diamonds with the maximum and minimum nitrogen concentrations, respectively. Despite the remarkable data spreading, the major part of the experimental points lies inside the predicted channel. Only three specific groups appear to be excluded from this channel.

The first group includes the HPHT high-doped diamonds, which are characterized by a saturation fluence that is 70%–100% above the theoretical estimation. The possible physical mechanism of the emission weakening here is a decrease in the mobility of carriers in high-nitrogen-impurity crystals. The second group covers the polycrystalline CVD diamonds with $N_S\approx 10$ ppm, whose saturation fluence exceeds approximately twice the theoretical limit. This can be caused, as in the first case, by damped electron mobility. The second important factor that obviously deteriorated the efficiency of the optical-to-THz conversion is just the strong optical scattering. In polycrystalline substrates, the backward and wide-angle scattering results in a remarkable non-absorptive attenuation of the pumping radiation that, in turn, leads to a diminished number of photocarriers and photocurrent-generating THz waves. In contrast, the performance demonstrated by the third group—two monocrystalline CVD diamonds—was about twice as good as the theoretical predictions. The mechanism of these efficiency spikes is currently unclear. Supposedly, this might be achieved at the expense of the laser excitation of other color centers in addition to the substitutional nitrogen.

On the whole, the diamonds behaved rather predictably in the THz generation experiments. Meanwhile, the $F_{sat}$ value calculated in this work for a set of 19 substrates revealed that a diamond PCA’s performance can vary by one order of magnitude with an approximately constant level of nitrogen. Future work, in order to achieve precise control of the THz generation efficiency, should explore the exact reasons for this dispersion and refine the techniques of diamond synthesis and doping.

4. Conclusions

In conclusion, this work investigated terahertz generation in PCAs based on nitrogen-doped diamonds and pumped by the second harmonic of a Ti:sapphire laser. The doping level was demonstrated to precisely govern the optical absorption in high-quality HPHT and CVD diamond substrates. Consequently, the tight correlation between the doping level and the magnitude of the saturation fluence in diamond PCAs arises. The efficiency of doping as a tool for controlling the performance of diamond emitters was proven: depending on the nitrogen level, the saturation fluence of diamond PCAs ranged from very high (∼12,000 $\mathsf{\mu }$J/cm${}^2$) to quite low (∼40 $\mathsf{\mu }$J/cm${}^2$) for dielectric materials. The current yield of THz radiation from diamond PCA is about ∼$0.2$ nJ, while the reported emission level for a GaAs large aperture PCA ($35\times 35$ mm${}^2$, 10.7 kV/cm) achieved ∼800 nJ [22]. Diamond-based antennas of comparable size are expected to emit a comparable power level. Moreover, this level can be significantly increased with increasing the applied electric field. Future work will focus on a necessity to form closely located buried electrodes in diamond bulk to provide the high bias field in a diamond PCA. These data and estimations corroborate the potential of doped diamond to be used as a material for extremely biased and efficient large-aperture photoconductive antennas.