Toward Real-Time Giga-Voxel Optoacoustic/Photoacoustic Microscopy: GPU-Accelerated Fourier Reconstruction with Quasi-3D Implementation
Abstract
:1. Introduction
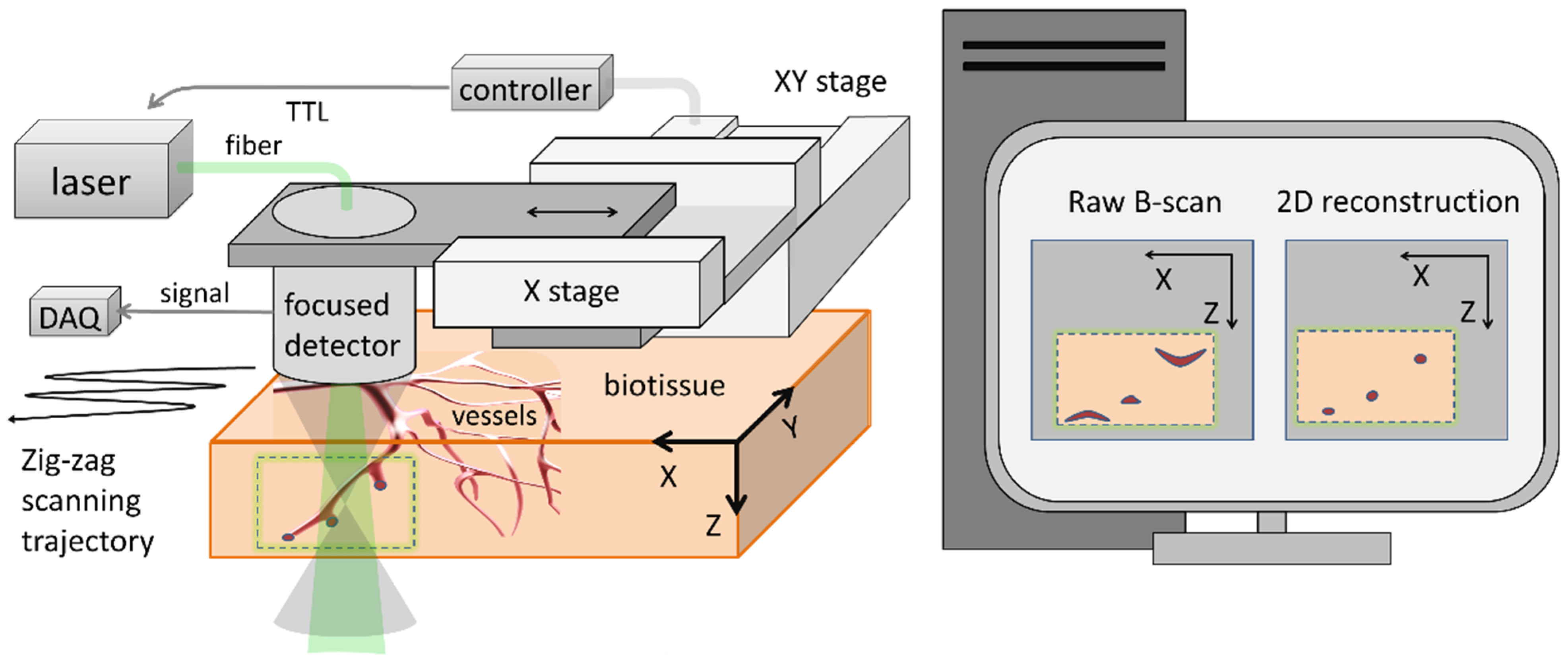
2. Materials and Methods
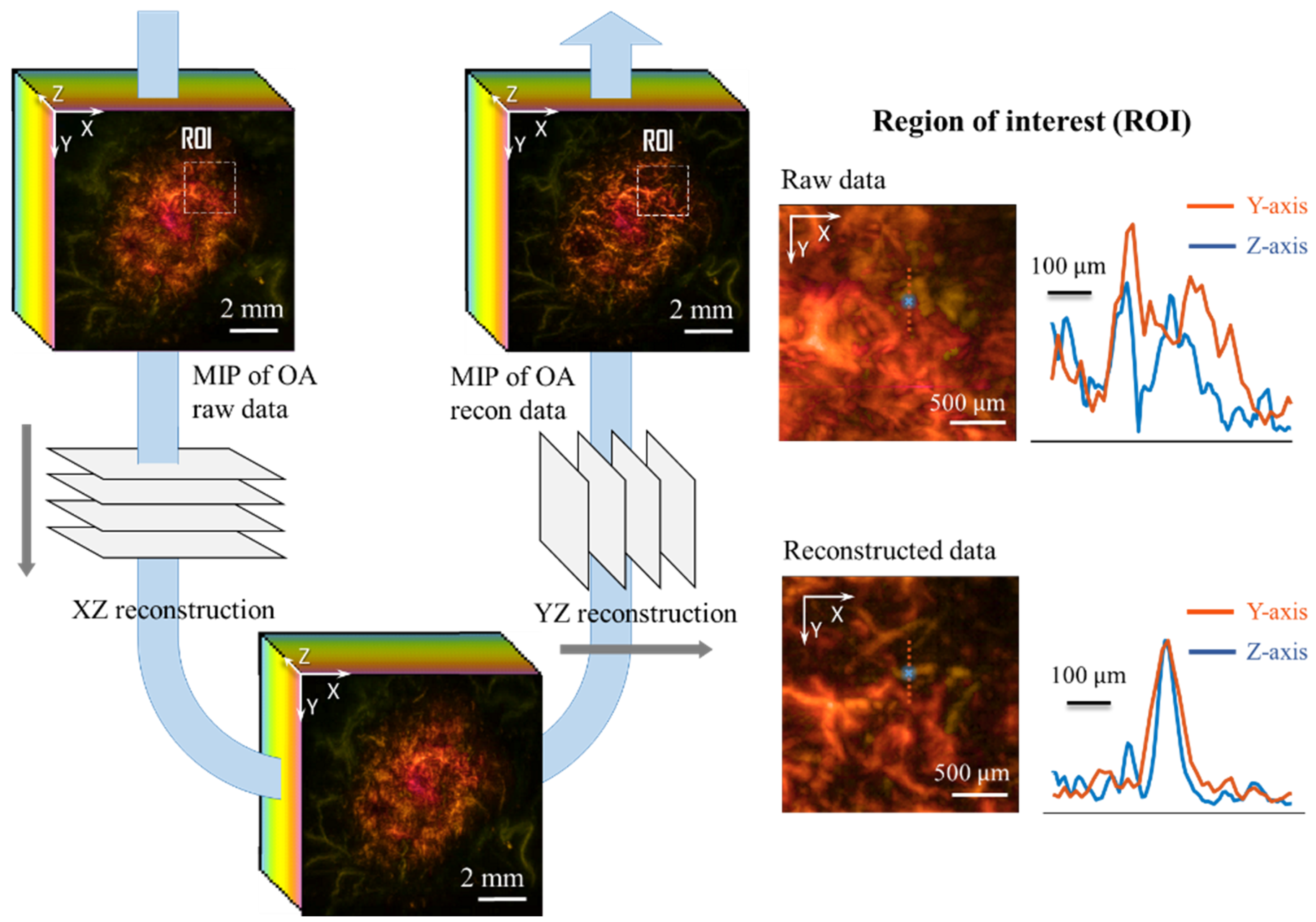
2.1. GPU-FD Accelerated Reconstruction
2.2. Experimental Data
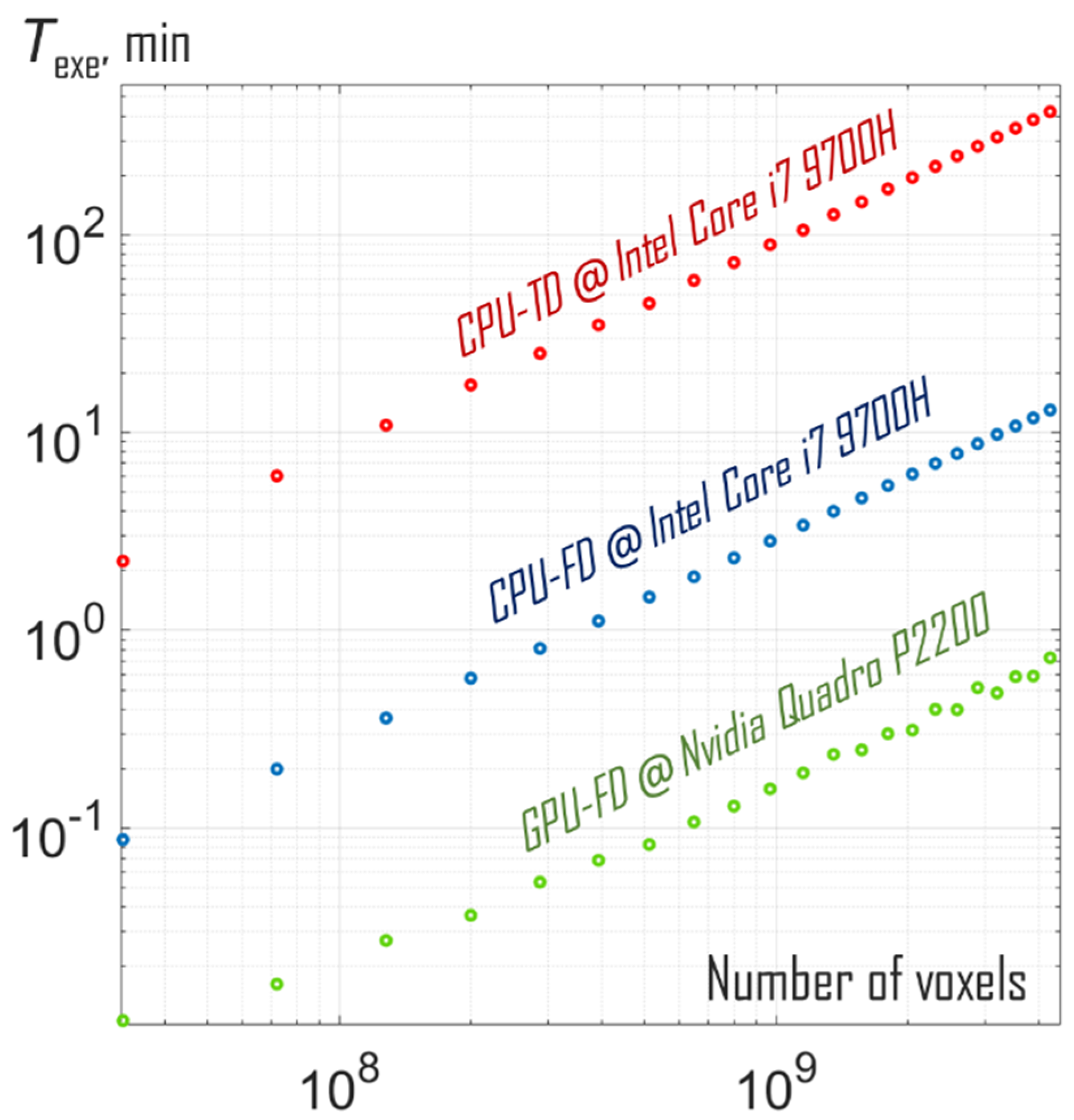
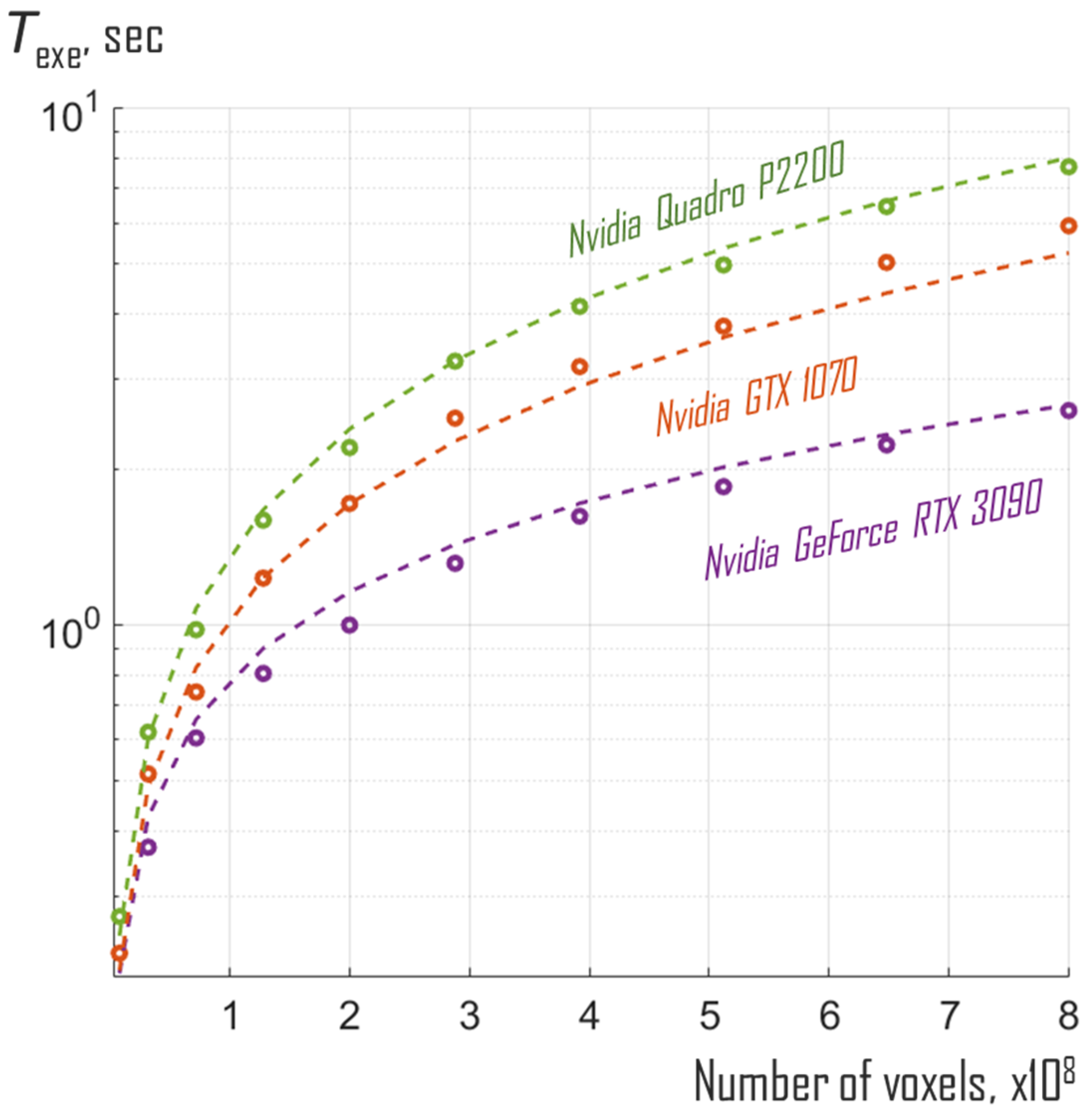
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, J.; Wang, L.V. Photoacoustic microscopy. Laser Photonics Rev. 2013, 7, 758–778. [Google Scholar] [CrossRef] [PubMed]
- Haedicke, K.; Agemy, L.; Omar, M.; Berezhnoi, A.; Roberts, S.; Longo-Machado, C.; Skubal, M.; Nagar, K.; Hsu, H.-T.; Kim, K. High-resolution optoacoustic imaging of tissue responses to vascular-targeted therapies. Nat. Biomed. Eng. 2020, 4, 286–297. [Google Scholar] [CrossRef] [PubMed]
- Saijo, Y.; Ida, T.; Iwazaki, H.; Miyajima, J.; Tang, H.; Shintate, R.; Sato, K.; Hiratsuka, T.; Yoshizawa, S.; Umemura, S. Visualization of skin morphology and microcirculation with high frequency ultrasound and dual-wavelength photoacoustic microscope. In Photons Plus Ultrasound: Imaging and Sensing 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; p. 108783E. [Google Scholar] [CrossRef]
- Hofmann, U.A.; Rebling, J.; Estrada, H.; Subochev, P.; Razansky, D. Rapid functional optoacoustic micro-angiography in a burst mode. Opt. Lett. 2020, 45, 2522–2525. [Google Scholar] [CrossRef] [PubMed]
- Baik, J.W.; Kim, J.Y.; Cho, S.; Choi, S.; Kim, J.; Kim, C. Super wide-field photoacoustic microscopy of animals and humans in vivo. IEEE Trans. Med. Imaging 2019, 39, 975–984. [Google Scholar] [CrossRef] [PubMed]
- Li, M.-L.; Zhang, H.F.; Maslov, K.; Stoica, G.; Wang, L.V. Improved in vivo photoacoustic microscopy based on a virtual-detector concept. Opt. Lett. 2006, 31, 474–476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwarz, M.; Garzorz-Stark, N.; Eyerich, K.; Aguirre, J.; Ntziachristos, V. Motion correction in optoacoustic mesoscopy. Sci. Rep. 2017, 7, 10386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lutzweiler, C.; Razansky, D. Optoacoustic imaging and tomography: Reconstruction approaches and outstanding challenges in image performance and quantification. Sensors 2013, 13, 7345–7384. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perekatova, V.V.; Kirillin, M.Y.; Turchin, I.V.; Subochev, P.V. Combination of virtual point detector concept and fluence compensation in acoustic resolution photoacoustic microscopy. J. Biomed. Opt. 2018, 23, 091414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jaeger, M.; Schüpbach, S.; Gertsch, A.; Kitz, M.; Frenz, M. Fourier reconstruction in optoacoustic imaging using truncated regularized inverse k-space interpolation. Inverse Probl. 2007, 23, S51. [Google Scholar] [CrossRef]
- Spadin, F.; Jaeger, M.; Nuster, R.; Subochev, P.; Frenz, M. Quantitative comparison of frequency-domain and delay-and-sum optoacoustic image reconstruction including the effect of coherence factor weighting. Photoacoustics 2020, 17, 100149. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Liu, S.; Zhang, R.; Liu, S.; Zheng, Y. Frequency domain based virtual detector for heterogeneous media in photoacoustic imaging. IEEE Trans. Comput. Imaging 2020, 6, 569–578. [Google Scholar] [CrossRef]
- Liu, S.; Feng, X.; Gao, F.; Jin, H.; Zhang, R.; Luo, Y.; Zheng, Y. Gpu-accelerated two dimensional synthetic aperture focusing for photoacoustic microscopy. APL Photonics 2018, 3, 026101. [Google Scholar] [CrossRef]
- Puchała, D.; Stokfiszewski, K.; Yatsymirskyy, M.; Szczepaniak, B. Effectiveness of fast fourier transform implementations on gpu and cpu. In Proceedings of the 2015 16th International Conference on Computational Problems of Electrical Engineering (CPEE), Lviv, Ukraine, 2–5 September 2015; pp. 162–164. [Google Scholar] [CrossRef]
- Smistad, E.; Falch, T.L.; Bozorgi, M.; Elster, A.C.; Lindseth, F. Medical image segmentation on gpus—A comprehensive review. Med. Image Anal. 2015, 20, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Chu, E.; George, A. Inside the FFT Black Box: Serial and Parallel Fast Fourier Transform Algorithms; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Subochev, P. Cost-effective imaging of optoacoustic pressure, ultrasonic scattering, and optical diffuse reflectance with improved resolution and speed. Opt. Lett. 2016, 41, 1006–1009. [Google Scholar] [CrossRef] [PubMed]
- Maslov, K.; Stoica, G.; Wang, L.V. In vivo dark-field reflection-mode photoacoustic microscopy. Opt. Lett. 2005, 30, 625–627. [Google Scholar] [CrossRef] [PubMed]
- Orlova, A.; Sirotkina, M.; Smolina, E.; Elagin, V.; Kovalchuk, A.; Turchin, I.; Subochev, P. Raster-scan optoacoustic angiography of blood vessel development in colon cancer models. Photoacoustics 2019, 13, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Kurnikov, A.A.; Pavlova, K.G.; Orlova, A.G.; Khilov, A.V.; Perekatova, V.V.; Kovalchuk, A.V.; Subochev, P.V. Broadband (100 kHz–100 MHz) ultrasound PVDF detectors for raster-scan optoacoustic angiography with acoustic resolution. Quantum Electron. 2021, 51, 383. [Google Scholar] [CrossRef]
- Subochev, P.V.; Prudnikov, M.; Vorobyev, V.; Postnikova, A.S.; Sergeev, E.; Perekatova, V.V.; Orlova, A.G.; Kotomina, V.; Turchin, I.V. Wideband linear detector arrays for optoacoustic imaging based on polyvinylidene difluoride films. J. Biomed. Opt. 2018, 23, 091408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ron, A.; Davoudi, N.; Deán-Ben, X.L.; Razansky, D. Self-gated respiratory motion rejection for optoacoustic tomography. Appl. Sci. 2019, 9, 2737. [Google Scholar] [CrossRef] [Green Version]

| Processing Unit | Clock Speed | Number of Cores | Execution Time, s | ||
|---|---|---|---|---|---|
| CPU-TD | CPU-FD | GPU-FD | |||
| Nvidia GeForce RTX 3090 | 1.7 GHz | 10,496 | n/a | n/a | 0.8 |
| Nvidia GTX 1070 | 1.7 GHz | 1920 | n/a | n/a | 1.2 |
| Nvidia Quadro P2200 | 1.5 GHz | 1280 | n/a | n/a | 1.6 |
| Intel Core i7 9700H | 4.7 GHz | 8 | 700 | 22 | n/a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subochev, P.; Spadin, F.; Perekatova, V.; Khilov, A.; Kovalchuk, A.; Pavlova, K.; Kurnikov, A.; Frenz, M.; Jaeger, M. Toward Real-Time Giga-Voxel Optoacoustic/Photoacoustic Microscopy: GPU-Accelerated Fourier Reconstruction with Quasi-3D Implementation. Photonics 2022, 9, 15. https://doi.org/10.3390/photonics9010015
Subochev P, Spadin F, Perekatova V, Khilov A, Kovalchuk A, Pavlova K, Kurnikov A, Frenz M, Jaeger M. Toward Real-Time Giga-Voxel Optoacoustic/Photoacoustic Microscopy: GPU-Accelerated Fourier Reconstruction with Quasi-3D Implementation. Photonics. 2022; 9(1):15. https://doi.org/10.3390/photonics9010015
Chicago/Turabian StyleSubochev, Pavel, Florentin Spadin, Valeriya Perekatova, Aleksandr Khilov, Andrey Kovalchuk, Ksenia Pavlova, Alexey Kurnikov, Martin Frenz, and Michael Jaeger. 2022. "Toward Real-Time Giga-Voxel Optoacoustic/Photoacoustic Microscopy: GPU-Accelerated Fourier Reconstruction with Quasi-3D Implementation" Photonics 9, no. 1: 15. https://doi.org/10.3390/photonics9010015
APA StyleSubochev, P., Spadin, F., Perekatova, V., Khilov, A., Kovalchuk, A., Pavlova, K., Kurnikov, A., Frenz, M., & Jaeger, M. (2022). Toward Real-Time Giga-Voxel Optoacoustic/Photoacoustic Microscopy: GPU-Accelerated Fourier Reconstruction with Quasi-3D Implementation. Photonics, 9(1), 15. https://doi.org/10.3390/photonics9010015






