Going Deeper into OSNR Estimation with CNN

Abstract

As optical performance monitoring (OPM) requires accurate and robust solutions to tackle the increasing dynamic and complicated optical network architectures, we experimentally demonstrate an end-to-end optical signal-to-noise (OSNR) estimation method based on the convolutional neural network (CNN), named OptInception. The design principles of the proposed scheme are specified. The idea behind the combination of the Inception module and finite impulse response (FIR) filter is elaborated as well. We experimentally evaluate the mean absolute error (MAE) and root-mean-squared error (RMSE) of the OSNR monitored in PDM-QPSK and PDM-16QAM signals under various symbol rates. The results suggest that the MAE reaches as low as 0.125 dB and RMSE is 0.246 dB in general. OptInception is also proved to be insensitive to the symbol rate, modulation format, and chromatic dispersion. The investigation of kernels in CNN indicates that the proposed scheme helps convolutional layers learn much more than a lowpass filter or bandpass filter. Finally, a comparison in performance and complexity presents the advantages of OptInception.

1. Introduction

Fiber-optic communication has experienced incredible advances in recent years for higher capacity. Advanced optical modulation formats, pulse-shaping techniques, along with multiplexing techniques contribute to higher spectral efficiency [1]. Moreover, reconfigurable optical add-drop multiplexers (ROADMs) bring flexible bandwidth assignment [2]. Nevertheless, the promotion of the optical network in dynamicity, flexibility, and better utilization of available transmission capacity comes at the price of a more complicated communication system with more noise sources introduced by new kinds of hardware units, where the communication link becomes path-dependent and dynamic due to the advent of ROADMs [3]. Therefore, transmission in fibers is more prone to be degraded, and real-time, comprehensive, and precise monitoring, referred to as optical performance monitoring (OPM), on the condition of optical networks is currently being urged.

OPM is considered as a key technology for elastic optical networks (EON) [4]. OSNR directly reflects the quality of communication links in fiber by quantifying noise, especially amplified spontaneous emission (ASE) noises, added into the optical signals. A direct relation between OSNR and bit-error rate (BER) [5] makes it become one of the most important parameters for the evaluation of the general health of links and fault diagnosis. The traditional measurement of OSNR typically relies on the optical spectrum analyzer (OSA) that needs to get access to optical fibers for out-of-signal band noise power measurement [6]. However, optical add-drop multiplexers (OADM) in wavelength division multiplexing (WDM) networks filter major ASE noises out of band, which makes traditional measurements fail [2]. Thus, many in-band measurement techniques are being put forward, such as spectral analysis after frequency down-conversion [7], polarization extinction [8], and usage of various interferometers [9,10]. The general drawback of these methods is the limitation on adaptation to dispersion impairment or different symbol rates. Moreover, the Refs. [11,12,13,14] estimated carrier-to-noise ratios (CNR) or signal-to-noise ratios (SNR) to calculate OSNR based on statistical moments of equalized signals. In [15], the utilization of empirical cumulative distribution function (CDF) of the signal’s amplitude overcame the degradation for signals employing multilevel constellations in moment-based OSNR estimation approaches mentioned above. In essence, this algorithm still estimates the SNR using Newton’s method to fit theoretical CDF to the empirical one. However, the requirement of equalization on signals leads to these methods being designed for the digital coherent receiver. The cost of receiving and equalization makes these methods non-economic and even impossible in the intermediate network nodes. Besides, conventional techniques have limitations in simultaneous and independent monitoring of multiple transmission impairments, of which the effects are often physically inseparable [4]. Fortunately, machine learning (ML) becomes a promising alternative for realizing highly impairment-tolerant and adaptive monitoring with easy deployment.

The emergence of deep learning made machine learning flourish in pattern recognition, speech recognition, and natural language processing. End-to-end deep learning has been used in waveform-to-symbol decoding in coherent fiber-optic communication [16]. The deep neural network (DNN) used in deep learning has proven to be effective in OSNR estimation [3]. By and large, the trend of deep learning methods in OPM can be listed as follows:

• Transparency to symbol rate, modulation format and impairments;
• Joint estimation of multiple parameters;
• Independence of signal receiving;
• Robust performance along with low complexity;
• End-to-end learning.

The majority of monitoring methods utilizing deep learning can be concluded as a combination of a statistic diagram or a statistic of received signals and one kind of neural network. The diagram can be an eye diagram [17], asynchronous delay-tap sampling (ADTS) 2D histogram [18], or amplitude histogram (AH) [19,20], while the statistic can be an error vector magnitude (EVM) [21] or Godard’s error [22]. The neural network can be an artificial neural network (ANN), k-nearest neighbors (KNN), support vector machine (SVM), or convolutional neural network (CNN). These methods have one common flaw that they all need to do extra information extraction or feature extraction manually. The Refs. [23,24,25] showed a CNN method that needs asynchronously sampled raw data from analog-to-digital converters (ADC) as input. The study of [25] probes the trained kernels in convolutional layers, which explains why CNN can process raw data directly.

CNN introduced in [26] develops a tradition model of pattern recognition with the idea of the training feature extractor itself. Based on the idea of CNN, deep convolutional neural networks (AlexNet) [27], networks using blocks (VGG) [28], network in network (NiN) [29], and so forth were proposed in succession and outperformed their predecessors on the ImageNet classification challenge. The trend of CNN has been increasing in size, including the depth and width of the network, to improve the performance at the cost of a surge in computation complexity. Overfitting simultaneously becomes another side effect. The sparsely connected architecture inside networks is the fundamental way to solve both problems mentioned above. However, the computation of infrastructures nowadays suffers from low efficiency in numerical calculation on the non-uniform sparse matrix. Therefore, the main idea of GoogLeNet in [30] focused on finding out how an optimal local sparse structure in a convolutional vision network can be approximated and covered by readily available dense components, and the inception module was also raised in this paper. Apart from that, the structure of parallel branches itself is thought-provoking as well.

In this paper, we dig deeper into OSNR estimation with CNN to realize end-to-end monitoring. A structure comprised of the Inception block, which is a critical component in GoogLeNet, is designed and explicated. Section 2 presents a review of the definition of OSNR and high-level consideration in CNN and Inception block. The ideas and principles behind the essential components in neural networks helped us to design the proposed scheme in Section 2.4. In Section 3, an experiment is set up to train and test the proposed scheme. The results are analyzed together with the architecture itself. Section 4 discusses the extent of training with the help of a learning curve. A comparison between the proposed scheme with state-of-the-art schemes in performance and complexity is presented as well. These come to a conclusion in Section 5.

2. Principle of Proposed Scheme

2.1. OSNR Measurement

The optical signal-to-noise ratio (OSNR) represents the transmission performance of optical links and has a direct relationship with BER [19,31]. A sufficiently high OSNR is an essential requirement to maintain communication within acceptable error limits. Thus, OSNR measurement can practically promote automatic fault detection and diagnosis, as well as in-service characterization of signal quality [32].

OSNR can be defined as the logarithmic ratio of the average optical signal power to average optical noise power over a specific spectral bandwidth measured at the input of an optical receiver photodiode [5].

$$\mathrm{OSNR}=10log\frac{P_{sig}}{P_{noise}}=10log\frac{P_{sig+noise}\left(B_0\right)-P_{noise}\left(B_0\right)}{P_{noise}\left(B_0\right)},$$

(1)

where $P_{sig}$ and $P_{noise}$ are the signal and noise power bound by the signal spectral bandwidth $B_0$. In practice, signal power $P_{sig}$, which is difficult to be measured directly due to being obscured by noise (where the same goes for noises at signal wavelength), is calculated by the difference between total power $P_{sig+noise}$ and noise power bound by the signal bandwidth $B_0$. A noise equivalent bandwidth (NEB) filter with a bandwidth of $B_m$ was applied to a signal skirt to estimate the power of noise in $B_0$ by interpolating the noise power measured outside the bandwidth, see (3). The instrument, the optical spectrum analyzer (OSA), calculates OSNR as (2), where the specific spectral bandwidth $B_r$ for signal and noise measurement is referred to as OSA’s resolution bandwidth (RBW) [5].

$$\mathrm{OSNR}=10log\frac{P_{sig}}{P_{noise}}+10log\frac{B_m}{B_r}$$

(2)

$$P_{noise}=\frac{P_{noise}\left({\lambda }_1\right)+P_{noise}\left({\lambda }_2\right)}{2}$$

(3)

Given the definition of the OSNR and OSA measurement method, separation of the noise and signal is the key point of the algorithm. Besides, OSNR describes the relationship between the second moment of two parts of the received optical signal, signal, and noise. Consequently, the trained neural network should learn how to extract the signal part from noise as well as a mapping from some characteristics of the second moment to the ultimate OSNR value. The Ref. [33] reveals a convolutional layer which has the potential of extraction while the mapping process can be realized in a fully connected network.

2.2. Design Principles of Basic CNN

Typical structure of CNN comprises convolutional layers for feature extraction and pooling layers for downsampling, following which fully connected (FC) layers learn nonlinear mapping from high-dimensional feature spaces to corresponding value spaces.

Despite different definitions of convolution in neural network and signal processing, the similarity in the mathematical formula reveals that the kernel in 1-D CNN could be considered as a finite impulse response (FIR) filter [25] with the taps already flipped around before doing multiplication with the signal sequence in a convolution operation.

$$s\left[i\right]=\sum _{j=0}^{N-1}x[i-j]\omega \left[j\right]$$

(4)

$$s\left[i\right]=f(\sum _{k=0}^{K-1}\sum _{j=0}^{N-1}{x}_k[i+j]{\omega }_k\left[j\right]+b\left[k\right]),$$

(5)

where $s\left[i\right]$ is the signal output, $x\left[i\right]$ is the signal input, $\omega \left[j\right]$ is the weight in the convolutional kernel, $b\left[k\right]$ is the bias, and k represents the channel number. In an investigation into the CNN kernels in [25], where two convolutional layers were placed in serial at the front end, the first trained convolutional layer performed a few types of bandpass filters to separate the signal from the noise, while the second one worked as a low-pass filter to extract a DC component for averaging values derived from the previous convolutional layer.

In pattern recognition, of which the aim is doing classification of the input, the pooling layer plays a role of dimension reduction with retaining basic features of the image. The pooling layer merges semantically similar features into one after computing the maximum or average of the local patch of units in feature maps [34]. Meanwhile, the pooling operation helps to make the representation approximately invariant to small translations of the input [35]. Namely, pooling brings image features invariance in translation, rotation, and scaling. The following example vividly shows the feature extraction function of pooling. In Figure 1, three different kinds of pooling are applied to the Girl with a Pearl Earring (an oil painting by Johannes Vermeer in 1665. The work has been in the collection of the Mauritshuis in The Hague since 1902). Downsampling samples the last pixel in each patch with a stride of 40 when max pooling and average pooling takes the patch’s maximum and average value in every channel of the image, respectively. It is still quite easy to recognize this famous girl even when the resolution drops to only 168 pixels from 268,800 pixels for all three pooling operations.

The success of the pooling layer applied to image recognition benefits from the sparse feature information in an image. A weak correlation between local patches also contributes to it. Specifically, features scatter in different regions of the 2D plane of an image while different regions conceal different features. However, signals in optical fiber have nothing to do with the property of sparsity. During a limited period, OSNR stays relatively unchanged and can be measured at any time of the signal. The definition of OSNR in Equation (1) also suggests that the information of OSNR is consistent at every time point and actually presents features in the frequency domain [5]. If pooling is applied in the raw signal at the very beginning, we could not derive much useful information from the time domain. The features concealed in the spectrum are damaged by pooling operation instead.

Multilayer feedforward networks with as little as one hidden layer are proven to have the potential of being universal approximators to any desired degree of accuracy, provided sufficient hidden units are available [36]. In many circumstances, a deeper network is more efficient to get a lower generalization error with less number of units required than a wider one when representing the desired function [35].

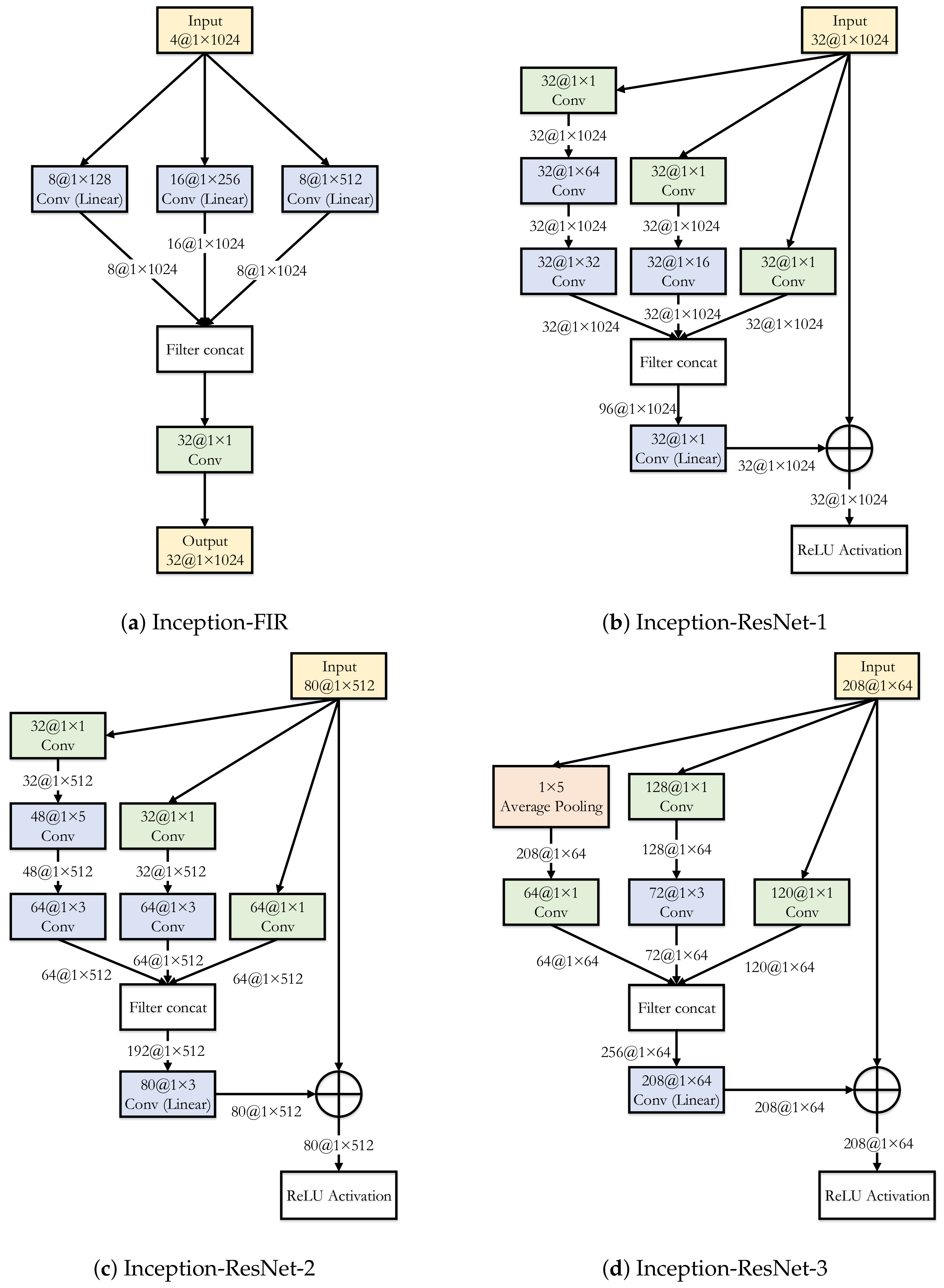
2.3. Inception Architecture

Given that sparsely connected architecture avoids overfitting without utilizing high computation efficiency on dense matrix multiplication, the Inception module aims at improving hardware computation speed when keeping the sparse structure of a network. The Inception block is a combination of variously sized kernels by concatenating several parallel branches of convolutional layers. An example structure is depicted in Figure 2.

In addition, the Ref. [30] introduces $1\times 1$ convolution for dimension reduction to alleviate the computation complexity of expensive $3\times 3$ and $5\times 5$ convolution. The following ReLU also provides a model with extra nonlinearity.

After various modifications made on Inception-v1 in [37], the latest work of [38] incorporates residual connections, which is argued to be necessary for deep networks to improve training speed empirically [39]. Furthermore, though Inception-v4 without residual connections can achieve similar performance with similar expensive Inception-ResNet-v2, the Ref. [38] admits that residual connections do accelerate training significantly. Secondly, residual connections are able to solve the degradation problem where training errors increase with a deeper network, and accuracy gets saturated or even degrades rapidly. The shortcut in ResNet endues the network with identity mapping, which is proved to be the best choice [40].

2.4. Proposed Scheme: OptInception

Figure 3 shows the whole architecture of the proposed network, OptInception, and its advanced version, OptInception-Pro, in this paper. We deepen the OptInception by cascading multiple Inception-ResNet modules in OptInception-Pro, which is inspired by Inception-v4. The input length of the network is $1\times 1024$ for four channels, which correspondingly represents sampled data from the optical field of in-phase and quadrature-phase components in both horizontal and vertical polarization. The detailed structures of Inception blocks and Reduction blocks are shown in Figure 4 and Figure 5, respectively. In the Figures, the sizes of data flowing in the networks and convolutional kernels are in the form of Channels@1 × Length of data(kernel) in every channel. The same padding is the default strategy, while ’Valid’ is marked in the convolutional layer if valid padding is used. Layers without an activation function are noted with ’Linear’ in parentheses. Concatenation of branches in Inception blocks is named ’Filter concat’ for short.

In order to estimate OSNR with neural networks, the key is the acquisition of characteristics of signal and noise power from raw data, as clarified above in (2). As clarified in [25], convolutional layers fed with four channels of raw data asynchronously sampled by ADC act as filters to extract various components of signals. Meanwhile, these filters in convolutional layers can be automatically trained by a back-propagation algorithm without any manual intervention. On this basis, longer convolutional kernels are applied for signal processing with higher resolution when feature separation of signal and noise can be more precise in an Inception-FIR block in a proposed scheme. Inspired by the structure of the Inception block itself, different lengths of CNN kernels are deployed in parallel and then concatenated by channels. Furthermore, it maintains integration of signals without the negative part being cut off, meaning that ReLU or other nonlinear activation functions are not applied to the convolution results. For max pooling in particular, pooling can lose a lot of information, ending with a deteriorating feature extraction effect in the successive network section, as explained in Section 2.2. Pooling layers which will not contribute to the separation were not laid out in this block.

Next, residual connections were introduced into subsequent Inception blocks to improve computation efficiency in deep network training. Considering that the network we design is definitely deep with multiple Inception blocks and fully connected layers, this practical structure is necessary and useful.

Following the Inception-ResNet blocks, reduction blocks named Reduction-1 and Reduction-2 were designed to help aggregate features and decrease the grid sizes of the feature maps. In the Reduction module, average pooling and $1\times 1$ convolution were both used. Only one of them should be used in a single branch of the Inception parallel structure as usual.

After three Inception-ResNet and two Reduction blocks, the trained feature maps were sent to average pooling before being flattened. Four fully connected layers with two hidden layers and without an activation function applied at the output of the network were arranged in order to fit the mapping to OSNR that is a continuous value.

All in all, the general architecture of OptInception can be divided into three procedures. In the beginning, the Inception-FIR is responsible for the reception of input data and feature separation. Secondly, feature extraction is conducted in Inception-ResNet and Reduction blocks. Finally, the features learned previously are mapped to a corresponding OSNR value in FC networks.

3. Experimental Result and Analysis

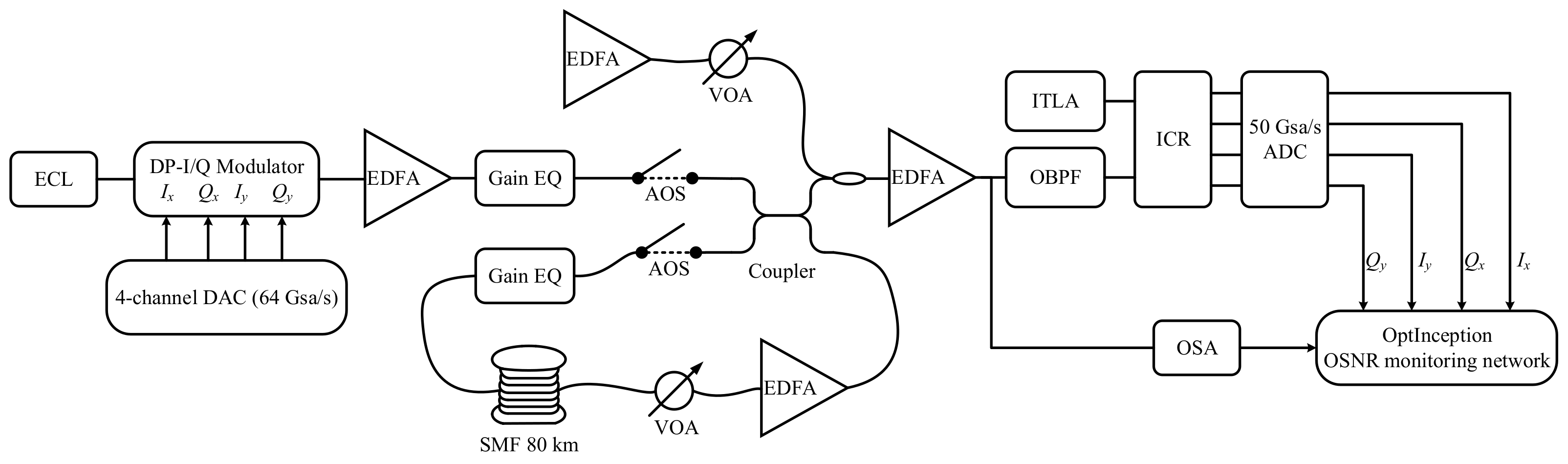
3.1. Experimental Setup

Figure 6 demonstrates the experiment platform our OSNR monitoring runs on. On the transceiver side, an external cavity laser (ECL) with less than 100 kHz linewidth generates a 194.1 THz carrier. PDM-QPSK and PDM-16QAM in 14 GBaud, 20 GBaud, and 28 GBaud Nyquist shaping optical signals with a 0.01 roll-off factor were generated in the DP-I/Q-modulator driven by a four-channel DAC with a 64 GSa/s sampling rate and 8-bit nominal resolution. Gain equalizers inserted in the link were aimed at making cascading of amplifiers possible so that the signal can be transmitted over long distances without distorting the envelope. Erbium-doped fiber amplifiers (EDFA) act as the amplified spontaneous emission (ASE) noise source in the experiment. Variable optical attenuators (VOA) along with EDFAs control the power of signal and noise and thereby adjust the OSNR at the receiver. A span of 80 km standard single-mode fibers (SSMF) with 16.75 ps/(km·nm) average dispersion simulates the real link for different transmission distances in the recirculating loop for the sake of the acousto-optic switches (AOS). These optical switches are integrated in the fiber-recirculating controller Ovlink IOM-601. After the transmission, the signal is filtered by an optical bandpass filter (OBPF) before being sent into an integrated coherent receiver. The signal is sampled at a rate of 50 GSa/s in an oscilloscope with 16 GHz bandwidth. Finally, the four-channel raw data go directly to the OSNR monitoring network. The measurements of OSA are used as labels in the training process.

3.2. Training Methodology

The number of data with a size of $4\times 1024$$(channels\times length)$ is 76,800. Within the dataset, 25% was classed as the test dataset and 75% served as the training dataset. In order to investigate monitoring performance under different chromatic dispersions (CD), we made optical signals travel different distances over the recirculation loop. Part of these data were included in the training dataset for generalization. We trained OptInception using the TensorFlow library based on graphics processing units (GPU) [41]. The mean square error was to be minimized after the forward propagation in every mini-batch training loop. The update of weights depends on the Adam optimization algorithm [42], where the individual adaptive learning rate is computed for different parameters and brings better training performance, higher computation efficiency, and lower computation resource occupation. In order to enhance generalization ability, batch normalization [43] was deployed inside convolutional layers while the dropout was put before a fully connected network. Bayesian optimization was used to find the best hyperparameters, such as learning rate and batch size [44,45]. A combination of a batch size of 40 and learning rate of 0.0005 seemed to be suitable in our training.

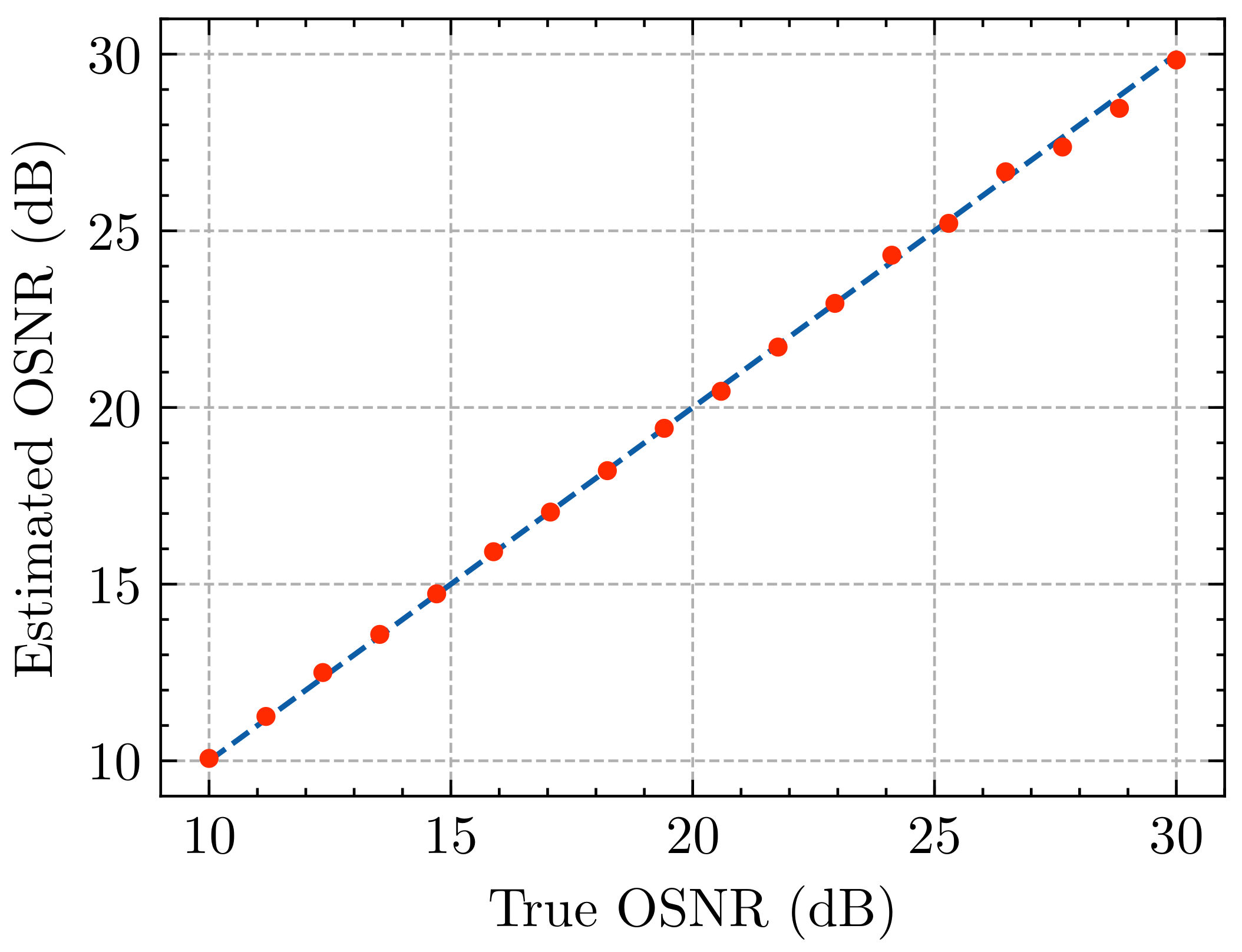
3.3. Results and Analysis

We trained OptInception and its variants in Figure 7. For variants with mini-Inception-FIR, the convolutional kernels were truncated to the lengths of 64, 32, and 16, respectively. The OptInception-AVG adds average pooling with a pooling size of eight in each branch following the convolutional layer. OptInception-Leaky adds one more layer into the hidden layer in the FC network and alter the ReLU function with the leaky-ReLU function. Moreover, Inception-v4 was modified to fit in with the 1D input format of raw data from ADC.

The 1D version of Inception-v4 and OptInception-AVG performed poorly, as shown in Figure 7. Violently inputting our data into a popular CNN designed for pattern recognition did not seem to work. The failure of OptInception-AVG proves that pooling will drop much useful information at the beginning of the networks, as shown by the design principle mentioned above. Pooling always plays a vital role in integrating similar features, but not in an information extraction step. The rest learn better on the training dataset.

Next, the estimation accuracy of OSNR on the test dataset depicted in Figure 8 reveals the generalization ability and feasibility in the reality of the networks. It is obvious that the modifications in OptInception-Leaky are not successful for its rigorous fluctuation and poorer and poorer generalization with training going on. In contrast, OptInception improves continuously and can finally reach quite a high level of accuracy of estimation in the test. The ones with mini-Inception-FIR do not deteriorate performance much, but are not stable in the early stages of training. OptInception-Pro trades much steadier learning improvement with more expensive learning prices. Metaphorically, OptInception is more like an intelligent student who learns fast with less time and energy but who also occasionally makes mistakes, while OptInception-Pro is a hardworking student who polishes up their score patiently, step by step.

The following monitoring results are estimated by OptInception-Pro to exploit the potential of the proposed scheme, considering its steady learning process.

In Figure 9, the estimation of the proposed OptInception-Pro is generally precise. However, degradation occurs with OSNR climbing because it becomes harder to measure the exact noise power from raw data when OSNR is higher. Nevertheless, this phenomenon does not affect its applications since it is more important to monitor the quality of transmission links in poor condition when the OSNR is always low in practice.

Figure 10 shows the test performance on different symbol rates and modulations, with Figure 10a showing mean absolute error (MAE) and Figure 10b showing root-mean-square error (RMSE). The MAE remains only about 0.125 dB when RMSE is 0.246 dB. The general performance does not fluctuate much, so the proposed scheme is almost transparent to modulations and symbol rates as long as the combinations are trained thoroughly.

The tolerance against chromatic dispersion is investigated in Figure 11 as well. The number of loops is controlled to acquire different CD. 28 GBaud PDM-QPSK signals when 20 dB OSNR are tested. The errors of estimation basically have a weak relationship with chromatic dispersion. Thus, OptInception is also transparent to impairment of chromatic dispersion.

When it comes to the effect of the convolutional layers in monitoring, we probed the weights in convolutional kernels again, as [25] did. For best demonstration, OptInception with mini-Inception-FIR was selected. The fast Fourier transform (FFT) of the shortest kernel with $1\times 16$ size in the third branch was ultimately presented. The zero-frequency was shifted to the center of the spectrum. In Figure 12, the OptInception learns more than bandpass filters. Lowpass filters and highpass filters were also formed during the training process. Some kernels selected various frequencies simultaneously. The variance of filters brought out variable characteristics. The functions of many other filters, however, cannot be explained intuitively. It is indeed true that the neural network is a veritable black box.

4. Discussion

4.1. Learning Curve

The learning curves of OptInception are further investigated in this section to show the extent of training. The term ’learning curve’ has different variables on the x-axis under the contexts of an artificial neural network and general machine learning. The ANN literature shows the performance on training and test datasets as a function of training iteration, while general ML shows the predictive generalization performance as a function of the number of training examples [46].

Considering the size of the training set is large enough, we investigate the training error and generalization error as a function of the number of iterations in Figure 13. After every epoch, the mean absolute error of prediction on the training dataset and test dataset is evaluated. As expected, the MAE on the training dataset drops slowly at a later stage, while the MAE on the test dataset fluctuates between 0.15 and 0.20 for a relatively long time. Overfitting does not become tricky, profiting from the techniques used in the architecture of OptInception, like ResNet, batch normalization, and dropout. The learning curve proves that the model has been trained thoroughly.

4.2. Comparison

In this section, comparisons between our proposed architecture and the state-of-the-art OSNR monitoring schemes are shown in the following with regard to performance and complexity. We evaluate the performance with MAE and RMSE for accuracy and precision, respectively. The complexity of an algorithm can be divided into time complexity and space complexity. Time complexity, which is defined as the time of calculation on the algorithm, can be quantitatively analyzed with floating-point operations (FLOPs). Space complexity describes the memory occupation when the algorithm runs.

In [47], He investigated the relationship between the accuracy of CNNs and the complexity. The paper calculated the total time complexity of all convolutional layers as (6).

$$O(\sum _{l=1}^d{n}_{l-1}·s_l^2·n_l·m_l^2),$$

(6)

where l is the index of a conventional layer, while $l-1$ represents the index of the previous one, and d is the number of conventional layers. $n_l$ is the number of convolutional kernels of the l-th layer when $n_{l-1}$ is regarded as the number of input channels of the l-th layer received from the output of the previous layer. Considering the kernel and feature map are both square, $s_l$ represents the spatial size of the kernel, and $m_l$ is the spatial size of the output feature map.

When it comes to space complexity, the memory occupation always includes two parts: the memory for weights, and the memory for output of every layer. For CNN, the space complexity is proportional to (7).

$$O\left(\sum _{l=1}^d(s_l^2·n_{l-1}·n_l+m_l^2·n_l)\right).$$

(7)

For the FC layer, the time and space complexity is determined by the number of nodes in output $n_l$ and that in input $n_{l-1}$. Thus, the FLOPs can be computed as $O\left(2n_{l-1}{n}_l\right)$ and the occupied memory is proportional to $O(n_{l-1}·n_l+n_l)$.

Therefore, a comparison is invited among the proposed OptInception scheme, CNN monitoring scheme in [25], and the CDF estimation algorithm in [15], as

Table 1. The comparison of various state-of-the-art OSNR monitoring schemes with the proposed scheme in performance and complexity.

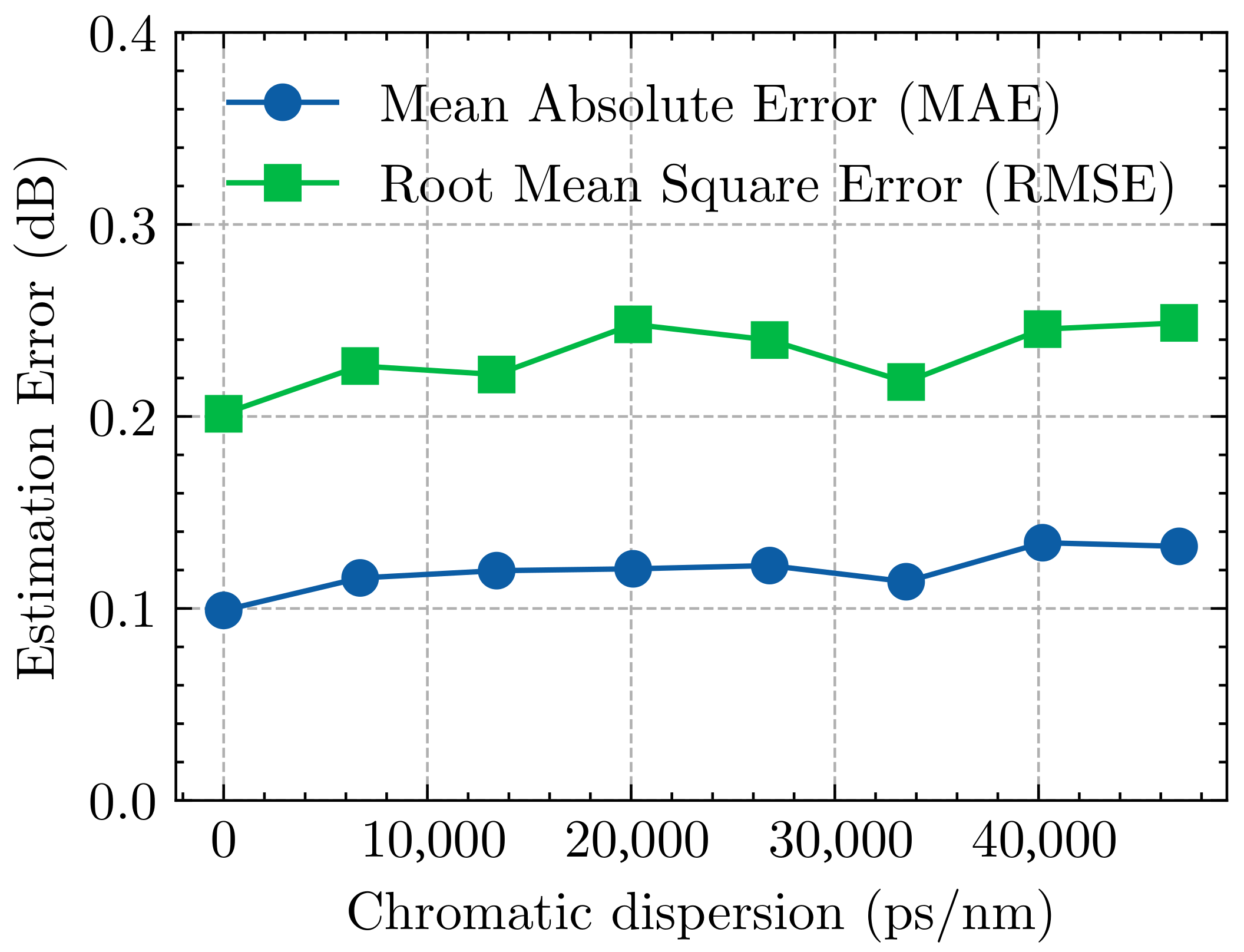
Scheme	Performance		Complexity
	MAE (dB)	RMSE (dB)	FLOPs	Params (Bytes)
OptInception	0.148	0.277	12,482,975	25,001,732
OptInception-Pro	0.125	0.246	16,833,798	56,378,116
Basic CNN scheme in [25]	0.357	0.449	28,135,393	33,751,492
CDF-based algorithm in [15]	0.478	0.525	71,264	-

depicts. All schemes were tested on our test dataset. The CNN model in [25] was trained with the same training dataset of OptInception. The parameters in the CDF algorithm were assigned with the same typical values in [15]. The parameters were stored in the data type of 32-bit floating-point numbers, and the space complexity was presented in bytes.

Table 1 vividly shows that the conventional method based on CDF has much lower computing complexity and memory occupation than schemes based on neural networks. However, the cost of low complexity is the relatively low estimation performance and the difficulty in deployment on devices without equalization. It makes sense that the deeper model, OptInception, monitors OSNR more accurately and precisely with lower values in MAE and RMSE than the scheme in [25] only using the basic CNN module. Surprisingly, the complexity of OptInception is obviously less than the basic CNN scheme in both time and space. In fact, when the node number in the FC layer grows, the number of weights becomes considerable along with addition and multiplication operations. The number of weights in FC layers of [25] accounts for 99.46%, but only 5.54% for Inception. Thanks to the averaging pooling layer before the FC network, the widths of FC layers shrink markedly. Last but not least, more than two-fold the space complexity and one-third of the time complexity increment in OptInception-Pro brought almost no more than a 15% improvement in performance. This phenomenon suggests that the marginal utility is diminishing as the depth of the network increases.

5. Conclusions

In this paper, a high-performance neural network scheme, namely, OptInception, was proposed for OSNR monitoring in OPM applications. We elaborated on the design of the scheme by reviewing structures and functions we used. Additionally, their principles or the ideas behind them decided whether and how we used them. An experiment was set up to verify the transparency of OptInception to the symbol rate, modulation format, and chromatic dispersion. The mean absolute error in the test dataset was approximately 0.125 dB, while the root-mean-square error was 0.246 dB. The kernels in trained the network were also investigated to reveal the complexity of neural networks. Finally, a learning curve was drawn to show the training extent of OptInception. A comparison in performance and complexity presented the advantage of the proposed scheme. In a nutshell, the training process and experimental results indicate that the design principles function as expected.