Study on Aberration Correction of Adaptive Optics Based on Convolutional Neural Network
Abstract
:1. Introduction
2. Methods
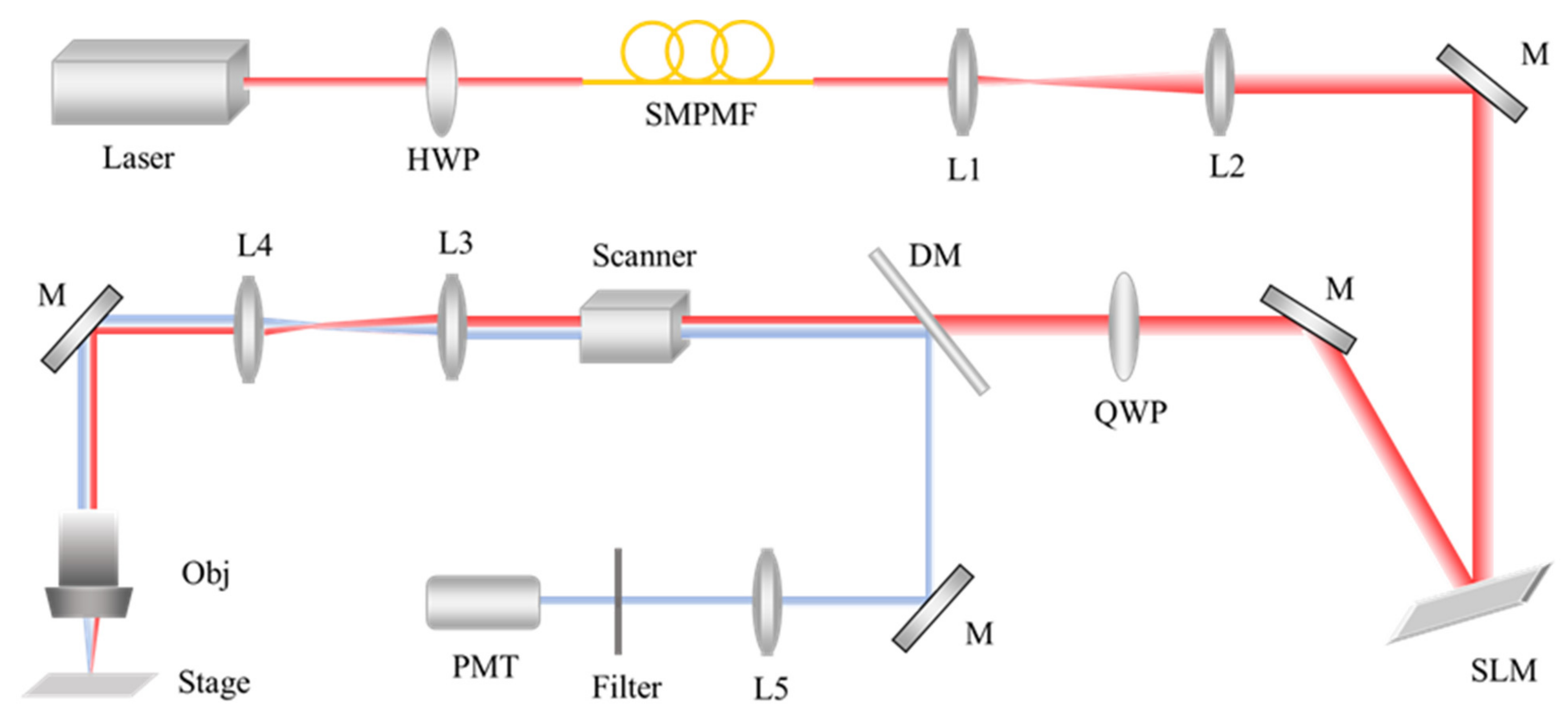
2.1. Experimental Setup
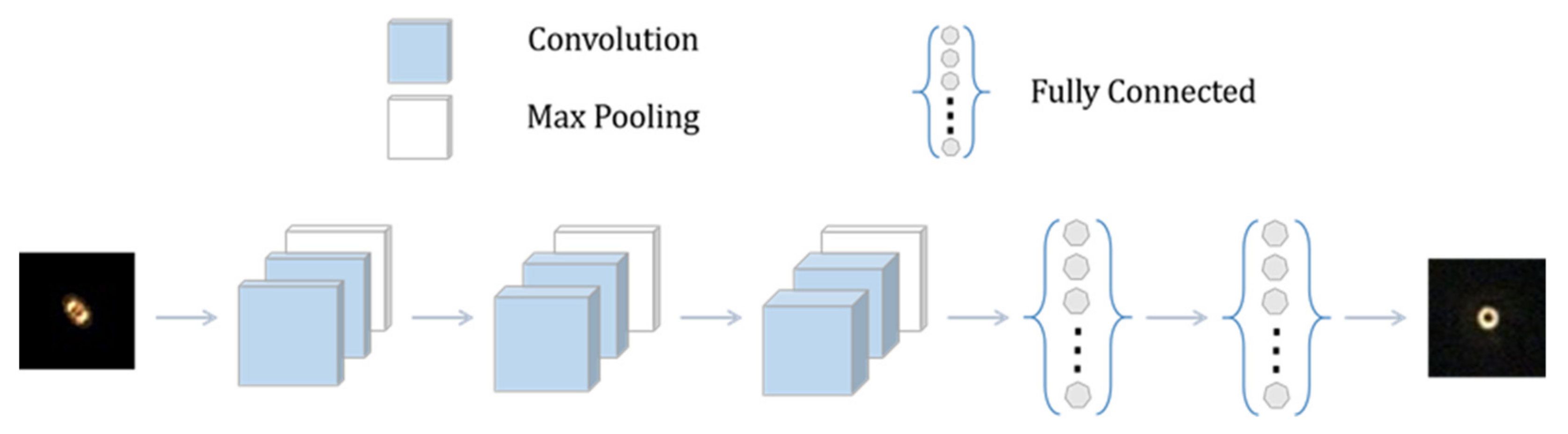
2.2. Convolutional Neural Network Structure
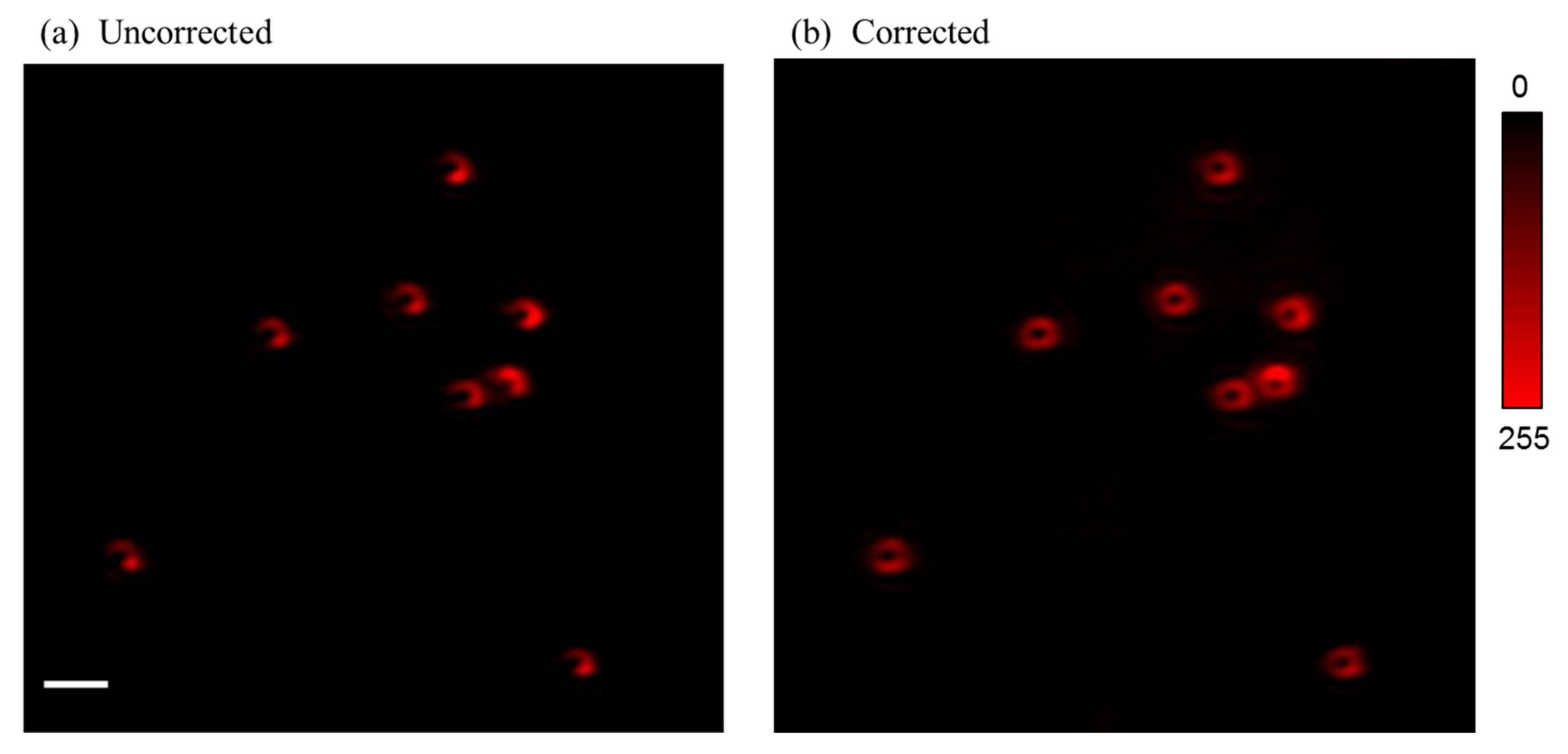
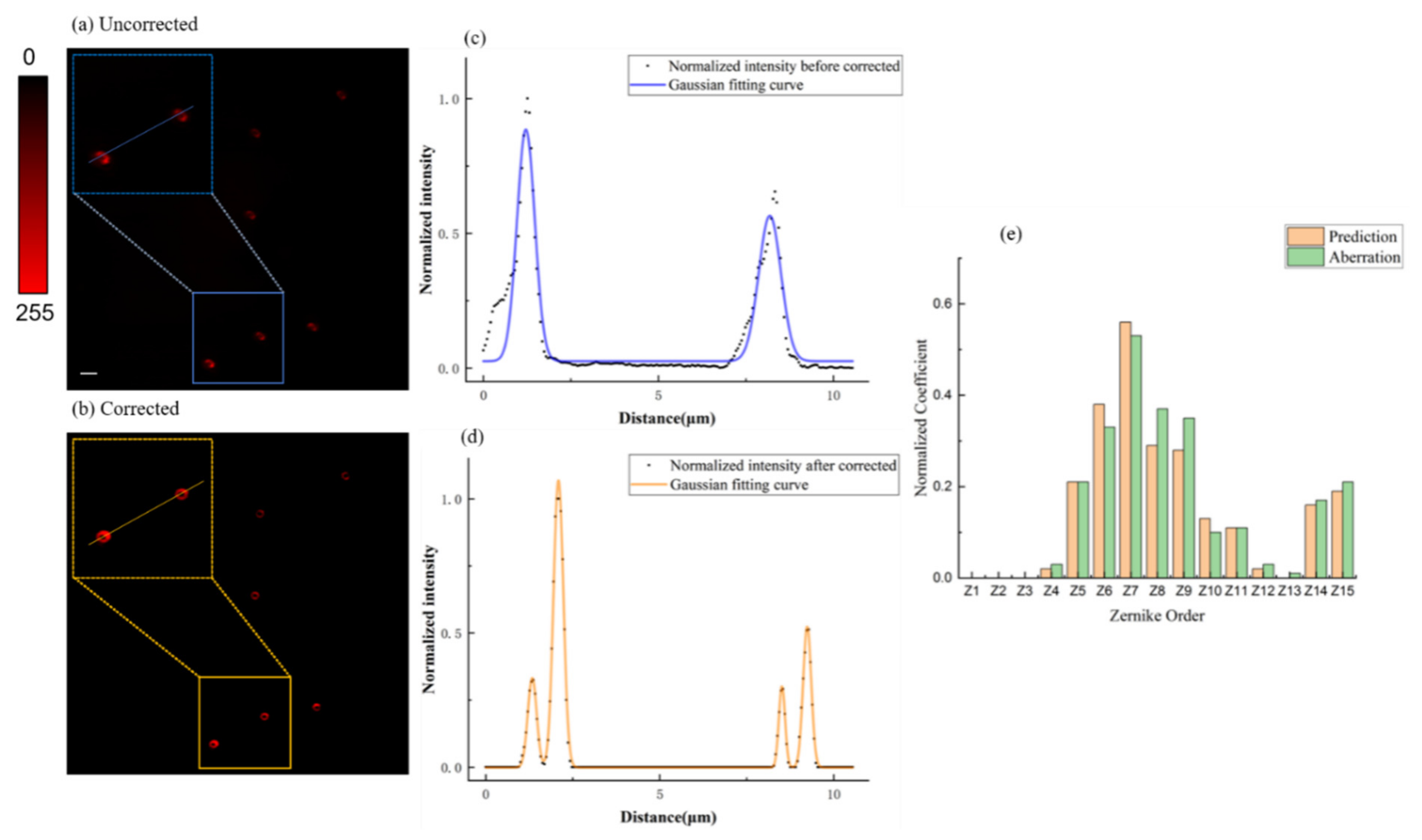
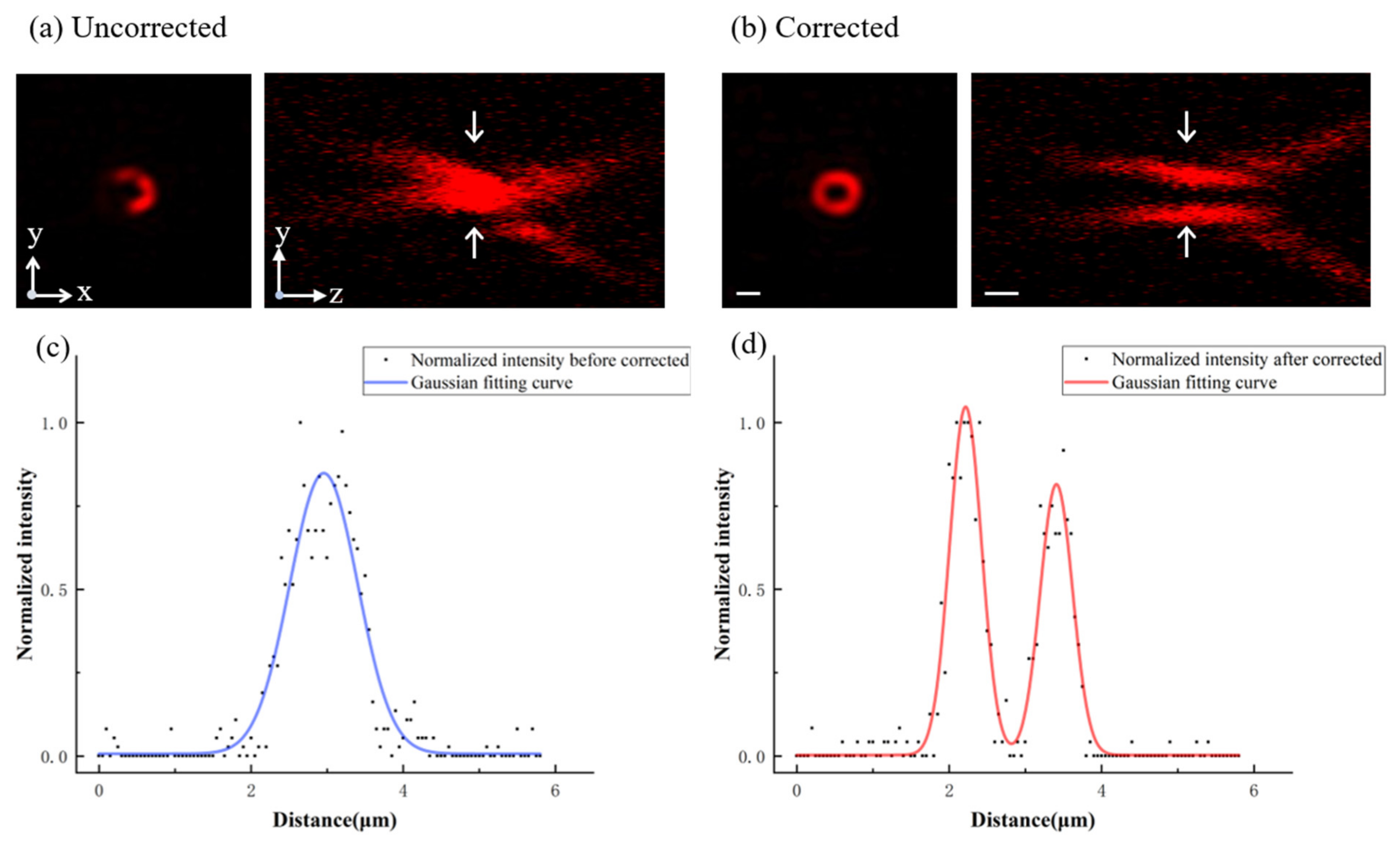
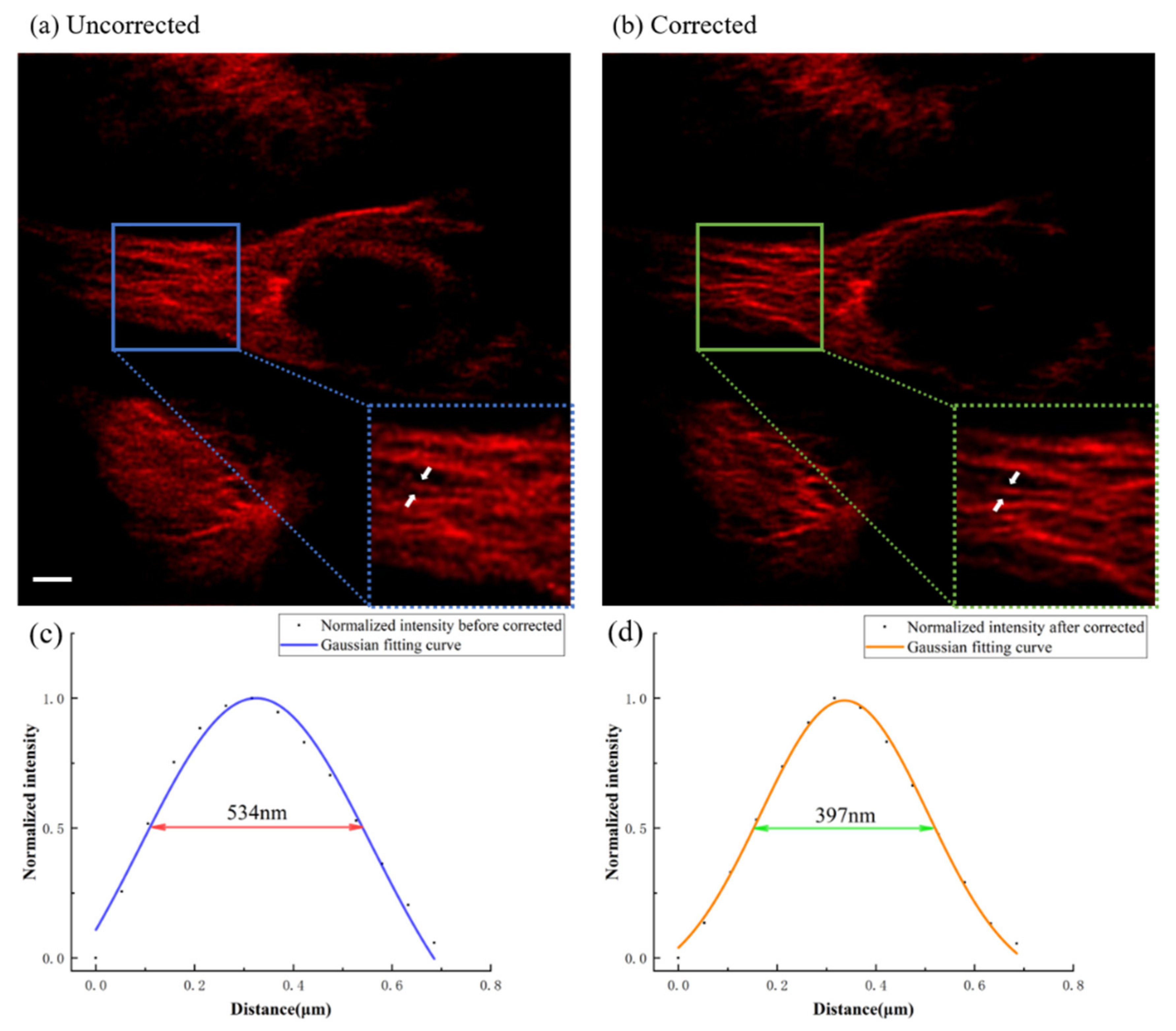
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Babcock, H.W. Adaptive optics revisited. Science 1990, 249, 253–257. [Google Scholar] [CrossRef]
- Booth, M.J. Adaptive optics in microscopy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 2829–2843. [Google Scholar] [CrossRef] [PubMed]
- Azucena, O.; Crest, J.; Cao, J.; Sullivan, W.; Kner, P.; Gavel, D.; Dillon, D.; Olivier, S.; Kubby, J. Wavefront aberration measurements and corrections through thick tissue using fluorescent microsphere reference beacons. Opt. Express 2010, 18, 17521–17532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tao, X.; Norton, A.; Kissel, M.; Azucena, O.; Kubby, J. Adaptive optics two photon microscopy with direct wavefront sensing using autofluorescent guide-stars[C]//MEMS Adaptive Optics VIII. Int. Soc. Opt. Photonics 2014, 8978, 89780D. [Google Scholar]
- Reinig, M.R.; Novack, S.W.; Tao, X.; Ermini, F.; Bentolila, L.A.; Roberts, D.G.; MacKenzie-Graham, A.; Godshalk, S.E.; Raven, M.A.; Kubby, J. Adaptive optics microscopy enhances image quality in deep layers of CLARITY processed brains of YFP-H mice[C]//Clinical and Translational Neurophotonics; Neural Imaging and Sensing; and Optogenetics and Optical Manipulation. Int. Soc. Opt. Photonics 2016, 9690, 969008. [Google Scholar]
- Wang, K.; Milkie, D.E.; Saxena, A.; Engerer, P.; Misgeld, T.; Bronner, M.E.; Mumm, J.; Betzig, E. Rapid adaptive optical recovery of optimal resolution over large volumes. Nat. Methods 2014, 11, 625–628. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.; Yang, Y.; Tan, Y.; Chen, X.; Li, Y.; Qu, J.; Ye, T. Coherent optical adaptive technique improves the spatial resolution of STED microscopy in thick samples. Photonics Res. 2017, 5, 176–181. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Yan, W.; Li, R.; Weng, X.; Zhang, J.; Yang, Z.; Liu, L.; Ye, T.; Qu, J. Aberration correction for improving the image quality in STED microscopy using the genetic algorithm. Nanophotonics 2018, 7, 1971–1980. [Google Scholar] [CrossRef]
- Marsh, P.N.; Burns, D.; Girkin, J.M. Practical implementation of adaptive optics in multiphoton microscopy. Opt. Express 2003, 11, 1123–1130. [Google Scholar] [CrossRef]
- Débarre, D.; Botcherby, E.J.; Watanabe, T.; Srinivas, S.; Booth, M.J.; Wilson, T. Image-based adaptive optics for two-photon microscopy. Opt. Lett. 2009, 34, 2495–2497. [Google Scholar] [CrossRef] [Green Version]
- Ji, N.; Sato, T.R.; Betzig, E. Characterization and adaptive optical correction of aberrations during in vivo imaging in the mouse cortex. Proc. Natl. Acad. Sci. USA 2012, 109, 22–27. [Google Scholar] [CrossRef] [Green Version]
- Montera, D.A.; Welsh, B.M.; Roggemann, M.C.; Ruck, D.W. Prediction of wavefront sensor slope measurements with artificial neural networks. Appl. Opt. 1997, 36, 675–681. [Google Scholar] [CrossRef]
- Rivenson, Y.; Göröcs, Z.; Günaydin, H.; Zhang, Y.; Wang, H.; Ozcan, A. Deep learning microscopy. Optica 2017, 4, 1437–1443. [Google Scholar] [CrossRef] [Green Version]
- Turpin, A.; Vishniakou, I.; Seelig, J.D. Light scattering control in transmission and reflection with neural networks. Opt. Express 2018, 26, 30911–30929. [Google Scholar] [CrossRef]
- Rodin, I.A.; Khonina, S.N.; Serafimovich, P.G.; Popov, S.B. Recognition of wavefront aberrations types corresponding to single Zernike functions from the pattern of the point spread function in the focal plane using neural networks. Comput. Opt. 2020, 44, 923–930. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Porfirev, A.P. Wavefront aberration sensor based on a multichannel difractive optical element. Sensors 2020, 20, 3850. [Google Scholar] [CrossRef]
- Vishniakou, I.; Seelig, J.D. Wavefront correction for adaptive optics with reflected light and deep neural networks. Opt. Express 2020, 28, 15459–15471. [Google Scholar] [CrossRef]
- Saha, D.; Schmidt, U.; Zhang, Q.; Barbotin, A.; Hu, Q.; Ji, N.; Booth, M.J.; Weigert, M.; Myers, E.W. Practical sensorless aberration estimation for 3D microscopy with deep learning. Opt. Express 2020, 28, 29044–29053. [Google Scholar] [CrossRef]
- Cumming, B.P.; Gu, M. Direct determination of aberration functions in microscopy by an artificial neural network. Opt. Express 2020, 28, 14511–14521. [Google Scholar] [CrossRef]
- Möckl, L.; Petrov, P.N.; Moerner, W.E. Accurate phase retrieval of complex 3D point spread functions with deep residual neural networks. Appl. Phys. Lett. 2019, 115, 251106. [Google Scholar] [CrossRef]
- Xin, Q.; Ju, G.; Zhang, C.; Xu, S. Object-independent image-based wavefront sensing approach using phase diversity images and deep learning. Opt. Express 2019, 27, 26102–26119. [Google Scholar] [CrossRef] [PubMed]
- Sinha, A.; Lee, J.; Li, S.; Barbastathis, G. Lensless computational imaging through deep learning. Optica 2017, 4, 1117–1125. [Google Scholar] [CrossRef] [Green Version]
- Jia-Lin, W.; Wei, Y.; Jia, Z.; Lu-Wei, W.; Zhi-Gang, Y.; Jun-Le, Q. New advances in the research of stimulated emission depletion super-resolution microscopy. Acta Phys. Sin. 2020, 69, 10. [Google Scholar]
- Wang, L.W.; Chen, Y.; Yan, W.; Weng, X.Y.; Yang, Z.G.; Ye, T.; Qu, J.L. Increasing fluorescence lifetime for resolution improvement in stimulated emission depletion nanoscopy. J. Biophotonics 2019, 12, e201800315. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, L.; Zhang, J.; Yang, Z.; Yan, W.; Qu, J. Improving the image quality in STED nanoscopy using frequency spectrum modulation. J. Biophotonics 2021, 14, e202000402. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, J.; Wang, L.; Gao, X.; Shao, Y.; Liu, L.; Yang, Z.; Yan, W.; Qu, J. Dual-color STED super-resolution microscope using a single laser source. J. Biophotonics 2020, 13, e202000057. [Google Scholar] [CrossRef] [PubMed]
- Delabie, T.; De Schutter, J.; Vandenbussche, B. An Accurate and Efficient Gaussian Fit Centroiding Algorithm for Star Trackers. J. Astronaut. Sci. 2014, 61, 60–84. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, L.; Guo, Y.; Huang, Y.; Yang, Z.; Yan, W.; Qu, J. Study on Aberration Correction of Adaptive Optics Based on Convolutional Neural Network. Photonics 2021, 8, 377. https://doi.org/10.3390/photonics8090377
Li J, Wang L, Guo Y, Huang Y, Yang Z, Yan W, Qu J. Study on Aberration Correction of Adaptive Optics Based on Convolutional Neural Network. Photonics. 2021; 8(9):377. https://doi.org/10.3390/photonics8090377
Chicago/Turabian StyleLi, Jin, Luwei Wang, Yong Guo, Yangrui Huang, Zhigang Yang, Wei Yan, and Junle Qu. 2021. "Study on Aberration Correction of Adaptive Optics Based on Convolutional Neural Network" Photonics 8, no. 9: 377. https://doi.org/10.3390/photonics8090377
APA StyleLi, J., Wang, L., Guo, Y., Huang, Y., Yang, Z., Yan, W., & Qu, J. (2021). Study on Aberration Correction of Adaptive Optics Based on Convolutional Neural Network. Photonics, 8(9), 377. https://doi.org/10.3390/photonics8090377






