Abstract
In a coherent diffraction imaging (CDI) system, the information of the sample is retrieved from the diffraction patterns recorded by the image sensor via multiple iterations. The limited dynamic range of the image sensor restricts the resolution of the reconstructed sample information. To alleviate this problem, the high dynamic range imaging technology is adopted to increase the signal-to-noise ratio of the diffraction patterns. A sequence of raw diffraction images with differently exposure time are recorded by the image sensor. Then, they are fused to generate a high quality diffraction pattern based on the response function of the image sensor. With the fused diffraction patterns, the resolution of the coherent diffraction imaging can be effectively improved. The experiments on USAF resolution card is carried out to verify the effectiveness of our proposed method, in which the spatial resolution is improved by 1.8 times using the high dynamic range imaging technology.
1. Introduction
Coherent diffraction imaging (CDI) [1,2,3,4,5,6] is a promising phase retrieval technique that uses the intensity of diffraction patterns to recover the amplitude and phase distribution of the sample by iterative phase algorithm. Due to its advantages such as no reference light wave being required and a low requirement on optical device processing accuracy, it has been actively applied in many fields, such as nanomaterials science [7], industrial measurement [8], and biomedical science [9]. In recent years, many researchers have proposed various modifications to improve the performance of CDI to meet requirements in different applications, including ptychographic iterative engine (PIE) [10,11,12,13], coherent modulation imaging [14,15,16], Fourier ptychographic microscopy [17,18], etc. [19,20,21]. In those techniques, the diffraction patterns are usually recorded by a image sensor, and then they are employed to reconstruct the complex amplitude distribution of sample. Due to the limitation of the dynamic range of the image sensor, they cannot provide a high signal-to-noise ratio to record the full diffraction information of the sample with a single exposure. For most real samples, its high-frequency diffraction components are very weak, and they will be lost because these weak signal will be covered by noise. It is worth noting that the proposed method in this paper is suitable for imaging systems that integration detectors such as CCD and CMOS serve as the recording elements, because these detectors have readout noise and dark current. That is to say, the insufficiency of high-frequency information due to the limited dynamic range of image sensor will degrade the quality of the reconstructed image. To alleviate the above problem, we present the coherent diffraction imaging using high dynamic-range (HDR) imaging, which can improve the quality of the reconstructed image.
High dynamic range (HDR) images have greater dynamic range and irradiance contrast and contain richer real-world lighting information [22,23]. The most classic method is to merge a HDR image from multiple photographs of a scene taken with different amounts of exposure [24], which is realized by calibrating a set of images with different exposure time to obtain the sensor response curve. Since obtaining the sensor response function is a linear least squares problem, the overdetermined system of linear equations is robustly solved using the singular value decomposition (SVD) method [24,25]. Additionally, the resultant HDR image is affected by a nonlinear mapping so typically it is necessary to carry out an additional normalization process.
Inspired by the idea of multiple exposures in HDR, we introduce HDR technology into the image acquisition of CDI. During the multi-exposure diffraction patterns acquisition process, more sample low-frequency information and high-frequency information can be obtained under low-exposure and over-exposure conditions, respectively. Therefore, it is necessary to extend the dynamic range of the image by mixing differently exposed images. In this letter, we propose a improved HDR method specially designed for CDI system to compensate the degradation of image quality due to insufficient dynamic range of the detector. Our main work is focused to the generation of a reliable diffraction information from diffractive images with different exposure conditions. In this case, our method only requires us to input a set of differently exposed diffraction patterns, typically five or six, and then these images used to recover the response function of the detector sensor through a simple operation, which will be explained in detail in the later experiment. According to the intensity response function curve of the detector, a HDR diffraction image can be derived. Finally, we demonstrate the resolution of the reconstructed image can be obviously improved using the HDR diffraction image via the phase retrieval process.
2. Materials and Methods
2.1. Proposed Method
For a test object , the diffraction distribution formed at the distance d behind the object can be determined by Fresnel diffraction formula, as shown in Equation (1), where is the incident wavelength, k is the wave number, and represents the fast Fourier transform.
The real diffraction intensity, , usually changes continuously and can have an arbitrary non-negative value. However, for most diffraction imaging systems, a charge coupled device (CCD) is used to record the intensity of diffraction information, which means that there is a minimum recording intensity threshold due to the quantization sampling. For an 8-bit image sensor, its recording intensity range is 0–255. The recorded intensity of the image can be describe as
where and are the real diffraction intensity and the recorded intensity by the camera, respectively. and represent the minimum intensity and the maximum intensity that the camera can quantitatively detect, respectively. K represents the gain coefficient of the detection system, which can describe the relationship between the real intensity and the recorded intensity. Generally, the gain coefficient can be found in the camera company report. For example, the gain has been designed by the manufacturer and different manufacturers may have different gain values and adjustable gain number settings. Int refers to the integer operation of CCD during sampling quantization. In any case, from Equation (2), the recorded pixel values fall into 3 categories: (1) “under-exposed pixels”, which are pixels with a value below the minimum images sensor threshold pixel value; they appear black and its value is 0. (2) “normal-exposed pixels”, whose intensity is within image sensor dynamic range and can be accurately recorded. (3) “over-exposed pixels”, which are pixels with a value beyond the maximum image sensor pixel value, they appear bright because of the sensor saturation and they are recorded as 255. As shown in Figure 1a, because the intensity of high frequency component and low frequency component of diffraction information is different, revealing details of the low-frequency information of sample requires low exposures, while preserving details of the high-frequency components of sample requires high exposures. For example, when a longer exposure time is adopted, more high-frequency components will become strong enough and recordable. Figure 1b shows that different diffraction information of the sample can be recorded under different exposure times. In this method, one of the key technology is to record the diffraction information of the object as much as possible by reasonably designing the exposure time of the detector in the image acquisition stage. For example, the underexposed diffraction pattern contains more low-frequency information of the object, while the overexposed diffraction pattern contains more high frequency information of the object. Another key technology in proposed method is to compute the intensity response function of the image sensor based on exposure time, and then combine these images into a reliable HDR diffraction image, which forms the input for later image reconstruction. Therefore, more high-frequency components corresponding to the fine structures of the sample can be used to improve the resolution of reconstruction image in phase retrieval process.
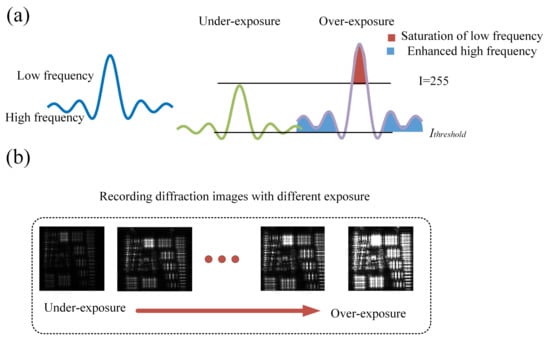
Figure 1.
(a) The intensity distribution of the object’s high-frequency information and low-frequency information; The blue area shows the enhanced high-frequency components in an over-exposed diffraction pattern; (b) Acquisition of multiple diffraction patterns at different levels of exposure.
After the acquisition of diffraction images under different exposure conditions, we collect several groups of diffraction patterns with different exposures at each wavelength. A simpler HDR method algorithm is applied to calculate the intensity response function of the detector, which avoids the cumbersome calibration process of traditional methods [24]. In this case, it requires only as input a set of differently exposed diffraction image. Then, a scale factor to describe the relationship between the pixel intensity of different exposure images. This relationship can also be seen as a function of the parameters of the detector. When changing the exposure time, it is understandable that the corresponding pixel value is multiplied by a constant coefficient. Although the diffraction image recorded under over-exposure condition contains more high-frequency components of sample, some low-frequency information have been lost due to the saturation, and their values are unknown. In this case, the value of overexposed pixels can be fitted according to the function of the parameters of the detector between different exposure conditions, which is an effective method to compensate the low-frequency information lost. The intensity distribution of HDR image can be described as:
where w is value of the coefficient calculated by the least square method, (x, y) and (x, y) represent the intensity distribution under low exposure condition and high exposure condition, respectively. Next, we briefly introduce how to use the least square method to calculate the scaling factor w. Firstly, two raw diffraction images under different exposure conditions are (x, y) and (x, y), respectively. Select n pixels on the (x, y), where n is the number of the pixels, and its intensity values to form the vector X(,, …). Correspondingly, the pixel values at the same positions on (x, y) to form the vector Y(,, …). Then, a first-order linear fitting operation based on the least squares is performed on vectors X and Y, and the slope of the fitting curve is also the scaling coefficient in this paper. The coefficient values between different exposure conditions can be obtained by the above operation. Once the scaling coefficients between any two diffraction patterns are obtained, according to Equation (3), the HDR image can be realized by fusion.
2.2. Experimental Setup
To demonstrate the effectiveness our method, we conducted a verification experiment based on a multi-wavelength diffraction imaging system. In our previous work [4], we have already demonstrated that the information of sample can be retrieved by using diffraction patterns at three different wavelengths. Here, three wavelengths, 457 nm, 633 nm, and850 nm, are served as the light sources. The experimental system setup is illustrated in Figure 2a. Different wavelengths are coupled into a single-mode fiber through a coupler (3 × 1), and the beam is collimated and expanded by a reflective collimator (RC, RC08FC-F01, Thorlabs). Diffraction patterns at three wavelengths can be recorded by turning the laser on and off in sequence, which is realized by the light switch, as shown in Figure 2a. This operation can avoid the mechanical movement, so this imaging system has high stability and robustness. A monochrome CCD camera (GEV-B2320U, 1768 × 2352 pixels, 5.5 × 5.5 m pixel pitch, 8 bit) is applied to record the diffraction information of sample at three wavelengths. A standard negative resolution board (USAF1951) is used as the test target, and the sample is located at a distance of 60 mm from the recording plane. To capture more diffraction information of object, we record multiple diffraction patterns sequentially from under-exposure to over-exposure.

Figure 2.
(a) The optical setup of the experiment. CL, collimator. Light switch, a light switch is used for laser on and off. (b) HDR diffraction images used in multi-wavelength diffraction imaging system to improve the resolution.
Here, six diffraction images with exposure time of 0.2 ms, 0.5 ms, 0.9 ms, 1.3 ms, 1.7 ms, and 2 ms are recorded at each wavelength. As shown in Figure 2b, for each wavelength, six raw images recorded with different conditions are used to generate a HDR image at corresponding wavelengths in digital reconstruction phase. Finally, three HDR images at three wavelengths are used for image recovery. Next we will explain how to obtain a single HDR image using intensity distributions for six different exposure times. Here, taking six diffraction patterns at wavelength 457 nm as an example for illustration, Figure 3a depicts the pixel intensities of different exposure images at the same pixel position. Obviously, the pixel intensity increases with the exposure time, which is consistent with the theoretical analysis. For the sake of simplicity, the six raw diffraction patterns are denoted as , , , , , and according to the exposure time from low to high. The scaling coefficients between any two images can be calculated by the least square method. For example, represents the value of scaling factor between the and . Finally, according to these scale factors, in this case (n = 2, 3, 4, 5, 6), the HDR diffraction images can be generated from to using Equation (3), respectively. Through this way of image fusion, we can combine the complementary of the images with different exposure time and obtain new images with more abundant information.

Figure 3.
(a) Pixel intensity recorded at the same location have different values in different exposure conditions. (b) Six raw diffraction images with different exposure times at 457 nm. (c) The HDR diffraction image at 457 nm.
A HDR diffraction image containing more information on the sample can be calculated as shown in Figure 3c. Obviously, after applying HDR imaging, the maximum light intensity can reach 2500, which is much higher than the maximum intensity of 255 under normal exposure conditions. Once we obtain HDR diffraction images of three wavelengths, we can use them for subsequent image reconstruction. The iterative phase retrieval algorithm starts with the random definition of the initial complex amplitudes at wavelength , and then propagates to and according to Equation (1). The angular spectrum transmission equation is used to carry out the forward and backward propagation between the object plane and recording plane in spatial domain and frequency domain. The diffraction patterns at each wavelength can constrain the iterative algorithm for convergence. The process is repeated until the evaluation function of the reconstructed image at the object plane is less than a certain threshold. This algorithm is described in detail in our previous work [4].
3. Results and Discussion
In order to quantitatively evaluate the enhancement of resolution, we use a standard USAF (United States Air Force) resolution board as the experimental sample and define resolution according to the closest set of bars that can be discriminated. Figure 4a,b show the results of the reconstructed image of the USAF resolution board without HDR technology and with HDR technology, respectively. Comparisons between the details of dashed box in Figure 4a,b, the recovered image with HDR method shows the high accuracy and the detail of sample. Specifically, the reconstructed images under normal exposure in Figure 4c present more background noise and a blurred reconstructed result with a resolution of 12.4 m (40.32 LP/mm). By comparison, our method can able to resolve Element 2, Group 6, giving a resolution of 6.96 m (71.84 LP/mm), as shown in Figure 4d. It is demonstrated experimentally that by properly selecting the exposure time and accordingly applying HDR method in the phase retrieval process, the resolution can be easily improved by 1.8 times in our experiments.
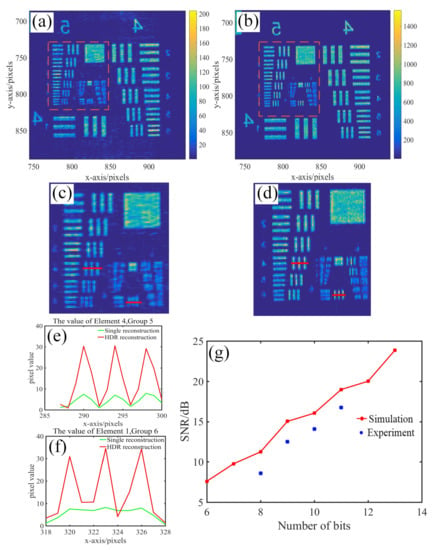
Figure 4.
Experiment results. (a) Reconstructed image with normal exposure conditions. (b) Reconstructed image with HDR method based on multiple diffraction patterns. (c,d) are the enlarged areas in the red dashed box of (a,b), respectively. (e) The intensity profiles of Element 4, Group 5. (f) The intensity profiles of Element 1, Group 6. (g) The relationship between the enhancement of SNR and the number of bits in simulation and experiment.
To verify the spatial resolution quantitatively, intensity profile taken across the red line in (c) and (d) are plotted as shown in Figure 4e,f, respectively. Comparing the intensity profiles of Element 4, Group 5 and Element 1, Group 6, it is verified that our suggested method not only improve the reconstruction resolution, but also enhanced the contrast by increasing the signal-to-noise ratio, as expected. In addition, we calculate the enhancement of SNR and compare it with the simulation. Here, the initial parameters used in simulations are basically the same as those used in the actual experiment. The image of USAF target board is selected in MATLAB as complex-valued object. The number of sampling point N is set to 800 × 800, and the pixel size is 5.5 m. Three wavelengths used in the simulation are 457 nm, 633 nm, and 850 nm, respectively. The diffraction intensity distribution can be calculated by Fresnel diffraction formula, as shown in Equation (1). It is worth noting that the number of different bits are used to quantize the intensity value in the simulation, where the number of bits are set to an integer of 6–14. The above operation is equivalent to the sampling record of CCD. Once the diffraction images of three wavelengths at different numbers of bit are obtained, the phase retrieval algorithm can be used to recover the object, and then the SNR of recover image can be calculated. The relationship between the enhancement of SNR and the number of bits in simulation and experiment are shown in Figure 4g. This can be concluded that the performance of using HDR method to enhance SNR is basically consistent with the simulation results. The reason why the experimental effect is slightly lower than that of simulation may be the environmental noise in recording plane. For example, the common influence of experimental factors such as intensity saturation and background noise might randomly degrade the quality of experimental results. In addition, integration detectors such as CCD and CMOS can generate readout noise and dark current, which will also introduce measurement noise.
In addition, what needs to be pointed out here is that this method can enhance the dynamic range of the detector to a certain extent, but it cannot make up for the degradation of image quality without limitation. Specifically, we find that when the illumination power or exposure time increases more than 10 times more than normal exposure condition the saturation area is larger than the effective information of the target on the detection plane. In this situation, the information lost caused by the saturation cannot be recovered completely and resulting in the degradation of reconstructed image quality. It can be understood that with the increase of exposure time, the common influence of experimental factors such as intensity saturation and background noise also have a negative impact on the recovered image.
4. Conclusions
In summary, in order to overcome the problem of the degradation of image quality caused by the limited dynamic range of detector sensor, we propose a technique for expanding the dynamic range of the diffraction image by using HDR method to improve the resolution. This method is simple and easy to implement, and it needs no additional hardware facilities. The feasibility of our proposed method is verified in a multiple wavelength CDI system. The experimental results show that the resolution can be easily improved by 1.8 times with our proposed HDR method, and the image quality has also improved by increasing the signal-to-noise ratio. Based on this work, we believe that HDR as a technology that can expand the detection range of image sensors can be extended its application to various fields of optical engineering.
Author Contributions
Conceptualization, Y.L. and Q.L.; methodology, Q.L.; software, Y.L.; validation, S.Z. and W.S.; formal analysis, B.X.; resources, Z.H.; writing—review and editing, Y.L.; supervision, Q.L.; funding acquisition, Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Financial support was provided by National Natural Science Foundation of China under Grants (Grant Nos. 61875121, 61975116, 61620106015).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gerchberg, R.W.; Saxton, W.O.A. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–250. [Google Scholar]
- Gerchberg, R. Super-resolution through Error Energy Reduction. Opt. Acta Int. J. Opt. 1974, 21, 709–720. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 35, 21. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Liu, Q.; Li, Y.; Xu, B.; He, Z. High-resolution multi-wavelength lensless diffraction imaging with adaptive dispersion correction. Opt. Express 2021, 5, 29. [Google Scholar]
- Beata, Z.; Zoltan, J.; Nikita, M. Towards Realistic Simulations of Macromolecules Irradiated under the Conditions of Coherent Diffraction Imaging with an X-ray Free-Electron Laser. Photonics 2015, 2, 256–269. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Liu, Q.; Li, Y.; Zhang, J.; He, Z. High-resolution multi-planar coherent diffraction imaging with multimode fiber source. Opt. Lasers Eng. 2021, 140, 106530. [Google Scholar] [CrossRef]
- Miao, J.; Ishikawa, T.; Robinson, I.K.; Murnane, M.M. Beyond crystallography: Diffractive imaging using coherent x-ray light sources. Science 2015, 348, 530–535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chowdhury, S.; Eldridge, W.J.; Wax, A.; Izatt, J. Refractive index tomography with structured illumination. Optica 2017, 4, 537–545. [Google Scholar] [CrossRef] [Green Version]
- Horstmeyer, R.; Yang, C. Diffraction tomography with Fourier ptychography. Optica 2015, 3, 827–835. [Google Scholar] [CrossRef] [PubMed]
- Faulkner, H.; Rodenburg, J.M. Movable Aperture Lensless Transmission Microscopy: A Novel Phase Retrieval Algorithm. Phys. Rev. Lett. 2004, 93, 023903. [Google Scholar] [CrossRef] [Green Version]
- Rodenburg, J.M.; Faulkner, H. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 2004, 91, 233117. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wen, D.; Song, Z.; Jiang, T.; Zhang, W.; Liu, G.; Wei, X. Imaging Correlography Using Ptychography. Appl. Sci. 2019, 9, 4377. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Burdet, N.; Batey, D.; Robinson, I. Multi-Modal Ptychography: Recent Developments and Applications. Appl. Sci. 2018, 8, 1054. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Bo, C.; Morrison, G.R.; Vila-Comamala, J.; Robinson, I.K. Phase retrieval by coherent modulation imaging. Nat. Commun. 2016, 7, 13367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, X.; Hua, T.; Pan, X.; Cheng, L.; Zhu, J. High-quality laser beam diagnostics using modified coherent phase modulation imaging. Opt. Express 2018, 26, 6239. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Dong, Z.; Fan, F.; Feng, Y.; Lou, Y.; Jiang, X. Characterization of Spatial Light Modulator Based on the Phase in Fourier Domain of the Hologram and Its Applications in Coherent Imaging. Appl. Sci. 2018, 8, 1146. [Google Scholar] [CrossRef] [Green Version]
- Zheng, G.; Horstmeyer, R.; Yang, C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7, 739. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Sun, J.; Li, J.; Asundi, A.; Chen, Q. Wide-field high-resolution 3D microscopy with Fourier ptychographic diffraction tomography. Opt. Lasers Eng. 2020, 128, 106003. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Qi, M.; Liu, Y.; Xue, X.; Chen, D.; Qu, J. Super-Resolution Image Reconstruction Based on Single-Molecule Localization Algorithm. Photonics 2021, 8, 273. [Google Scholar] [CrossRef]
- Cocco, D. Recent Developments in UV Optics for Ultra-Short, Ultra-Intense Coherent Light Sources. Photonics 2015, 1, 10–49. [Google Scholar] [CrossRef]
- Bao, P.; Zhang, F.; Pedrini, G.; Osten, W. Phase retrieval using multiple illumination wavelengths. Opt. Lett. 2008, 4, 309. [Google Scholar] [CrossRef]
- Lucat, A.; Hegedus, R.; Pacanowski, R. Diffraction effects detection for HDR image-based measurements. Opt. Express 2017, 25, 27146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, Z.; Pan, X.; Yan, K.; Qian, W.; Cheng, L. Partial saturation-aided resolution enhancement for digital holography. Appl. Opt. 2018, 57, 3884. [Google Scholar] [CrossRef] [PubMed]
- Debevec, P.E.; Malik, J. Recovering high dynamic range radiance maps from photographs. Siggraph 1997. [Google Scholar] [CrossRef]
- Golub, G.H. Singular value decomposition and least squares solutions. Numer. Math. 1970, 14, 403–420. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).